Skip to main content
Global

16.3E: Exercícios para a Seção 16.3

  1. Last updated
  2. Save as PDF
  • Page ID
    188509

    • Edwin “Jed” Herman & Gilbert Strang
    • OpenStax
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    1. Verdadeiro ou falso? Se o campo vetorial\(\vecs F\) for conservador na região aberta e conectada\(D\), as integrais de linha de\(\vecs F\) são independentes do caminho\(D\), independentemente da forma de\(D\).

    Resposta
    É verdade

    2. Verdadeiro ou falso? Função\(\vecs r(t)=\vecs a+t(\vecs b−\vecs a)\), onde\(0≤t≤1\), parametriza o segmento em linha reta de\(\vecs a\) até\(\vecs b\).

    Resposta
    É verdade

    3. Verdadeiro ou falso? O campo vetorial\(\vecs F(x,y,z)=(y\sin z)\,\mathbf{\hat i}+(x\sin z)\,\mathbf{\hat j}+(xy\cos z)\,\mathbf{\hat k}\) é conservador.

    Resposta
    É verdade

    4. Verdadeiro ou falso? O campo vetorial\(\vecs F(x,y,z)=y\,\mathbf{\hat i}+(x+z)\,\mathbf{\hat j}−y\,\mathbf{\hat k}\) é conservador.

    5. Justifique o teorema fundamental das integrais de linha para o caso\(\displaystyle \int _C\vecs F·d\vecs r\) em que\(\vecs{F}(x,y)=(2x+2y)\,\mathbf{\hat i}+(2x+2y)\,\mathbf{\hat j}\) e\(C\) é uma parte do círculo orientado positivamente\(x^2+y^2=25\) de\((5, 0)\) para\((3, 4).\)

    Resposta
    \(\displaystyle \int _C \vecs F·d\vecs r=24\)unidades de trabalho

    6. [T] Descubra\(\displaystyle \int _C\vecs F·d\vecs r,\) onde\(\vecs{F}(x,y)=(ye^{xy}+\cos x)\,\mathbf{\hat i}+\left(xe^{xy}+\frac{1}{y^2+1}\right)\,\mathbf{\hat j}\) e\(C\) é uma parte da curva\(y=\sin x\)\(x=0\) de\(x=\frac{π}{2}\) a.

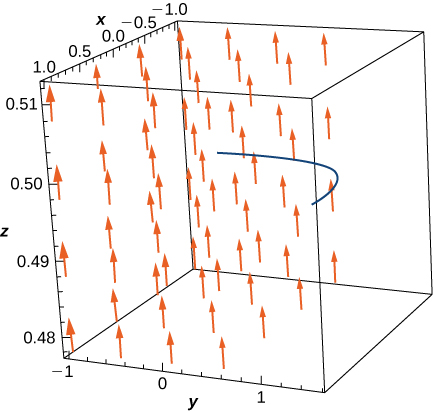
    7. [T] Avalie a integral da linha\(\displaystyle \int _C\vecs F·d\vecs r\)\(\vecs{F}(x,y)=(e^x\sin y−y)\,\mathbf{\hat i}+(e^x\cos y−x−2)\,\mathbf{\hat j}\), onde, e\(C\) é o caminho dado\(\vecs r(t)=(t^3\sin\frac{πt}{2})\,\mathbf{\hat i}−(\frac{π}{2}\cos(\frac{πt}{2}+\frac{π}{2}))\,\mathbf{\hat j}\) por for\(0≤t≤1\).

    CNX_Calc_Figure_16_03_201.jpg

    Resposta
    \(\displaystyle \int _C\vecs F·d\vecs r=\left(e−\frac{3π}{2}\right)\)unidades de trabalho

    Para os exercícios a seguir, determine se o campo vetorial é conservador e, se for, encontre a função potencial.

    8. \(\vecs{F}(x,y)=2xy^3\,\mathbf{\hat i}+3y^2x^2\,\mathbf{\hat j}\)

    9. \(\vecs{F}(x,y)=(−y+e^x\sin y)\,\mathbf{\hat i}+((x+2)e^x\cos y)\,\mathbf{\hat j}\)

    Resposta
    Não conservador

    10. \(\vecs{F}(x,y)=(e^{2x}\sin y)\,\mathbf{\hat i}+(e^{2x}\cos y)\,\mathbf{\hat j}\)

    11. \(\vecs{F}(x,y)=(6x+5y)\,\mathbf{\hat i}+(5x+4y)\,\mathbf{\hat j}\)

    Resposta
    Conservador,\(f(x,y)=3x^2+5xy+2y^2+k\)

    12. \(\vecs{F}(x,y)=(2x\cos(y)−y\cos(x))\,\mathbf{\hat i}+(−x^2\sin(y)−\sin(x))\,\mathbf{\hat j}\)

    13. \(\vecs{F}(x,y)=(ye^x+\sin(y))\,\mathbf{\hat i}+(e^x+x\cos(y))\,\mathbf{\hat j}\)

    Resposta
    Conservador,\(f(x,y)=ye^x+x\sin(y)+k\)

    Para os exercícios a seguir, avalie as integrais de linha usando o Teorema Fundamental das Integrais de Linha.

    14. \(\displaystyle ∮_C(y\,\mathbf{\hat i}+x\,\mathbf{\hat j})·d\vecs r,\)onde\(C\) está qualquer caminho de\((0, 0)\) até\((2, 4)\)

    15. \(\displaystyle ∮_C(2y\,dx+2x\,dy),\)onde\(C\) está o segmento de linha de\((0, 0)\) até\((4, 4)\)

    Resposta
    \(\displaystyle ∮_C(2y\,dx+2x\,dy)=32\)unidades de trabalho

    16. [T]\(\displaystyle ∮_C\left[\arctan\dfrac{y}{x}−\dfrac{xy}{x^2+y^2}\right]\,dx+\left[\dfrac{x^2}{x^2+y^2}+e^{−y}(1−y)\right]\,dy\), onde\(C\) está qualquer curva suave de\((1, 1)\) a\((−1,2).\)

    17. Encontre o campo vetorial conservador para a função potencial\(f(x,y)=5x^2+3xy+10y^2.\)

    Resposta
    \(\vecs{F}(x,y)=(10x+3y)\,\mathbf{\hat i}+(3x+20y)\,\mathbf{\hat j}\)

    Para os exercícios a seguir, determine se o campo vetorial é conservador e, em caso afirmativo, encontre uma função potencial.

    18. \(\vecs{F}(x,y)=(12xy)\,\mathbf{\hat i}+6(x^2+y^2)\,\mathbf{\hat j}\)

    19. \(\vecs{F}(x,y)=(e^x\cos y)\,\mathbf{\hat i}+6(e^x\sin y)\,\mathbf{\hat j}\)

    Resposta
    \(\vecs F\)não é conservador.

    20. \(\vecs{F}(x,y)=(2xye^{x^2y})\,\mathbf{\hat i}+6(x^2e^{x^2y})\,\mathbf{\hat j}\)

    21. \(\vecs F(x,y,z)=(ye^z)\,\mathbf{\hat i}+(xe^z)\,\mathbf{\hat j}+(xye^z)\,\mathbf{\hat k}\)

    Resposta
    \(\vecs F\)é conservador e uma função potencial é\(f(x,y,z)=xye^z+k\).

    22. \(\vecs F(x,y,z)=(\sin y)\,\mathbf{\hat i}−(x\cos y)\,\mathbf{\hat j}+\,\mathbf{\hat k}\)

    23. \(\vecs F(x,y,z)=\dfrac{1}{y}\,\mathbf{\hat i}-\dfrac{x}{y^2}\,\mathbf{\hat j}+(2z−1)\,\mathbf{\hat k}\)

    Resposta
    \(\vecs F\)é conservador e uma função potencial é\(f(x,y,z)=\dfrac{x}{y}+z^2-z+k.\)

    24. \(\vecs F(x,y,z)=3z^2\,\mathbf{\hat i}−\cos y\,\mathbf{\hat j}+2xz\,\mathbf{\hat k}\)

    25. \(\vecs F(x,y,z)=(2xy)\,\mathbf{\hat i}+(x^2+2yz)\,\mathbf{\hat j}+y^2\,\mathbf{\hat k}\)

    Resposta
    \(\vecs F\)é conservador e uma função potencial é\(f(x,y,z)=x^2y+y^2z+k.\)

    Para os exercícios a seguir, determine se o campo vetorial fornecido é conservador e encontre uma função potencial.

    26. \(\vecs{F}(x,y)=(e^x\cos y)\,\mathbf{\hat i}+6(e^x\sin y)\,\mathbf{\hat j}\)

    27. \(\vecs{F}(x,y)=(2xye^{x^2y})\,\mathbf{\hat i}+(x^2e^{x^2y})\,\mathbf{\hat j}\)

    Resposta
    \(\vecs F\)é conservador e uma função potencial é\(f(x,y)=e^{x^2y}+k\)

    Para os exercícios a seguir, avalie a integral usando o Teorema Fundamental das Integrais de Linha.

    28. Avalie\(\displaystyle \int _C\vecs ∇f·d\vecs r\), onde\(f(x,y,z)=\cos(πx)+\sin(πy)−xyz\) e\(C\) está qualquer caminho que começa\((1,12,2)\) e termina em\((2,1,−1)\).

    29. [T] Avalie\(\displaystyle \int _C\vecs ∇f·d\vecs r\), onde\(f(x,y)=xy+e^x\) e\(C\) é uma linha reta de\((0,0)\) até\((2,1)\).

    Resposta
    \(\displaystyle \int _C\vecs F·d\vecs r=\left(e^2+1\right)\)unidades de trabalho

    30. [T] Avalie\(\displaystyle \int _C\vecs ∇f·d\vecs r,\) onde\(f(x,y)=x^2y−x\) e\(C\) está qualquer caminho em um plano de (1, 2) a (3, 2).

    31. Avalie\(\displaystyle \int _C\vecs ∇f·d\vecs r,\) onde\(f(x,y,z)=xyz^2−yz\) e\(C\) tem ponto inicial\((1, 2, 3)\) e ponto terminal\((3, 5, 2).\)

    Resposta
    \(\displaystyle \int _C\vecs F·d\vecs r=38\)unidades de trabalho

    Para os exercícios a seguir, seja\(\vecs{F}(x,y)=2xy^2\,\mathbf{\hat i}+(2yx^2+2y)\,\mathbf{\hat j}\) e\(G(x,y)=(y+x)\,\mathbf{\hat i}+(y−x)\,\mathbf{\hat j}\), e\(C_1\) seja a curva que consiste no círculo de raio 2, centrado na origem e orientado no sentido anti-horário, e\(C_2\) seja a curva que consiste em um segmento de linha de\((0, 0)\) a\((1, 1)\) seguido por um segmento de linha de\((1, 1)\) até\((3, 1).\)

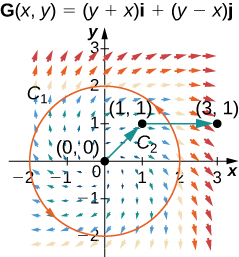
    CNX_Calc_Figure_16_03_203.jpg

    32. Calcule a integral da linha de\(\vecs F\) over\(C_1\).

    33. Calcule a integral da linha de\(\vecs G\) over\(C_1\).

    Resposta
    \(\displaystyle ∮_{C_1}\vecs G·d\vecs r=−8π\)unidades de trabalho

    34. Calcule a integral da linha de\(\vecs F\) over\(C_2\).

    35. Calcule a integral da linha de\(\vecs G\) over\(C_2\).

    Resposta
    \(\displaystyle ∮_{C_2}\vecs F·d\vecs r=7\)unidades de trabalho

    36. [T] Deixe\(\vecs F(x,y,z)=x^2\,\mathbf{\hat i}+z\sin(yz)\,\mathbf{\hat j}+y\sin(yz)\,\mathbf{\hat k}\). \(\displaystyle ∮_C\vecs F·d\vecs{r}\)Calcule, de onde\(C\) está um caminho de\(A=(0,0,1)\) até\(B=(3,1,2)\).

    37. [T] Encontre a integral\(\displaystyle ∮_C\vecs F·dr\) da linha do campo vetorial\(\vecs F(x,y,z)=3x^2z\,\mathbf{\hat i}+z^2\,\mathbf{\hat j}+(x^3+2yz)\,\mathbf{\hat k}\) ao longo da curva\(C\) parametrizada por\(\vecs r(t)=(\frac{\ln t}{\ln 2})\,\mathbf{\hat i}+t^{3/2}\,\mathbf{\hat j}+t\cos(πt),1≤t≤4.\)

    Resposta
    \(\displaystyle \int _C\vecs F·d\vecs r=150\)unidades de trabalho

    Para os exercícios 38 a 40, mostre que os seguintes campos vetoriais são conservadores. Em seguida, calcule\(\displaystyle \int _C\vecs F·d\vecs r\) para a curva dada.

    38. \(\vecs{F}(x,y)=(xy^2+3x^2y)\,\mathbf{\hat i}+(x+y)x^2\,\mathbf{\hat j}\);\(C\) é a curva que consiste em segmentos de linha de\((1,1)\)\((0,2)\) até\((3,0).\)

    39. \(\vecs{F}(x,y)=\dfrac{2x}{y^2+1}\,\mathbf{\hat i}−\dfrac{2y(x^2+1)}{(y^2+1)^2}\,\mathbf{\hat j}\);\(C\) é parametrizado por\(x=t^3−1,\;y=t^6−t\), para\(0≤t≤1.\)

    Resposta
    \(\displaystyle \int _C\vecs F·d\vecs r=−1\)unidades de trabalho

    40. [T]\(\vecs{F}(x,y)=[\cos(xy^2)−xy^2\sin(xy^2)]\,\mathbf{\hat i}−2x^2y\sin(xy^2)\,\mathbf{\hat j}\);\(C\) é a curva\(\langle e^t,e^{t+1}\rangle,\) para\(−1≤t≤0\).

    41. A massa da Terra é de aproximadamente\(6×10^{27}g\) e a do Sol é 330.000 vezes maior. A constante gravitacional é\(6.7×10^{−8}cm^3/s^2·g\). A distância entre a Terra e o Sol é de aproximadamente\(1.5×10^{12}cm\). Calcule, aproximadamente, o trabalho necessário para aumentar a distância da Terra do Sol em\(1\;cm\).

    Resposta
    \(4×10^{31}\)erg

    42. [T] Deixe\(\vecs{F}(x,y,z)=(e^x\sin y)\,\mathbf{\hat i}+(e^x\cos y)\,\mathbf{\hat j}+z^2\,\mathbf{\hat k}\). Avalie a integral\(\displaystyle \int _C\vecs F·d\vecs r\), onde\(\vecs r(t)=\langle\sqrt{t},t^3,e^{\sqrt{t}}\rangle,\) para\(0≤t≤1.\)

    43. [T]\(C:[1,2]→ℝ^2\) Seja dado por\(x=e^{t−1},y=\sin\left(\frac{π}{t}\right)\). Use um computador para calcular a integral\(\displaystyle \int _C\vecs F·d\vecs r=\int _C 2x\cos y\,dx−x^2\sin y\,dy\), onde\(\vecs{F}(x,y)=(2x\cos y)\,\mathbf{\hat i}−(x^2\sin y)\,\mathbf{\hat j}.\)

    Resposta
    \(\displaystyle \int _C\vecs F·d\vecs s=0.4687\)unidades de trabalho

    44. [T] Use um sistema computacional de álgebra para encontrar a massa de um fio que está ao longo da curva\(\vecs r(t)=(t^2−1)\,\mathbf{\hat j}+2t\,\mathbf{\hat k},\) onde\(0≤t≤1\), se a densidade for dada por\(d(t) = \dfrac{3}{2}t\).

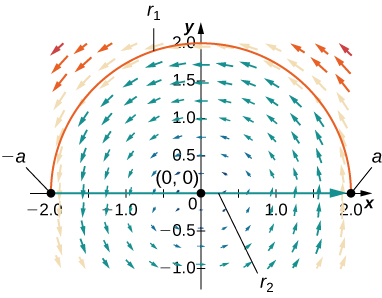
    45. Encontre a circulação e o fluxo de campo\(\vecs{F}(x,y)=−y\,\mathbf{\hat i}+x\,\mathbf{\hat j}\) ao redor e através do caminho semicircular fechado que consiste em arco semicircular\(\vecs r_1(t)=(a\cos t)\,\mathbf{\hat i}+(a\sin t)\,\mathbf{\hat j},\quad 0≤t≤π\), seguido por segmento de linha\(\vecs r_2(t)=t\,\mathbf{\hat i},\quad −a≤t≤a.\)

    CNX_Calc_Figure_16_03_204.jpg

    Resposta
    \(\text{circulation}=πa^2\)e\(\text{flux}=0\)

    46. Calcule\(\displaystyle \int _C\cos x\cos y\,dx−\sin x\sin y\,dy,\) onde\(\vecs r(t)=\langle t,t^2 \rangle, \quad 0≤t≤1.\)

    47. Complete a prova do teorema intitulado THE PATH INDEPENDENCE TEST FOR CONSERVATIVE FIELDS mostrando que\(f_y=Q(x,y).\)