16.3: Campos vetoriais conservadores

Objetivos de

• Descreva curvas simples e fechadas; defina regiões conectadas e simplesmente conectadas.
• Explique como encontrar uma função potencial para um campo vetorial conservador.
• Use o Teorema Fundamental para Integrais de Linha para avaliar uma integral de linha em um campo vetorial.
• Explique como testar um campo vetorial para determinar se ele é conservador.

Nesta seção, continuamos o estudo de campos vetoriais conservadores. Examinamos o Teorema Fundamental para Integrais de Linha, que é uma generalização útil do Teorema Fundamental do Cálculo para integrais de linha de campos vetoriais conservadores. Também descobrimos como testar se um determinado campo vetorial é conservador e determinar como construir uma função potencial para um campo vetorial conhecido por ser conservador.

Curvas e regiões

Antes de continuar nosso estudo de campos vetoriais conservadores, precisamos de algumas definições geométricas. Todos os teoremas nas seções subsequentes dependem da integração de certos tipos de curvas e regiões, então desenvolvemos as definições dessas curvas e regiões aqui. Primeiro definimos dois tipos especiais de curvas: curvas fechadas e curvas simples. Como aprendemos, uma curva fechada é aquela que começa e termina no mesmo ponto. Uma curva simples é aquela que não se cruza sozinha. Uma curva que é ao mesmo tempo fechada e simples é uma curva fechada simples (Figura\(\PageIndex{1}\)).

Figura\(\PageIndex{1}\). Tipos de curvas que são simples ou não simples e fechadas ou não fechadas.

DEFINIÇÃO: Curvas fechadas

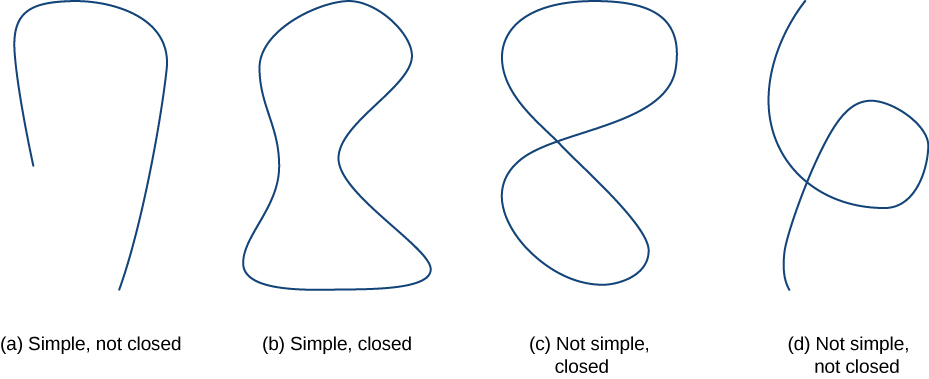
Curva\(C\) é uma curva fechada se houver uma parametrização\(\vecs r(t)\),\(a≤t≤b\) de\(C\) tal forma que a parametrização atravessa a curva exatamente uma vez\(\vecs r(a)=\vecs r(b)\) e. \(C\)A curva é uma curva simples se\(C\) não se cruza sozinha. Ou seja,\(C\) é simples se existe uma parametrização\(\vecs r(t)\),\(a≤t≤b\) de\(C\) tal que\(\vecs r\) seja de um para um\((a,b)\). É possível para\(\vecs r(a)=\vecs r(b)\), o que significa que a curva simples também está fechada.

Exemplo\(\PageIndex{1}\): Determining Whether a Curve Is Simple and Closed

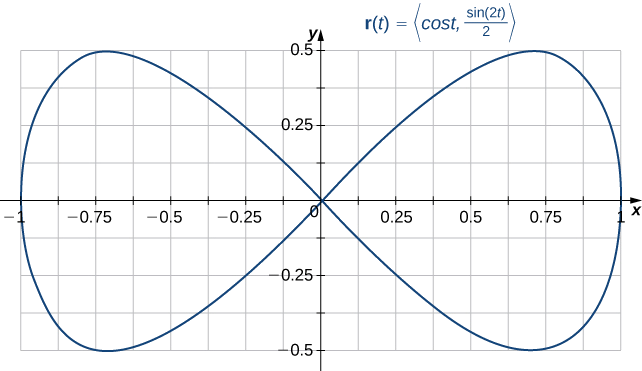
A curva com parametrização\(\vecs{r}(t)=\left\langle\cos t,\frac{\sin(2t)}{2}\right\rangle\) é\(0≤t≤2\pi\) uma curva fechada simples?

Solução

Observe que\(\vecs{r}(0)=⟨1,0⟩=\vecs r(2\pi)\), portanto, a curva está fechada. No entanto, a curva não é simples. Para ver isso, observe que\(\vecs{r}\left(\frac{\pi}{2}\right)=⟨0,0⟩=\vecs{r}\left(\frac{3\pi}{2}\right)\), e portanto, a curva se cruza na origem (Figura\(\PageIndex{2}\)).

Figura\(\PageIndex{2}\) . Uma curva fechada, mas não simples.

Exercício\(\PageIndex{1}\)

A curva é dada pela parametrização\(\vecs{r}(t)=⟨2\cos t,3\sin t⟩\)\(0≤t≤6\pi\), uma curva fechada simples?

Dica

Esboce a curva.

Responda

sim

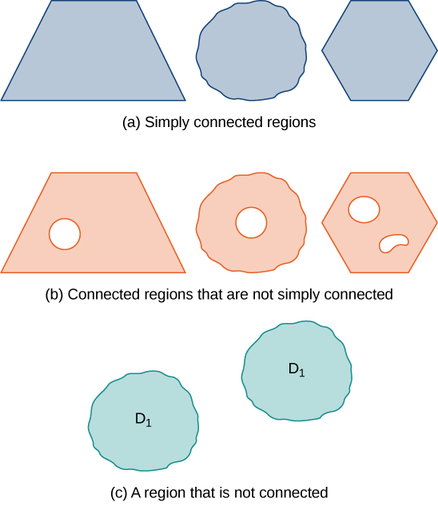
Muitos dos teoremas deste capítulo relacionam uma integral sobre uma região a uma integral sobre o limite da região, onde o limite da região é uma curva fechada simples ou uma união de curvas fechadas simples. Para desenvolver esses teoremas, precisamos de duas definições geométricas para regiões: a de uma região conectada e a de uma região simplesmente conectada. Uma região conectada é aquela em que há um caminho na região que conecta quaisquer dois pontos que estejam dentro dessa região. Uma região simplesmente conectada é uma região conectada que não tem nenhum buraco nela. Essas duas noções, junto com a noção de uma curva fechada simples, nos permitem declarar várias generalizações do Teorema Fundamental do Cálculo mais adiante neste capítulo. Essas duas definições são válidas para regiões em qualquer número de dimensões, mas estamos preocupados apenas com regiões em duas ou três dimensões.

DEFINIÇÃO: regiões conectadas

Uma região D é uma região conectada se, para quaisquer dois pontos\(P_1\) e\(P_2\), houver um caminho de\(P_1\) até\(P_2\) com um traço contido inteiramente dentro de D. Uma região D é uma região simplesmente conectada se D estiver conectada a qualquer curva fechada simples C que esteja dentro de D, e a curva C puder ser reduzida continuamente até um ponto, permanecendo inteiramente dentro de D. Em duas dimensões, uma região é simplesmente conectada se estiver conectada e não tiver furos.

Todas as regiões simplesmente conectadas estão conectadas, mas nem todas as regiões conectadas estão simplesmente conectadas (Figura\(\PageIndex{3}\)).

Figura\(\PageIndex{3}\): Nem todas as regiões conectadas estão simplesmente conectadas. (a) Regiões simplesmente conectadas não têm buracos. (b) As regiões conectadas que não estão simplesmente conectadas podem ter furos, mas você ainda pode encontrar um caminho na região entre quaisquer dois pontos. (c) Uma região que não está conectada tem alguns pontos que não podem ser conectados por um caminho na região.

Exercício\(\PageIndex{2}\)

A região na imagem abaixo está conectada? A região está simplesmente conectada?

Dica

Considere as definições.

Responda

A região na figura está conectada. A região na figura não está simplesmente conectada.

Teorema fundamental para integrais de linha

Agora que entendemos algumas curvas e regiões básicas, vamos generalizar o Teorema Fundamental do Cálculo para integrais de linha. Lembre-se de que o Teorema Fundamental do Cálculo diz que se uma função\(f\) tem uma antiderivada\(F\), então a integral\(f\) de de\(a\) para\(b\) depende apenas dos valores de\(F\) at\(a\) e at\(b\) —isto é,

\[\int_a^bf(x)\,dx=F(b)−F(a). \nonumber \]

Se pensarmos no gradiente como uma derivada, o mesmo teorema vale para integrais de linha vetorial. Mostramos como isso funciona usando um exemplo motivacional.

Exemplo\(\PageIndex{2}\): Evaluating a Line Integral and the Antiderivatives of the Endpoints

Deixe\(\vecs{F}(x,y)=⟨2x,4y⟩\). Calcule\(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}\), onde C é o segmento de linha de\((0,0)\) até\((2,2)\) (Figura\(\PageIndex{4}\)).

Solução

Usamos o método da seção anterior para calcular\(\int_C \vecs{F} \cdot d\vecs{r}\). A curva C pode ser parametrizada por\(\vecs{r}(t)=⟨2t,2t⟩\),\(0≤t≤1\). Então,\(\vecs{F}(\vecs r(t))=⟨4t,8t⟩\) e\(\vecs r′(t)=⟨2,2⟩\), o que implica que

\[\begin{align*} \int_C \vecs{F}·d\vecs{r} &=\int_0^1⟨4t,8t⟩·⟨2,2⟩dt \\[4pt] &=\int_0^1(8t+16t)dt=\int_0^1 24tdt\\[4pt] &={\big[12t^2\big]}_0^1=12. \end{align*}\]

Figura\(\PageIndex{4}\): O valor da integral\(\int_C \vecs{F} \cdot d\vecs{r}\) da linha depende apenas do valor da função potencial de\(\vecs{F}\) nas extremidades da curva.

Observe isso\(\vecs{F}=\vecs \nabla f\), onde\(f(x,y)=x^2+2y^2\). Se pensarmos no gradiente como uma derivada, então\(f\) é uma “antiderivada” de\(\vecs{F}\). No caso de integrais de variável única, a integral da derivada\(g′(x)\) é\(g(b)−g(a)\), onde a é o ponto inicial do intervalo de integração e b é o ponto final. Se as integrais de linha vetorial funcionarem como integrais de variável única, então esperaríamos que\(\vecs{F}\) a integral fosse\(f(P_1)−f(P_0)\), onde\(P_1\) é o ponto final da curva de integração e\(P_0\) é o ponto inicial. Observe que esse é o caso deste exemplo:

\[\int_C \vecs{F} \cdot d\vecs{r}=\int_C \vecs \nabla f \cdot d\vecs{r}=12 \nonumber \]

e

\[f(2,2)−f(0,0)=4+8−0=12. \nonumber \]

Em outras palavras, a integral de uma “derivada” pode ser calculada avaliando uma “antiderivada” nos pontos finais da curva e subtraindo-a, assim como para integrais de variável única.

O teorema a seguir diz que, sob certas condições, o que aconteceu no exemplo anterior vale para qualquer campo de gradiente. O mesmo teorema vale para integrais de linha vetorial, que chamamos de Teorema Fundamental para Integrais de Linha.

Teorema: O TEOREMA FUNDAMENTAL PARA INTEGRAIS DE LINHA

Seja C uma curva suave por partes com parametrização\(\vecs r(t)\),\(a≤t≤b\). \(f\)Seja uma função de duas ou três variáveis com derivadas parciais de primeira ordem que existem e são contínuas em C. Em seguida,

\[\int_C \vecs \nabla f \cdot d\vecs{r}=f(\vecs r(b))−f(\vecs r(a)). \label{FunTheLine} \]

Prova

Em primeiro lugar,

\[\int_C \vecs \nabla f \cdot d \vecs{r}=\int_a^b \vecs \nabla f( \vecs r(t)) \cdot \vecs r′(t)\,dt. \nonumber \]

Pela regra da cadeia,

\[\dfrac{d}{dt}(f( \vecs r(t))= \vecs \nabla f( \vecs r(t)) \cdot \vecs r′(t) \nonumber \]

Portanto, pelo Teorema Fundamental do Cálculo,

\[\begin{align*} \int_C \vecs \nabla f \cdot d \vecs{r} &=\int_a^b \vecs \nabla f( \vecs r(t)) \cdot \vecs r′(t)dt \\[4pt] &=\int_a^b\dfrac{d}{dt}(f( \vecs r(t))dt \\[4pt] &={\big[f( \vecs r(t))\big]}_{t=a}^{t=b}\\[4pt] &=f( \vecs r(b))−f( \vecs r(a)). \end{align*}\]

\(\square\)

Sabemos que se\(\vecs{F}\) é um campo vetorial conservador, existe uma função potencial\(f\) tal\( \vecs \nabla f= \vecs F\). Portanto

\[\int_C \vecs F·d\vecs r=\int_C\vecs \nabla f·d\vecs{r}=f(\vecs r(b))−f(\vecs r(a)). \nonumber \]

Em outras palavras, assim como no Teorema Fundamental do Cálculo, calcular a integral da linha\(\int_C \vecs F·d\vecs{r}\), onde\(\vecs{F}\) é conservador, é um processo de duas etapas:

1. Encontre uma função potencial (“antiderivada”)\(f\) para\(\vecs{F}\) e
2. Calcule o valor de\(f\) nas extremidades de\(C\) e calcule sua diferença\(f(\vecs r(b))−f(\vecs r(a))\).

Lembre-se, no entanto, de que há uma grande diferença entre o Teorema Fundamental do Cálculo e o Teorema Fundamental das Integrais de Linha:
Uma função de uma variável que é contínua deve ter uma antiderivada. No entanto, um campo vetorial, mesmo que seja contínuo, não precisa ter uma função potencial.

Exemplo\(\PageIndex{3}\): Applying the Fundamental Theorem

Calcule integral\(\int_C \vecs{F} \cdot d\vecs{r}\), onde\(\vecs{F}(x,y,z)=⟨2x\ln y,\dfrac{x^2}{y}+z^2,2yz⟩\) e\(C\) é uma curva com parametrização\(\vecs{r}(t)=⟨t^2,t,t⟩\),\(1≤t≤e\)

1. sem usar o Teorema Fundamental das Integrais de Linha e
2. usando o Teorema Fundamental das Integrais de Linha.

Solução

1. Primeiro, vamos calcular a integral sem o Teorema Fundamental para Integrais de Linha e, em vez disso, usar o método que aprendemos na seção anterior:

\[\begin{align*} \int_C \vecs{F} \cdot dr &=\int_1^e\vecs F(\vecs r(t)) \cdot \vecs r′(t)\,dt\\[4pt] &=\int_1^e⟨2t^2\ln t,\dfrac{t^4}{t}+t^2,2t^2⟩ \cdot ⟨2t,1,1⟩\,dt\\[4pt] &=\int_1^e(4t^3\ln t+t^3+3t^2)\,dt \\[4pt] &=\int_1^e 4t^3\ln t \,dt+\int_1^e(t^3+3t^2)\,dt \\[4pt] &=\int_1^e 4t^3\ln t\,dt+{\Big[\dfrac{t^4}{4}+t^3\Big]}_1^e \\[4pt] &=\int_1^e 4t^3\ln t\,dt+\dfrac{e^4}{4}+e^3 −\dfrac{1}{4} −1 \\[4pt] &= \int_1^e 4t^3\ln t\,dt+\dfrac{e^4}{4}+e^3 −\dfrac{5}{4}\end{align*}\]

Integral\(\displaystyle \int_1^e t^3\ln t\,dt\) requer integração por partes. Deixe\(u=\ln t\)\(dv=t^3\) e. Em seguida\(u=\ln t\),\(dv=t^3\)

e

\[du=\dfrac{1}{t}\,dt, \;\;v=\dfrac{t^4}{4}.\nonumber \]

Portanto,

\[\begin{align*} \int_1^e t^3\ln t\,dt &={\Big[\dfrac{t^4}{4}\ln t\Big]}_1^e−\dfrac{1}{4}\int_1^e t^3\,dt \\[4pt] &=\dfrac{e^4}{4}−\dfrac{1}{4}\left(\dfrac{e^4}{4}−\dfrac{1}{4}\right). \end{align*}\]

Assim,

\[\begin{align*} \int_C \vecs F \cdot d\vecs{r} &= 4\int_1^e t^3\ln t\, dt\quad +\quad \dfrac{e^4}{4}+e^3 − \dfrac{5}{4} \\[4pt] &=4\left(\dfrac{e^4}{4}−\dfrac{1}{4}\left(\dfrac{e^4}{4}−\dfrac{1}{4}\right)\right)+\dfrac{e^4}{4}+e^3−\dfrac{5}{4}\\[4pt] &=e^4−\dfrac{e^4}{4}+\dfrac{1}{4}+\dfrac{e^4}{4}+e^3−\dfrac{5}{4} \\[4pt] &=e^4+e^3−1. \end{align*}\]

2. Dado que essa\(f(x,y,z)=x^2\ln y+yz^2\) é uma função potencial para\(\vecs F\), vamos usar o Teorema Fundamental para Integrais de Linha para calcular a integral. Note que

\[\begin{align*} \int_C \vecs F \cdot d\vecs{r} &=\int_C \vecs \nabla f \cdot d\vecs{r} \\[4pt] &=f(\vecs r(e))−f(\vecs r(1)) \\[4pt] &=f(e^2,e,e)−f(1,1,1)\\[4pt] &=e^4+e^3−1. \end{align*}\]

Esse cálculo é muito mais simples do que o cálculo que fizemos em (a). Desde que tenhamos uma função potencial, calcular uma integral de linha usando o Teorema Fundamental para Integrais de Linha é muito mais fácil do que calcular sem o teorema.

O exemplo\(\PageIndex{3}\) ilustra um bom recurso do Teorema Fundamental das Integrais de Linha: ele nos permite calcular mais facilmente muitas integrais de linha vetorial. Enquanto tivermos uma função potencial, calcular a integral da linha é apenas uma questão de avaliar a função potencial nos pontos finais e subtrair.

Exercício\(\PageIndex{3}\)

Dado que essa\(f(x,y)={(x−1)}^2y+{(y+1)}^2x\) é uma função potencial para\(\vecs F(x,y)=⟨2xy−2y+{(y+1)}^2,{(x−1)}^2+2yx+2x⟩\), calcule integral\(\int_C \vecs F·d\vecs r\), onde\(C\) está a metade inferior do círculo unitário orientada no sentido anti-horário.

Dica

O teorema fundamental para intervalos de linha diz que essa integral depende apenas do valor de\(f\) nas extremidades de\(C\).

Responda

2

O teorema fundamental para integrais de linha tem duas consequências importantes. A primeira consequência é que, se\(\vecs{F}\) for conservadora e\(C\) for uma curva fechada, a circulação de\(\vecs{F}\) along\(C\) é zero, ou seja,\(\int_C \vecs F·d\vecs r=0\). Para ver por que isso é verdade,\(f\) seja uma função potencial para\(\vecs{F}\). Como\(C\) é uma curva fechada, o ponto terminal\(\vecs r(b)\) de\(C\) é o mesmo que a inicial\(\vecs r(a)\) de\(C\) —isto é,\(\vecs r(a)=\vecs r(b)\). Portanto, pelo Teorema Fundamental para Integrais de Linha,

\[\begin{align} \oint_C \vecs F·d\vecs r &=\oint_C \vecs \nabla f·d\vecs r\\[4pt] &=f(\vecs r(b))−f(\vecs r(a)) \\[4pt] &=f(\vecs r(b))−f(\vecs r(b)) \\[4pt] &=0. \end{align} \nonumber \]

Lembre-se de que a razão pela qual um campo vetorial conservador\(\vecs{F}\) é chamado de “conservador” é porque esses campos vetoriais modelam forças nas quais a energia é conservada. Mostramos que a gravidade é um exemplo dessa força. Se pensarmos\(\vecs{F}\) no campo vetorial na integral\(\oint_C \vecs F·d\vecs r\) como um campo gravitacional, a equação\(\oint_C \vecs{F}·d\vecs{r}=0\) segue. Se uma partícula percorre um caminho que começa e termina no mesmo local, o trabalho realizado pela gravidade na partícula é zero.

A segunda consequência importante do Teorema Fundamental para Integrais de Linha (Equation\ ref {FunTheLine}) é que as integrais de linha de campos vetoriais conservadores são independentes do caminho, ou seja, elas dependem apenas dos pontos finais da curva dada e não dependem do caminho entre as extremidades.

DEFINIÇÃO: Path Independence

\(\vecs{F}\)Seja um campo vetorial com domínio\(D\); ele é independente do caminho (ou independente do caminho) se

\[\int_{C_1} \vecs{F}·d\vecs{r}=\int_{C_2} \vecs{F}·d\vecs{r} \nonumber \]

para qualquer caminho\(C_1\) e\(C_2\)\(D\) com os mesmos pontos iniciais e terminais.

A segunda consequência é declarada formalmente no seguinte teorema.

Teorema: CAMPOS CONSERVADORES

Se\(\vecs{F}\) for um campo vetorial conservador, então\(\vecs{F}\) é independente do caminho.

Prova

Vamos\(D\) denotar o domínio de\(\vecs{F}\)\(C_1\) e deixar e\(C_2\) ser dois caminhos\(D\) com os mesmos pontos iniciais e terminais (Figura\(\PageIndex{5}\)). Chame o ponto inicial\(P_1\) e o ponto terminal\(P_2\). Como\(\vecs{F}\) é conservador, existe uma função potencial\(f\) para\(\vecs{F}\). Pelo teorema fundamental para integrais de linha,

\[\int_{C_1} \vecs{F}·d\vecs{r}=f(P_2)−f(P_1)=\int_{C_2} \vecs{F}·d\vecs{r}. \nonumber \]

Portanto,\(\int_{C_1}\vecs F·d\vecs r=\int_{C_2}\vecs F·d\vecs r\) e\(\vecs{F}\) é independente do caminho.

\(\square\)

Para visualizar o que significa independência de caminho, imagine três caminhantes subindo do acampamento base até o topo de uma montanha. O Hiker 1 faz uma rota íngreme diretamente do acampamento até o topo. O Hiker 2 segue uma rota sinuosa que não é íngreme do acampamento até o topo. O Hiker 3 começa seguindo a rota íngreme, mas na metade do caminho até o topo decide que é muito difícil para ele. Portanto, ele retorna ao acampamento e segue o caminho não íngreme até o topo. Todos os três caminhantes estão viajando por caminhos em um campo gravitacional. Como a gravidade é uma força na qual a energia é conservada, o campo gravitacional é conservador. Pela independência do caminho, a quantidade total de trabalho realizado por gravidade em cada um dos caminhantes é a mesma porque todos começaram no mesmo lugar e terminaram no mesmo lugar. O trabalho realizado pelos caminhantes inclui outros fatores, como atrito e movimento muscular, portanto, a quantidade total de energia que cada um gasta não é a mesma, mas a energia líquida gasta contra a gravidade é a mesma para todos os três caminhantes.

Figura\(\PageIndex{4}\): O campo vetorial é conservador e, portanto, independente do caminho.

Mostramos que se\(\vecs{F}\) é conservador, então\(\vecs{F}\) é independente do caminho. Acontece que, se o domínio de\(\vecs{F}\) estiver aberto e conectado, o inverso também será verdadeiro. Ou seja, se\(\vecs{F}\) é independente do caminho e o domínio do\(\vecs{F}\) está aberto e conectado, então\(\vecs{F}\) é conservador. Portanto, o conjunto de campos vetoriais conservadores em domínios abertos e conectados é precisamente o conjunto de campos vetoriais independentes do caminho.

Teorema: O TESTE DE INDEPENDÊNCIA DE CAMINHO PARA CAMPOS CONSERVADORES

Se\(\vecs{F}\) for um campo vetorial contínuo que é independente do caminho e o domínio\(D\) de\(\vecs{F}\) está aberto e conectado, então\(\vecs{F}\) é conservador.

Prova

Provamos o teorema para campos vetoriais em\(ℝ^2\). A prova dos campos vetoriais em\(ℝ^3\) é semelhante. Para mostrar que isso\(\vecs F=⟨P,Q⟩\) é conservador, devemos encontrar uma função potencial\(f\) para\(\vecs{F}\). Para esse fim,\(X\) seja um ponto fixo em\(D\). Para qualquer ponto\((x,y)\)\(D\),\(C\) seja um caminho de\(X\) para\((x,y)\). Defina\(f(x,y)\) por\(f(x,y)=\int_C \vecs F·d\vecs r\). (Note que essa definição de só\(f\) faz sentido porque\(\vecs{F}\) é independente do caminho. Se não\(\vecs{F}\) fosse independente do caminho, talvez fosse possível encontrar outro caminho\(C′\) de\(X\) para\((x,y)\) tal que\(\int_C \vecs F·d\vecs r≠\int_C \vecs F·d\vecs r\), nesse caso, não\(f(x,y)\) fosse uma função.) Queremos mostrar que\(f\) tem a propriedade\(\vecs \nabla f=\vecs F\).

Como o domínio\(D\) está aberto, é possível encontrar um disco centralizado de\((x,y)\) forma que o disco fique totalmente contido em seu interior\(D\). Que\((a,y)\)\(a<x\) seja um ponto nesse disco. \(C\)Seja um caminho de\(X\) até lá\((x,y)\) que consiste em duas peças:\(C_1\)\(C_2\) e. A primeira peça,\(C_1\), é qualquer caminho de\(C\) até\((a,y)\) que permaneça dentro\(D\);\(C_2\) é o segmento da linha horizontal de\((a,y)\) para\((x,y)\) (Figura\(\PageIndex{6}\)). Então

\[f(x,y)=\int_{C_1} \vecs F·d\vecs r+\int_{C_2}\vecs F \cdot d\vecs r.\nonumber \]

A primeira integral não depende de\(x\), então

\[f_x(x,y)=\dfrac{∂}{∂x}\int_{C_2} \vecs F \cdot d\vecs r. \nonumber \]

Se parametrizarmos\(C_2\) por\(\vecs r(t)=⟨t,y⟩\)\(a≤t≤x\), então

\[\begin{align*} f_x(x,y) &=\dfrac{∂}{∂x}\int_{C_2} \vecs F \cdot d\vecs r \\[4pt] &=\dfrac{∂}{∂x}\int_a^x \vecs F(\vecs r(t)) \cdot \vecs r′(t)\,dt \\[4pt] &=\dfrac{∂}{∂x}\int_a^x \vecs F(\vecs r(t)) \cdot \dfrac{d}{dt}(⟨t,y⟩)\,dt \\[4pt] &=\dfrac{∂}{∂x}\int_a^x \vecs F(\vecs r(t)) \cdot ⟨1,0⟩\,dt \\[4pt] &=\dfrac{∂}{∂x}\int_a^x P(t,y)\,dt.\\[4pt] \end{align*}\]

Pelo Teorema Fundamental do Cálculo (parte 1),

\[f_x(x,y)=\dfrac{∂}{∂x}\int_a^x P(t,y)\,dt=P(x,y).\nonumber \]

Figura\(\PageIndex{6}\). Aqui,\(C_1\) é qualquer caminho de\(C\) até\((a,y)\) que permaneça dentro\(D\), e\(C_2\) é o segmento de linha horizontal de\((a,y)\) para\((x,y)\).

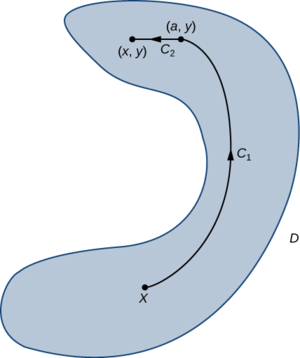
Um argumento semelhante usando um segmento de linha vertical em vez de um segmento de linha horizontal mostra isso\(f_y(x,y)=Q(x,y)\).

Portanto,\(\vecs \nabla f=\vecs F\) e\(\vecs{F}\) é conservador.

\(\square\)

Passamos muito tempo discutindo e provando os teoremas acima, mas podemos resumi-los de forma simples: um campo vetorial\(\vecs F\) em um domínio aberto e conectado é conservador se e somente se for independente do caminho. É importante saber isso porque campos vetoriais conservadores são extremamente importantes em aplicações, e esses teoremas nos dão uma maneira diferente de ver o que significa ser conservador usando a independência de caminhos.

Exemplo\(\PageIndex{4}\): Showing That a Vector Field Is Not Conservative

Use a independência do caminho para mostrar que o campo vetorial não\(\vecs F(x,y)=⟨x^2y,y+5⟩\) é conservador.

Solução

Podemos indicar que não\(\vecs{F}\) é conservador, mostrando que não\(\vecs{F}\) é independente do caminho. Fazemos isso dando dois caminhos diferentes\(C_2\), que começam\(C_1\) e terminam em\((0,0)\)\((1,1)\), e ainda assim\(\int_{C_1} \vecs F \cdot d\vecs r≠\int_{C_2} \vecs F \cdot d\vecs r\).

\(C_1\)Seja a curva com parametrização\(\vecs r_1(t)=⟨t,\,t⟩\)\(0≤t≤1\) e\(C_2\) seja a curva com parametrização\(\vecs r_2(t)=⟨t,\,t^2⟩\)\(0≤t≤1\) (Figura\(\PageIndex{7}\).). Então

\[\begin{align*} \int_{C_1} \vecs{F}·d\vecs r &=\int_0^1 \vecs F(\vecs r_1(t))·\vecs r_1′(t)\,dt \\[4pt] &=\int_0^1⟨t^3,t+5⟩·⟨1,1⟩\,dt=\int_0^1(t^3+t+5)\,dt\\[4pt] &={\Big[\dfrac{t^4}{4}+\dfrac{t^2}{2}+5t\Big]}_0^1=\dfrac{23}{4} \end{align*}\]

e

\[\begin{align*} \int_{C_2}\vecs F·d\vecs r &=\int_0^1 \vecs F(\vecs r_2(t))·\vecs r_2′(t)\,dt \\[4pt] &=\int_0^1⟨t^4,t^2+5⟩·⟨1,2t⟩\,dt=\int_0^1(t^4+2t^3+10t)\,dt \\[4pt] &={\Big[\dfrac{t^5}{5}+\dfrac{t^4}{2}+5t^2\Big]}_0^1=\dfrac{57}{10}. \end{align*}\]

Uma vez que\(\int_{C_1} \vecs F \cdot d\vecs r≠\int_{C_2} \vecs F \cdot d\vecs r\), o valor de uma linha integral de\(\vecs{F}\) depende do caminho entre dois pontos dados. Portanto, não\(\vecs{F}\) é independente do caminho e não\(\vecs{F}\) é conservador.

Figura\(\PageIndex{7}\): Curvas\(C_1\) e\(C_2\) ambas orientadas da esquerda para a direita.

Exercício\(\PageIndex{4}\)

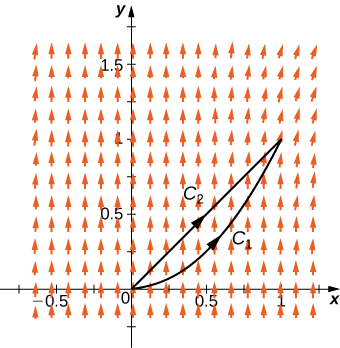
Mostre que não\(\vecs{F}(x,y)=⟨xy,\,x^2y^2⟩\) é independente do caminho considerando o segmento de linha de\((0,0)\) para\((0,2)\) e a parte do gráfico\(y=\dfrac{x^2}{2}\) que vai de\((0,0)\) para\((0,2)\).

Dica

Calcule as integrais de linha correspondentes.

Responda

Se\(C_1\) e\(C_2\) representar as duas curvas, então\[\int_{C_1} \vecs F \cdot d\vecs r≠\int_{C_2} \vecs F \cdot d\vecs r. \nonumber \]

Campos vetoriais conservadores e funções potenciais

Como aprendemos, o Teorema Fundamental para Integrais de Linha diz que, se\(\vecs{F}\) for conservador, o cálculo\(\int_C \vecs F·d\vecs r\) tem duas etapas: primeiro, encontre uma função potencial\(f\) para\(\vecs{F}\) e, segundo, calcule\(f(P_1)−f(P_0)\), onde\(P_1\) está o ponto final de\(C\) e\(P_0\) é o ponto de partida. Para usar esse teorema para um campo conservador\(\vecs{F}\), devemos ser capazes de encontrar uma função potencial\(f\) para\(\vecs{F}\). Portanto, devemos responder à seguinte pergunta: Dado um campo vetorial conservador\(\vecs{F}\), como podemos encontrar uma função\(f\) como essa\(\vecs \nabla f=\vecs{F}\)? Antes de fornecer um método geral para encontrar uma função potencial, vamos motivar o método com um exemplo.

Exemplo\(\PageIndex{5}\): Finding a Potential Function

Encontre uma função potencial para\(\vecs F(x,y)=⟨2xy^3,3x^2y^2+\cos(y)⟩\), mostrando assim que\(\vecs{F}\) é conservadora.

Solução

Suponha que essa\(f(x,y)\) seja uma função potencial para\(\vecs{F}\). Então\(\vecs \nabla f=\vecs F\), e portanto

\[f_x(x,y)=2xy^3 \; \; \text{and} \;\; f_y(x,y)=3x^2y^2+\cos y. \nonumber \]

Integrar a equação em\(f_x(x,y)=2xy^3\) relação a\(x\) produz a equação

\[f(x,y)=x^2y^3+h(y). \nonumber \]

Observe que, como estamos integrando uma função de duas variáveis em relação a\(x\), devemos adicionar uma constante de integração que seja uma constante em relação a\(x\), mas ainda pode ser uma função de\(y\). A equação\(f(x,y)=x^2y^3+h(y)\) pode ser confirmada tomando a derivada parcial em relação a\(x\):

\[\dfrac{∂f}{∂x}=\dfrac{∂}{∂x}(x^2y^3)+\dfrac{∂}{∂x}(h(y))=2xy^3+0=2xy^3. \nonumber \]

Uma vez que\(f\) é uma função potencial para\(\vecs{F}\),

\[f_y(x,y)=3x^2y^2+\cos(y), \nonumber \]

e, portanto,

\[3x^2y^2+g′(y)=3x^2y^2+\cos(y). \nonumber \]

Isso implica que\(h′(y)=\cos y\), então\(h(y)=\sin y+C\). Portanto, qualquer função do formulário\(f(x,y)=x^2y^3+\sin(y)+C\) é uma função potencial. Tomar, em particular,\(C=0\) dá a função potencial\(f(x,y)=x^2y^3+\sin(y)\).

Para verificar se\(f\) é uma função potencial, observe isso\(\vecs \nabla f(x,y)=⟨2xy^3,3x^2y^2+\cos y⟩=\vecs F\).

Exercício\(\PageIndex{5}\)

Encontre uma função potencial para\(\vecs{F}(x,y)=⟨e^xy^3+y,3e^xy^2+x⟩\).

Dica

Siga as etapas em Exemplo\(\PageIndex{5}\).

Responda

\(f(x,y)=e^xy^3+xy\)

A lógica do exemplo anterior se estende a encontrar a função potencial para qualquer campo vetorial conservador em\(ℝ^2\). Assim, temos a seguinte estratégia de resolução de problemas para encontrar funções potenciais:

ESTRATÉGIA DE RESOLUÇÃO DE PROBLEMAS: ENCONTRAR UMA FUNÇÃO POTENCIAL PARA UM CAMPO VETORIAL CONSERVADOR\(\vecs{F}(x,y)=⟨P(x,y),Q(x,y)⟩\)

1. Integre\(P\) com relação\(x\) a. Isso resulta em uma função do formulário\(g(x,y)+h(y)\), onde\(h(y)\) é desconhecida.
2. Pegue a derivada parcial de em\(g(x,y)+h(y)\) relação a\(y\), que resulta na função\(gy(x,y)+h′(y)\).
3. Use a equação\(gy(x,y)+h′(y)=Q(x,y)\) para encontrar\(h′(y)\).
4. Integre\(h′(y)\) para encontrar\(h(y)\).
5. Qualquer função da forma\(f(x,y)=g(x,y)+h(y)+C\), onde\(C\) é uma constante, é uma função potencial para\(\vecs{F}\).

Podemos adaptar essa estratégia para encontrar funções potenciais para campos vetoriais em\(ℝ^3\), conforme mostrado no próximo exemplo.

Exemplo\(\PageIndex{6}\): Finding a Potential Function in \(ℝ^3\)

Encontre uma função potencial para\(F(x,y,z)=⟨2xy,x^2+2yz^3,3y^2z^2+2z⟩\), mostrando assim que\(\vecs{F}\) é conservadora.

Solução

Suponha que\(f\) seja uma função potencial. Então,\(\vecs \nabla f= \vecs{F}\) e portanto\(f_x(x,y,z)=2xy\). A integração dessa equação em relação a\(x\) produz a equação\(f(x,y,z)=x^2y+g(y,z)\) para alguma função\(g\). Observe que, nesse caso, a constante de integração em relação a\(x\) é uma função de\(y\)\(z\) e.

Uma vez que\(f\) é uma função potencial,

\[x^2+2yz^3=f_y(x,y,z)=x^2+g_y(y,z). \nonumber \]

Portanto,

\[g_y(y,z)=2yz^3. \nonumber \]

Integrando essa função com relação aos\(y\) rendimentos

\[g(y,z)=y^2z^3+h(z) \nonumber \]

para alguma função\(h(z)\) de\(z\) sozinho. (Observe que, porque sabemos que isso\(g\) é uma função de apenas\(y\) e\(z\), não precisamos escrever\(g(y,z)=y^2z^3+h(x,z)\).) Portanto,

\[f(x,y,z)=x^2y+g(y,z)=x^2y+y^2z^3+h(z). \nonumber \]

Para encontrar\(f\), agora só precisamos encontrar\(h\). Uma vez que\(f\) é uma função potencial,

\[3y^2z^2+2z=g_z(y,z)=3y^2z^2+h′(z). \nonumber \]

Isso implica que\(h′(z)=2z\), então\(h(z)=z^2+C\). Deixar\(C=0\) dá a função potencial

\[f(x,y,z)=x^2y+y^2z^3+z^2. \nonumber \]

Para verificar se\(f\) é uma função potencial, observe isso\(\vecs \nabla f(x,y,z)=⟨2xy,x^2+2yz^3,3y^2z^2+2z⟩=\vecs F(x,y,z)\).

Exercício\(\PageIndex{6}\)

Encontre uma função potencial para\(\vecs{F}(x,y,z)=⟨12x^2,\cos y\cos z,1−\sin y\sin z⟩\).

Dica

Exemplo a seguir\(\PageIndex{6}\), comece integrando com relação\(x\) a.

Responda

\(f(x,y,z)=4x^3+\sin y\cos z+z\)

Podemos aplicar o processo de encontrar uma função potencial a uma força gravitacional. Lembre-se de que, se um objeto tem massa unitária e está localizado na origem, a força gravitacional\(ℝ^2\) que o objeto exerce sobre outro objeto de massa unitária no ponto\((x,y)\) é dada pelo campo vetorial

\(\vecs F(x,y)=−G\left\langle\dfrac{x}{ {(x^2+y^2)}^{3/2} },\dfrac{y}{ {(x^2+y^2)}^{3/2} }\right\rangle\),

onde\(G\) está a constante gravitacional universal. No próximo exemplo, construímos uma função potencial para\(\vecs{F}\), confirmando assim o que já sabemos: que a gravidade é conservadora.

Exemplo\(\PageIndex{7}\): Finding a Potential Function

Encontre uma função potencial\(f\) para\(\vecs{F}(x,y)=−G\left\langle\dfrac{x}{ {(x^2+y^2)}^{3/2} },\dfrac{y}{ {(x^2+y^2)}^{3/2} }\right\rangle\).

Solução

Suponha que\(f\) seja uma função potencial. Então,\(\vecs \nabla f= \vecs{F}\) e portanto

\[f_x(x,y)=\dfrac{−Gx}{ {(x^2+y^2)}^{3/2} }.\nonumber \]

Para integrar essa função em relação a\(x\), podemos usar\(u\) -substitution. Se\(u=x^2+y^2\), então\(\dfrac{du}{2}=x\,dx\), sim

\[\begin{align*} \int \dfrac{−Gx}{ {(x^2+y^2)}^{3/2} }\,dx &=\int \dfrac{−G}{2u^{3/2}} \,du \\[4pt] &=\dfrac{G}{\sqrt{u}}+h(y) \\[4pt] &=\dfrac{G}{\sqrt{x^2+y^2}}+h(y) \end{align*}\]

para alguma função\(h(y)\). Portanto,

\[f(x,y)=\dfrac{G}{ \sqrt{x^2+y^2}}+h(y).\nonumber \]

Uma vez que\(f\) é uma função potencial para\(\vecs{F}\),

\[f_y(x,y)=\dfrac{−Gy}{ {(x^2+y^2)}^{3/2} }\nonumber \].

Desde então\(f(x,y)=\dfrac{G}{ \sqrt{x^2+y^2}}+h(y)\),\(f_y(x,y)\) também é igual\(\dfrac{−Gy}{ {(x^2+y^2)}^{3/2} }+h′(y)\).

Portanto,

\[\dfrac{−Gy}{ {(x^2+y^2)}^{3/2} }+h′(y)=\dfrac{−Gy}{ {(x^2+y^2)}^{3/2} }, \nonumber \]

o que implica isso\(h′(y)=0\). Assim, podemos\(h(y)\) considerar qualquer constante; em particular, podemos deixar\(h(y)=0\). A função

\[f(x,y)=\dfrac{G}{ \sqrt{x^2+y^2} } \nonumber \]

é uma função potencial para o campo gravitacional\(\vecs{F}\). Para confirmar que\(f\) é uma função potencial, observe que

\[\begin{align*} \vecs\nabla f(x,y) &=⟨−\dfrac{1}{2} \dfrac{G}{ {(x^2+y^2)}^{3/2} } (2x),−\dfrac{1}{2} \dfrac{G}{ {(x^2+y^2)}^{3/2} }(2y)⟩ \\[4pt] &=⟨\dfrac{−Gx}{ {(x^2+y^2)}^{3/2} },\dfrac{−Gy}{ {(x^2+y^2)}^{3/2} }⟩\\[4pt] &=\vecs F(x,y). \end{align*}\]

Exercício\(\PageIndex{7}\)

Encontre uma função potencial\(f\) para a força gravitacional tridimensional\(\vecs{F}(x,y,z)=\left\langle\dfrac{−Gx}{ {(x^2+y^2+z^2)}^{3/2} },\dfrac{−Gy}{ {(x^2+y^2+z^2)}^{3/2} },\dfrac{−Gz}{ {(x^2+y^2+z^2)}^{3/2} }\right\rangle\).

Dica

Siga a estratégia de resolução de problemas.

Responda

\(f(x,y,z)=\dfrac{G}{\sqrt{x^2+y^2+z^2}}\)

Testando um campo vetorial

Até agora, trabalhamos com campos vetoriais que sabemos serem conservadores, mas se não nos disserem que um campo vetorial é conservador, precisamos ser capazes de testar se ele é conservador. Lembre-se de que, se\(\vecs{F}\) for conservador, então\(\vecs{F}\) tem a propriedade parcial cruzada (consulte A propriedade parcial cruzada de campos vetoriais conservadores). Ou seja, se\(\vecs F=⟨P,Q,R⟩\) for conservador\(P_y=Q_x\), então\(P_z=R_x\),\(Q_z=R_y\) e. Então, se\(\vecs{F}\) tem a propriedade parcial cruzada, então é\(\vecs{F}\) conservador? Se o domínio do\(\vecs{F}\) estiver aberto e simplesmente conectado, a resposta será sim.

Teorema: O TESTE PARCIAL CRUZADO PARA CAMPOS CONSERVADORES

Se\(\vecs{F}=⟨P,Q,R⟩\) é um campo vetorial em uma região aberta, simplesmente conectada\(D\) e\(P_y=Q_x\)\(P_z=R_x\), e\(Q_z=R_y\) por toda parte\(D\), então\(\vecs{F}\) é conservador.

Embora uma prova desse teorema esteja além do escopo do texto, podemos descobrir seu poder com alguns exemplos. Posteriormente, vemos por que é necessário que a região esteja simplesmente conectada.

Combinando esse teorema com a propriedade parcial cruzada, podemos determinar se um determinado campo vetorial é conservador:

Teorema: PROPRIEDADE PARCIAL CRUZADA DE CAMPOS CONSERVADORES

\(\vecs{F}=⟨P,Q,R⟩\)Seja um campo vetorial em uma região aberta e simplesmente conectada\(D\). Então\(P_y=Q_x\)\(P_z=R_x\), e\(Q_z=R_y\) por toda parte,\(D\) se e somente se\(\vecs{F}\) for conservador.

A versão desse teorema em também\(ℝ^2\) é verdadeira. Se\(\vecs F(x,y)=⟨P,Q⟩\) for um campo vetorial em um domínio aberto, simplesmente conectado em\(ℝ^2\), então\(\vecs F\) é conservador se e somente se\(P_y=Q_x\).

Exemplo\(\PageIndex{8}\): Determining Whether a Vector Field Is Conservative

Determine se o campo vetorial\(\vecs F(x,y,z)=⟨xy^2z,x^2yz,z^2⟩\) é conservador.

Solução

Observe que o domínio de\(\vecs{F}\) é todo\(ℝ^2\) e\(ℝ^3\) está simplesmente conectado. Portanto, podemos usar The Cross-Partial Property of Conservative Vector Fields para determinar se\(\vecs{F}\) é conservador. Deixe

\[P(x,y,z)=xy^2z \nonumber \]

\[Q(x,y,z)=x^2yz \nonumber \]

e

\[R(x,y,z)=z^2.\nonumber \]

Desde\(Q_z(x,y,z)=x^2y\) e\(R_y(x,y,z)=0\), o campo vetorial não é conservador.

Exemplo\(\PageIndex{9}\): Determining Whether a Vector Field Is Conservative

Determinar campo vetorial\(\vecs{F}(x,y)=⟨x\ln (y), \,\dfrac{x^2}{2y}⟩\) é conservador.

Solução

Observe que o domínio de\(\vecs{F}\) é a parte\(ℝ^2\) da qual\(y>0\). Assim, o domínio de\(\vecs{F}\) faz parte de um plano acima do\(x\) eixo -, e esse domínio é simplesmente conectado (não há buracos nessa região e essa região está conectada). Portanto, podemos usar The Cross-Partial Property of Conservative Vector Fields para determinar se\(\vecs{F}\) é conservador. Deixe

\[P(x,y)=x\ln (y) \;\; \text{and} \;\;\ Q(x,y)=\dfrac{x^2}{2y}. \nonumber \]

Então,\(P_y(x,y)=\dfrac{x}{y}=Q_x(x,y)\) e assim,\(\vecs{F}\) é conservador.

Exercício\(\PageIndex{8}\)

Determine se\(\vecs{F}(x,y)=⟨\sin x\cos y,\,\cos x\sin y⟩\) é conservador.

Dica

Use a propriedade parcial cruzada dos campos vetoriais conservadores da seção anterior.

Responda

É conservador.

Ao usar a propriedade parcial cruzada de campos vetoriais conservadores, é importante lembrar que um teorema é uma ferramenta e, como qualquer ferramenta, ele só pode ser aplicado sob as condições corretas. No caso de The Cross-Partial Property of Conservative Vector Fields, o teorema só pode ser aplicado se o domínio do campo vetorial estiver simplesmente conectado.

Para ver o que pode dar errado ao aplicar incorretamente o teorema, considere o campo vetorial de Example\(\PageIndex{4}\):

\[\vecs F(x,y)=\dfrac{y}{x^2+y^2}\,\hat{\mathbf i}+\dfrac{−x}{x^2+y^2}\,\hat{\mathbf j}. \nonumber \]

Esse campo vetorial satisfaz a propriedade parcial cruzada, já que

\[\dfrac{∂}{∂y}\left(\dfrac{y}{x^2+y^2}\right)=\dfrac{(x^2+y^2)−y(2y)}{ {(x^2+y^2)}^2}=\dfrac{x^2−y^2}{ {(x^2+y^2)}^2} \nonumber \]

e

\[\dfrac{∂}{∂x}\left(\dfrac{−x}{x^2+y^2}\right)=\dfrac{−(x^2+y^2)+x(2x)}{ {(x^2+y^2)}^2}=\dfrac{x^2−y^2}{ {(x^2+y^2)}^2}. \nonumber \]

Como\(\vecs{F}\) satisfaz a propriedade parcial cruzada, podemos ficar tentados a concluir que\(\vecs{F}\) é conservador. No entanto, não\(\vecs{F}\) é conservador. Para ver isso, deixe

\[\vecs r(t)=⟨\cos t,\sin t⟩,\;\; 0≤t≤\pi \nonumber \]

seja uma parametrização da metade superior de um círculo unitário orientado no sentido anti-horário (denote isso\(C_1\)) e deixe

\[\vecs s(t)=⟨\cos t,−\sin t⟩,\;\; 0≤t≤\pi \nonumber \]

seja uma parametrização da metade inferior de um círculo unitário orientado no sentido horário (denote isso\(C_2\)). Observe isso\(C_1\) e\(C_2\) tenha o mesmo ponto inicial e final. Uma vez que\({\sin}^2 t+{\cos}^2 t=1\),

\[\vecs F(\vecs r(t)) \cdot \vecs r′(t)=⟨\sin(t),−\cos(t)⟩ \cdot ⟨−\sin(t), \cos(t)⟩=−1 \nonumber \]

e

\[\vecs F(\vecs s(t))·\vecs s′(t)=⟨−\sin t,−\cos t⟩·⟨−\sin t,−\cos t⟩={\sin}^2 t+{\cos}^2t=1. \nonumber \]

Portanto,

\[\int_{C_1} \vecs F·d\vecs r=\int_0^{\pi}−1\,dt=−\pi \nonumber \]

e

\[\int_{C_2}\vecs F·d\vecs r=\int_0^{\pi} 1\,dt=\pi. \nonumber \]

Portanto,\(C_1\) e\(C_2\) têm o mesmo ponto de partida e ponto final, mas\(\int_{C_1} \vecs F·d\vecs r≠\int_{C_2} \vecs F·d\vecs r\). Portanto, não\(\vecs{F}\) é independente do caminho e não\(\vecs{F}\) é conservador.

Resumindo:\(\vecs{F}\) satisfaz a propriedade parcial cruzada e ainda não\(\vecs{F}\) é conservadora. O que deu errado? Isso contradiz a propriedade parcial cruzada dos campos vetoriais conservadores? O problema é que o domínio de\(\vecs{F}\) é todo\(ℝ^2\), exceto a origem. Em outras palavras, o domínio de\(\vecs{F}\) tem um buraco na origem e, portanto, o domínio não está simplesmente conectado. Como o domínio não está simplesmente conectado, a propriedade parcial cruzada dos campos vetoriais conservadores não se aplica\(\vecs{F}\) a.

Fechamos esta seção examinando um exemplo da utilidade do Teorema Fundamental para integrais de linha. Agora que podemos testar se um campo vetorial é conservador, sempre podemos decidir se o Teorema Fundamental para integrais de linha pode ser usado para calcular uma integral de linha vetorial. Se nos pedirem que calculemos uma integral do formulário\(\int_C \vecs F·d\vecs r\), nossa primeira pergunta deve ser: é\(\vecs{F}\) conservador? Se a resposta for sim, então devemos encontrar uma função potencial e usar o Teorema Fundamental para Integrais de Linha para calcular a integral. Se a resposta for não, então o Teorema Fundamental para Integrais de Linha não pode nos ajudar e temos que usar outros métodos, como usar o método da seção anterior (usando\(\vecs F(\vecs r(t))\) e\(\vecs r'(t)\)).

Exemplo\(\PageIndex{10}\): Using the Fundamental Theorem for Line Integrals

Calcule a integral da linha\(\int_C \vecs F·d\vecs r\), onde\(\vecs F(x,y,z)=⟨2xe^yz+e^xz,\,x^2e^yz,\,x^2e^y+e^x⟩\) e\(C\) é qualquer curva suave que vai da origem até\((1,1,1)\).

Solução

Antes de tentar calcular a integral, precisamos determinar se\(\vecs{F}\) é conservador e se o domínio de\(\vecs{F}\) está simplesmente conectado. O domínio de\(\vecs{F}\) é todo\(ℝ^3\), que está conectado e não tem buracos. Portanto, o domínio de\(\vecs{F}\) está simplesmente conectado. Deixe

\[P(x,y,z)=2xe^yz+e^xz, \;\; Q(x,y,z)=x^2e^yz, \;\; \text{and} \;\; R(x,y,z)=x^2e^y+e^x \nonumber \]

para que\(\vecs{F}(x,y,z)=⟨P,Q,R⟩\). Como o domínio de\(\vecs{F}\) está simplesmente conectado, podemos verificar os parciais cruzados para determinar se\(\vecs{F}\) é conservador. Note que

\[\begin{align*} P_y(x,y,z) &=2xe^yz=Q_x(x,y,z) \\[4pt]P_z(x,y,z) &=2xe^y+e^x=R_x(x,y,z) \\[4pt] Q_z(x,y,z) &=x^2e^y=R_y(x,y,z).\end{align*}\]

Portanto,\(\vecs{F}\) é conservador.

Para avaliar\(\int_C \vecs F·d\vecs r\) usando o Teorema Fundamental para Integrais de Linha, precisamos encontrar uma função potencial\(f\) para\(\vecs{F}\). \(f\)Seja uma função potencial para\(\vecs{F}\). Então\(\vecs \nabla f=\vecs F\), e portanto\(f_x(x,y,z)=2xe^yz+e^xz\). Integrar essa equação em relação a\(x\) fornece\(f(x,y,z)=x^2e^yz+e^xz+h(y,z)\) para alguma função\(h\). Diferenciar essa equação em relação a\(y\) dá\(x^2e^yz+h_y(y,z)=Q(x,y,z)=x^2e^yz\), o que implica isso\(h_y(y,z)=0\). Portanto,\(h\) é uma função de\(z\) apenas,\(f(x,y,z)=x^2e^yz+e^xz+h(z)\) e. Para encontrar\(h\), observe isso\(f_z=x^2e^y+e^x+h′(z)=R=x^2e^y+e^x\). Portanto,\(h′(z)=0\) e podemos pegar\(h(z)=0\). Uma função potencial para\(\vecs{F}\) é\(f(x,y,z)=x^2e^yz+e^xz\).

Agora que temos uma função potencial, podemos usar o Teorema Fundamental para Integrais de Linha para calcular a integral. Pelo teorema,

\[\begin{align*} \int_C \vecs F·d\vecs r &=\int_C \vecs \nabla f·d\vecs r\\[4pt] &=f(1,1,1)−f(0,0,0)\\[4pt] &=2e. \end{align*}\]

Análise

Observe que, se não tivéssemos reconhecido que isso\(\vecs{F}\) é conservador, teríamos que parametrizar\(C\) e usar o método da seção anterior. Como a curva\(C\) é desconhecida, usar o Teorema Fundamental para integrais de linha é muito mais simples.

Exercício\(\PageIndex{9}\)

Calcule integral\(\int_C \vecs F·d\vecs r\), onde\(\vecs{F}(x,y)=⟨\sin x\sin y, 5−\cos x\cos y⟩\) e\(C\) é um semicírculo com ponto inicial\((0,\pi)\) e ponto final\((0,−\pi)\).

Dica

Use o teorema fundamental para integrais de linha.

Responda

\(−10\pi\)

Exemplo\(\PageIndex{11}\): Work Done on a Particle

\(\vecs F(x,y)=⟨2xy^2,2x^2y⟩\)Seja um campo de força. Suponha que uma partícula comece seu movimento na origem e termine seu movimento em qualquer ponto em um plano que não esteja no\(x\) eixo -ou no\(y\) eixo -. Além disso, o movimento da partícula pode ser modelado com uma parametrização suave. Mostre que\(\vecs{F}\) faz um trabalho positivo na partícula.

Solução

Mostramos que\(\vecs{F}\) faz um trabalho positivo na partícula, mostrando que ela\(\vecs{F}\) é conservadora e, em seguida, usando o Teorema Fundamental para Integrais de Linha.

Para mostrar que isso\(\vecs{F}\) é conservador, suponha\(f(x,y)\) que sejam uma função potencial para\(\vecs{F}\). Então,\(\vecs \nabla f(x,y)=\vecs F(x,y)=⟨2xy^2,2x^2y⟩\)\(f_x(x,y)=2xy^2\) e portanto\(f_y(x,y)=2x^2y\) e. A equação\(fx(x,y)=2xy^2\) implica isso\(f(x,y)=x^2y^2+h(y)\). Derivando os dois lados em relação aos\(y\) rendimentos\(f_y(x,y)=2x^2y+h′(y)\). Portanto,\(h′(y)=0\) e podemos pegar\(h(y)=0\).

Se\(f(x,y)=x^2y^2\), então observe isso e\(\vecs \nabla f(x,y)=⟨2xy^2,2x^2y⟩=\vecs F\), portanto,\(f\) é uma função potencial para\(\vecs{F}\).

\((a,b)\)Seja o ponto em que a partícula para o movimento e\(C\) denote a curva que modela o movimento da partícula. O trabalho realizado pela\(\vecs{F}\) partícula é\(\int_C \vecs{F}·d\vecs{r}\). Pelo teorema fundamental para integrais de linha,

\[\begin{align*} \int_C \vecs F·d\vecs r &=\int_C \nabla f·d\vecs r \\[4pt] &=f(a,b)−f(0,0)\\[4pt] &=a^2b^2. \end{align*}\]

Desde\(a≠0\) e\(b≠0\), por suposição,\(a^2b^2>0\). Portanto,\(\int_C \vecs F·d\vecs r>0\), e\(\vecs{F}\) faz um trabalho positivo na partícula.

Análise

Observe que esse problema seria muito mais difícil sem usar o Teorema Fundamental para integrais de linha. Para aplicar as ferramentas que aprendemos, precisaríamos fornecer uma parametrização da curva e usar o método da seção anterior. Como o caminho do movimento\(C\) pode ser tão exótico quanto desejamos (desde que seja suave), pode ser muito difícil parametrizar o movimento da partícula.

Exercício\(\PageIndex{10}\)

Suponha que uma partícula se mova de um ponto\((4,4)\) para outro ao\((1,1)\) longo de qualquer curva suave.\(\vecs{F}(x,y)=⟨4x^3y^4,4x^4y^3⟩\) O trabalho realizado\(\vecs{F}\) com a partícula é positivo, negativo ou zero?

Dica

Use o teorema fundamental para integrais de linha.

Responda

Negativo

Conceitos-chave

• Os teoremas desta seção exigem curvas fechadas, simples ou ambas, e regiões conectadas ou simplesmente conectadas.
• A integral de linha de um campo vetorial conservador pode ser calculada usando o Teorema Fundamental para Integrais de Linha. Este teorema é uma generalização do Teorema Fundamental do Cálculo em dimensões superiores. O uso desse teorema geralmente facilita o cálculo da integral da linha.
• Os campos conservadores são independentes do caminho. A integral de linha de um campo conservador depende somente do valor da função potencial nas extremidades da curva de domínio.
• Dado o campo vetorial\(\vecs{F}\), podemos testar se\(\vecs{F}\) é conservador usando a propriedade parcial cruzada. Se\(\vecs{F}\) tem a propriedade parcial cruzada e o domínio está simplesmente conectado, então\(\vecs{F}\) é conservador (e, portanto, tem uma função potencial). Se\(\vecs{F}\) for conservador, podemos encontrar uma função potencial usando a Estratégia de Solução de Problemas.
• A circulação de um campo vetorial conservador em um domínio simplesmente conectado sobre uma curva fechada é zero.

Equações-chave

• Teorema fundamental para integrais de linha
  \(\displaystyle \int_C \vecs \nabla f·d\vecs r=f(\vecs r(b))−f(\vecs r(a))\)
• Circulação de um campo conservador sobre a curva C que envolve uma região simplesmente conectada
  \(\displaystyle \oint_C \vecs \nabla f·d\vecs r=0\)

Glossário

curva fechada

uma curva que começa e termina no mesmo ponto

região conectada

uma região na qual quaisquer dois pontos podem ser conectados por um caminho com um traço contido inteiramente dentro da região

Teorema fundamental para integrais de linha

o valor da integral\(\displaystyle \int_C\vecs ∇f⋅d\vecs r\) da linha depende somente do valor de\(f\) nas extremidades de\(C: \displaystyle \int_C \vecs ∇f⋅d\vecs r=f(\vecs r(b))−f(\vecs r(a))\)

independência do caminho

um campo vetorial\(\vecs{F}\) tem independência de caminho se for\(\displaystyle \int_{C_1} \vecs F⋅d\vecs r=\displaystyle \int_{C_2} \vecs F⋅d\vecs r\) para qualquer curva\(C_1\) e\(C_2\) no domínio de\(\vecs{F}\) com os mesmos pontos iniciais e terminais

curva simples

uma curva que não se cruza

região simplesmente conectada

uma região que está conectada e tem a propriedade de que qualquer curva fechada que esteja inteiramente dentro da região engloba pontos que estão inteiramente dentro da região