16.2E: Exercícios para a Seção 16.2

Last updated
Save as PDF

Page ID: 188553

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

1. Verdadeiro ou falso? $\displaystyle\int _C f(x,y)\,ds$A integral de linha é igual a uma integral definida se$C$ for uma curva suave definida em$[a,b]$ e se a função$f$ for contínua em alguma região que contém curva$C$.

Resposta: É verdade

2. Verdadeiro ou falso? Funções vetoriais$\vecs r_1=t\,\hat{\mathbf i}+t^2\,\hat{\mathbf j}, \quad 0≤t≤1,$ e$\vecs r_2=(1−t)\,\hat{\mathbf i}+(1−t)^2\,\hat{\mathbf j}, \quad 0≤t≤1$ definem a mesma curva orientada.

3. Verdadeiro ou falso? $\displaystyle\int _{−C}(P\,dx+Q\,dy)=\int _C(P\,dx−Q\,dy)$

Resposta: Falso

4. Verdadeiro ou falso? Uma curva suave por partes$C$ consiste em um número finito de curvas suaves que são unidas de ponta a ponta.

5. Verdadeiro ou falso? Se$C$ for dado por$x(t)=t,\quad y(t)=t, \quad 0≤t≤1$, então$\displaystyle\int _Cxy\,ds=\int ^1_0t^2\,dt.$

Resposta: Falso

Para os exercícios a seguir, use um sistema computacional de álgebra (CAS) para avaliar as integrais de linha ao longo do caminho indicado.

6. [T]$\displaystyle\int _C(x+y)\,ds$

$C:x=t,y=(1−t),z=0$de$(0, 1, 0)$ para$(1, 0, 0)$

7. [T]$\displaystyle \int _C(x−y)ds$

$C:\vecs r(t)=4t\,\hat{\mathbf i}+3t\,\hat{\mathbf j}$quando$0≤t≤2$

Resposta: $\displaystyle\int _C(x−y)\,ds=10$

8. [T]$\displaystyle\int _C(x^2+y^2+z^2)\,ds$

$C:\vecs r(t)=\sin t\,\hat{\mathbf i}+\cos t\,\hat{\mathbf j}+8t\,\hat{\mathbf k}$quando$0≤t≤\dfrac{π}{2}$

9. [T] Avalie$\displaystyle\int _Cxy^4\,ds$, onde$C$ está a metade direita do círculo$x^2+y^2=16$ e é percorrido no sentido horário.

Resposta: $\displaystyle\int _Cxy^4\,ds=\frac{8192}{5}$

10. [T] Avalie$\displaystyle\int _C4x^3ds$, onde C é o segmento de linha$(−2,−1)$ de$(1, 2)$ a.

Para os exercícios a seguir, encontre o trabalho realizado.

11. Encontre o trabalho realizado por campo vetorial$\vecs F(x,y,z)=x\,\hat{\mathbf i}+3xy\,\hat{\mathbf j}−(x+z)\,\hat{\mathbf k}$ em uma partícula que se move ao longo de um segmento de linha que vai$(1,4,2)$ de$(0,5,1)$ a.

Resposta: $W=8$unidades de trabalho

12. Encontre o trabalho realizado por uma pessoa pesando 150 libras caminhando exatamente uma volta subindo uma escada circular em espiral de raio de 3 pés se a pessoa subir 10 pés.

13. Encontre o trabalho realizado pelo campo de força$\vecs F(x,y,z)=−\dfrac{1}{2}x\,\hat{\mathbf i}−\dfrac{1}{2}y\,\hat{\mathbf j}+\dfrac{1}{4}\,\hat{\mathbf k}$ em uma partícula à medida que ela se move ao longo da hélice$\vecs r(t)=\cos t\,\hat{\mathbf i}+\sin t\,\hat{\mathbf j}+t\,\hat{\mathbf k}$ de um ponto$(1,0,0)$ a outro$(−1,0,3π)$.

Resposta: $W=\frac{3π}{4}$unidades de trabalho

14. Encontre o trabalho realizado pelo campo$\vecs{F}(x,y)=y\,\hat{\mathbf i}+2x\,\hat{\mathbf j}$ vetorial ao mover um objeto ao longo do caminho$C$, que une pontos$(1, 0)$$(0, 1)$ e.

15. Encontre o trabalho realizado pela força$\vecs{F}(x,y)=2y\,\hat{\mathbf i}+3x\,\hat{\mathbf j}+(x+y)\,\hat{\mathbf k}$ ao mover um objeto ao longo da curva$\vecs r(t)=\cos(t)\,\hat{\mathbf i}+\sin(t)\,\hat{\mathbf j}+16\,\hat{\mathbf k}$, onde$0≤t≤2π$.

Resposta: $W=π$unidades de trabalho

16. Encontre a massa de um fio na forma de um círculo de raio 2 centrado em (3, 4) com densidade de massa linear$ρ(x,y)=y^2$.

Para os exercícios a seguir, avalie as integrais de linha.

17. Avalie$\displaystyle\int_C\vecs F·d\vecs{r}$$\vecs{F}(x,y)=−1\,\hat{\mathbf j}$, onde e$C$ é a parte do gráfico$y=\frac{1}{2}x^3−x$ de$(2,2)$ para$(−2,−2)$.

Resposta: $\displaystyle\int _C\vecs F·d\vecs{r}=4$unidades de trabalho

18. Avalie$\displaystyle\int _γ(x^2+y^2+z^2)^{−1}ds$, onde$γ$ está a hélice$x=\cos t,y=\sin t,z=t,$ com$0≤t≤T.$

19. Avalie$\displaystyle\int _Cyz\,dx+xz\,dy+xy\,dz$ o segmento de linha de$(1,1,1) $ até$(3,2,0).$

Resposta: $\displaystyle\int _Cyz\,dx+xz\,dy+xy\,dz=−1$

20. $C$Seja o segmento de linha do ponto (0, 1, 1) ao ponto (2, 2, 3). Avaliar a integral da linha$\displaystyle\int _Cy\,ds.$

21. [T] Use um sistema computacional de álgebra para avaliar a integral da linha$\displaystyle\int _Cy^2\,dx+x\,dy$, onde$C$ está o arco da parábola$x=4−y^2$$(−5, −3)$ de$(0, 2)$ a.

Resposta: $\displaystyle\int _C(y^2)\,dx+(x)\,dy=\dfrac{245}{6}$

22. [T] Use um sistema de álgebra computacional para avaliar a integral da linha$\displaystyle\int _C (x+3y^2)\,dy$ ao longo do caminho$C$ dado por$x=2t,y=10t,$ onde$0≤t≤1.$

23. [T] Use um CAS para avaliar a integral da linha$\displaystyle\int _C xy\,dx+y\,dy$ sobre o caminho$C$ dado por$x=2t,y=10t$, onde$0≤t≤1$.

Resposta: $\displaystyle\int _Cxy\,dx+y\,dy=\dfrac{190}{3}$

24. Calcule a integral da linha$\displaystyle\int _C(2x−y)\,dx+(x+3y)\,dy$, onde$C$ fica ao longo do$x$ eixo$x=0$ -de$x=5$ a.

26. [T] Use um CAS para avaliar$\displaystyle\int _C\dfrac{y}{2x^2−y^2}\,ds$, onde$C$ é definido pelas equações paramétricas$x=t,y=t$, para$1≤t≤5.$

Resposta: $\displaystyle\int _C\frac{y}{2x^2−y^2}\,ds=\sqrt{2}\ln 5$

27. [T] Use um CAS para avaliar$\displaystyle\int _Cxy\,ds$, onde$C$ é definido pelas equações paramétricas$x=t^2,y=4t$, para$0≤t≤1.$

Nos exercícios a seguir, encontre o trabalho realizado pelo campo de força$\vecs F$ em um objeto que se move ao longo do caminho indicado.

28. $\vecs{F}(x,y)=−x \,\hat{\mathbf i}−2y\,\hat{\mathbf j}$

$C:y=x^3$de$(0, 0)$ para$(2, 8)$

Resposta: $W=−66$unidades de trabalho

29. $\vecs{F}(x,y)=2x\,\hat{\mathbf i}+y\,\hat{\mathbf j}$

<$C$: no sentido anti-horário ao redor do triângulo com vértices$(0, 0), (1, 0), $ e$(1, 1)$

30. $\vecs F(x,y,z)=x\,\hat{\mathbf i}+y\,\hat{\mathbf j}−5z\,\hat{\mathbf k}$

$C:\vecs r(t)=2\cos t\,\hat{\mathbf i}+2\sin t\,\hat{\mathbf j}+t\,\hat{\mathbf k},\; 0≤t≤2π$

Resposta: $W=−10π^2$unidades de trabalho

31. $\vecs F$Seja um campo vetorial$\vecs{F}(x,y)=(y^2+2xe^y+1)\,\hat{\mathbf i}+(2xy+x^2e^y+2y)\,\hat{\mathbf j}$. Calcule o trabalho da integral$\displaystyle\int _C\vecs F·d\vecs{r}$, onde$C$ está o caminho$\vecs r(t)=\sin t\,\hat{\mathbf i}+\cos t\,\hat{\mathbf j},\quad 0≤t≤\dfrac{π}{2}$.

32. Calcule o trabalho realizado à força ao$\vecs F(x,y,z)=2x\,\hat{\mathbf i}+3y\,\hat{\mathbf j}−z\,\hat{\mathbf k}$ longo do caminho$\vecs r(t)=t\,\hat{\mathbf i}+t^2\,\hat{\mathbf j}+t^3\,\hat{\mathbf k}$, onde$0≤t≤1$.

Resposta: $W=2$unidades de trabalho

33. Avalie$\displaystyle\int _C\vecs F·d\vecs{r}$, onde$\vecs{F}(x,y)=\dfrac{1}{x+y}\,\hat{\mathbf i}+\dfrac{1}{x+y}\,\hat{\mathbf j}$ e$C$ é o segmento do círculo unitário indo no sentido anti-horário de$(1,0)$ para$(0, 1)$.

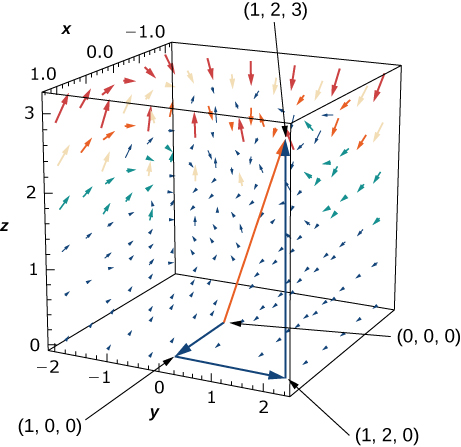
34. A força$\vecs F(x,y,z)=zy\,\hat{\mathbf i}+x\,\hat{\mathbf j}+z^2x\,\hat{\mathbf k}$ atua sobre uma partícula que viaja da origem ao ponto$(1, 2, 3)$. Calcule o trabalho realizado se a partícula viajar:

ao longo do caminho$(0,0,0)→(1,0,0)→(1,2,0)→(1,2,3)$ ao longo de segmentos em linha reta que unem cada par de extremidades;
ao longo da linha reta que une os pontos inicial e final.
O trabalho é o mesmo nos dois caminhos?
$clipboard_e7c787ff46860b19ec57c0669a08914af.png$

Resposta: a.$W=11$ unidades de trabalho;
b.$W=\dfrac{39}{4}=9\frac{3}{4}$ unidades de trabalho;
c. Não

35. Encontre o trabalho realizado por campo vetorial$\vecs F(x,y,z)=x\,\hat{\mathbf i}+3xy\,\hat{\mathbf j}−(x+z)\,\hat{\mathbf k}$ em uma partícula que se move ao longo de um segmento de linha que vai$(1, 4, 2)$ de$(0, 5, 1).$

36. Quanto trabalho é necessário para mover um objeto no campo vetorial$\vecs{F}(x,y)=y\,\hat{\mathbf i}+3x\,\hat{\mathbf j}$ ao longo da parte superior da elipse$\dfrac{x^2}{4}+y^2=1$ de$(2, 0)$ para$(−2,0)$?

Resposta: $W=2π$unidades de trabalho

37. Um campo vetorial é dado por$\vecs{F}(x,y)=(2x+3y)\,\hat{\mathbf i}+(3x+2y)\,\hat{\mathbf j}$. Avalie a integral da linha do campo em torno de um círculo de raio unitário percorrido no sentido horário.

38. Avalie a integral de linha da função escalar$xy$ ao longo do caminho parabólico$y=x^2$ conectando a origem ao ponto$(1, 1)$.

Resposta: $\displaystyle\int _C f\,ds=\dfrac{25\sqrt{5}+1}{120}$

39. Encontre$\displaystyle\int _Cy^2\,dx+(xy−x^2)\,dy$$C: y=3x$ de$(0, 0)$ até$(1, 3).$

40. Encontre$\displaystyle\int _Cy^2\,dx+(xy−x^2)\,dy$$C: y^2=9x$ de$(0, 0)$ até$(1, 3).$

Resposta: $\displaystyle\int _Cy^2\,dx+(xy−x^2)\,dy=6.15$

Para os exercícios a seguir, use um CAS para avaliar as integrais de linha fornecidas.

41. [T] Avalie$\vecs F(x,y,z)=x^2z\,\hat{\mathbf i}+6y\,\hat{\mathbf j}+yz^2\,\hat{\mathbf k}$, onde$C$ é representado por$\vecs r(t)=t\,\hat{\mathbf i}+t^2\,\hat{\mathbf j}+\ln t \,\hat{\mathbf k},1≤t≤3$.

42. [T] Avalie a integral da linha$\displaystyle\int _γxe^y\,ds$ onde,$γ$ é o arco$x=e^y$ da curva$(1,0)$ de$(e,1)$ a.

Resposta: $\displaystyle\int _γxe^y\,ds≈7.157$

43. [T] Avalie a integral$\displaystyle\int _γxy^2\,ds$, onde$γ$ está um triângulo com vértices$(0, 1, 2), (1, 0, 3)$,$(0,−1,0)$ e.

44. [T] Avalie a integral da linha$\displaystyle\int _γ(y^2−xy)\,dx$, onde$γ$ é$y=\ln x$ a curva de$(1, 0)$ direção$(e,1)$.

Resposta: $\displaystyle\int _γ(y^2−xy)\,dx≈−1.379$

45. [T] Calcule a integral da linha$\displaystyle\int_γ xy^4\,ds$, onde$γ$ está a metade direita do círculo$x^2+y^2=16$.

46. [T] Avalie$\int C \vecs F⋅d\vecs{r},\int C \vecs F·d\vecs{r},$ onde$\vecs F(x,y,z)=x^2y\,\mathbf{\hat i}+(x−z)\,\mathbf{\hat j}+xyz\,\mathbf{\hat k}$ e

$C: \vecs r(t)=t\,\mathbf{\hat i}+t^2\,\mathbf{\hat j}+2\,\mathbf{\hat k},0≤t≤1$.

Resposta: $\displaystyle\int _C \vecs F⋅d\vecs{r}≈−1.133$unidades de trabalho

47. Avalie$\displaystyle\int _C \vecs F⋅d\vecs{r}$, onde$\vecs{F}(x,y)=2x\sin y\,\mathbf{\hat i}+(x^2\cos y−3y^2)\,\mathbf{\hat j}$ e

$C$é qualquer caminho de$(−1,0)$ para$(5, 1)$.

48. Encontre a integral da linha de$\vecs F(x,y,z)=12x^2\,\mathbf{\hat i}−5xy\,\mathbf{\hat j}+xz\,\mathbf{\hat k}$$C$ sobreposição definida$y=x^2, z=x^3$ de ponto$(0, 0, 0)$ a ponto$(2, 4, 8)$.

Resposta: $\displaystyle\int _C \vecs F⋅d\vecs{r}≈22.857$unidades de trabalho

49. Encontre a integral da linha de$\displaystyle\int _C(1+x^2y)\,ds$, de onde$C$ vem a elipse$\vecs r(t)=2\cos t\,\mathbf{\hat i}+3\sin t\,\mathbf{\hat j}$$0≤t≤π.$

Para os exercícios a seguir, encontre o fluxo.

50. Calcule o fluxo de$\vecs{F}=x^2\,\mathbf{\hat i}+y\,\mathbf{\hat j}$ um segmento de linha de$(0, 0)$ para$(1, 2).$

Resposta: $\text{flux}=−\frac{1}{3}$

51. Deixe$\vecs{F}=5\,\mathbf{\hat i}$ e$C$ deixe fazer uma curva$y=0,$ com$0≤x≤4$. Encontre o fluxo do outro lado$C$.

52. Deixe$\vecs{F}=5\,\mathbf{\hat j}$ e$C$ deixe fazer uma curva$y=0,$ com$0≤x≤4$. Encontre o fluxo do outro lado$C$.

Resposta: $\text{flux}=-20$

53. Deixe$\vecs{F}=−y\,\mathbf{\hat i}+x\,\mathbf{\hat j}$ e deixe$C: \vecs r(t)=\cos t\,\mathbf{\hat i}+\sin t\,\mathbf{\hat j}$ para$0≤t≤2π$. Calcule o fluxo transversal$C$.

54. Deixe$\vecs{F}=(x^2+y^3)\,\mathbf{\hat i}+(2xy)\,\mathbf{\hat j}$. Calcule o fluxo$\vecs F$ orientado no sentido anti-horário ao longo da curva$C: x^2+y^2=9.$

Resposta: $\text{flux}=0$

Complete o resto dos exercícios conforme indicado.

55. Encontre a integral da linha de$\displaystyle\int _C z^2\,dx+y\,dy+2y\,dz,$ onde$C$ consiste em duas partes:$C_1$ e$C_2.$$C_1$ é a interseção do cilindro$x^2+y^2=16$ e$z=3$ do plano de$(0, 4, 3)$ para$(−4,0,3).$$C_2$ é um segmento de linha de$(−4,0,3)$ para$(0, 1, 5)$.

56. Uma mola é feita de um fio fino torcido na forma de uma hélice circular.$x=2\cos t,\;y=2\sin t,\;z=t.$ Encontre a massa de duas voltas da mola se o fio tiver uma densidade de massa constante de$ρ$ gramas por cm.

Resposta: $m=4πρ\sqrt{5}$gramas

57. Um fio fino é dobrado na forma de um semicírculo de raio$a$. Se a densidade de massa linear no ponto$P$ for diretamente proporcional à distância da linha até as extremidades, encontre a massa do fio.

58. Um objeto se move no campo de força no$\vecs F(x,y,z)=y^2\,\mathbf{\hat i}+2(x+1)y\,\mathbf{\hat j}$ sentido anti-horário a partir do ponto$(2, 0)$ ao longo do caminho$x^2+4y^2=4$ elíptico e de volta ao ponto$(2, 0)$ ao longo do$x$ eixo.$(−2,0)$ Quanto trabalho é feito pelo campo de força no objeto?

Resposta: $W=0$unidades de trabalho

59. Encontre o trabalho realizado quando um objeto se move no campo de força$\vecs F(x,y,z)=2x\,\mathbf{\hat i}−(x+z)\,\mathbf{\hat j}+(y−x)\,\mathbf{\hat k}$ ao longo do caminho dado por$\vecs r(t)=t^2\,\mathbf{\hat i}+(t^2−t)\,\mathbf{\hat j}+3\,\mathbf{\hat k}, \; 0≤t≤1.$

60. Se um campo de força inverso$\vecs F$ for dado por$\vecs F(x,y,z)=\dfrac{k}{‖r‖^3}r$, onde$k$ é uma constante, encontre o trabalho realizado à$\vecs F$ medida que seu ponto de aplicação se move ao longo do$x$ eixo -de$A(1,0,0)$ para$B(2,0,0)$.

Resposta: $W=\frac{k}{2}$unidades de trabalho

61. David e Sandra planejam avaliar a integral da linha$\displaystyle\int _C\vecs F·d\vecs{r}$ ao longo de um caminho no$xy$ plano$(0, 0)$ -de$(1, 1)$ a. O campo de força é$\vecs{F}(x,y)=(x+2y)\,\mathbf{\hat i}+(−x+y^2)\,\mathbf{\hat j}$. David escolhe o caminho que percorre o$x$ eixo -de$(0, 0)$ até$(1, 0)$ e, em seguida, percorre a linha vertical$x=1$ de$(1, 0)$ até o ponto final$(1, 1)$. Sandra escolhe o caminho direto ao longo da linha diagonal$y=x$ de$(0, 0)$ até$(1, 1)$. Cuja integral de linha é maior e em quanto?

Colaboradores

Template:contribopenstaxcalc