16.2: Integrais de linha
- Page ID
- 188540
Intro
- Calcule uma integral de linha escalar ao longo de uma curva.
- Calcule uma integral de linha vetorial ao longo de uma curva orientada no espaço.
- Use uma integral de linha para calcular o trabalho realizado ao mover um objeto ao longo de uma curva em um campo vetorial.
- Descreva o fluxo e a circulação de um campo vetorial.
Estamos familiarizados com integrais de variável única do formulário\(\displaystyle \int_{a}^{b}f(x)\,dx\), em que o domínio da integração é um intervalo\([a,b]\). Esse intervalo pode ser considerado como uma curva no\(xy\) plano -, já que o intervalo define um segmento de linha com pontos finais\((a,0)\) e\((b,0)\) —em outras palavras, um segmento\(x\) de linha localizado no eixo. Suponha que desejemos integrar qualquer curva no plano, não apenas sobre um segmento\(x\) de linha no eixo. Essa tarefa requer um novo tipo de integral, chamado integral de linha.
As integrais de linha têm muitas aplicações em engenharia e física. Eles também nos permitem fazer várias generalizações úteis do Teorema Fundamental do Cálculo. E eles estão intimamente ligados às propriedades dos campos vetoriais, como veremos.
Integrais de linha escalar
Uma integral de linha nos dá a capacidade de integrar funções multivariáveis e campos vetoriais em curvas arbitrárias em um plano ou no espaço. Existem dois tipos de integrais de linha: integrais de linha escalar e integrais de linha vetorial. Integrais de linha escalar são integrais de uma função escalar sobre uma curva em um plano ou no espaço. Integrais de linha vetorial são integrais de um campo vetorial sobre uma curva em um plano ou no espaço. Vamos examinar primeiro as integrais de linha escalar.
Uma integral de linha escalar é definida assim como uma integral de variável única é definida, exceto que para uma integral de linha escalar, o integrando é uma função de mais de uma variável e o domínio de integração é uma curva em um plano ou no espaço, em oposição a uma curva no\(x\) eixo.
Para uma integral de linha escalar, deixamos\(C\) ser uma curva suave em um plano ou no espaço e deixamos ff uma função com um domínio que inclui\(C\). Nós cortamos a curva em pequenos pedaços. Para cada peça, escolhemos o ponto\(P\) dessa peça e avaliamos\(f\) em\(P\). (Podemos fazer isso porque todos os pontos na curva estão no domínio de\(f\).) Multiplicamos\(f(P)\) pelo comprimento do arco da peça\(\Delta s\), adicionamos o produto\(f(P)\Delta s\) sobre todas as peças e, em seguida, deixamos o comprimento do arco das peças encolher até zero, estabelecendo um limite. O resultado é a integral da linha escalar da função sobre a curva.
Para uma descrição formal de uma integral de linha escalar,\(C\) seja uma curva suave no espaço dada pela parametrização\(\vecs r(t)=⟨x(t),y(t),z(t)⟩\),\(a≤t≤b\). \(f(x,y,z)\)Seja uma função com um domínio que inclui curva\(C\). Para definir a integral de linha da função\(f\) over\(C\), começamos quando a maioria das definições de uma integral começa: cortamos a curva em pequenos pedaços. Divida o intervalo do parâmetro\([a,b]\) em\(n\) subintervalos\([t_{i−l},t_i]\) de igual largura para\(1≤i≤n\), onde\(t_0=a\) e\(t_n=b\) (Figura\(\PageIndex{1}\)). \(t_{i}^*\)Seja um valor no\(i^{th}\) intervalo\([t_{i−l},t_i]\). Denote os pontos finais de\(\vecs r(t_0)\),\(\vecs r(t_1)\),...,\(\vecs r(t_n)\) por\(P_0\),...,\(P_n\). Os pontos P dividem a curva\(C\) em\(n\) pedaços\(C_1\)\(C_2\),,...\(C_n\),, com comprimentos\(\Delta s_1\)\(\Delta s_2\),,...\(\Delta s_n\), respectivamente. Vamos\(P_{i}^*\) indicar o ponto final de\(\vecs r(t_{i}^*)\) for\(1≤i≤n\). Agora, avaliamos a função\(f\) no ponto\(P_{i}^*\) de\(1≤i≤n\). Observe que\(P_{i}^*\) está em peça e\(C_1\), portanto,\(P_{i}^*\) está no domínio de\(f\). Multiplique\(f(P_{i}^*)\) pelo comprimento\(\Delta s_1\) de\(C_1\), o que dá a área da “folha” com base\(C_1\) e altura\(f(P_{i}^{*})\). Isso é semelhante ao uso de retângulos para aproximar a área em uma integral de variável única. Agora, formamos a soma\(\displaystyle \sum_{i=1}^{n} f(P_{i}^{*})\,\Delta s_i\).
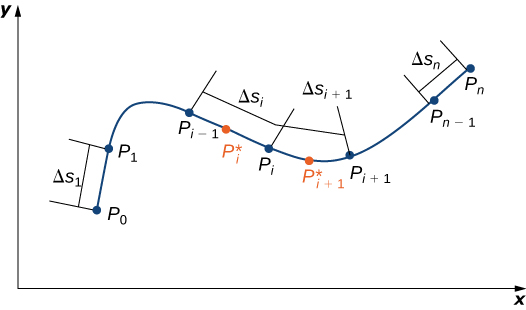
Observe a semelhança dessa soma versus uma soma de Riemann; na verdade, essa definição é uma generalização de uma soma de Riemann para curvas arbitrárias no espaço. Assim como com as somas e integrais de forma de Riemann\(\displaystyle \int_{a}^{b}g(x)\,dx\), definimos uma integral deixando a largura das partes da curva encolher a zero tomando um limite. O resultado é a integral da linha escalar de\(f\) along\(C\).
Você pode ter notado uma diferença entre essa definição de integral de linha escalar e integral de variável única. Nessa definição, os comprimentos dos\(\Delta s_1\) arcos,,...,\(\Delta s_n\) não são necessariamente os mesmos; na definição de uma integral de variável única, a curva no\(x\) eixo -é dividida em partes de igual comprimento.\(\Delta s_2\) Essa diferença não tem nenhum efeito no limite. À medida que reduzimos os comprimentos dos arcos para zero, seus valores se tornam próximos o suficiente para que qualquer pequena diferença se torne irrelevante.
\(f\)Seja uma função com um domínio que inclui a curva suave\(C\) que é parametrizada por\(\vecs r(t)=⟨x(t),y(t),z(t)⟩\),\(a≤t≤b\). A integral da linha escalar de\(f\) along\(C\) é
\[\int_C f(x,y,z) \,ds=\lim_{n\to\infty}\sum_{i=1}^{n}f(P_{i}^{*})\,\Delta s_i \label{eq12a} \]
se esse limite existir (\(t_i ^{*}\)e\(\Delta s_i\) forem definidos como nos parágrafos anteriores). Se\(C\) for uma curva plana, então\(C\) pode ser representada pelas equações paramétricas\(x=x(t)\)\(y=y(t)\),\(a≤t≤b\) e. Se\(C\) for suave e\(f(x,y)\) for uma função de duas variáveis, então a integral da linha escalar de\(f\) along\(C\) é definida da mesma forma como
\[\int_C f(x,y) \,ds=\lim_{n\to\infty}\sum_{i=1}^{n} f(P_{i}^{*})\,\Delta s_i, \label{eq13} \]
se esse limite existir.
Se\(f\) for uma função contínua em uma curva suave\(C\), então\(\displaystyle \int_C f \,ds\) sempre existe. Como\(\displaystyle \int_C f \,ds\) é definido como um limite das somas de Riemann, a continuidade de\(f\) é suficiente para garantir a existência do limite, assim como a integral\(\displaystyle \int_{a}^{b}g(x)\,dx\) existe se\(g\) for contínua\([a,b]\).
Antes de ver como calcular uma integral de linha, precisamos examinar a geometria capturada por essas integrais. Suponha que\(f(x,y)≥0\) para todos os pontos\((x,y)\) em uma curva plana suave\(C\). Imagine pegar a curva\(C\) e projetá-la “acima” na superfície definida por\(f(x,y)\), criando assim uma nova curva\(C′\) que está no gráfico de\(f(x,y)\) (Figura\(\PageIndex{2}\)). Agora, soltamos uma “folha” de\(C′\) baixo para o\(xy\) plano. A área desta folha é\(\displaystyle \int_C f(x,y)ds\). Se for\(f(x,y)≤0\) para alguns pontos em\(C\), então o valor de\(\displaystyle \int_C f(x,y)\,ds\) é a área acima do\(xy\) plano -menos a área abaixo do\(xy\) plano -. (Observe a semelhança com as integrais do formulário\(\displaystyle \int_{a}^{b}g(x)\,dx\).)
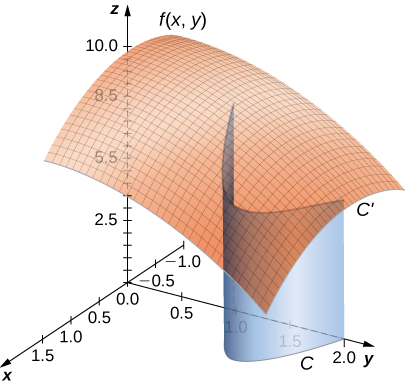
A partir dessa geometria, podemos ver que a integral da linha\(\displaystyle \int_C f(x,y)\,ds\) não depende da parametrização\(\vecs r(t)\) de\(C\). Desde que a curva seja percorrida exatamente uma vez pela parametrização, a área da folha formada pela função e pela curva é a mesma. Esse mesmo tipo de argumento geométrico pode ser estendido para mostrar que a integral da linha de uma função de três variáveis sobre uma curva no espaço não depende da parametrização da curva.
Encontre o valor da integral\(\displaystyle \int_C 2\,ds\), onde\(C\) está a metade superior do círculo unitário.
Solução
O integrando é\(f(x,y)=2\). A figura\(\PageIndex{3}\) mostra o gráfico\(f(x,y)=2\), a curva C e a folha formada por eles. Observe que essa folha tem a mesma área de um retângulo com largura\(\pi\) e comprimento\(2\). Portanto,\(\displaystyle \int_C 2 \,ds=2\pi\,\text{units}^2\).
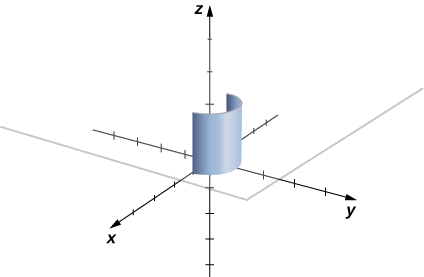
Para ver que\(\displaystyle \int_C 2 \,ds=2\pi\) usando a definição de integral de linha, deixamos\(\vecs r(t)\) ser uma parametrização de\(C\). Então,\(f(\vecs r(t_i))=2\) para qualquer número\(t_i\) no domínio de\(\vecs r\). Portanto,
\[\begin{align*} \int_C f \,ds &=\lim_{n\to\infty}\sum_{i=1}^{n} f(\vecs r(t_{i}^{*}))\,\Delta s_i \\[4pt] &=\lim_{n\to\infty}\sum_{i=1}^{n}2\,\Delta s_i \\[4pt] &=2\lim_{n\to\infty}\sum_{i=1}^{n}\,\Delta s_i \\[4pt] &=2(\text{length}\space \text{of}\space C) \\[4pt] &=2\pi \,\text{units}^2. \end{align*}\]
Encontre o valor de\(\displaystyle \int_C(x+y)\,ds\), onde\(C\) está a curva parametrizada por\(x=t\),\(y=t\),\(0≤t≤1\).
- Dica
-
Encontre a forma formada por\(C\) e o gráfico da função\(f(x,y)=x+y\).
- Responda
-
\(\sqrt{2}\)
Observe que em uma integral de linha escalar, a integração é feita com relação ao comprimento do arco\(s\), o que pode dificultar o cálculo de uma integral de linha escalar. Para facilitar os cálculos, podemos traduzir\(\displaystyle \int_C f\,ds\) em uma integral com uma variável de integração, ou seja,\(t\).
Que\(\vecs r(t)=⟨x(t),y(t),z(t)⟩\)\(a≤t≤b\) seja uma parametrização de\(C\). Como estamos assumindo que\(C\) é suave,\(\vecs r′(t)=⟨x′(t),y′(t),z′(t)⟩\) é contínuo para todos\(t\)\([a,b]\). Em particular,\(x′(t)\),\(y′(t)\), e\(z′(t)\) existem para todos\(t\)\([a,b]\). De acordo com a fórmula do comprimento do arco, temos
\[\text{length}(C_i)=\Delta s_i=\int_{t_{i−1}}^{t_i} ‖\vecs r′(t)‖\,dt. \nonumber \]
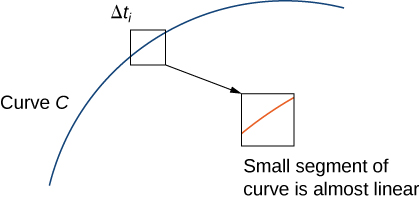
Se a largura\(\Delta t_i=t_i−t_{i−1}\) for pequena, então a função\(\displaystyle \int_{t_{i−1}}^{t_i} ‖\vecs r′(t)‖\,dt\,≈\,‖\vecs r′(t_i^*)‖\,\Delta t_i\),\(‖\vecs r′(t)‖\) é quase constante ao longo do intervalo\([t_{i−1},t_i]\). Portanto,
\[\int_{t_{i−1}}^{t_i} ‖\vecs r′(t)‖\,dt\,≈\,‖\vecs r′(t_{i}^{*})‖\,\Delta t_i, \label{approxLineIntEq1} \]
e nós temos
\[\sum_{i=1}^{n} f(\vecs r(t_i^*))\,\Delta s_i\approx\sum_{i=1}^{n} f(\vecs r(t_{i}^{*})) ‖\vecs r′(t_{i}^{*})‖\,\Delta t_i. \nonumber \]
Veja a Figura\(\PageIndex{4}\).
Note que
\[\lim_{n\to\infty}\sum_{i=1}^{n} f(\vecs r(t_i^*))‖\vecs r′(t_{i}^{*})‖\,\Delta t_i=\int_a^b f(\vecs r(t))‖\vecs r′(t)‖\,dt. \nonumber \]
Em outras palavras, à medida que as larguras dos intervalos\([t_{i−1},t_i]\) diminuem para zero, a soma\(\displaystyle \sum_{i=1}^{n} f(\vecs r(t_i^{*}))‖\vecs r′(t_{i}^{*})‖\,\Delta t_i\) converge para a integral\(\displaystyle \int_{a}^{b}f(\vecs r(t))‖\vecs r′(t)‖\,dt\). Portanto, temos o seguinte teorema.
\(f\)Seja uma função contínua com um domínio que inclui a curva suave\(C\) com parametrização\(\vecs r(t)\),\(a≤t≤b\). Então
\[\int_C f \,ds=\int_{a}^{b} f(\vecs r(t))‖\vecs r′(t)‖\,dt.\label{scalerLineInt1} \]
Embora tenhamos rotulado Equation\ ref {approxLineInteq1} como uma equação, ela é considerada com mais precisão uma aproximação porque podemos mostrar que o lado esquerdo da Equação\ ref {approxLineInteq1} se aproxima do lado direito como\(n\to\infty\). Em outras palavras, deixar as larguras das peças encolherem para zero torna a soma à direita arbitrariamente próxima da soma esquerda. Desde
\[‖\vecs r′(t)‖=\sqrt{{(x′(t))}^2+{(y′(t))}^2+{(z′(t))}^2}, \nonumber \]
obtemos o seguinte teorema, que usamos para calcular integrais de linha escalar.
\(f\)Seja uma função contínua com um domínio que inclui a curva suave\(C\) com parametrização\(\vecs r(t)=⟨x(t),y(t),z(t)⟩\),\(a≤t≤b\). Então
\[\int_C f(x,y,z) \,ds=\int_{a}^{b} f(\vecs r(t))\sqrt{({x′(t))}^2+{(y′(t))}^2+{(z′(t))}^2} \,dt. \nonumber \]
Da mesma forma,
\[\int_C f(x,y) \,ds=\int_{a}^{b}f(\vecs r(t))\sqrt{{(x′(t))}^2+{(y′(t))}^2} \,dt \nonumber \]
if\(C\) é uma curva plana e\(f\) é uma função de duas variáveis.
Observe que uma consequência desse teorema é a equação\(ds=‖\vecs r′(t)‖ \,dt\). Em outras palavras, a mudança no comprimento do arco pode ser vista como uma mudança no\(t\) domínio -, dimensionada pela magnitude do vetor\(\vecs r′(t)\).
Encontre o valor da integral\(\displaystyle \int_C(x^2+y^2+z) \,ds\), onde\(C\) é parte da hélice parametrizada por\(\vecs r(t)=⟨\cos t,\sin t,t⟩\),\(0≤t≤2\pi\).
Solução
Para calcular uma integral de linha escalar, começamos convertendo a variável de integração do comprimento do arco\(s\) para\(t\). Então, podemos usar a Equação\ ref {eq12a} para calcular a integral em relação\(t\) a. Note que
\[f(\vecs r(t))={\cos}^2 t+{\sin}^2 t+t=1+t \nonumber \]
e
\[\sqrt{{(x′(t))}^2+{(y′(t))}^2+{(z′(t))}^2} =\sqrt{{(−\sin(t))}^2+{\cos}^2(t)+1} =\sqrt{2}.\nonumber \]
Portanto,
\[\int_C(x^2+y^2+z) \,ds=\int_{0}^{2\pi} (1+t)\sqrt{2} \,dt. \nonumber \]
Observe que a Equação\ ref {eq12a} traduziu a integral original da linha difícil em uma integral de variável única gerenciável. Desde
\ [\ begin {align*}\ int_ {0} ^ {2\ pi} (1+t)\ sqrt {2}\, dt &= {\ left [\ sqrt {2} t+\ dfrac {\ sqrt {2} t^2} {2}\ direita]} _ {0} ^ {2\ pi}\\ [4pt]
&=2\ sqrt {2}\ pi+2\ sqrt {2} {\ pi} ^2,\ end {align*}\]
nós temos
\[\int_C(x^2+y^2+z) \,ds=2\sqrt{2}\pi+2\sqrt{2}{\pi}^2. \nonumber \]
Avalie\(\displaystyle \int_C(x^2+y^2+z)ds\), onde C é a curva com parametrização\(\vecs r(t)=⟨\sin(3t),\cos(3t)⟩\),\(0≤t≤\dfrac{\pi}{4}\).
- Dica
-
Use a versão de duas variáveis da definição integral da linha escalar (Equação\ ref {eq13}).
- Responda
-
\[\dfrac{1}{3}+\dfrac{\sqrt{2}}{6}+\dfrac{3\pi}{4} \nonumber \]
Encontre o valor da integral\(\displaystyle \int_C(x^2+y^2+z) \,ds\), onde\(C\) é parte da hélice parametrizada por\(\vecs r(t)=⟨\cos(2t),\sin(2t),2t⟩\),\(0≤t≤π\). Observe que essa função e a curva são as mesmas do exemplo anterior; a única diferença é que a curva foi reparametrizada para que o tempo seja duas vezes mais rápido.
Solução
Como no exemplo anterior, usamos a Equação\ ref {eq12a} para calcular a integral em relação\(t\) a. Observe que\(f(\vecs r(t))={\cos}^2(2t)+{\sin}^2(2t)+2t=2t+1\) e
\ [\ begin {align*}\ sqrt {{(x′( t)))} ^2+ {(y′( t))} ^2+ {(z′( t)))} ^2} &=\ sqrt {(−\ sin t+\ cos t+4)}\\ [4pt] &=22
\ end {align*}\]
então temos
\[\begin{align*} \int_C(x^2+y^2+z)ds &=2\sqrt{2}\int_{0}^{\pi}(1+2t)dt\\[4pt] &=2\sqrt{2}\Big[t+t^2\Big]_0^{\pi} \\[4pt] &=2\sqrt{2}(\pi+{\pi}^2). \end{align*}\]
Observe que isso está de acordo com a resposta do exemplo anterior. A alteração da parametrização não alterou o valor da integral da linha. Integrais de linha escalar são independentes da parametrização, desde que a curva seja percorrida exatamente uma vez pela parametrização.
Avalie a integral da linha\(\displaystyle \int_C(x^2+yz) \,ds\), onde\(C\) está a linha com parametrização\(\vecs r(t)=⟨2t,5t,−t⟩\),\(0≤t≤10\). Reparametrize C com parametrização\(s(t)=⟨4t,10t,−2t⟩\)\(0≤t≤5\), recalcule a integral\(\displaystyle \int_C(x^2+yz) \,ds\) da linha e observe que a mudança da parametrização não teve efeito sobre o valor da integral.
- Dica
-
Use a equação\ ref {eq12a}.
- Responda
-
As duas integrais de linha são iguais\(−\dfrac{1000\sqrt{30}}{3}\).
Agora que podemos calcular integrais de linha, podemos usá-los para calcular o comprimento do arco. Se\(f(x,y,z)=1\), então
\[\begin{align*} \int_C f(x,y,z) \,ds &=\lim_{n\to\infty} \sum_{i=1}^{n} f(t_{i}^{*}) \,\Delta s_i \\[4pt] &=\lim_{n\to\infty} \sum_{i=1}^{n} \,\Delta s_i \\[4pt] &=\lim_{n\to\infty} \text{length} (C)\\[4pt] &=\text{length} (C). \end{align*}\]
Portanto,\(\displaystyle \int_C 1 \,ds\) é o comprimento do arco de\(C\).
Um fio tem uma forma que pode ser modelada com a parametrização\(\vecs r(t)=⟨\cos t,\sin t,\frac{2}{3} t^{3/2}⟩\),\(0≤t≤4\pi\). Encontre o comprimento do fio.
Solução
O comprimento do fio é dado por\(\displaystyle \int_C 1 \,ds\), onde\(C\) está a curva com parametrização\(\vecs r\). Portanto,
\[\begin{align*} \text{The length of the wire} &=\int_C 1 \,ds \\[4pt] &=\int_{0}^{4\pi} ||\vecs r′(t)||\,dt \\[4pt] &=\int_{0}^{4\pi} \sqrt{(−\sin t)^2+\cos^2 t+t}dt \\[4pt] &=\int_{0}^{4\pi} \sqrt{1+t} dt \\[4pt] &=\left.\dfrac{2{(1+t)}^{\frac{3}{2}}}{3} \right|_{0}^{4\pi} \\[4pt] &=\frac{2}{3}\left((1+4\pi)^{3/2}−1\right). \end{align*}\]
Encontre o comprimento de um fio com parametrização\(\vecs r(t)=⟨3t+1,4−2t,5+2t⟩\),\(0≤t≤4\).
- Dica
-
Encontre a integral da linha de um sobre a curva correspondente.
- Responda
-
\(4\sqrt{17}\)
Integrais de linha vetorial
O segundo tipo de integrais de linha são integrais de linha vetorial, nas quais nos integramos ao longo de uma curva por meio de um campo vetorial. Por exemplo, deixe
\[\vecs F(x,y,z)=P(x,y,z)\,\hat{\mathbf i}+Q(x,y,z)\,\hat{\mathbf j}+R(x,y,z)\,\hat{\mathbf k} \nonumber \]
seja um campo vetorial contínuo\(ℝ^3\) que represente uma força sobre uma partícula, e\(C\) seja uma curva suave\(ℝ^3\) contida no domínio de\(\vecs F\). Como computaríamos o trabalho realizado ao\(\vecs F\) mover uma partícula\(C\)?
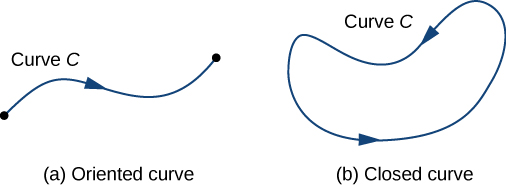
Para responder a essa pergunta, primeiro observe que uma partícula pode viajar em duas direções ao longo de uma curva: uma direção para frente e outra para trás. O trabalho realizado pelo campo vetorial depende da direção na qual a partícula está se movendo. Portanto, devemos especificar uma direção ao longo da curva\(C\); essa direção especificada é chamada de orientação de uma curva. A direção especificada é a direção positiva ao longo\(C\); a direção oposta é a direção negativa ao longo\(C\). Quando\(C\) recebe uma orientação,\(C\) é chamada de curva orientada (Figura\(\PageIndex{5}\)). O trabalho realizado na partícula depende da direção ao longo da curva na qual a partícula está se movendo.
Uma curva fechada é aquela para a qual existe uma parametrização\(\vecs r(t)\)\(a≤t≤b\), de forma que\(\vecs r(a)=\vecs r(b)\) a curva seja percorrida exatamente uma vez. Em outras palavras, a parametrização é individual no domínio\((a,b)\).
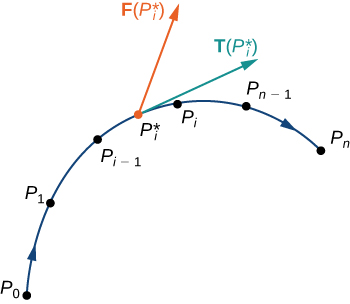
\(\vecs r(t)\)Seja uma parametrização de\(C\) para\(a≤t≤b\) que a curva seja percorrida exatamente uma vez pela partícula e a partícula se mova na direção positiva\(C\). Divida o intervalo do parâmetro\([a,b]\) em n subintervalos\([t_{i−1},t_i]\),\(0≤i≤n\), de igual largura. Denote os pontos finais de\(r(t_0)\),\(r(t_1)\),...,\(r(t_n)\) por\(P_0\),...,\(P_n\). Os pontos\(C\) são\(P_i\) divididos em n partes. Denote o comprimento da peça de\(P_{i−1}\) a\(P_i\) por\(\Delta s_i\). Para cada um\(i\), escolha um valor\(t_i^*\) no subintervalo\([t_{i−1},t_i]\). Então, o ponto final de\(\vecs r(t_i^*)\) é um ponto na parte\(C\) entre\(P_{i−1}\) e\(P_i\) (Figura\(\PageIndex{6}\)). Se\(\Delta s_i\) for pequeno, então, à medida que a partícula se move de\(P_{i−1}\) para\(P_i\) o outro\(C\), ela se move aproximadamente na direção de\(\vecs T(P_i)\), o vetor tangente unitário na extremidade de\(\vecs r(t_i^*)\). Vamos\(P_i^*\) indicar o ponto final de\(\vecs r(t_i^*)\). Então, o trabalho realizado pelo campo vetorial de força ao mover a partícula de\(P_{i−1}\) para\(P_i\) é\(\vecs F(P_i^*)·(\Delta s_i \vecs T(P_i^*))\), então o trabalho total realizado junto\(C\) é
\[\sum_{i=1}^n \vecs F(P_i^*)·(\Delta s_i \vecs T(P_i^*))=\sum_{i=1}^n \vecs F(P_i^*)·\vecs T(P_i^*)\,\Delta s_i. \nonumber \]
Deixar o comprimento do arco das peças\(C\) ficar arbitrariamente pequeno ao tomar um limite, como nos\(n\rightarrow \infty\) dá o trabalho realizado pelo campo ao mover a partícula\(C\). Portanto, o trabalho realizado ao\(\vecs{F}\) mover a partícula na direção positiva\(C\) é definido como
\[W=\int_C \vecs{F} \cdot \vecs{T}\,ds, \nonumber \]
o que nos dá o conceito de uma integral de linha vetorial.
A linha vetorial integral do campo vetorial\(\vecs{F}\) ao longo da curva suave orientada\(C\) é
\[\int_C \vecs{F} \cdot \vecs{T}\, ds=\lim_{n\to\infty} \sum_{i=1}^{n} \vecs{F}(P_i^*) \cdot \vecs{T}(P_i^*)\Delta s_i \nonumber \]
se esse limite existir.
Com integrais de linha escalar, nem a orientação nem a parametrização da curva são importantes. Desde que a curva seja percorrida exatamente uma vez pela parametrização, o valor da integral da linha permanece inalterado. Com integrais de linha vetorial, a orientação da curva é importante. Se pensarmos na integral da linha como um trabalho computacional, isso faz sentido: se você subir uma montanha, a força gravitacional da Terra faz um trabalho negativo em você. Se você descer a montanha exatamente pelo mesmo caminho, a força gravitacional da Terra fará um trabalho positivo em você. Em outras palavras, reverter o caminho muda o valor do trabalho de negativo para positivo nesse caso. Note que se\(C\) for uma curva orientada, então vamos\(−C\) representar a mesma curva, mas com orientação oposta.
Assim como acontece com integrais de linha escalar, é mais fácil calcular uma integral de linha vetorial se a expressarmos em termos da função de parametrização\(\vecs{r}\) e da variável\(t\). Para traduzir a integral\(\displaystyle \int_C \vecs{F} \cdot \vecs{T}ds\) em termos de\(t\), observe que o vetor tangente unitário\(\vecs{T}\) ao longo\(C\) é dado por\(\vecs{T}=\dfrac{\vecs{r}′(t)}{‖\vecs{r}′(t)‖}\) (assumindo\(‖\vecs{r}′(t)‖≠0\)). Uma vez que\(ds=‖\vecs r′(t)‖\,dt\), como vimos ao discutir integrais de linha escalar, temos
\[\vecs F·\vecs T\,ds=\vecs F(\vecs r(t))·\dfrac{\vecs r′(t)}{‖\vecs r′(t)‖}‖\vecs r′(t)‖dt=\vecs F(\vecs r(t))·\vecs r′(t)\,dt. \nonumber \]
Assim, temos a seguinte fórmula para calcular integrais de linha vetorial:
\[\int_C\vecs F·\vecs T\,ds=\int_a^b \vecs F(\vecs r(t))·\vecs r′(t)\,dt.\label{lineintformula} \]
Por causa da Equação\ ref {lineintformula}, geralmente usamos a notação\(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}\) para a integral da linha\(\displaystyle \int_C \vecs F·\vecs T\,ds\).
Se\(\vecs r(t)=⟨x(t),y(t),z(t)⟩\), então\(\dfrac{d\vecs{r}}{dt}\) denota vetor\(⟨x′(t),y′(t),z′(t)⟩\)\(d\vecs{r} = \vecs r'(t)\,dt\) e.
Encontre o valor da integral\(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}\), onde\(C\) está o semicírculo parametrizado por\(\vecs{r}(t)=⟨\cos t,\sin t⟩\),\(0≤t≤\pi\)\(\vecs F=⟨−y,x⟩\) e.
Solução
Podemos usar Equation\ ref {lineintformula} para converter a variável de integração de\(s\) para\(t\). Em seguida, temos
\[\vecs F(\vecs r(t))=⟨−\sin t,\cos t⟩ \; \text{and} \; \vecs r′(t)=⟨−\sin t,\cos t⟩ . \nonumber \]
Portanto,
\[\begin{align*} \int_C \vecs{F} \cdot d\vecs{r} &=\int_0^{\pi}⟨−\sin t,\cos t⟩·⟨−\sin t,\cos t⟩ \,dt \\[4pt] &=\int_0^{\pi} {\sin}^2 t+{\cos}^2 t \,dt \\[4pt] &=\int_0^{\pi}1 \,dt=\pi.\end{align*}\]
Veja a Figura\(\PageIndex{7}\).
Encontre o valor da integral\(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}\), onde\(C\) está o semicírculo parametrizado por\(\vecs r(t)=⟨\cos (t+π),\sin t⟩\),\(0≤t≤\pi\)\(\vecs F=⟨−y,x⟩\) e.
Solução
Observe que esse é o mesmo problema do Example\(\PageIndex{5}\), exceto que a orientação da curva foi percorrida. Neste exemplo, a parametrização começa em\(\vecs r(0)=⟨-1,0⟩\) e termina em\(\vecs r(\pi)=⟨1,0⟩\). Pela Equação\ ref {lineintformula},
\[\begin{align*} \int_C \vecs{F} \cdot d\vecs{r} &=\int_0^{\pi} ⟨−\sin t,\cos (t+\pi)⟩·⟨−\sin (t+\pi), \cos t⟩dt\\[4pt] &=\int_0^{\pi}⟨−\sin t,−\cos t⟩·⟨\sin t,\cos t⟩dt\\[4pt] &=\int_{0}^{π}(−{\sin}^2 t−{\cos}^2 t)dt \\[4pt] &=\int_{0}^{\pi}−1dt\\[4pt] &=−\pi. \end{align*}\]
Observe que esse é o negativo da resposta em Exemplo\(\PageIndex{5}\). Faz sentido que essa resposta seja negativa porque a orientação da curva vai contra o “fluxo” do campo vetorial.
\(C\)Seja uma curva orientada e\(-C\) denote a mesma curva, mas com a orientação invertida. Em seguida, os dois exemplos anteriores ilustram o seguinte fato:
\[\int_{-C} \vecs{F} \cdot d\vecs{r}=−\int_C\vecs{F} \cdot d\vecs{r}. \nonumber \]
Ou seja, reverter a orientação de uma curva altera o sinal de uma integral de linha.
\(\vecs F=x\,\hat{\mathbf i}+y \,\hat{\mathbf j}\)Seja um campo vetorial e\(C\) seja a curva com parametrização\(⟨t,t^2⟩\) para\(0≤t≤2\). O que é maior:\(\displaystyle \int_C\vecs F·\vecs T\,ds\) ou\(\displaystyle \int_{−C} \vecs F·\vecs T\,ds\)?
- Dica
-
Imagine seguir o caminho e computar o produto escalar\(\vecs F·\vecs T\) à medida que avança.
- Responda
-
\[\int_C \vecs F·\vecs T \,ds \nonumber \]
Outra notação padrão para integral\(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}\) é\(\displaystyle \int_C P\,dx+Q\,dy+R \,dz\). Nessa notação,\(P,\, Q\), e\(R\) são funções, e pensamos em vetores\(⟨dx,dy,dz⟩\).\(d\vecs{r}\) Para justificar essa convenção, lembre-se disso\(d\vecs{r}=\vecs T\,ds=\vecs r′(t) \,dt=\left\langle\dfrac{dx}{dt},\dfrac{dy}{dt},\dfrac{dz}{dt}\right\rangle\,dt\). Portanto,
\[\vecs{F} \cdot d\vecs{r}=⟨P,Q,R⟩·⟨dx,dy,dz⟩=P\,dx+Q\,dy+R\,dz. \nonumber \]
Se\(d\vecs{r}=⟨dx,dy,dz⟩\), então\(\dfrac{dr}{dt}=\left\langle\dfrac{dx}{dt},\dfrac{dy}{dt},\dfrac{dz}{dt}\right\rangle\), o que implica isso\(d\vecs{r}=\left\langle\dfrac{dx}{dt},\dfrac{dy}{dt},\dfrac{dz}{dt}\right\rangle\,dt\). Portanto
\[\begin{align} \int_C \vecs{F} \cdot d\vecs{r} &=\int_C P\,dx+Q\,dy+R\,dz \\[4pt] &=\int_a^b\left(P\big(\vecs r(t)\big)\dfrac{dx}{dt}+Q\big(\vecs r(t)\big)\dfrac{dy}{dt}+R\big(\vecs r(t)\big)\dfrac{dz}{dt}\right)\,dt. \label{eq14}\end{align} \]
Encontre o valor da integral\(\displaystyle \int_C z\,dx+x\,dy+y\,dz\), onde\(C\) está a curva parametrizada por\(\vecs r(t)=⟨t^2,\sqrt{t},t⟩\),\(1≤t≤4\).
Solução
Como em nossos exemplos anteriores, para calcular essa integral de linha, devemos realizar uma mudança de variáveis para escrever tudo em termos de\(t\). Nesse caso, a Equação\ ref {eq14} nos permite fazer essa alteração:
\[\begin{align*} \int_C z\,dx+x\,dy+y\,dz &=\int_1^4 \left(t(2t)+t^2\left(\frac{1}{2\sqrt{t}}\right)+\sqrt{t}\right)\,dt \\[4pt] &=\int_1^4\left(2t^2+\frac{t^{3/2}}{2}+\sqrt{t}\right)\,dt \\[4pt] &={\left[\dfrac{2t^3}{3}+\dfrac{t^{5/2}}{5}+\dfrac{2t^{3/2}}{3} \right]}_{t=1}^{t=4} \\[4pt] &=\dfrac{793}{15}.\end{align*}\]
Encontre o valor de\(\displaystyle \int_C 4x\,dx+z\,dy+4y^2\,dz\), onde\(C\) está a curva parametrizada por\(\vecs r(t)=⟨4\cos(2t),2\sin(2t),3⟩\),\(0≤t≤\dfrac{\pi}{4}\).
- Dica
-
Escreva a integral em termos de\(t\) uso da Equação\ ref {eq14}.
- Responda
-
\(−26\)
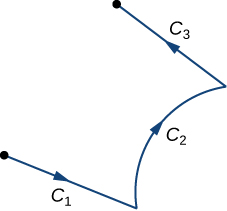
Aprendemos como integrar curvas orientadas suaves. Agora, suponha que\(C\) seja uma curva orientada que não seja suave, mas que possa ser escrita como a união de muitas curvas suaves. Nesse caso, dizemos que\(C\) é uma curva suave por partes. Para ser mais preciso, a curva\(C\) é suave por partes se\(C\) puder ser escrita como uma união de n curvas suaves\(C_1\),\(C_2\),...,\(C_n\) de forma que o ponto final de\(C_i\) seja o ponto inicial de\(C_{i+1}\) (Figura\(\PageIndex{8}\)). Quando as curvas\(C_i\) satisfazem a condição de que o ponto final de\(C_i\) é o ponto de partida de\(C_{i+1}\), escrevemos sua união como\(C_1+C_2+⋯+C_n\).
O próximo teorema resume várias propriedades principais das integrais de linhas vetoriais.
\(\vecs G\)Seja\(\vecs F\) e seja campos vetoriais contínuos com domínios que incluem a curva suave orientada\(C\). Então
- \(\displaystyle \int_C(\vecs F+\vecs G)·d\vecs{r}=\int_C \vecs{F} \cdot d\vecs{r}+\int_C \vecs G·d\vecs{r}\)
- \(\displaystyle \int_C k\vecs{F} \cdot d\vecs{r}=k\int_C \vecs{F} \cdot d\vecs{r}\), onde\(k\) é uma constante
- \(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}=\int_{−C}\vecs{F} \cdot d\vecs{r}\)
- Em vez disso, suponha que\(C\) seja uma curva suave por partes nos domínios de\(\vecs F\) e\(\vecs G\), onde\(C=C_1+C_2+⋯+C_n\) e\(C_1,C_2,…,C_n\) são curvas suaves, de forma que o ponto final de\(C_i\) seja o ponto inicial de\(C_{i+1}\). Então
\[\int_C \vecs F·d\vecs{r}=\int_{C_1} \vecs F·d\vecs{r}+\int_{C_2} \vecs F·d\vecs{r}+⋯+\int_{C_n} \vecs F·d\vecs{r}. \nonumber \]
Observe as semelhanças entre esses itens e as propriedades de integrais de variável única. As propriedades i. e ii. dizem que as integrais de linha são lineares, o que também vale para integrais de variável única. A propriedade iii. diz que inverter a orientação de uma curva altera o sinal da integral. Se pensarmos na integral como computar o trabalho realizado em uma partícula viajando\(C\), isso faz sentido. Se a partícula se mover para trás em vez de avançar, o valor do trabalho realizado tem o sinal oposto. Isso é análogo à equação\(\displaystyle \int_a^b f(x)\,dx=−\int_b^af(x)\,dx\). Finalmente, se\([a_1,a_2]\),\([a_2,a_3]\),...,\([a_{n−1},a_n]\) são intervalos, então
\[\int_{a_1}^{a_n}f(x) \,dx=\int_{a_1}^{a_2}f(x)\,dx+\int_{a_1}^{a_3}f(x)\,dx+⋯+\int_{a_{n−1}}^{a_n} f(x)\,dx, \nonumber \]
que é análoga à propriedade iv.
Encontre o valor de integral\(\displaystyle \int_C \vecs F·\vecs T \,ds\), onde\(C\) está o retângulo (orientado no sentido anti-horário) em um plano com vértices\((0,0)\)\((2,0)\),\((2,1)\),\((0,1)\), e e onde\(\vecs F=⟨x−2y,y−x⟩\) (Figura\(\PageIndex{9}\)).

Solução
Observe que a curva\(C\) é a união de seus quatro lados e cada lado é suave. Portanto,\(C\) é suave por partes. Vamos\(C_1\) representar o lado de\((0,0)\) para\((2,0)\), vamos\(C_2\) representar o lado de\((2,0)\) para\((2,1)\), vamos\(C_3\) representar o lado de\((2,1)\) para\((0,1)\) e vamos\(C_4\) representar o lado de\((0,1)\) para\((0,0)\) (Figura\(\PageIndex{9}\)). Então,
\[\int_C \vecs F·\vecs T \,dr=\int_{C_1} \vecs F·\vecs T \,dr+\int_{C_2} \vecs F·\vecs T \,dr+\int_{C_3} \vecs F·\vecs T \,dr+\int_{C_4} \vecs F·\vecs T \,dr. \nonumber \]
Queremos calcular cada uma das quatro integrais no lado direito usando a Equação\ ref {eq12a}. Antes de fazer isso, precisamos de uma parametrização de cada lado do retângulo. Aqui estão quatro parametrizações (observe que elas se deslocam\(C\) no sentido anti-horário):
\[\begin{align*} C_1&: ⟨t,0⟩,0≤t≤2\\[4pt] C_2&: ⟨2,t⟩, 0≤t≤1 \\[4pt] C_3&: ⟨2−t,1⟩, 0≤t≤2\\[4pt] C_4&: ⟨0,1−t⟩, 0≤t≤1. \end{align*}\]
Portanto,
\[\begin{align*} \int_{C_1} \vecs F·\vecs T \,dr &=\int_0^2 \vecs F(\vecs r(t))·\vecs r′(t) \,dt \\[4pt] &=\int_0^2 ⟨t−2(0),0−t⟩·⟨1,0⟩ \,dt=\int_0^2 t \,dt \\[4pt] &=\Big[\tfrac{t^2}{2}\Big]_0^2=2. \end{align*}\]
Observe que o valor dessa integral é positivo, o que não deve ser surpreendente. À medida que nos movemos ao longo\(C_1\) da curva da esquerda para a direita, nosso movimento flui na direção geral do próprio campo vetorial. Em qualquer ponto\(C_1\), o vetor tangente à curva e o vetor correspondente no campo formam um ângulo menor que 90°. Portanto, o vetor tangente e o vetor de força têm um produto escalar positivo o tempo todo\(C_1\), e a integral da linha terá valor positivo.
Os cálculos para as outras três integrais de linha são feitos da mesma forma:
\[\begin{align*} \int_{C_2} \vecs{F} \cdot d\vecs{r} &=\int_{0}^{1}⟨2−2t,t−2⟩·⟨0,1⟩ \,dt \\[4pt] &=\int_{0}^{1} (t−2) \,dt \\[4pt] &=\Big[\tfrac{t^2}{2}−2t\Big]_0^1=−\dfrac{3}{2}, \end{align*}\]
\[\begin{align*} \int_{C_3} \vecs F·\vecs T \,ds &=\int_0^2⟨(2−t)−2,1−(2−t)⟩·⟨−1,0⟩ \,dt \\[4pt] &=\int_0^2t \,dt=2, \end{align*}\]
e
\[\begin{align*} \int_{C_4} \vecs{F} \cdot d\vecs{r} &=\int_0^1⟨−2(1−t),1−t⟩·⟨0,−1⟩ \,dt \\[4pt] &=\int_0^1(t−1) \,dt \\[4pt] &=\Big[\tfrac{t^2}{2}−t\Big]_0^1=−\dfrac{1}{2}. \end{align*}\]
Assim, nós temos\(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}=2\).
Calcule a integral da linha\(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}\), onde\(\vecs F\) é o campo vetorial\(⟨y^2,2xy+1⟩\) e\(C\) é um triângulo com vértices\((0,0)\)\((4,0)\),\((0,5)\), e, orientado no sentido anti-horário.
- Dica
-
Escreva o triângulo como uma união de seus três lados e calcule três integrais de linha separados.
- Responda
-
0
Aplicações de integrais de linha
Integrais de linha escalar têm muitas aplicações. Eles podem ser usados para calcular o comprimento ou a massa de um fio, a área da superfície de uma folha de uma determinada altura ou o potencial elétrico de um fio carregado, dada uma densidade de carga linear. Integrais de linhas vetoriais são extremamente úteis em física. Eles podem ser usados para calcular o trabalho realizado em uma partícula à medida que ela se move através de um campo de força ou a taxa de fluxo de um fluido em uma curva. Aqui, calculamos a massa de um fio usando uma integral de linha escalar e o trabalho realizado por uma força usando uma integral de linha vetorial.
Suponha que um pedaço de arame seja modelado pela curva C no espaço. A massa por unidade de comprimento (a densidade linear) do fio é uma função contínua\(\rho(x,y,z)\). Podemos calcular a massa total do fio usando a integral da linha escalar\(\displaystyle \int_C \rho(x,y,z) \,ds\). A razão é que a massa é a densidade multiplicada pelo comprimento e, portanto, a densidade de um pequeno pedaço do fio pode ser aproximada\(\rho(x^*,y^*,z^*) \,\Delta s\)\((x^*,y^*,z^*)\) em algum ponto da peça. Deixar o comprimento das peças encolher até zero com um limite produz a integral da linha\(\displaystyle \int_C \rho(x,y,z) \,ds\).
Calcule a massa de uma mola na forma de uma curva parametrizada por\(⟨t,2\cos t,2\sin t⟩\)\(0≤t≤\dfrac{\pi}{2}\),, com uma função de densidade dada por\(\rho(x,y,z)=e^x+yz\) kg/m (Figura\(\PageIndex{10}\)).
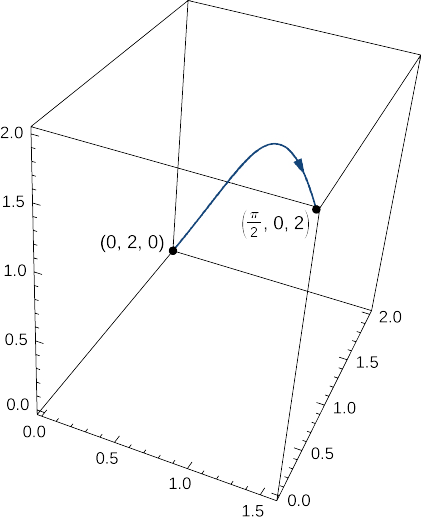
Solução
Para calcular a massa da mola, devemos encontrar o valor da integral da linha escalar\(\displaystyle \int_C(e^x+yz)\,ds\), onde\(C\) está a hélice dada. Para calcular essa integral, nós a escrevemos em termos de\(t\) uso da Equação\ ref {eq12a}:
\[\begin{align*} \int_C \left(e^x+yz\right) \,ds &=\int_0^{\tfrac{\pi}{2}} \left((e^t+4\cos t\sin t)\sqrt{1+(−2\cos t)^2+(2\sin t)^2}\right)\,dt\\[4pt] &=\int_0^{\tfrac{\pi}{2}}\left((e^t+4\cos t\sin t)\sqrt{5}\right) \,dt \\[4pt] &=\sqrt{5}\Big[e^t+2\sin^2 t\Big]_{t=0}^{t=\pi/2}\\[4pt] &=\sqrt{5}(e^{\pi/2}+1). \end{align*}\]
Portanto, a massa é de\(\sqrt{5}(e^{\pi/2}+1)\) kg.
Calcule a massa de uma mola na forma de uma hélice parametrizada por\(\vecs r(t)=⟨\cos t,\sin t,t⟩\)\(0≤t≤6\pi\),, com uma função de densidade dada por\(\rho (x,y,z)=x+y+z\) kg/m.
- Dica
-
Calcule a integral da linha\(\rho\) acima da curva com parametrização\(\vecs r\).
- Resposta
-
\(18\sqrt{2}{\pi}^2\)kg
Quando definimos pela primeira vez integrais de linha vetorial, usamos o conceito de trabalho para motivar a definição. Portanto, não é surpreendente que o cálculo do trabalho realizado por um campo vetorial representando uma força seja um uso padrão de integrais de linha vetorial. Lembre-se de que, se um objeto se move ao longo da curva\(C\) no campo de força\(\vecs F\), o trabalho necessário para mover o objeto é dado por\(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}\).
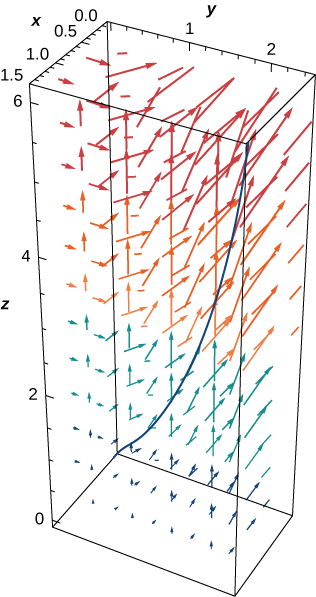
Quanto trabalho é necessário para mover um objeto no campo de força vetorial\(\vecs F=⟨yz,xy,xz⟩\) ao longo do caminho.\(\vecs r(t)=⟨t^2,t,t^4⟩,\, 0≤t≤1?\) Veja a Figura\(\PageIndex{11}\).
Solução
Vamos\(C\) denotar o caminho fornecido. Precisamos encontrar o valor de\(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}\). Para fazer isso, usamos Equation\ ref {lineintformula}:
\[\begin{align*}\int_C \vecs{F} \cdot d\vecs{r} &=\int_0^1(⟨t^5,t^3,t^6⟩·⟨2t,1,4t^3⟩) \,dt \\[4pt] &=\int_0^1(2t^6+t^3+4t^9) \,dt \\[4pt] &={\Big[\dfrac{2t^7}{7}+\dfrac{t^4}{4}+\dfrac{2t^{10}}{5}\Big]}_{t=0}^{t=1}=\dfrac{131}{140}\;\text{units of work}. \end{align*}\]
Fluxo
Encerramos esta seção discutindo dois conceitos-chave relacionados às integrais de linha: fluxo através de uma curva plana e circulação ao longo de uma curva plana. O fluxo é usado em aplicações para calcular o fluxo de fluido em uma curva, e o conceito de circulação é importante para caracterizar campos de gradiente conservadores em termos de integrais de linha. Ambos os conceitos são muito usados ao longo do restante deste capítulo. A ideia de fluxo é especialmente importante para o teorema de Green e em dimensões mais altas para o teorema de Stokes e o teorema da divergência.
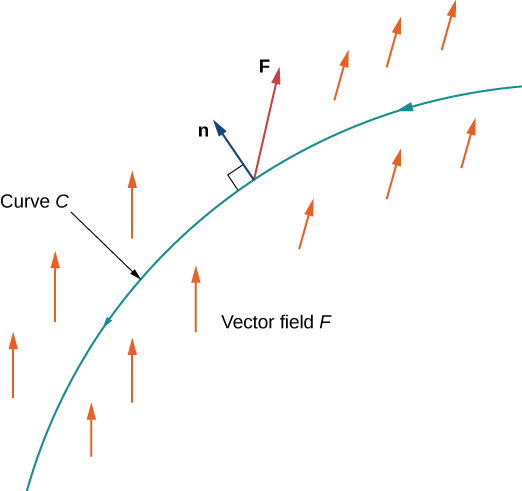
\(C\)Seja uma curva plana e\(\vecs F\) seja um campo vetorial no plano. Imagine\(C\) uma membrana através da qual o fluido flui, mas\(C\) não impede o fluxo do fluido. Em outras palavras,\(C\) é uma membrana idealizada invisível ao fluido. Suponha que\(\vecs F\) represente o campo de velocidade do fluido. Como podemos quantificar a taxa na qual o fluido está cruzando\(C\)?
Lembre-se de que a integral da linha de\(\vecs F\) along\(C\) é\(\displaystyle \int_C \vecs F·\vecs T \,ds\) —em outras palavras, a integral da linha é o produto escalar do campo vetorial com o vetor tangencial unitário em relação ao comprimento do arco. Se substituirmos o vetor tangencial unitário pelo vetor normal unitário\(\vecs N(t)\) e, em vez disso\(\int_C \vecs F·\vecs N \,ds\), computarmos a integral, determinaremos o fluxo transversal\(C\). Para ser mais preciso, a definição de integral\(\displaystyle \int_C \vecs F·\vecs N \,ds\) é a mesma de integral\(\displaystyle \int_C \vecs F·\vecs T \,ds\), exceto que a\(\vecs T\) soma de Riemann é substituída por\(\vecs N\). Portanto, o fluxo transversal\(C\) é definido como
\[\int_C \vecs F·\vecs N \,ds=\lim_{n\to\infty}\sum_{i=1}^{n} \vecs F(P_i^*)·\vecs N(P_i^*)\,\Delta s_i, \nonumber \]
onde\(P_i^*\) e\(\Delta s_i\) são definidos como eram para integral\(\displaystyle \int_C \vecs F·\vecs T \,ds\). Portanto, uma integral de fluxo é uma integral que é perpendicular a uma integral de linha vetorial, porque\(\vecs N\) e\(\vecs T\) são vetores perpendiculares.
Se\(\vecs F\) for um campo de velocidade de um fluido e\(C\) uma curva que representa uma membrana, então o fluxo\(\vecs F\) transversal\(C\) é a quantidade de fluido fluindo\(C\) por unidade de tempo, ou a taxa de fluxo.
Mais formalmente,\(C\) seja uma curva plana parametrizada por\(\vecs r(t)=⟨x(t),\,y(t)⟩\),\(a≤t≤b\). \(\vecs n(t)=⟨y′(t),\,−x′(t)⟩\)Seja o vetor que é normal\(C\) no ponto final de\(\vecs r(t)\) e aponta para a direita à medida que atravessamos\(C\) na direção positiva (Figura\(\PageIndex{12}\)). Então,\(\vecs N(t)=\dfrac{\vecs n(t)}{‖\vecs n(t)‖}\) é o vetor normal unitário\(C\) no ponto final\(\vecs r(t)\) desse ponto à direita à medida que atravessamos\(C\).
O fluxo de\(\vecs F\) cross\(C\) é integral de linha
\[\int_C \vecs F·\dfrac{\vecs n(t)}{‖\vecs n(t)‖} \,ds. \nonumber \]
Agora damos uma fórmula para calcular o fluxo em uma curva. Essa fórmula é análoga à fórmula usada para calcular uma integral de linha vetorial (veja Equação\ ref {lineintformula}).
\(\vecs F\)Seja um campo vetorial e\(C\) seja uma curva suave com parametrização\(r(t)=⟨x(t),y(t)⟩\),\(a≤t≤b\) .Let\(\vecs n(t)=⟨y′(t),−x′(t)⟩\). O fluxo de\(\vecs F\) cruzamento\(C\) é
\[\int_C \vecs F·\vecs N\,ds=\int_a^b\vecs F(\vecs r(t))·\vecs n(t) \,dt. \label{eq84} \]
Antes de derivar a fórmula, observe que
\[‖\vecs n(t)‖=‖⟨y′(t),−x′(t)⟩‖=\sqrt{{(y′(t))}^2+{(x′(t))}^2}=‖\vecs r′(t)‖. \nonumber \]
Portanto,
\[\begin{align*}\int_C \vecs F·\vecs N \,ds &=\int_C \vecs F·\dfrac{\vecs n(t)}{‖\vecs n(t)‖} \,ds \\[4pt] &=\int_a^b \vecs F·\dfrac{\vecs n(t)}{‖\vecs n(t)‖}‖\vecs r′(t)‖ \,dt \\[4pt] &=\int_a^b \vecs F(\vecs r(t))·\vecs n(t) \,dt. \end{align*}\]
\(\square\)
Calcule o fluxo de\(\vecs F=⟨2x,2y⟩\) um círculo unitário orientado no sentido anti-horário (Figura\(\PageIndex{13}\)).
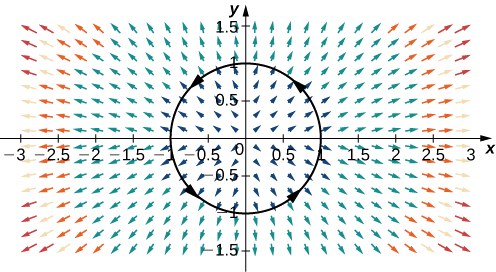
Solução
Para calcular o fluxo, primeiro precisamos de uma parametrização do círculo unitário. Podemos usar a parametrização padrão\(\vecs r(t)=⟨\cos t,\sin t⟩\),\(0≤t≤2\pi\). O vetor normal para um círculo unitário é\(⟨\cos t,\sin t⟩\). Portanto, o fluxo é
\[\begin{align*} \int_C \vecs F·\vecs N \,ds &=\int_0^{2\pi}⟨2\cos t,2\sin t⟩·⟨\cos t,\sin t⟩ \,dt\\[4pt] &=\int_0^{2\pi}(2{\cos}^2t+2{\sin}^2t) \,dt \\[4pt] &=2\int_0^{2\pi}({\cos}^2t+{\sin}^2t) \,dt \\[4pt] &=2\int_0^{2\pi} \,dt=4\pi.\end{align*}\]
Calcule o fluxo do\(\vecs F=⟨x+y,2y⟩\) segmento de linha de\((0,0)\) para\((2,3)\), onde a curva é orientada da esquerda para a direita.
- Dica
-
Use a Equação\ ref {eq84}.
- Resposta
-
\(3/2\)
\(\vecs F(x,y)=⟨P(x,y),Q(x,y)⟩\)Seja um campo vetorial bidimensional. Lembre-se de que integral às vezes\(\displaystyle \int_C \vecs F·\vecs T \,ds\) é escrito como\(\displaystyle \int_C P\,dx+Q\,dy\). Analogamente, o fluxo às vezes\(\displaystyle \int_C \vecs F·\vecs N \,ds\) é escrito na notação\(\displaystyle \int_C −Q\,dx+P\,dy\), porque o vetor normal unitário\(\vecs N\) é perpendicular à tangente unitária\(\vecs T\). Girar o vetor\(d\vecs{r}=⟨dx,dy⟩\) em 90° resulta em vetor\(⟨dy,−dx⟩\). Portanto, a integral da linha em Example\(\PageIndex{8}\) pode ser escrita como\(\displaystyle \int_C −2y\,dx+2x\,dy\).
Circulação
Agora que definimos o fluxo, podemos voltar nossa atenção para a circulação. A integral da linha do campo vetorial\(\vecs F\) ao longo de uma curva fechada orientada é chamada de circulação de\(\vecs F\) along\(C\). As integrais da linha de circulação têm sua própria notação:\(\oint_C \vecs F·\vecs T \,ds\). O círculo no símbolo integral indica que\(C\) é “circular” porque não tem pontos finais. \(\PageIndex{5}\)O exemplo mostra um cálculo da circulação.
Para ver de onde vem o termo circulação e o que ele mede, vamos\(\vecs v\) representar o campo de velocidade de um fluido e\(C\) ser uma curva fechada orientada. Em um ponto específico\(P\), quanto mais próxima a direção de\(\vecs v(P)\) estiver da direção de\(\vecs T(P)\), maior será o valor do produto escalar\(\vecs v(P)·\vecs T(P)\). O valor máximo de\(\vecs v(P)·\vecs T(P)\) ocorre quando os dois vetores estão apontando exatamente na mesma direção; o valor mínimo de\(\vecs v(P)·\vecs T(P)\) ocorre quando os dois vetores estão apontando em direções opostas. Assim, o valor da circulação\(\oint_C \vecs v·\vecs T \,ds\) mede a tendência do fluido de se mover na direção de\(C\).
\(\vecs F=⟨−y,\,x⟩\)Seja o campo vetorial do Example\(\PageIndex{3}\) e\(C\) representemos o círculo unitário orientado no sentido anti-horário. Calcule a circulação de um\(\vecs F\) longo\(C\).
Solução
Usamos a parametrização padrão do círculo unitário:\(\vecs r(t)=⟨\cos t,\sin t⟩\),\(0≤t≤2\pi\). Então,\(\vecs F(\vecs r(t))=⟨−\sin t,\cos t⟩\)\(\vecs r′(t)=⟨−\sin t,\cos t⟩\) e. Portanto, a circulação de\(\vecs F\) along\(C\) é
\[\begin{align*} \oint_C \vecs F·\vecs T \,ds &=\int_0^{2\pi}⟨−\sin t,\cos t⟩·⟨−\sin t,\cos t⟩ \,dt \\[4pt] &=\int_0^{2\pi} ({\sin}^2 t+{\cos}^2 t) \,dt \\[4pt] &=\int_0^{2\pi} \,dt=2\pi \;\text{units of work}. \end{align*}\]
Observe que a circulação é positiva. A razão para isso é que a orientação de\(C\) “flui” com a direção de\(\vecs F\). Em qualquer ponto ao longo do círculo, o vetor tangente e o vetor de\(\vecs F\) formam um ângulo menor que 90° e, portanto, o produto escalar correspondente é positivo.
No exemplo\(\PageIndex{12}\), e se tivéssemos orientado o círculo unitário no sentido horário? Nós denotamos o círculo unitário orientado no sentido horário por\(−C\). Então
\[\oint_{−C} \vecs F·\vecs T \,ds=−\oint_C \vecs F·\vecs T \,ds=−2\pi \;\text{units of work}. \nonumber \]
Observe que a circulação é negativa nesse caso. A razão para isso é que a orientação da curva flui contra a direção de\(\vecs F\).
Calcule a circulação\(\vecs F(x,y)=⟨−\dfrac{y}{x^2+y^2},\,\dfrac{x}{x^2+y^2}⟩\) ao longo de um círculo unitário orientado no sentido anti-horário.
- Dica
-
Use a Equação\ ref {eq84}.
- Resposta
-
\(2\pi\)unidades de trabalho
Calcule o trabalho realizado em uma partícula que atravessa um círculo\(C\) de raio 2 centrado na origem, orientado no sentido anti-horário, por campo\(\vecs F(x,y)=⟨−2,\,y⟩\). Suponha que a partícula comece seu movimento em\((1,\,0)\).
Solução
O trabalho realizado pela\(\vecs F\) partícula é a circulação de\(\vecs F\) ao longo\(C\):\(\oint_C \vecs F·\vecs T \,ds\). Usamos a parametrização\(\vecs r(t)=⟨2\cos t,\,2\sin t⟩\),\(0≤t≤2\pi\) para\(C\). Então,\(\vecs r′(t)=⟨−2\sin t,\,2\cos t⟩\)\(\vecs F(\vecs r(t))=⟨−2,\,2\sin t⟩\) e. Portanto, a circulação de\(\vecs F\) along\(C\) é
\[\begin{align*} \oint_C \vecs F·\vecs T \,ds &=\int_0^{2\pi} ⟨−2,2\sin t⟩·⟨−2\sin t,2\cos t⟩ \,dt\\[4pt] &=\int_0^{2\pi} (4\sin t+4\sin t\cos t) \,dt\\[4pt] &={\Big[−4\cos t+4{\sin}^2 t\Big]}_0^{2\pi}\\[4pt] &=\left(−4\cos(2\pi)+2{\sin}^2(2\pi)\right)−\left(−4\cos(0)+4{\sin}^2(0)\right)\\[4pt] &=−4+4=0\;\text{units of work}.\end{align*}\]
O campo de força não faz nenhum trabalho na partícula.
Observe que a circulação de\(\vecs F\) along\(C\) é zero. Além disso, observe que, uma vez que\(\vecs F\) é o gradiente de\(f(x,y)=−2x+\dfrac{y^2}{2}\),\(\vecs F\) é conservador. Provamos em uma seção posterior que, sob certas condições gerais, a circulação de um campo vetorial conservador ao longo de uma curva fechada é zero.
Calcule o trabalho realizado por campo\(\vecs F(x,y)=⟨2x,\,3y⟩\) em uma partícula que atravessa o círculo unitário. Suponha que a partícula comece seu movimento em\((−1,\,0)\).
- Dica
-
Use a Equação\ ref {eq84}.
- Resposta
-
\(0\)unidades de trabalho
Conceitos-chave
- Integrais de linha generalizam a noção de integral de variável única para dimensões mais altas. O domínio de integração em uma integral de variável única é um segmento de linha ao longo do\(x\) eixo -, mas o domínio de integração em uma integral de linha é uma curva em um plano ou no espaço.
- Se\(C\) for uma curva, então o comprimento de\(C\) é\(\displaystyle \int_C \,ds\).
- Existem dois tipos de integrais de linha: integrais de linha escalar e integrais de linha vetorial. Integrais de linha escalar podem ser usadas para calcular a massa de um fio; integrais de linha vetorial podem ser usadas para calcular o trabalho realizado em uma partícula viajando por um campo.
- Integrais de linha escalar podem ser calculadas usando a Equação\ ref {eq12a}; integrais de linha vetorial podem ser calculadas usando Equation\ ref {lineintformula}.
- Dois conceitos-chave expressos em termos de integrais de linha são fluxo e circulação. O fluxo mede a taxa com que um campo cruza uma determinada linha; a circulação mede a tendência de um campo se mover na mesma direção de uma determinada curva fechada.
Equações-chave
- Calculando uma integral de linha escalar
\(\displaystyle \int_C f(x,y,z) \,ds=\int_a^bf(\vecs r(t))\sqrt{{(x′(t))}^2+{(y′(t))}^2+{(z′(t))}^2} \,dt\) - Calculando uma integral de linha vetorial
\(\displaystyle \int_C \vecs F·d\vecs{r}=\int_C \vecs F·\vecs T \,ds=\int_a^b\vecs F(\vecs r(t))·\vecs r′(t)\,dt\)
ou
\(\displaystyle \int_C P\,dx+Q\,dy+R\,dz=\int_a^b \left(P\big(\vecs r(t)\big)\dfrac{dx}{dt}+Q\big(\vecs r(t)\big)\dfrac{dy}{dt}+R\big(\vecs r(t)\big)\dfrac{dz}{dt}\right) \,dt\) - Calculando o fluxo
\(\displaystyle \int_C \vecs F·\dfrac{\vecs n(t)}{‖\vecs n(t)‖}\,ds=\int_a^b \vecs F(\vecs r(t))·\vecs n(t) \,dt\)
Glossário
- circulação
- a tendência de um fluido se mover na direção da curva\(C\). Se\(C\) for uma curva fechada, então a circulação de\(\vecs F\) along\(C\) é integral de linha\(∫_C \vecs F·\vecs T \,ds\), o que também denotamos\(∮_C\vecs F·\vecs T \,ds\).
- curva fechada
- uma curva para a qual existe uma parametrização\(\vecs r(t), a≤t≤b\), tal que\(\vecs r(a)=\vecs r(b)\), e a curva é percorrida exatamente uma vez
- fluem
- a taxa de um fluido fluindo através de uma curva em um campo vetorial; o fluxo do campo vetorial\(\vecs F\) através da curva plana\(C\) é integral da linha\(∫_C \vecs F·\frac{\vecs n(t)}{‖\vecs n(t)‖} \,ds\)
- linha integral
- a integral de uma função ao longo de uma curva em um plano ou no espaço
- orientação de uma curva
- a orientação de uma curva\(C\) é uma direção especificada de\(C\)
- curva suave por partes
- uma curva orientada que não é suave, mas pode ser escrita como a união de muitas curvas suaves
- integral de linha escalar
- a integral da linha escalar de uma função\(f\) ao longo de uma curva em\(C\) relação ao comprimento do arco é a integral\(\displaystyle \int_C f\,ds\), é a integral de uma função escalar\(f\) ao longo de uma curva em um plano ou no espaço; tal integral é definida em termos de uma soma de Riemann, assim como uma integral de variável única
- integral de linha vetorial
- a integral da linha vetorial do campo vetorial\(\vecs F\) ao longo da curva\(C\) é a integral do produto escalar de\(\vecs F\) com vetor tangente unitário\(\vecs T\) de\(C\) em relação ao comprimento do arco,\(∫_C \vecs F·\vecs T\, ds\); tal integral é definida em termos de uma soma de Riemann, semelhante a uma integral de variável única


