Skip to main content
Global

16.1E: Exercícios para a Seção 16.1

  1. Last updated
  2. Save as PDF
  • Page ID
    188584

    • Edwin “Jed” Herman & Gilbert Strang
    • OpenStax
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    1. O domínio do campo vetorial\(\vecs{F}=\vecs{F}(x,y)\) é um conjunto de pontos\((x,y)\) em um plano, e o alcance de\(\vecs F\) é um conjunto do que no plano?

    Responda
    Vetores

    Para os exercícios 2 a 4, determine se a afirmação é verdadeira ou falsa.

    2. \(\vecs{F}=⟨3x^2,1⟩\)O campo vetorial é um campo de gradiente para\(ϕ_1(x,y)=x^3+y\) e\(ϕ_2(x,y)=y+x^3+100.\)

    3. \(\vecs{F}=\dfrac{⟨y,x⟩}{\sqrt{x^2+y^2}}\)O campo vetorial é constante em direção e magnitude em um círculo unitário.

    Responda
    Falso

    4. \(\vecs{F}=\dfrac{⟨y,x⟩}{\sqrt{x^2+y^2}}\)O campo vetorial não é um campo radial nem um campo de rotação.

    Para os exercícios 5 a 13, descreva cada campo vetorial desenhando alguns de seus vetores.

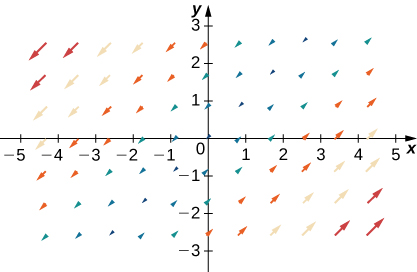
    5. [T]\(\vecs{F}(x,y)=x\,\hat{\mathbf i}+y\,\hat{\mathbf j}\)

    Responda

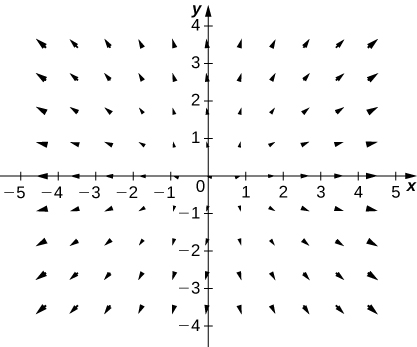
    clipboard_ed15464787a3931076aab028ddc5b12d7.png

    6. [T]\(\vecs{F}(x,y)=−y\,\hat{\mathbf i}+x\,\hat{\mathbf j}\)

    7. [T]\(\vecs{F}(x,y)=x\,\hat{\mathbf i}−y\,\hat{\mathbf j}\)

    Responda

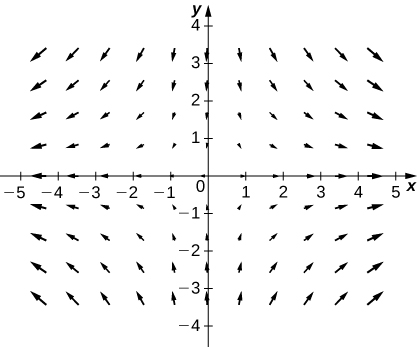
    clipboard_ec0907b086839ad5c262019c65af7add7.png

    8. [T]\(\vecs{F}(x,y)=\,\hat{\mathbf i}+\,\hat{\mathbf j}\)

    9. [T]\(\vecs{F}(x,y)=2x\,\hat{\mathbf i}+3y\,\hat{\mathbf j}\)

    Responda

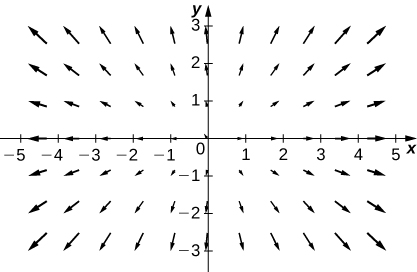
    clipboard_ef331d6cd76b60efd3886d0df3b197637.png

    10. [T] \(\vecs{F}(x,y)=3\,\hat{\mathbf i}+x\,\hat{\mathbf j}\)

    11. [T]\(\vecs{F}(x,y)=y\,\hat{\mathbf i}+\sin x\,\hat{\mathbf j}\)

    Responda

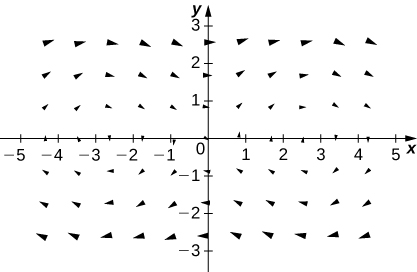
    clipboard_e90f52faea8df656c5e8538475924d4a3.png

    12. [T]\(\vecs F(x,y,z)=x\,\hat{\mathbf i}+y\,\hat{\mathbf j}+z\,\hat{\mathbf k}\)

    13. [T]\(\vecs F(x,y,z)=2x\,\hat{\mathbf i}−2y\,\hat{\mathbf j}−2z\,\hat{\mathbf k}\)

    Responda

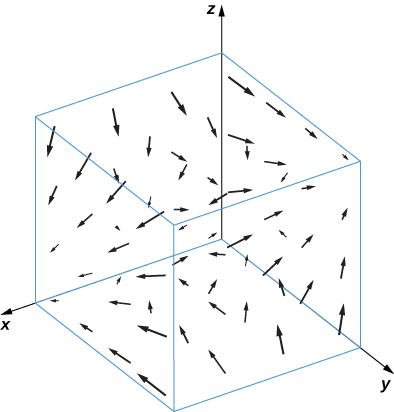
    clipboard_e1eb143e779ce49ea2a01af87d7a3548d.png

    14. [T]\(\vecs F(x,y,z)=yz\,\hat{\mathbf i}−xz\,\hat{\mathbf j}\)

    Para os exercícios 15 a 20, encontre o campo vetorial de gradiente de cada função\(f\).

    15. \(f(x,y)=x\sin y+\cos y\)

    Responda
    \(\vecs{F}(x,y)=\sin(y)\,\hat{\mathbf i}+(x\cos y−\sin y)\,\hat{\mathbf j}\)

    16. \(f(x,y,z)=ze^{−xy}\)

    17. \(f(x,y,z)=x^2y+xy+y^2z\)

    Responda
    \(\vecs F(x,y,z)=(2xy+y)\,\hat{\mathbf i}+(x^2+x+2yz)\,\hat{\mathbf j}+y^2\,\hat{\mathbf k}\)

    18. \(f(x,y)=x^2\sin(5y)\)

    19. \(f(x,y)=\ln(1+x^2+2y^2)\)

    Responda
    \(\vecs{F}(x,y)=\dfrac{2x}{1+x^2+2y^2}\,\hat{\mathbf i}+\dfrac{4y}{1+x^2+2y^2}\,\hat{\mathbf j}\)

    20. \(f(x,y,z)=x\cos\left(\frac{y}{z}\right)\)

    21. O que é um campo vetorial\(\vecs{F}(x,y)\) com um valor de comprimento unitário e aponta para\((1,0)\)?\((x,y)\)

    Responda
    \(\vecs{F}(x,y)=\dfrac{(1−x)\,\hat{\mathbf i}−y\,\hat{\mathbf j}}{\sqrt{(1−x)^2+y^2}}\)

    Para os exercícios 22 a 24, escreva fórmulas para os campos vetoriais com as propriedades fornecidas.

    22. Todos os vetores são paralelos ao\(x\) eixo -e todos os vetores em uma linha vertical têm a mesma magnitude.

    23. Todos os vetores apontam para a origem e têm comprimento constante.

    Responda
    \(\vecs{F}(x,y)=\dfrac{(y\,\hat{\mathbf i}−x\,\hat{\mathbf j})}{\sqrt{x^2+y^2}}\)

    24. Todos os vetores são de comprimento unitário e são perpendiculares ao vetor de posição nesse ponto.

    25. Dê uma fórmula\(\vecs{F}(x,y)=M(x,y)\,\hat{\mathbf i}+N(x,y)\,\hat{\mathbf j}\) para o campo vetorial em um plano que tenha as propriedades que\(\vecs{F}=\vecs 0\) em\((0,0)\) e que em qualquer outro ponto\((a,b), \vecs F\) é tangente ao círculo\(x^2+y^2=a^2+b^2\) e aponta no sentido horário com magnitude\(\|\vecs F\|=\sqrt{a^2+b^2}\).

    Responda
    \(\vecs{F}(x,y)=y\,\hat{\mathbf i}−x\,\hat{\mathbf j}\)

    26. O campo vetorial é\(\vecs{F}(x,y)=(P(x,y),Q(x,y))=(\sin x+y)\,\hat{\mathbf i}+(\cos y+x)\,\hat{\mathbf j}\) um campo de gradiente?

    27. Encontre uma fórmula para o campo vetorial,\(\vecs{F}(x,y)=M(x,y)\,\hat{\mathbf i}+N(x,y)\,\hat{\mathbf j}\) considerando o fato de que, para todos os\(\vecs F\) pontos\((x,y)\), aponta para a origem\(\|\vecs F\|=\dfrac{10}{x^2+y^2}\) e.

    Responda
    \(\vecs{F}(x,y)=\dfrac{−10}{(x^2+y^2)^{3/2}}(x\,\hat{\mathbf i}+y\,\hat{\mathbf j})\)

    Para os exercícios 28 a 29, suponha que um campo elétrico no\(xy\) plano -causado por uma linha infinita de carga ao longo do\(x\) eixo -seja um campo de gradiente com função potencial\(V(x,y)=c\ln\left(\frac{r_0}{\sqrt{x^2+y^2}}\right)\), onde\(c>0\) é uma constante e\(r_0\) é uma distância de referência na qual o o potencial é considerado zero.

    28. Encontre os componentes do campo elétrico nas\(y\) direções\(x\) - e -, onde\(\vecs E(x,y)=−\vecs ∇V(x,y).\)

    29. Mostre que o campo elétrico em um ponto do\(xy\) plano -é direcionado para fora da origem e tem magnitude\(\|\vecs E\|=\dfrac{c}{r}\), onde\(r=\sqrt{x^2+y^2}\).

    Responda
    \(\|\vecs E\|=\dfrac{c}{|r|^2}r=\dfrac{c}{|r|}\dfrac{r}{|r|}\)

    Uma linha de fluxo (ou linha de fluxo) de um campo vetorial\(\vecs F\) é uma curva\(\vecs r(t)\) como essa\(d\vecs{r}/dt=\vecs F(\vecs r(t))\). Se\(\vecs F\) representa o campo de velocidade de uma partícula em movimento, então as linhas de fluxo são caminhos percorridos pela partícula. Portanto, as linhas de fluxo são tangentes ao campo vetorial.

    Para os exercícios 30 e 31, mostre que a curva dada\(\vecs c(t)\) é uma linha de fluxo do campo vetorial de velocidade fornecido\(\vecs F(x,y,z)\).

    30. \(\vecs c(t)=⟨ e^{2t},\ln|t|,\frac{1}{t} ⟩,\,t≠0;\quad \vecs F(x,y,z)=⟨2x,z,−z^2⟩\)

    31. \(\vecs c(t)=⟨ \sin t,\cos t,e^t⟩;\quad \vecs F(x,y,z) =〈y,−x,z〉\)

    Responda
    \(\vecs c′(t)=⟨ \cos t,−\sin t,e^{−t}⟩=\vecs F(\vecs c(t))\)

    Para os exercícios 32 a 34\(\vecs{F}=x\,\hat{\mathbf i}+y\,\hat{\mathbf j}\), deixe\(\vecs G=−y\,\hat{\mathbf i}+x\,\hat{\mathbf j}\),\(\vecs H=x\,\hat{\mathbf i}−y\,\hat{\mathbf j}\) e. Combine\(\vecs F\)\(\vecs G\),, e\(\vecs H\) com seus gráficos.

    32.

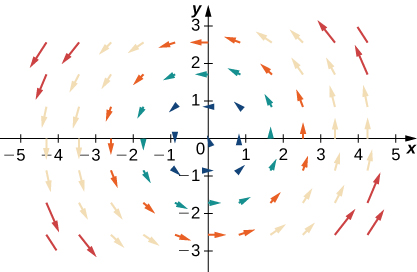
    clipboard_ed92420bb9a2a79bf7e0737bdf653eee9.png

    33.

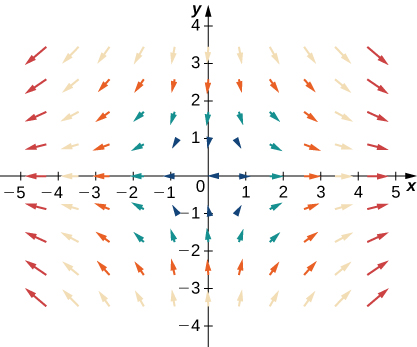
    clipboard_eb5a596effc35031ee81697fe6f857207.png

    Responda
    \(\vecs H\)

    34.

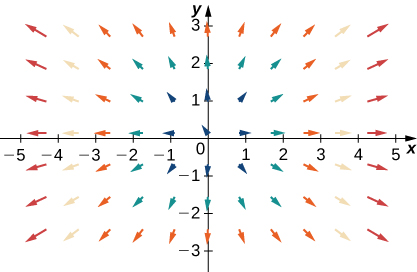
    clipboard_ec5488ed5d7cc242a516fe39456391eaa.png

    Para os exercícios 35 a 38\(\vecs{F}=x\,\hat{\mathbf i}+y\,\hat{\mathbf j}\), deixe\(\vecs G=−y\,\hat{\mathbf i}+x\,\hat{\mathbf j}\),\(\vecs H=−x\,\hat{\mathbf i}+y\,\hat{\mathbf j}\) e. Combine os campos vetoriais com seus gráficos em (I) − (IV).

    1. \(\vecs F+\vecs G\)
    2. \(\vecs F+\vecs H\)
    3. \(\vecs G+\vecs H\)
    4. \(−\vecs F+\vecs G\)

    35.

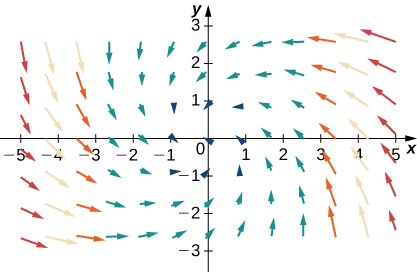
    clipboard_eddbf3f9c662003d8e6e632e520b53134.png

    Responda
    d.\(−\vecs F+\vecs G\)

    36.

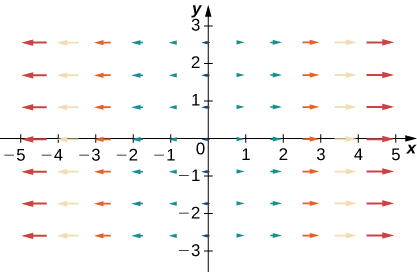
    clipboard_e75a38125572207465d05c29854873433.png

    37.

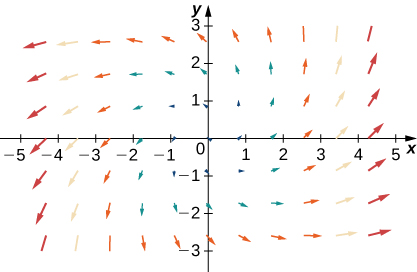
    clipboard_e0404b6b216ac76764fdd9b22d61f3e46.png

    Responda
    uma.\(\vecs F+\vecs G\)

    38.

    clipboard_e3db08e2f2eec3aeb28cd303fd451bb14.png