16.1: Campos vetoriais
- Page ID
- 188568
- Reconheça um campo vetorial em um plano ou no espaço.
- Esboce um campo vetorial a partir de uma determinada equação.
- Identifique um campo conservador e sua função potencial associada.
Os campos vetoriais são uma ferramenta importante para descrever muitos conceitos físicos, como gravitação e eletromagnetismo, que afetam o comportamento dos objetos em uma grande região de um plano ou do espaço. Eles também são úteis para lidar com comportamentos em grande escala, como tempestades atmosféricas ou correntes oceânicas de alto mar. Nesta seção, examinamos as definições básicas e os gráficos dos campos vetoriais para que possamos estudá-los com mais detalhes no restante deste capítulo.
Exemplos de campos vetoriais
Como podemos modelar a força gravitacional exercida por vários objetos astronômicos? Como podemos modelar a velocidade das partículas de água na superfície de um rio? A figura\(\PageIndex{1}\) fornece representações visuais de tais fenômenos.
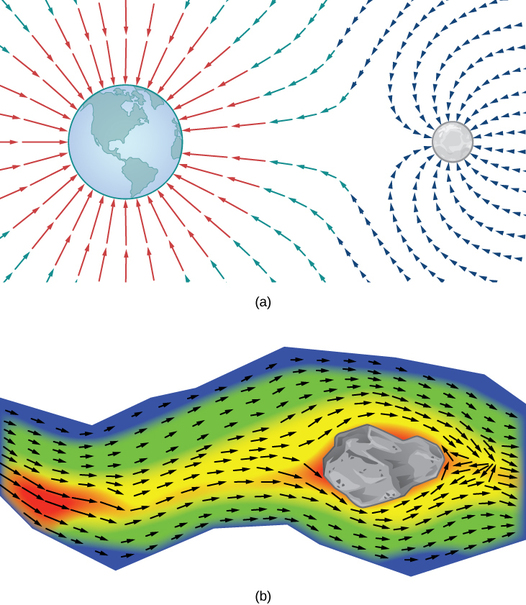
\(\PageIndex{1a}\)A figura mostra um campo gravitacional exercido por dois objetos astronômicos, como uma estrela e um planeta ou um planeta e uma lua. Em qualquer ponto da figura, o vetor associado a um ponto fornece a força gravitacional líquida exercida pelos dois objetos em um objeto de massa unitária. Os vetores de maior magnitude na figura são os vetores mais próximos do objeto maior. O objeto maior tem maior massa, então ele exerce uma força gravitacional de maior magnitude do que o objeto menor.
A figura\(\PageIndex{1b}\) mostra a velocidade de um rio em pontos de sua superfície. O vetor associado a um determinado ponto na superfície do rio fornece a velocidade da água nesse ponto. Como os vetores à esquerda da figura são pequenos em magnitude, a água está fluindo lentamente nessa parte da superfície. À medida que a água se move da esquerda para a direita, ela encontra algumas corredeiras ao redor de uma rocha. A velocidade da água aumenta e um redemoinho ocorre em parte das corredeiras.
Cada figura ilustra um exemplo de um campo vetorial. Intuitivamente, um campo vetorial é um mapa de vetores. Nesta seção, estudamos campos vetoriais em\(ℝ^2\)\(ℝ^3\) e.
- Um campo vetorial\(\vecs{F}\) em\(ℝ^2\) é uma atribuição de um vetor bidimensional\(\vecs{F}(x,y)\) a cada ponto\((x,y)\) de um subconjunto\(D\) de\(ℝ^2\). O subconjunto\(D\) é o domínio do campo vetorial.
- Um campo vetorial\(\vecs{F}\) em\(ℝ^3\) é uma atribuição de um vetor tridimensional\(\vecs{F}(x,y,z)\) a cada ponto\((x,y,z)\) de um subconjunto\(D\) de\(ℝ^3\). O subconjunto\(D\) é o domínio do campo vetorial.
Campos vetoriais em\(ℝ^2\)
Um campo vetorial em\(ℝ^2\) pode ser representado de duas formas equivalentes. A primeira maneira é usar um vetor com componentes que são funções com duas variáveis:
\[\vecs{F}(x,y)=⟨P(x,y),Q(x,y)⟩ \nonumber \]
A segunda maneira é usar os vetores unitários padrão:
\[\vecs{F}(x,y)=P(x,y) \,\hat{\mathbf i}+Q(x,y) \,\hat{\mathbf j}. \nonumber \]
Diz-se que um campo vetorial é contínuo se suas funções componentes forem contínuas.
\(\vecs{F} (x,y)=(2y^2+x−4)\,\hat{\mathbf i}+\cos(x)\,\hat{\mathbf j}\)Seja um campo vetorial em\(ℝ^2\). Observe que esse é um exemplo de campo vetorial contínuo, já que ambas as funções dos componentes são contínuas. Qual vetor está associado ao ponto\((0,−1)\)?
Solução
Substitua os valores dos pontos por\(x\) e\(y\):
\[\begin{align*} \vecs{F} (0,-1) &=(2{(−1)}^2+0−4) \,\hat{\mathbf i}+\cos(0) \,\hat{\mathbf j} \\[4pt] &=−2 \,\hat{\mathbf i} + \hat{\mathbf j}. \end{align*}\]
\(\vecs{G}(x,y)=x^2y\,\hat{\mathbf i}−(x+y)\,\hat{\mathbf j}\)Seja um campo vetorial em\(ℝ^2\). Qual vetor está associado ao ponto\((−2,3)\)?
- Dica
-
Substitua os valores dos pontos na função vetorial.
- Resposta
-
\(\vecs{G}(−2,3)=12\hat{\mathbf i}−\hat{\mathbf j}\)
Desenhando um campo vetorial
Agora podemos representar um campo vetorial em termos de seus componentes de funções ou vetores unitários, mas representá-lo visualmente esboçando-o é mais complexo porque o domínio de um campo vetorial está dentro\(ℝ^2\), assim como o alcance. Portanto, o “gráfico” de um campo vetorial\(ℝ^2\) vive no espaço quadridimensional. Como não podemos representar visualmente o espaço quadridimensional, desenhamos campos vetoriais\(ℝ^2\) em um plano em si. Para fazer isso, desenhe o vetor associado a um determinado ponto no ponto de um plano. Por exemplo, suponha que o vetor associado ao ponto\((4,−1)\) seja\(⟨3,1⟩\). Em seguida, desenharíamos o vetor\(⟨3,1⟩\) no ponto\((4,−1)\).
Devemos traçar vetores suficientes para ver a forma geral, mas não tantos para que o esboço se torne uma bagunça confusa. Se fôssemos traçar o vetor da imagem em cada ponto da região, ele preencheria a região completamente e seria inútil. Em vez disso, podemos escolher pontos nas interseções das linhas da grade e traçar uma amostra de vários vetores de cada quadrante de um sistema de coordenadas retangulares em\(ℝ^2\).
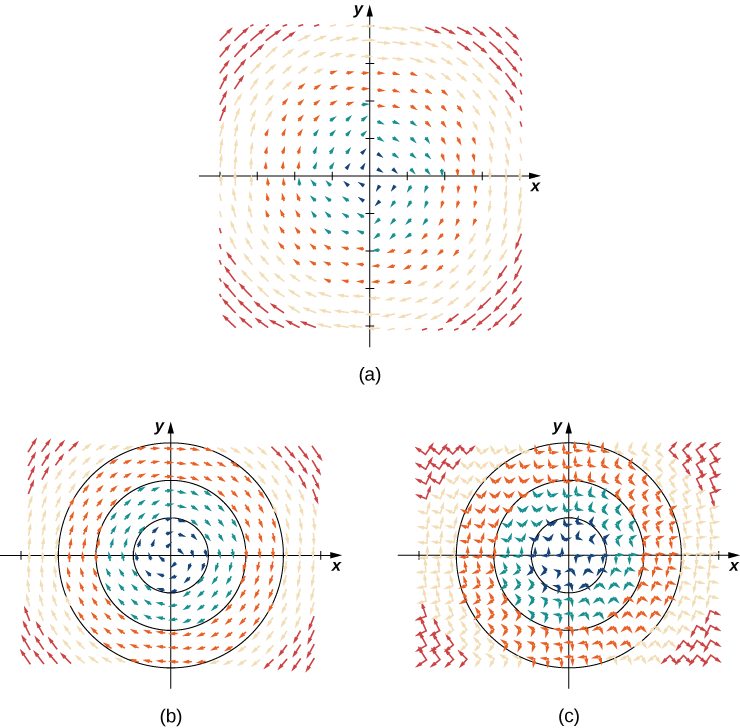
Há dois tipos de campos vetoriais nos\(ℝ^2\) quais este capítulo se concentra: campos radiais e campos rotacionais. Campos radiais modelam certos campos gravitacionais e campos de fontes de energia, e campos rotacionais modelam o movimento de um fluido em um vórtice. Em um campo radial, todos os vetores apontam diretamente para ou diretamente para longe da origem. Além disso, a magnitude de qualquer vetor depende apenas de sua distância da origem. Em um campo radial, o vetor localizado no ponto\((x,y)\) é perpendicular ao círculo centrado na origem que contém o ponto\((x,y)\), e todos os outros vetores desse círculo têm a mesma magnitude.
Desenhe o campo vetorial\(\vecs{F} (x,y)=\dfrac{x}{2}\hat{\mathbf i}+\dfrac{y}{2}\hat{\mathbf j}\).
Solução
Para esboçar esse campo vetorial, escolha uma amostra de pontos de cada quadrante e calcule o vetor correspondente. A tabela a seguir fornece uma amostra representativa dos pontos em um plano e dos vetores correspondentes.
| \((x,y)\) | \(\vecs{F}(x,y)\) | \((x,y)\) | \(\vecs{F}(x,y)\) | \((x,y)\) | \(\vecs{F}(x,y)\) |
|---|---|---|---|---|---|
| \ ((x, y)\)” style="alinhamento vertical: meio; ">\((1,0)\) | \ (\ vecs {F} (x, y)\)” style="alinhamento vertical: meio; ">\(⟨\dfrac{1}{2},0⟩\) | \ ((x, y)\)” style="alinhamento vertical: meio; ">\((2,0)\) | \ (\ vecs {F} (x, y)\)” style="alinhamento vertical: meio; ">\(⟨1,0⟩\) | \ ((x, y)\)” style="alinhamento vertical: meio; ">\((1,1)\) | \ (\ vecs {F} (x, y)\)” style="alinhamento vertical: meio; ">\(⟨\dfrac{1}{2},\dfrac{1}{2}⟩\) |
| \ ((x, y)\)” style="alinhamento vertical: meio; ">\((0,1)\) | \ (\ vecs {F} (x, y)\)” style="alinhamento vertical: meio; ">\(⟨0,\dfrac{1}{2}⟩\) | \ ((x, y)\)” style="alinhamento vertical: meio; ">\((0,2)\) | \ (\ vecs {F} (x, y)\)” style="alinhamento vertical: meio; ">\(⟨0,1⟩\) | \ ((x, y)\)” style="alinhamento vertical: meio; ">\((−1,1)\) | \ (\ vecs {F} (x, y)\)” style="alinhamento vertical: meio; ">\(⟨−\dfrac{1}{2},\dfrac{1}{2}⟩\) |
| \ ((x, y)\)” style="alinhamento vertical: meio; ">\((−1,0)\) | \ (\ vecs {F} (x, y)\)” style="alinhamento vertical: meio; ">\(⟨−\dfrac{1}{2},0⟩\) | \ ((x, y)\)” style="alinhamento vertical: meio; ">\((−2,0)\) | \ (\ vecs {F} (x, y)\)” style="alinhamento vertical: meio; ">\(⟨−1,0⟩\) | \ ((x, y)\)” style="alinhamento vertical: meio; ">\((−1,−1)\) | \ (\ vecs {F} (x, y)\)” style="alinhamento vertical: meio; ">\(⟨−\dfrac{1}{2},−\dfrac{1}{2}⟩\) |
| \ ((x, y)\)” style="alinhamento vertical: meio; ">\((0,−1)\) | \ (\ vecs {F} (x, y)\)” style="alinhamento vertical: meio; ">\(⟨0,−\dfrac{1}{2}⟩\) | \ ((x, y)\)” style="alinhamento vertical: meio; ">\((0,−2)\) | \ (\ vecs {F} (x, y)\)” style="alinhamento vertical: meio; ">\(⟨0,−1⟩\) | \ ((x, y)\)” style="alinhamento vertical: meio; ">\((1,−1)\) | \ (\ vecs {F} (x, y)\)” style="alinhamento vertical: meio; ">\(⟨\dfrac{1}{2},−\dfrac{1}{2}⟩\) |
A figura\(\PageIndex{2a}\) mostra o campo vetorial. Para ver se cada vetor é perpendicular ao círculo correspondente, a Figura\(\PageIndex{2b}\) mostra círculos sobrepostos no campo vetorial.
Desenhe o campo radial\(\vecs{F} (x,y)=−\dfrac{x}{3}\hat{\mathbf i}−\dfrac{y}{3}\hat{\mathbf j}\).
- Dica
-
Desenhe vetores suficientes para ter uma ideia da forma.
- Resposta
-

Em contraste com os campos radiais, em um campo rotacional, o vetor no ponto\((x,y)\) é tangente (não perpendicular) a um círculo com raio\(r=\sqrt{x^2+y^2}\). Em um campo rotacional padrão, todos os vetores apontam no sentido horário ou no sentido anti-horário, e a magnitude de um vetor depende apenas de sua distância da origem. Ambos os exemplos a seguir são campos rotacionais no sentido horário, e vemos em suas representações visuais que os vetores parecem girar em torno da origem.
Desenhe o campo vetorial\(\vecs{F} (x,y)=⟨y,\,−x⟩\).
Solução
Crie uma tabela (veja a tabela a seguir) usando uma amostra representativa de pontos em um plano e seus vetores correspondentes. A figura\(\PageIndex{3}\) mostra o campo vetorial resultante.
| \((x,y)\) | \(\vecs{F}(x,y)\) | \((x,y)\) | \(\vecs{F}(x,y)\) | \((x,y)\) | \(\vecs{F}(x,y)\) |
|---|---|---|---|---|---|
| \ ((x, y)\)” style="alinhamento vertical: meio; ">\((1,0)\) | \ (\ vecs {F} (x, y)\)” style="alinhamento vertical: meio; ">\(⟨0,−1⟩\) | \ ((x, y)\)” style="alinhamento vertical: meio; ">\((2,0)\) | \ (\ vecs {F} (x, y)\)” style="alinhamento vertical: meio; ">\(⟨0,−2⟩\) | \ ((x, y)\)” style="alinhamento vertical: meio; ">\((1,1)\) | \ (\ vecs {F} (x, y)\)” style="alinhamento vertical: meio; ">\(⟨1,−1⟩\) |
| \ ((x, y)\)” style="alinhamento vertical: meio; ">\((0,1)\) | \ (\ vecs {F} (x, y)\)” style="alinhamento vertical: meio; ">\(⟨1,0⟩\) | \ ((x, y)\)” style="alinhamento vertical: meio; ">\((0,2)\) | \ (\ vecs {F} (x, y)\)” style="alinhamento vertical: meio; ">\(⟨2,0⟩\) | \ ((x, y)\)” style="alinhamento vertical: meio; ">\((−1,1)\) | \ (\ vecs {F} (x, y)\)” style="alinhamento vertical: meio; ">\(⟨1,1⟩\) |
| \ ((x, y)\)” style="alinhamento vertical: meio; ">\((−1,0)\) | \ (\ vecs {F} (x, y)\)” style="alinhamento vertical: meio; ">\(⟨0,1⟩\) | \ ((x, y)\)” style="alinhamento vertical: meio; ">\((−2,0)\) | \ (\ vecs {F} (x, y)\)” style="alinhamento vertical: meio; ">\(⟨0,2⟩\) | \ ((x, y)\)” style="alinhamento vertical: meio; ">\((−1,−1)\) | \ (\ vecs {F} (x, y)\)” style="alinhamento vertical: meio; ">\(⟨−1,1⟩\) |
| \ ((x, y)\)” style="alinhamento vertical: meio; ">\((0,−1)\) | \ (\ vecs {F} (x, y)\)” style="alinhamento vertical: meio; ">\(⟨−1,0⟩\) | \ ((x, y)\)” style="alinhamento vertical: meio; ">\((0,−2)\) | \ (\ vecs {F} (x, y)\)” style="alinhamento vertical: meio; ">\(⟨−2,0⟩\) | \ ((x, y)\)” style="alinhamento vertical: meio; ">\((1,−1)\) | \ (\ vecs {F} (x, y)\)” style="alinhamento vertical: meio; ">\(⟨−1,−1⟩\) |
Análise
Observe que o vetor\(\vecs{F}(a,b)=⟨b,−a⟩\) aponta no sentido horário e é perpendicular ao vetor radial\(⟨a,b⟩\). (Podemos verificar essa afirmação calculando o produto escalar dos dois vetores:\(⟨a,b⟩·⟨−b,a⟩=−ab+ab=0\).) Além disso, o vetor\(⟨b,−a⟩\) tem comprimento\(r=\sqrt{a^2+b^2}\). Assim, temos uma descrição completa desse campo vetorial rotacional: o vetor associado ao ponto\((a,b)\) é o vetor com comprimento r tangente ao círculo com raio r e aponta no sentido horário.
Esboços como os da Figura\(\PageIndex{3}\) são frequentemente usados para analisar grandes sistemas de tempestades, incluindo furacões e ciclones. No hemisfério norte, as tempestades giram no sentido anti-horário; no hemisfério sul, as tempestades giram no sentido horário. (Esse é um efeito causado pela rotação da Terra em torno de seu eixo e é chamado de Efeito Coriolis.)

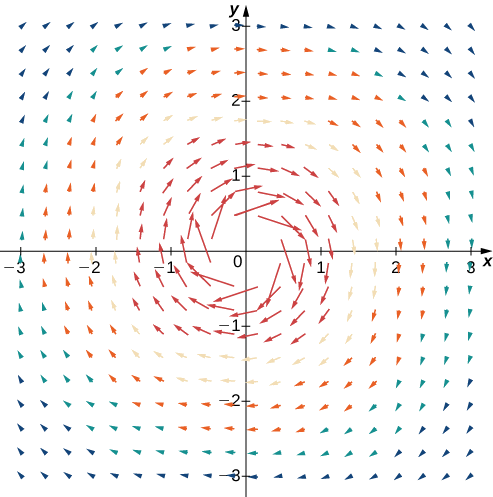
Esboce o campo vetorial\(\vecs{F}(x,y)=\dfrac{y}{x^2+y^2}\hat{\mathbf i}, -\dfrac{x}{x^2+y^2}\hat{\mathbf j}\).
Solução
Para visualizar esse campo vetorial, primeiro observe que o produto escalar\(\vecs{F}(a,b)·(a \,\hat{\mathbf i}+b \,\hat{\mathbf j})\) é zero para qualquer ponto\((a,b)\). Portanto, cada vetor é tangente ao círculo no qual está localizado. Além disso\((a,b)\rightarrow(0,0)\), a magnitude de\(\vecs{F}(a,b)\) vai para o infinito. Para ver isso, observe que
\(||\vecs{F}(a,b)||=\sqrt{\dfrac{a^2+b^2}{ {(a^2+b^2)}^2 }} =\sqrt{\dfrac{1}{a^2+b^2}}\).
\(\dfrac{1}{a^2+b^2}\rightarrow \infty\)Desde\((a,b)\rightarrow (0,0)\) então\(||\vecs F(a,b)||\rightarrow \infty\) como\((a,b)\rightarrow (0,0)\). Esse campo vetorial é semelhante ao campo vetorial em Exemplo\(\PageIndex{3}\), mas nesse caso as magnitudes dos vetores próximos à origem são grandes. A tabela\(\PageIndex{3}\) mostra uma amostra de pontos e os vetores correspondentes, e a Figura\(\PageIndex{5}\) mostra o campo vetorial. Observe que esse campo vetorial modela o movimento do redemoinho do rio na Figura\(\PageIndex{5}\) (b). O domínio desse campo vetorial é todo\(ℝ^2\), exceto o ponto\((0,0)\).
| \((x,y)\) | \(\vecs{F}(x,y)\) | \((x,y)\) | \(\vecs{F}(x,y)\) | \((x,y)\) | \(\vecs{F}(x,y)\) |
|---|---|---|---|---|---|
| \ ((x, y)\)” style="alinhamento vertical: meio; ">\((1,0)\) | \ (\ vecs {F} (x, y)\)” style="alinhamento vertical: meio; ">\(⟨0,−1⟩\) | \ ((x, y)\)” style="alinhamento vertical: meio; ">\((2,0)\) | \ (\ vecs {F} (x, y)\)” style="alinhamento vertical: meio; ">\(⟨0,−\dfrac{1}{2}⟩\) | \ ((x, y)\)” style="alinhamento vertical: meio; ">\((1,1)\) | \ (\ vecs {F} (x, y)\)” style="alinhamento vertical: meio; ">\(⟨\dfrac{1}{2},−\dfrac{1}{2}⟩\) |
| \ ((x, y)\)” style="alinhamento vertical: meio; ">\((0,1)\) | \ (\ vecs {F} (x, y)\)” style="alinhamento vertical: meio; ">\(⟨1,0⟩\) | \ ((x, y)\)” style="alinhamento vertical: meio; ">\((0,2)\) | \ (\ vecs {F} (x, y)\)” style="alinhamento vertical: meio; ">\(⟨\dfrac{1}{2},0⟩\) | \ ((x, y)\)” style="alinhamento vertical: meio; ">\((−1,1)\) | \ (\ vecs {F} (x, y)\)” style="alinhamento vertical: meio; ">\(⟨\dfrac{1}{2},\dfrac{1}{2}⟩\) |
| \ ((x, y)\)” style="alinhamento vertical: meio; ">\((−1,0)\) | \ (\ vecs {F} (x, y)\)” style="alinhamento vertical: meio; ">\(⟨0,1⟩\) | \ ((x, y)\)” style="alinhamento vertical: meio; ">\((−2,0)\) | \ (\ vecs {F} (x, y)\)” style="alinhamento vertical: meio; ">\(⟨0,\dfrac{1}{2}⟩\) | \ ((x, y)\)” style="alinhamento vertical: meio; ">\((−1,−1)\) | \ (\ vecs {F} (x, y)\)” style="alinhamento vertical: meio; ">\(⟨−\dfrac{1}{2},\dfrac{1}{2}⟩\) |
| \ ((x, y)\)” style="alinhamento vertical: meio; ">\((0,−1)\) | \ (\ vecs {F} (x, y)\)” style="alinhamento vertical: meio; ">\(⟨−1,0⟩\) | \ ((x, y)\)” style="alinhamento vertical: meio; ">\((0,−2)\) | \ (\ vecs {F} (x, y)\)” style="alinhamento vertical: meio; ">\(⟨−\dfrac{1}{2},0⟩\) | \ ((x, y)\)” style="alinhamento vertical: meio; ">\((1,−1)\) | \ (\ vecs {F} (x, y)\)” style="alinhamento vertical: meio; ">\(⟨−\dfrac{1}{2},−\dfrac{1}{2}⟩\) |
Esboce o campo vetorial\(\vecs{F}(x,y)=⟨−2y,\,2x⟩\). O campo vetorial é radial, rotacional ou nenhum?
- Dica
-
Substitua pontos suficientes\(\vecs{F}\) para ter uma ideia da forma.
- Resposta
-
Rotacional

Suponha que esse\(\vecs{v} (x,y)=−\dfrac{2y}{x^2+y^2}\hat{\mathbf i}+\dfrac{2x}{x^2+y^2}\hat{\mathbf j}\) seja o campo de velocidade de um fluido. Com que rapidez o fluido está se movendo em um ponto\((1,−1)\)? (Suponha que as unidades de velocidade sejam metros por segundo.)
Solução
Para encontrar a velocidade do fluido no ponto\((1,−1)\), substitua o ponto em\(\vecs{v} \):
\(\vecs{v}(1,−1)=\dfrac{−2(−1)}{1+1}\hat{\mathbf i}+\dfrac{2(1)}{1+1}\hat{\mathbf j}=\hat{\mathbf i}+\hat{\mathbf j}\).
A velocidade do fluido em\((1,−1)\) é a magnitude desse vetor. Portanto, a velocidade é\(||\hat{\mathbf i}+\hat{\mathbf j}||=\sqrt{2}\) m/seg.
O campo vetorial\(\vecs{v} (x,y)=⟨4|x|,\,1⟩\) modela a velocidade da água na superfície de um rio. Qual é a velocidade da água no ponto\((2,3)\)? Use metros por segundo como unidades.
- Dica
-
Lembre-se de que a velocidade é a magnitude da velocidade.
- Resposta
-
\(\sqrt{65}\)m/seg
Examinamos campos vetoriais que contêm vetores de várias magnitudes, mas assim como temos vetores unitários, também podemos ter um campo vetorial unitário. Um campo vetorial\(\vecs{F}\) é um campo vetorial unitário se a magnitude de cada vetor no campo for 1. Em um campo vetorial unitário, a única informação relevante é a direção de cada vetor.
Mostre que o campo vetorial\(\vecs{F} (x,y)=\left\langle\dfrac{y}{\sqrt{x^2+y^2}},−\dfrac{x}{\sqrt{x^2+y^2}}\right\rangle\) é um campo vetorial unitário.
Solução
Para mostrar que\(\vecs{F}\) é um campo unitário, devemos mostrar que a magnitude de cada vetor é\(1\). Note que
\[\begin{align*} \sqrt{ \left(\dfrac{y}{\sqrt{x^2+y^2}}\right)^2+\left(−\dfrac{x}{\sqrt{x^2+y^2}}\right)^2} &=\sqrt{ \dfrac{y^2}{x^2+y^2}+\dfrac{x^2}{x^2+y^2}} \\[4pt] &=\sqrt{\dfrac{x^2+y^2}{x^2+y^2}} \\[4pt] &=1 \end{align*}\]
Portanto,\(\vecs{F} \) é um campo vetorial unitário.
O campo vetorial é\(\vecs{F} (x,y)=⟨−y,\,x⟩\) um campo vetorial unitário?
- Dica
-
Calcule a magnitude de\(\vecs{F} \) em um ponto arbitrário\((x,y)\).
- Resposta
-
Não.
Por que os campos vetoriais unitários são importantes? Suponha que estejamos estudando o fluxo de um fluido e nos preocupamos apenas com a direção na qual o fluido está fluindo em um determinado ponto. Nesse caso, a velocidade do fluido (que é a magnitude do vetor de velocidade correspondente) é irrelevante, porque tudo o que importa é a direção de cada vetor. Portanto, o campo vetorial unitário associado à velocidade é o campo que estudaríamos.
Se\(\vecs{F} =⟨P,Q,R⟩\) for um campo vetorial, o campo vetorial unitário correspondente será\(\big\langle\tfrac{P}{||\vecs F||},\tfrac{Q}{||\vecs F||},\tfrac{R}{||\vecs F||}\big\rangle\). Observe que se\(\vecs{F}(x,y)=⟨y,\,−x⟩\) for o campo vetorial de Example\(\PageIndex{6}\), então a magnitude de\(\vecs{F} \) é e\(\sqrt{x^2+y^2}\), portanto, o campo vetorial unitário correspondente é o campo\(\vecs{G} \) do exemplo anterior.
Se\(\vecs{F} \) for um campo vetorial, o processo de divisão\(\vecs{F} \) por sua magnitude para formar um campo vetorial unitário\(\vecs{F}/||\vecs{F}||\) é chamado de normalização do campo\(\vecs{F} \).
Campos vetoriais em\(ℝ^3\)
Vimos vários exemplos de campos vetoriais em\(ℝ^2\); vamos agora voltar nossa atenção para campos vetoriais em\(ℝ^3\). Esses campos vetoriais podem ser usados para modelar campos gravitacionais ou eletromagnéticos e também podem ser usados para modelar fluxo de fluido ou fluxo de calor em três dimensões. Na verdade, um campo vetorial bidimensional só pode modelar o movimento da água em uma fatia bidimensional de um rio (como a superfície do rio). Como um rio passa por três dimensões espaciais, para modelar o fluxo de toda a profundidade do rio, precisamos de um campo vetorial em três dimensões.
A dimensão extra de um campo tridimensional pode tornar os campos vetoriais\(ℝ^3\) mais difíceis de visualizar, mas a ideia é a mesma. Para visualizar um campo vetorial em\(ℝ^3\), plote vetores suficientes para mostrar a forma geral. Podemos usar um método semelhante para visualizar um campo vetorial em\(ℝ^2\) escolhendo pontos em cada octante.
Assim como com os campos vetoriais em\(ℝ^2\), podemos representar campos vetoriais\(ℝ^3\) com funções de componentes. Nós simplesmente precisamos de uma função de componente extra para a dimensão extra. Nós também escrevemos
\[\vecs{F}(x,y,z)=⟨P(x,y,z),Q(x,y,z),R(x,y,z)⟩ \nonumber \]
ou
\[\vecs{F}(x,y,z)=P(x,y,z)\hat{\mathbf i}+Q(x,y,z)\hat{\mathbf j}+R(x,y,z)\hat{\mathbf k}. \nonumber \]
Descreva o campo\(\vecs{F}(x,y,z)=⟨1,\,1,\,z⟩\) vetorial
Solução
Para esse campo vetorial, os\(y\) componentes\(x\) - e -são constantes, então cada ponto em\(ℝ^3\) tem um vetor associado com\(y\) componentes\(x\) - e -igual a um. Para visualizar\(\vecs{F}\), primeiro consideramos a aparência do campo no\(xy\) plano. No\(xy\) plano -,\(z=0\). Portanto, cada ponto da forma\((a,b,0)\) tem um vetor\(⟨1,1,0⟩\) associado a ele. Para pontos que não estão no\(xy\) plano -, mas um pouco acima dele, o vetor associado tem um\(z\) componente pequeno, mas positivo, e, portanto, o vetor associado aponta ligeiramente para cima. Para pontos que estão muito acima do\(xy\) plano -, o\(z\) componente -é grande, então o vetor é quase vertical. A figura\(\PageIndex{6}\) mostra esse campo vetorial.
Figura\(\PageIndex{6}\): Uma representação visual do campo vetorial\(\vecs{F}(x,y,z)=⟨1,1,z⟩\).
Esboce o campo vetorial\(\vecs{G}(x,y,z)=⟨2,\,\dfrac{z}{2},\,1⟩\).
- Dica
-
Substitua pontos suficientes no campo vetorial para ter uma ideia da forma geral.
- Resposta
No próximo exemplo, exploraremos um dos casos clássicos de um campo vetorial tridimensional: um campo gravitacional.
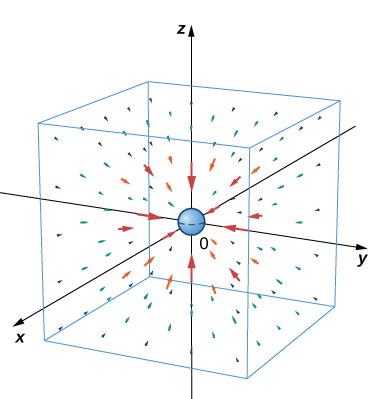
A lei da gravitação de Newton afirma que\(\vecs{F}=−G\dfrac{m_1m_2}{r^2}\hat{\mathbf r}\), onde G é a constante gravitacional universal. Ele descreve o campo gravitacional exercido por um objeto (objeto 1) de massa\(m_1\) localizado na origem de outro objeto (objeto 2) de massa\(m_2\) localizado no ponto\((x,y,z)\). Campo\(\vecs{F}\) indica a força gravitacional que o objeto 1 exerce sobre o objeto 2,\(r\) é a distância entre os dois objetos e\(\hat{\mathbf r}\) indica o vetor unitário do primeiro objeto ao segundo. O sinal de menos mostra que a força gravitacional atrai em direção à origem; ou seja, a força do objeto 1 é atraente. Esboce o campo vetorial associado a essa equação.
Solução
Como o objeto 1 está localizado na origem, a distância entre os objetos é dada por\(r=\sqrt{x^2+y^2+z^2}\). O vetor unitário do objeto 1 para o objeto 2 é\(\hat{\mathbf r}=\dfrac{⟨x,y,z⟩}{||⟨x,y,z⟩||}\), e portanto\(\hat{\mathbf r}=\big\langle\dfrac{x}{r},\dfrac{y}{r},\dfrac{z}{r}\big\rangle\). Portanto, o campo vetorial gravitacional\(\vecs{F}\) exercido pelo objeto 1 no objeto 2 é
\[ \vecs{F}=−Gm_1m_2\big\langle\dfrac{x}{r^3},\dfrac{y}{r^3},\dfrac{z}{r^3}\big\rangle. \nonumber \]
Este é um exemplo de um campo vetorial radial em\(ℝ^3\).
A figura\(\PageIndex{7}\) mostra a aparência desse campo gravitacional para uma grande massa na origem. Observe que as magnitudes dos vetores aumentam à medida que os vetores se aproximam da origem.
A massa do asteróide 1 é 750.000 kg e a massa do asteróide 2 é 130.000 kg. Suponha que o asteróide 1 esteja localizado na origem e o asteróide 2 esteja localizado em\((15,−5,10)\), medido em unidades de 10 até o oitavo quilômetro de potência. Dado que a constante gravitacional universal é\(G=6.67384×10^{−11}m^3{kg}^{−1}s^{−2}\), encontre o vetor de força gravitacional que o asteróide 1 exerce sobre o asteróide 2.
- Dica
-
Siga o exemplo\(\PageIndex{8}\) e primeiro calcule a distância entre os asteróides.
- Resposta
-
\(1.49063×{10}^{−18}\),\(4.96876×{10}^{−19}\),\(9.93752×{10}^{−19}\) N
Campos de gradiente (campos conservadores)
Nesta seção, estudamos um tipo especial de campo vetorial chamado campo de gradiente ou campo conservador. Esses campos vetoriais são extremamente importantes na física porque podem ser usados para modelar sistemas físicos nos quais a energia é conservada. Campos gravitacionais e campos elétricos associados a uma carga estática são exemplos de campos de gradiente.
Lembre-se de que se\(f\) é uma função (escalar) de\(x\) e\(y\), então o gradiente de\(f\) é
\[ \text{grad}\, f =\vecs \nabla f(x,y) =f_x(x,y) \hat{\mathbf i} +f_y(x,y) \hat{\mathbf j}. \nonumber \]
Podemos ver pela forma em que o gradiente está escrito que\(\vecs \nabla f\) é um campo vetorial em\(ℝ^2\). Da mesma forma, se\(f\) é uma função de\(x\)\(y\), e\(z\), então o gradiente de\(f\) é
\[ \text{grad}\, f =\vecs \nabla f(x,y,z) = f_x(x,y,z) \hat{\mathbf i}+f_y(x,y,z) \hat{\mathbf j}+f_z(x,y,z)\hat{\mathbf k}. \nonumber \]
O gradiente de uma função de três variáveis é um campo vetorial em\(ℝ^3\). Um campo de gradiente é um campo vetorial que pode ser escrito como o gradiente de uma função, e temos a seguinte definição.
Um campo vetorial\(\vecs{F}\) dentro\(ℝ^2\) ou dentro\(ℝ^3\) é um campo de gradiente se existir uma função escalar\(f\) como essa\(\vecs \nabla f=\vecs{F}\).
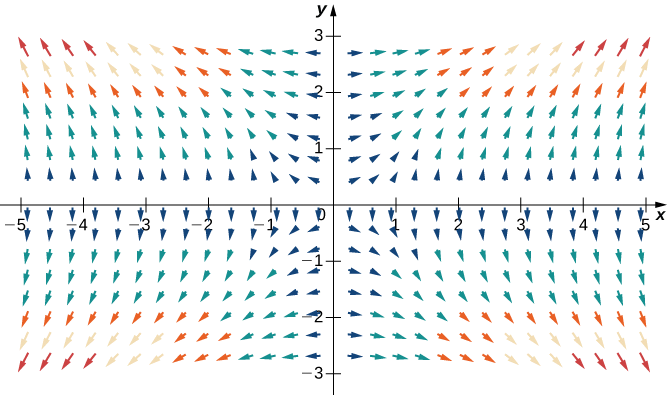
Use a tecnologia para traçar o campo vetorial de gradiente de\(f(x,y)=x^2y^2\).
Solução
O gradiente de\(f\) é\(\vecs \nabla f(x,y)=⟨2xy^2,\,2x^2y⟩\). Para esboçar o campo vetorial, use um sistema computacional de álgebra como o Mathematica. A figura\(\PageIndex{8}\) mostra\(\vecs \nabla f\).
Use a tecnologia para traçar o campo vetorial de gradiente de\(f(x,y)=\sin x\cos y\).
- Dica
-
Encontre o gradiente de\(f\).
- Resposta
-
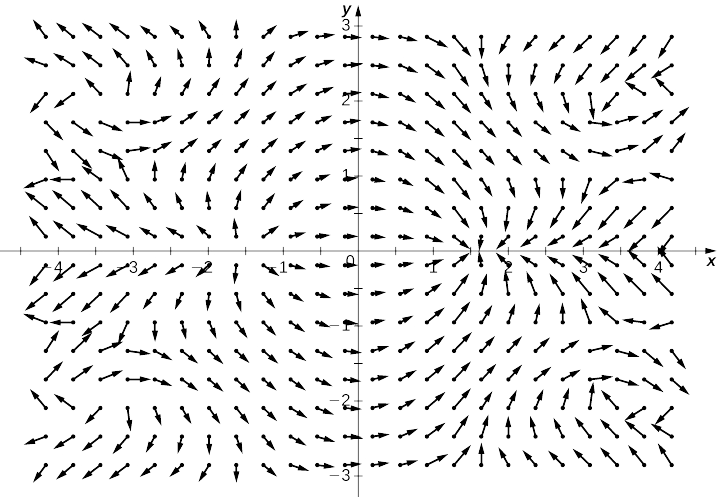
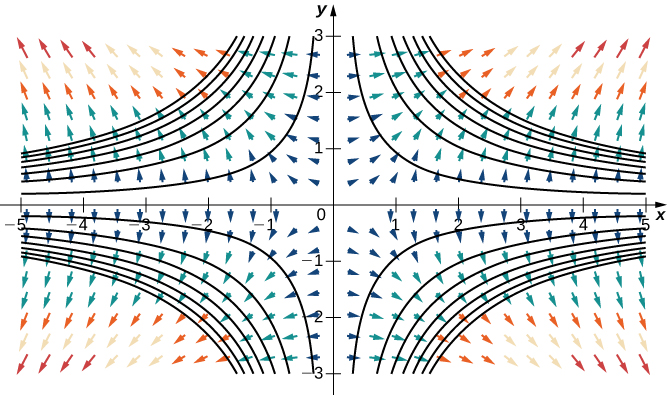
Considere a função\(f(x,y)=x^2y^2\) de Example\(\PageIndex{9}\). A figura\(\PageIndex{9}\) mostra as curvas de nível dessa função sobrepostas no campo vetorial de gradiente da função. Os vetores de gradiente são perpendiculares às curvas de nível, e as magnitudes dos vetores aumentam à medida que as curvas de nível se aproximam, porque curvas de nível bem agrupadas indicam que o gráfico é íngreme e a magnitude do vetor de gradiente é o maior valor da derivada direcional. Portanto, você pode ver a inclinação local de um gráfico investigando o campo de gradiente da função correspondente.
Como aprendemos anteriormente, um campo vetorial\(\vecs{F}\) é um campo vetorial conservador ou um campo de gradiente se existir uma função escalar\(f\) como essa\(\vecs \nabla f=\vecs{F}\). Nessa situação,\(f\) é chamada de função potencial para\(\vecs{F}\). Campos vetoriais conservadores surgem em muitas aplicações, particularmente na física. A razão pela qual esses campos são chamados de conservadores é que eles modelam forças de sistemas físicos nos quais a energia é conservada. Estudamos campos vetoriais conservadores com mais detalhes posteriormente neste capítulo.
Você pode notar que, em alguns aplicativos, uma função potencial\(f\) para\(\vecs{F}\) é definida como uma função como essa\(−\vecs \nabla f=\vecs{F}\). Esse é o caso de certos contextos da física, por exemplo.
É\(f(x,y,z)=x^2yz−\sin(xy)\) uma função potencial para campo vetorial
\(\vecs{F}(x,y,z)=⟨2xyz−y\cos(xy),x^2z−x\cos(xy),x^2y⟩\)?
Solução
Precisamos confirmar se\(\vecs \nabla f=\vecs{F}\). Nós temos
\[ \begin{align*} f_x(x,y) =2xyz−y\cos(xy) \\[4pt] f_y(x,y) =x^2z−x\cos(xy) \\[4pt] f_z(x,y) =x^2y \end{align*}. \nonumber \]
Portanto,\(\vecs \nabla f=\vecs{F}\) e\(f\) é uma função potencial para\(\vecs{F}\).
É\(f(x,y,z)=x^2\cos(yz)+y^2z^2\) uma função potencial para\(\vecs{F}(x,y,z)=⟨2x\cos(yz),−x^2z \sin(yz)+2yz^2,y^2⟩\)?
- Dica
-
Calcule o gradiente de\(f\).
- Resposta
-
Não
A velocidade de um fluido é modelada por campo\(\vecs v(x,y)=⟨xy,\tfrac{x^2}{2}−y⟩\). Verifique se\(f(x,y)=\dfrac{x^2y}{2}−\dfrac{y^2}{2}\) é uma função potencial do\(\vecs{v}\).
Solução
Para mostrar que essa\(f\) é uma função potencial, devemos mostrar isso\(\vecs \nabla f=\vecs v\). Observe isso\(f_x(x,y)=xy\)\(f_y(x,y)=\dfrac{x^2}{2}−y\) e. Portanto,\(\vecs \nabla f(x,y)=⟨xy,\tfrac{x^2}{2}−y⟩\) e\(f\) é uma função potencial para\(\vecs{v}\) (Figura\(\PageIndex{10}\)).

Verifique se\(f(x,y)=x^3y^2+x\) é uma função potencial para o campo de velocidade\(\vecs{v}(x,y)=⟨3x^2y^2+1,2x^3y⟩\).
- Dica
-
Calcule o gradiente.
- Resposta
-
\(\vecs \nabla f(x,y)=\vecs{v}(x,y)\)
Se\(\vecs{F}\) for um campo vetorial conservador, então há pelo menos uma função potencial\(f\) como essa\(\vecs \nabla f=\vecs{F}\). Mas, poderia haver mais de uma função potencial? Em caso afirmativo, existe alguma relação entre duas funções potenciais para o mesmo campo vetorial? Antes de responder a essas perguntas, vamos relembrar alguns fatos do cálculo de variável única para guiar nossa intuição. Lembre-se de que se\(k(x)\) é uma função integrável, então\(k\) tem infinitas antiderivadas. Além disso, se\(\vecs{F}\) e\(\vecs{G}\) são ambas antiderivadas de\(k\), então\(\vecs{F}\) e\(\vecs{G}\) diferem apenas por uma constante. Ou seja, há algum número\(C\) desse tipo\(\vecs{F}(x)=\vecs{G}(x)+C\).
Agora,\(\vecs{F}\) sejamos um campo vetorial conservador\(f\) e\(g\) sejam funções potenciais para\(\vecs{F}\). Como o gradiente é como uma derivada,\(\vecs{F}\) ser conservador significa que\(\vecs{F}\) é “integrável” com “antiderivadas”\(f\)\(g\) e. Portanto, se a analogia com o cálculo de variável única for válida, esperamos que haja alguma constante\(C\) como essa\(f(x)=g(x)+C\). O próximo teorema diz que esse é realmente o caso.
Para declarar o próximo teorema com precisão, precisamos assumir que o domínio do campo vetorial está conectado e aberto. Estar conectado significa se\(P_1\) e\(P_2\) existem dois pontos no domínio, então você pode caminhar de a para o\(P_1\) ao\(P_2\) longo de um caminho que permanece inteiramente dentro do domínio.
\(\vecs{F}\)Seja um campo vetorial conservador em um domínio aberto e conectado e deixe\(f\) e\(g\) seja funções de tal forma que\(\vecs \nabla f=\vecs{F}\)\(\vecs \nabla g=\vecs{F}\) e. Então, há uma constante\(C\) como essa\(f=g+C\).
Uma vez que\(f\) e ambas\(g\) são funções potenciais para\(\vecs{F}\), então\(\vecs \nabla (f−g)=\vecs \nabla f−\vecs \nabla g=\vecs{F}−\vecs{F}=\vecs 0\). Vamos\(h=f−g\), então temos\(\vecs \nabla h=\vecs 0\) .Gostaríamos de mostrar que\(h\) é uma função constante.
Suponha que\(h\) seja uma função de\(x\) e\(y\) (a lógica dessa prova se estende a qualquer número de variáveis independentes). Desde então\(\vecs \nabla h=\vecs 0\), nós temos\(h_x(x,y)=0\)\(h_y(x,y)=0\) e. A expressão\(h_x(x,y)=0\) implica que\(h\) é uma função constante em relação a\(x\) —isto é,\(h(x,y)=k_1(y)\) para alguma função\(k_1\). Da mesma forma,\(h_y(x,y)=0\) implica\(h(x,y)=k_2(x)\) em alguma função\(k_2\). Portanto, a função\(h\) depende apenas de\(y\) e também depende apenas de\(x\). Assim,\(h(x,y)=C\) para alguma constante\(C\) no domínio conectado de\(\vecs{F}\). Observe que realmente precisamos de conexão neste momento; se o domínio de\(\vecs{F}\) veio em duas partes separadas, então\(k\) poderia ser uma constante\(C_1\) em uma peça, mas poderia ser uma constante diferente\(C_2\) na outra peça. Desde então\(f−g=h=C\), temos isso\(f=g+C\), conforme desejado.
\(\square\)
Os campos vetoriais conservadores também têm uma propriedade especial chamada propriedade parcial cruzada. Essa propriedade ajuda a testar se um determinado campo vetorial é conservador.
\(\vecs{F}\)Seja um campo vetorial em duas ou três dimensões, de modo que as funções componentes de\(\vecs{F}\) tenham derivadas parciais mistas contínuas de segunda ordem no domínio de\(\vecs{F}\).
Se\(\vecs{F}(x,y)=⟨P(x,y),Q(x,y)⟩\) for um campo vetorial conservador em\(ℝ^2\), então
\[\dfrac{\partial P}{\partial y}=\dfrac{\partial Q}{\partial x}. \nonumber \]
Se\(\vecs{F}(x,y,z)=⟨P(x,y,z),Q(x,y,z),R(x,y,z)⟩\) for um campo vetorial conservador em\({\mathbb{R}}^3\), então
\[ \begin{align*} \dfrac{\partial P}{\partial y} =\dfrac{\partial Q}{\partial x} \\[4pt] \dfrac{\partial Q}{\partial z} =\dfrac{\partial R}{\partial y} \\[4pt] \dfrac{\partial R}{\partial x} =\dfrac{\partial P}{\partial z}. \end{align*}\]
Como\(\vecs{F}\) é conservador, existe uma função\(f(x,y)\) como essa\(\vecs \nabla f=\vecs{F}\). Portanto, pela definição do gradiente,\(f_x=P\)\(f_y=Q\) e. Pelo teorema de Clairaut\(f_{xy}=f_{yx}\), Mas,\(f_{xy}=P_y\) e\(f_{yx}=Q_{x}\), e assim\(P_y=Q_x\).
\(\square\)
O teorema de Clairaut fornece uma prova rápida da propriedade parcial cruzada dos campos vetoriais conservadores em\(ℝ^3\), assim como fez com os campos vetoriais em\(ℝ^2\).
A propriedade parcial cruzada dos campos vetoriais conservadores mostra que a maioria dos campos vetoriais não é conservadora. A propriedade parcial cruzada é difícil de satisfazer em geral, então a maioria dos campos vetoriais não terá parciais cruzados iguais.
Mostre que o campo vetorial rotacional não\(\vecs{F}(x,y)=⟨y,\,−x⟩\) é conservador.
Solução
Deixe\(P(x,y)=y\)\(Q(x,y)=−x\) e. Se\(\vecs{F}\) for conservador, então os interparciais seriam iguais, ou seja,\(P_y\) seriam iguais\(Q_x\). Portanto, para mostrar que não \(\vecs{F}\)é conservador, verifique isso\(P_y≠Q_x\). Desde\(P_y=1\) e\(Q_x=−1\), o campo vetorial não é conservador.
Mostre que o campo vetorial não\(\vecs F(x,y)=xy\,\hat{\mathbf i}−x^2y\,\hat{\mathbf j}\) é conservador.
- Dica
-
Verifique as parciais cruzadas.
- Resposta
-
\(P_y(x,y)=x\)\(Q_x(x,y)=−2xy\)e. Desde então\(P_y(x,y) ≠ Q_x(x,y)\), não\(\vecs F\) é conservador.
O campo vetorial é\(\vecs{F}(x,y,z)=⟨7,−2,x^3⟩\) conservador?
Solução
Deixe\(P(x,y,z)=7\)\(Q(x,y,z)=−2\),\(R(x,y,z)=x^3\) e. Se\(\vecs{F}\) for conservador, então todas as três equações parciais cruzadas serão satisfeitas — isto é, se for\(\vecs{F}\) conservador, então\(P_y\) seria igual\(Q_x\),\(Q_z\) seria igual\(R_y\) e\(R_x\) seria igual\(P_z\). Note que
\[P_y=Q_x=R_y=Q_z=0 \nonumber \]
então as duas primeiras igualdades necessárias se mantêm. No entanto,\(R_x(x,y,z)=x^3\) e\(P_z(x,y,z)=0\) assim por diante\(R_x≠P_z\). Portanto, não\(\vecs{F}\) é conservador.
O campo vetorial é\(\vecs{G}(x,y,z)=⟨y,\,x,\,xyz⟩\) conservador?
- Dica
-
Verifique as parciais cruzadas.
- Resposta
-
Não
Concluímos esta seção com uma palavra de advertência: A propriedade parcial cruzada dos campos vetoriais conservadores diz que, se\(\vecs{F}\) for conservadora,\(\vecs{F}\) tem a propriedade parcial cruzada. O teorema não diz que, se\(\vecs{F}\) tem a propriedade parcial cruzada, então\(\vecs{F}\) é conservador (o inverso de uma implicação não é logicamente equivalente à implicação original). Em outras palavras, a propriedade parcial cruzada de campos vetoriais conservadores só pode ajudar a determinar se um campo não é conservador; ela não permite concluir que um campo vetorial é conservador.
Por exemplo, considere o campo vetorial\(\vecs{F}(x,y)=⟨x^2y,\dfrac{x^3}{3}⟩\). Esse campo tem a propriedade parcial cruzada, então é natural tentar usar a propriedade parcial cruzada dos campos vetoriais conservadores para concluir que esse campo vetorial é conservador. No entanto, isso é uma aplicação incorreta do teorema. Aprenderemos mais tarde como concluir que isso\(\vecs F\) é conservador.
Conceitos-chave
- Um campo vetorial atribui um vetor\(\vecs{F}(x,y)\) a cada ponto\((x,y)\) em um subconjunto\(D\) de\(ℝ^2\) ou\(ℝ^3\). \(\vecs{F}(x,y,z)\)para cada ponto\((x,y,z)\) em um subconjunto\(D\) de\(ℝ^3\).
- Os campos vetoriais podem descrever a distribuição de quantidades vetoriais, como forças ou velocidades, em uma região do plano ou do espaço. Eles são de uso comum em áreas como física, engenharia, meteorologia e oceanografia.
- Podemos esboçar um campo vetorial examinando sua equação definidora para determinar magnitudes relativas em vários locais e, em seguida, desenhar vetores suficientes para determinar um padrão.
- Um campo vetorial\(\vecs{F}\) é chamado de conservador se existir uma função escalar\(f\) como essa\(\vecs \nabla f=\vecs{F}\).
Equações-chave
- Campo vetorial em\(ℝ^2\)
\(\vecs{F}(x,y)=⟨P(x,y),\,Q(x,y)⟩\)
ou
\(\vecs{F}(x,y)=P(x,y) \,\hat{\mathbf i}+Q(x,y) \,\hat{\mathbf j}\) - Campo vetorial em\(ℝ^3\)
\(\vecs{F}(x,y,z)=⟨P(x,y,z),\,Q(x,y,z),\,R(x,y,z)⟩\)
ou
\(\vecs{F}(x,y,z)=P(x,y,z) \,\hat{\mathbf i} +Q(x,y,z) \,\hat{\mathbf j}+R(x,y,z) \,\hat{\mathbf k}\)
Glossário
- campo conservador
- um campo vetorial para o qual existe uma função escalar\(f\) tal que\(\vecs ∇f=\vecs{F}\)
- campo de gradiente
- um campo vetorial\(\vecs{F}\) para o qual existe uma função escalar\(f\) tal que\(\vecs ∇f=\vecs{F}\); em outras palavras, um campo vetorial que é o gradiente de uma função; esses campos vetoriais também são chamados de conservadores
- função potencial
- uma função escalar\(f\) tal que\(\vecs ∇f=\vecs{F}\)
- campo radial
- um campo vetorial no qual todos os vetores apontam diretamente para ou diretamente para longe da origem; a magnitude de qualquer vetor depende apenas de sua distância da origem
- campo rotacional
- um campo vetorial no qual o vetor em um ponto\((x,y)\) é tangente a um círculo com raio\(r=\sqrt{x^2+y^2}\); em um campo rotacional, todos os vetores fluem no sentido horário ou anti-horário, e a magnitude de um vetor depende apenas de sua distância da origem
- campo vetorial unitário
- um campo vetorial no qual a magnitude de cada vetor é 1
- campo vetorial
- medido em\(ℝ^2\), uma atribuição de um vetor\(\vecs{F}(x,y)\) a cada ponto\((x,y)\) de um subconjunto\(D\) de\(ℝ^2\); em\(ℝ^3\), uma atribuição de um vetor\(\vecs{F}(x,y,z)\) a cada ponto\((x,y,z)\) de um subconjunto\(D\) de\(ℝ^3\)


