16.4: Teorema de Green
- Page ID
- 188552
- Aplique a forma de circulação do teorema de Green.
- Aplique a forma de fluxo do teorema de Green.
- Calcule a circulação e o fluxo em regiões mais gerais.
Nesta seção, examinamos o teorema de Green, que é uma extensão do Teorema Fundamental do Cálculo para duas dimensões. O teorema de Green tem duas formas: uma forma de circulação e uma forma de fluxo, ambas as quais exigem que a região\(D\) na integral dupla seja simplesmente conectada. No entanto, estenderemos o teorema de Green para regiões que não estão simplesmente conectadas.
Simplificando, o teorema de Green relaciona uma integral de linha em torno de uma curva plana simplesmente fechada\(C\) e uma integral dupla sobre a região delimitada por\(C\). O teorema é útil porque nos permite traduzir integrais de linha difíceis em integrais duplas mais simples ou integrais duplas difíceis em integrais de linha mais simples.
Estendendo o Teorema Fundamental do Cálculo
Lembre-se de que o Teorema Fundamental do Cálculo diz que
\[\int_a^b F′(x)\,dx=F(b)−F(a). \nonumber \]
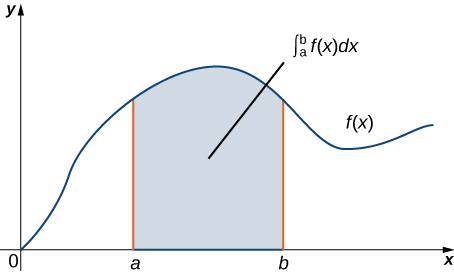
Como afirmação geométrica, essa equação diz que a integral sobre a região abaixo do gráfico\(F′(x)\) e acima do segmento de linha\([a,b]\) depende apenas do valor de\(F\) nas extremidades\(a\) e\(b\) desse segmento. Como os números\(a\) e\(b\) são o limite do segmento de reta\([a,b]\), o teorema diz que podemos calcular integral\(\int_a^b F′(x)\,dx\) com base em informações sobre o limite do segmento de reta\([a,b]\) (Figura\(\PageIndex{1}\)). A mesma ideia se aplica ao Teorema Fundamental para Integrais de Linha:
\[\int_C \vecs \nabla f·d\vecs r=f(\vecs r(b))−f(\vecs r(a)). \nonumber \]
Quando temos uma função potencial (uma “antiderivada”), podemos calcular a integral da linha com base somente em informações sobre o limite da curva\(C\).
O teorema de Green pega essa ideia e a estende ao cálculo de integrais duplos. O teorema de Green diz que podemos calcular uma integral dupla sobre a região\(D\) com base apenas em informações sobre o limite de\(D\). O teorema de Green também diz que podemos calcular uma integral de linha sobre uma curva fechada simples\(C\) com base apenas em informações sobre a região que o\(C\) circunda. Em particular, o teorema de Green conecta uma integral dupla sobre\(D\) a região a uma integral reta ao redor do limite de\(D\).
Forma de circulação do teorema de Green
A primeira forma do teorema de Green que examinamos é a forma de circulação. Essa forma do teorema relaciona a integral da linha vetorial sobre uma curva simples de plano fechado\(C\) com uma integral dupla sobre a região delimitada por\(C\). Portanto, a circulação de um campo vetorial ao longo de uma curva fechada simples pode ser transformada em uma integral dupla e vice-versa.
\(D\)Seja uma região aberta, simplesmente conectada, com uma curva limite\(C\) que é uma curva fechada simples, suave em partes, orientada no sentido anti-horário (Figura\(\PageIndex{1}\)). \(\vecs F=⟨P,Q⟩\)Seja um campo vetorial com funções de componentes que têm derivadas parciais contínuas ativadas\(D\). Então,
\[ \begin{align} \oint_C \vecs F·d\vecs r =\oint_C P\,dx+Q\,dy \\[4pt] =\iint_D (Q_x−P_y)\,dA. \end{align} \nonumber \]
Observe que o teorema de Green só pode ser usado para um campo vetorial bidimensional\(\vecs F\). Se\(\vecs F\) for um campo tridimensional, o teorema de Green não se aplica. Desde
\[\displaystyle \int_C P\,dx+Q\,dy=\int_C \vecs F·\vecs T\,ds \nonumber \]
esta versão do teorema de Green às vezes é chamada de forma tangencial do teorema de Green.
A prova do teorema de Green é bastante técnica e está além do escopo deste texto. Aqui, examinamos uma prova do teorema no caso especial que\(D\) é um retângulo. Por enquanto, observe que podemos confirmar rapidamente que o teorema é verdadeiro para o caso especial em que\(\vecs F=⟨P,Q⟩\) é conservador. Nesse caso,
\[\oint_C P\,dx+Q\,dy=0 \nonumber \]
porque a circulação é zero em campos vetoriais conservadores. \(\vecs F\)satisfaz a condição parcial cruzada, então\(P_y=Q_x\). Portanto,
\[\iint_D (Q_x−P_y)\,dA=\int_D 0\,dA=0=\oint_C P\,dx+Q\,dy \nonumber \]
o que confirma o teorema de Green no caso de campos vetoriais conservadores.
Vamos agora provar que a forma de circulação do teorema de Green é verdadeira quando a região\(D\) é um retângulo. \(D\)Seja o retângulo\([a,b]×[c,d]\) orientado no sentido anti-horário. Então, o limite\(C\) de\(D\) consiste em quatro peças lisas por partes\(C_1\),\(C_2\)\(C_3\), e\(C_4\) (Figura\(\PageIndex{3}\)). Parametrizamos cada lado da\(D\) seguinte forma:
\(C_1: \vecs r_1(t)=⟨t,c⟩\),\(a≤t≤b\)
\(C_2: \vecs r_2(t)=⟨b,t⟩\),\(c≤t≤d\)
\(−C_3: \vecs r_3(t)=⟨t,d⟩\),\(a≤t≤b\)
\(−C_4: \vecs r_4(t)=⟨a,t⟩\),\(c≤t≤d\).
Então,
\[\begin{align*} \int_C \vecs F·d \vecs r &=\int_{C_1} \vecs F·d \vecs r+\int_{C_2} \vecs F·d \vecs r+\int_{C_3} \vecs F·d \vecs r+\int_{C_4} \vecs F·d \vecs r \\[4pt] &=\int_{C_1} \vecs F·d \vecs r+\int_{C_2} \vecs F·d \vecs r−\int_{−C_3} \vecs F·d \vecs r−\int_{−C_4} \vecs F·d \vecs r \\[4pt] &=\int_a^b \vecs F( \vecs r_1(t))· \vecs r_1'(t)\,dt+\int_c^d \vecs F( \vecs r_2(t))· \vecs r_2'(t)\,dt−\int_a^b \vecs F( \vecs r_3(t))· \vecs r_3'(t)\,dt−\int_c^d \vecs F( \vecs r_4(t))·\vecs r_4'(t)\,dt\\[4pt] &=\int_a^b P(t,c)\,dt+\int_c^dQ(b,t)\,dt−\int_a^bP(t,d)\,dt−\int_c^dQ(a,t)\,dt \\[4pt] &=\int_a^b(P(t,c)−P(t,d))\,dt+\int_c^d(Q(b,t)−Q(a,t))\,dt\\[4pt] &=−\int_a^b(P(t,d)−P(t,c))\,dt+\int_c^d(Q(b,t)−Q(a,t))\,dt. \end{align*}\]
Pelo Teorema Fundamental do Cálculo,
\[P(t,d)−P(t,c)=\int_c^d \dfrac{\partial}{\partial y}P(t,y)dy \nonumber \]
e
\[Q(b,t)−Q(a,t)=\int_a^b \dfrac{\partial}{\partial x} Q(x,t)\,dx. \nonumber \]
Portanto,
\[−\int_a^b(P(t,d)−P(t,c))\,dt+\int_c^d(Q(b,t)−Q(a,t))\,dt=−\int_a^b\int_c^d \dfrac{\partial}{\partial y} P(t,y)\,dy\,dt+\int_c^d\int_a^b \dfrac{\partial}{\partial x}Q(x,t)\,dx\,dt. \nonumber \]
Mas,
\[\begin{align*} −\int_a^b\int_c^d \dfrac{\partial}{\partial y}P(t,y)\,dy\,dt+\int_c^d\int_a^b \dfrac{\partial}{\partial x}Q(x,t)\,dx\,dt &=−\int_a^b\int_c^d \dfrac{\partial}{\partial y}P(x,y)\,dy\,dx+\int_c^d\int_a^b \dfrac{\partial}{\partial x}Q(x,y)\,dx\,dy \\[4pt] &=\int_a^b\int_c^d(Q_x−P_y)\,dy\,dx\\[4pt] &=\iint_D(Q_x−P_y)\,dA. \end{align*}\]
Portanto,\(\displaystyle \int_C \vecs F\cdot d\vecs r=\iint_D(Q_x−P_y)\,dA\) e provamos o teorema de Green no caso de um retângulo.
\(\square\)
Para provar o teorema de Green sobre uma região geral\(D\), podemos nos decompor\(D\) em muitos retângulos minúsculos e usar a prova de que o teorema funciona sobre retângulos. Os detalhes são técnicos, no entanto, e estão além do escopo deste texto.
Calcule a integral da linha
\[\oint_C x^2ydx+(y−3)dy, \nonumber \]
onde\(C\) é um retângulo com vértices\((1,1)\),\((4,1)\)\((4,5)\), e\((1,5)\) orientado no sentido anti-horário.
Solução
Deixe\( \vecs F(x,y)=⟨P(x,y),Q(x,y)⟩=⟨x^2y,y−3⟩\). Então,\(Q_x(x,y)=0\)\(P_y(x,y)=x^2\) e. Portanto,\(Q_x−P_y=−x^2\).
\(D\)Seja a região retangular delimitada por\(C\) (Figura\(\PageIndex{4}\)). Pelo teorema de Green,
\[\begin{align*} \oint_C x^2ydx+(y−3)\,dy &=\iint_D (Q_x−P_y)\,dA \\[4pt] &=\iint_D −x^2 \,dA=\int_1^5\int_1^4−x^2\,dx\,dy \\[4pt] &=\int_1^5−21\,dy=−84.\end{align*}\]

Análise
Se calculássemos essa integral de linha sem usar o teorema de Green, precisaríamos parametrizar cada lado do retângulo, quebrar a integral de linha em quatro integrais de linha separadas e usar os métodos da seção intitulada Integrais de linha para avaliar cada integral. Além disso, como o campo vetorial aqui não é conservador, não podemos aplicar o Teorema Fundamental para integrais de linha. O teorema de Green torna o cálculo muito mais simples.
Calcule o trabalho realizado em uma partícula por campo de força
\[\vecs F(x,y)=⟨y+\sin x,e^y−x⟩ \nonumber \]
à medida que a partícula atravessa o círculo\(x^2+y^2=4\) exatamente uma vez no sentido anti-horário, começando e terminando no ponto\((2,0)\).
Solução
Vamos\(C\) denotar o círculo e deixar\(D\) ser o disco delimitado por\(C\). O trabalho realizado na partícula é
\[W=\oint_C (y+\sin x)\,dx+(e^y−x)\,dy. \nonumber \]
Como no exemplo\(\PageIndex{1}\), essa integral pode ser calculada usando ferramentas que aprendemos, mas é mais fácil usar a integral dupla dada pelo teorema de Green (Figura\(\PageIndex{5}\)).
Deixe\(\vecs F(x,y)=⟨P(x,y),Q(x,y)⟩=⟨y+\sin x,e^y−x⟩\). Então,\(Q_x=−1\)\(P_y=1\) e. Portanto,\(Q_x−P_y=−2\).
Pelo teorema de Green,
\[\begin{align*} W &=\oint_C(y+\sin(x))dx+(e^y−x)\,dy \\[4pt] &=\iint_D (Q_x−P_y)\,dA \\[4pt] &=\iint_D−2\,dA \\[4pt] &=−2(area(D))=−2\pi (2^2)=−8\pi. \end{align*}\]
Use o teorema de Green para calcular a integral da linha
\[\oint_C \sin(x^2)\,dx+(3x−y)\,dy. \nonumber \]
onde\(C\) é um triângulo reto com vértices\((−1,2)\) e\((4,5)\) orientado no sentido anti-horário.\((4,2)\)
- Dica
-
Transforme a integral da linha em uma integral dupla.
- Responda
-
\(\dfrac{45}{2}\)
Nos dois exemplos anteriores, a integral dupla no teorema de Green era mais fácil de calcular do que a integral de linha, então usamos o teorema para calcular a integral de linha. No próximo exemplo, a integral dupla é mais difícil de calcular do que a integral de linha, então usamos o teorema de Green para traduzir uma integral dupla em uma integral de linha.
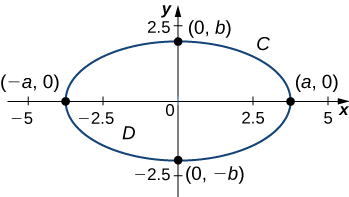
Calcule a área delimitada pela elipse\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\) (Figura\(\PageIndex{6}\)).
Solução
Vamos\(C\) denotar a elipse e\(D\) seja a região delimitada por\(C\). Lembre-se de que a elipse\(C\) pode ser parametrizada por
- \(x=a\cos t\),
- \(y=b \sin t\),
- \(0≤t≤2\pi\).
Calcular a área de\(D\) é equivalente a calcular a integral dupla\(\iint_D \,dA\). Para calcular essa integral sem o teorema de Green, precisaríamos\(D\) dividir em duas regiões: a região acima do eixo x e a região abaixo. A área da elipse é
\[\int_{−a}^a\int_0^{\sqrt{b^2−{(bx/a)}^2}} \,dy\,dx+\int_{−a}^{a} \int_{−\sqrt{b^2−{(bx/a)}^2}}^{0} \,dy\,dx. \nonumber \]
Essas duas integrais não são fáceis de calcular (embora quando sabemos o valor da primeira integral, saibamos o valor da segunda por simetria). Em vez de tentar calculá-los, usamos o teorema de Green para\(\iint_D \,dA\) nos transformar em uma linha integral ao redor do limite\(C\).
Considere o campo vetorial
\[F(x,y)=⟨P,Q⟩=⟨−\dfrac{y}{2},\dfrac{x}{2}⟩. \nonumber \]
Então,\(Q_x=\dfrac{1}{2}\) e\(P_y=−\dfrac{1}{2}\), e portanto\(Q_x−P_y=1\). Observe que\(\vecs F\) foi escolhido para ter a propriedade que\(Q_x−P_y=1\). Como esse é o caso, o teorema de Green transforma a integral reta de\(\vecs F\) over\(C\) na integral dupla de 1 over\(D\).
Pelo teorema de Green,
\[\begin{align*} \iint_D \,dA &=\iint_D (Q_x−P_y)\,dA \\[4pt] &=\int_C \vecs F\cdot d\vecs r=\dfrac{1}{2}\int_C −y\,dx+x\,dy \\[4pt] &=\dfrac{1}{2}\int_0^{2\pi}−b \sin t(−a\sin t)+a(\cos t)b\cos t\,dt \\[4pt] &=\dfrac{1}{2}\int_0^{2\pi} ab \cos^2 t+ab \sin^2 t\,dt \\[4pt] &=\dfrac{1}{2}\int_0^{2\pi} ab\,dt =\pi ab. \end{align*}\]
Portanto, a área da elipse é\(\pi ab\;\text{units}^2\).
No exemplo\(\PageIndex{3}\), usamos o campo vetorial\(\vecs F(x,y)=⟨P,Q⟩=⟨−\dfrac{y}{2},\dfrac{x}{2}⟩\) para encontrar a área de qualquer elipse. A lógica do exemplo anterior pode ser estendida para derivar uma fórmula para a área de qualquer região\(D\). \(D\)Seja qualquer região com um limite que seja uma curva fechada simples\(C\) orientada no sentido anti-horário. Se\(F(x,y)=⟨P,Q⟩=⟨−\dfrac{y}{2},\dfrac{x}{2}⟩\), então\(Q_x−P_y=1\). Portanto, pela mesma lógica do Exemplo\(\PageIndex{3}\),
\[ \text{area of} \; D=\iint_D dA=\dfrac{1}{2}\oint_C−ydx+xdy. \label{greenarea} \]
É importante notar que, se\(F=⟨P,Q⟩\) houver algum campo vetorial com\(Q_x−P_y=1\), a lógica do parágrafo anterior funciona. Então. A equação\ ref {greenarea} não é a única equação que usa os parciais mistos de um campo vetorial para obter a área de uma região.
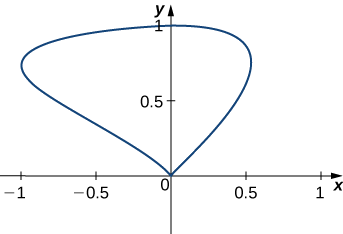
Encontre a área da região delimitada pela curva com parametrização\(r(t)=⟨\sin t\cos t,\sin t⟩\),\(0≤t≤\pi\).
- Dica
-
Use a Equação\ ref {greenarea}.
- Responda
-
\(\dfrac{4}{3}\)
Forma de fluxo do teorema de Green
A forma de circulação do teorema de Green relaciona uma integral dupla sobre região\(D\) com integral de linha\(\oint_C \vecs F·\vecs Tds\), onde\(C\) é o limite de\(D\). A forma de fluxo do teorema de Green relaciona uma integral dupla sobre\(D\) a região com o fluxo através do limite\(C\). O fluxo de um fluido em uma curva pode ser difícil de calcular usando a integral da linha de fluxo. Essa forma do teorema de Green nos permite traduzir uma integral de fluxo difícil em uma integral dupla que geralmente é mais fácil de calcular.
\(D\)Seja uma região aberta, simplesmente conectada, com uma curva limite\(C\) que é uma curva fechada simples e suave em partes, orientada no sentido anti-horário (Figura\(\PageIndex{7}\)). \(\vecs F=⟨P,Q⟩\)Seja um campo vetorial com funções de componentes que tenham derivadas parciais contínuas em uma região aberta contendo\(D\). Então,
\[\oint_C \vecs F·\vecs N\,ds=\iint_D P_x+Q_y\,dA. \label{GreenN} \]
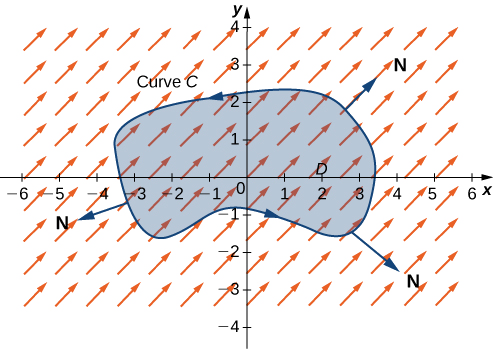
Como essa forma do teorema de Green contém vetor normal unitário\(\vecs N\), às vezes é chamada de forma normal do teorema de Green.
Lembre-se disso\(\displaystyle \oint_C \vecs F·\vecs N\,ds=\oint_C −Q\,dx+P\,dy\). Deixe\(M=−Q\)\(N=P\) e. Pela forma de circulação do teorema de Green,
\[\begin{align*} \oint_C−Q\,dx+P\,dy &=\oint_C M\,dx+N\,dy\\[4pt] &=\iint_D N_x−M_y \,dA\\[4pt] &=\iint_D P_x−{(−Q)}_y \,dA\\[4pt] &=\iint_D P_x+Q_y \,dA. \end{align*}\]
\(\square\)
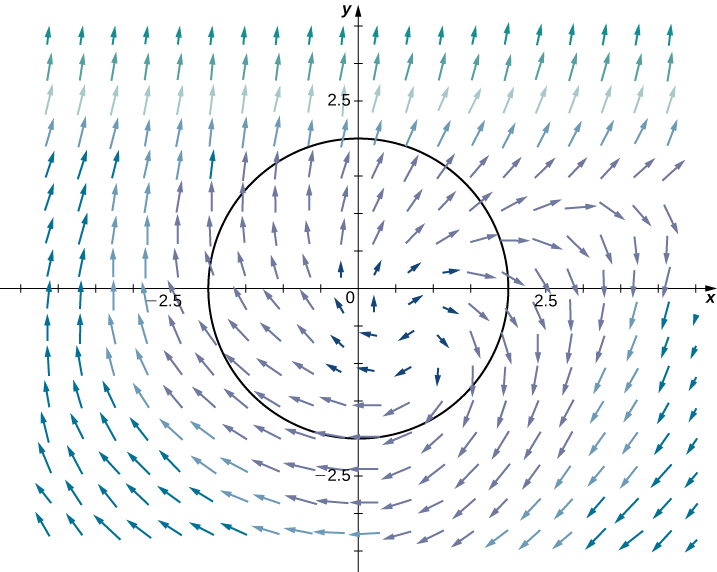
\(C\)Seja um círculo de raio\(r\) centrado na origem (Figura\(\PageIndex{8}\)) e deixe\(\vecs F(x,y)=⟨x,y⟩\). Calcule o fluxo transversal\(C\).

Solução
\(D\)Seja o disco delimitado por\(C\). O fluxo que atravessa\(C\) é\(\displaystyle \oint_C \vecs F·\vecs N\,ds\). Poderíamos avaliar essa integral usando ferramentas que aprendemos, mas o teorema de Green torna o cálculo muito mais simples. Deixe\(P(x,y)=x\) e\(Q(x,y)=y\) faça isso\(\vecs F=⟨P,Q⟩\). Observe isso e\(P_x=1=Q_y\), portanto,\(P_x+Q_y=2\). Pelo teorema de Green,
\[\int_C \vecs F\cdot\vecs N\,ds=\iint_D 2\,dA=2\iint_D \,dA. \nonumber \]
Uma vez que\(\displaystyle \iint_D \,dA\) é a área do círculo,\(\displaystyle \iint_D \,dA=\pi r^2\). Portanto, o fluxo que atravessa\(C\) é\(2\pi r^2\).
\(S\)Seja o triângulo com vértices\((0,0)\) e\((0,3)\) orientado no sentido horário (Figura\(\PageIndex{9}\)).\((1,0)\) Calcule o fluxo da\(\vecs F(x,y)=⟨P(x,y),Q(x,y)⟩=⟨x^2+e^y,x+y⟩\) cruz\(S\).
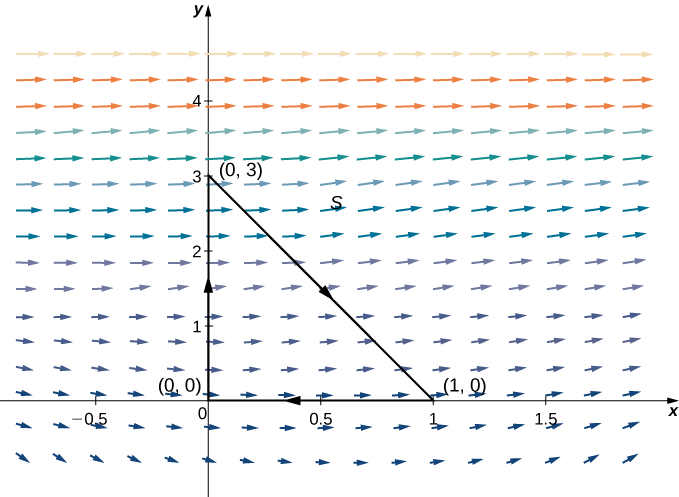
Solução
Para calcular o fluxo sem o teorema de Green, precisaríamos quebrar a integral do fluxo em três integrais de linha, uma integral para cada lado do triângulo. Usar o teorema de Green para traduzir a integral da linha de fluxo em uma única integral dupla é muito mais simples.
\(D\)Seja a região cercada por\(S\). Observe isso\(P_x=2x\) e\(Q_y=1\); portanto,\(P_x+Q_y=2x+1\). O teorema de Green se aplica apenas a curvas fechadas simples orientadas no sentido anti-horário, mas ainda podemos aplicar o teorema porque ele\(\displaystyle \oint_C \vecs F·\vecs N\,ds=−\oint_{−S} \vecs F·\vecs N\,ds\)\(−S\) é orientado no sentido anti-horário. Pelo teorema de Green, o fluxo é
\[\begin{align*} \oint_C \vecs F·\vecs N\,ds &= \oint_{−S} \vecs F·\vecs N\,ds\\[4pt] &=−\iint_D (P_x+Q_y)\,dA \\[4pt] &=−\iint_D (2x+1)\,dA.\end{align*}\]
Observe que a borda superior do triângulo é a linha\(y=−3x+3\). Portanto, na integral dupla iterada, os\(y\) valores -vão de\(y=0\) até\(y=−3x+3\), e temos
\[\begin{align*} −\iint_D (2x+1)\,dA &= −\int_0^1\int_0^{−3x+3}(2x+1)\,dy\,dx \\[4pt] &=−\int_0^1(2x+1)(−3x+3)\,dx \\[4pt] &=−\int_0^1(−6x^2+3x+3)\,dx\\[4pt] &=−{[−2x^3+\dfrac{3x^2}{2}+3x]}_0^1 \\[4pt] &=−\dfrac{5}{2}. \end{align*}\]
Calcule o fluxo de\(\vecs F(x,y)=⟨x^3,y^3⟩\) um círculo unitário orientado no sentido anti-horário.
- Dica
-
Aplique o teorema de Green e use coordenadas polares.
- Responda
-
\(\dfrac{3\pi}{2}\)
A água flui de uma fonte localizada na origem. A velocidade da água é modelada pelo campo vetorial\(\vecs v(x,y)=⟨5x+y,x+3y⟩\) m/seg. Encontre a quantidade de água por segundo que flui pelo retângulo com os vértices\((−1,−2)\)\((1,−2)\),\((1,3)\), e\((−1,3)\), orientados no sentido anti-horário (Figura\(\PageIndex{10}\)).

Solução
Vamos\(C\) representar o retângulo dado e\(D\) ser a região retangular delimitada por\(C\). Para encontrar a quantidade de água que flui\(C\), calculamos o fluxo\(\int_C \vecs v\cdot d\vecs r\). Deixe\(P(x,y)=5x+y\) e\(Q(x,y)=x+3y\) faça isso\(\vecs v=⟨P,Q⟩\). Então,\(P_x=5\)\(Q_y=3\) e. Pelo teorema de Green,
\[\begin{align*} \int_C \vecs v\cdot d\vecs r &=\iint_D (P_x+Q_y)\,dA \\ &=\iint_D 8\,dA \\ &=8(area\space of\space D)=80. \end{align*}\]
Portanto, o fluxo de água é de 80 m 2 /seg.
Lembre-se de que, se o campo vetorial\(\vecs F\) for conservador, não\(\vecs F\) funciona com curvas fechadas, ou seja, a circulação\(\vecs F\) ao redor de uma curva fechada é zero. De fato, se o domínio de\(\vecs F\) estiver simplesmente conectado, então\(\vecs F\) é conservador se e somente se a circulação\(\vecs F\) ao redor de qualquer curva fechada for zero. Se substituirmos “circulação de\(\vecs F\)” por “fluxo de”\(\vecs F\), obteremos a definição de um campo vetorial sem fonte. Todas as declarações a seguir são formas equivalentes de definir um campo sem fonte\(\vecs F=⟨P,Q⟩\) em um domínio simplesmente conectado (observe as semelhanças com as propriedades de campos vetoriais conservadores):
- O fluxo\( \displaystyle \oint_C \vecs F·\vecs N\,ds\) em qualquer curva fechada\(C\) é zero.
- Se\(C_1\) e\(C_2\) são curvas no domínio de\(\vecs F\) com os mesmos pontos iniciais e finais, então\(\displaystyle \int_{C_1} \vecs F·\vecs N\,ds=\int_{C_2} \vecs F·\vecs N\,ds\). Em outras palavras, o fluxo é independente do caminho.
- Existe uma função de transmissão\(g(x,y)\) para\(\vecs F\). Uma função de fluxo para\(\vecs F=⟨P,Q⟩\) é uma função g tal que\(P=g_y\) e\(Q=−g_x\) .Geometricamente,\(\vecs F=\langle a,b\rangle\) é tangencial à curva de nível de\(g\) at\((a,b)\). Como o gradiente de\(g\) é perpendicular à curva de nível de\(g\) at\((a,b)\), a função stream\(g\) tem a propriedade\(\vecs F(a,b)\cdot\vecs\nabla g(a,b)=0\) de qualquer ponto\((a,b)\) no domínio de\(g\). (As funções de fluxo desempenham o mesmo papel para campos sem fonte que as funções potenciais desempenham para campos conservadores.)
- \(P_x+Q_y=0\)
Verifique se o campo vetorial de rotação\(\vecs F(x,y)=⟨y,−x⟩\) não tem fonte e encontre uma função de fluxo para\(\vecs F\).
Solução
Observe que o domínio de\(\vecs F\) é tudo de\(ℝ^2\), que está simplesmente conectado. Portanto, para mostrar\(\vecs F\) que não tem fonte, podemos mostrar que qualquer um dos itens 1 a 4 da lista anterior é verdadeiro. Neste exemplo, mostramos que o item 4 é verdadeiro. Deixe\(P(x,y)=y\)\(Q(x,y)=−x\) e. Então\(P_x+0=Q_y\), e portanto\(P_x+Q_y=0\). Portanto,\(\vecs F\) é livre de fonte.
Para encontrar uma função de fluxo para\(\vecs F\), proceda da mesma maneira que encontrar uma função potencial para um campo conservador. \(g\)Seja uma função de transmissão para\(\vecs F\). Então\(g_y=y\), o que implica que
\(g(x,y)=\dfrac{y^2}{2}+h(x)\).
Desde então\(−g_x=Q=−x\), nós temos\(h′(x)=x\). Portanto,
\(h(x)=\dfrac{x^2}{2}+C\).
Deixar\(C=0\) dar função de transmissão
\(g(x,y)=\dfrac{x^2}{2}+\dfrac{y^2}{2}\).
Para confirmar que\(g\) é uma função de transmissão para\(\vecs F\), observe que\(g_y=y=P\)\(−g_x=−x=Q\) e.
Observe que o campo vetorial de rotação sem fonte\(\vecs F(x,y)=⟨y,−x⟩\) é perpendicular ao campo vetorial radial conservador\(\vecs \nabla g=⟨x,y⟩\) (Figura\(\PageIndex{11}\)).
Encontre uma função de fluxo para o campo vetorial\(\vecs F(x,y)=⟨x \sin y,\cos y⟩\).
- Dica
-
Siga o esboço fornecido no exemplo anterior.
- Responda
-
\(g(x,y)=−x\cos y\)
Campos vetoriais que são conservadores e livres de fontes são campos vetoriais importantes. Uma característica importante dos campos vetoriais conservadores e sem fonte em um domínio simplesmente conectado é que qualquer função potencial\(f\) desse campo satisfaz a equação de Laplace\(f_{xx}+f_{yy}=0\). A equação de Laplace é fundamental no campo das equações diferenciais parciais porque modela fenômenos como os potenciais gravitacionais e magnéticos no espaço e o potencial de velocidade de um fluido ideal. Uma função que satisfaz a equação de Laplace é chamada de função harmônica. Portanto, qualquer função potencial de um campo vetorial conservador e sem fonte é harmônica.
Para ver que qualquer função potencial de um campo vetorial conservador e sem fonte em um domínio simplesmente conectado é harmônica,\(f\) seja essa função potencial do campo vetorial\(\vecs F=⟨P,Q⟩\). Então,\(f_x=P\) e\(f_x=Q\) porque\(\vecs \nabla f=\vecs F\). Portanto,\(f_{xx}=P_x\)\(f_{yy}=Q_y\) e. Uma vez que\(\vecs F\) é livre de fontes\(f_{xx}+f_{yy}=P_x+Q_y=0\), e nós temos isso\(f\) é harmônico.
Para campo vetorial\(\vecs F(x,y)=⟨e^x\sin y,e^x\cos y⟩\), verifique se o campo é conservador e livre de fontes, encontre uma função potencial para\(\vecs F\) e verifique se a função potencial é harmônica.
Solução
Deixe\(P(x,y)=e^x\sin y\)\(Q(x,y)=e^x \cos y\) e. Observe que o domínio de\(\vecs F\) é todo de dois espaços, que é simplesmente conectado. Portanto, podemos verificar os parciais cruzados de\(\vecs F\) para determinar se\(\vecs F\) é conservador. Note que\(P_y=e^x \cos y=Q_x\), assim como\(\vecs F\) é conservador. Uma vez que\(P_x=e^x \sin y\) e\(Q_y=e^x \sin y\),\(P_x+Q_y=0\) e o campo é livre de fonte.
Para encontrar uma função potencial para\(\vecs F\),\(f\) seja uma função potencial. Então\(\vecs \nabla f=\vecs F\), então\(f_x(x,y)=e^x \sin y\). Integrar essa equação em relação a x dá\(f(x,y)=e^x \sin y+h(y)\). Uma vez que\(f_y(x,y)=e^x \cos y\), diferenciar em\(f\) relação a y dá\(e^x\cos y=e^x\cos y+h′(y)\). Portanto, podemos assumir\(h(y)=0\), e\(f(x,y)=e^x\sin y\) é uma função potencial para\(f\).
Para verificar se\(f\) é uma função harmônica, observe que\(f_{xx}(x,y)=\dfrac{\partial}{\partial x}(e^x\sin y)=e^x \sin y\) e
\(f_{yy}(x,y)=\dfrac{\partial}{\partial x}(e^x\cos y)=−e^x\sin y\). Portanto,\(f_{xx}+f_{yy}=0\), e\(f\) satisfaz a equação de Laplace.
A função é\(f(x,y)=e^{x+5y}\) harmônica?
- Dica
-
Determine se a função satisfaz a equação de Laplace.
- Responda
-
Não
Teorema de Green sobre regiões gerais
O teorema de Green, conforme declarado, se aplica apenas a regiões que estão simplesmente conectadas, ou seja, o teorema de Green, conforme declarado até agora, não pode lidar com regiões com buracos. Aqui, estendemos o teorema de Green para que ele funcione em regiões com finitos buracos (Figura\(\PageIndex{12}\)).
Antes de discutir extensões do teorema de Green, precisamos examinar algumas terminologias sobre o limite de uma região. \(D\)Seja uma região e\(C\) seja um componente do limite de\(D\). Dizemos que\(C\) é orientado positivamente se, à medida que caminhamos\(C\) na direção da orientação, a região\(D\) estiver sempre à nossa esquerda. Portanto, a orientação anti-horária do limite de um disco é uma orientação positiva, por exemplo. \(C\)A curva é orientada negativamente se, à medida que caminhamos\(C\) na direção da orientação, a região\(D\) estiver sempre à nossa direita. A orientação no sentido horário do limite de um disco é negativa, por exemplo.
\(D\)Seja uma região com finitos furos (de modo que\(D\) tenha finitas curvas de limite) e denote o limite de\(D\) por\(\partial D\) (Figura\(\PageIndex{13}\)). Para estender o teorema de Green para que ele possa lidar\(D\), dividimos a região\(D\) em duas regiões,\(D_1\)\(\partial D_1\) e\(D_2\) (com os respectivos limites e\(\partial D_2\)), de tal forma que\(D=D_1\cup D_2\)\(D_1\) nem\(D_2\) tenha buracos (Figura\(\PageIndex{13}\)).
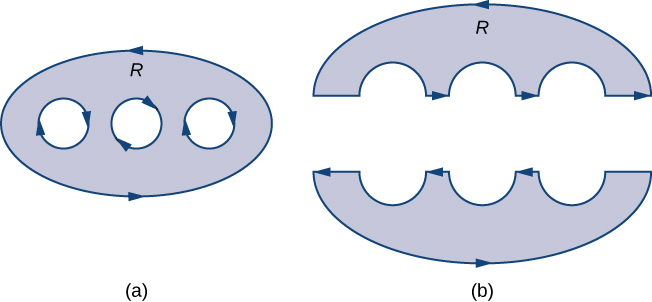
Suponha que o limite de\(D\) esteja orientado como na figura, com os orifícios internos com orientação negativa e o limite externo com orientação positiva. O limite de cada região\(D_1\) simplesmente conectada\(D_2\) é orientado positivamente. Se\(\vecs F\) for um campo vetorial definido em\(D\), então o teorema de Green diz que
\[\begin{align} \oint_{\partial D} \vecs F·d\vecs{r} &=\oint_{\partial D_1}\vecs F·d\vecs{r}+\oint_{\partial D_2}\vecs F·d\vecs{r} \\ &=\iint_{D_1}Q_x−P_y\,dA+\iint_{D_2}Q_x−P_y\,dA \\ &=\iint_D (Q_x−P_y)\,dA.\end{align} \nonumber \]
Portanto, o teorema de Green ainda funciona em uma região com buracos.
Para ver como isso funciona na prática, considere o anel\(D\) na Figura\(\PageIndex{14}\) e suponha que\(F=⟨P,Q⟩\) seja um campo vetorial definido nesse anel. \(D\)A região tem um buraco, então não está simplesmente conectada. Oriente o círculo externo do anel no sentido anti-horário e o círculo interno no sentido horário (Figura\(\PageIndex{14}\)) para que, ao dividirmos a região em\(D_1\) e\(D_2\), possamos manter a região à nossa esquerda enquanto caminhamos por um caminho que atravessa a fronteira. \(D_1\)Seja a metade superior do anel e\(D_2\) seja a metade inferior. Nenhuma dessas regiões tem buracos, então nos\(D\) dividimos em duas regiões simplesmente conectadas.
Rotulamos cada pedaço desses novos limites como\(P_i\) para alguns\(i\), como na Figura\(\PageIndex{14}\). Se começarmos\(P\) e viajarmos ao longo do limite orientado, o primeiro segmento é\(P_1\)\(P_2\), então\(P_3\),\(P_4\) e. Agora atravessamos\(D_1\) e voltamos para\(P\). Em seguida, começamos de\(P\) novo e atravessamos\(D_2\). Como a primeira parte do limite é a mesma que\(P_4\) em\(D_1\), mas orientada na direção oposta, a primeira parte do\(D_2\) é\(−P_4\). Em seguida, temos\(P_5\)\(−P_2\), então e finalmente\(P_6\).
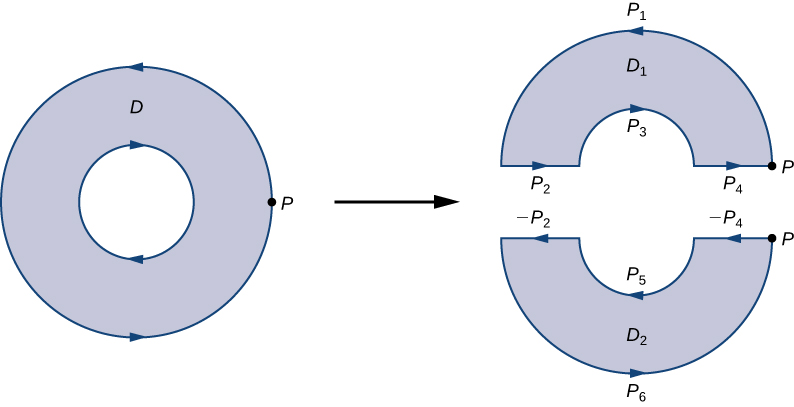
A figura\(\PageIndex{14}\) mostra um caminho que atravessa o limite de\(D\). Observe que esse caminho atravessa o limite da região\(D_1\), retorna ao ponto de partida e, em seguida, atravessa o limite da região\(D_2\). Além disso, à medida que caminhamos pelo caminho, a região está sempre à nossa esquerda. Observe que essa travessia dos\(P_i\) caminhos cobre todo o limite da região\(D\). Se tivéssemos atravessado apenas uma parte do limite de\(D\), então não podemos aplicar o teorema de Green\(D\) a.
O limite da metade superior do anel, portanto, é\(P_1\cup P_2\cup P_3\cup P_4\) e o limite da metade inferior do anel é\(−P_4\cup P_5\cup −P_2\cup P_6\). Então, o teorema de Green implica
\[\begin{align} \oint_{\partial D}\vecs F·d\vecs{r} &=\int_{P_1}\vecs F·d\vecs{r}+\int_{P_2}\vecs F·d\vecs{r}+\int_{P_3}\vecs F·d\vecs{r}+\int_{P_4}\vecs F·d\vecs{r}+\int_{−P_4}\vecs F·d\vecs{r}+\int_{P_5}\vecs F·d\vecs{r}+\int_{−P_2}\vecs F·d\vecs{r}+\int_{P_6}\vecs F·d\vecs{r} \\ &=\int_{P_1}\vecs F·d\vecs{r}+\int_{P_2}\vecs F·d\vecs{r}+\int_{P_3}\vecs F·d\vecs{r}+\int_{P_4}\vecs F·d\vecs{r}+\int_{P_4}\vecs F·d\vecs{r}+\int_{P_5}\vecs F·d\vecs{r}+\int_{−P_2}\vecs F·d\vecs{r}+\int_{P_6}\vecs F·d\vecs{r} \\ &=\int_{P_1}\vecs F·d\vecs{r}+\int_{P_3}\vecs F·d\vecs{r}+\int_{P_5}\vecs F·d\vecs{r}+\int_{P_6}\vecs F·d\vecs{r} \\ &=\oint_{\partial D_1}\vecs F·d\vecs{r}+\oint_{\partial D_2}\vecs F·d\vecs{r}\\ &=\iint_{D_1}(Q_x−P_y)\,dA+\iint_{D_2}(Q_x−P_y)\,dA \\ &=\iint_D(Q_x−P_y)\,dA. \end{align} \nonumber \]
Portanto, chegamos à equação encontrada no teorema de Green, a saber,
\[\oint_{\partial D}\vecs F·d\vecs{r}=\iint_D (Q_x−P_y)\,dA. \nonumber \]
A mesma lógica implica que a forma de fluxo do teorema de Green também pode ser estendida para uma região com finitos buracos:
\[\oint_C F·N\,ds=\iint_D (P_x+Q_y)\,dA. \nonumber \]
Calcule a integral
\[\oint_{\partial D}(\sin x−\dfrac{y^3}{3})dx+(\dfrac{y^3}{3}+\sin y)dy, \nonumber \]
onde\(D\) está o anel dado pelas desigualdades polares\(1≤r≤2\),\(0≤\theta≤2\pi\).
Solução
Embora não\(D\) esteja simplesmente conectado, podemos usar a forma estendida do teorema de Green para calcular a integral. Como a integração ocorre sobre um anel, convertemos em coordenadas polares:
\[\begin{align*} \oint_{\partial D}(\sin x−\dfrac{y^3}{3})\,dx+(\dfrac{x^3}{3}+\sin y)\,dy &=\iint_D (Q_x−P_y)\,dA \\ &=\iint_D (x^2+y^2)\,dA\\ &=\int_0^{2\pi}\int_1^2 r^3\,drd\theta=\int_0^{2\pi} \dfrac{15}{4}\,d\theta \\ &=\dfrac{15\pi}{2}. \end{align*}\]
Seja\(\vecs F=⟨P,Q⟩=⟨\dfrac{y}{x^2+y^2},-\dfrac{x}{x^2+y^2}⟩\) e\(C\) seja qualquer curva fechada simples em um plano orientado no sentido anti-horário. Quais são os valores possíveis de\(\oint_C \vecs F·d\vecs{r}\)?
Solução
Usamos a forma estendida do teorema de Green para mostrar que\(\oint_C \vecs F·d\vecs{r}\) é\(0\) ou\(−2\pi\) - isto é, não importa o quão louca\(C\) seja a curva, a integral da reta de\(\vecs F\) along\(C\) pode ter apenas um dos dois valores possíveis. Consideramos dois casos: o caso quando\(C\) engloba a origem e o caso em\(C\) que não engloba a origem.
Caso 1: C não abrange a origem
Nesse caso, a região delimitada por\(C\) é simplesmente conectada porque o único orifício no domínio de\(\vecs F\) está na origem. Mostramos em nossa discussão sobre parciais cruzados que\(\vecs F\) satisfazem a condição parcial cruzada. Se restringirmos o domínio de\(\vecs F\) apenas a\(C\) e a região que ele abrange, então,\(\vecs F\) com esse domínio restrito, agora é definido em um domínio conectado de forma simples. Como\(\vecs F\) satisfaz a propriedade parcial cruzada em seu domínio restrito, o campo\(\vecs F\) é conservador nessa região simplesmente conectada e, portanto, a circulação\(\oint_C \vecs F·d\vecs{r}\) é zero.
Caso 2: C abrange a origem
Nesse caso, a região delimitada não\(C\) está simplesmente conectada porque contém um orifício na origem. \(C_1\)Seja um círculo de raio a centrado na origem de forma que\(C_1\) fique inteiramente dentro da região delimitada por\(C\) (Figura\(\PageIndex{15}\)). Dê\(C_1\) uma orientação no sentido horário.
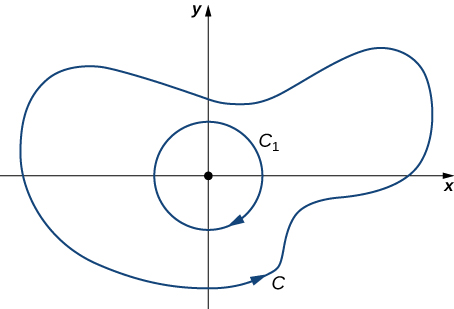
\(D\)Seja a região entre\(C_1\) e\(C\), e\(C\) seja orientada no sentido anti-horário. Pela versão estendida do teorema de Green,
\[\begin{align*} \int_C \vecs F·d\vecs{r}+\int_{C_1}\vecs F·d\vecs{r} &=\iint_D Qx_−P_y \,dA \\[4pt] &=\iint_D−\dfrac{y^2−x^2}{{(x^2+y^2)}^2}+\dfrac{y^2−x^2}{{(x^2+y^2)}^2}dA \\[4pt] &=0, \end{align*}\]
e, portanto,
\[\int_C \vecs F·d\vecs{r}=−\int_{C_1} \vecs F·d\vecs{r}. \nonumber \]
Como\(C_1\) é uma curva específica, podemos avaliar\(\int_{C_1}\vecs F·d\vecs{r}\). Deixe
\[ x=a\cos t, \;\; y=a\sin t, \;\; 0≤t≤2\pi \nonumber \]
seja uma parametrização de\(C_1\). Então,
\[\begin{align*} \int_{C_1}\vecs F·d\vecs{r} &=\int_0^{2\pi} F(r(t))·r′(t)dt \\[4pt] &=\int_0^{2\pi} ⟨−\dfrac{\sin(t)}{a},−\dfrac{\cos(t)}{a}⟩·⟨−a\sin(t),−a\cos(t)⟩dt \\[4pt] &=\int_0^{2\pi}{\sin}^2(t)+{\cos}^2(t)dt \\[4pt] &=\int_0^{2\pi}dt=2\pi. \end{align*}\]
Portanto,\(\int_C F·ds=−2\pi\).
Calcule integral\(\oint_{\partial D}\vecs F·d\vecs{r}\), onde\(D\) está o anel dado pelas desigualdades polares\(2≤r≤5\)\(0≤\theta≤2\pi\),,\(F(x,y)=⟨x^3,5x+e^y\sin y⟩\) e.
- Dica
-
Use a versão estendida do teorema de Green.
- Responda
-
\(105\pi\)
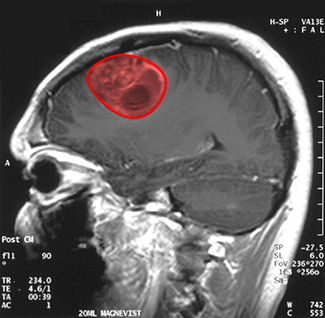
Imagine que você é um médico que acaba de receber uma imagem de ressonância magnética do cérebro do seu paciente. O cérebro tem um tumor (Figura\(\PageIndex{16}\)). Qual é o tamanho do tumor? Para ser mais preciso, qual é a área da região vermelha? A seção transversal vermelha do tumor tem uma forma irregular e, portanto, é improvável que você consiga encontrar um conjunto de equações ou desigualdades para a região e depois calcular sua área por meios convencionais. Você pode aproximar a área cortando a região em pequenos quadrados (uma abordagem de soma de Riemann), mas esse método sempre fornece uma resposta com algum erro.
Em vez de tentar medir a área da região diretamente, podemos usar um dispositivo chamado planímetro rolante para calcular exatamente a área da região, simplesmente medindo seu limite. Neste projeto, você investiga como um planímetro funciona e usa o teorema de Green para mostrar que o dispositivo calcula a área corretamente.
Um planímetro rolante é um dispositivo que mede a área de uma região plana traçando o limite dessa região (Figura\(\PageIndex{17}\)). Para medir a área de uma região, simplesmente passamos o traçador do planímetro ao redor do limite da região. O planímetro mede o número de voltas pelas quais a roda gira à medida que traçamos o limite; a área da forma é proporcional a esse número de voltas da roda. Podemos derivar a equação de proporcionalidade precisa usando o teorema de Green. Conforme o traçador se move ao redor do limite da região, o braço traçador gira e o rolo se move para frente e para trás (mas não gira).
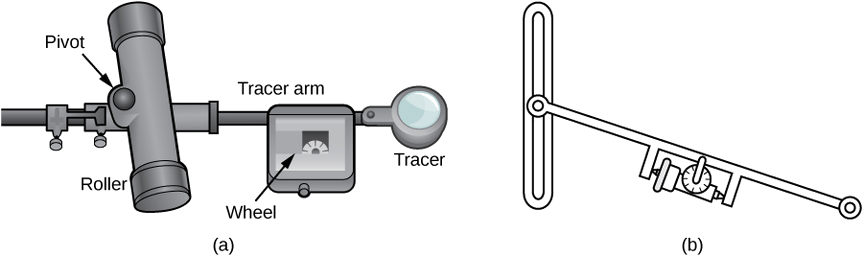
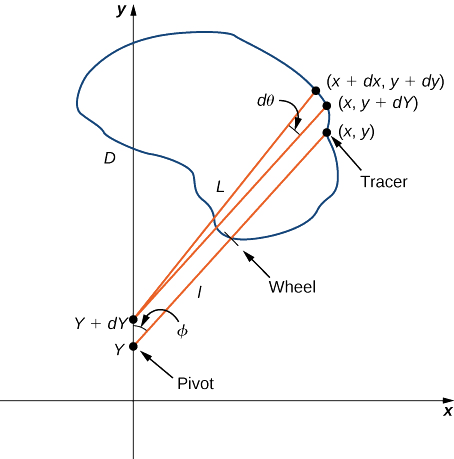
Vamos\(C\) indicar o limite da região\(D\), a área a ser calculada. À medida que o traçador atravessa a curva\(C\), suponha que o rolo se mova ao longo do eixo y (como o rolo não gira, pode-se supor que ele se move ao longo de uma linha reta). Use as coordenadas\((x,y)\) para representar pontos no limite\(C\) e coordenadas\((0,Y)\) para representar a posição do pivô. Conforme o planímetro traça\(C\), o pivô se move ao longo do eixo y enquanto o braço traçador gira no pivô.
Assista a uma breve animação de um planímetro em ação.
Comece a análise considerando o movimento do traçador à medida que ele se move do ponto\((x,y)\) no sentido anti-horário para o ponto\((x+dx,y+dy)\) próximo de\((x,y)\) (Figura\(\PageIndex{18}\)). O pivô também se move, de um ponto\((0,Y)\) para outro\((0,Y+dY)\). Quanto a roda gira como resultado desse movimento? Para responder a essa pergunta, divida o movimento em duas partes. Primeiro, role o pivô ao longo do eixo y de\((0,Y)\) para\((0,Y+dY)\) sem girar o braço traçador. O braço traçador então termina no ponto,\((x,y+dY)\) mantendo um ângulo constante\(\phi\) com o eixo x. Em segundo lugar, gire o braço traçador em um ângulo\(d\theta\) sem mover o rolo. Agora, o traçador está no ponto certo\((x+dx,y+dy)\). Seja ll a distância do pivô até a roda e L seja a distância do pivô até o traçador (o comprimento do braço traçador).

- Explique por que a distância total pela qual a roda rola o pequeno movimento que acabamos de descrever é\(\sin \phi dY+ld\theta=\dfrac{x}{L}dY+ld\theta\).
- Mostre isso\(\oint_C d\theta=0\).
- Use a etapa 2 para mostrar que a distância total de rolamento da roda à medida que o traçador percorre a curva\(C\) é a rotação
total da roda\(=\dfrac{1}{L}\oint_C xdY\).
Agora que você tem uma equação para a distância total de rolamento da roda, conecte essa equação ao teorema de Green para calcular a área\(D\) delimitada por\(C\). - Mostre isso\(x^2+(y−Y)^2=L^2\).
- Suponha que a orientação do planímetro seja a mostrada na Figura\(\PageIndex{18}\). Explique por que\(Y≤y\), e use essa desigualdade para mostrar que há um valor único de\(Y\) para cada ponto\((x,y)\):\(Y=y=\sqrt{L^2−x^2}\).
- Use a etapa 5 para mostrar que\(dY=dy+\dfrac{x}{L^2−x^2}dx.\)
- Use o teorema de Green para mostrar isso\(\displaystyle \oint_C \dfrac{x}{L^2−x^2}dx=0\).
- Use a etapa 7 para mostrar que o rolamento total da roda é
\[\text{Total wheel roll}\quad =\quad 1L\oint_C x\,dy. \nonumber \]
Deu um pouco de trabalho, mas essa equação diz que a variável de integração Y na etapa 3 pode ser substituída por y.
- Use o teorema de Green para mostrar que a área de\(D\) é\(\oint_C xdy\). A lógica é semelhante à lógica usada para mostrar que a área de\(\displaystyle D=12\oint_C −y\,dx+x\,dy\).
- Conclua que a área de\(D\) é igual ao comprimento do braço traçador multiplicado pela distância total de rolamento da roda.
Agora você sabe como um planímetro funciona e usou o teorema de Green para justificar que ele funciona. Para calcular a área de uma região plana\(D\), use um planímetro para traçar o limite da região. A área da região é o comprimento do braço traçador multiplicado pela distância em que a roda rolou.
Conceitos-chave
- O teorema de Green relaciona a integral sobre uma região conectada a uma integral sobre o limite da região. O teorema de Green é uma versão do Teorema Fundamental do Cálculo em uma dimensão superior.
- O Teorema de Green tem duas formas: uma forma de circulação e uma forma de fluxo. Na forma de circulação, o integrando é\(\vecs F·\vecs T\). Na forma de fluxo, o integrando é\(\vecs F·\vecs N\).
- O teorema de Green pode ser usado para transformar uma integral de linha difícil em uma integral dupla mais fácil ou para transformar uma integral dupla difícil em uma integral de linha mais fácil.
- Um campo vetorial não tem fonte se tiver uma função de fluxo. O fluxo de um campo vetorial sem fonte em uma curva fechada é zero, assim como a circulação de um campo vetorial conservador em uma curva fechada é zero.
Equações-chave
- Teorema de Green, forma de circulação
\(\displaystyle ∮_C P\,dx+Q\,dy=∬_D Q_x−P_y\,dA\), onde\(C\) está o limite de\(D\) - Teorema de Green, forma de fluxo
\(\displaystyle ∮_C\vecs F·\vecs N\,ds=∬_D P_x+Q_y\,dA\), onde\(C\) está o limite de\(D\) - Teorema de Green, versão estendida
\(\displaystyle ∮_{\partial D}\vecs F·d\vecs{r}=∬_D Q_x−P_y\,dA\)
Glossário
- Teorema de Green
- relaciona a integral sobre uma região conectada a uma integral sobre o limite da região
- função de fluxo
- se\(\vecs F=⟨P,Q⟩\) é um campo vetorial sem fonte, então a função stream\(g\) é uma função tal que\(P=g_y\) e\(Q=−g_x\)


