16.4E: Exercícios para a Seção 16.4

Last updated
Save as PDF

Page ID: 188567

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Para os exercícios a seguir, avalie as integrais de linha aplicando o teorema de Green.

1. $\displaystyle \int_C 2xy\,dx+(x+y)\,dy$, onde$C$ é o caminho de$(0, 0)$ para$(1, 1)$ ao longo do gráfico de$y=x^3$ e de$(1, 1)$ para$(0, 0)$ ao longo do gráfico de$y=x$ orientado no sentido anti-horário

2. $\displaystyle \int_C 2xy\,dx+(x+y)\,dy$, onde$C$ é o limite da região situada entre os gráficos$y=0$ e$y=4−x^2$ orientada no sentido anti-horário

Resposta: $\displaystyle \int_C2xy\,dx+(x+y)\,dy=\frac{32}{3}$unidades de trabalho

3. $\displaystyle \int_C 2\arctan\left(\frac{y}{x}\right)\,dx+\ln(x^2+y^2)\,dy$, onde$C$ é definido por$x=4+2\cos θ,\;y=4\sin θ$ orientado no sentido anti-horário

4. $\displaystyle \int_C \sin x\cos y\,dx+(xy+\cos x\sin y)\,dy$, onde$C$ é o limite da região situada entre os gráficos$y=x$ e$y=\sqrt{x}$ orientada no sentido anti-horário

Resposta: $\displaystyle \int_C\sin x\cos y\,dx+(xy+\cos x\sin y)\,dy=\frac{1}{12}$unidades de trabalho

5. $\displaystyle \int_C xy\,dx+(x+y)\,dy$, onde$C$ é o limite da região situada entre os gráficos$x^2+y^2=1$ e$x^2+y^2=9$ orientada no sentido anti-horário

6. $\displaystyle ∮_C (−y\,dx+x\,dy)$, onde$C$ consiste no segmento$C_1$ de linha de$(−1,0)$ até$(1, 0)$, seguido pelo arco semicircular$C_2$ de$(1, 0)$ trás para$(-1, 0)$

Resposta: $\displaystyle ∮_C (−y\,\,dx+x\,\,dy)=π$unidades de trabalho

Para os exercícios a seguir, use o teorema de Green.

7. $C$Seja a curva que consiste em segmentos de linha de$(0, 0)$ para$(1, 1)$ para$(0, 1)$ e de volta para$(0, 0)$. Encontre o valor de$\displaystyle \int_C xy\,dx+\sqrt{y^2+1}\,dy$.

8. Calcule a integral da linha$\displaystyle \int_C xe^{−2x}\,dx+(x^4+2x^2y^2)\,dy$, onde$C$ é o limite da região entre os círculos$x^2+y^2=1$ e$x^2+y^2=4$, e é uma curva orientada positivamente.

Resposta: $\displaystyle \int_C xe^{−2x}\,dx+(x^4+2x^2y^2)\,dy=0$unidades de trabalho

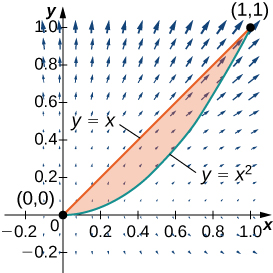
9. Encontre a circulação de campo no sentido anti-horário$\vecs F(x,y)=xy\,\mathbf{\hat i}+y^2\,\mathbf{\hat j}$ ao redor e acima do limite da região delimitada por curvas$y=x^2$ e$y=x$ no primeiro quadrante e orientada no sentido anti-horário.

$CNX_Calc_Figure_16_04_201.jpg$

10. Avalie$\displaystyle ∮_C y^3\,dx−x^3y^2\,dy$, onde$C$ está o círculo de raio orientado positivamente$2$ centrado na origem.

Resposta: $\displaystyle ∮_C y^3\,dx−x^3y^2\,dy=−20π$unidades de trabalho

11. Avalie$\displaystyle ∮_C y^3\,dx−x^3\,dy$, onde$C$ inclui os dois círculos de raio$2$ e raio$1$ centrado na origem, ambos com orientação positiva.

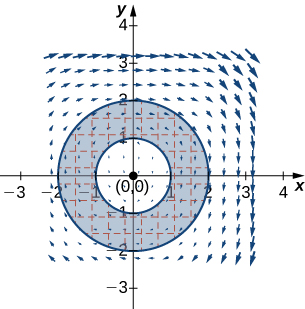
$CNX_Calc_Figure_16_04_202.jpg$

12. Calcule$\displaystyle ∮_C −x^2y\,dx+xy^2\,dy$, onde$C$ está um círculo de raio$2$ centrado na origem e orientado no sentido anti-horário.

Resposta: $\displaystyle ∮_C −x^2y\,dx+xy^2\,dy=8π$unidades de trabalho

13. Calcule a integral$\displaystyle ∮_C 2[y+x\sin(y)]\,dx+[x^2\cos(y)−3y^2]\,dy$ ao longo do triângulo$C$ com vértices$(0, 0), \,(1, 0)$ e$(1, 1)$, orientada no sentido anti-horário, usando o teorema de Green.

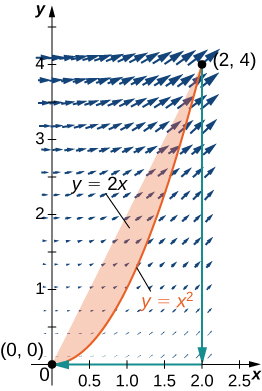
14. Calcule integral$\displaystyle ∮_C (x^2+y^2)\,dx+2xy\,dy$, onde$C$ está a curva que segue a parábola a$y=x^2$ partir de$(0,0), \,(2,4),$ então a linha de$(2, 4)$ para e$(2, 0)$, finalmente, a linha de$(2, 0)$ para$(0, 0)$.

$CNX_Calc_Figure_16_04_203.jpg$

Resposta: $\displaystyle ∮_C (x^2+y^2)\,dx+2xy\,dy=0$unidades de trabalho

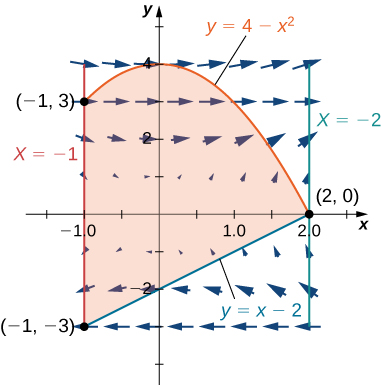
15. Calcule a integral da linha$\displaystyle ∮_C (y−\sin(y)\cos(y))\,dx+2x\sin^2(y)\,dy$, onde$C$ está orientada em um caminho anti-horário em torno da região delimitada por$x=−1, \,x=2, \,y=4−x^2$, e$y=x−2.$

$CNX_Calc_Figure_16_04_204.jpg$

Para os exercícios a seguir, use o teorema de Green para encontrar a área.

16. Encontre a área entre a elipse$\frac{x^2}{9}+\frac{y^2}{4}=1$ e o círculo$x^2+y^2=25$.

Resposta: $A=19π\;\text{units}^2$

17. Encontre a área da região delimitada pela equação paramétrica

$\vecs p(θ)=(\cos(θ)−\cos^2(θ))\,\mathbf{\hat i}+(\sin(θ)−\cos(θ)\sin(θ))\,\mathbf{\hat j}$para$0≤θ≤2π.$

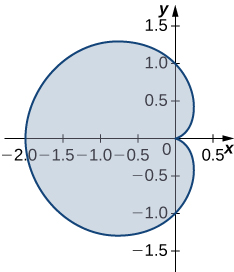
$CNX_Calc_Figure_16_04_205.jpg$

18. Encontre a área da região delimitada pelo hipociclóide$\vecs r(t)=\cos^3(t)\,\mathbf{\hat i}+\sin^3(t)\,\mathbf{\hat j}$. A curva é parametrizada por$t∈[0,2π].$

Resposta: $A=\frac{3}{8π}\;\text{units}^2$

19. Encontre a área de um pentágono com vértices$(0,4), \,(4,1), \,(3,0), \,(−1,−1),$$(−2,2)$ e.

20. Use o teorema de Green para calcular$\displaystyle \int_{C^+}(y^2+x^3)\,dx+x^4\,dy$, onde$C^+$ está o perímetro do quadrado$[0,1]×[0,1]$ orientado no sentido anti-horário.

Resposta: $\displaystyle \int_{C^+} (y^2+x^3)\,dx+x^4\,dy=0$

21. Use o teorema de Green para provar que a área de um disco com raio$a$ é$A=πa^2\;\text{units}^2$.

22. Use o teorema de Green para encontrar a área de um laço de uma rosa de quatro folhas$r=3\sin 2θ$. (Dica:$x\,dy−y\,dx=r^2\,dθ$).

Resposta: $A=\frac{9π}{8}\;\text{units}^2$

23. Use o teorema de Green para encontrar a área sob um arco do ciclóide dada pelas equações paramétricas:$x=t−\sin t,\;y=1−\cos t,\;t≥0.$

24. Use o teorema de Green para encontrar a área da região delimitada pela curva

$\vecs r(t)=t^2\,\mathbf{\hat i}+\left(\frac{t^3}{3}−t\right)\,\mathbf{\hat j},$para$−\sqrt{3}≤t≤\sqrt{3}$.

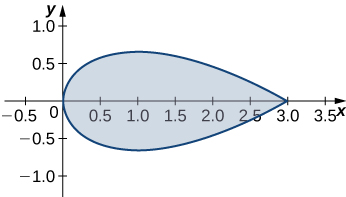
$CNX_Calc_Figure_16_04_206.jpg$

Resposta: $A=\frac{8\sqrt{3}}{5}\;\text{units}^2$

25. [T] Avalie o teorema de Green usando um sistema de álgebra computacional para calcular a integral$\displaystyle \int_C xe^y\,dx+e^x\,dy$, onde$C$ está o círculo dado por$x^2+y^2=4$ e é orientado no sentido anti-horário.

26. Avalie$\displaystyle \int_C(x^2y−2xy+y^2)\,ds$, onde$C$ está o limite da unidade quadrada$0≤x≤1,\;0≤y≤1$, percorrido no sentido anti-horário.

Resposta: $\displaystyle \int_C (x^2y−2xy+y^2)\,ds=3$

27. Avalie$\displaystyle \int_C \frac{−(y+2)\,dx+(x−1)\,dy}{(x−1)^2+(y+2)^2}$, onde$C$ está qualquer curva fechada simples com um interior que não contém ponto$(1,−2)$ percorrido no sentido anti-horário.

28. Avalie$\displaystyle \int_C \frac{x\,dx+y\,dy}{x^2+y^2}$, onde$C$ está qualquer curva fechada simples e suave em partes, envolvendo a origem, percorrida no sentido anti-horário.

Resposta: $\displaystyle \int_C \frac{x\,dx+y\,dy}{x^2+y^2}=2π$

Para os exercícios a seguir, use o teorema de Green para calcular o trabalho realizado pela força$\vecs F$ em uma partícula que está se movendo no sentido anti-horário em torno de um caminho fechado$C$.

29. $\vecs F(x,y)=xy\,\mathbf{\hat i}+(x+y)\,\mathbf{\hat j}, \quad C:x^2+y^2=4$

30. $\vecs F(x,y)=(x^{3/2}−3y)\,\mathbf{\hat i}+(6x+5\sqrt{y})\,\mathbf{\hat j}, \quad C$: boundary of a triangle with vertices $(0, 0), \,(5, 0),$ and $(0, 5)$

Answer: $W=\frac{225}{2}$ units of work

31. Evaluate $\displaystyle \int_C (2x^3−y^3)\,dx+(x^3+y^3)\,dy$, where $C$ is a unit circle oriented in the counterclockwise direction.

32. A particle starts at point $(−2,0)$, moves along the $x$-axis to $(2, 0)$, and then travels along semicircle $y=\sqrt{4−x^2}$ to the starting point. Use Green’s theorem to find the work done on this particle by force field $\vecs F(x,y)=x\,\mathbf{\hat i}+(x^3+3xy^2)\,\mathbf{\hat j}$.

Answer: $W=12π$ units of work

33. David and Sandra are skating on a frictionless pond in the wind. David skates on the inside, going along a circle of radius $2$ in a counterclockwise direction. Sandra skates once around a circle of radius $3$, also in the counterclockwise direction. Suppose the force of the wind at point $(x,y)$ is $\vecs F(x,y)=(x^2y+10y)\,\mathbf{\hat i}+(x^3+2xy^2)\,\mathbf{\hat j}$. Use Green’s theorem to determine who does more work.

34. Use Green’s theorem to find the work done by force field $\vecs F(x,y)=(3y−4x)\,\mathbf{\hat i}+(4x−y)\,\mathbf{\hat j}$ when an object moves once counterclockwise around ellipse $4x^2+y^2=4.$

Answer: $W=2π$ units of work

35. Use Green’s theorem to evaluate line integral $\displaystyle ∮_C e^{2x}\sin 2y\,dx+e^{2x}\cos 2y\,dy$, where $C$ is ellipse $9(x−1)^2+4(y−3)^2=36$ oriented counterclockwise.

36. Evaluate line integral $\displaystyle ∮_C y^2\,dx+x^2\,dy$, where $C$ is the boundary of a triangle with vertices $(0,0), \,(1,1)$, and $(1,0)$, with the counterclockwise orientation.

Answer: $\displaystyle ∮_C y^2\,dx+x^2\,dy=\frac{1}{3}$ units of work

37. Use Green’s theorem to evaluate line integral $\displaystyle \int_C \vecs h·d\vecs r$ if $\vecs h(x,y)=e^y\,\mathbf{\hat i}−\sin πx\,\mathbf{\hat j}$, where $C$ is a triangle with vertices $(1, 0), \,(0, 1),$ and $(−1,0),$ traversed counterclockwise.

38. Use Green’s theorem to evaluate line integral $\displaystyle \int_C\sqrt{1+x^3}\,dx+2xy\,dy$ where $C$ is a triangle with vertices $(0, 0), \,(1, 0),$ and $(1, 3)$ oriented clockwise.

Answer: $\displaystyle \int_C \sqrt{1+x^3}\,dx+2xy\,dy=3$ units of work

39. Use Green’s theorem to evaluate line integral $\displaystyle \int_C x^2y\,dx−xy^2\,dy$ where $C$ is a circle $x^2+y^2=4$ oriented counterclockwise.

40. Use Green’s theorem to evaluate line integral $\displaystyle \int_C \left(3y−e^{\sin x}\right)\,dx+\left(7x+\sqrt{y^4+1}\right)\,dy$ where $C$ is circle $x^2+y^2=9$ oriented in the counterclockwise direction.

Answer: $\displaystyle \int_C \left(3y−e^{\sin x}\right)\,dx+\left(7x+\sqrt{y^4+1}\right)\,dy=36π$ units of work

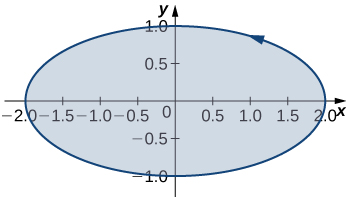
41. Use Green’s theorem to evaluate line integral $\displaystyle \int_C (3x−5y)\,dx+(x−6y)\,dy$, where $C$ is ellipse $\frac{x^2}{4}+y^2=1$ and is oriented in the counterclockwise direction.

$A horizontal oval oriented counterclockwise with vertices at (-2,0), (0,-1), (2,0), and (0,1). The region enclosed is shaded.$

42. Let $C$ be a triangular closed curve from $(0, 0)$ to $(1, 0)$ to $(1, 1)$ and finally back to $(0, 0).$ Let $\vecs F(x,y)=4y\,\mathbf{\hat i}+6x^2\,\mathbf{\hat j}.$ Use Green’s theorem to evaluate $\displaystyle ∮_C\vecs F·d\vecs r.$

Answer: $\displaystyle ∮_C\vecs F·d\vecs r=2$ units of work

43. Use Green’s theorem to evaluate line integral $\displaystyle ∮_C y\,dx−x\,dy$, where $C$ is circle $x^2+y^2=a^2$ oriented in the clockwise direction.

44. Use Green’s theorem to evaluate line integral $\displaystyle ∮_C (y+x)\,dx+(x+\sin y)\,dy,$ where $C$ is any smooth simple closed curve joining the origin to itself oriented in the counterclockwise direction.

Answer: $\displaystyle ∮_C (y+x)\,dx+(x+\sin y)\,dy=0$ units of work

45. Use Green’s theorem to evaluate line integral $\displaystyle ∮_C \left(y−\ln(x^2+y^2)\right)\,dx+\left(2\arctan \frac{y}{x}\right)\,dy,$ where $C$ is the positively oriented circle $(x−2)^2+(y−3)^2=1.$

46. Use Green’s theorem to evaluate $\displaystyle ∮_C xy\,dx+x^3y^3\,dy,$ where $C$ is a triangle with vertices $(0, 0), \,(1, 0),$ and $(1, 2)$ with positive orientation.

Answer: $\displaystyle ∮_C xy\,dx+x^3y^3\,dy=2221$ units of work

47. Use Green’s theorem to evaluate line integral $\displaystyle \int_C \sin y\,dx+x\cos y\,dy,$ where $C$ is ellipse $x^2+xy+y^2=1$ oriented in the counterclockwise direction.

48. Let $\vecs F(x,y)=\left(\cos(x^5)−13y^3\right)\,\mathbf{\hat i}+13x^3\,\mathbf{\hat j}.$ Find the counterclockwise circulation $\displaystyle ∮_C\vecs F·d\vecs r,$ where $C$ is a curve consisting of the line segment joining $(−2,0)$ and $(−1,0),$ half circle $y=\sqrt{1−x^2},$ the line segment joining $(1, 0)$ and $(2, 0),$ and half circle $y=\sqrt{4−x^2}.$

Answer: $\displaystyle ∮_C\vecs F·d\vecs r=15π^4$ units of work

49. Use Green’s theorem to evaluate line integral $\displaystyle ∫_C \sin(x^3)\,dx+2ye^{x^2}\,dy,$ where $C$ is a triangular closed curve that connects the points $(0, 0), \,(2, 2),$ and $(0, 2)$ counterclockwise.

50. Let $C$ be the boundary of square $0≤x≤π,\;0≤y≤π,$ traversed counterclockwise. Use Green’s theorem to find $\displaystyle ∫_C \sin(x+y)\,dx+\cos(x+y)\,dy.$

Answer: $\displaystyle \int_C\sin(x+y)\,dx+\cos(x+y)\,dy=4$ units of work

51. Use Green’s theorem to evaluate line integral $\displaystyle ∫_C \vecs F·d\vecs r,$ where $\vecs F(x,y)=(y^2−x^2)\,\mathbf{\hat i}+(x^2+y^2)\,\mathbf{\hat j},$ and $C$ is a triangle bounded by $y=0,\;x=3,$ and $y=x,$ oriented counterclockwise.

52. Use Green’s Theorem to evaluate integral $\displaystyle ∫_C \vecs F·d\vecs r,$ where $\vecs F(x,y)=(xy^2)\,\mathbf{\hat i}+x\,\mathbf{\hat j},$ and $C$ is a unit circle oriented in the counterclockwise direction.

Answer: $\displaystyle ∫_C \vecs F·d\vecs r=π$ units of work

53. Use Green’s theorem in a plane to evaluate line integral $\displaystyle ∮_C (xy+y^2)\,dx+x^2\,dy,$ where $C$ is a closed curve of a region bounded by $y=x$ and $y=x^2$ oriented in the counterclockwise direction.

54. Calculate the outward flux of $\vecs F(x,y)=−x\,\mathbf{\hat i}+2y\,\mathbf{\hat j}$ over a square with corners $(±1,\,±1),$ where the unit normal is outward pointing and oriented in the counterclockwise direction.

Answer: $\displaystyle ∮_C\vecs F·\vecs N \,ds=4$

55. [T] Let $C$ be circle $x^2+y^2=4$ oriented in the counterclockwise direction. Evaluate $\displaystyle ∮_C \left[\left(3y−e^{\arctan x})\,dx+(7x+\sqrt{y^4+1}\right)\,dy\right]$ using a computer algebra system.

56. Find the flux of field $\vecs F(x,y)=−x\,\mathbf{\hat i}+y\,\mathbf{\hat j}$ across $x^2+y^2=16$ oriented in the counterclockwise direction.

Answer: $\displaystyle ∮_C \vecs F·\vecs N\,ds=32π$

57. Let $\vecs F=(y^2−x^2)\,\mathbf{\hat i}+(x^2+y^2)\,\mathbf{\hat j},$ and let $C$ be a triangle bounded by $y=0, \,x=3,$ and $y=x$ oriented in the counterclockwise direction. Find the outward flux of $\vecs F$ through $C$.

58. [T] Let $C$ be unit circle $x^2+y^2=1$ traversed once counterclockwise. Evaluate $\displaystyle ∫_C \left[−y^3+\sin(xy)+xy\cos(xy)\right]\,dx+\left[x^3+x^2\cos(xy)\right]\,dy$ by using a computer algebra system.

Answer: $\displaystyle ∫_C \left[−y^3+\sin(xy)+xy\cos(xy)\right]\,dx+\left[x^3+x^2\cos(xy)\right]\,dy=4.7124$ units of work

59. [T] Find the outward flux of vector field $\vecs F(x,y)=xy^2\,\mathbf{\hat i}+x^2y\,\mathbf{\hat j}$ across the boundary of annulus $R=\big\{(x,y):1≤x^2+y^2≤4\big\}=\big\{(r,θ):1≤r≤2,\,0≤θ≤2π\big\}$ using a computer algebra system.

60. Consider region $R$ bounded by parabolas $y=x^2$ and $x=y^2.$ Let $C$ be the boundary of $R$ oriented counterclockwise. Use Green’s theorem to evaluate $\displaystyle ∮_C \left(y+e^{\sqrt{x}}\right)\,dx+\left(2x+\cos(y^2)\right)\,dy.$

Answer: $\displaystyle ∮_C \left(y+e^{\sqrt{x}}\right)\,dx+\left(2x+\cos(y^2)\right)\,dy=13$ units of work

Contributors

Template:contribopenstaxcalc