16.5: Divergência e curvatura
- Page ID
- 188523
- Determine a divergência da fórmula para um determinado campo vetorial.
- Determine a curvatura a partir da fórmula para um determinado campo vetorial.
- Use as propriedades de curvatura e divergência para determinar se um campo vetorial é conservador.
Nesta seção, examinamos duas operações importantes em um campo vetorial: divergência e curvatura. Eles são importantes para o campo do cálculo por vários motivos, incluindo o uso de curvatura e divergência para desenvolver algumas versões de maior dimensão do Teorema Fundamental do Cálculo. Além disso, curvatura e divergência aparecem em descrições matemáticas da mecânica dos fluidos, eletromagnetismo e teoria da elasticidade, que são conceitos importantes em física e engenharia. Também podemos aplicar curl e divergência a outros conceitos que já exploramos. Por exemplo, sob certas condições, um campo vetorial é conservador se e somente se sua curvatura for zero.
Além de definir curvatura e divergência, examinamos algumas interpretações físicas delas e mostramos sua relação com campos vetoriais conservadores e livres de fontes.
Divergência
A divergência é uma operação em um campo vetorial que nos diz como o campo se comporta em direção ou longe de um ponto. Localmente, a divergência de um campo vetorial\(\vecs{F}\)\(\mathbb{R}^3\) em\(\mathbb{R}^2\) ou em um ponto específico\(P\) é uma medida da “saída” do campo vetorial em\(P\). Se\(\vecs{F}\) representa a velocidade de um fluido, então a divergência de\(\vecs{F}\) at\(P\) mede a taxa líquida de variação em relação ao tempo da quantidade de fluido que sai\(P\) (a tendência do fluido de fluir “para fora” de P). Em particular, se a quantidade de fluido que flui para dentro\(P\) for a mesma que sai, então a divergência em\(P\) é zero.
Se\(\vecs{F} = \langle P,Q,R \rangle\) é um campo vetorial em\(\mathbb{R}^3\)\(P_x, \, Q_y, \) e\(R_z\) todos existem, então a divergência de\(\vecs{F}\) é definida por
\[\begin{align} \text{div}\, F &= P_x + Q_y + R_z \\[4pt] &= \dfrac{\partial P}{\partial x} + \dfrac{\partial Q}{\partial y} + \dfrac{\partial R}{\partial z}. \end{align} \nonumber \]
Observe que a divergência de um campo vetorial não é um campo vetorial, mas uma função escalar. Em termos do operador de gradiente
\[\vecs \nabla = \langle \dfrac{\partial}{\partial x}, \dfrac{\partial}{\partial y}, \dfrac{\partial}{\partial z} \rangle \nonumber \]
a divergência pode ser escrita simbolicamente como o produto escalar
\[\text{div}\, \vecs F = \vecs \nabla \cdot \vecs{F}. \nonumber \]
Observe que isso é apenas uma notação útil, porque o produto escalar de um vetor de operadores e um vetor de funções não está definido de forma significativa, dada a nossa definição atual de produto escalar.
Se\(\vecs{F} = \langle P,Q \rangle\) for um campo vetorial em\(\mathbb{R}^2\),\(P_x\) e\(Q_y\) ambos existirem, então a divergência de\(\vecs{F}\) é definida de forma semelhante como
\[\begin{align*} \text{div}\, \vecs{F} &= P_x + Q_y \\[4pt] &= \dfrac{\partial P}{\partial x} + \dfrac{\partial Q}{\partial y} \\[4pt] &= \vecs \nabla \cdot \vecs{F}. \end{align*}\]
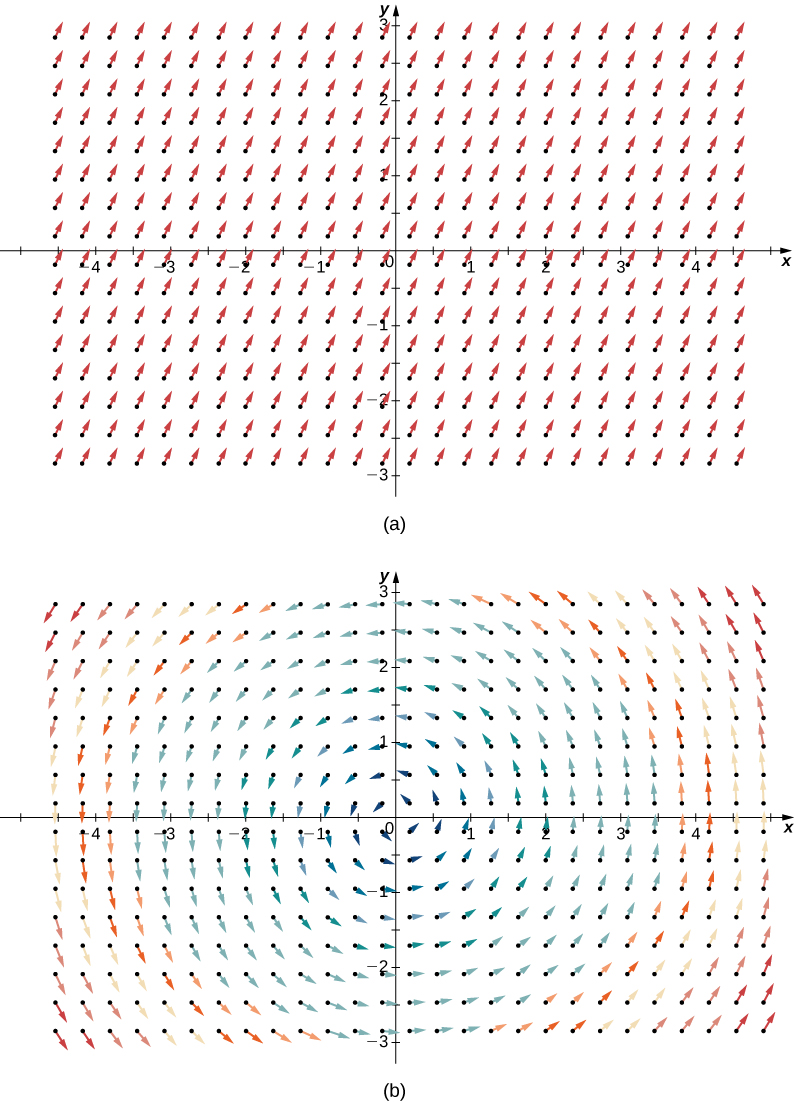
Para ilustrar esse ponto, considere os dois campos vetoriais na Figura\(\PageIndex{1}\). Em qualquer ponto específico, a quantidade que entra é a mesma que sai, então, em cada ponto, a “saída” do campo é zero. Portanto, esperamos que a divergência de ambos os campos seja zero, e esse é realmente o caso, como
\[\text{div}(\langle 1,2 \rangle ) = \dfrac{\partial}{\partial x} (1) + \dfrac{\partial}{\partial y}(2) = 0 \nonumber \]
e
\[\text{div}(\langle -y,x \rangle ) = \dfrac{\partial}{\partial x} (-y) + \dfrac{\partial}{\partial y} (x) = 0. \nonumber \]
Por outro lado, considere o campo vetorial radial\(\vecs{R} (x,y) = \langle -x, -y \rangle\) na Figura\(\PageIndex{2}\). Em qualquer ponto, mais fluido está fluindo para dentro do que está fluindo para fora e, portanto, a “saída” do campo é negativa. Esperamos que a divergência desse campo seja negativa, e esse é realmente o caso, pois
\[\text{div}(\vecs{R}) = \dfrac{\partial}{\partial x} (-x) + \dfrac{\partial}{\partial y} (-y) = -2. \nonumber \]
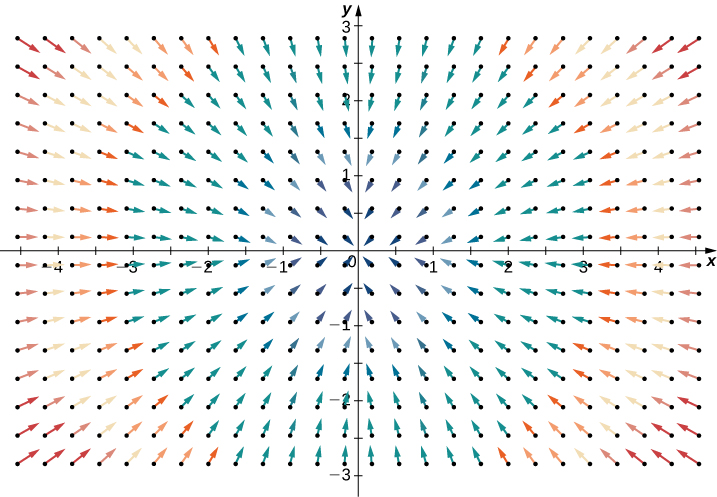
Para ter uma noção global do que a divergência está nos dizendo, suponha que um campo vetorial em\(\mathbb{R}^2\) represente a velocidade de um fluido. Imagine pegar um círculo elástico (um círculo com uma forma que pode ser alterada pelo campo vetorial) e soltá-lo em um fluido. Se o círculo mantiver sua área exata à medida que flui pelo fluido, a divergência será zero. Isso ocorreria para os dois campos vetoriais na Figura\(\PageIndex{1}\). Por outro lado, se a forma do círculo estiver distorcida de forma que sua área encolha ou se expanda, a divergência não será zero. Imagine soltar esse círculo elástico no campo vetorial radial na Figura\(\PageIndex{2}\) para que o centro do círculo caia no ponto\((3, 3)\). O círculo fluiria em direção à origem e, ao fazê-lo, a frente do círculo viajaria mais lentamente do que a de trás, fazendo com que o círculo se “apertasse” e perdesse área. É assim que você pode ver uma divergência negativa.
Se\(\vecs{F}(x,y,z) = e^x \hat{i} + yz \hat{j} - yz^2 \hat{k}\), então encontre a divergência de\(\vecs{F}\) at\((0,2,-1)\).
Solução
A divergência de\(\vecs{F}\) é
\[\dfrac{\partial}{\partial x} (e^x) + \dfrac{\partial}{\partial y}(yz) - \dfrac{\partial}{\partial z} (y z^2) = e^x + z - 2yz. \nonumber \]
Portanto, a divergência em\((0,2,-1)\) é\(e^0 - 1 + 4 = 4\). Se\(\vecs{F}\) representa a velocidade de um fluido, então mais fluido está fluindo para fora do que fluindo para dentro no ponto\((0,2,-1)\).
Encontre\(\text{div}\, \vecs{F}\) para
\[\vecs{F}(x,y,z) = \langle xy, \, 5-z^2, \, x^2 + y^2 \rangle \nonumber. \nonumber \]
- Dica
-
Siga o exemplo\(\PageIndex{1}\).
- Responda
-
\(\text{div}\, \vecs{F} = y \)
Outra aplicação para divergência é detectar se um campo é livre de fonte. Lembre-se de que um campo sem fonte é um campo vetorial que tem uma função de fluxo; equivalentemente, um campo sem fonte é um campo com um fluxo zero ao longo de qualquer curva fechada. Os próximos dois teoremas dizem que, sob certas condições, os campos vetoriais sem fonte são precisamente os campos vetoriais com divergência zero.
Se\(\vecs{F} = \langle P,Q \rangle\) for um campo vetorial contínuo sem fonte com funções de componentes diferenciáveis, então\(\text{div}\, \vecs{F} = 0\).
Como\(\vecs{F}\) é livre de fonte, existe uma função\(g(x,y)\) com\(g_y = P\)\(-g_x = Q\) e. Portanto,\(\vecs{F} = \langle g_y, -g_x \rangle\) e\(\text{div}\, \vecs{F} = g_{yx} - g_{xy} = 0\) pelo teorema de Clairaut.
\(\square\)
O inverso da divergência de um campo vetorial sem fonte é verdadeiro em regiões simplesmente conectadas, mas a prova é técnica demais para ser incluída aqui. Assim, temos o seguinte teorema, que pode testar se um campo vetorial em\(\mathbb{R}^2\) é livre de fonte.
\(\vecs{F} = \langle P,Q \rangle \)Seja um campo vetorial contínuo com funções de componentes diferenciáveis com um domínio que é simplesmente conectado. Então,\(\text{div}\, \vecs{F} = 0\) se e somente se\(\vecs{F}\) for livre de fonte.
A\(\vecs{F} (x,y) = \langle x^2 y, \, 5 - xy^2 \rangle\) fonte de campo é gratuita?
Solução
Observe\(\mathbb{R}^2\) que o domínio de\(\vecs{F}\) is está simplesmente conectado. Além disso,\(\vecs{F}\) é contínuo com funções de componentes diferenciáveis. Portanto, podemos usar o Teste de Divergência para campos vetoriais sem fonte para analisar\(\vecs{F}\). A divergência de\(\vecs{F}\) é
\[\dfrac{\partial}{\partial x} (x^2 y) + \dfrac{\partial}{\partial y} (5 - xy^2 ) = 2xy - 2xy = 0. \nonumber \]
Portanto,\(\vecs{F}\) é livre de fontes pelo Teste de Divergência para Campos Vetoriais Sem Fonte.
\(\vecs{F} (x,y) = \langle -ay, bx \rangle\)Seja um campo rotacional onde\(a\) e\(b\) são constantes positivas. A\(\vecs{F}\) fonte é gratuita?
- Dica
-
Calcule a divergência.
- Responda
-
sim
Lembre-se de que a forma de fluxo do teorema de Green diz que
\[\oint_C \vecs F \cdot \vecs N \; ds = \iint_D P_x + Q_y \;dA, \nonumber \]
onde\(C\) é uma curva fechada simples e\(D\) é a região delimitada por\(C\). Desde então\(P_x + Q_y = \text{div}\,\vecs F\), o teorema de Green às vezes é escrito como
\[\oint_C \vecs F \cdot \vecs N\; ds = \iint_D \text{div}\, \vecs F \;dA. \nonumber \]
Portanto, o teorema de Green pode ser escrito em termos de divergência. Se pensarmos na divergência como uma espécie de derivada, então o teorema de Green diz que a “derivada” de\(\vecs{F}\) em uma região pode ser traduzida em uma linha integral\(\vecs{F}\) ao longo do limite da região. Isso é análogo ao Teorema Fundamental do Cálculo, no qual a derivada de uma função\(f\) em um segmento de reta\([a,b]\) pode ser traduzida em uma afirmação\(f\) sobre o limite de\([a,b]\). Usando a divergência, podemos ver que o teorema de Green é um análogo de maior dimensão do Teorema Fundamental do Cálculo.
Podemos usar tudo o que aprendemos na aplicação da divergência. \(\vecs{v}\)Seja um campo vetorial modelando a velocidade de um fluido. Como a divergência de\(\vecs{v}\) no ponto\(P\) mede a “saída” do fluido em\(P\),\(\text{div}\, v(P) > 0\) implica que mais fluido está saindo\(P\) do que fluindo para dentro. Da mesma forma,\(\text{div}\, v(P) < 0\) implica que quanto mais fluido está fluindo para dentro\(P\) do que está fluindo para fora, e\(\text{div}\, \vecs{v}(P) = 0\) implica que a mesma quantidade de fluido está fluindo para dentro e para fora.
Suponha que\(\vecs{v}(x,y) = \langle -xy,y \rangle, \, y > 0\) modele o fluxo de um fluido. Há mais fluido fluindo para o ponto\((1,4)\) do que fluindo para fora?
Solução
Para determinar se mais fluido está fluindo para dentro\((1,4)\) do que está fluindo para fora, calculamos a divergência de\(\vecs v\) em\((1,4)\):
\[div(\vecs{v}) = \dfrac{\partial}{\partial x} (-xy) + \dfrac{\partial}{\partial y} (y) = -y + 1. \nonumber \]
Para encontrar a divergência,\((1,4)\) substitua o ponto pela divergência:\(-4 + 1 = -3\). Como a divergência de\(\vecs v\) at\((1,4)\) é negativa, mais fluido está fluindo para dentro do que saindo (Figura\(\PageIndex{4}\)).

Para o campo vetorial\(\vecs{v}(x,y) = \langle -xy, y \rangle , \, y > 0\), encontre todos os pontos de\(P\) forma que a quantidade de fluido fluindo para seja\(P\) igual à quantidade de fluido que sai\(P\).
- Dica
-
Descubra onde a divergência é zero.
- Responda
-
Todos os pontos em linha\(y = 1\).
Ondulação
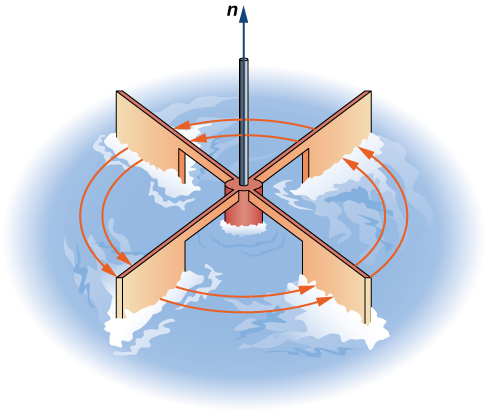
A segunda operação em um campo vetorial que examinamos é a curvatura, que mede a extensão da rotação do campo em torno de um ponto. Suponha que isso\(\vecs{F}\) represente o campo de velocidade de um fluido. Então, a curvatura de um\(\vecs{F}\) ponto\(P\) é um vetor que mede a tendência das partículas próximas de\(P\) girar em torno do eixo que aponta na direção desse vetor. A magnitude do vetor de curvatura em\(P\) mede a rapidez com que as partículas giram em torno desse eixo. Em outras palavras, a curvatura em um ponto é uma medida da “rotação” do campo vetorial nesse ponto. Visualmente, imagine colocar uma roda de pás em um fluido em\(P\), com o eixo da roda alinhado com o vetor de curvatura (Figura\(\PageIndex{5}\)). A curvatura mede a tendência da roda de girar.
Considere os campos vetoriais na Figura\(\PageIndex{1}\). Na parte (a), o campo vetorial é constante e não há rotação em nenhum ponto. Portanto, esperamos que a curvatura do campo seja zero, e esse é realmente o caso. A parte (b) mostra um campo rotacional, então o campo tem rotação. Em particular, se você colocar uma roda de pás em um campo em qualquer ponto para que o eixo da roda fique perpendicular a um plano, a roda gira no sentido anti-horário. Portanto, esperamos que a curvatura do campo seja diferente de zero, e esse é realmente o caso (a curvatura é\(2\,\mathbf{\hat k}\)).
Para ver o que a ondulação está medindo globalmente, imagine jogar uma folha no fluido. Conforme a folha se move junto com o fluxo de fluido, a curvatura mede a tendência da folha de girar. Se a ondulação for zero, a folha não gira enquanto se move pelo fluido.
Se\(\vecs{F} = \langle P,Q,R \rangle\) for um campo vetorial em\(\mathbb{R}^3\)\(P_x, \, Q_y\), e\(R_z\) todos existirem, então a curvatura de\(\vecs{F}\) é definida por
\ [\ begin {align}\ text {curl}\,\ vecs {F} &= (R_y - Q_z)\,\ mathbf {\ hat i} + (P_z - R_x)\,\ mathbf {\ hat j} + (Q_x - P_y)\,\ mathbf {\ hat k}\\ [4pt]
&=\ left (\ dfrac {\ partial R} {\ partial y} -\ dfrac {\ partial Q} {\ partial z}\ direita)\,\ mathbf {\ hat i} +\ left (\ dfrac {\ partial P} {\ partial z} -\ dfrac {\ partial R} {\ partial x}\ right)\,\ mathbf {\ hat j} +\ left (\ dfrac {\ partial Q} {\ partial x} -\ dfrac {\ partial P} {\ partial y}\ direita)\,\ mathbf {\ hat k}. \ end {align}\ nonumber\]
Observe que a curvatura de um campo vetorial é um campo vetorial, em contraste com a divergência.
A definição de curvatura pode ser difícil de lembrar. Para ajudar na lembrança, usamos a notação\(\vecs \nabla \times \vecs{F}\) para representar um “determinante” que fornece a fórmula da curvatura:
\[\begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ \dfrac{\partial}{\partial x} & \dfrac{\partial}{\partial y} & \dfrac{\partial}{\partial z} \\ P & Q & R \end{vmatrix}. \nonumber \]
O determinante dessa matriz é
\[(R_y - Q_z) \,\mathbf{\hat i} - (R_x - P_z) \,\mathbf{\hat j} + (Q_x - P_y) \,\mathbf{\hat k} = (R_y - Q_z) \,\mathbf{\hat i} + (P_z - R_x) \,\mathbf{\hat j} + (Q_x - P_y)\,\mathbf{\hat k} = \text{curl}\, \vecs{F}. \nonumber \]
Portanto, essa matriz é uma forma de ajudar a lembrar a fórmula da curvatura. Lembre-se, porém, de que a palavra determinante é usada de forma muito vaga. Um determinante não é realmente definido em uma matriz com entradas que são três vetores, três operadores e três funções.
Se\(\vecs{F} = \langle P,Q \rangle\) for um campo vetorial em\(\mathbb{R}^2\), então a curvatura de\(\vecs{F}\), por definição, é
\[\text{curl}\, \vecs{F} = (Q_x - P_y)\,\mathbf{\hat k} = \left(\dfrac{\partial Q}{\partial x} - \dfrac{\partial P}{\partial y} \right)\,\mathbf{\hat k}. \nonumber \]
Encontre a curvatura de\(\vecs{F}(P,Q,R) = \langle x^2 z, e^y + xz, xyz \rangle\).
Solução
A curvatura é
\[\begin{align*} \text{curl}\, f &= \vecs\nabla \times \vecs{F} \\ &= \begin{vmatrix} \mathbf{\hat i} & \mathbf{\hat j} & \mathbf{\hat k} \\ \partial/\partial x & \partial/\partial y & \partial / \partial z \\ P & Q & R \end{vmatrix} \\ &= (R_y - Q_z)\,\mathbf{\hat i} + (P_z - R_x)\,\mathbf{\hat j} + (Q_x - P_y)\,\mathbf{\hat k} \\ &= (xz - x)\,\mathbf{\hat i} + (x^2 - yz)\,\mathbf{\hat j} + z \,\mathbf{\hat k}. \end{align*}\]
Encontre a curvatura de\(\vecs{F} = \langle \sin x \, \cos z, \, \sin y \, \sin z, \, \cos x \, \cos y \rangle \) no ponto\(\left(0, \dfrac{\pi}{2}, \dfrac{\pi}{2} \right)\).
- Dica
-
Encontre o determinante da matriz\(\vecs \nabla \times \vecs{F}\).
- Responda
-
\(-\hat{i}\)
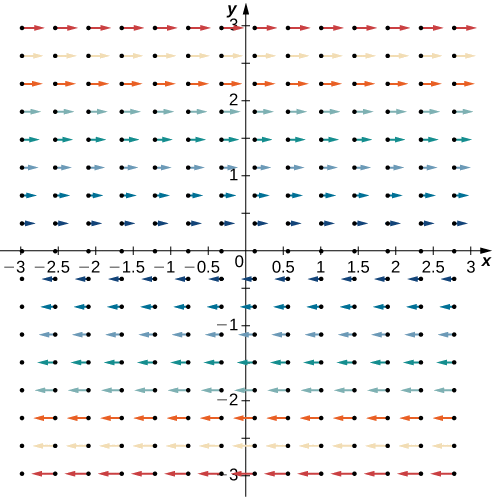
Encontre a curvatura de\(\vecs{F} = \langle P,Q \rangle = \langle y,0\rangle\).
Solução
Observe que esse campo vetorial consiste em vetores que são todos paralelos. Na verdade, cada vetor no campo é paralelo ao eixo x. Esse fato pode nos levar à conclusão de que o campo não tem giro e que a curvatura é zero. Para testar essa teoria, observe que
\[\text{curl}\, \vecs{F} = (Q_x - P_y)\,\mathbf{\hat k} = -\,\mathbf{\hat k} \neq \vecs 0. \nonumber \]
Portanto, esse campo vetorial tem spin. Para ver o porquê, imagine colocar uma roda de pás em qualquer ponto do primeiro quadrante (Figura\(\PageIndex{6}\)). As maiores magnitudes dos vetores na parte superior da roda fazem com que a roda gire. A roda gira no sentido horário (negativo), fazendo com que o coeficiente de curvatura seja negativo.
Note que se\(\vecs{F} = \langle P,Q\rangle\) é um campo vetorial em um plano, então\(\text{curl}\, \vecs{F} \cdot \mathbf{\hat k} = (Q_x - P_y)\,\mathbf{\hat k} \cdot \mathbf{\hat k} = Q_x - P_y\). Portanto, a forma de circulação do teorema de Green às vezes é escrita como
\[\oint_C \vecs{F} \cdot d\vecs{r} = \iint_D \text{curl}\, \vecs F \cdot \,\mathbf{\hat k}\,dA, \nonumber \]
onde\(C\) é uma curva fechada simples e\(D\) é a região delimitada por\(C\). Portanto, a forma de circulação do teorema de Green pode ser escrita em termos de curvatura. Se pensarmos em curl como uma espécie de derivada, então o teorema de Green diz que a “derivada” de\(\vecs{F}\) em uma região pode ser traduzida em uma linha integral\(\vecs{F}\) ao longo do limite da região. Isso é análogo ao Teorema Fundamental do Cálculo, no qual a derivada de uma função\(f\) no segmento de linha\([a,b]\) pode ser traduzida em uma afirmação\(f\) sobre o limite de\([a,b]\). Usando curl, podemos ver que a forma de circulação do teorema de Green é um análogo de maior dimensão do Teorema Fundamental do Cálculo.
Agora podemos usar o que aprendemos sobre curl para mostrar que os campos gravitacionais não têm “rotação”. Suponha que haja um objeto na origem com massa\(m_1\) na origem e um objeto com massa\(m_2\). Lembre-se de que a força gravitacional que o objeto 1 exerce sobre o objeto 2 é dada pelo campo
\[ \vecs{F}(x,y,z) = - Gm_1m_2 \left\langle \dfrac{x}{(x^2 + y^2 + z^2 )^{3/2}}, \dfrac{y}{(x^2 + y^2 + z^2 )^{3/2}}, \dfrac{z}{(x^2 + y^2 + z^2 )^{3/2}}\right\rangle. \nonumber \]
Mostre que um campo gravitacional não tem rotação.
Solução
Para mostrar que não\(\vecs{F}\) tem rotação, calculamos sua curvatura. Deixe
- \(P(x,y,z) = \dfrac{x}{(x^2 + y^2 + z^2 )^{3/2}}\),
- \(Q(x,y,z) = \dfrac{y}{(x^2 + y^2 + z^2 )^{3/2}}\), e
- \(R(x,y,z) = \dfrac{z}{(x^2 + y^2 + z^2 )^{3/2}}\).
Então,
\ [\ begin {align*}\ text {curl}\,\ vecs {F} &= - GM_1m_2 [(R_y - Q_z)\ mathbf {\ hat i} + (P_z - R_x)\ mathbf {\ hat j} + (Q_x - P_y)\ mathbf {\ hat k}\ [4pt]
&= - GM_1m_2\ begin {pmatrix}\ left (\ dfrac {-3yz} {(x^2 + y^2 + z^2) ^ {5/2}} -\ left (\ dfrac {-3yz} {(x^2 + y^2 + z^2) ^ {5/2}}\ direita)\ direita)\ mathbf {\ hat is}\ nonumber\\ [4pt]
+\ left (\ dfrac {-3xz} {(x^2 + y^2 + z^2) ^ {5/2}} -\ left (\ dfrac {-3xz} {(x^2 + y^2 + z^2) ^ {5/2}}\ direita)\ direita)\ mathbf {\ hat j}\ nonumber\\ [4pt]
+\ left (\ dfrac {-3xy} {(x^2 + y^2 + z^2) ^ {5/2}} -\ left (\ dfrac {-3xy} {(x^2 + y^2 + z^2) ^ {5/2}}\ direita)\ direita)\ direita)\ mathbf {\ hat k}\ end {pmatrix}\\ [4pt]
&=\ vecs 0. \ end {align*}\]
Como a curvatura do campo gravitacional é zero, o campo não tem rotação.
O campo\(\vecs{v}(x,y) = \langle - \dfrac{y}{x^2+y^2}, \dfrac{x}{x^2+y^2} \rangle \) modela o fluxo de um fluido. Mostre que se você soltar uma folha nesse fluido, à medida que a folha se move ao longo do tempo, a folha não gira.
- Dica
-
Calcule a curvatura.
- Responda
-
\(\text{curl}\, \vecs{v} = \vecs 0\)
Usando Divergence e Curl
Agora que entendemos os conceitos básicos de divergência e curvatura, podemos discutir suas propriedades e estabelecer relações entre elas e campos vetoriais conservadores.
Se\(\vecs{F}\) for um campo vetorial em\(\mathbb{R}^3\), a curvatura de também\(\vecs{F}\) é um campo vetorial em\(\mathbb{R}^3\). Portanto, podemos considerar a divergência de uma onda. O próximo teorema diz que o resultado é sempre zero. Esse resultado é útil porque nos dá uma forma de mostrar que alguns campos vetoriais não são a curvatura de nenhum outro campo. Para dar a esse resultado uma interpretação física, lembre-se de que a divergência de um campo de velocidade\(\vecs{v}\) em um ponto\(P\) mede a tendência do fluido correspondente de sair\(P\). Desde então\(\text{div}(\text{curl}\,\vecs v) = 0\), a taxa líquida de fluxo no campo vetorial\(\text{curl}\;\vecs v\) em qualquer ponto é zero. Obter a curvatura do campo vetorial\(\vecs{F}\) elimina qualquer divergência presente\(\vecs{F}\).
\(\vecs{F} = \langle P,Q,R \rangle \)Seja um campo vetorial de\(\mathbb{R}^3\) forma que todas as funções dos componentes tenham derivadas parciais contínuas de segunda ordem. Então,
\[\text{div}(\text{curl}\, \vecs{F}) = \vecs\nabla \cdot (\vecs \nabla \times \vecs F) = 0. \nonumber \]
Pelas definições de divergência e curvatura, e pelo teorema de Clairaut,
\[\begin{align*} \text{div}(\text{curl}\, \vecs{F}) = \text{div}[(R_y - Q_z)\,\mathbf{\hat i} + (P_z - R_x)\,\mathbf{\hat j} + (Q_x - P_y)\,\mathbf{\hat k}] \\ = R_{yx} - Q_{xz} + P_{yz} - R_{yx} + Q_{zx} - P_{zy}\\ = 0. \end{align*}\]
\(\Box\)
Mostre que não\(\vecs{F}(x,y,z) = e^x\,\mathbf{\hat i}+ yz\,\mathbf{\hat j} + xz^2\,\mathbf{\hat k}\) é a curvatura de outro campo vetorial. Ou seja, mostre que não há outro vetor\(\vecs{G}\) com\(\text{curl} \, \vecs G = \vecs F\).
Solução
Observe que o domínio de\(\vecs{F}\) é tudo de\(\mathbb{R}^3\) e os parciais de segunda ordem de\(\vecs{F}\) são todos contínuos. Portanto, podemos aplicar o teorema anterior\(\vecs{F}\) a.
A divergência de\(\vecs{F}\) é\(e^x + z + 2xz\). Se\(\vecs{F}\) fosse a curvatura do campo vetorial\(\vecs{G}\), então\(\text{div}\, \vecs F = \text{div}(\text{curl} \,\vecs G) = 0\). Mas, a divergência de não\(\vecs{F}\) é zero e, portanto, não\(\vecs{F}\) é a curvatura de nenhum outro campo vetorial.
É possível que seja\(\vecs G(x,y,z) = \langle \sin x, \, \cos y, \, \sin (xyz)\rangle \) a curvatura de um campo vetorial?
- Dica
-
Encontre a divergência de\(\vecs{G}\).
- Responda
-
Não.
Com os próximos dois teoremas, mostramos que se\(\vecs{F}\) é um campo vetorial conservador, sua curvatura é zero, e se o domínio de\(\vecs{F}\) estiver simplesmente conectado, o inverso também é verdadeiro. Isso nos dá outra maneira de testar se um campo vetorial é conservador.
\(\vecs{F} = \langle P,Q,R\rangle\)É conservador, então\(\text{curl} \, \vecs{F} = \vecs 0\).
Como os campos vetoriais conservadores satisfazem a propriedade de parciais cruzados, todos os parciais\(\vecs F\) cruzados de são iguais. Portanto,
\[\begin{align*} \text{curl}\, \vecs{F} &= (R_y - Q_z)\,\mathbf{\hat i} + (P_z - R_x)\,\mathbf{\hat j} + (Q_x - P_y)\,\mathbf{\hat k} \\[4pt] &= \vecs 0. \end{align*}\]
\(\Box\)
O mesmo teorema é verdadeiro para campos vetoriais em um plano.
Como um campo vetorial conservador é o gradiente de uma função escalar, o teorema anterior diz isso\(\text{curl}\, (\vecs \nabla f) = \vecs 0\) para qualquer função escalar\(f\). Em termos de nossa notação curl,\(\vecs \nabla \times \vecs \nabla (f) = \vecs 0\). Essa equação faz sentido porque o produto cruzado de um vetor consigo mesmo é sempre o vetor zero. Às vezes, a equação\(\vecs \nabla \times \vecs \nabla (f) = \vecs 0\) é simplificada como\(\vecs \nabla \times \vecs \nabla = \vecs 0\).
\(\vecs{F} = \langle P,Q,R\rangle\)Seja um campo vetorial no espaço em um domínio simplesmente conectado. Se\(\text{curl}\;\vecs F = \vecs 0\), então\(\vecs{F}\) é conservador.
Desde então\(\text{curl}\, \vecs F = \vecs 0\), nós temos isso\(R_y = Q_z, \, P_z = R_x\),\(Q_x = P_y\) e. Portanto,\(\vecs{F}\) satisfaz a propriedade interparcial em um domínio simplesmente conectado, e a propriedade parcial cruzada de campos conservadores implica que\(\vecs{F}\) é conservadora.
\(\Box\)
O mesmo teorema também é verdadeiro em um plano. Portanto, se\(\vecs{F}\) é um campo vetorial em um plano ou no espaço e o domínio está simplesmente conectado, então\(\vecs{F}\) é conservador se e somente se\(\text{curl}\, \vecs F = \vecs 0\).
Use a curvatura para determinar se\(\vecs{F}(x,y,z) = \langle yz, xz, xy\rangle\) é conservadora.
Solução
Observe que o domínio de\(\vecs{F}\) é tudo\(\mathbb{R}^3\) o que está simplesmente conectado (Figura\(\PageIndex{7}\)). Portanto, podemos testar se\(\vecs{F}\) é conservador calculando sua curvatura.
A ondulação de\(\vecs{F}\) é
\[\left(\dfrac{\partial}{\partial y}xy - \dfrac{\partial}{\partial z} xz \right) \,\mathbf{\hat i} + \left(\dfrac{\partial}{\partial y}yz - \dfrac{\partial}{\partial z} xy \right) \,\mathbf{\hat j} + \left(\dfrac{\partial}{\partial y}xz - \dfrac{\partial}{\partial z} yz \right)\,\mathbf{\hat k}= (x - x)\,\mathbf{\hat i} + (y - y)\,\mathbf{\hat j} + (z - z)\,\mathbf{\hat k} = \vecs 0. \nonumber \]
Assim,\(\vecs{F}\) é conservador.
Vimos que a curvatura de um gradiente é zero. Qual é a divergência de um gradiente? Se\(f\) é uma função de duas variáveis, então\(\text{div}(\vecs \nabla f) = \vecs \nabla \cdot (\vecs \nabla f) = f_{xx} + f_{yy}\). Abreviamos esse “produto de dois pontos” como\(\vecs \nabla^2\). Esse operador é chamado de operador de Laplace e, nessa notação, a equação de Laplace se torna\(\vecs \nabla^2 f = 0\). Portanto, uma função harmônica é uma função que se torna zero após a divergência de um gradiente.
Da mesma forma, se\(f\) é uma função de três variáveis, então
\[\text{div}(\vecs \nabla f) = \vecs \nabla \cdot (\vecs \nabla f) = f_{xx} + f_{yy} + f_{zz}. \nonumber \]
Usando essa notação, obtemos a equação de Laplace para funções harmônicas de três variáveis:
\[\vecs \nabla^2 f = 0. \nonumber \]
As funções harmônicas surgem em muitas aplicações. Por exemplo, a função potencial de um campo eletrostático em uma região do espaço que não tem carga estática é harmônica.
É possível que seja\(f(x,y) = x^2 + x - y\) a função potencial de um campo eletrostático localizado em uma região\(\mathbb{R}^2\) livre de carga estática?
Solução
Se\(f\) fosse uma função tão potencial, então\(f\) seria harmônica. Observe isso\(f_{xx} = 2\) e\(f_{yy} = 0\), e assim por diante\(f_{xx} + f_{yy} \neq 0\). Portanto, não\(f\) é harmônico e\(f\) não pode representar um potencial eletrostático.
É possível que a função seja\(f(x,y) = x^2 - y^2 + x\) a função potencial de um campo eletrostático localizado em uma região\(\mathbb{R}^2\) livre de carga estática?
- Dica
-
Determine se a função é harmônica.
- Responda
-
Sim.
Conceitos-chave
- A divergência de um campo vetorial é uma função escalar. A divergência mede a “saída” de um campo vetorial. Se\(\vecs{v}\) for o campo de velocidade de um fluido, a divergência de\(\vecs{v}\) em um ponto é a saída do fluido menos a entrada no ponto.
- A curvatura de um campo vetorial é um campo vetorial. A curvatura de um campo vetorial em um ponto\(P\) mede a tendência das partículas em\(P\) girarem em torno do eixo que aponta na direção da curvatura\(P\).
- Um campo vetorial com um domínio simplesmente conectado é conservador se e somente se sua curvatura for zero.
Equações-chave
- Ondulação
\[\vecs \nabla \times \vecs{F} = (R_y - Q_z)\,\mathbf{\hat i} + (P_z - R_x)\,\mathbf{\hat j} + (Q_x - P_y)\,\mathbf{\hat k} \nonumber \]
- Divergência
\[\vecs \nabla \cdot \vecs{F} = P_x + Q_y + R_z\nonumber \]
- A divergência da curvatura é zero
\[\vecs \nabla \cdot (\vecs \nabla \times \vecs F) = 0\nonumber \]
- A curvatura de um gradiente é o vetor zero
\[\vecs \nabla \times (\vecs \nabla f) = 0 \nonumber \]
Glossário
- ondulação
- a curvatura do campo vetorial\(\vecs{F}=⟨P,Q,R⟩\), denotada\(\vecs ∇× \vecs{F}\) é a “determinante” da matriz\[\begin{vmatrix} \mathbf{\hat i} & \mathbf{\hat j} & \mathbf{\hat k} \\ \dfrac{\partial}{\partial x} & \dfrac{\partial}{\partial y} & \dfrac{\partial}{\partial z} \\ P & Q & R \end{vmatrix}. \nonumber \] e é dada pela expressão\((R_y−Q_z)\,\mathbf{\hat i} +(P_z−R_x)\,\mathbf{\hat j} +(Q_x−P_y)\,\mathbf{\hat k} \); ela mede a tendência das partículas em um ponto de girarem em torno do eixo que aponta na direção da curvatura no ponto
- divergência
- a divergência de um campo vetorial\(\vecs{F}=⟨P,Q,R⟩\), denotada\(\vecs ∇× \vecs{F}\), é\(P_x+Q_y+R_z\); ela mede a “saída” de um campo vetorial



Uma aplicação para divergência ocorre na física, quando se trabalha com campos magnéticos. Um campo magnético é um campo vetorial que modela a influência de correntes elétricas e materiais magnéticos. Os físicos usam a divergência na lei de Gauss para magnetismo, que afirma que se\(\vecs{B}\) é um campo magnético, então\(\vecs \nabla \cdot \vecs{B} = 0\); em outras palavras, a divergência de um campo magnético é zero.
Exemplo\(\PageIndex{2}\): Determining Whether a Field Is Magnetic
É possível que\(\vecs{F} (x,y) = \langle x^2 y, \, y - xy^2 \rangle \) seja um campo magnético?
Solução
Se\(\vecs{F}\) fosse magnético, sua divergência seria zero. A divergência de\(\vecs{F}\) é
\[\dfrac{\partial}{\partial x} (x^2y) + \dfrac{\partial}{\partial y} (y - xy^2) = 2 xy + 1 - 2 xy = 1 \nonumber \]
e, portanto,\(\vecs{F}\) não pode modelar um campo magnético (Figura\(\PageIndex{3}\)).