14.6: Derivadas direcionais e o gradiente

Last updated
Save as PDF

Page ID: 187917

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

objetivos de aprendizagem

Determine a derivada direcional em uma determinada direção para uma função de duas variáveis.
Determine o vetor de gradiente de uma determinada função de valor real.
Explique a importância do vetor de gradiente em relação à direção da mudança ao longo de uma superfície.
Use o gradiente para encontrar a tangente a uma curva de nível de uma determinada função.
Calcule derivadas direcionais e gradientes em três dimensões.

Uma função$z=f(x,y)$ tem duas derivadas parciais:$∂z/∂x$$∂z/∂y$ e. Essas derivadas correspondem a cada uma das variáveis independentes e podem ser interpretadas como taxas instantâneas de mudança (ou seja, como inclinações de uma reta tangente). Por exemplo,$∂z/∂x$ representa a inclinação de uma reta tangente passando por um determinado ponto na superfície definida$z=f(x,y),$ assumindo que a linha tangente é paralela ao $x$eixo. Da mesma forma,$∂z/∂y$ representa a inclinação da reta tangente paralela ao $y$eixo y. Agora, consideramos a possibilidade de uma reta tangente paralela a nenhum dos eixos.

Derivadas direcionais

Começamos com o gráfico de uma superfície definida pela equação$z=f(x,y)$. Dado um ponto$(a,b)$ no domínio de$f$, escolhemos uma direção para viajar a partir desse ponto. Medimos a direção usando um ângulo$θ$, que é medido no sentido anti-horário no$xy$ plano -, começando em zero a partir do$x$ eixo positivo (Figura$\PageIndex{1}$). A distância que viajamos é$h$ e a direção que viajamos é dada pelo vetor unitário.$\vecs u=(\cos θ)\,\hat{\mathbf i}+(\sin θ)\,\hat{\mathbf j}.$ Portanto, a$z$ coordenada -do segundo ponto no gráfico é dada por$z=f(a+h\cos θ,b+h\sin θ).$

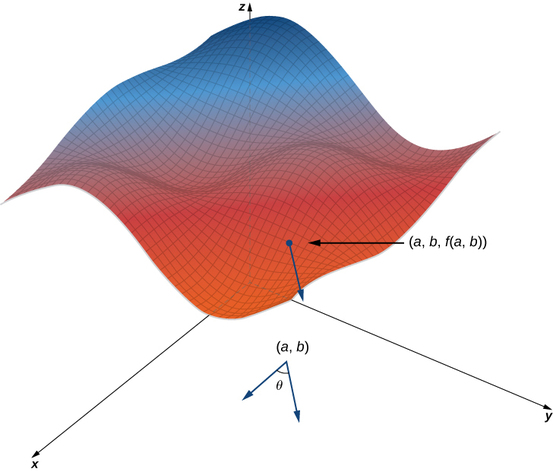
Uma forma no espaço xyz com ponto (a, b, f (a, b)). A partir do ponto, há uma seta que representa a derivada direcional. No plano xy, o ponto (a, b) é marcado e um ângulo de tamanho θ é feito entre a projeção da derivada direcional no plano e uma linha paralela ao eixo x. — Figura$\PageIndex{1}$: Encontrando a derivada direcional em um ponto no gráfico de$z=f(x,y)$. A inclinação da seta azul no gráfico indica o valor da derivada direcional nesse ponto.

Podemos calcular a inclinação da linha secante dividindo a diferença nos$z$ valores -pelo comprimento do segmento de linha conectando os dois pontos no domínio. O comprimento do segmento de linha é$h$. Portanto, a inclinação da linha secante é

\[m_{sec}=\dfrac{f(a+h\cos θ,b+h\sin θ)−f(a,b)}{h} \nonumber \]

Para encontrar a inclinação da reta tangente na mesma direção, tomamos o limite quando$h$ se aproxima de zero.

Definição: Derivadas direcionais

Suponha que$z=f(x,y)$ seja uma função de duas variáveis com um domínio de$D$. Deixe$(a,b)∈D$ e defina$\vecs u=(\cos θ)\,\hat{\mathbf i}+(\sin θ)\,\hat{\mathbf j}$. Então, a derivada direcional de$f$ na direção de$\vecs u$ é dada por

\[D_{\vecs u}f(a,b)=\lim_{h→0}\dfrac{f(a+h \cos θ,b+h\sin θ)−f(a,b)}{h} \label{DD} \]

desde que o limite exista.

A equação\ ref {DD} fornece uma definição formal da derivada direcional que pode ser usada em muitos casos para calcular uma derivada direcional.

Observe que, como o ponto$(a, b)$ é escolhido aleatoriamente$D$ do domínio da função$f$, podemos usar essa definição para encontrar a derivada direcional em função de$x$$y$ e.

Ou seja,

\[D_{\vecs u}f(x,y)=\lim_{h→0}\dfrac{f(x+h \cos θ,y+h\sin θ)−f(x,y)}{h} \label{DDxy} \]

Exemplo$\PageIndex{1}$: Finding a Directional Derivative from the Definition

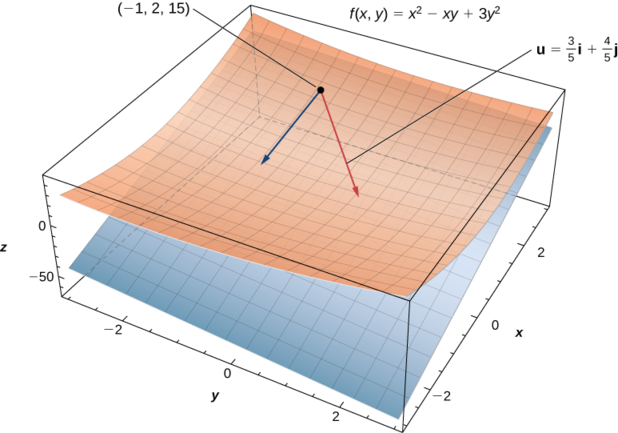
Vamos$θ=\arccos(3/5).$ encontrar a derivada direcional$D_{\vecs u}f(x,y)$ de$f(x,y)=x^2−xy+3y^2$ na direção de$\vecs u=(\cos θ)\,\hat{\mathbf i}+(\sin θ)\,\hat{\mathbf j}$.

Em seguida, determine$D_{\vecs u}f(−1,2)$.

Solução

Em primeiro lugar, uma vez que$\cos θ=3/5$ e$θ$ é agudo, isso implica

\[\sin θ=\sqrt{1−\left(\dfrac{3}{5}\right)^2}=\sqrt{\dfrac{16}{25}}=\dfrac{4}{5}. \nonumber \]

Usando$f(x,y)=x^2−xy+3y^2,$, primeiro calculamos$f(x+h\cos θ,y+h\sin θ)$:

\ [\ begin {align*} f (x+h\ cos θ, y+h\ sin θ) &= (x+h\ cos θ) ^2− (x+h\ cos θ) (y+h\ sin θ) +3 (y+h\ sin θ) ^2\\
&=x^2+2xh\ cos θ+h^2\ cos^2 θ−xy−xh\ sin θ−yh\ cos θ−h^2\ sin θ\ cos θ+3y^2+6yh\ sin θ+3h^2\ sin^2 θ\\
&=x^2+2xh (\ frac {3} {5}) +\ frac {9h^2} {25} −xy−\ frac {4xh} {5} −\ frac {3yh} {5} −\ frac {12h ^2} {25} +3y^2+6yh (\ frac {4} {5}) +3h^2 (\ frac {16} {25})\\
&=x^2−xy+3y^2+\ frac {2xh} {5} +\ frac {9h^2} {5} {5} {5} +\ frac {21yh} {5}. \ end {align*}\]

Substituímos essa expressão na Equação\ ref {DD} por$a = x$ e$b = y$:

\ [\ begin {align*} D_ {\ vecs u} f (x, y) &=\ lim_ {h→0}\ frac {f (x+h\ cos θ, y+h\ sin θ) −f (x, y)} {h}\\
&=\ lim_ {h→0}\ frac {(x^2−xy+3y^2+\ frac {2xh} {5} +\ frac {9h^2} {5} +\ frac {21yh} {5}) − (x^2−xy+3y^2)} {h}\\
&=\ lim_ {h→0}\ frac {\ frac {2xh} {5} +\ frac {9h^2} {5} +\ frac {21c yh} {5} {h}\\
& ; =\ lim_ {h→0}\ frac {2x} {5} +\ frac {9h} {5} +\ frac {21y} {5}\\
&=\ frac {2x+21y} {5}. \ end {align*}\]

Para calcular,$D_{\vecs u}f(−1,2),$$y=2$ substituímos$x=−1$ e nesta resposta (Figura$\PageIndex{2}$):

\[ D_{\vecs u}f(−1,2)=\dfrac{2(−1)+21(2)}{5}=\dfrac{−2+42}{5}=8. \nonumber \]

A forma f (x, y) = x2 — xy + 3y2 no espaço xyz com plano tangente no ponto (—1, 2, 15). Há duas flechas a partir do ponto, uma aparentemente ao longo da superfície da forma e a outra na direção do plano. O que corresponde ao plano está marcado com u = 3/5 i + 4/5 j. — Figura$\PageIndex{2}$: Encontrando a derivada direcional em uma determinada direção$\vecs u$ em um determinado ponto de uma superfície. O plano é tangente à superfície em um determinado ponto$(−1,2,15).$

Uma abordagem mais fácil para calcular derivadas direcionais que envolvem derivadas parciais é descrita no teorema a seguir.

Derivada direcional de uma função de duas variáveis

$z=f(x,y)$Seja uma função de duas variáveis$x$ e$y$, e suponha que$f_x$$f_y$ exista. Então, a derivada direcional de$f$ na direção de$\vecs u=(\cos θ)\,\hat{\mathbf i}+(\sin θ)\,\hat{\mathbf j}$ é dada por

\[D_{\vecs u}f(x,y)=f_x(x,y)\cos θ+f_y(x,y)\sin θ. \label{DD2v} \]

Prova

Aplicando a definição de uma derivada direcional indicada acima na Equação\ ref {DD}, a derivada direcional de$f$ na direção de$\vecs u=(\cos θ)\,\hat{\mathbf i}+(\sin θ)\,\hat{\mathbf j}$$(x_0, y_0)$ em um ponto no domínio de$f$ pode ser escrita

\[D_{\vecs u}f((x_0, y_0))=\lim_{t→0}\dfrac{f(x_0+t \cos θ,y_0+t\sin θ)−f(x_0,y_0)}{t}. \nonumber \]

Deixe$x=x_0+t\cos θ$$y=y_0+t\sin θ,$ e defina$g(t)=f(x,y)$. Como$f_x$$f_y$ ambas existem, podemos usar a regra da cadeia para calcular funções de duas variáveis$g′(t)$:

\[g′(t)=\dfrac{∂f}{∂x}\dfrac{dx}{dt}+\dfrac{∂f}{∂y}\dfrac{dy}{dt}=f_x(x,y)\cos θ+f_y(x,y)\sin θ. \nonumber \]

Se$t=0,$ então$x=x_0$ e$y=y_0,$ assim

\[g′(0)=f_x(x_0,y_0)\cos θ+f_y(x_0,y_0)\sin θ \nonumber \]

Pela definição$g′(t),$, também é verdade que

\[g′(0)=\lim_{t→0}\dfrac{g(t)−g(0)}{t}=\lim_{t→0}\dfrac{f(x_0+t\cos θ,y_0+t\sin θ)−f(x_0,y_0)}{t}. \nonumber \]

Portanto,$D_{\vecs u}f(x_0,y_0)=f_x(x_0,y_0)\cos θ+f_y(x_0,y_0)\sin θ$.

Como o ponto$ (x_0,y_0) $ é um ponto arbitrário do domínio de$f$, esse resultado vale para todos os pontos no domínio dos$f$ quais$f_y$ existem$f_x$ os parciais.

Portanto,\[D_{\vecs u}f(x,y)=f_x(x,y)\cos θ+f_y(x,y)\sin θ. \nonumber \]

□

Exemplo$\PageIndex{2}$: Finding a Directional Derivative: Alternative Method

Vamos$θ=\arccos (3/5).$ encontrar a derivada direcional$D_{\vecs u}f(x,y)$ de$f(x,y)=x^2−xy+3y^2$ na direção de$\vecs u=(\cos θ)\,\hat{\mathbf i}+(\sin θ)\,\hat{\mathbf j}$.

Em seguida, determine$D_{\vecs u}f(−1,2)$.

Solução

Primeiro, devemos calcular as derivadas parciais de$f$:

\[\begin{align*}f_x(x,y) &=2x−y \\ f_y(x,y) &=−x+6y, \end{align*}\]

Em seguida, usamos a Equação\ ref {DD2v} com$θ=\arccos (3/5)$:

\ [\ begin {align*} D_ {\ vecs u} f (x, y) &=f_x (x, y)\ cos θ+f_y (x, y)\ sin θ\\
& =( 2x−y)\ dfrac {3} {5} + (−x+6y)\ dfrac {4} {5}\\
&=\ dfrac {6 x} {5} −\ dfrac {3y} {5} −\ dfrac {4x} {5} +\ dfrac {24y} {5}\\
&=\ dfrac {2x+21y} {5}. \ end {align*}\]

Para calcular$D_{\vecs u}f(−1,2),$ let$x=−1$ e$y=2$:

\[D_{\vecs u}f(−1,2)=\dfrac{2(−1)+21(2)}{5}=\dfrac{−2+42}{5}=8.\nonumber \]

Essa é a mesma resposta obtida no Example$\PageIndex{1}$.

Exercício$\PageIndex{1}$:

Encontre a derivada direcional$D_{\vecs u}f(x,y)$ de$f(x,y)=3x^2y−4xy^3+3y^2−4x$ na direção de$\vecs u=(\cos \dfrac{π}{3})\,\hat{\mathbf i}+(\sin \dfrac{π}{3})\,\hat{\mathbf j}$ usar a Equação\ ref {DD2v}.

O que é$D_{\vecs u} f(3,4)$?

Dica

Calcule as derivadas parciais e determine o valor de$θ$.

Resposta

$D_{\vecs u}f(x,y)=\dfrac{(6xy−4y^3−4)(1)}{2}+\dfrac{(3x^2−12xy^2+6y)\sqrt{3}}{2}$

$D_{\vecs u}f(3,4)=\dfrac{72−256−4}{2}+\dfrac{(27−576+24)\sqrt{3}}{2}=−94−\dfrac{525\sqrt{3}}{2}$

Se o vetor que é dado para a direção da derivada não for um vetor unitário, então só é necessário dividir pela norma do vetor. Por exemplo, se quiséssemos encontrar a derivada direcional da função em Exemplo$\PageIndex{2}$ na direção do vetor$⟨−5,12⟩$, primeiro dividiríamos por sua magnitude para obter$\vecs u$. Isso nos dá$\vecs u=⟨−\frac{5}{13},\frac{12}{13}⟩$.

Então

\ [\ begin {align*} D_ {\ vecs u} f (x, y) &=f_x (x, y)\ cos θ+f_y (x, y)\ sin θ\\
&=−\ dfrac {5} {13} (2x−y) +\ dfrac {12} {13} (−x+6y)\\
&=−\ dfrac {22} {13} x+\ dfrac {17} {13} y\ end {align*}\]

Gradiente

O lado direito da Equação\ ref {DD2v} é igual a$f_x(x,y)\cos θ+f_y(x,y)\sin θ$, o que pode ser escrito como produto escalar de dois vetores. Defina o primeiro vetor como$\vecs ∇f(x,y)=f_x(x,y)\,\hat{\mathbf i}+f_y(x,y)\,\hat{\mathbf j}$ e o segundo vetor como$\vecs u=(\cos θ)\,\hat{\mathbf i}+(\sin θ)\,\hat{\mathbf j}$. Em seguida, o lado direito da equação pode ser escrito como o produto escalar desses dois vetores:

\[D_{\vecs u}f(x,y)=\vecs ∇f(x,y)⋅\vecs u. \label{gradDirDer} \]

O primeiro vetor em Equation\ ref {gradDirder} tem um nome especial: o gradiente da função$f$. O símbolo$∇$ é chamado nabla e o vetor$\vecs ∇f$ é lido como “del”$f$.

Definição: O gradiente

$z=f(x,y)$Seja uma função de$x$ e$y$ tal que$f_x$$f_y$ exista. O vetor$\vecs ∇f(x,y)$ é chamado de gradiente de$f$ e é definido como

\[\vecs ∇f(x,y)=f_x(x,y)\,\hat{\mathbf i}+f_y(x,y)\,\hat{\mathbf j}. \label{grad} \]

O vetor também$\vecs ∇f(x,y)$ é escrito como “graduado”$f$.

Exemplo$\PageIndex{3}$: Finding Gradients

Encontre o gradiente$\vecs ∇f(x,y)$ de cada uma das seguintes funções:

$f(x,y)=x^2−xy+3y^2$
$f(x,y)=\sin 3 x \cos 3y$

Solução

Para ambas as partes a. e b., primeiro calculamos as derivadas parciais$f_x$ e$f_y$, em seguida, usamos a Equação\ ref {grad}.

a.$ f_x(x,y)=2x−y$ e$f_y(x,y)=−x+6y$, então

\[\begin{align*} \vecs ∇f(x,y) &=f_x(x,y)\,\hat{\mathbf i}+f_y(x,y)\,\hat{\mathbf j}\\ &=(2x−y)\,\hat{\mathbf i}+(−x+6y)\,\hat{\mathbf j}.\end{align*}\]

b.$ f_x(x,y)=3\cos 3x \cos 3y$ e$f_y(x,y)=−3\sin 3x \sin 3y$, então

\ [\ begin {align*}\ vecs f (x, y) &=f_x (x, y)\,\ hat {\ mathbf i} +f_y (x, y)\,\ hat {\ mathbf j}\\
& =( 3\ cos 3x\ cos 3y)\,\ hat {\ mathbf i} − (3\ sin 3x\ sin 3y)\,\ hat {\ mathbf j}. \ end {align*}\]

Exercício$\PageIndex{2}$

Encontre o gradiente$\vecs ∇f(x,y)$ de$f(x,y)=\dfrac{x^2−3y^2}{2x+y}$.

Dica: Calcule as derivadas parciais e, em seguida, use a Equação\ ref {grad}.
Resposta: $\vecs ∇f(x,y)=\dfrac{2x^2+2xy+6y^2}{(2x+y)^2}\,\hat{\mathbf i}−\dfrac{x^2+12xy+3y^2}{(2x+y)^2}\,\hat{\mathbf j}$

O gradiente tem algumas propriedades importantes. Já vimos uma fórmula que usa o gradiente: a fórmula para a derivada direcional. Lembre-se do The Dot Product que se o ângulo entre dois vetores$\vecs a$ e$\vecs b$ é$φ$, então$\vecs a⋅\vecs b=‖\vecs a‖‖\vecs b‖\cos φ.$ Portanto, se o ângulo entre$\vecs ∇f(x_0,y_0)$ e$\vecs u=(cosθ)\,\hat{\mathbf i}+(sinθ)\,\hat{\mathbf j}$ for$φ$, temos

\[D_{\vecs u}f(x_0,y_0)=\vecs ∇f(x_0,y_0)⋅\vecs u=\|\vecs ∇f(x_0,y_0)\|‖\vecs u‖\cos φ=\|\vecs ∇f(x_0,y_0)\|\cos φ. \nonumber \]

O$‖\vecs u‖$ desaparece porque$\vecs u$ é um vetor unitário. Portanto, a derivada direcional é igual à magnitude do gradiente avaliado$(x_0,y_0)$ multiplicado por$\cos φ$. Lembre-se de que$\cos φ$ varia$−1$ de$1$ a.

Se$φ=0,$ então$\cos φ=1$$\vecs ∇f(x_0,y_0)$ e$\vecs u$ ambos apontarem na mesma direção.

Se$φ=π$, então$\cos φ=−1$ e$\vecs ∇f(x_0,y_0)$ e$\vecs u$ apontam em direções opostas.

No primeiro caso, o valor de$D_{\vecs u}f(x_0,y_0)$ é maximizado; no segundo caso, o valor de$D_{\vecs u}f(x_0,y_0)$ é minimizado.

Também podemos ver que se$\vecs ∇f(x_0,y_0)=\vecs 0$, então

\[ D_{\vecs u}f(x_0,y_0)=\vecs ∇f(x_0,y_0)⋅\vecs u=0 \nonumber \]

para qualquer vetor$\vecs u$. Esses três casos são descritos no seguinte teorema.

Propriedades do gradiente

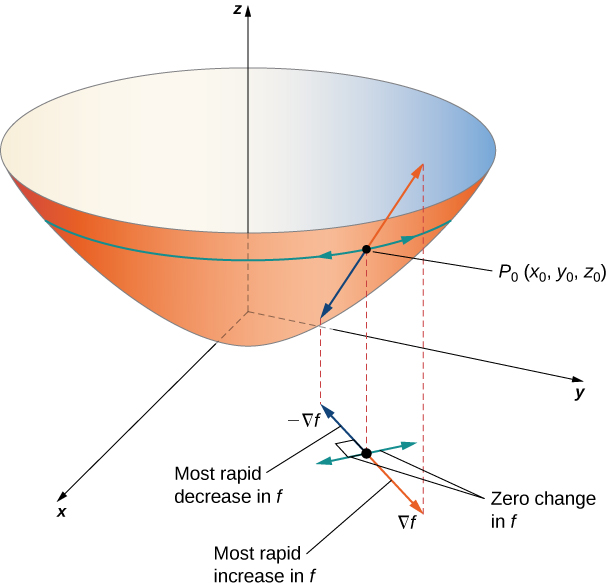
Suponha que a função$z=f(x,y)$ seja diferenciável em$(x_0,y_0)$ (Figura$\PageIndex{3}$).

Se$\vecs ∇f(x_0,y_0)=\vecs 0$, então$D_{\vecs u}f(x_0,y_0)=0$ para qualquer vetor unitário$\vecs u$.
Se$\vecs ∇f(x_0,y_0)≠ \vecs 0$, então$D_{\vecs u}f(x_0,y_0)$ é maximizado quando$\vecs u$ aponta na mesma direção que$\vecs ∇f(x_0,y_0)$. O valor máximo de$D_{\vecs u}f(x_0,y_0)$ é$\|\vecs ∇f(x_0,y_0)\|$.
Se$\vecs ∇f(x_0,y_0)≠\vecs 0$, então$D_{\vecs u}f(x_0,y_0)$ é minimizado quando$\vecs u$ aponta na direção oposta de$\vecs ∇f(x_0,y_0)$. O valor mínimo de$D_{\vecs u}f(x_0,y_0)$ é$−\|\vecs ∇f(x_0,y_0)\|$.

Um parabolóide voltado para cima no espaço xyz com o ponto P0 (x0, y0, z0). A partir desse ponto, há flechas subindo, descendo e contornando o parabolóide. No plano xy, o ponto (x0, y0) é marcado e as setas correspondentes são desenhadas no plano: a seta para baixo corresponde a −f (diminuição mais rápida em f), a seta para cima corresponde a f (aumento mais rápido em f) e as setas ao redor não correspondem a nenhuma mudança em f. As setas para cima/para baixo são perpendiculares a as setas ao redor em sua projeção no avião. — Figura$\PageIndex{3}$: O gradiente indica os valores máximo e mínimo da derivada direcional em um ponto.

Exemplo$\PageIndex{4}$: Finding a Maximum Directional Derivative

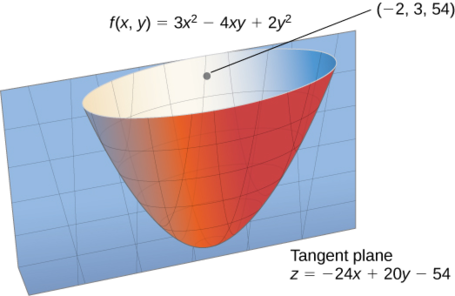
Encontre a direção para a qual a derivada direcional de$f(x,y)=3x^2−4xy+2y^2$ at$(−2,3)$ é máxima. Qual é o valor máximo?

Solução

O valor máximo da derivada direcional ocorre quando$\vecs ∇f$ e o vetor unitário aponta na mesma direção. Portanto, começamos calculando$\vecs ∇f(x,y$):

\[f_x(x,y)=6x−4y \; \text{and}\; f_y(x,y)=−4x+4y \nonumber \]

então

\[\vecs ∇f(x,y)=f_x(x,y)\,\hat{\mathbf i}+f_y(x,y)\,\hat{\mathbf j}=(6x−4y)\,\hat{\mathbf i}+(−4x+4y)\,\hat{\mathbf j}. \nonumber \]

Em seguida, avaliamos o gradiente em$(−2,3)$:

\[\vecs ∇f(−2,3)=(6(−2)−4(3))\,\hat{\mathbf i}+(−4(−2)+4(3))\,\hat{\mathbf j}=−24\,\hat{\mathbf i}+20\,\hat{\mathbf j}. \nonumber \]

Precisamos encontrar um vetor unitário que aponte na mesma direção$\vecs ∇f(−2,3),$, então o próximo passo é dividir$\vecs ∇f(−2,3)$ por sua magnitude, que é$\sqrt{(−24)^2+(20)^2}=\sqrt{976}=4\sqrt{61}$. Portanto,

\[\dfrac{\vecs ∇f(−2,3)}{\|\vecs ∇f(−2,3)\|}=\dfrac{−24}{4\sqrt{61}}i+\dfrac{20}{4\sqrt{61}}j=−\dfrac{6\sqrt{61}}{61}\,\hat{\mathbf i}+\dfrac{5\sqrt{61}}{61}\,\hat{\mathbf j}. \nonumber \]

Este é o vetor unitário que aponta na mesma direção que$\vecs ∇f(−2,3).$ Para encontrar o ângulo correspondente a esse vetor unitário, resolvemos as equações

\[\cos θ=\dfrac{−6\sqrt{61}}{61}\; \text{and}\; \sin θ=\dfrac{5\sqrt{61}}{61} \nonumber \]

para$θ$. Como o cosseno é negativo e o seno é positivo, o ângulo deve estar no segundo quadrante. Portanto,$θ=π−\arcsin((5\sqrt{61})/61)≈2.45$ rad.

O valor máximo da derivada direcional em$(−2,3)$ é$\|\vecs ∇f(−2,3)\|=4\sqrt{61}$ (Figura$\PageIndex{4}$).

Um parabolóide voltado para cima f (x, y) = 3x2 — 4xy + 2y2 com plano tangente no ponto (—2, 3, 54). O plano tangente tem a equação z = —24x + 20y — 54. — Figura$\PageIndex{4}$: O valor máximo da derivada direcional em$(−2,3)$ está na direção do gradiente.

Exercício$\PageIndex{3}$

Encontre a direção para a qual a derivada direcional de$g(x,y)=4x−xy+2y^2$ at$(−2,3)$ é máxima. Qual é o valor máximo?

Dica

Avalie o gradiente de$g$ no ponto$(−2,3)$.

Resposta

O gradiente de$g$ at$(−2,3)$ é$\vecs ∇g(−2,3)=\,\hat{\mathbf i}+14\,\hat{\mathbf j}$. O vetor unitário que aponta na mesma direção que$\vecs ∇g(−2,3)$ é

\[\dfrac{\vecs ∇g(−2,3)}{\|\vecs ∇g(−2,3)\|}=\dfrac{1}{\sqrt{197}}\,\hat{\mathbf i}+\dfrac{14}{\sqrt{197}}\,\hat{\mathbf j}=\dfrac{\sqrt{197}}{197}\,\hat{\mathbf i}+\dfrac{14\sqrt{197}}{197}\,\hat{\mathbf j},\nonumber \]

o que dá um ângulo de$θ=\arcsin ((14\sqrt{197})/197)≈1.499$ rad.

O valor máximo da derivada direcional é$\|\vecs ∇g(−2,3)\|=\sqrt{197}$.

A figura$\PageIndex{5}$ mostra uma parte do gráfico da função$f(x,y)=3+\sin x \sin y$. Dado um ponto$(a,b)$ no domínio de$f$, o valor máximo da derivada direcional nesse ponto é dado por$\|\vecs ∇f(a,b)\|$. Isso seria igual à taxa de maior subida se a superfície representasse um mapa topográfico. Se formos na direção oposta, seria a taxa de maior descida.

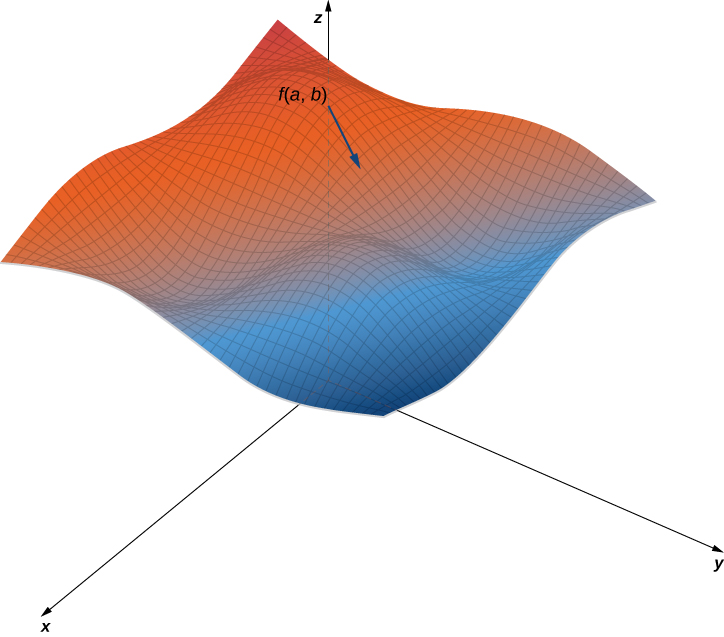
Uma superfície no espaço xyz com ponto em f (a, b). Há uma flecha na direção da maior descida. — Figura$\PageIndex{5}$: Uma superfície típica em$\mathbb R^3$. Dado um ponto na superfície, a derivada direcional pode ser calculada usando o gradiente.

Ao usar um mapa topográfico, a inclinação mais íngreme está sempre na direção em que as linhas de contorno estão mais próximas (Figura$\PageIndex{6}$). Isso é análogo ao mapa de contorno de uma função, supondo que as curvas de nível sejam obtidas para valores igualmente espaçados em todo o intervalo dessa função.

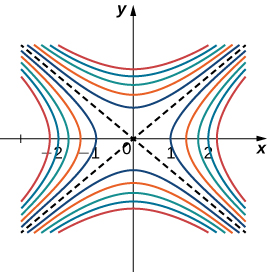
Duas linhas tracejadas cruzadas que passam pela origem e uma série de linhas curvas se aproximando das cruzes linhas tracejadas como se fossem assíntotas. — Figura$\PageIndex{6}$: Mapa de contorno da função$f(x,y)=x^2−y^2$ usando valores de nível entre$−5$$5$ e.

Gradientes e curvas de nível

Lembre-se de que, se uma curva for definida parametricamente pelo par de funções$(x(t),y(t)),$, o vetor$x′(t)\,\hat{\mathbf i}+y′(t)\,\hat{\mathbf j}$ será tangente à curva para cada valor de$t$ no domínio. Agora, vamos supor que$z=f(x,y)$ seja uma função diferenciável de$x$ e$y$, e$(x_0,y_0)$ esteja em seu domínio. Vamos supor ainda que$x_0=x(t_0)$ e$y_0=y(t_0)$ para algum valor de$t$, e considere a curva de nível$f(x,y)=k$. Defina$g(t)=f(x(t),y(t))$ e calcule$g′(t)$ na curva de nível. Pela regra da cadeia,

\[g′(t)=f_x(x(t),y(t))x′(t)+f_y(x(t),y(t))y′(t). \nonumber \]

Mas$g′(t)=0$ porque$g(t)=k$ para todos$t$. Portanto, por um lado,

\[f_x(x(t),y(t))x′(t)+f_y(x(t),y(t))y′(t)=0; \nonumber \]

por outro lado,

\[f_x(x(t),y(t))x′(t)+f_y(x(t),y(t))y′(t)=\vecs ∇f(x,y)⋅⟨x′(t),y′(t)⟩. \nonumber \]

Portanto,

\[\vecs ∇f(x,y)⋅⟨x′(t),y′(t)⟩=0. \nonumber \]

Assim, o produto escalar desses vetores é igual a zero, o que implica que eles são ortogonais. No entanto, o segundo vetor é tangente à curva de nível, o que implica que o gradiente deve ser normal à curva de nível, o que dá origem ao seguinte teorema.

O gradiente é normal em relação à curva de nível

Suponha que a função$z=f(x,y)$ tenha derivadas parciais contínuas de primeira ordem em um disco aberto centrado em um ponto$(x_0,y_0)$. Se$\vecs ∇f(x_0,y_0)≠0$, então$\vecs ∇f(x_0,y_0)$ é normal para a curva de nível de$f$ em$(x_0,y_0).$

Podemos usar esse teorema para encontrar vetores tangentes e normais para nivelar as curvas de uma função.

Exemplo$\PageIndex{5}$: Finding Tangents to Level Curves

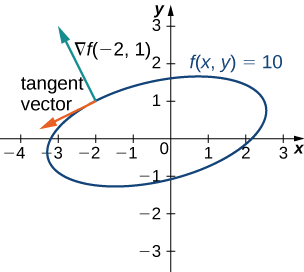
Para a função,$f(x,y)=2x^2−3xy+8y^2+2x−4y+4,$ encontre um vetor tangente à curva de nível no ponto$(−2,1)$. Faça um gráfico da curva de nível correspondente$f(x,y)=18$ e desenhe um vetor tangente.$\vecs ∇f(−2,1)$

Solução

Primeiro, devemos calcular$\vecs ∇f(x,y):$

\[f_x(x,y)=4x−3y+2 \;\text{and}\; f_y=−3x+16y−4 \;\text{so}\; \vecs ∇f(x,y)=(4x−3y+2)\,\hat{\mathbf i}+(−3x+16y−4)\,\hat{\mathbf j}.\nonumber \]

Em seguida, avaliamos$\vecs ∇f(x,y)$ em$(−2,1):$

\[\vecs ∇f(−2,1)=(4(−2)−3(1)+2)\,\hat{\mathbf i}+(−3(−2)+16(1)−4)\,\hat{\mathbf j}=−9\,\hat{\mathbf i}+18\,\hat{\mathbf j}.\nonumber \]

Esse vetor é ortogonal à curva no ponto$(−2,1)$. Podemos obter um vetor tangente invertendo os componentes e multiplicando qualquer um por$−1$. Assim, por exemplo,$−18\,\hat{\mathbf i}−9\,\hat{\mathbf j}$ é um vetor tangente (Figura$\PageIndex{7}$).

Uma elipse girada com a equação f (x, y) = 10. No ponto (—2, 1) da elipse, são desenhadas duas setas, um vetor tangente e um vetor normal. O vetor normal é marcado com f (—2, 1) e é perpendicular ao vetor tangente. — Figura$\PageIndex{7}$: Vetores tangentes e normais$2x^2−3xy+8y^2+2x−4y+4=18$ em relação ao ponto$(−2,1)$.

Exercício$\PageIndex{4}$

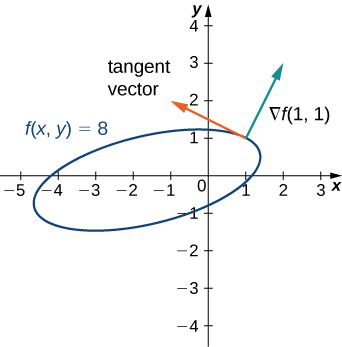
Para a função$f(x,y)=x^2−2xy+5y^2+3x−2y+3$, encontre a tangente à curva de nível no ponto$(1,1)$. Desenhe o gráfico da curva de nível correspondente a$f(x,y)=8$$\vecs ∇f(1,1)$ e desenhe um vetor tangente.

Dica

Calcule o gradiente no ponto$(1,1)$.

Resposta

$\vecs ∇f(x,y)=(2x−2y+3)\,\hat{\mathbf i}+(−2x+10y−2)\,\hat{\mathbf j}$

$\vecs ∇f(1,1)=3\,\hat{\mathbf i}+6\,\hat{\mathbf j}$

Vetor tangente:$6\,\hat{\mathbf i}−3\,\hat{\mathbf j}$ ou$−6\,\hat{\mathbf i}+3\,\hat{\mathbf j}$

$Uma elipse girada com a equação f (x, y) = 8. No ponto (1, 1) da elipse, são desenhadas duas setas, um vetor tangente e um vetor normal. O vetor normal é marcado com f (1, 1) e é perpendicular ao vetor tangente.$

Gradientes tridimensionais e derivadas direcionais

A definição de um gradiente pode ser estendida para funções de mais de duas variáveis.

Definição: Gradientes em 3D

$w=f(x, y, z)$Seja uma função de três variáveis como essa$f_x, \, f_y$ $fx,fy,andfzfx,fy,andfz" role="presentation" tabindex="0"> e$f_z$$ exista. O vetor$\vecs ∇f(x,y,z)$ é chamado de gradiente de $ff" role="presentation" tabindex="0">$f$$ e é definido como

\[\vecs ∇f(x,y,z)=f_x(x,y,z)\,\hat{\mathbf i}+f_y(x,y,z)\,\hat{\mathbf j}+f_z(x,y,z)\,\hat{\mathbf k}.\label{grad3d} \]

$\vecs ∇f(x,y,z)$também pode ser escrito como graduado$f(x,y,z).$

Calcular o gradiente de uma função em três variáveis é muito semelhante ao cálculo do gradiente de uma função em duas variáveis. Primeiro, calculamos as derivadas parciais$f_x, \, f_y,$ e$f_z$, em seguida, usamos a Equação\ ref {grad3d}.

Exemplo$\PageIndex{6}$: Finding Gradients in Three Dimensions

Encontre o gradiente$\vecs ∇f(x,y,z)$ de cada uma das seguintes funções:

$f(x,y,z)=5x^2−2xy+y^2−4yz+z^2+3xz$
$f(x,y,z)=e^{−2z}\sin 2x \cos 2y$

Solução

Para ambas as partes a. e b., primeiro calculamos as derivadas parciais$f_x,f_y,$ e$f_z$, em seguida, usamos a Equação\ ref {grad3d}.

a.$f_x(x,y,z)=10x−2y+3z$,$f_y(x,y,z)=−2x+2y−4z$, e$ f_z(x,y,z)=3x−4y+2z$, então

\ [\ begin {align*}\ vecs f (x, y, z) &=f_x (x, y, z)\,\ hat {\ mathbf i} +f_y (x, y, z)\,\ hat {\ mathbf j} +f_z (x, y, z)\,\ hat {\ mathbf k}\\
& =( 10x−2y+3z)\,\ hat {\ mathbf i} + (−2x+2y−4z)\,\ hat {\ mathbf j} + (3x-4y+2z)\,\ hat {\ mathbf k}. \ end {align*}\]

b.$f_x(x,y,z) =2e^{−2z}\cos 2x \cos 2y$,$ f_y(x,y,z)=−2e^{−2z} \sin 2x \sin 2y$, e$f_z(x,y,z)=−2e^{−2z}\sin 2x \cos 2y$, assim

\[\begin{align*} \vecs ∇f(x,y,z) &=f_x(x,y,z)\,\hat{\mathbf i}+f_y(x,y,z)\,\hat{\mathbf j}+f_z(x,y,z)\,\hat{\mathbf k} \\ &=(2e^{−2z}\cos 2x \cos 2y)\,\hat{\mathbf i}+(−2e^{−2z} \sin 2x \sin 2y)\,\hat{\mathbf j}+(−2e^{−2z}\sin 2x \cos 2y)\,\hat{\mathbf k} \\ &=2e^{−2z}(\cos 2x \cos 2y \,\hat{\mathbf i}−\sin 2x \sin 2y\,\hat{\mathbf j}−\sin 2x \cos 2y\,\hat{\mathbf k}). \end{align*}\]

Exercício$\PageIndex{5}$:

Encontre o gradiente$\vecs ∇f(x,y,z)$ de$f(x,y,z)=\dfrac{x^2−3y^2+z^2}{2x+y−4z.}$

Resposta: \[\vecs ∇f(x,y,z)=\dfrac{2x^2+2xy+6y^2−8xz−2z^2}{(2x+y−4z)^2}\,\hat{\mathbf i}−\dfrac{x^2+12xy+3y^2−24yz+z^2}{(2x+y−4z)^2}\,\hat{\mathbf j}+\dfrac{4x^2−12y^2−4z^2+4xz+2yz}{(2x+y−4z)^2}\,\hat{\mathbf k}\nonumber \]

A derivada direcional também pode ser generalizada para funções de três variáveis. Para determinar uma direção em três dimensões, é necessário um vetor com três componentes. Esse vetor é um vetor unitário e os componentes do vetor unitário são chamados de cossenos direcionais. Dado um vetor unitário tridimensional$\vecs u$ na forma padrão (ou seja, o ponto inicial está na origem), esse vetor forma três ângulos diferentes com os$z$ eixos positivos$x$$y$ -, - e -. Vamos chamar esses ângulos$α,β,$$γ$ e. Em seguida, os cossenos direcionais são dados por$\cos α,\cos β,$$\cos γ$ e. Esses são os componentes do vetor unitário$\vecs u$; como$\vecs u$ é um vetor unitário, é verdade que$\cos^2 α+\cos^2 β+\cos^2 γ=1.$

Definição: Derivada direcional de uma função de três variáveis

Suponha que$w=f(x,y,z)$ seja uma função de três variáveis com um domínio de$D$. Seja$(x_0,y_0,z_0)∈D$ e$\vecs u=\cos α\,\hat{\mathbf i}+\cos β\,\hat{\mathbf j}+\cos γ\,\hat{\mathbf k}$ seja um vetor unitário. Então, a derivada direcional de$f$ na direção de$u$ é dada por

\[D_{\vecs u}f(x_0,y_0,z_0)=\lim_{t→0}\dfrac{f(x_0+t \cos α,y_0+t\cos β,z_0+t\cos γ)−f(x_0,y_0,z_0)}{t} \nonumber \]

desde que o limite exista.

Podemos calcular a derivada direcional de uma função de três variáveis usando o gradiente, levando a uma fórmula que é análoga à Equação\ ref {DD2v}.

Derivada direcional de uma função de três variáveis

$f(x,y,z)$Seja uma função diferenciável de três variáveis e$\vecs u=\cos α\,\hat{\mathbf i}+\cos β\,\hat{\mathbf j}+\cos γ\,\hat{\mathbf k}$ seja um vetor unitário. Então, a derivada direcional de$f$ na direção de$\vecs u$ é dada por

\[D_{\vecs u}f(x,y,z)=\vecs ∇f(x,y,z)⋅\vecs u=f_x(x,y,z)\cos α+f_y(x,y,z)\cos β+f_z(x,y,z)\cos γ. \label{DDv3} \]

Os três ângulos$α,β,$ e$γ$ determinam o vetor unitário$\vecs u$. Na prática, podemos usar um vetor arbitrário (não unitário) e depois dividir por sua magnitude para obter um vetor unitário na direção desejada.

Exemplo$\PageIndex{7}$: Finding a Directional Derivative in Three Dimensions

Calcule$D_{\vecs v}f(1,−2,3)$ na direção de$\vecs v=−\,\hat{\mathbf i}+2\,\hat{\mathbf j}+2\,\hat{\mathbf k}$ para a função

\[ f(x,y,z)=5x^2−2xy+y^2−4yz+z^2+3xz. \nonumber \]

Solução:

Primeiro, encontramos a magnitude de$v$:

\[‖\vecs v‖=\sqrt{(−1)^2+(2)^2+(2)^2}=\sqrt{9}=3. \nonumber \]

Portanto,$\dfrac{\vecs v}{‖\vecs v‖}=\dfrac{−\hat{\mathbf i}+2\,\hat{\mathbf j}+2\,\hat{\mathbf k}}{3}=−\dfrac{1}{3}\,\hat{\mathbf i}+\dfrac{2}{3}\,\hat{\mathbf j}+\dfrac{2}{3}\,\hat{\mathbf k}$ é um vetor unitário na direção de$\vecs v$, so$\cos α=−\dfrac{1}{3},\cos β=\dfrac{2}{3},$$\cos γ=\dfrac{2}{3}$ e. Em seguida, calculamos as derivadas parciais de$f$:

\ [\ begin {align*} f_x (x, y, z) &=10x−2y+3z\\
f_y (x, y, z) &=−2x+2y−4z\\
f_z (x, y, z) &=−4y+2z+3x,\ end {align*}\ nonumber\]

em seguida, substitua-os na Equação\ ref {ddV3}:

\ [\ begin {align*} D_ {\ vecs v} f (x, y, z) &=f_x (x, y, z)\ cos α+f_y (x, y, z)\ cos β+f_z (x, y, z)\ cos γ\\
& =( 10x−2y+3z) (−\ dfrac {1} {3}) + (−2x+2y−4z) (\ dfrac {2} {3}) + (−4y+2z+3x) (\ dfrac {2} {3})\\
&=−\ dfrac {10x} {3} +\ dfrac {2y} {3} −\ dfrac {3z} {3} −\ dfrac {4x} {3} +\ dfrac {4y} {3} −\ dfrac {8z} {3} −\ dfrac { 8y} {3} +\ dfrac {4z} {3} +\ dfrac {6x} {3}\\
&=−\ dfrac {8x} {3} −\ dfrac {2y} {3} −\ dfrac {7z} {3}. \ end {align*}\]

Por último, para encontrar$D_{\vecs v}f(1,−2,3),$ um substituto$x=1,\, y=−2$, e$z=3:$

\ [\ begin {align*} D_ {\ vecs v} f (1, −2,3) &=−\ dfrac {8 (1)} {3} −\ dfrac {2 (−2)} {3} −\ dfrac {7 (3)} {3}\\
&=−\ dfrac {8} {3} +\ dfrac {4} {3} −\ dfrac {21} {3}\\
&=−\ dfrac {25} {3}. \ end {align*}\]

Exercício$\PageIndex{6}$:

$D_{\vecs v}f(x,y,z)$Calcule e$D_{\vecs v}f(0,−2,5)$ na direção de$\vecs v=−3\,\hat{\mathbf i}+12\,\hat{\mathbf j}−4\,\hat{\mathbf k}$ para a função

\[f(x,y,z)=3x^2+xy−2y^2+4yz−z^2+2xz.\nonumber \]

Dica

Primeiro, divida$\vecs v$ por sua magnitude, calcule as derivadas parciais de e$f$, em seguida, use a Equação\ ref {ddV3}.

Resposta

$D_{\vecs v}f(x,y,z)=−\dfrac{3}{13}(6x+y+2z)+\dfrac{12}{13}(x−4y+4z)−\dfrac{4}{13}(2x+4y−2z)$

$D_{\vecs v}f(0,−2,5)=\dfrac{384}{13}$

Resumo

Uma derivada direcional representa a taxa de variação de uma função em qualquer direção dada.
O gradiente pode ser usado em uma fórmula para calcular a derivada direcional.
O gradiente indica a direção da maior mudança de uma função de mais de uma variável.

Equações-chave

derivada direcional (duas dimensões)\[D_{\vecs u}f(a,b)=\lim_{h→0}\dfrac{f(a+h\cos θ,b+h\sin θ)−f(a,b)}{h} \nonumber \] ou\[D_{\vecs u}f(x,y)=f_x(x,y)\cos θ+f_y(x,y)\sin θ\nonumber \]
gradiente (duas dimensões)\[\vecs ∇f(x,y)=f_x(x,y)\,\hat{\mathbf i}+f_y(x,y)\,\hat{\mathbf j}\nonumber \]
gradiente (três dimensões)\[\vecs ∇f(x,y,z)=f_x(x,y,z)\,\hat{\mathbf i}+f_y(x,y,z)\,\hat{\mathbf j}+f_z(x,y,z)\,\hat{\mathbf k}\nonumber \]
derivada direcional (três dimensões)\[D_{\vecs u}f(x,y,z)=\vecs ∇f(x,y,z)⋅\vecs u=f_x(x,y,z)\cos α+f_y(x,y,z)\cos β+f_x(x,y,z)\cos γ\nonumber \]

Glossário

derivada direcional: a derivada de uma função na direção de um determinado vetor unitário
gradiente: o gradiente da função$f(x,y)$ é definido como$\vecs ∇f(x,y)=(∂f/∂x)\,\hat{\mathbf i}+(∂f/∂y)\,\hat{\mathbf j},$ sendo o que pode ser generalizado para uma função de qualquer número de variáveis independentes

Definição: Derivadas direcionais

Exemplo\(\PageIndex{1}\): Finding a Directional Derivative from the Definition

Derivada direcional de uma função de duas variáveis

Prova

Exemplo\(\PageIndex{2}\): Finding a Directional Derivative: Alternative Method

Exercício\(\PageIndex{1}\):

Definição: O gradiente

Exemplo\(\PageIndex{3}\): Finding Gradients

Exercício\(\PageIndex{2}\)

Propriedades do gradiente

Exemplo\(\PageIndex{4}\): Finding a Maximum Directional Derivative

Exercício\(\PageIndex{3}\)

O gradiente é normal em relação à curva de nível

Exemplo\(\PageIndex{5}\): Finding Tangents to Level Curves

Exercício\(\PageIndex{4}\)

Definição: Gradientes em 3D

Exemplo\(\PageIndex{6}\): Finding Gradients in Three Dimensions

Exercício\(\PageIndex{5}\):

Definição: Derivada direcional de uma função de três variáveis

Derivada direcional de uma função de três variáveis

Exemplo\(\PageIndex{7}\): Finding a Directional Derivative in Three Dimensions

Exercício\(\PageIndex{6}\):