14.5E: Exercícios para a Seção 14.5

Last updated
Save as PDF

Page ID: 187954

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Nos exercícios 1 a 6, use as informações fornecidas para resolver o problema.

1) Deixe$ w(x,y,z)=xy\cos z,$ onde$ x=t,y=t^2,$ e$ z=\arcsin t.$ encontre$ \dfrac{dw}{dt}$.

Responda: $ \dfrac{dw}{dt}=y\cos z+x\cos z(2t)−\dfrac{xy\sin z}{\sqrt{1−t^2}}$

2) Deixe$ w(t,v)=e^{tv}$ onde$ t=r+s$$ v=rs$ e. Encontre$ \dfrac{∂w}{∂r}$$ \dfrac{∂w}{∂s}$ e.

3) Se$ w=5x^2+2y^2, \quad x=−3u+v,$$ \dfrac{∂w}{∂u}$ e$ y=u−4v,$ encontre$ \dfrac{∂w}{∂v}$ e.

Responda: $ \dfrac{∂w}{∂u}=−30x+4y \quad\ = \quad -30(-3u + v) + 4(u - 4v) \quad = \quad 90u -30v + 4u - 16v \quad = \quad 94u - 46v$,
$\dfrac{∂w}{∂v}=10x−16y \quad\ = \quad 10(-3u + v) - 16(u - 4v) \quad = \quad -30u +10v - 16u + 64v \quad = \quad -46u + 74v$

4) Se$ w=xy^2,x=5\cos(2t),$ e$ y=5\sin(2t)$, encontre$ \dfrac{∂w}{∂t}$.

5) Se$ f(x,y)=xy,x=r\cos θ,$ e$ y=r\sin θ$, encontre$\dfrac{∂f}{∂r}$ e expresse a resposta em termos de$ r$$ θ$ e.

Responda: $ \dfrac{∂f}{∂r}=r\sin(2θ)$

6) Suponha$ f(x,y)=x+y,u=e^x\sin y,\quad x=t^2$ e$ y=πt$, onde$ x=r\cos θ$$ y=r\sin θ$ e. Encontre$ \dfrac{∂f}{∂θ}$.

Nos exercícios 7 a 12, encontre$ \dfrac{dz}{dt}$ de duas maneiras, primeiro usando a regra da cadeia e depois por substituição direta.

7)$ z=x^2+y^2, \quad x=t,y=t^2$

Responda: $ \dfrac{dz}{dt}=2t+4t^3$

8)$ z=\sqrt{x^2+y^2},\quad y=t^2,x=t$

9)$ z=xy,\quad x=1−\sqrt{t},y=1+\sqrt{t}$

Responda: $ \dfrac{dz}{dt}=−1$

10)$ z=\frac{x}{y},\quad x=e^t,y=2e^t$

11)$ z=\ln(x+y), \quad x=e^t,y=e^t$

Responda: $ \dfrac{dz}{dt}=1$

12)$ z=x^4,\quad x=t,y=t$

13) Deixe$ w(x,y,z)=x^2+y^2+z^2, \quad x=cost,y=sint,$$ z=e^t$ e. $ w$Expresse em função de$ t$ e encontre$ \dfrac{dw}{dt}$ diretamente. Em seguida, encontre$ \dfrac{dw}{dt}$ usando a regra da cadeia.

Responda: $ \dfrac{dw}{dt}=2e^{2t}$em ambos os casos

14) Deixe$ z=x^2y,$ onde$ x=t^2$$ y=t^3$ e. Encontre$ \dfrac{dz}{dt}$.

15) Deixe$ u=e^x\sin y,$ onde$ x=-\ln 2t$$ y=πt$ e. Descubra$ \dfrac{du}{dt}$ quando$ x=\ln 2$$ y=\frac{π}{4}$ e.

Responda: $ \dfrac{du}{dt} = \sqrt{2}\big(\pi - 4\big)$

Nos exercícios 16 a 33, determine$ \dfrac{dy}{dx}$ usando derivadas parciais.

16)$ \sin(6x)+\tan(8y)+5=0$

17)$ x^3+y^2x−3=0$

Responda: $ \dfrac{dy}{dx}=−\dfrac{3x^2+y^2}{2xy}$

18)$ \sin(x+y)+\cos(x−y)=4$

19)$ x^2−2xy+y^4=4$

Responda: $ \dfrac{dy}{dx}=\dfrac{y−x}{−x+2y^3}$

20)$ xe^y+ye^x−2x^2y=0$

21)$ x^{2/3}+y^{2/3}=a^{2/3}$

Responda: $ \dfrac{dy}{dx}=−\sqrt[3]{\frac{y}{x}}$

22)$ x\cos(xy)+y\cos x=2$

23)$ e^{xy}+ye^y=1$

Responda: $ \dfrac{dy}{dx}=−\dfrac{ye^{xy}}{xe^{xy}+e^y(1+y)}$

24)$ x^2y^3+\cos y=0$

25) Encontre$ \dfrac{dz}{dt}$ usando a regra da cadeia onde$ z=3x^2y^3,\,\,x=t^4,$$ y=t^2$ e.

Responda: $ \dfrac{dz}{dt}=42t^{13}$

26) Deixe$ z=3\cos x−\sin(xy),x=\frac{1}{t},$ e$ y=3t.$ encontre$ \dfrac{dz}{dt}$.

27) Deixe$ z=e^{1−xy},\,\, x=t^{1/3},$$ y=t^3$ e. Encontre$ \dfrac{dz}{dt}$.

Responda: $ \dfrac{dz}{dt}=−\frac{10}{3}t^{7/3}×e^{1−t^{10/3}}$

28) Encontre$ \dfrac{dz}{dt}$ pela regra da cadeia onde$ z=\cosh^2(xy),\,\,x=\frac{1}{2}t,$$ y=e^t$ e.

29) Deixe$ z=\dfrac{x}{y},\,\, x=2\cos u,$$ \dfrac{∂z}{∂u}$ e$ y=3\sin v.$ encontre$ \dfrac{∂z}{∂v}$ e.

Responda: $ \dfrac{∂z}{∂u}=\dfrac{−2\sin u}{3\sin v}$e$ \dfrac{∂z}{∂v}=\dfrac{−2\cos u\cos v}{3\sin^2v}$

30) Deixe$ z=e^{x^2y}$, onde$ x=\sqrt{uv}$$ y=\frac{1}{v}$ e. Encontre$ \dfrac{∂z}{∂u}$$ \dfrac{∂z}{∂v}$ e.

31) Se$ z=xye^{x/y},\,\, x=r\cos θ,$ e$ y=r\sin θ$, encontre$ \dfrac{∂z}{∂r}$$ r=2$ e$ \dfrac{∂z}{∂θ}$ quando$ θ=\frac{π}{6}$ e.

Responda: $ \dfrac{∂z}{∂r}=\sqrt{3}e^{\sqrt{3}}, \dfrac{∂z}{∂θ}=(2−4\sqrt{3})e^{\sqrt{3}}$

32) Descubra$ \dfrac{∂w}{∂s}$ se$ w=4x+y^2+z^3,\,\,x=e^{rs^2},\,\,y=\ln(\frac{r+s}{t}),$$ z=rst^2$ e.

33) Se$ w=\sin(xyz),\,\,x=1−3t,\,\,y=e^{1−t},$ e$ z=4t$, encontre$ \dfrac{∂w}{∂t}$.

Responda: $ \dfrac{∂w}{∂t}=-3yz\cos(xyz)−xze^{1−t}\cos(xyz)+4xy\cos(xyz)$

Nos exercícios 34 a 36, use esta informação: Diz-se que uma função$ f(x,y)$ é homogênea em grau$ n$ if$ f(tx,ty)=t^nf(x,y)$. Para todas as funções homogêneas de grau$ n$, a seguinte equação é verdadeira:$ x\dfrac{∂f}{∂x}+y\dfrac{∂f}{∂y}=nf(x,y)$. Mostre que a função dada é homogênea e verifique isso$ x\dfrac{∂f}{∂x}+y\dfrac{∂f}{∂y}=nf(x,y)$.

34)$ f(x,y)=3x^2+y^2$

(35)$ f(x,y)=\sqrt{x^2+y^2}$

Resposta: $ f(tx,ty)=\sqrt{t^2x^2+t^2y^2}=t^1f(x,y), \quad \dfrac{∂f}{∂y}=x\frac{1}{2}(x^2+y^2)^{−1/2}×2x+y\frac{1}{2}(x^2+y^2)^{−1/2}×2y=1f(x,y)$

36)$ f(x,y)=x^2y−2y^3$

37) O volume de um cilindro circular reto é dado por$ V(x,y)=πx^2y,$ onde$ x$ está o raio do cilindro e$ y$ a altura do cilindro. Suponha$ x$ e$ y$ sejam funções$ t$ dadas por$ x=\frac{1}{2}t$ e$ y=\frac{1}{3}t$ para que$ x$ ambas$ y$ estejam aumentando com o tempo. Com que rapidez o volume está aumentando quando$ x=2$ e$ y=5$? Suponha que o tempo seja medido em segundos.

Resposta: $ \ddfrac{dV}{dt} = \frac{34π}{3}\,\text{units}^3/\text{s}$

38) A pressão$ P$ de um gás está relacionada ao volume e à temperatura pela fórmula$ PV=kT$, onde a temperatura é expressa em kelvins. Expresse a pressão do gás em função de ambos$ V$$ T$ e. Descubra$ \dfrac{dP}{dt}$ quando$ k=1, \dfrac{dV}{dt}=2$ cm ³ /min,$ \dfrac{dT}{dt}=12$ K/min$ V=20 cm^3$,$ T=20°F$ e.

39) O raio de um cone circular reto está aumentando em$ 3$ cm/min, enquanto a altura do cone está diminuindo em$ 2$ cm/min. Encontre a taxa de variação do volume do cone quando o raio é$ 13$ cm e a altura é$ 18$ cm.

Resposta: $ \dfrac{dV}{dt}=\frac{1066π}{3}\,\text{cm}^3/\text{min}$

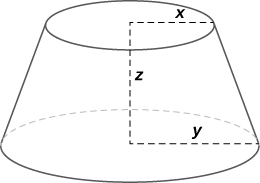
40) O volume de um tronco de um cone é dado pela fórmula$ V=\frac{1}{3}πz(x^2+y^2+xy),$ onde$ x$ é o raio do círculo menor,$ y$ é o raio do círculo maior e$ z$ é a altura do tronco (veja a figura). Encontre a taxa de variação do volume desse tronco quando$ x=10$ em.,$y=12$ em. e$ z=18$ dentro.

$Tronco de um cone com altura z, raio superior de x e raio inferior de y.$

41) Uma caixa fechada tem a forma de um sólido retangular com dimensões$ x,y,$$ z$ e. (As dimensões estão em polegadas.) Suponha que cada dimensão esteja mudando na taxa de$ 0.5$ in. /min. Encontre a taxa de variação da área total da superfície da caixa quando$ x=2$ em.,$y=3$ em. e$ z=1$ dentro.

Resposta: $ \dfrac{dA}{dt}=12\, \text{in.}^2/\text{min}$

42) A resistência total em um circuito que tem três resistências individuais representadas$ x,y,$ e$ z$ é dada pela fórmula$ R(x,y,z)=\dfrac{xyz}{yz+xz+xy}$. Suponha que em um determinado momento a$ x$ resistência seja$ 100\,Ω$, a$ y$ resistência seja$ 200\,Ω,$ e a$ z$ resistência seja$ 300\,Ω.$ Além disso, suponha que a$ x$ resistência esteja mudando$ 2\,Ω/\text{min},$ a uma taxa de que a$ y$ resistência esteja mudando na taxa de$ 1\,Ω/\text{min}$, e o $ z$a resistência não muda. Encontre a taxa de variação da resistência total neste circuito neste momento.

43) A temperatura$ T$ em um ponto$ (x,y)$ é$ T(x,y)$ e é medida usando a escala Celsius. Uma mosca rasteja de forma que sua posição após$ t$ segundos seja dada por$ x=\sqrt{1+t}$ e$ y=2+\frac{1}{3}t$, onde$ x$ e$ y$ seja medida em centímetros. A função de temperatura satisfaz$ T_x(2,3)=4$$ T_y(2,3)=3$ e. Com que rapidez a temperatura está aumentando na trajetória da mosca após um$ 3$ segundo?

Resposta: $ 2$°C/seg

44) Os$ y$ componentes$ x$ e de um fluido que se move em duas dimensões são dados pelas seguintes funções:$ u(x,y)=2y$$x≥0$ e$ v(x,y)=−2x$ com$y≥0$ e. A velocidade do fluido no ponto$ (x,y)$ é$ s(x,y)=\sqrt{u(x,y)^2+v(x,y)^2}$. Encontre$ \dfrac{∂s}{∂x}$ e$ \dfrac{∂s}{∂y}$ use a regra da cadeia.

45) Deixe$ u=u(x,y,z),$ onde$ x=x(w,t),\, y=y(w,t),\, z=z(w,t),\, w=w(r,s)$ e$ t=t(r,s).$ use um diagrama de árvore e a regra da cadeia para encontrar uma expressão para$ \dfrac{∂u}{∂r}$.

Resposta: $ \frac{∂u}{∂r}=\frac{∂u}{∂x}(\frac{∂x}{∂w}\frac{∂w}{∂r}+\frac{∂x}{∂t}\frac{∂t}{∂r})+\frac{∂u}{∂y}(\frac{∂y}{∂w}\frac{∂w}{∂r}+\frac{∂y}{∂t}\frac{∂t}{∂r})+\frac{∂u}{∂z}(\frac{∂z}{∂w}\frac{∂w}{∂r}+\frac{∂z}{∂t}\frac{∂t}{∂r})$