14.5: A regra da cadeia para funções multivariáveis
- Page ID
- 187940
- Defina as regras da cadeia para uma ou duas variáveis independentes.
- Use diagramas de árvore como uma ajuda para entender a regra da cadeia para várias variáveis independentes e intermediárias.
- Execute a diferenciação implícita de uma função de duas ou mais variáveis.
No cálculo de variável única, descobrimos que uma das regras de diferenciação mais úteis é a regra da cadeia, que nos permite encontrar a derivada da composição de duas funções. O mesmo vale para o cálculo multivariável, mas desta vez temos que lidar com mais de uma forma da regra da cadeia. Nesta seção, estudamos extensões da regra da cadeia e aprendemos como obter derivadas de composições de funções de mais de uma variável.
Regras de cadeia para uma ou duas variáveis independentes
Lembre-se de que a regra da cadeia para a derivada de um composto de duas funções pode ser escrita na forma
\[\dfrac{d}{dx}\Big(f(g(x))\Big)=f′\big(g(x)\big)g′(x). \nonumber \]
Nessa equação, ambos\(f(x)\) e\(g(x)\) são funções de uma variável. Agora, suponha que\(f\) seja uma função de duas variáveis e\(g\) seja uma função de uma variável. Ou talvez ambas sejam funções de duas variáveis, ou até mais. Como calcularíamos a derivada nesses casos? O teorema a seguir nos dá a resposta para o caso de uma variável independente.
Suponha que\(x=g(t)\) e\(y=h(t)\) sejam funções diferenciáveis de\(t\) e\(z=f(x,y)\) seja uma função diferenciável de\(x\)\(y\) e. Então\(z=f(x(t),y(t))\) é uma função diferenciável de\(t\) e
\[\dfrac{dz}{dt}=\dfrac{∂z}{∂x}⋅\dfrac{dx}{dt}+\dfrac{∂z}{∂y}⋅\dfrac{dy}{dt}, \label{chain1} \]
onde as derivadas ordinárias são avaliadas em\(t\) e as derivadas parciais são avaliadas em\((x,y)\).
A prova desse teorema usa a definição de diferenciabilidade de uma função de duas variáveis. Suponha que\(f\) seja diferenciável no\(P(x_0,y_0),\) ponto em que\(x_0=g(t_0)\) e\(y_0=h(t_0)\) para um valor fixo de\(t_0\). Queremos provar que\(z=f\big(x(t),y(t)\big)\) é diferenciável em\(t=t_0\) e que a Equação\ ref {chain1} também se mantém nesse ponto.
Como\(f\) é diferenciável em\(P\), sabemos que
\[z(t)=f(x,y)=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0)+E(x,y), \nonumber \]
onde
\[ \lim_{(x,y)→(x_0,y_0)}\dfrac{E(x,y)}{\sqrt{(x−x_0)^2+(y−y_0)^2}}=0. \nonumber \]
Em seguida, subtraímos\(z_0=f(x_0,y_0)\) dos dois lados dessa equação:
\[ \begin{align*} z(t)−z(t_0) &=f(x(t),y(t))−f(x(t_0),y(t_0)) \\[4pt] &=f_x(x_0,y_0)(x(t)−x(t_0))+f_y(x_0,y_0)(y(t)−y(t_0))+E(x(t),y(t)). \end{align*}\]
Em seguida, dividimos os dois lados por\(t−t_0\):
\[\frac{z(t)−z(t_0)}{t−t_0}=f_x(x_0,y_0)\frac{x(t)−x(t_0)}{t−t_0}+f_y(x_0,y_0)\frac{y(t)−y(t_0)}{t−t_0}+\frac{E(x(t),y(t))}{t−t_0}. \nonumber \]
Em seguida, tomamos o limite conforme\(t\) se aproxima\(t_0\):
\[\begin{align*} \lim_{t→t_0}\dfrac{z(t)−z(t_0)}{t−t_0} &= f_x(x_0,y_0)\lim_{t→t_0} \left (\dfrac{x(t)−x(t_0)}{t−t_0} \right) \\[4pt] &+f_y(x_0,y_0)\lim_{t→t_0}\left (\dfrac{y(t)−y(t_0)}{t−t_0}\right)\\[4pt] &+\lim_{t→t_0}\dfrac{E(x(t),y(t))}{t−t_0}. \end{align*}\]
O lado esquerdo dessa equação é igual a\(dz/dt\), o que leva a
\[\dfrac{dz}{dt}=f_x(x_0,y_0)\dfrac{dx}{dt}+f_y(x_0,y_0)\dfrac{dy}{dt}+\lim_{t→t_0}\dfrac{E(x(t),y(t))}{t−t_0}. \nonumber \]
O último termo pode ser reescrito como
\[\begin{align*} \lim_{t→t_0}\dfrac{E(x(t),y(t))}{t−t_0} &=\lim_{t→t_0}\dfrac{E(x,y)}{\sqrt{(x−x_0)^2+(y−y_0)^2}}\dfrac{\sqrt{(x−x_0)^2+(y−y_0)^2}}{t−t_0}) \\[4pt] &=\lim_{t→t_0}\left(\dfrac{E(x,y)}{\sqrt{(x−x_0)^2+(y−y_0)^2}}\right)\lim_{t→t_0}\left(\dfrac{\sqrt{(x−x_0)^2+(y−y_0)^2}}{t−t_0}\right). \end{align*} \nonumber \]
À medida\(\big(x(t_0),y(t_0)\big),\) que\(t_0, \big(x(t),y(t)\big)\) se\(t\) aproxima, podemos reescrever o último produto como
\[\lim_{(x,y)→(x_0,y_0)}\dfrac{E(x,y)}{\sqrt{(x−x_0)^2+(y−y_0)^2}}\lim_{(x,y)→(x_0,y_0)}\left(\dfrac{\sqrt{(x−x_0)^2+(y−y_0)^2}}{t−t_0}\right). \nonumber \]
Como o primeiro limite é igual a zero, precisamos apenas mostrar que o segundo limite é finito:
\[ \begin{align*} \lim_{(x,y)→(x_0,y_0)} \dfrac{\sqrt{ (x−x_0)^2+(y−y_0)^2 }} {t−t+0} =\lim_{(x,y)→(x_0,y_0)} \sqrt{ \dfrac { (x−x_0)^2+(y−y_0)^2 } {(t−t_0)^2} } \\[4pt] =\lim_{(x,y)→(x_0,y_0)}\sqrt{ \left(\dfrac{x−x_0}{t−t_0}\right)^2+\left(\dfrac{y−y_0}{t−t_0}\right)^2} \\[4pt] =\sqrt{ \left[\lim_{(x,y)→(x_0,y_0)} \left(\dfrac{x−x_0}{t−t_0}\right)\right]^2+\left[\lim_{(x,y)→(x_0,y_0)} \left(\dfrac{y−y_0}{t−t_0}\right)\right]^2}. \end{align*} \nonumber \]
Uma vez que\(x(t)\) ambas\(y(t)\) são funções diferenciáveis de\(t\), existem ambos os limites dentro do último radical. Portanto, esse valor é finito. Isso prova a regra da cadeia em\(t=t_0\); o resto do teorema segue da suposição de que todas as funções são diferenciáveis em todos os seus domínios.
□
Um exame mais detalhado da Equação\ ref {chain1} revela um padrão interessante. O primeiro termo na equação é\(\dfrac{∂f}{∂x} \cdot \dfrac{dx}{dt}\) e o segundo termo é\(\dfrac{∂f}{∂y}⋅\dfrac{dy}{dt}\). Lembre-se de que, ao multiplicar frações, o cancelamento pode ser usado. Se tratarmos esses derivados como frações, cada produto “simplifica” para algo parecido\(∂f/dt\). As variáveis\(x\) e\(y\) que desaparecem nessa simplificação são frequentemente chamadas de variáveis intermediárias: elas são variáveis independentes para a função\(f\), mas são variáveis dependentes para a variável\(t\). Dois termos aparecem no lado direito da fórmula e\(f\) são uma função de duas variáveis. Esse padrão também funciona com funções de mais de duas variáveis, como veremos mais adiante nesta seção.
Calcule\(dz/dt\) para cada uma das seguintes funções:
- \(z=f(x,y)=4x^2+3y^2,\quad x=x(t)=\sin t,\quad y=y(t)=\cos t\)
- \(z=f(x,y)=\sqrt{x^2−y^2},\quad x=x(t)=e^{2t},\quad y=y(t)=e^{−t}\)
Solução
a. Para usar a regra da cadeia, precisamos de quatro quantidades—\(∂z/∂x,\; ∂z/∂y, \; dx/dt\) e\(dy/dt\):
- \(\dfrac{∂z}{∂x}=8x\)
- \(\dfrac{dx}{dt}=\cos t\)
- \(\dfrac{∂z}{∂y}=6y\)
- \(\dfrac{dy}{dt}=−\sin t\)
Agora, substituímos cada um deles na Equação\ ref {chain1}:
\ [\ begin {align*}\ dfrac {dz} {dt} &=\ dfrac {\ partial z} {\ partial x}\ cdot\ dfrac {dx} {dt} +\ dfrac {\ partial z} {\ partial y}\ cdot\ dfrac {dy} {dt}\\ [4pt]
& =( 8x) (\ cos t) + (6y) (−\ sin t)\\ [4pt]
&=8x\ cos t−6y\ sin t.\ end {align*}\]
Essa resposta contém três variáveis. Para reduzi-lo a uma variável, use o fato de que\(x(t)=\sin t\) e\(y(t)=\cos t.\) Nós obtemos
\ [\ begin {align*}\ dfrac {dz} {dt} &=8x\ cos t−6y\ sin t\\ [4pt]
&=8 (\ sin t)\ cos t−6 (\ cos t)\ sin t\\ [4pt]
&=2\ sin t\ cos t.\ end {align*}\]
Essa derivada também pode ser calculada substituindo primeiro\(x(t)\) e\(f(x,y),\) depois diferenciando\(y(t)\) em relação a\(t\):
\ [\ begin {align*} z =f (x, y) &=f\ big (x (t), y (t)\ grande)\\ [4pt]
&=4 (x (t)) ^2+3 (y (t)) ^2\\ [4pt]
&=4\ sin^2 t+3\ cos^2 t.\ end {align*}\]
Então
\ [\ begin {align*}\ dfrac {dz} {dt} &=2 (4\ sin t) (\ cos t) +2 (3\ cos t) (−\ sin t)\\ [4pt]
&=8\ sin t\ cos t−6\ sin t\ cos t\ cos t\\ [4pt]
&=2\ sin t\ cos t,\ end {align*}\]
que é a mesma solução. No entanto, nem sempre é tão fácil diferenciar dessa forma.
b. Para usar a regra da cadeia, precisamos novamente de quatro quantidades —\(∂z/∂x,∂z/dy,dx/dt,\) e\(dy/dt:\)
- \(\dfrac{∂z}{∂x}=\dfrac{x}{\sqrt{x^2−y^2}}\)
- \(\dfrac{dx}{dt}=2e^{2t}\)
- \(\dfrac{∂z}{∂y}=\dfrac{−y}{\sqrt{x^2−y^2}}\)
- \(\dfrac{dx}{dt}=−e^{−t}.\)
Substituímos cada um deles na Equação\ ref {chain1}:
\ [\ begin {align*}\ dfrac {dz} {dt} &=\ dfrac {\ partial z} {\ partial x}\ cdot\ dfrac {dx} {dt} +\ dfrac {\ partial z} {\ partial y}\ cdot\ dfrac {dy} {dt}\\ [4pt] &=\ left (\ dfrac {x} {\ sqrt {x^2−y^2}}\ direita) (2e^ {2t}) +\ left (\ dfrac {−y} {\ sqrt {x^2−y^2}}\ direita) (−e^ {−t})\ [4pt]
&=\ dfrac {2xe^ {2t} −ye^ {−t}} {\ sqrt {x^2−y^2}}. \ end {align*}\ nonumber\]
Para reduzir isso a uma variável, usamos o fato de que\(x(t)=e^{2t}\)\(y(t)=e^{−t}\) e. Portanto,
\ [\ begin {align*}\ dfrac {dz} {dt} &=\ dfrac {2xe^2t+ye^ {−t}} {\ sqrt {x^2−y^2}}\ [4pt]
&=\ dfrac {2 (e^ {2t}) e^ {2t} + (e^ {−t}) e^ {−t}}} {\ sqrt {e^ {4t} −e^ {−2t}}}\\ [4pt]
&=\ dfrac {2e^ {4t} +e^ {−2t}} {\ sqrt {e^ {4t} −e^ {−2t}}}. \ end {align*}\ nonumber\]
Para eliminar expoentes negativos, multiplicamos a parte superior por\(e^{2t}\) e a inferior por\(\sqrt{e^{4t}}\):
\ [\ begin {align*}\ dfrac {dz} {dt} &=\ dfrac {2e^ {4t} +e^ {−2t}} {\ sqrt {e^ {4t} −e^ {−2t}} ^\ dfrac {e^ {2t}} {\ sqrt {e^ {4t}}\\ [4pt]
&=\ dfrac {2e^ {6t} +1} {\ sqrt {e^ {8t} −e^ {2t}}\\ [4pt]
&=\ dfrac {2e^ {6t} +1} {\ sqrt {e^ {2t} (e^ {6t} −1)}\\ [4pt]
&=\ dfrac {22t} e^ {6t} +1} {e^t\ sqrt {e^ {6t} −1}}. \ end {align*}\]
Novamente, essa derivada também pode ser calculada substituindo primeiro\(x(t)\) e\(f(x,y),\) depois diferenciando\(y(t)\) em relação a\(t\):
\[\begin{align*} z &=f(x,y) \\[4pt] &=f(x(t),y(t)) \\[4pt] &=\sqrt{(x(t))^2−(y(t))^2} \\[4pt] &=\sqrt{e^{4t}−e^{−2t}} \\[4pt] &=(e^{4t}−e^{−2t})^{1/2}. \end{align*} \nonumber \]
Então
\[ \begin{align*} \dfrac{dz}{dt} &= \dfrac{1}{2} (e^{4t}−e^{−2t})^{−1/2} \left(4e^{4t}+2e^{−2t} \right) \\[4pt] &=\dfrac{2e^{4t}+e^{−2t}}{\sqrt{e^{4t}−e^{−2t}}}. \end{align*}\]
Essa é a mesma solução.
\(dz/dt \)Calcule com as seguintes funções. Expresse a resposta final em termos de\(t\).
\[ \begin{align*} z =f(x,y) &=x^2−3xy+2y^2,\\[4pt] x =x(t) &=3\sin 2t,\\[4pt] y=y(t) &=4\cos 2t \end{align*}\]
- Dica
-
\(∂z/∂x,∂z/dy,dx/dt,\)Calcule e\(dy/dt\), em seguida, use a Equação\ ref {chain1}.
- Resposta
-
\ (\ begin {align*}\ dfrac {dz} {dt} &=\ dfrac {f} {x}\ dfrac {dx} {dt} +\ dfrac {f} {y}\ dfrac {dy} {dt}\\ [5pt]
& =( 2x−3y) (6\ cos 2t) + (−3x+4y) (−8\ sin 2t)\\ [5pt]
&=−92\ sin 2t\ cos 2t−72 (\ cos ^22t−\ sin^2 2t)\\ [5pt]
&=−46\ sin 4t−72\ cos 4t. \ end {align*}\)
Muitas vezes, é útil criar uma representação visual da Equação\ ref {chain1} para a regra da cadeia. Isso é chamado de diagrama de árvore para a regra em cadeia para funções de uma variável e fornece uma maneira de lembrar a fórmula (Figura\(\PageIndex{1}\)). Esse diagrama pode ser expandido para funções de mais de uma variável, como veremos em breve.
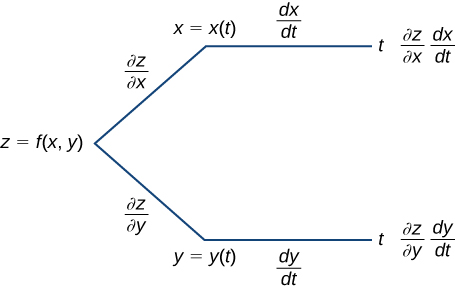
Neste diagrama, o canto mais à esquerda corresponde\(z=f(x,y)\) a. Como\(f\) tem duas variáveis independentes, há duas linhas saindo desse canto. O ramo superior corresponde à variável\(x\) e o ramo inferior corresponde à variável\(y\). Como cada uma dessas variáveis é então dependente de uma variável\(t\), uma ramificação vem\(x\) e uma ramificação vem de\(y\). Por último, cada um dos galhos na extrema direita tem uma etiqueta que representa o caminho percorrido para chegar a esse galho. O ramo superior é alcançado seguindo o\(x\) galho, depois o ramo t; portanto, é rotulado\((∂z/∂x)×(dx/dt).\) O ramo inferior é semelhante: primeiro o\(y\) galho, depois o\(t\) galho. Esse ramo é rotulado\((∂z/∂y)×(dy/dt)\). Para obter a fórmula,\(dz/dt,\) adicione todos os termos que aparecem no lado mais à direita do diagrama. Isso nos dá a equação.
No Note,\(z=f(x,y)\) é uma função de\(x\) e\(y\),\(x=g(u,v)\) e ambos e\(y=h(u,v)\) são funções das variáveis independentes\(u\)\(v\) e.
Suponha que\(x=g(u,v)\) e\(y=h(u,v)\) sejam funções diferenciáveis de\(u\) e\(v\), e\(z=f(x,y)\) seja uma função diferenciável de\(x\)\(y\) e. Então,\(z=f(g(u,v),h(u,v))\) é uma função diferenciável de\(u\) e\(v\), e
\[\dfrac{∂z}{∂u}=\dfrac{∂z}{∂x}\dfrac{∂x}{∂u}+\dfrac{∂z}{∂y}\dfrac{∂y}{∂u} \label{chain2a} \]
e
\[\dfrac{∂z}{∂v}=\dfrac{∂z}{∂x}\dfrac{∂x}{∂v}+\dfrac{∂z}{∂y}\dfrac{∂y}{∂v}. \label{chain2b} \]
Podemos desenhar um diagrama de árvore para cada uma dessas fórmulas da seguinte forma.
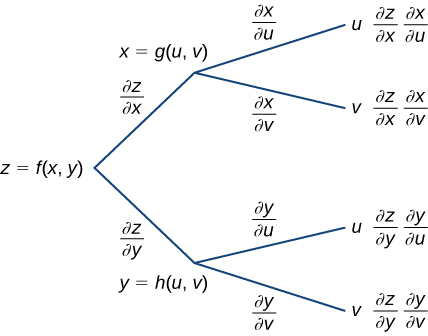
Para derivar a fórmula de\(∂z/∂u\), comece do lado esquerdo do diagrama, siga somente as ramificações que terminam com\(u\) e adicione os termos que aparecem no final dessas ramificações. Para a fórmula de\(∂z/∂v\), siga somente as ramificações que terminam com\(v\) e adicione os termos que aparecem no final dessas ramificações.
Há uma diferença importante entre esses dois teoremas da regra da cadeia. No Note, o lado esquerdo da fórmula para a derivada não é uma derivada parcial, mas no Note é. A razão é que, no Note,\(z\) é em última análise uma função de\(t\) sozinho, enquanto no Note,\(z\) é uma função de ambos\(u\)\(v\) e.
\(∂z/∂u\)Calcule e\(∂z/∂v\) use as seguintes funções:
\[z=f(x,y)=3x^2−2xy+y^2,\; x=x(u,v)=3u+2v,\; y=y(u,v)=4u−v. \nonumber \]
Solução
Para implementar a regra da cadeia para duas variáveis, precisamos de seis derivadas parciais —\(∂z/∂x,\; ∂z/∂y,\; ∂x/∂u,\; ∂x/∂v,\; ∂y/∂u,\) e\(∂y/∂v\):
\[\begin{align*} \dfrac{∂z}{∂x} &=6x−2y & & \dfrac{∂z}{∂y}=−2x+2y \\[4pt] \dfrac{∂x}{∂u} &=3 & & \dfrac{∂x}{∂v}=2 \\[4pt] \dfrac{∂y}{∂u} &=4 & & \dfrac{∂y}{∂v}=−1. \end{align*}\]
Para encontrar,\(∂z/∂u,\) usamos a Equação\ ref {chain2a}:
\ [\ begin {align*}\ dfrac {z} {u} &=\ dfrac {z} {x}\ dfrac {x} {u} +\ dfrac {z} {y}\ dfrac {y} {u}\\ [4pt]
&=3 (6x−2y) +4 (−2x−2y) +4 (−2x−2y) +4 (−2x−2y) +2y)\\ [4pt]
&=10x+2y. \ end {align*}\]
Em seguida, substituímos\(x(u,v)=3u+2v\) e\(y(u,v)=4u−v:\)
\[\begin{align*} \dfrac{∂z}{∂u} &=10x+2y \\[4pt] &=10(3u+2v)+2(4u−v) \\[4pt] &=38u+18v. \end{align*}\]
Para encontrar,\(∂z/∂v,\) usamos a Equação\ ref {chain2b}:
\[\begin{align*} \dfrac{∂z}{∂v} &=\dfrac{∂z}{∂x}\dfrac{∂x}{∂v}+\dfrac{∂z}{∂y}\dfrac{∂y}{∂v} \\[4pt] &=2(6x−2y)+(−1)(−2x+2y) \\[4pt] &=14x−6y. \end{align*}\]
Em seguida, substituímos\(x(u,v)=3u+2v\) e\(y(u,v)=4u−v:\)
\[\begin{align*} \dfrac{∂z}{∂v} &=14x−6y \\[4pt] &=14(3u+2v)−6(4u−v) \\[4pt] &=18u+34v \end{align*}\]
\(∂z/∂u\)Calcule e\(∂z/∂v\) receba as seguintes funções:
\[ z=f(x,y)=\dfrac{2x−y}{x+3y},\quad x(u,v)=e^{2u}\cos 3v,\quad y(u,v)=e^{2u}\sin 3v. \nonumber \]
- Dica
-
\(∂z/∂x,\; ∂z/∂y,\; ∂x/∂u,\; ∂x/∂v,\; ∂y/∂u,\)Calcule e\(∂y/∂v\), em seguida, use a Equação\ ref {chain2a} e a Equação\ ref {chain2b}.
- Resposta
-
\(\dfrac{∂z}{∂u}=0,\quad \dfrac{∂z}{∂v}=\dfrac{−21}{(3\sin 3v+\cos 3v)^2}\)
A regra da cadeia generalizada
Agora que vimos como estender a regra da cadeia original para funções de duas variáveis, é natural perguntar: podemos estender a regra para mais de duas variáveis? A resposta é sim, como afirma a regra generalizada da cadeia.
\(w=f(x_1,x_2,…,x_m)\)Seja uma função diferenciável de variáveis\(m\) independentes e, para cada uma,\(i∈{1,…,m},\)\(x_i=x_i(t_1,t_2,…,t_n)\) seja uma função diferenciável de variáveis\(n\) independentes. Então
\[\dfrac{∂w}{∂t_j}=\dfrac{∂w}{∂x_1}\dfrac{∂x_1}{∂t_j}+\dfrac{∂w}{∂x_2}\dfrac{∂x_2}{∂t_j}+⋯+\dfrac{∂w}{∂x_m}\dfrac{∂x_m}{∂t_j} \nonumber \]
para qualquer\(j∈{1,2,…,n}.\)
No próximo exemplo, calculamos a derivada de uma função de três variáveis independentes em que cada uma das três variáveis é dependente de duas outras variáveis.
\(∂w/∂u\)Calcule e\(∂w/∂v\) use as seguintes funções:
\[\begin{align*} w &=f(x,y,z)=3x^2−2xy+4z^2 \\[4pt] x &=x(u,v)=e^u\sin v \\[4pt] y &=y(u,v)=e^u\cos v \\[4pt] z &=z(u,v)=e^u. \end{align*}\]
Solução
As fórmulas para\(∂w/∂u\) e\(∂w/∂v\) são
\[\begin{align*} \dfrac{∂w}{∂u} =\dfrac{∂w}{∂x}⋅\dfrac{∂x}{∂u}+\dfrac{∂w}{∂y}⋅\dfrac{∂y}{∂u}+\dfrac{∂w}{∂z}⋅\dfrac{∂z}{∂u} \\[4pt] \dfrac{∂w}{∂v} =\dfrac{∂w}{∂x}⋅\dfrac{∂x}{∂v}+\dfrac{∂w}{∂y}⋅\dfrac{∂y}{∂v}+\dfrac{∂w}{∂z}⋅\dfrac{∂z}{∂v}. \end{align*}\]
Portanto, existem nove derivadas parciais diferentes que precisam ser calculadas e substituídas. Precisamos calcular cada um deles:
\[\begin{align*} \dfrac{∂w}{∂x}&=6x−2y \dfrac{∂w}{∂y}=−2x \dfrac{∂w}{∂z}=8z \\[4pt] \dfrac{∂x}{∂u}&=e^u\sin v \dfrac{∂y}{∂u}=e^u\cos v \dfrac{∂z}{∂u}=e^u \\[4pt] \dfrac{∂x}{∂v}&=e^u\cos v \dfrac{∂y}{∂v}=−e^u\sin v \dfrac{∂z}{∂v}=0. \end{align*}\]
Agora, substituímos cada um deles na primeira fórmula para calcular\( ∂w/∂u\):
\ [\ begin {align*}\ dfrac {w} {u} &=\ dfrac {w} {x}\ dfrac {x} {u} +\ dfrac {w} {y},\ dfrac {y} {u} +\ dfrac {w} {z} ↑\ dfrac {z} {u}\\ [4pt]
& =( 6x−2y) e^u\ sin v−2xe^u\ cos v+8ze^u,\ end {align*}\]
em seguida,\(z(u,v)=e^u\) substitua\(x(u,v)=e^u \sin v, \, y(u,v)=e^u\cos v,\) e nesta equação:
\[\begin{align*} \dfrac{∂w}{∂u} &=(6x−2y)e^u\sin v−2xe^u\cos v+8ze^u \\[4pt] &=(6e^u\sin v−2eu\cos v)e^u\sin v−2(e^u\sin v)e^u\cos v+8e^{2u} \\[4pt] &=6e^{2u}\sin^2 v−4e^{2u}\sin v\cos v+8e^{2u} \\[4pt] &=2e^{2u}(3\sin^2 v−2\sin v\cos v+4). \end{align*}\]
Em seguida, calculamos\(∂w/∂v\):
\[\begin{align*} \dfrac{∂w}{∂v} &=\dfrac{∂w}{∂x}⋅\dfrac{∂x}{∂v}+\dfrac{∂w}{∂y}⋅\dfrac{∂y}{∂v}+\dfrac{∂w}{∂z}⋅\dfrac{∂z}{∂v} \\[4pt] &=(6x−2y)e^u\cos v−2x(−e^u\sin v)+8z(0), \end{align*}\]
então substituímos\(x(u,v)=e^u\sin v,\, y(u,v)=e^u\cos v,\) e\(z(u,v)=e^u\) nesta equação:
\[\begin{align*} \dfrac{∂w}{∂v} &=(6x−2y)e^u\cos v−2x(−e^u\sin v) \\[4pt] &=(6e^u \sin v−2e^u\cos v)e^u\cos v+2(e^u\sin v)(e^u\sin v) \\[4pt] &=2e^{2u}\sin^2 v+6e^{2u}\sin v\cos v−2e^{2u}\cos^2 v \\[4pt] &=2e^{2u}(\sin^2 v+\sin v\cos v−\cos^2 v). \end{align*}\]
\(∂w/∂u\)Calcule e\(∂w/∂v\) receba as seguintes funções:
\[\begin{align*} w &=f(x,y,z)=\dfrac{x+2y−4z}{2x−y+3z} \\[4pt] x &=x(u,v)=e^{2u}\cos3v \\[4pt] y &=y(u,v)=e^{2u}\sin 3v \\[4pt] z &=z(u,v)=e^{2u}. \end{align*}\]
- Dica
-
Calcule nove derivadas parciais e use as mesmas fórmulas do Example\(\PageIndex{3}\).
- Resposta
-
\(\dfrac{∂w}{∂u}=0\)
\(\dfrac{∂w}{∂v}=\dfrac{15−33\sin 3v+6\cos 3v}{(3+2\cos 3v−\sin 3v)^2}\)
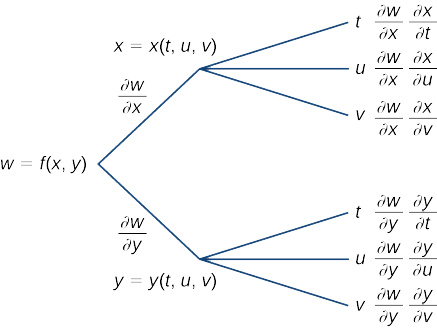
Crie um diagrama de árvore para o caso quando
\[ w=f(x,y,z),\quad x=x(t,u,v),\quad y=y(t,u,v),\quad z=z(t,u,v) \nonumber \]
e escreva as fórmulas para as três derivadas parciais de\(w\).
Solução
Começando pela esquerda, a função\(f\) tem três variáveis independentes:\(x,\, y\),\(z\) e. Portanto, três ramos devem estar emanando do primeiro nó. Cada uma dessas três ramificações também tem três ramificações, para cada uma das variáveis\(t,\, u,\)\(v\) e.

As três fórmulas são
\[\begin{align*} \dfrac{∂w}{∂t} &=\dfrac{∂w}{∂x}\dfrac{∂x}{∂t}+\dfrac{∂w}{∂y}\dfrac{∂y}{∂t}+\dfrac{∂w}{∂z}\dfrac{∂z}{∂t} \\[4pt] \dfrac{∂w}{∂u} &=\dfrac{∂w}{∂x}\dfrac{∂x}{∂u}+\dfrac{∂w}{∂y}\dfrac{∂y}{∂u}+\dfrac{∂w}{∂z}\dfrac{∂z}{∂u} \\[4pt] \dfrac{∂w}{∂v} &=\dfrac{∂w}{∂x}\dfrac{∂x}{∂v}+\dfrac{∂w}{∂y}\dfrac{∂y}{∂v}+\dfrac{∂w}{∂z}\dfrac{∂z}{∂v}. \end{align*}\]
Crie um diagrama de árvore para o caso quando
\[w=f(x,y),\quad x=x(t,u,v),\quad y=y(t,u,v) \nonumber \]
e escreva as fórmulas para as três derivadas parciais de\(w.\)
- Dica
-
Determine o número de galhos que emanam de cada nó na árvore.
- Resposta
-
\[\begin{align*}\dfrac{∂w}{∂t} &=\dfrac{∂w}{∂x}\dfrac{∂x}{∂t}+\dfrac{∂w}{∂y}\dfrac{∂y}{∂t} \\[4pt] \dfrac{∂w}{∂u} &=\dfrac{∂w}{∂x}\dfrac{∂x}{∂u}+\dfrac{∂w}{∂y}\dfrac{∂y}{∂u} \\[4pt] \dfrac{∂w}{∂v} &=\dfrac{∂w}{∂x}\dfrac{∂x}{∂v}+\dfrac{∂w}{∂y}\dfrac{∂y}{∂v} \end{align*}\]
Diferenciação implícita
A recuperação da diferenciação implícita fornece um método para descobrir\(dy/dx\) quando\(y\) é definido implicitamente como uma função de\(x\). O método envolve diferenciar os dois lados da equação que define a função em relação a e\(x\), em seguida, a resolução de derivadas\(dy/dx.\) parciais fornece uma alternativa a esse método.
Considere a elipse definida pela equação da\(x^2+3y^2+4y−4=0\) seguinte forma.
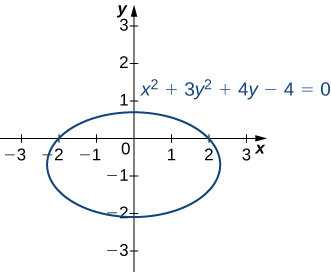
Essa equação se define implicitamente\(y\) como uma função de\(x\). Dessa forma, podemos encontrar a derivada\(dy/dx\) usando o método de diferenciação implícita:
\[\begin{align*} \dfrac{d}{dx}(x^2+3y^2+4y−4) &=\dfrac{d}{dx}(0) \\[4pt] 2x+6y\dfrac{dy}{dx}+4\dfrac{dy}{dx} &=0 \\[4pt] (6y+4)\dfrac{dy}{dx} &=−2x\\[4pt] \dfrac{dy}{dx} &=−\dfrac{x}{3y+2}\end{align*}\]
Também podemos definir uma função\(z=f(x,y)\) usando o lado esquerdo da equação que define a elipse. Em seguida,\(f(x,y)=x^2+3y^2+4y−4.\) a elipse\(x^2+3y^2+4y−4=0\) pode então ser descrita pela equação\(f(x,y)=0\). Usar essa função e o seguinte teorema nos dá uma abordagem alternativa para calcular\(dy/dx.\)
Suponha que a função\(z=f(x,y)\) defina\(y\) implicitamente como uma função\(y=g(x)\) de\(x\) através da equação\(f(x,y)=0.\) Então
\[\dfrac{dy}{dx}=−\dfrac{∂f/∂x}{∂f/∂y} \label{implicitdiff1} \]
fornecido\(f_y(x,y)≠0.\)
Se a equação for\(f(x,y,z)=0\) definida\(z\) implicitamente como uma função diferenciável de\(x\) e\(y\), então
\[\dfrac{dz}{dx}=−\dfrac{∂f/∂x}{∂f/∂z} \qquad\text{and}\qquad \dfrac{dz}{dy}=−\dfrac{∂f/∂y}{∂f/∂z}\label{implicitdiff2} \]
contanto que\(f_z(x,y,z)≠0.\)
A equação\ ref {implicitdiff1} é uma consequência direta da Equação\ ref {chain2a}. Em particular, se assumirmos que\(y\) é definido implicitamente como uma função de\(x\) via equação\(f(x,y)=0\), podemos aplicar a regra da cadeia para encontrar\(dy/dx:\)
\[\begin{align*} \dfrac{d}{dx}f(x,y) &=\dfrac{d}{dx}(0) \\[4pt] \dfrac{∂f}{∂x}⋅\dfrac{dx}{dx}+\dfrac{∂f}{∂y}⋅\dfrac{dy}{dx} &=0 \\[4pt]\dfrac{∂f}{∂x}+\dfrac{∂f}{∂y}⋅\dfrac{dy}{dx} &=0. \end{align*}\]
Resolver esta equação para\(dy/dx\) dá a Equação\ ref {implicitdiff1}. A equação\ ref {implicitdiff1} pode ser derivada de forma semelhante.
Vamos agora voltar ao problema que começamos antes do teorema anterior. Usando o Note e a função\(f(x,y)=x^2+3y^2+4y−4,\) que obtemos
\[\begin{align*} \dfrac{∂f}{∂x} &=2x\\[4pt] \dfrac{∂f}{∂y} &=6y+4. \end{align*}\]
Então a Equação\ ref {implicitdiff1} fornece
\[\dfrac{dy}{dx}=−\dfrac{∂f/∂x}{∂f/∂y}=−\dfrac{2x}{6y+4}=−\dfrac{x}{3y+2}, \nonumber \]
que é o mesmo resultado obtido pelo uso anterior da diferenciação implícita.
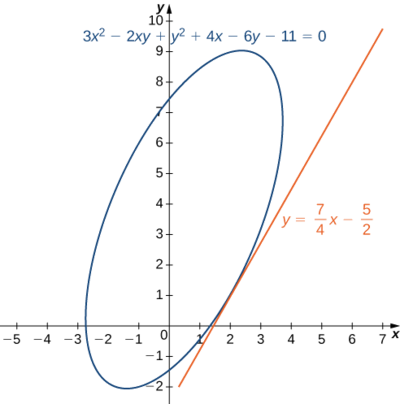
- Calcule\(dy/dx\) se\(y\) é definido implicitamente como uma função de\(x\) via equação\(3x^2−2xy+y^2+4x−6y−11=0\). Qual é a equação da reta tangente ao gráfico dessa curva no ponto\((2,1)\)?
- \(∂z/∂x\)Calcule e\(∂z/∂y,\) forneça\(x^2e^y−yze^x=0.\)
Solução
a. Defina e\(f(x,y)=3x^2−2xy+y^2+4x−6y−11=0,\), em seguida,\(f_x\) calcule e\(f_y: f_x(x,y)=6x−2y+4\) e\(f_y(x,y)=−2x+2y−6.\)
A derivada é dada por
\[\dfrac{dy}{dx}=−\dfrac{∂f/∂x}{∂f/∂y}=\dfrac{6x−2y+4}{−2x+2y−6}=\dfrac{3x−y+2}{x−y+3}. \nonumber \]
A inclinação da reta tangente no ponto\((2,1)\) é dada por
\[\dfrac{dy}{dx}\Bigg|_{(x,y)=(2,1)}=\dfrac{3(2)−1+2}{2−1+3}=\dfrac{7}{4} \nonumber \]
Para encontrar a equação da reta tangente, usamos a forma ponto-inclinação (Figura\(\PageIndex{5}\)):
\[\begin{align*} y−y_0 &=m(x−x_0)\\[4pt]y−1 &=\dfrac{7}{4}(x−2) \\[4pt] y &=\dfrac{7}{4}x−\dfrac{7}{2}+1\\[4pt] y &=\dfrac{7}{4}x−\dfrac{5}{2}.\end{align*}\]
b. Temos\(f(x,y,z)=x^2e^y−yze^x.\), portanto,
\[\begin{align*} \dfrac{∂f}{∂x} &=2xe^y−yze^x \\[4pt] \dfrac{∂f}{∂y} &=x^2e^y−ze^x \\[4pt] \dfrac{∂f}{∂z} &=−ye^x\end{align*}\]
Usando a Equação\ ref {implicitdiff2},
\[\begin{align*} \dfrac{∂z}{∂x} &=−\dfrac{∂f/∂x}{∂f/∂y} & &\text{and} & \dfrac{∂z}{∂y} =−\dfrac{∂f/∂y}{∂f/∂z} \\[4pt] &=−\dfrac{2xe^y−yze^x}{−ye^x} & & &=−\dfrac{x^2e^y−ze^x}{−ye^x} \\[4pt] &=\dfrac{2xe^y−yze^x}{ye^x} & & & =\dfrac{x^2e^y−ze^x}{ye^x} \end{align*}\]
Descubra\(dy/dx\) se\(y\) é definido implicitamente como uma função de\(x\) pela equação\(x^2+xy−y^2+7x−3y−26=0\). Qual é a equação da reta tangente ao gráfico dessa curva no ponto\((3,−2)\)?
- Dica
-
\(∂f/dx\)Calcule e\(∂f/dy\), em seguida, use Equation\ ref {implicitdiff1}.
- Solução
-
\[\dfrac { d y } { d x } = \left. \frac { 2 x + y + 7 } { 2 y - x + 3 } \right| _ { ( 3 , - 2 ) } = \dfrac { 2 ( 3 ) + ( - 2 ) + 7 } { 2 ( - 2 ) - ( 3 ) + 3 } = - \dfrac { 11 } { 4 } \nonumber \]
Equação da reta tangente:\(y=−\dfrac{11}{4}x+\dfrac{25}{4}\)
Conceitos chave
- A regra da cadeia para funções de mais de uma variável envolve as derivadas parciais em relação a todas as variáveis independentes.
- Os diagramas de árvore são úteis para derivar fórmulas para a regra da cadeia para funções de mais de uma variável, em que cada variável independente também depende de outras variáveis.
Equações chave
- Regra em cadeia, uma variável independente
\(\dfrac{dz}{dt}=\dfrac{∂z}{∂x}⋅\dfrac{dx}{dt}+\dfrac{∂z}{∂y}⋅\dfrac{dy}{dt}\)
- Regra da cadeia, duas variáveis independentes
\(\dfrac{dz}{du}=\dfrac{∂z}{∂x}⋅\dfrac{∂x}{∂u}+\dfrac{∂z}{∂y}⋅\dfrac{∂y}{∂u}\dfrac{dz}{dv}=\dfrac{∂z}{∂x}⋅\dfrac{∂x}{∂v}+\dfrac{∂z}{∂y}⋅\dfrac{∂y}{∂v}\)
- Regra de cadeia generalizada
\(\dfrac{∂w}{∂t_j}=\dfrac{∂w}{∂x_1}\dfrac{∂x_1}{∂t_j}+\dfrac{∂w}{∂x_2}\dfrac{∂x_1}{∂t_j}+⋯+\dfrac{∂w}{∂x_m}\dfrac{∂x_m}{∂t_j}\)
Glossário
- regra de cadeia generalizada
- a regra da cadeia se estendeu às funções de mais de uma variável independente, na qual cada variável independente pode depender de uma ou mais outras variáveis
- variável intermediária
- dada uma composição de funções (por exemplo\(f(x(t),y(t)))\), as variáveis intermediárias são as variáveis que são independentes na função externa, mas também dependem de outras variáveis; na função,\(f(x(t),y(t)),\) as variáveis\(x\) e\(y\) são exemplos de variáveis intermediárias
- diagrama de árvore
- ilustra e deriva fórmulas para a regra da cadeia generalizada, na qual cada variável independente é contabilizada


