Skip to main content
Global

14.4E: Exercícios para a Seção 14.4

  1. Last updated
  2. Save as PDF
  • Page ID
    187926

    • Edwin “Jed” Herman & Gilbert Strang
    • OpenStax
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Nos exercícios 1 a 2, encontre um vetor normal unitário na superfície no ponto indicado.

    1)\( f(x,y)=x^3,\quad (2,−1,8)\)

    Resposta
    \( (\frac{\sqrt{145}}{145})(12\hat{\mathbf i}−\hat{\mathbf k})\)

    2)\( \ln\left(\dfrac{x}{y−z}\right)=0\) quando\( x=y=1\)

    Nos exercícios 3 a 7, encontre um vetor normal e um vetor tangente no ponto\( P\).

    3)\( x^2+xy+y^2=3,\quad P(−1,−1)\)

    Resposta
    Vetor normal:\( \hat{\mathbf i}+\hat{\mathbf j}\), vetor tangente:\( \hat{\mathbf i}−\hat{\mathbf j}\)

    4)\( (x^2+y^2)^2=9(x^2−y^2),\quad P(\sqrt{2},1)\)

    5)\( xy^2−2x^2+y+5x=6,\quad P(4,2)\)

    Resposta
    Vetor normal:\( 7\hat{\mathbf i}−17\hat{\mathbf j}\), vetor tangente:\( 17\hat{\mathbf i}+7\hat{\mathbf j}\)

    6)\( 2x^3−x^2y^2=3x−y−7,\quad P(1,−2)\)

    7)\( ze^{x^2−y^2}−3=0, \quad P(2,2,3)\)

    Resposta
    Vetor normal:\( -12\hat{\mathbf i}+12\hat{\mathbf j}-\hat{\mathbf k}\) ou\( 12\hat{\mathbf i}-12\hat{\mathbf j}+\hat{\mathbf k}\), vetor
    tangente:\( 0\hat{\mathbf i}+1\hat{\mathbf j}+12\hat{\mathbf k}\) ou\( 1\hat{\mathbf i}+0\hat{\mathbf j}-12\hat{\mathbf k}\)

    Nos exercícios 8 a 19, encontre a equação do plano tangente à superfície no ponto indicado. (Dica: se a função dada ainda não tiver sido resolvida\(z\), comece resolvendo-a\( z\) em termos de\( x\)\( y\) e.)

    8)\( −8x−3y−7z=−19,\quad P(1,−1,2)\)

    9)\( z=−9x^2−3y^2,\quad P(2,1,−39)\)

    Resposta
    \( −36x−6y−z=−39\)

    10)\( x^2+10xyz+y^2+8z^2=0,\quad P(−1,−1,−1)\)

    11)\( z=\ln(10x^2+2y^2+1),\quad P(0,0,0)\)

    Resposta
    \( z=0\)

    12)\( z=e^{7x^2+4y^2}, \quad P(0,0,1)\)

    13)\( xy+yz+zx=11,\quad P(1,2,3)\)

    Resposta
    \( 5x+4y+3z−22=0\)

    14)\( x^2+4y^2=z^2,\quad P(3,2,5)\)

    15)\( x^3+y^3=3xyz,\quad P(1,2,\frac{3}{2})\)

    Resposta
    \( 4x−5y+4z=0\)

    16)\( z=axy,\quad P(1,\frac{1}{a},1)\)

    17)\( z=\sin x+\sin y+\sin(x+y),\quad P(0,0,0)\)

    Resposta
    \( 2x+2y−z=0\)

    18)\( h(x,y)=\ln\sqrt{x^2+y^2},\quad P(3,4)\)

    19)\( z=x^2−2xy+y^2,\quad P(1,2,1)\)

    Resposta
    \( −2(x−1)+2(y−2)−(z−1)=0\)

    Nos exercícios 20 a 25, encontre equações paramétricas para a linha normal em relação à superfície no ponto indicado. (Lembre-se de que, para encontrar a equação de uma linha no espaço, você precisa de um ponto na linha e de um vetor\( \vecs v=⟨a,b,c⟩\) paralelo à linha.\( P_0(x_0,y_0,z_0)\) Então, as equações da linha são:\(\quad x=x_0+at,\quad y=y_0+bt, \quad z=z_0+ct.)\)

    20)\( −3x+9y+4z=−4,\quad P(1,−1,2)\)

    21)\( z=5x^2−2y^2,\quad P(2,1,18)\)

    Resposta
    \( x=20t+2,y=−4t+1,z=−t+18\)

    22)\( x^2−8xyz+y^2+6z^2=0,\quad P(1,1,1)\)

    23)\( z=\ln(3x^2+7y^2+1),\quad P(0,0,0)\)

    Resposta
    \( x=0,y=0,z=t\)

    24)\( z=e^{4x^2+6y^2},\quad P(0,0,1)\)

    25)\( z=x^2−2xy+y^2\) no ponto\( P(1,2,1)\)

    Resposta
    \( x−1=2t;y−2=−2t;z−1=t\)

    Nos exercícios 26 a 28, use a figura mostrada aqui.

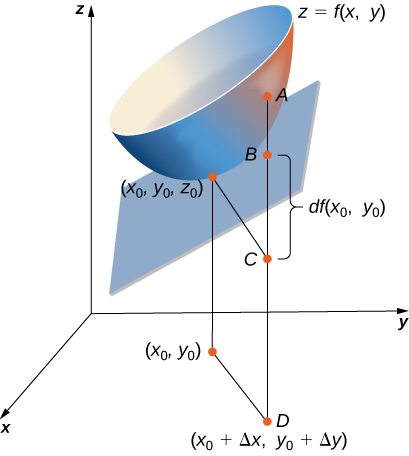
    Diagrama mostrando o diferencial de f no ponto (x_0, y_0)

    26) O comprimento do segmento de linha\( AC\) é igual a qual expressão matemática?

    27) O comprimento do segmento de linha\( BC\) é igual a qual expressão matemática?

    Resposta
    O diferencial da função\( z(x,y)=dz=f_xdx+f_ydy\)

    28) Usando a figura, explique o que o comprimento do segmento de linha\( AB\) representa.

    29) Mostre que\( f(x,y)=e^{xy}x\) é diferenciável no ponto\( (1,0).\)

    Resposta
    Usando a definição de diferenciabilidade, temos\( e^{xy}x≈x+y\).

    30) Mostre que\( f(x,y)=x^2+3y\) é diferenciável em cada ponto. Em outras palavras, mostre que\( Δz=f(x+Δx,y+Δy)−f(x,y)=f_xΔx+f_yΔy+ε_1Δx+ε_2Δy\), onde ambos\( ε_1\) se\( ε_2\) aproximam de zero como\( (Δx,Δy)\) abordagens\( (0,0).\)

    Resposta
    \( Δz=2xΔx+3Δy+(Δx)^2.(Δx)^2→0\)para pequenos\( Δx\) e\( z\) satisfaz a definição de diferenciabilidade.

    31) Encontre o diferencial total de cada função:

    1. \( z=x^3 + y^3 - 5\)
    2. \( z=e^{xy}\)
    3. \( z=y\cos x+\sin y\)
    4. \(P = t^2 + 3t + tu^3\)
    5. \( w=e^y\cos(x)+z^2\)
    Respostas:
    1. \( dz = 3x^2\,dx +3y^2\,dy \)
    2. \( dz = ye^{xy}\,dx +xe^{xy}\,dy \)
    3. \( dz = -y\sin x\,dx +(\cos x + \cos y)\,dy \)
    4. \( dP = (2t + 3 + u^3)\, dt + 3t u^2 \,du \)
    5. \( dw = -e^y\sin(x)\,dx +e^y\cos(x)\,dy +2z\,dz\)

    32) a. Encontre o diferencial total\(dz\) da função\( z=\dfrac{xy}{y+x}\) e, em seguida,
    b. Indique seu valor onde\( x\) muda de\( 10\) para\( 10.5\) e\( y\) muda de\( 15\) para\( 13\).

    Resposta
    a.\( dz = \dfrac{y^2}{(x+y)^2}\, dx + \dfrac{x^2}{(x+y)^2} \,dy \)
    b.\(dx = 0.5\) e\(dy = -2\) assim

    \ (\ begin {align*} dz &= f_x (10, 15)\, dx + f_y (10,15)\, dy\\
    &=\ frac {15^2} {25^2}\, dx +\ frac {10^2} {25^2}\, dy\\
    &=\ frac {225} {625}, (0,5) +\ frac {100} { 625} (-2)\\
    &=\ frac {9} {25}\ left (\ frac {1} {2}\ right) +\ frac {4} {25} (-2)\\
    &=\ frac {18} {100} -\ frac {32} {100}\\
    &= .18 - .32 = -0,14\ end {align*}\)

    33) Deixe\( z=f(x,y)=xe^y.\) declarar seu diferencial total. Em seguida, calcule\( Δz\) de\( P(1,2)\) para\( Q(1.05,2.1)\) e, em seguida, encontre a mudança aproximada em\( z\)\(dz\),, de ponto\( P\) a ponto\( Q\). Lembre-se\( Δz=f(x+Δx,y+Δy)−f(x,y)\), e\( dz\) e\( Δz\) devem ser aproximadamente iguais, se\(dx\) e\(dy\) forem razoavelmente pequenos.

    Resposta
    Diferencial total:\(dz = e^y\,dx + xe^y\, dy \)
    \( Δz≈1.185422\) e\( dz≈1.108.\) observe que eles estão relativamente próximos.

    34) O volume de um cilindro circular reto é dado por\( V(r,h)=πr^2h.\) Encontre o diferencial\( dV\). Interprete a fórmula geometricamente.

    Resposta
    \( dV = 2 \pi r h\, dr + \pi r^2 \,dh \)

    35) Veja o problema anterior. Use diferenciais para estimar a quantidade de alumínio em uma lata de alumínio fechada com diâmetro\( 8.0cm\) e altura\( 12cm\) se o alumínio tiver\( 0.04\) cm de espessura.

    Resposta
    \( 16\,\text{cm}^3\)

    36) Use o diferencial\( dz\) para aproximar a mudança na\( z=\sqrt{4−x^2−y^2}\) medida em que\( (x,y)\) se move de um ponto\( (1,1)\) a outro.\( (1.01,0.97).\) Compare essa aproximação com a mudança real na função.

    37) Vamos\( z=f(x,y)=x^2+3xy−y^2.\) encontrar a mudança exata na função e a mudança aproximada na função à medida que\( x\) muda de\( 2.00\) para\( 2.05\) e\( y\) muda de\( 3.00\) para\( 2.96\).

    Resposta
    \( Δz=\)mudança exata\( =0.6449\), mudança aproximada é\( dz=0.65\). Os dois valores estão próximos.

    38) A aceleração centrípeta de uma partícula que se move em um círculo\( v\) é dada por\( a(r,v)=\frac{v^2}{r},\) onde está a velocidade e\( r\) é o raio do círculo. Aproxime o erro percentual máximo na medição da aceleração resultante de erros\( 3\%\) de entrada\( v\) e\( 2\%\) entrada\( r\). (Lembre-se de que o erro percentual é a razão entre a quantidade de erro e a quantidade original. Portanto, nesse caso, o erro percentual em a é dado por\( \frac{da}{a}\).)

    39) O raio\( r\) e a altura\( h\) de um cilindro circular reto são medidos com possíveis erros de\( 4\%\) e\( 5\%\), respectivamente. Aproxime o erro percentual máximo possível na medição do volume (lembre-se de que o erro percentual é a razão entre a quantidade de erro e a quantidade original). Portanto, nesse caso, o erro percentual em\( V\) é dado por\( \frac{dV}{V}\).)

    Resposta
    \( 13\%\)ou\( 0.13\)

    40) O raio base e a altura de um cone circular reto são medidos\( 25\) em\( 10\) pol. e in., respectivamente, com um possível erro na medição de até. cada um.\( 0.1\) Use diferenciais para estimar o erro máximo no volume calculado do cone.

    41) A resistência elétrica\( R\) produzida pelos resistores de fiação\( R_1\) e\( R_2\) em paralelo pode ser calculada a partir da fórmula\( \frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}\). Se\( R_1\) e\( R_2\) forem medidos como sendo\( 7Ω\) e\( 6Ω\), respectivamente, e se essas medições forem precisas de dentro\( 0.05Ω\), estime o máximo possível de erro na computação\( R\). (O símbolo\( Ω\) representa um ohm, a unidade de resistência elétrica.)

    Resposta
    \( 0.025\)

    42) A área de uma elipse com eixos de comprimento\( 2a\) e\( 2b\) é dada pela fórmula\( A=πab\). Aproxime a variação percentual na área quando\( a\) aumenta em\( 2\%\) e\( b\) aumenta em\( 1.5\%.\)

    43) O período\( T\) de um pêndulo simples com pequenas oscilações é calculado a partir da fórmula\( T=2π\sqrt{\frac{L}{g}}\), onde\( L\) é o comprimento do pêndulo e\( g\) é a aceleração resultante da gravidade. Suponha isso\( L\) e\( g\) tenha erros de, no máximo,\( 0.5\%\) e\( 0.1\%\), respectivamente. Use diferenciais para aproximar o erro percentual máximo no valor calculado de\( T\).

    Resposta
    \( 0.3\%\)

    44) A energia elétrica\( P\) é dada por\( P=\frac{V^2}{R}\), onde\( V\) está a tensão e\( R\) é a resistência. Aproxime o erro percentual máximo no cálculo da potência se\( 120 V\) for aplicado a um\( 2000−Ω\) resistor e os possíveis erros percentuais na medição\( V\) e\( R\) são\( 3\%\) e\( 4\%\), respectivamente.

    Para os exercícios 45 a 49, encontre a aproximação linear de cada função no ponto indicado.

    45)\( f(x,y)=x\sqrt{y},\quad P(1,4)\)

    Resposta
    \( L(x,y) = 2x+\frac{1}{4}y−1\)

    (46)\( f(x,y)=e^x\cos y;\quad P(0,0)\)

    47)\( f(x,y)=\arctan(x+2y),\quad P(1,0)\)

    Resposta
    \( L(x,y) = \frac{1}{2}x+y+\frac{1}{4}π−\frac{1}{2}\)

    48)\( f(x,y)=\sqrt{20−x^2−7y^2},\quad P(2,1)\)

    49)\( f(x,y,z)=\sqrt{x^2+y^2+z^2},\quad P(3,2,6)\)

    Resposta
    \( L(x,y,z) = \frac{3}{7}x+\frac{2}{7}y+\frac{6}{7}z\)

    50) [T] Encontre a equação do plano tangente à superfície\( f(x,y)=x^2+y^2\) no ponto\( (1,2,5),\) e represente graficamente a superfície e o plano tangente no ponto.

    51) [T] Encontre a equação para o plano tangente à superfície no ponto indicado e represente graficamente a superfície e o plano tangente:\( z=\ln(10x^2+2y^2+1),\quad P(0,0,0).\)

    Resposta

    \( z=0\)

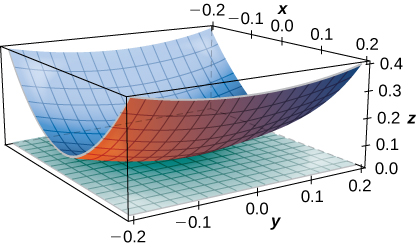
    Superfície representando a função z=ln (10x^2+2y^2+1) e seu plano tangente no ponto (0, 0)

    52) [T] Encontre a equação do plano tangente à superfície\( z=f(x,y)=\sin(x+y^2)\) no ponto\( \left(\frac{π}{4},0,\frac{\sqrt{2}}{2}\right)\) e represente graficamente a superfície e o plano tangente.

    Colaboradores