14.4: Planos tangentes e aproximações lineares
- Page ID
- 187916
- Determine a equação de um plano tangente a uma determinada superfície em um ponto.
- Use o plano tangente para aproximar uma função de duas variáveis em um ponto.
- Explique quando uma função de duas variáveis é diferenciável.
- Use o diferencial total para aproximar a mudança em uma função de duas variáveis.
Nesta seção, consideramos o problema de encontrar o plano tangente a uma superfície, que é análogo a encontrar a equação de uma reta tangente a uma curva quando a curva é definida pelo gráfico de uma função de uma variável,\( y=f(x)\). A inclinação da reta tangente no ponto\( x=a\) é dada por\( m=f′(a)\); qual é a inclinação de um plano tangente? Aprendemos sobre a equação de um plano em Equações de Linhas e Planos no Espaço; nesta seção, vemos como ela pode ser aplicada ao problema em questão.
Planos tangentes
Intuitivamente, parece claro que, em um plano, apenas uma linha pode ser tangente a uma curva em um ponto. No entanto, no espaço tridimensional, muitas linhas podem ser tangentes a um determinado ponto. Se essas linhas estiverem no mesmo plano, elas determinarão o plano tangente nesse ponto. Uma maneira mais intuitiva de pensar em um plano tangente é assumir que a superfície é lisa nesse ponto (sem cantos). Então, uma linha tangente à superfície nesse ponto em qualquer direção não tem nenhuma mudança abrupta na inclinação porque a direção muda suavemente. Portanto, em uma vizinhança pequena o suficiente ao redor do ponto, um plano tangente toca a superfície somente nesse ponto.
\( P_0=(x_0,y_0,z_0)\)Seja um ponto em uma superfície\( S\), e\( C\) seja qualquer curva que passe por ela\( P_0\) e esteja inteiramente nela\( S\). Se as linhas tangentes a todas essas curvas\( P_0\) estiverem\( C\) no mesmo plano, esse plano será chamado de plano tangente a\( S\) at\( P_0\) (Figura\(\PageIndex{1}\)).

Para que um plano tangente a uma superfície exista em um ponto dessa superfície, é suficiente que a função que define a superfície seja diferenciável nesse ponto. Definimos o termo plano tangente aqui e depois exploramos a ideia intuitivamente.
\( S\)Seja uma superfície definida por uma função diferenciável\( z=f(x,y),\) e\( P_0=(x_0,y_0)\) seja um ponto no domínio de\( f\). Então, a equação do plano tangente a\( S\) at\( P_0\) é dada por
\[z=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0). \label{tanplane} \]
Para ver por que essa fórmula está correta, vamos primeiro encontrar duas linhas tangentes à superfície\( S\). A equação da reta tangente à curva que é representada pela interseção de\( S\) com o traço vertical dado por\( x=x_0\) is\( z=f(x_0,y_0)+f_y(x_0,y_0)(y−y_0)\). Da mesma forma, a equação da reta tangente à curva que é representada pela interseção de\( S\) com o traço vertical dado por\( y=y_0\) é\( z=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)\). Um vetor paralelo à primeira reta tangente é\( \vecs a=\,\hat{\mathbf j}+f_y(x_0,y_0)\,\hat{\mathbf k}\); um vetor paralelo à segunda reta tangente é\(\vecs b=\hat{\mathbf i}+f_x(x_0,y_0)\,\hat{\mathbf k}\). Podemos pegar o produto cruzado desses dois vetores:
\[\begin{align*} \vecs a\times \vecs b &=(\,\hat{\mathbf j}+f_y(x_0,y_0)\,\hat{\mathbf k})×(\,\hat{\mathbf i}+f_x(x_0,y_0)\,\hat{\mathbf k})\\[4pt] &=\begin{vmatrix}\hat{\mathbf i} & \hat{\mathbf j} & \hat{\mathbf k}\\[4pt] 0 & 1 & f_y(x_0,y_0)\\[4pt] 1 & 0 & f_x(x_0,y_0)\end{vmatrix} \\[4pt] &=f_x(x_0,y_0)\,\hat{\mathbf i}+f_y(x_0,y_0)\,\hat{\mathbf j}−\,\hat{\mathbf k}. \end{align*}\]
Esse vetor é perpendicular às duas linhas e, portanto, é perpendicular ao plano tangente. Podemos usar esse vetor como um vetor normal ao plano tangente, junto com o ponto\( P_0=(x_0,y_0,f(x_0,y_0))\) na equação de um plano:
\[ \begin{align*}\vecs n·((x−x_0)\,\hat{\mathbf i}+(y−y_0)\,\hat{\mathbf j}+(z−f(x_0,y_0))\,\hat{\mathbf k}) &=0 \\[4pt] (f_x(x_0,y_0)\,\hat{\mathbf i}+f_y(x_0,y_0)\,\hat{\mathbf j}-\,\hat{\mathbf k})·((x−x_0)\,\hat{\mathbf i}+(y−y_0)\,\hat{\mathbf j}+(z−f(x_0,y_0))\,\hat{\mathbf k}) &=0 \\[4pt] f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0)−(z−f(x_0,y_0)) &=0. \end{align*}\]
Resolver essa equação para\(z\) fornece a Equação\ ref {tanplane}.
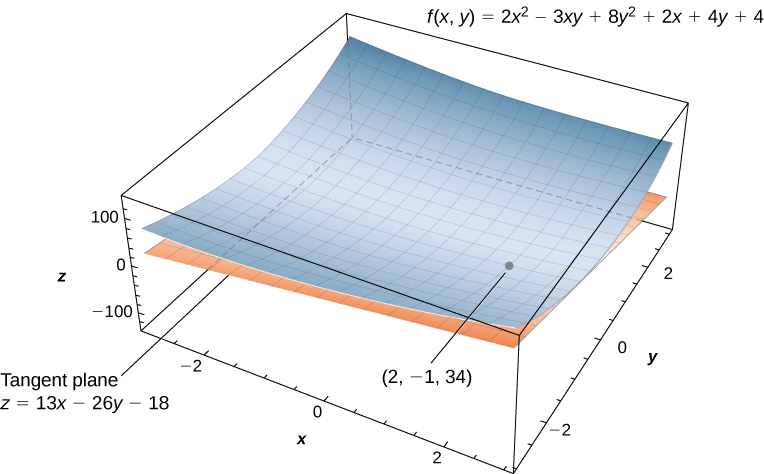
Encontre a equação do plano tangente à superfície definida pela função\( f(x,y)=2x^2−3xy+8y^2+2x−4y+4\) no ponto\( (2,−1).\)
Solução
Primeiro, devemos calcular\( f_x(x,y)\) e\( f_y(x,y)\), em seguida, usar a Equação com\( x_0=2\) e\( y_0=−1\):
\[\begin{align*} f_x(x,y) &=4x−3y+2 \\[4pt] f_y(x,y) &=−3x+16y−4 \\[4pt] f(2,−1) &=2(2)^2−3(2)(−1)+8(−1)^2+2(2)−4(−1)+4=34 \\[4pt] f_x(2,−1) &=4(2)−3(−1)+2=13 \\[4pt] f_y(2,−1) &=−3(2)+16(−1)−4=−26.\end{align*}\]
Então Equation\ ref {tanplane} se torna
\[\begin{align*} z &=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0) \\[4pt] z &=34+13(x−2)−26(y−(−1)) \\[4pt] z &=34+13x−26−26y−26 \\[4pt] z &=13x−26y−18. \end{align*}\]
(Veja a figura a seguir).
Encontre a equação do plano tangente à superfície definida pela função\( f(x,y)=x^3−x^2y+y^2−2x+3y−2\) no ponto\( (−1,3)\).
- Dica
-
Primeiro,\( f_x(x,y)\) calcule e\( f_y(x,y)\), em seguida, use Equation\ ref {tanplane}.
- Resposta
-
\( z=7x+8y−3\)
Encontre a equação do plano tangente à superfície definida pela função\( f(x,y)=\sin(2x)\cos(3y)\) no ponto\( (π/3,π/4).\)
Solução
Primeiro,\( f_x(x,y)\) calcule e\( f_y(x,y)\), em seguida, use a Equação\ ref {tanplane} com\( x_0=π/3\) e\( y_0=π/4\):
\[\begin{align*} f_x(x,y) &=2\cos(2x)\cos(3y) \\[4pt] f_y(x,y) &=−3\sin(2x)\sin(3y) \\[4pt] f\left(\dfrac{π}{3},\dfrac{π}{4}\right) &=\sin\left(2\left(\dfrac{π}{3}\right)\right)\cos\left(3\left(\dfrac{π}{4}\right)\right)=\left(\dfrac{\sqrt{3}}{2}\right)\left(−\dfrac{\sqrt{2}}{2}\right)=−\dfrac{\sqrt{6}}{4} \\[4pt] f_x\left(\dfrac{π}{3},\dfrac{π}{4}\right) &=2\cos\left(2\left(\dfrac{π}{3}\right)\right)\cos\left(3\left(\dfrac{π}{4}\right)\right)=2\left(−\dfrac{1}{2}\right)\left(−\dfrac{\sqrt{2}}{2}\right)=\dfrac{\sqrt{2}}{2} \\[4pt] f_y \left(\dfrac{π}{3},\dfrac{π}{4}\right) &=−3\sin\left(2\left(\dfrac{π}{3}\right)\right)\sin\left(3\left(\dfrac{π}{4}\right)\right)=−3\left(\dfrac{\sqrt{3}}{2}\right)\left(\dfrac{\sqrt{2}}{2}\right)=−\dfrac{3\sqrt{6}}{4}. \end{align*}\]
Então Equation\ ref {tanplane} se torna
\[\begin{align*} z &=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0) \\[4pt] &=−\dfrac{\sqrt{6}}{4}+\dfrac{\sqrt{2}}{2}\left(x−\dfrac{π}{3}\right)−\dfrac{3\sqrt{6}}{4}\left(y−\dfrac{π}{4}\right) \\[4pt] &=\dfrac{\sqrt{2}}{2}x−\dfrac{3\sqrt{6}}{4}y−\dfrac{\sqrt{6}}{4}−\dfrac{π\sqrt{2}}{6}+\dfrac{3π\sqrt{6}}{16} \end{align*}\]
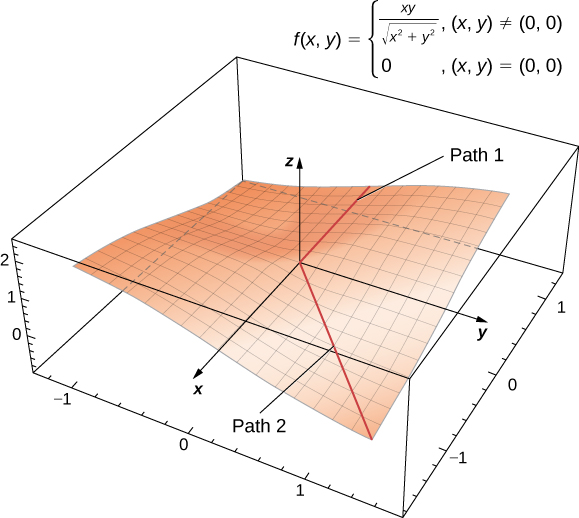
Nem sempre existe um plano tangente a uma superfície em todos os pontos da superfície. Considere a função por partes
\[f(x,y)=\begin{cases}\dfrac{xy}{\sqrt{x^2+y^2}}, & & (x,y)≠(0,0)\\[4pt] 0, & & (x,y)=(0,0)\end{cases}. \label{oddfunction} \]
O gráfico dessa função segue.
Figura\(\PageIndex{3}\): Gráfico de uma função que não tem um plano tangente na origem. Figura dinâmica alimentada por CalcPlot3D.
Se for um\( x=0\) ou\( y=0\),\( f(x,y)=0,\) então o valor da função não muda no eixo\(x\) - ou\(y\) -. Portanto\( f_x(x,0)=f_y(0,y)=0\), quando um\( x\) ou outro se\( y\) aproxima de zero, essas derivadas parciais permanecem iguais a zero. Substituí-los na Equação\( z=0\) é a equação da reta tangente. No entanto, se abordarmos a origem de uma direção diferente, teremos uma história diferente. Por exemplo, suponha que nos aproximemos da origem ao longo da linha\( y=x\). Se colocarmos\( y=x\) na função original, ela se torna
\[f(x,x)=\dfrac{x(x)}{\sqrt{x^2+(x)^2}}=\dfrac{x^2}{\sqrt{2x^2}}=\dfrac{|x|}{\sqrt{2}}. \nonumber \]
Quando\( x>0,\) a inclinação dessa curva é igual a\( \sqrt{2}/2\); quando\( x<0\), a inclinação dessa curva é igual a\( −(\sqrt{2}/2).\) Isso apresenta um problema. Na definição de plano tangente, presumimos que todas as retas tangentes que passam pelo ponto\( P\) (neste caso, a origem) estão no mesmo plano. Isso claramente não é o caso aqui. Quando estudamos funções diferenciáveis, veremos que essa função não é diferenciável na origem.
Aproximações lineares
Lembre-se, a partir de Aproximações e Diferenciais Lineares, que a fórmula para a aproximação linear de uma função\( f(x)\) no ponto\( x=a\) é dada por
\[y≈f(a)+f'(a)(x−a). \nonumber \]
O diagrama para a aproximação linear de uma função de uma variável aparece no gráfico a seguir.
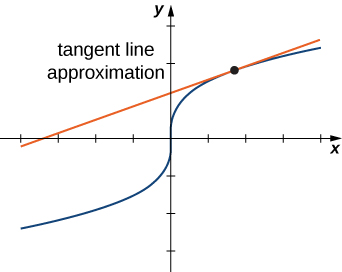
A reta tangente pode ser usada como uma aproximação da função\( f(x)\) para valores\( x\) razoavelmente próximos\( x=a\) a. Ao trabalhar com uma função de duas variáveis, a reta tangente é substituída por um plano tangente, mas a ideia de aproximação é praticamente a mesma.
Dada uma função\( z=f(x,y)\) com derivadas parciais contínuas que existem no ponto\( (x_0,y_0)\), a aproximação linear de\(f\) no ponto\( (x_0,y_0)\) é dada pela equação
\[L(x,y)=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0). \label{approx} \]
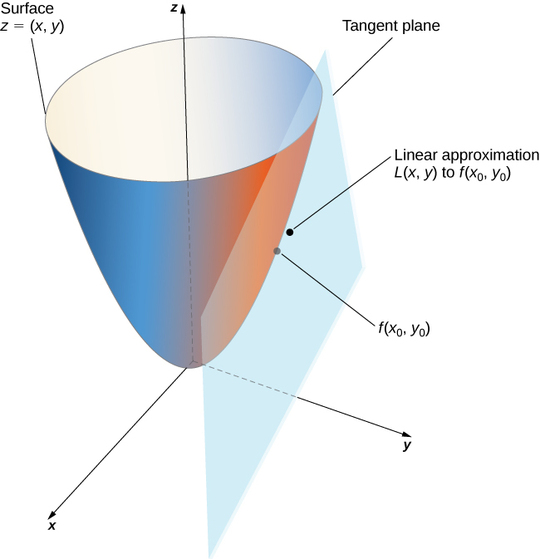
Observe que essa equação também representa o plano tangente à superfície definido por\( z=f(x,y)\) no ponto\( (x_0,y_0)\). A ideia por trás do uso de uma aproximação linear é que, se houver um ponto\( (x_0,y_0)\) no qual o valor preciso de\( f(x,y)\) é conhecido, então, para valores\( (x,y)\) razoavelmente próximos\( (x_0,y_0)\), a aproximação linear (ou seja, plano tangente) produz um valor que também é razoavelmente próximo do valor exato de\( f(x,y)\) (Figura). Além disso, o plano usado para encontrar a aproximação linear também é o plano tangente à superfície no ponto.\( (x_0,y_0).\)
Dada a função\( f(x,y)=\sqrt{41−4x^2−y^2}\), aproxime\( f(2.1,2.9)\) o ponto de uso\( (2,3)\) para\( (x_0,y_0).\) Qual é o valor aproximado de\( f(2.1,2.9)\) até quatro casas decimais?
Solução
Para aplicar a Equação\ ref {approx}, primeiro devemos calcular\( f(x_0,y_0), f_x(x_0,y_0),\) e\( f_y(x_0,y_0)\) usar\( x_0=2\) e\( y_0=3:\)
\[\begin{align*} f(x_0,y_0) &=f(2,3)=\sqrt{41−4(2)^2−(3)^2}=\sqrt{41−16−9}=\sqrt{16}=4 \\[4pt] f_x(x,y) &=−\dfrac{4x}{\sqrt{41−4x^2−y^2}} \text{ so} \; f_x(x_0,y_0)=−\dfrac{4(2)}{\sqrt{41−4(2)^2−(3)^2}}=−2 \\[4pt] f_y(x,y) &=−\dfrac{y}{\sqrt{41−4x^2−y^2}} \text{ so}\; f_y(x_0,y_0)=−\dfrac{3}{\sqrt{41−4(2)^2−(3)^2}}=−\dfrac{3}{4}. \end{align*}\]
Agora substituímos esses valores na Equação\ ref {approx}:
\[\begin{align*} L(x,y) &=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0) \\[4pt] &=4−2(x−2)−\dfrac{3}{4}(y−3) \\[4pt] &=\dfrac{41}{4}−2x−\dfrac{3}{4}y. \end{align*}\]
Por último, substituímos\( x=2.1\) e\( y=2.9\) entramos\(L(x,y):\)
\[ L(2.1,2.9)=\dfrac{41}{4}−2(2.1)−\dfrac{3}{4}(2.9)=10.25−4.2−2.175=3.875. \nonumber \]
O valor aproximado de\( f(2.1,2.9)\) até quatro casas decimais é
\[ f(2.1,2.9)=\sqrt{41−4(2.1)^2−(2.9)^2}=\sqrt{14.95}≈3.8665, \nonumber \]
o que corresponde a um\( 0.2%\) erro na aproximação.
Dada a função\( f(x,y)=e^{5−2x+3y},\) aproximada\( f(4.1,0.9)\) usando o ponto\( (4,1)\) para\( (x_0,y_0)\). Qual é o valor aproximado de\( f(4.1,0.9)\) até quatro casas decimais?
- Dica
-
Primeiro\( f(x_0,y_0),f_x(x_0,y_0),\) calcule e\( f_y(x_0,y_0)\) use\( x_0=4\) e\( y_0=1\), em seguida, use Equation\ ref {approx}.
- Resposta
-
\( L(x,y)=6−2x+3y,\)então\( L(4.1,0.9)=6−2(4.1)+3(0.9)=0.5\)\( f(4.1,0.9)=e^{5−2(4.1)+3(0.9)}=e^{−0.5}≈0.6065.\)
Diferenciabilidade
Ao trabalhar com uma função\( y=f(x)\) de uma variável, diz-se que a função é diferenciável em um ponto,\( x=a\) se\( f′(a)\) existir. Além disso, se uma função de uma variável é diferenciável em um ponto, o gráfico é “suave” nesse ponto (ou seja, não existem cantos) e uma reta tangente está bem definida nesse ponto.
A ideia por trás da diferenciabilidade de uma função de duas variáveis está conectada à ideia de suavidade nesse ponto. Nesse caso, uma superfície é considerada lisa no ponto\( P\) se existir um plano tangente à superfície nesse ponto. Se uma função é diferenciável em um ponto, então existe um plano tangente à superfície nesse ponto. Lembre-se de que a fórmula (Equação\ ref {tanplane}) para um plano tangente em um ponto\( (x_0,y_0)\) é dada por
\[z=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0) \nonumber \]
Para que um plano tangente exista no ponto,\( (x_0,y_0),\) as derivadas parciais devem, portanto, existir nesse ponto. No entanto, essa não é uma condição suficiente para a suavidade, conforme ilustrado na Figura. Nesse caso, as derivadas parciais existiam na origem, mas a função também tinha um canto no gráfico na origem.
Uma função\( f(x,y)\) é diferenciável em um ponto\( P(x_0,y_0)\) se, para todos os pontos\( (x,y)\) em um\( δ\) disco ao redor\( P\), pudermos escrever
\[f(x,y)=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0)+E(x,y), \label{diff1} \]
onde o termo de erro é\( E\) satisfatório
\[\lim_{(x,y)→(x_0,y_0)}\dfrac{E(x,y)}{\sqrt{(x−x_0)^2+(y−y_0)^2}}=0. \label{diff2} \]
O último termo na Equação\ ref {diff1} é to como o termo de erro e representa a proximidade com que o plano tangente chega à superfície em uma pequena vizinhança (\( δ\)disco) do ponto\( P\). Para que\( f\) a função seja diferenciável em\( P\), a função deve ser suave, ou seja, o gráfico de\( f\) deve estar próximo ao plano tangente para pontos próximos\( P\).
Mostre que a função\( f(x,y)=2x^2−4y\) é diferenciável no ponto\( (2,−3).\)
Solução
Primeiro, calculamos\( f(x_0,y_0),f_x(x_0,y_0),\) e\( f_y(x_0,y_0)\) usamos\( x_0=2\) e\( y_0=−3,\) depois usamos a Equação\ ref {diff1}:
\[\begin{align*} f(2,−3) &=2(2)^2−4(−3)=8+12=20 \\[4pt] f_x(2,−3) &=4(2)=8 \\[4pt] f_y(2,−3) &=−4. \end{align*}\]
Portanto,\( m_1=8\) e\( m_2=−4,\) e a Equação\ ref {diff1} se torna
\[ \begin{align*} f(x,y) &=f(2,−3)+f_x(2,−3)(x−2)+f_y(2,−3)(y+3)+E(x,y) \\[4pt] 2x^2−4y &=20+8(x−2)−4(y+3)+E(x,y) \\[4pt] 2x^2−4y &=20+8x−16−4y−12+E(x,y) \\[4pt] 2x^2−4y &=8x−4y−8+E(x,y) \\[4pt] E(x,y) &=2x^2−8x+8. \end{align*}\]
Em seguida, calculamos o limite na Equação\ ref {diff2}:
\ [\ begin {align*}\ lim_ {(x, y) → (x_0, y_0)}\ dfrac {E (x, y)} {\ sqrt {(x−x+0) ^2+ (y−y_0) ^2}} &=\ lim_ {(x, y) → (2, −3)}\ dfrac {2x^2−−8x+8} {\ sqrt {(x−2) ^2+ (y+3) ^2}}\\ [4pt]
&=\ lim_ {(x, y) → (2, −3)}\ dfrac {2 (x^2−4x+4)} {\ sqrt {(x−2) ^2+ (y+3) ^2}}\\ [4 pt]
&=\ lim_ {(x, y) → (2, −3)}\ dfrac {2 (x−2) ^2} {\ sqrt {(x −2) ^2+ (y+3) ^2}\\ [4pt]
&=\ lim_ {(x, y) → (2, −3)}\ dfrac {2 (x−2) ^2+ (y+3) ^2)} {\ sqrt {(x−2) ^2+ (y+3) ^2}}\\ [4pt]
&=\ lim_ {(x, y) → (2, −3)} 2\ sqrt {(x−2) ^2+ (y+3) ^2}\\ [4pt]
&=0. \ end {align*}\]
Já que\( E(x,y)≥0\) para qualquer valor de\( x\) ou\( y\), o limite original deve ser igual a zero. Portanto,\( f(x,y)=2x^2−4y\) é diferenciável em alguns pontos\( (2,−3)\).
Mostre que a função\( f(x,y)=3x−4y^2\) é diferenciável no ponto\((−1,2)\).
- Dica
-
Primeiro,\( f(x_0,y_0),f_x(x_0,y_0),\) calcule e\( f_y(x_0,y_0)\) use\( x_0=−1\) e\( y_0=2\), em seguida, use a Equação\ ref {diff2} para encontrar\( E(x,y)\). Por último, calcule o limite.
- Resposta
-
\ [\ begin {align*} f (−1,2) &=−19,\ quad f_x (−1,2) =3,\ quad f_y (−1,2) =−16,\ quad E (x, y) =−4 (y−2) ^2.\\ [4pt]
\ lim_ {(x, y) → (x_0, y_0)}\ dfrac {E (x, y)} {\ sqrt {(x−x_0) ^2+ (y−y_0) ^2}} &=\ lim_ {(x, y) → (−1,2)}\ dfrac {−4 (y−2) ^2} {\ sqrt {(x+1) ^2+ (y−2) ^2}}\\ [4pt]
\ lim_ {(x, y) → (−1,2)}\ dfrac {−4 (x+1) ^2+ (y−2) ^2)} {\ sqrt {(x+1) ^2+ (y−2) ^2}}\\ [4pt]
&=\ lim_ {(x, y) → (2, −3)} −4\ sqrt {(x+1) ^2+ (y−2) ^2}\\ [4pt]
&=0. \ end {align*}\]
Esta função de (Equation\ ref {oddfunction})
\[ f(x,y)=\begin{cases}\dfrac{xy}{\sqrt{x^2+y^2}}, & & (x,y)≠(0,0)\\[4pt] 0, & & (x,y)=(0,0)\end{cases} \nonumber \]
não é diferenciável na origem (Figura\(\PageIndex{3}\)). Podemos ver isso calculando as derivadas parciais. Essa função apareceu anteriormente na seção, onde mostramos isso\( f_x(0,0)=f_y(0,0)=0\). Substituindo essas informações nas Equações\ ref {diff1} e\ ref {diff2} usando\( x_0=0\) e\( y_0=0\), obtemos
\[\begin{align*} f(x,y) &=f(0,0)+f_x(0,0)(x−0)+f_y(0,0)(y−0)+E(x,y) \\[4pt] E(x,y) &=\dfrac{xy}{\sqrt{x^2+y^2}}. \end{align*}\]
Calculando
\[ \lim_{(x,y)→(x_0,y_0)}\dfrac{E(x,y)}{\sqrt{(x−x_0)^2+(y−y_0)^2}} \nonumber \]
concede
\[\begin{align*} \lim_{(x,y)→(x_0,y_0)}\dfrac{E(x,y)}{\sqrt{(x−x_0)^2+(y−y_0)^2}} &=\lim_{(x,y)→(0,0)}\dfrac{\dfrac{xy}{\sqrt{x^2+y^2}}}{\sqrt{x^2+y^2}} \\[4pt] &=\lim_{(x,y)→(0,0)}\dfrac{xy}{x^2+y^2}. \end{align*}\]
Dependendo do caminho percorrido em direção à origem, esse limite assume valores diferentes. Portanto, o limite não existe e a função não\( f\) é diferenciável na origem, conforme mostrado na figura a seguir.
Diferenciabilidade e continuidade para funções de duas ou mais variáveis estão conectadas, da mesma forma que para funções de uma variável. Na verdade, com alguns ajustes de notação, o teorema básico é o mesmo.
\( z=f(x,y)\)Seja uma função de duas variáveis com\( (x_0,y_0)\) no domínio de\( f\). Se\( f(x,y)\) é diferenciável em\( (x_0,y_0)\), então\( f(x,y)\) é contínuo em\( (x_0,y_0).\)
A nota mostra que, se uma função é diferenciável em um ponto, ela é contínua lá. No entanto, se uma função é contínua em um ponto, ela não é necessariamente diferenciável nesse ponto. Por exemplo, a função discutida acima (Equation\ ref {oddfunction})
\[f(x,y)=\begin{cases}\dfrac{xy}{\sqrt{x^2+y^2}}, & & (x,y)≠(0,0)\\[4pt] 0, & & (x,y)=(0,0)\end{cases} \nonumber \]
é contínuo na origem, mas não é diferenciável na origem. Essa observação também é semelhante à situação no cálculo de variável única.
Podemos explorar ainda mais a conexão entre continuidade e diferenciabilidade em um ponto. O próximo teorema diz que se a função e suas derivadas parciais forem contínuas em um ponto, a função é diferenciável.
\( z=f(x,y)\)Seja uma função de duas variáveis com\( (x_0,y_0)\) no domínio de\( f\). Se\(f(x,y)\)\(f_x(x,y)\), e\(f_y(x,y)\) todos existem em uma vizinhança de\((x_0,y_0)\) e são contínuos em\((x_0,y_0)\), então\(f(x,y)\) é diferenciável lá.
Lembre-se de que anteriormente mostramos que a função na Equação\ ref {oddfunction} não era diferenciável na origem. Vamos calcular as derivadas parciais\( f_x\) e\( f_y\):
\[ \dfrac{∂f}{∂x}=\dfrac{y^3}{(x^2+y^2)^{3/2}} \nonumber \]
e
\[\dfrac{∂f}{∂y}=\dfrac{x^3}{(x^2+y^2)^{3/2}}. \nonumber \]
O contrapositivo do teorema anterior afirma que, se uma função não é diferenciável, pelo menos uma das hipóteses deve ser falsa. Vamos explorar a condição que\( f_x(0,0)\) deve ser contínua. Para que isso seja verdade, deve ser verdade que
\[ \lim_{(x,y)→(0,0)} f_x(x,y)=f_x(0,0) \nonumber \]
por isso
\[ \lim_{(x,y)→(0,0)}f_x(x,y)=\lim_{(x,y)→(0,0)}\dfrac{y^3}{(x^2+y^2)^{3/2}}. \nonumber \]
Deixe\( x=ky\). Então
\ [\ begin {align*}\ lim_ {(x, y) → (0,0)}\ dfrac {y^3} {(x^2+y^2) ^ {3/2}} &=\ lim_ {y→0}\ dfrac {y^3} {((ky) ^2+y^2) ^ {3/2}}\\ [4pt]
&=\ lim_ {y→0}\ dfrac {y^3} {(k^2y^2+y^2) ^ {3/2}}\\ [4pt]
&=\ lim_ {y→0}\ dfrac {y^3} {|y|^3 (k^2+1) ^ {3/2}}\\ [4pt]
&=\ dfrac {1} {(k ^2+1) ^ {3/2}}\ lim_ {y →0}\ frac {|y|} {y}. \ end {align*}\]
Se\( y>0\), então essa expressão é igual\( 1/(k^2+1)^{3/2}\); se\( y<0\), então é igual\( −(1/(k^2+1)^{3/2})\). Em ambos os casos, o valor depende de\( k\), portanto, o limite não existe.
Diferenciais
Em Aproximações e Diferenciais Lineares, primeiro estudamos o conceito de diferenciais. O diferencial de\( y\), escrito\( dy\), é definido como\( f′(x)dx\). O diferencial é usado para aproximar\( Δy=f(x+Δx)−f(x)\), onde\( Δx=dx\). Estender essa ideia para a aproximação linear de uma função de duas variáveis no ponto\( (x_0,y_0)\) produz a fórmula para o diferencial total de uma função de duas variáveis.
\( z=f(x,y)\)Seja uma função de duas variáveis com\( (x_0,y_0)\) no domínio de\( f\),\( Δx\) e\( Δy\) seja escolhida de forma que também\( (x_0+Δx,y_0+Δy)\) esteja no domínio de\( f\). Se\( f\) for diferenciável no ponto\( (x_0,y_0)\), então os diferenciais\( dx\) e\( dy\) são definidos como
\[dx=Δx \nonumber \]
e
\[dy=Δy. \nonumber \]
O diferencial\( dz\), também chamado de diferencial total de\( z=f(x,y)\) at\( (x_0,y_0)\), é definido como
\[dz=f_x(x_0,y_0)dx+f_y(x_0,y_0)dy. \label{total} \]
Observe que o símbolo não\( ∂\) é usado para indicar o diferencial total; em vez disso,\( d\) aparece na frente de\( z\). Agora, vamos definir\( Δz=f(x+Δx,y+Δy)−f(x,y).\) Nós usamos\( dz\) para aproximar\( Δz\), então
\[Δz≈dz=f_x(x_0,y_0)dx+f_y(x_0,y_0)dy. \nonumber \]
Portanto, o diferencial é usado para aproximar a mudança na função\( z=f(x_0,y_0)\) no ponto\( (x_0,y_0)\) para determinados valores de\( Δx\)\( Δy\) e. Uma vez que\( Δz=f(x+Δx,y+Δy)−f(x,y)\), isso pode ser usado ainda mais para aproximar\( f(x+Δx,y+Δy):\)
\[ f(x+Δx,y+Δy)=f(x,y)+Δz≈f(x,y)+fx(x_0,y_0)Δx+f_y(x_0,y_0)Δy. \nonumber \]
Veja a figura a seguir.

Uma dessas aplicações dessa ideia é determinar a propagação do erro. Por exemplo, se estivermos fabricando um gadget e estivermos atrasados na medição de uma determinada quantidade, o diferencial pode ser usado para estimar o erro no volume total do dispositivo.
Encontre o diferencial\( dz\) da função\( f(x,y)=3x^2−2xy+y^2\) e use-o para aproximar o\( Δz\) ponto\( (2,−3).\) Use\( Δx=0.1\) e\( Δy=−0.05.\) Qual é o valor exato de\( Δz\)?
Solução
Primeiro, devemos calcular\( f(x_0,y_0),f_x(x_0,y_0),\) e\( f_y(x_0,y_0)\) usar\( x_0=2\) e\( y_0=−3:\)
\[\begin{align*} f(x_0,y_0) &=f(2,−3)=3(2)^2−2(2)(−3)+(−3)^2=12+12+9=33 \\[4pt] f_x(x,y) &=6x−2y \\[10pt] f_y(x,y) &=−2x+2y \\[4pt] f_x(x_0,y_0) &= fx(2,−3) \\[4pt] &=6(2)−2(−3)=12+6=18 \\[10pt] f_y(x_0,y_0) &=f_y(2,−3) \\[4pt] &=−2(2)+2(−3) \\[4pt] &=−4−6=−10. \end{align*}\]
Em seguida, substituímos essas quantidades na Equação\ ref {total}:
\[\begin{align*} dz &=f_x(x_0,y_0)dx+f_y(x_0,y_0)dy \\[4pt] dz &=18(0.1)−10(−0.05)=1.8+0.5=2.3. \end{align*}\]
Esta é a aproximação de\( Δz=f(x_0+Δx,y_0+Δy)−f(x_0,y_0).\) O valor exato de\( Δz\) é dado por
\[\begin{align*} Δz &=f(x_0+Δx,y_0+Δy)−f(x_0,y_0) \\[4pt] &=f(2+0.1,−3−0.05)−f(2,−3) \\[4pt] &=f(2.1,−3.05)−f(2,−3) \\[4pt] &=2.3425. \end{align*}\]
Encontre o diferencial\( dz\) da função\( f(x,y)=4y^2+x^2y−2xy\) e use-o para aproximar o\( Δz\) ponto\( (1,−1)\). Use\( Δx=0.03\)\( Δy=−0.02\) e. Qual é o valor exato de\( Δz\)?
- Dica
-
Primeiro,\( f_x(x_0,y_0)\) calcule e\( f_y(x_0,y_0)\) use\( x_0=1\) e\( y_0=−1\), em seguida, use Equation\ ref {total}.
- Resposta
-
\( dz=0.18\)
\( Δz=f(1.03,−1.02)−f(1,−1)=0.180682\)
Diferenciabilidade de uma função de três variáveis
Todos os resultados anteriores para diferenciabilidade de funções de duas variáveis podem ser generalizados para funções de três variáveis. Primeiro, a definição:
Uma função\( f(x,y,z)\) é diferenciável em um ponto\( P(x_0,y_0,z_0)\) se, para todos os pontos\( (x,y,z)\) em um\( δ\) disco ao redor,\( P\) pudermos escrever
\[f(x,y)=f(x_0,y_0,z_0)+f_x(x_0,y_0,z_0)(x−x_0)+f_y(x_0,y_0,z_0)(y−y_0)+f_z(x_0,y_0,z_0)(z−z_0)+E(x,y,z), \nonumber \]
onde o termo de erro E satisfaz
\[\lim_{(x,y,z)→(x_0,y_0,z_0)}\dfrac{E(x,y,z)}{\sqrt{(x−x_0)^2+(y−y_0)^2+(z−z_0)^2}}=0. \nonumber \]
Se uma função de três variáveis é diferenciável em um ponto\( (x_0,y_0,z_0)\), ela é contínua lá. Além disso, a continuidade das primeiras derivadas parciais nesse ponto garante diferenciabilidade.
Conceitos-chave
- O análogo de uma reta tangente a uma curva é um plano tangente a uma superfície para funções de duas variáveis.
- Planos tangentes podem ser usados para aproximar valores de funções próximos a valores conhecidos.
- Uma função é diferenciável em um ponto se for “suave” nesse ponto (ou seja, não existem cantos ou descontinuidades nesse ponto).
- O diferencial total pode ser usado para aproximar a mudança em uma função\( z=f(x_0,y_0)\) no ponto\( (x_0,y_0)\) para determinados valores de\( Δx\)\( Δy\) e.
Equações-chave
- Plano tangente
\( z=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0)\)
- Aproximação linear
\( L(x,y)=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0)\)
- Diferencial total
\( dz=f_x(x_0,y_0)dx+f_y(x_0,y_0)dy\).
- Diferenciabilidade (duas variáveis)
\( f(x,y)=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0)+E(x,y),\)
onde o termo de erro é\( E\) satisfatório
\(\displaystyle \lim_{(x,y)→(x_0,y_0)}\dfrac{E(x,y)}{\sqrt{(x−x_0)^2+(y−y_0)^2}}=0\).
- Diferenciabilidade (três variáveis)
\( f(x,y)=f(x_0,y_0,z_0)+f_x(x_0,y_0,z_0)(x−x_0)+f_y(x_0,y_0,z_0)(y−y_0)+f_z(x_0,y_0,z_0)(z−z_0)+E(x,y,z),\)
onde o termo de erro é\( E\) satisfatório
\(\displaystyle \lim_{(x,y,z)→(x_0,y_0,z_0)}\dfrac{E(x,y,z)}{\sqrt{(x−x_0)^2+(y−y_0)^2+(z−z_0)^2}}=0\).
Glossário
- diferenciável
-
uma função\( f(x,y)\) é diferenciável em\( (x_0,y_0)\) se\( f(x,y)\) puder ser expressa na forma\( f(x,y)=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0)+E(x,y),\)
onde o termo de erro é\( E(x,y)\) satisfatório\( \lim_{(x,y)→(x_0,y_0)}\dfrac{E(x,y)}{\sqrt{(x−x_0)^2+(y−y_0)^2}}=0\)
- aproximação linear
- dada uma função\( f(x,y)\) e um plano tangente à função em um ponto\( (x_0,y_0)\), podemos aproximar os pontos\( f(x,y)\) próximos\( (x_0,y_0)\) usando a fórmula do plano tangente
- plano tangente
- dada uma função\( f(x,y)\) que é diferenciável em um ponto\( (x_0,y_0)\), a equação do plano tangente à superfície\( z=f(x,y)\) é dada por\( z=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0)\)
- diferencial total
- o diferencial total da função\( f(x,y)\) at\( (x_0,y_0)\) é dado pela fórmula\( dz=f_x(x_0,y_0)dx+fy(x_0,y_0)dy\)


