Skip to main content
Global

14.3E: Exercícios para a Seção 14.3

  1. Last updated
  2. Save as PDF
  • Page ID
    187992

    • Edwin “Jed” Herman & Gilbert Strang
    • OpenStax
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    No exercício a seguir, calcule a derivada parcial usando somente as definições de limite.

    1)\(\dfrac{∂z}{∂y}\) para\( z=x^2−3xy+y^2\)

    Responda
    \(\dfrac{∂z}{∂y}=−3x+2y\)

    Para os exercícios 2 a 5, calcule o sinal da derivada parcial usando o gráfico da superfície.

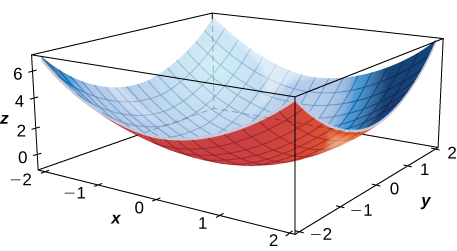
    Gráfico de superfície de um parabolóide que é côncavo e tem seu vértice na origem

    2)\( f_x(1,1)\)

    3)\( f_x(−1,1)\)

    Responda
    O sinal é negativo.

    4)\( f_y(1,1)\)

    5)\( f_x(0,0)\)

    Responda
    A derivada parcial é zero na origem.

    Nos exercícios 6 a 16, calcule as derivadas parciais solicitadas.

    6)\( \dfrac{∂z}{∂x}\) para\( z=\sin(3x)\cos(3y)\)

    7)\( \dfrac{∂z}{∂y}\) para\( z=\sin(3x)\cos(3y)\)

    Responda
    \( \dfrac{∂z}{∂y}=−3\sin(3x)\sin(3y)\)

    8)\( \dfrac{∂z}{∂x}\) e\( \dfrac{∂z}{∂y}\) para\( z=x^8e^3y\)

    9)\( \dfrac{∂z}{∂x}\) e\( \dfrac{∂z}{∂y}\) para\( z=\ln(x^6+y^4)\)

    Responda
    \( \dfrac{∂z}{∂x}=\frac{6x^5}{x^6+y^4};\quad \dfrac{∂z}{∂y}=\frac{4y^3}{x^6+y^4}\)

    10) Encontre\( f_y(x,y)\) para\( f(x,y)=e^{xy}\cos(x)\sin(y).\)

    11) Deixe\( z=e^{xy}.\) encontrar\( \dfrac{∂z}{∂x}\)\( \dfrac{∂z}{∂y}\) e.

    Responda
    \( \dfrac{∂z}{∂x}=ye^{xy};\quad \dfrac{∂z}{∂y}=xe^{xy}\)

    12) Deixe\( z=\ln(\frac{x}{y})\). Encontre\( \dfrac{∂z}{∂x}\)\( \dfrac{∂z}{∂y}\) e.

    13) Deixe\( z=\tan(2x−y).\) encontrar\( \dfrac{∂z}{∂x}\)\( \dfrac{∂z}{∂y}\) e.

    Responda
    \( \dfrac{∂z}{∂x}=2\sec^2(2x−y),\quad \dfrac{∂z}{∂y}=−\sec^2(2x−y)\)

    14) Deixe\( z=\sinh(2x+3y).\) encontrar\( \dfrac{∂z}{∂x}\)\( \dfrac{∂z}{∂y}\) e.

    15) Vamos\( f(x,y)=\arctan(\frac{y}{x}).\) avaliar\( f_x(2,−2)\)\( f_y(2,−2)\) e.

    Responda
    \( f_x(2,−2)=\frac{1}{4}=f_y(2,−2)\)

    16) Vamos\( f(x,y)=\dfrac{xy}{x−y}.\) encontrar\( f_x(2,−2)\) e\( f_y(2,−2).\)

    17) Encontre\( \dfrac{∂z}{∂x}\) em\( (0,1)\) para\( z=e^{−x}cos(y)\).

    Responda
    \( \dfrac{∂z}{∂x}=−\cos(1)\)

    18) Dado\( f(x,y,z)=x^3yz^2,\) achado\( \dfrac{∂^2f}{∂x∂y}\) e\( f_z(1,1,1).\)

    19) Dado\( f(x,y,z)=2\sin(x+y),\) achado\( f_x(0,\frac{π}{2},−4)\)\(f_y(0,\frac{π}{2},−4)\),\( f_z(0,\frac{π}{2},−4)\) e.

    Responda
    \( f_x(x,y,z)=0,\quad f_y(x,y,z)=0,\quad f_z(x,y,z)=0\)

    20) A área de um paralelogramo com comprimentos laterais adjacentes que são\( a\) e\( b\), e na qual o ângulo entre esses dois lados é\( θ\), é dada pela função\( A(a,b,θ)=ba\sin(θ).\) Encontre a taxa de variação da área do paralelogramo em relação ao seguinte:

    a. Lado\(a\)

    b. Lado\(b\)

    c. Ângulo\(θ\)

    21) Expresse o volume de um cilindro circular reto em função de duas variáveis:

    a. seu raio\( r\) e sua altura\( h\).

    b. Mostre que a taxa de variação do volume do cilindro em relação ao seu raio é o produto de sua circunferência multiplicada por sua altura.

    c. Mostre que a taxa de variação do volume do cilindro em relação à sua altura é igual à área da base circular.

    Responda
    \( a. V(r,h)=πr^2h\)
    \( b. \dfrac{∂V}{∂r}=2πrh\)
    \( c. \dfrac{∂V}{∂h}=πr^2\)

    22) Calcular\( \dfrac{∂w}{∂z}\) para\( w=z\sin(xy^2+2z).\)

    Nos exercícios 23 a 39, encontre as derivadas parciais de ordem superior indicadas.

    23)\( f_{xy}(x,y)\) para\( f(x,y)=\ln(x−y)\)

    Responda
    \( f_{xy}(x,y)=\frac{1}{(x−y)^2}\)

    24)\( f_{yx}(x,y)\) para\( f(x, y)=\ln(x−y)\)

    25) Deixe\( z=x^2+3xy+2y^2.\) encontrar\( \dfrac{∂^2z}{∂x^2}\)\( \dfrac{∂^2z}{∂y^2}\) e.

    Responda
    \( \dfrac{∂^2z}{∂x^2}=2,\quad \dfrac{∂^2z}{∂y^2}=4\)

    26) Dado\( z=e^x\tan y\), encontre\( \dfrac{∂^2z}{∂x∂y}\)\( \dfrac{∂^2z}{∂y∂x}\) e.

    27) Dado\( f(x,y,z)=xyz,\) o achado\( f_{xyy}(x,y,z),\, f_{yxy}(x,y,z),\)\( f_{yyx}(x,y,z)\) e.

    Responda
    \( f_{xyy}(x,y,z)=f_{yxy}(x,y,z)=f_{yyx}(x,y,z)=0\)

    28) Dado\( f(x,y,z)=e^{−2x}\sin(z^2y),\) mostrar que\( f_{xyy}(x,y,z)=f_{yxy}(x,y,z)\).

    29) Mostre que\( z=\frac{1}{2}(e^y−e^{−y})\sin x\) é uma solução da equação diferencial\( \dfrac{∂^2z}{∂x^2}+\dfrac{∂^2z}{∂y^2}=0.\)

    Responda
    \( \dfrac{d^2z}{dx^2}=−\frac{1}{2}(e^y−e^{−y})\sin x\)
    \( \dfrac{d^2z}{dy^2}=\frac{1}{2}(e^y−e^{−y})\sin x\)
    \( \dfrac{d^2z}{dx^2}+\dfrac{d^2z}{dy^2}=0\)

    30) Encontre\( f_{xx}(x,y)\) por\( f(x,y)=\frac{4x^2}{y}+\frac{y^2}{2x}.\)

    31) Deixe\( f(x,y,z)=x^2y^3z−3xy^2z^3+5x^2z−y^3z.\) encontrar\( f_{xyz}.\)

    Responda
    \( f_{xyz}(x,y,z)=6y^2x−18yz^2\)

    32) Deixe\( F(x,y,z)=x^3yz^2−2x^2yz+3xz−2y^3z.\) encontrar\( F_{xyz}(x,y,z)\).

    33) Dado\( f(x,y)=x^2+x−3xy+y^3−5,\) encontre todos os pontos em que\( f_x(x,y)=f_y(x,y)=0\) simultaneamente.

    Responda
    \( (\frac{1}{4},\frac{1}{2}),\quad (1,1)\)

    34) Dado\( f(x,y)=2x^2+2xy+y^2+2x−3,\) encontre todos os pontos em que\( \dfrac{∂f}{∂x}=0\) e\( \dfrac{∂f}{∂y}=0\) simultaneamente.

    35) Dado\( f(x,y)=y^3−3yx^2−3y^2−3x^2+1\), encontre todos os pontos\( f\) nos quais\( f_x(x, y)=f_y(x, y)=0\) simultaneamente.

    Responda
    \( (0,0),\quad (0,2),\quad (\sqrt{3},−1), \quad (−\sqrt{3},−1)\)

    36) Dado\( f(x,y)=15x^3−3xy+15y^3,\) encontre todos os pontos em que\( f_x(x,y)=f_y(x,y)=0\) simultaneamente.

    37) Mostre que\( z=e^x\sin y\) satisfaz a equação\( \dfrac{∂^2z}{∂x^2}+\dfrac{∂^2z}{∂y^2}=0.\)

    Responda
    \( \dfrac{∂^2z}{∂x^2}+\dfrac{∂^2z}{∂y^2}=e^x\sin y−e^x\sin y=0\)

    38) Mostre que\( f(x,y)=\ln(x^2+y^2)\) resolve a equação de Laplace\( \dfrac{∂^2z}{∂x^2}+\dfrac{∂^2z}{∂y^2}=0.\)

    39) Mostre que\( z=e^{−t}\cos(\frac{x}{c})\) satisfaz a equação do calor\( \dfrac{∂z}{∂t}=−e^{−t}\cos(\frac{x}{c}).\)

    Responda
    \( c^2\dfrac{∂^2z}{∂x^2}=e^{−t}\cos(\frac{x}{c})\)

    40) Encontre\(\displaystyle \lim_{Δx→0}\frac{f(x+Δx)−f(x,y)}{Δx}\) por\( f(x,y)=−7x−2xy+7y.\)

    41) Encontre\(\displaystyle \lim_{Δy→0}\frac{f(x,y+Δy)−f(x,y)}{Δy}\) por\( f(x,y)=−7x−2xy+7y.\)

    Responda
    \( \dfrac{∂f}{∂y}=−2x+7\)

    42) Encontre\(\displaystyle \lim_{Δx→0}\frac{Δf}{Δx}=\lim_{Δx→0}\frac{f(x+Δx,y)−f(x,y)}{Δx}\) por\( f(x,y)=x^2y^2+xy+y.\)

    43) Encontre\(\displaystyle \lim_{Δx→0}\frac{Δf}{Δx}=\lim_{Δx→0}\frac{f(x+Δx,y)−f(x,y)}{Δx}\) por\( f(x,y)=\sin(xy).\)

    Responda
    \( \dfrac{∂f}{∂x}=y\cos xy\)

    44) A função\( P(T,V)=\dfrac{nRT}{V}\) fornece a pressão em um ponto de um gás em função da temperatura\( T\) e do volume\( V\). As letras\( n\) e\( R\) são constantes. Encontre\( \dfrac{∂P}{∂V}\) e\( \dfrac{∂P}{∂T}\) explique o que essas quantidades representam.

    45) A equação para o fluxo de calor no\( xy\) plano -é\( \dfrac{∂f}{∂t}=\dfrac{∂^2f}{∂x^2}+\dfrac{∂^2f}{∂y^2}\). Mostre que isso\( f(x,y,t)=e^{−2t}\sin x\sin y\) é uma solução.

    46) A equação básica da onda é\( f_{tt}=f_{xx}.\) Verificar se\( f(x,t)=\sin(x+t)\)\( f(x,t)=\sin(x−t)\) são soluções.

    47) A lei dos cossenos pode ser pensada como uma função de três variáveis. \( θ\)Seja\( x,y,\) e seja os dois lados de qualquer triângulo em que o ângulo\( θ\) seja o ângulo incluído entre os dois lados. Em seguida,\( F(x,y,θ)=x^2+y^2−2xy\cos θ\) dá o quadrado do terceiro lado do triângulo. Encontre\( \dfrac{∂F}{∂θ}\) e\( \dfrac{∂F}{∂x}\) quando\( x=2,\,y=3,\) e\( θ=\frac{π}{6}.\)

    Responda
    \( \dfrac{∂F}{∂θ}=6,\quad \dfrac{∂F}{∂x}=4−3\sqrt{3}\)

    48) Suponha que os lados de um retângulo estejam mudando em relação ao tempo. O primeiro lado está mudando a uma taxa\( 2\) de entrada. /sec, enquanto o segundo lado está mudando na taxa de\( 4\) in/seg. Com que rapidez a diagonal do retângulo muda quando o primeiro lado mede\( 16\) em. e o segundo lado mede\( 20\) em.? (Arredonde a resposta para três casas decimais.)

    49) Uma função de produção da Cobb-Douglas é\( f(x,y)=200x^{0.7}y^{0.3},\) onde\( x\) e\( y\) representa a quantidade de mão de obra e capital disponível. Let\( x=500\) and\( y=1000.\) Find\( \dfrac{∂f}{∂x}\) e\( \dfrac{∂f}{∂y}\) com esses valores, que representam a produtividade marginal do trabalho e do capital, respectivamente.

    Responda
    \( \dfrac{∂f}{∂x}\)\( (500,1000)=172.36, \quad \dfrac{∂f}{∂y}\)em\( (500,1000)=36.93\)

    50) O índice de temperatura aparente é uma medida da sensação da temperatura e é baseado em duas variáveis:\( h\), que é umidade relativa e\( t\), qual é a temperatura do ar.

    \( A=0.885t−22.4h+1.20th−0.544.\)Encontre\( \dfrac{∂A}{∂t}\) e\( \dfrac{∂A}{∂h}\) quando\( t=20°F\) e\( h=0.90.\)