14.3: Derivadas parciais
- Page ID
- 187980
- Calcule as derivadas parciais de uma função de duas variáveis.
- Calcule as derivadas parciais de uma função de mais de duas variáveis.
- Determine as derivadas de ordem superior de uma função de duas variáveis.
- Explique o significado de uma equação diferencial parcial e dê um exemplo.
Agora que examinamos os limites e a continuidade das funções de duas variáveis, podemos prosseguir com o estudo de derivadas. Encontrar derivadas de funções de duas variáveis é o conceito-chave neste capítulo, com tantas aplicações em matemática, ciências e engenharia quanto a diferenciação de funções de variável única. No entanto, já vimos que os limites e a continuidade das funções multivariáveis têm novos problemas e exigem novas terminologias e ideias para lidar com eles. Isso também se transforma em diferenciação.
Derivadas de uma função de duas variáveis
Ao estudar derivadas de funções de uma variável, descobrimos que uma interpretação da derivada é uma taxa de variação instantânea de\(y\) como uma função da notação de\(x.\) Leibniz para a derivada é o\(dy/dx,\) que implica que\(y\) é a variável dependente e\(x\) é a variável independente. Para uma função\(z=f(x,y)\) de duas variáveis,\(x\) e\(y\) são as variáveis independentes e\(z\) é a variável dependente. Isso levanta duas questões imediatamente: Como adaptamos a notação de Leibniz para funções de duas variáveis? Além disso, o que é uma interpretação da derivada? A resposta está nas derivadas parciais.
\(f(x,y)\)Seja uma função de duas variáveis. Então, a derivada parcial de\(f\) com relação a\(x\), escrita como\(∂f/∂x,\) ou\(f_x,\) é definida como
\[\dfrac{∂f}{∂x}=f_x(x,y)=\lim_{h→0}\dfrac{f(x+h,y)−f(x,y)}{h} \label{pd1} \]
A derivada parcial de\(f\) com relação a\(y\), escrita como\(∂f/∂y\) ou\(f_y,\) é definida como
\[\dfrac{∂f}{∂y}=f_y(x,y)=\lim_{k→0}\dfrac{f(x,y+k)−f(x,y)}{k}. \label{pd2} \]
Essa definição já mostra duas diferenças. Primeiro, a notação muda, no sentido de que ainda usamos uma versão da notação de Leibniz, mas a\(d\) da notação original é substituída pelo símbolo\(∂\). (Esse arredondado geralmente\(“d”\) é chamado de “parcial”, então\(∂f/∂x\) é falado como o “parcial de em\(f\) relação\(x\) a.”) Essa é a primeira dica de que estamos lidando com derivadas parciais. Segundo, agora temos duas derivadas diferentes que podemos usar, já que existem duas variáveis independentes diferentes. Dependendo da variável que escolhermos, podemos criar diferentes derivadas parciais, e muitas vezes o fazemos.
Use a definição da derivada parcial como um limite para calcular\(∂f/∂x\) e\(∂f/∂y\) para a função
\[f(x,y)=x^2−3xy+2y^2−4x+5y−12. \nonumber \]
Solução
Primeiro, calcule\(f(x+h,y).\)
\[\begin{align*} f(x+h,y) &=(x+h)^2−3(x+h)y+2y^2−4(x+h)+5y−12 \\ &=x^2+2xh+h^2−3xy−3hy+2y^2−4x−4h+5y−12. \end{align*} \nonumber \]
Em seguida, substitua isso na Equação\ ref {pd1} e simplifique:
\ [\ begin {align*}\ dfrac {f} {x} &=\ lim_ {h→0}\ dfrac {f (x+h, y) −f (x, y)} {h}\\
&=\ lim_ {h→0}\ dfrac {(x^2+2xh+h^2−3xy−3hy+2y^2−2−3hy+2y^2−2−2−3hy+2y^2−2−2−2−3hy+2y^2−2−2−2−3hy+2y^2−2−4x−4h+5y−12) − (x^2−3xy+2y^2−4x+5y−12)} {h}\\ &=\ lim_ {h→0}\ dfrac {x^2+2xh+h^2−3xy−3hy+2y^2−4x−4h+5y−12−x^2+3xy−2y^2+4x−5y+12} {h}\\
&=\ lim_ {h→0}\ dfrac {2 xh+h^2−3hy−4h} {h}\\
&=\ lim_ {h→0}\ dfrac {h (2x+h−3y−4)} {h}\\
&=\ lim_ {h→0} (2x+h−3y−4)\\
&=2x−3y−4. \ end {align*}\]
Para calcular\(\dfrac{∂f}{∂y}\), primeiro calcule\(f(x,y+h):\)
\[\begin{align*} f(x+h,y) &=x^2−3x(y+h)+2(y+h)^2−4x+5(y+h)−12 \\ &=x^2−3xy−3xh+2y^2+4yh+2h^2−4x+5y+5h−12. \end{align*}\]
Em seguida, substitua isso na Equação\ ref {pd2} e simplifique:
\ [\ begin {align*}\ dfrac {f} {y} &=\ lim_ {h→0}\ dfrac {f (x, y+h) −f (x, y)} {h}\\
&=\ lim_ {h→0}\ dfrac {(x^2−3xy−3xh+2y^2+4yh+2h+2h+2h+4h+2h^2+4h+2h+2h^2+4yh+2h+2h+2h^2+4h+2h^2h+2h^22−4x+5y+5h−12) − (x^2−3xy+2y^2−4x+5y−12)} {h}\\ &=\ lim_ {h→0}\ dfrac {x^2−3xy−3xh+2y^2+4yh+2h^2−4x+5y+5h−12−x^2=2h^2−4x+5h−12−x^2^2−4x+5h−12−x^2^2−4x+2h−4x+5h−12−x^2−+3xy−2y^2+4x−5y+12} {h}\\
&=\ lim_ {h→0}\ dfrac {−3xh+4h+2h^2+5h} {h}\\
&=\ lim_ {h→0}\ dfrac {h (−3x+4y+2h+5)} {h}\\
&=\ lim_ {h→0} (−3x+4y+2h+5)\\
&=−3x+4y+4 5\ end {align*}\]
Use a definição da derivada parcial como um limite para calcular\(∂f/∂x\) e\(∂f/∂y\) para a função
\[f(x,y)=4x^2+2xy−y^2+3x−2y+5.\nonumber \]
- Dica
-
Use as equações\ ref {pd1} e\ ref {pd2} da definição de derivadas parciais.
- Responda
-
\(\dfrac{∂f}{∂x}=8x+2y+3\)
\(\dfrac{∂f}{∂y}=2x−2y−2\)
A ideia a ter em mente ao calcular derivadas parciais é tratar todas as variáveis independentes, exceto a variável em relação à qual estamos diferenciando, como constantes. Em seguida, proceda à diferenciação como acontece com uma função de uma única variável. Para ver por que isso é verdade, primeiro corrija\(y\) e defina\(g(x)=f(x,y)\) como uma função de\(x\). Então
\[\begin{align*} g′(x) &=\lim_{h→0}\dfrac{g(x+h)−g(x)}{h} \\[6pt] &=\lim_{h→0}\dfrac{f(x+h,y)−f(x,y)}{h} \\[6pt] &=\dfrac{∂f}{∂x}. \end{align*}\]
O mesmo vale para calcular a derivada parcial de em\(f\) relação\(y\) a. Desta vez, corrija\(x\) e\(h(y)=f(x,y)\) defina em função de\(y\). Então
\[\begin{align*} h′(x) &=\lim_{k→0}\dfrac{h(x+k)−h(x)}{k} \\[6pt] &=\lim_{k→0}\dfrac{f(x,y+k)−f(x,y)}{k} \\[6pt] &=\dfrac{∂f}{∂y}. \end{align*}\]
Todas as regras de diferenciação se aplicam.
\(∂f/∂x\)Calcule e\(∂f/∂y\) para as seguintes funções mantendo a variável oposta constante e depois diferenciando:
- \(f(x,y)=x^2−3xy+2y^2−4x+5y−12\)
- \(g(x,y)=\sin(x^2y−2x+4)\)
Solução:
a. Para calcular\(∂f/∂x\), trate a variável\(y\) como uma constante. Em seguida, diferencie em\(f(x,y)\) relação ao\(x\) uso das regras de soma, diferença e poder:
\[\begin{align*}\dfrac{∂f}{∂x} &=\dfrac{∂}{∂x}\left[x^2−3xy+2y^2−4x+5y−12\right] \\[6pt] &=\dfrac{∂}{∂x}[x^2]−\dfrac{∂}{∂x}[3xy]+\dfrac{∂}{∂x}[2y^2]−\dfrac{∂}{∂x}[4x]+\dfrac{∂}{∂x}[5y]−\dfrac{∂}{∂x}[12] \\[6pt] &=2x−3y+0−4+0−0 \\ &=2x−3y−4. \end{align*}\]
As derivadas do terceiro, quinto e sexto termos são todas zero porque não contêm a variável e\(x\), portanto, são tratadas como termos constantes. A derivada do segundo termo é igual ao coeficiente de\(x\), que é\(−3y\). Calculando\(∂f/∂y\):
\[\begin{align*} \dfrac{∂f}{∂y} &=\dfrac{∂}{∂y}\left[x^2−3xy+2y^2−4x+5y−12\right] \\[6pt] &=\dfrac{∂}{∂y}[x^2]−\dfrac{∂}{∂y}[3xy]+\dfrac{∂}{∂y}[2y^2]−\dfrac{∂}{∂y}[4x]+\dfrac{∂}{∂y}[5y]−\dfrac{∂}{∂y}[12] \\[6pt] &=−3x+4y−0+5−0 \\ &=−3x+4y+5. \end{align*} \nonumber \]
Essas são as mesmas respostas obtidas no Example\(\PageIndex{1}\).
b. Para calcular,\(∂g/∂x,\) trate a variável y como uma constante. Em seguida, diferencie em\(g(x,y)\) relação ao\(x\) uso da regra da cadeia e da regra de poder:
\[\begin{align*}\dfrac{∂g}{∂x} &=\dfrac{∂}{∂x}\left[\sin(x^2y−2x+4)\right] \\[6pt] &=\cos(x^2y−2x+4)\dfrac{∂}{∂x}[x^2y−2x+4] \\[6pt] &=(2xy−2)\cos(x^2y−2x+4). \end{align*}\]
Para calcular,\(∂g/∂y,\) trate a variável\(x\) como uma constante. Em seguida, diferencie em\(g(x,y)\) relação ao\(y\) uso da regra da cadeia e da regra de poder:
\[ \begin{align*} \dfrac{∂g}{∂y} &=\dfrac{∂}{∂y}\left[\sin(x^2y−2x+4)\right] \\[6pt] &=\cos(x^2y−2x+4)\dfrac{∂}{∂y}[x^2y−2x+4] \\[6pt] &=x^2\cos(x^2y−2x+4). \end{align*} \nonumber \]
\(∂f/∂x\)Calcule e\(∂f/∂y\) para a função
\[f(x,y)=\tan(x^3−3x^2y^2+2y^4) \nonumber \]
mantendo constante a variável oposta e, em seguida, diferenciando.
- Dica
-
Use as equações\ ref {pd1} e\ ref {pd1} da definição de derivadas parciais.
- Responda
-
\(\dfrac{∂f}{∂x}=(3x^2−6xy^2)\sec^2(x^3−3x^2y^2+2y^4)\)
\(\dfrac{∂f}{∂y}=(−6x^2y+8y^3)\sec^2(x^3−3x^2y^2+2y^4)\)
Como podemos interpretar essas derivadas parciais? Lembre-se de que o gráfico de uma função de duas variáveis é uma superfície em\(R^3\). Se removermos o limite da definição da derivada parcial em relação a\(x\), o quociente de diferença permanece:
\[\dfrac{f(x+h,y)−f(x,y)}{h}. \nonumber \]
Isso se assemelha ao quociente de diferença para a derivada de uma função de uma variável, exceto pela presença da\(y\) variável. A figura\(\PageIndex{1}\) ilustra uma superfície descrita por uma função arbitrária\(z=f(x,y).\)
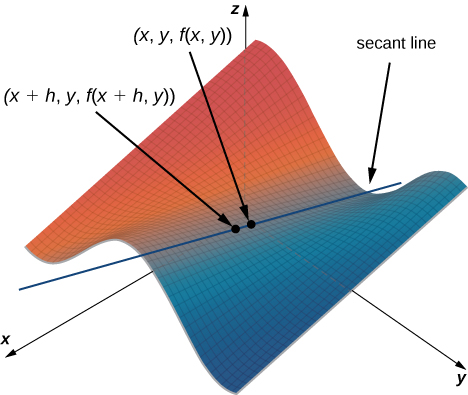
Na Figura\(\PageIndex{1}\), o valor de\(h\) é positivo. Se representarmos graficamente\(f(x,y)\) e\(f(x+h,y)\) para um ponto arbitrário\((x,y),\), a inclinação da linha secante que passa por esses dois pontos é dada por
\[\dfrac{f(x+h,y)−f(x,y)}{h}. \nonumber \]
Essa linha é paralela ao\(x\) eixo y. Portanto, a inclinação da linha secante representa uma taxa média de mudança da função à\(f\) medida que viajamos paralelamente ao\(x\) eixo. À medida que\(h\) se aproxima de zero, a inclinação da linha secante se aproxima da inclinação da reta tangente.
Se escolhermos mudar\(y\) em vez de\(x\) pelo mesmo valor incremental\(h\), a linha secante é paralela ao\(y\) eixo -, assim como a linha tangente. Portanto,\(∂f/∂x\) representa a inclinação da reta tangente que passa pelo ponto\((x,y,f(x,y))\) paralelo ao\(x\) eixo -e\(∂f/∂y\) representa a inclinação da reta tangente passando pelo ponto\((x,y,f(x,y))\) paralelo ao\(y\) eixo. Se quisermos encontrar a inclinação de uma reta tangente passando pelo mesmo ponto em qualquer outra direção, precisamos das chamadas derivadas direcionais.
Agora voltamos à ideia de mapas de contorno, que introduzimos em Funções de várias variáveis. Podemos usar um mapa de contorno para estimar derivadas parciais de uma função\(g(x,y)\).
Use um mapa de\(∂g/∂x\) contorno para estimar o ponto\((\sqrt{5},0)\) da função
\[g(x,y)=\sqrt{9−x^2−y^2}. \nonumber \]
Solução
\(\PageIndex{2}\)A figura representa um mapa de contorno da função\(g(x,y)\).
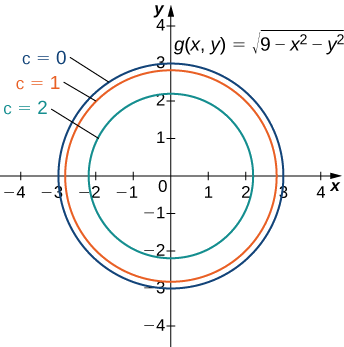
O círculo interno no mapa de contorno corresponde a\(c=2\) e o próximo círculo de saída corresponde\(c=1\) a. A primeira circunferência é dada pela equação\(2=\sqrt{9−x^2−y^2}\); a segunda circunferência é dada pela equação\(1=\sqrt{9−x^2−y^2}\). A primeira equação simplifica para\(x^2+y^2=5\) e a segunda equação simplifica para\(x^2+y^2=8.\) O\(x\) intercepto -do primeiro círculo é\((\sqrt{5},0)\) e o\(x\) intercepto -do segundo círculo é\((2\sqrt{2},0)\). Podemos estimar o valor de\(∂g/∂x\) avaliado no ponto\((\sqrt{5},0)\) usando a fórmula da inclinação:
\[ \begin{align*} \left.\dfrac{∂g}{∂x}\right|_{(x,y) = (\sqrt{5},0)} &≈ \dfrac{g(\sqrt{5},0)−g(2\sqrt{2},0)}{\sqrt{5}−2\sqrt{2}} \\ &= \dfrac{2−1}{\sqrt{5}−2\sqrt{2}} \\ &=\dfrac{1}{\sqrt{5}−2\sqrt{2}} ≈−1.688. \end{align*}\]
Para calcular o valor exato de\(∂g/∂x\) avaliado no ponto\((\sqrt{5},0)\), começamos encontrando\(∂g/∂x\) usando a regra da cadeia. Primeiro, reescrevemos a função como
\[g(x,y)=\sqrt{9−x^2−y^2}=(9−x^2−y^2)^{1/2} \nonumber \]
e, em seguida, diferencie em relação a\(x\) enquanto mantém\(y\) constante:
\[ \begin{align*} \dfrac{∂g}{∂x} &=\dfrac{1}{2}(9−x^2−y^2)^{−1/2}(−2x) \\[4pt] &=−\dfrac{x}{\sqrt{9−x^2−y^2}}. \end{align*}\]
Em seguida, avaliamos essa expressão usando\(x=\sqrt{5}\) e\(y=0\):
\ [\ begin {align*}\ dfrac {g} {x} _ {(x, y) = (\ sqrt {5} ,0)} &=−\ dfrac {\ sqrt {5}} {\ sqrt {9− (\ sqrt {5}) ^2− (0) ^2}}\\ [4pt]
&=−\ dfrac {sqrt {5}} {\ sqrt {4}}\\ [4pt]
&=−\ dfrac {\ sqrt {5}} {2} ≈ −1,118. \ end {align*}\ nonumber\]
A estimativa da derivada parcial corresponde à inclinação da linha secante que passa pelos pontos\((\sqrt{5},0,g(\sqrt{5},0))\)\((2\sqrt{2},0,g(2\sqrt{2},0))\) e. Representa uma aproximação da inclinação da reta tangente à superfície através do ponto\((\sqrt{5},0,g(\sqrt{5},0)),\) que é paralelo ao\(x\) eixo y.
Use um mapa de\(∂f/∂y\) contorno para estimar o ponto\((0,\sqrt{2})\) da função
\[ f(x,y)=x^2−y^2.\nonumber \]
Compare isso com a resposta exata.
- Dica
-
Crie um mapa de contorno para\(f\) usar valores\(c\) de\(−3\) até\(3\). Qual dessas curvas passa pelo ponto\((0,\sqrt{2})?\)
- Responda
-
Usando as curvas correspondentes a\(c=−2\) e\(c=−3,\) obtemos
\ [\ begin {align*}\ left. \ dfrac {f} {y}\ right|_ {(x, y) = (0,\ sqrt {2})} &≈\ dfrac {f (0,\ sqrt {3}) −f (0,\ sqrt {2})} {\ sqrt {3} −\ sqrt {2}}\\ [4pt]
&=\ dfrac {−−1 3− (−2)} {\ sqrt {3} −\ sqrt {2}}\ dfrac {\ sqrt {3} +\ sqrt {2}} {\ sqrt {3} +\ sqrt {2}}\\ [4pt]
&=−\ sqrt {3} −\ sqrt {2} ≈ −3,146. \ end {align*}\]A resposta exata é
\[ \left. \dfrac{∂f}{∂y} \right|_{(x,y)=(0,\sqrt{2})}=(−2y|_{(x,y)=(0,\sqrt{2})}=−2\sqrt{2}≈−2.828. \nonumber \]
Funções de mais de duas variáveis
Suponha que tenhamos uma função de três variáveis, como\(w=f(x,y,z).\) Podemos calcular derivadas parciais de em\(w\) relação a qualquer uma das variáveis independentes, simplesmente como extensões das definições para derivadas parciais de funções de duas variáveis.
\(f(x,y,z)\)Seja uma função de três variáveis. Então, a derivada parcial de\(f\) com relação a\(x\), escrita como\(∂f/∂x,\) ou\(f_x,\) é definida como
\[\dfrac{∂f}{∂x}=f_x(x,y,z)=\lim_{h→0}\dfrac{f(x+h,y,z)−f(x,y,z)}{h}. \label{PD2a} \]
A derivada parcial de\(f\) com relação a\(y\), escrita como\(∂f/∂y\), ou\(f_y\), é definida como
\[\dfrac{∂f}{∂y}=f_y(x,y,z)=\lim_{k→0}\dfrac{f(x,y+k,z)−f(x,y,z)}{k.} \label{PD2b} \]
A derivada parcial de\(f\) com relação a\(z\), escrita como\(∂f/∂z\), ou\(f_z\), é definida como
\[\dfrac{∂f}{∂z}=f_z(x,y,z)=\lim_{m→0}\dfrac{f(x,y,z+m)−f(x,y,z)}{m}. \label{PD2c} \]
Podemos calcular uma derivada parcial de uma função de três variáveis usando a mesma ideia que usamos para uma função de duas variáveis. Por exemplo, se tivermos uma função\(f\) de\(x,y\) e\(z\) e desejamos calcular\(∂f/∂x\), tratamos as outras duas variáveis independentes como se fossem constantes e, em seguida, diferenciamos em relação\(x\) a.
Use a definição de limite de derivadas parciais\(∂f/∂x\) para calcular a função
\[ f(x,y,z)=x^2−3xy+2y^2−4xz+5yz^2−12x+4y−3z. \nonumber \]
Em seguida, encontre\(∂f/∂y\) e\(∂f/∂z\) defina as outras duas variáveis como constantes e diferencie de acordo.
Solução:
Primeiro calculamos\(∂f/∂x\) usando a Equação\ ref {PD2a}, depois calculamos as outras duas derivadas parciais mantendo as variáveis restantes constantes. Para usar a equação para encontrar\(∂f/∂x\), primeiro precisamos calcular\(f(x+h,y,z):\)
\ [\ begin {align*} f (x+h, y, z) &= (x+h) ^2−3 (x+h) y+2y^2−4 (x+h) z+5yz^2−12 (x+h) +4y−3z\\ [4pt]
&=x^2+2xh+h^2−3xy−3xh+2xh+2−3xy−3xh+2xh+2−3xy−3xh+2xh+2−3xy−3xh+2xh+2−3xy−3xh+2y^2−4xz−4hz+5yz^2−12x−12h+4y−3z\ end {align*}\ nonumber\]
e lembre-se de que, em\(f(x,y,z)=x^2−3xy+2y^2−4zx+5yz^2−12x+4y−3z.\) seguida, substituímos essas duas expressões na equação:
\ [\ begin {align*}\ dfrac {f} {x} &=\ lim_ {h→0}\ left [\ dfrac {x^2+2xh+h^2−3xy−3hy+2y^2−4xz−4hz+5yz^2−12x−12h+4y−3zh−x^2−3xy+2−3xy+2−3xy+2−3xy+2xy+2−3xy+2−3xy+2−3xy+2−3xy+2−3xy+2−3xy+2−3xy+y^2−4xz+5yz^2−12x+4y−3z} {h}\ direita]\\ [4pt]
&=\ lim_ {h→0}\ left [\ dfrac {2xh+h^2−3hy−4hz−12h} {h}\ direita]\\ [4pt]
&=\ lim_ {h→0}\ esquerda [\ dfrac {h (2x+h−3y−4z−12) )} {h}\ right]\\ [4pt]
&=\ lim_ {h→0} (2x+h−3y−4z−12)\\ [4pt]
&=2x−3y−4z−12. \ end {align*}\ nonumber\]
Em seguida, encontramos\(∂f/∂y\) segurando\(x\) e\(z\) constantemente. Portanto, qualquer termo que não inclua a variável\(y\) é constante e sua derivada é zero. Podemos aplicar as regras de soma, diferença e potência para funções de uma variável:
\ [\ begin {align*} &\ dfrac {} {y}\ esquerda [x^2−3xy+2y^2−4xz+5yz^2−12x+4y−3z\ direita]\ [4pt]
&=\ dfrac {} {y} [x^2] −\ dfrac {} {y} [3xy]] +\ dfrac {} {y} [2y^2] −\ dfrac {} {y} [4xz] +\ dfrac {} {y} [5yz^2] −\ dfrac {} {y} [12x] +\ dfrac {} {y} [4y] −\ dfrac {} {z} [3z]\\ [4pt]
&=0−3x+4y−0+5z^2−0+4−0 \\ [4pt]
&=−3x+4y+5z^2+4. \ end {align*}\]
Para calcular,\(∂f/∂z,\) mantemos\(y\) uma constante\(x\) e aplicamos as regras de soma, diferença e potência para funções de uma variável:
\ [\ begin {align*} &\ dfrac {} {z} [x^2−3xy+2y^2−4xz+5yz^2−12x+4y−3z]\ [4pt]
&=\ dfrac {} {z} [x^2] −\ dfrac {} {z} [3xy]\ + frac {} {z} [2y^2] −\ dfrac {} {z} [4xz] +\ dfrac {} {z} [5yz^2] −\ dfrac {} {z} [12x] +\ dfrac {} {} {} {z} {z} [3z]\\ [4pt]
&=0−0+0−4x+10yz−0+0−3\\ [4pt]
&=−4x+10yz−3\ end {align*}\]
Use a definição de limite de derivadas parciais\(∂f/∂x\) para calcular a função
\[f(x,y,z)=2x^2−4x^2y+2y^2+5xz^2−6x+3z−8.\nonumber \]
Em seguida, encontre\(∂f/∂y\) e\(∂f/∂z\) defina as outras duas variáveis como constantes e diferencie de acordo.
- Dica
-
Use a estratégia do exemplo anterior.
- Responda
-
\(\dfrac{∂f}{∂x}=4x−8xy+5z^2−6,\dfrac{∂f}{∂y}=−4x^2+4y,\dfrac{∂f}{∂z}=10xz+3\)
Calcule as três derivadas parciais das seguintes funções.
- \(f(x,y,z)=x^2y−4xz+y^2x−3yz\)
- \(g(x,y,z)=\sin(x^2y−z)+\cos(x^2−yz)\)
Solução
Em cada caso, trate todas as variáveis como constantes, exceto aquela cuja derivada parcial você está calculando.
uma.
\ [\ begin {align*}\ dfrac {f} {x} &=\ dfrac {} {x}\ left [\ dfrac {x^2y−4xz+y^2} {x−3yz}\ direita]\\ [6pt]
&=\ dfrac {\ dfrac {} {x} (x^2y−4−4) xz+y^2) (x−3yz) − (x^2y−4xz+y^2)\ dfrac {} {x} (x−3yz)} {(x−3yz) ^2}\\ [6pt]
&=\ dfrac {(2xy−4z) (x−3yz) − (x^2y−4xx z+y^2) (1)} {(x−3yz) ^2}\\ [6 pontos]
&=\ dfrac {2x^2y−6xy^2z−4xz+12yz^2−x^2y+4xz−y^2} {(x−3yz) ^2}\\ [6pt]
&=\ dfrac {x^2y−6xy^2z−4xz+12yz^2+4xz−y^2} {(x−3yz) ^2}\ end {align*}\]
\ [\ begin {align*}\ dfrac {f} {y} &=\ dfrac {} {y}\ left [\ dfrac {x^2y−4xz+y^2} {x−3yz}\ direita]\\ [6pt]
&=\ dfrac {\ dfrac {} {y} (x^2y−4−4 xz+y^2) (x−3yz) − (x^2y−4xz+y^2)\ dfrac {} {y} (x−3yz)} {(x−3yz) ^2}\\ [6pt]
&=\ dfrac {(x^2+2y) (x−3yz) − (x^2y−4) xz+y^2) (−3z)} {(x−3yz) ^2}\\ [6 pontos]
&=\ dfrac {x^3−3x^2yz+2xy−6y^2z+3x^2yz−12xz^2+3y^2z} {(x−3yz) ^2}\\ [6pt]
&=\ dfrac {x^3+2xy−3y^2z−12xz^2} {(x−3y^2} {(x−3y−3y^2} {(x−3y^2} {(x−3y^2} {(x−3y^2} {(x−3y^2} {z) ^2}\ end {align*}\]
\ [\ begin {align*}\ dfrac {f} {z} &=\ dfrac {} {z}\ left [\ dfrac {x^2y−4xz+y^2} {x−3yz}\ direita]\\ [6pt]
&=\ dfrac {\ dfrac {} {z} (x^2y−4−4) xz+y^2) (x−3yz) − (x^2y−4xz+y^2)\ dfrac {} {z} (x−3yz)} {(x−3yz) ^2}\\ [6pt]
&=\ dfrac {(−4x) (x−3yz) − (x^2y−4xz+y^2) (−3y)} {(x−3yz) ^2}\\ [6pt]
&=\ dfrac {−4x^2+12xyz+3x^2y^2−12xyz+3y^3} {(x−3yz) ^2}\ [6pt]
&=\ dfrac {−4x^2+3x^2y^2+3y^3} {(x−3yz) ^2}\ end {alinhamento*}]
b.
\ [\ begin {align*}\ dfrac {f} {x} &=\ dfrac {} {x}\ left [\ sin (x^2y−z) +\ cos (x^2−yz)\ direita]\\ [6pt]
& =(\ cos (x^2y−z))\ dfrac {} {x} (x^2y−z) y−z) − (\ sin (x^2−yz))\ dfrac {} {x} (x^2−yz)\\ [6pt]
&=2xy\ cos (x^2y−z) −2x\ sin (x^2−yz)\ end {align*}\]
\ [\ begin {align*}\ dfrac {f} {y} &=\ dfrac {} {y} [\ sin (x^2y−z) +\ cos (x^2−yz)]\ [6pt]
& =(\ cos (x^2y−z))\ dfrac {} {y} (x^2y−z) − (\ sin (x^2−yz))\ dfrac {} {y} (x^2−yz)\\ [6pt]
&=x^2\ cos (x^2y−z) +z\ sin (x^2−yz)\ end {align*}\]
\ [\ begin {align*}\ dfrac {f} {z} &=\ dfrac {} {z} [\ sin (x^2y−z) +\ cos (x^2−yz)]\ [6pt]
& =(\ cos (x^2y−z))\ dfrac {} {z} (x^2y−z) − (\ sin (x^2−yz))\ dfrac {} {z} (x^2−yz)\\ [6pt]
&=−\ cos (x^2y−z) +y\ sin (x^2−yz)\ end {align*}\ nonumber\]
\(∂f/∂x, ∂f/∂y,\)Calcule e\(∂f/∂z\) para a função
\[f(x,y,z)=\sec(x^2y)−\tan(x^3yz^2). \nonumber \]
- Dica
-
Use a estratégia do exemplo anterior.
- Responda
-
\(\dfrac{∂f}{∂x}=2xy\sec(x^2y)\tan(x^2y)−3x^2yz^2\sec^2(x^3yz^2)\)
\(\dfrac{∂f}{∂y}=x^2\sec(x^2y)\tan(x^2y)−x^3z^2\sec^2(x^3yz^2)\)
\(\dfrac{∂f}{∂z}=−2x^3yz\sec^2(x^3yz^2)\)
Derivadas parciais de ordem superior
Considere a função
\[f(x,y)=2x^3−4xy^2+5y^3−6xy+5x−4y+12. \nonumber \]
Suas derivadas parciais são
\[\dfrac{∂f}{∂x}=6x^2−4y^2−6y+5 \nonumber \]
e
\[\dfrac{∂f}{∂y}=−8xy+15y^2−6x−4. \nonumber \]
Cada uma dessas derivadas parciais é uma função de duas variáveis, então podemos calcular derivadas parciais dessas funções. Assim como com derivadas de funções de variável única, podemos chamá-las de derivadas de segunda ordem, derivadas de terceira ordem e assim por diante. Em geral, eles são chamados de derivadas parciais de ordem superior. Existem quatro derivadas parciais de segunda ordem para qualquer função (desde que todas existam):
\ [\ begin {align*}\ dfrac {^2f} {x^2} &=\ dfrac {} {x}\ left [\ dfrac {f} {x}\ direita]\\ [4pt]\ dfrac {^2f} {yx} &=
\ dfrac {} {y}\ left\ dfrac {} {y}\ left\ dfrac {}\ left\ dfrac {} {y}\ left\ dfrac {frac {f} {x}
\ direita]\\ [4pt]\ dfrac {^2f} {xy} &=\ dfrac {} {x}\ left [\ dfrac {f} {y}\ direita]\
\ [4pt]\ dfrac {^2f} {y^2} &=\ dfrac {} {y}\ left [\ dfrac {f} {y}\ right]. \ end {align*}\]
Uma notação alternativa para cada um é\(f_{xx},f_{xy},f_{yx},\) e\(f_{yy}\), respectivamente. Derivadas parciais de ordem superior calculadas com relação a diferentes variáveis, como\(f_{xy}\) e\(f_{yx}\), são comumente chamadas de derivadas parciais mistas.
Calcule todas as derivadas parciais de quatro segundos para a função
\[f(x,y)=xe^{−3y}+\sin(2x−5y).\label{Ex6e1} \]
Solução:
Para calcular\(\dfrac{∂^2f}{∂x^2}\) e\(\dfrac{∂^2f}{∂y∂x}\), primeiro calculamos\(∂f/∂x\):
\[\dfrac{∂f}{∂x}=e^{−3y}+2\cos(2x−5y). \label{Ex6e2} \]
Para calcular\(\dfrac{∂^2f}{∂x^2}\), diferencie\(∂f/∂x\) (Equação\ ref {ex6E2}) em relação a\(x\):
\ [\ begin {align*}\ dfrac {^2f} {x^2} &=\ dfrac {} {x}\ left [\ dfrac {f} {x}\ direita]\ [6pt]
&=\ dfrac {} {x} [e^ {−3y} +2\ cos (2x−5y)]\ [6pt]
&=−4\ sin (2x−5y). \ end {align*}\ nonumber\]
Para calcular\(\dfrac{∂^2f}{∂y∂x}\), diferencie\(∂f/∂x\) (Equação\ ref {ex6E2}) em relação a\(y\):
\ [\ begin {align*}\ dfrac {^2f} {y\, x} &=\ dfrac {} {y}\ left [\ dfrac {f} {x}\ direita]\\ [6pt]
&=\ dfrac {} {y} [e^ {−3y} +2\ cos (2x−5y)]\\ [6pt]
&=−3e^ {−3y} +10\ sin (2x−5y). \ end {align*}\ nonumber\]
Para calcular\(\dfrac{∂^2f}{∂x∂y}\) e\(\dfrac{∂^2f}{∂y^2}\), primeiro calcule\(∂f/∂y\):
\[\dfrac{∂f}{∂y}=−3xe^{−3y}−5\cos(2x−5y). \label{Ex6e5} \]
Para calcular\(\dfrac{∂^2f}{∂x∂y}\), diferencie\(∂f/∂y\) (Equação\ ref {Ex6E5}) em relação a\(x\):
\ [\ begin {align*}\ dfrac {^2f} {xy} &=\ dfrac {} {x}\ left [\ dfrac {f} {y}\ direita]\ [6pt]
&=\ dfrac {} {x} [−3xe^ {−3y} −5\ cos (2x−5y)]\\ [6pt]
&=−3e^ {−3y} +10\ sin (2x−5y). \ end {align*}\ nonumber\]
Para calcular\(\dfrac{∂^2f}{∂y^2}\), diferencie\(∂f/∂y\) (Equação\ ref {Ex6E5}) em relação a\(y\):
\ [\ begin {align*}\ dfrac {^2f} {y^2} &=\ dfrac {} {y}\ left [\ dfrac {f} {y}\ direita]\ [6pt]
&=\ dfrac {} {y} [−3xe^ {−3y} −5\ cos (2x−5y)]\\ [6pt]
&=9xe^ {−3y} −25\ sin (2x−5y). \ end {align*}\ nonumber\]
Calcule todas as derivadas parciais de quatro segundos para a função
\[f(x,y)=\sin(3x−2y)+\cos(x+4y).\nonumber \]
- Dica
-
Siga as mesmas etapas do exemplo anterior.
- Responda
-
\(\dfrac{∂^2f}{∂x^2}=−9\sin(3x−2y)−\cos(x+4y)\)
\(\dfrac{∂^2f}{∂y∂x}=6\sin(3x−2y)−4\cos(x+4y)\)
\(\dfrac{∂^2f}{∂x∂y}=6\sin(3x−2y)−4\cos(x+4y)\)
\(\dfrac{∂^2f}{∂y^2}=−4\sin(3x−2y)−16\cos(x+4y)\)
Neste ponto, devemos notar que, tanto no Exemplo\(\PageIndex{6}\) quanto no ponto de verificação, era verdade que\(\dfrac{∂^2f}{∂y∂x}=\dfrac{∂^2f}{∂x∂y}\). Sob certas condições, isso é sempre verdade. Na verdade, é uma consequência direta do seguinte teorema.
Suponha que isso\(f(x,y)\) esteja definido em um disco aberto\(D\) que contém o ponto\((a,b)\). Se as funções\(f_{xy}\) e\(f_{yx}\) estiverem ativadas continuamente\(D\), então\(f_{xy}=f_{yx}\).
O teorema de Clairaut garante que, enquanto as derivadas mistas de segunda ordem forem contínuas, a ordem na qual escolhemos diferenciar as funções (ou seja, qual variável vai primeiro, depois segunda e assim por diante) não importa. Também pode ser estendido para derivativos de ordem superior. A prova do teorema de Clairaut pode ser encontrada nos livros de cálculo mais avançados.
Duas outras derivadas parciais de segunda ordem podem ser calculadas para qualquer função\(f(x,y).\). A derivada parcial\(f_{xx}\) é igual à derivada parcial de em\(f_x\) relação a\(x\), e\(f_{yy}\) é igual à derivada parcial de em\(f_y\) relação\(y\) a.
Equações diferenciais parciais
Anteriormente, estudamos equações diferenciais nas quais a função desconhecida tinha uma variável independente. Uma equação diferencial parcial é uma equação que envolve uma função desconhecida de mais de uma variável independente e uma ou mais de suas derivadas parciais. Exemplos de equações diferenciais parciais são
\[\underset{\text{heat equation in two dimensions}}{u_t=c^2(u_{xx}+u_{yy})} \nonumber \]
\[\underset{\text{wave equation in two dimensions}}{u_{tt}=c^2(u_{xx}+u_{yy})} \nonumber \]
\[\underset{\text{Laplace’s equation in two dimensions}} {u_{xx}+u_{yy}=0} \nonumber \]
Nas equações de calor e onda, a função desconhecida\(u\) tem três variáveis independentes:\(t\),\(x\), e\(y\) with\(c\) é uma constante arbitrária. As variáveis independentes\(x\) e\(y\) são consideradas variáveis espaciais, e a variável\(t\) representa o tempo. Na equação de Laplace, a função desconhecida\(u\) tem duas variáveis independentes\(x\)\(y\) e.
Verifique se
\[u(x,y,t)=5\sin(3πx)\sin(4πy)\cos(10πt) \nonumber \]
é uma solução para a equação da onda
\[u_{tt}=4(u_{xx}+u_{yy}). \label{Ex7Eq2} \]
Solução
Primeiro, calculamos\(u_{tt},u_{xx},\) e\(u_{yy}:\)
\ [\ begin {align*} u_ {tt} (x, y, t) &=\ dfrac {} {t}\ left [\ dfrac {u} {t}\ direita]\ [6pt]
&=\ dfrac {} {t} [5\ sin (3π)\ sin (4π) (−10π\ sin (10π) t))]\\ [6pt]
&=\ dfrac {} {t}\ left [−50π\ sin (3π x)\ sin (4π y)\ sin (10π t)\ direita]\\ [6pt]
&=−500π ^2\ sin (3π x)\ sin (4π y)\ cos (10π t)\ fim {align*}\]
\ [\ begin {align*} u_ {xx} (x, y, t) &=\ dfrac {} {x}\ left [\ dfrac {u} {x}\ direita]\ [6pt]
&=\ dfrac {} {x}\ left [15π\ cos (3π)\ sin (4π y)\ (cos 10π t)\ right]\\ [6pt]
&=−45π ^2\ sin (3π x)\ sin (4π y)\ cos (10π t)\ end {align*}\]
\ [\ begin {align*} u_ {yy} (x, y, t) &=\ dfrac {} {y}\ left [\ dfrac {u} {y}\ direita]\ [6pt]
&=\ dfrac {} {y}\ left [5\ sin (3π) (4π\ cos (4π))\ cos (4π))\ cos (4π))\ cos (4π))\ cos (4π))\ cos (10π t)\ direita]\\ [6pt]
&=\ dfrac {} {y}\ left [20π\ sin (3π x)\ cos (4π y)\ cos (10π t)\ direita]\\ [6pt]
&=−80π ^2\ sin (3π x)\ sin (4π y)\ cos ( 10 (t). \ end {align*}\ nonumber\]
Em seguida, substituímos cada um deles no lado direito da Equação\ ref {Ex7Eq2} e simplificamos:
\ [\ begin {align*} 4 (u_ {xx} +u_ {yy}) &=4 (−45π ^2\ sin (3π x)\ sin (4π y)\ cos (10π t) +−80π ^2\ sin (3π x)\ sin (4π y)\ cos (10π t))\\ [6pt]
&=4 (−125π ^ 2\ sin (3π)\ sin (4π y)\ cos (10π t))\\ [6pt]
&=−500π ^2\ sin (3π x)\ sin (4π y)\ cos (10π t)\\ [6pt]
&=u_ {tt}. \ end {align*}\]
Isso verifica a solução.
Verifique se
\[u(x,y,t)=2\sin \left(\dfrac{x}{3} \right)\sin\left(\dfrac{y}{4} \right)e^{−25t/16} \nonumber \]
é uma solução para a equação do calor
\[u_t=9(u_{xx}+u_{yy}). \nonumber \]
- Dica
-
Calcule as derivadas parciais e substitua-as no lado direito.
- Responda
-
TBA
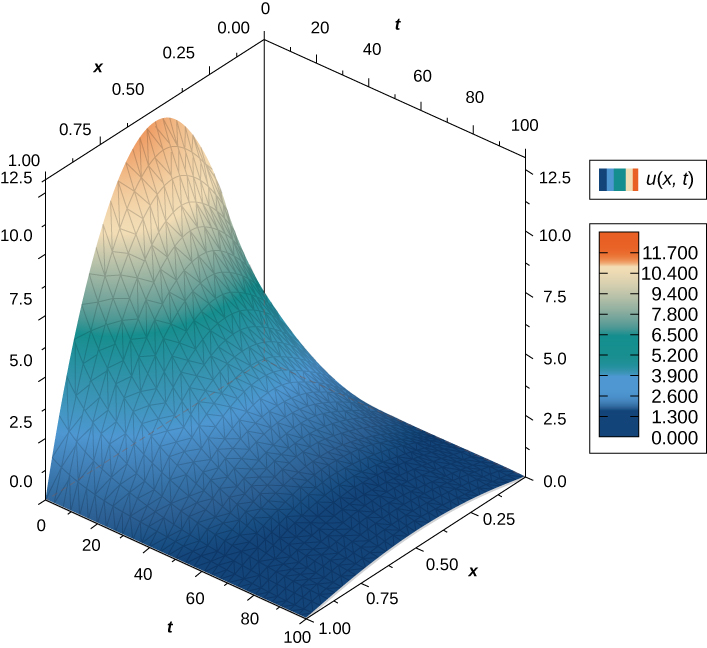
Como a solução para a equação bidimensional do calor é uma função de três variáveis, não é fácil criar uma representação visual da solução. Podemos representar graficamente a solução para valores fixos\(t,\), que equivalem a capturas instantâneas das distribuições de calor em horários fixos. Esses instantâneos mostram como o calor é distribuído em uma superfície bidimensional à medida que o tempo avança. O gráfico da solução anterior no momento\(t=0\) aparece na Figura\(\PageIndex{3}\). Conforme o tempo avança, os extremos se estabilizam, aproximando-se de zero à medida que\(t\) se aproxima do infinito.
Se considerarmos a equação do calor em uma dimensão, é possível representar graficamente a solução ao longo do tempo. A equação do calor em uma dimensão se torna
\[u_t=c^2u_{xx}, \nonumber \]
onde\(c^2\) representa a difusividade térmica do material em questão. Uma solução dessa equação diferencial pode ser escrita na forma
\[u_m(x,t)=e^{−π^2m^2c^2t}\sin(mπx) \nonumber \]
onde\(m\) é qualquer número inteiro positivo. Um gráfico dessa solução usando\(m=1\) aparece na Figura\(\PageIndex{4}\), onde a distribuição inicial da temperatura sobre um fio de comprimento\(1\) é dada pelo\(u(x,0)=\sin πx.\) Aviso de que, com o passar do tempo, o fio esfria. Isso ocorre porque, da esquerda para a direita, a temperatura mais alta (que ocorre no meio do fio) diminui e muda de cor do vermelho para o azul.
Durante o final do século XIX, os cientistas do novo campo da geologia chegaram à conclusão de que a Terra deveria ter “milhões e milhões” de anos. Mais ou menos na mesma época, Charles Darwin publicou seu tratado sobre evolução. A visão de Darwin era que a evolução precisou de muitos milhões de anos para ocorrer, e ele fez uma afirmação ousada de que os campos de giz de Weald, onde fósseis importantes foram encontrados, foram o resultado de\(300\) milhões de anos de erosão.

Naquela época, o eminente físico William Thomson (Lord Kelvin) usou uma importante equação diferencial parcial, conhecida como equação de difusão de calor, para estimar a idade da Terra determinando quanto tempo a Terra levaria para esfriar da rocha derretida até o que tínhamos naquela época. Sua conclusão foi de 20 a 400 milhões de anos, mas provavelmente cerca de 50 milhões de anos. Por muitas décadas, as proclamações desse ícone irrefutável da ciência não agradaram aos geólogos ou a Darwin.
Kelvin fez suposições razoáveis com base no que se sabia em sua época, mas também fez várias suposições que se revelaram erradas. Uma suposição incorreta era que a Terra é sólida e que o resfriamento era, portanto, apenas por condução, justificando assim o uso da equação de difusão. Mas o erro mais grave foi perdoável: a omissão do fato de a Terra conter elementos radioativos que continuamente fornecem calor sob o manto da Terra. A descoberta da radioatividade chegou perto do fim da vida de Kelvin e ele reconheceu que seu cálculo teria que ser modificado.
Kelvin usou o modelo unidimensional simples aplicado apenas à camada externa da Terra, e derivou a idade de gráficos e do gradiente de temperatura mais ou menos conhecido próximo à superfície da Terra. Vamos dar uma olhada em uma versão mais apropriada da equação de difusão em coordenadas radiais, que tem a forma
\[\dfrac{∂T}{∂t}=K\left[\dfrac{∂^2T}{∂^2r}+\dfrac{2}{r}\dfrac{∂T}{∂r}\right] \label{kelvin1} \].
Aqui,\(T(r,t)\) está a temperatura em função de\(r\) (medida a partir do centro da Terra) e o tempo\(t. K\) é a condutividade térmica — para a rocha derretida, neste caso. O método padrão para resolver essa equação diferencial parcial é pela separação de variáveis, onde expressamos a solução como o produto de funções que contêm cada variável separadamente. Nesse caso, escreveríamos a temperatura como
\[T(r,t)=R(r)f(t). \nonumber \]
- Substitua esta forma na Equação\ ref {kelvin1} e, observando que\(f(t)\) é constante em relação à distância\((r)\) e\(R(r)\) é constante em relação ao tempo\((t)\), mostre que\[\dfrac{1}{f}\dfrac{∂f}{∂t}=\dfrac{K}{R}\left[\dfrac{∂^2R}{∂r^2}+\dfrac{2}{r}\dfrac{∂R}{∂r}\right]. \nonumber \]
- Essa equação representa a separação das variáveis que queremos. O lado esquerdo é apenas uma função de\(t\) e o lado direito é apenas uma função de\(r\), e eles devem ser iguais para todos os valores de\(r\)\(t\) e. Portanto, ambos devem ser iguais a uma constante. Vamos chamar isso de constante\(−λ^2\). (A conveniência dessa escolha é vista na substituição.) Então, nós temos\[\dfrac{1}{f}\dfrac{∂f}{∂t}=−λ^2 \text{and} \dfrac{K}{R}\left[\dfrac{∂^2R}{∂r^2}+\dfrac{2}{r}\dfrac{∂R}{∂r}\right]=−λ^2. \nonumber \]
- Agora, podemos verificar por meio de substituição direta para cada equação se as soluções são\(f(t)=Ae^{−λ^2t}\) e\(R(r)=B\left(\dfrac{\sin αr}{r}\right)+C\left(\dfrac{\cos αr}{r}\right)\), onde\(α=λ/\sqrt{K}\). Observe que também\(f(t)=Ae^{+λn^2t}\) é uma solução válida, então poderíamos ter escolhido\(+λ^2\) nossa constante. Você consegue ver por que isso não seria válido para este caso à medida que o tempo aumenta?
- Agora, vamos aplicar as condições de limite.
- A temperatura deve ser finita no centro da Terra,\(r=0\). Qual das duas constantes,\(B\) ou, deve\(C\), portanto, ser zero para se manter\(R\) finita\(r=0\)? (Lembre-se disso\(\sin(αr)/r→α=\) como\(r→0\), mas\(\cos(αr)/r\) se comporta de maneira muito diferente.)
- Kelvin argumentou que quando o magma atinge a superfície da Terra, ele esfria muito rapidamente. Muitas vezes, uma pessoa pode tocar a superfície semanas após o fluxo. Portanto, a superfície atingiu uma temperatura moderada muito cedo e permaneceu quase constante à temperatura da superfície\(T_s\). Para simplificar, vamos definir\(T=0\) em\(r=R_E\) e encontrar α de forma que essa seja a temperatura lá para sempre\(t\). (Kelvin considerou que o valor era\(300K≈80°F\). Podemos adicionar essa\(300K\) constante à nossa solução posteriormente.) Para que isso seja verdade, o argumento seno deve ser zero em\(r=R_E\). Observe que α tem uma série infinita de valores que satisfazem essa condição. Cada valor de\(α\) representa uma solução válida (cada uma com seu próprio valor para\(A\)). A solução total ou geral é a soma de todas essas soluções.
- Em,\(t=0,\) assumimos que toda a Terra estava em uma temperatura inicial quente\(T_0\) (Kelvin considerou que isso era cerca de)\(7000K\). A aplicação dessa condição de contorno envolve a aplicação mais avançada dos coeficientes de Fourier. Conforme observado na parte b. cada valor de\(α_n\) representa uma solução válida, e a solução geral é a soma de todas essas soluções. Isso resulta em uma solução em série:\[T(r,t)=\left(\dfrac{T_0R_E}{π}\right)\sum_n\dfrac{(−1)^{n−1}}{n}e^{−λn^2t}\dfrac{\sin(α_nr)}{r} \nonumber \] onde\(\; α_n=nπ/R_E\).
Observe como os valores de\(α_n\) vêm da condição de contorno aplicada na parte b. O termo\(\dfrac{−1^{n−1}}{n}\) é a constante\(A_n\) para cada termo na série, determinada pela aplicação do método de Fourier. Vamos\(β=\dfrac{π}{R_E}\) examinar os primeiros termos dessa solução mostrada aqui e observar como\(λ^2\) no exponencial faz com que os termos mais altos diminuam rapidamente com o passar do tempo:
\[T(r,t)=\dfrac{T_0R_E}{πr}\left(e^{−Kβ^2t}(\sinβr)−\dfrac{1}{2}e^{−4Kβ^2t}(\sin2βr)+\dfrac{1}{3}e^{−9Kβ^2t}(\sin3βr)−\dfrac{1}{4}e^{−16Kβ^2t}(\sin4βr)+\dfrac{1}{5}e^{−25Kβ^2t}(\sin5βr)...\right). \nonumber \]
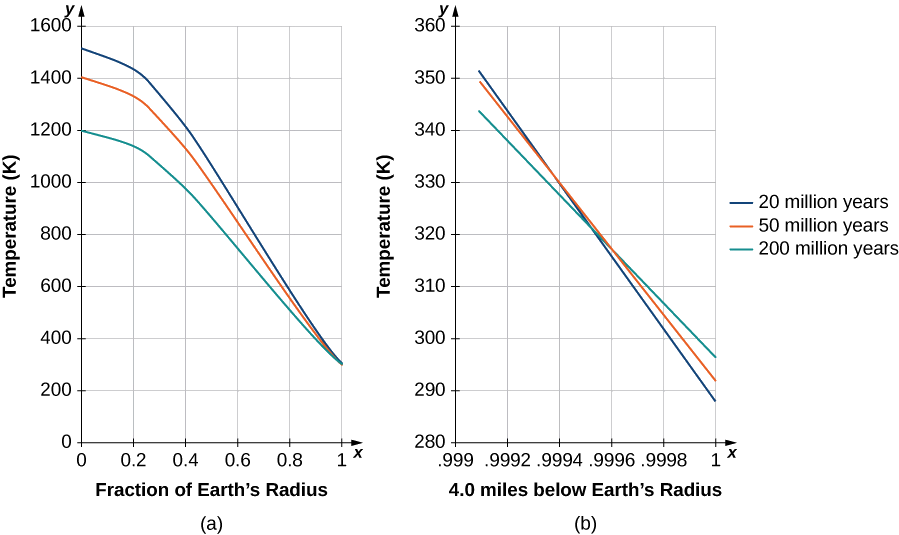
Quase no momento,\(t=0,\) muitos termos da solução são necessários para garantir a precisão. Inserindo valores para a condutividade\(K\) e\(β=π/R_E\) para um tempo que se aproxima de apenas milhares de anos, apenas os primeiros termos dão uma contribuição significativa. Kelvin só precisou observar a solução próxima à superfície da Terra (Figura\(\PageIndex{6}\)) e, depois de muito tempo, determinar em que momento melhor produziu o gradiente de temperatura estimado conhecido durante sua época (\(1°F\)aumento por\(50ft\)). Ele simplesmente escolheu um intervalo de tempos com um gradiente próximo a esse valor. Na Figura\(\PageIndex{6}\), as soluções são plotadas e dimensionadas, com a temperatura\(300−K\) da superfície adicionada. Observe que o centro da Terra seria relativamente frio. Na época, pensava-se que a Terra deveria ser sólida.
Epílogo
Em 20 de maio de 1904, o físico Ernest Rutherford falou na Royal Institution para anunciar um cálculo revisado que incluía a contribuição da radioatividade como fonte de calor da Terra. Nas próprias palavras de Rutherford:
“Entrei na sala, que estava meio escura, e atualmente vi Lord Kelvin na platéia e percebi que estava em apuros na última parte do meu discurso sobre a era da Terra, onde minhas opiniões conflitavam com as dele. Para meu alívio, Kelvin adormeceu profundamente, mas quando chego ao ponto importante, vi o velho pássaro sentar, abrir um olho e pestanejar com um olhar maldoso para mim.
Então, uma inspiração repentina veio, e eu disse que Lord Kelvin havia limitado a idade da Terra, desde que nenhuma nova fonte [de calor] fosse descoberta. Essa declaração profética se referia ao que estamos considerando agora esta noite, rádio! Eis! O velho garoto sorriu para mim.”
Rutherford calculou uma idade para a Terra de cerca de 500 milhões de anos. O valor aceito hoje da idade da Terra é de cerca de 4,6 bilhões de anos.
Conceitos-chave
- Uma derivada parcial é uma derivada que envolve uma função de mais de uma variável independente.
- Para calcular uma derivada parcial em relação a uma determinada variável, trate todas as outras variáveis como constantes e use as regras de diferenciação usuais.
- Derivadas parciais de ordem superior podem ser calculadas da mesma forma que derivadas de ordem superior.
Equações-chave
Derivada parcial de em\(f\) relação a\(x\)\[\dfrac{∂f}{∂x}=\displaystyle{\lim_{h→0}\dfrac{f(x+h,y)−f(x,y)}{h}} \nonumber \]
Derivada parcial de em\(f\) relação a\(y\)\[\dfrac{∂f}{∂y}=\displaystyle{\lim_{k→0}\dfrac{f(x,y+k)−f(x,y)}{k}} \nonumber \]
Glossário
- derivadas parciais de ordem superior
- derivadas parciais de segunda ordem ou superiores, independentemente de serem derivadas parciais mistas
- derivados parciais mistos
- derivadas parciais de segunda ordem ou superiores, nas quais pelo menos duas das diferenciações são em relação a variáveis diferentes
- derivada parcial
- uma derivada de uma função de mais de uma variável independente na qual todas as variáveis, exceto uma, são mantidas constantes
- equação diferencial parcial
- uma equação que envolve uma função desconhecida de mais de uma variável independente e uma ou mais de suas derivadas parciais


