14.2E: Exercícios para a Seção 14.2

Last updated
Save as PDF

Page ID: 188021

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

1) Use as leis de limite para funções de duas variáveis para avaliar cada limite abaixo, considerando que$\displaystyle \lim_{(x,y)→(a,b)}f(x,y) = 5$$\displaystyle \lim_{(x,y)→(a,b)}g(x,y) = 2$ e.

$\displaystyle \lim_{(x,y)→(a,b)}\left[f(x,y) + g(x,y)\right]$
$\displaystyle \lim_{(x,y)→(a,b)}\left[f(x,y) g(x,y)\right]$
$\displaystyle \lim_{(x,y)→(a,b)}\left[ \dfrac{7f(x,y)}{g(x,y)}\right]$
$\displaystyle \lim_{(x,y)→(a,b)}\left[\dfrac{2f(x,y) - 4g(x,y)}{f(x,y) - g(x,y)}\right]$

Responda

$\displaystyle \lim_{(x,y)→(a,b)}\left[f(x,y) + g(x,y)\right] = \displaystyle \lim_{(x,y)→(a,b)}f(x,y) + \displaystyle \lim_{(x,y)→(a,b)}g(x,y)= 5 + 2 = 7$
$\displaystyle \lim_{(x,y)→(a,b)}\left[f(x,y) g(x,y)\right] =\left(\displaystyle \lim_{(x,y)→(a,b)}f(x,y)\right) \left(\displaystyle \lim_{(x,y)→(a,b)}g(x,y)\right) = 5(2) = 10$
$\displaystyle \lim_{(x,y)→(a,b)}\left[ \dfrac{7f(x,y)}{g(x,y)}\right] = \frac{7\left(\displaystyle \lim_{(x,y)→(a,b)}f(x,y)\right)}{\displaystyle \lim_{(x,y)→(a,b)}g(x,y)}=\frac{7(5)}{2} = 17.5$
$\displaystyle \lim_{(x,y)→(a,b)}\left[\dfrac{2f(x,y) - 4g(x,y)}{f(x,y) - g(x,y)}\right] = \frac{2\left(\displaystyle \lim_{(x,y)→(a,b)}f(x,y)\right) - 4 \left(\displaystyle \lim_{(x,y)→(a,b)}g(x,y)\right)}{\displaystyle \lim_{(x,y)→(a,b)}f(x,y) - \displaystyle \lim_{(x,y)→(a,b)}g(x,y)}= \frac{2(5) - 4(2)}{5 - 2} = \frac{2}{3}$

Nos exercícios 2 a 4, determine o limite da função.

2)$\displaystyle \lim_{(x,y)→(1,2)}x$

3)$\displaystyle \lim_{(x,y)→(1,2)}\frac{5x^2y}{x^2+y^2}$

Responda: $\displaystyle \lim_{(x,y)→(1,2)}\frac{5x^2y}{x^2+y^2} = 2$

4) Mostre que o limite$\displaystyle \lim_{(x,y)→(0,0)}\frac{5x^2y}{x^2+y^2}$ existe e é o mesmo ao longo dos caminhos:$y$ -eixo e$x$ -eixo, e ao longo$ y=x$.

Nos exercícios 5 a 19, avalie os limites nos valores indicados de$x$$y$ e. Se o limite não existir, indique isso e explique por que o limite não existe.

5)$\displaystyle \lim_{(x,y)→(0,0)}\frac{4x^2+10y^2+4}{4x^2−10y^2+6}$

Responda: $\displaystyle \lim_{(x,y)→(0,0)}\frac{4x^2+10y^2+4}{4x^2−10y^2+6} = \frac{2}{3} $

6)$\displaystyle \lim_{(x,y)→(11,13)}\sqrt{\frac{1}{xy}}$

7)$\displaystyle \lim_{(x,y)→(0,1)}\frac{y^2\sin x}{x}$

Responda: $\displaystyle \lim_{(x,y)→(0,1)}\frac{y^2\sin x}{x} = 1$

8)$\displaystyle \lim_{(x,y)→(0,0)}\sin(\frac{x^8+y^7}{x−y+10})$

9)$\displaystyle \lim_{(x,y)→(π/4,1)}\frac{y\tan x}{y+1}$

Responda: $\displaystyle \lim_{(x,y)→(π/4,1)}\frac{y\tan x}{y+1}=\frac{1}{2}$

10)$\displaystyle \lim_{(x,y)→(0,π/4)}\frac{\sec x+2}{3x−\tan y}$

11)$\displaystyle \lim_{(x,y)→(2,5)}(\frac{1}{x}−\frac{5}{y})$

Responda: $\displaystyle \lim_{(x,y)→(2,5)}(\frac{1}{x}−\frac{5}{y}) = −\frac{1}{2}$

12)$\displaystyle \lim_{(x,y)→(4,4)}x\ln y$

13)$\displaystyle \lim_{(x,y)→(4,4)}e^{−x^2−y^2}$

Responda: $\displaystyle \lim_{(x,y)→(4,4)}e^{−x^2−y^2} = e^{−32}$

14)$\displaystyle \lim_{(x,y)→(0,0)}\sqrt{9−x^2−y^2}$

15)$\displaystyle \lim_{(x,y)→(1,2)}(x^2y^3−x^3y^2+3x+2y)$

Responda: $\displaystyle \lim_{(x,y)→(1,2)}(x^2y^3−x^3y^2+3x+2y) = 11$

16)$\displaystyle \lim_{(x,y)→(π,π)}x\sin(\frac{x+y}{4})$

17)$\displaystyle \lim_{(x,y)→(0,0)}\frac{xy+1}{x^2+y^2+1}$

Responda: $\displaystyle \lim_{(x,y)→(0,0)}\frac{xy+1}{x^2+y^2+1} = 1$

18)$\displaystyle \lim_{(x,y)→(0,0)}\frac{x^2+y^2}{\sqrt{x^2+y^2+1}−1}$

19)$\displaystyle \lim_{(x,y)→(0,0)}\ln(x^2+y^2)$

Responda: O limite não existe porque quando$x$ e$y$ ambas se aproximam de zero, a função se aproxima$ \ln 0$, o que é indefinido (se aproxima do infinito negativo).

Nos exercícios 20 a 21, complete a declaração.

20) Um ponto$ (x_0,y_0)$ em uma região plana$ R$ é um ponto interior de$R$ se _________________.

21) Um ponto$ (x_0,y_0)$ em uma região plana$R$ é chamado de ponto limite de$R$ se ___________.

Responda: Cada disco aberto centrado em$ (x_0,y_0)$ contém pontos internos$ R$ e externos$ R$.

Nos exercícios 22 a 25, use técnicas algébricas para avaliar o limite.

22)$\displaystyle \lim_{(x,y)→(2,1)}\frac{x−y−1}{\sqrt{x−y}−1}$

23)$\displaystyle \lim_{(x,y)→(0,0)}\frac{x^4−4y^4}{x^2+2y^2}$

Responda: $\displaystyle \lim_{(x,y)→(0,0)}\frac{x^4−4y^4}{x^2+2y^2} = 0$

24)$\displaystyle \lim_{(x,y)→(0,0)}\frac{x^3−y^3}{x−y}$

25)$\displaystyle \lim_{(x,y)→(0,0)}\frac{x^2−xy}{\sqrt{x}−\sqrt{y}}$

Responda: $\displaystyle \lim_{(x,y)→(0,0)}\frac{x^2−xy}{\sqrt{x}−\sqrt{y}} = 0$

Nos exercícios 26 a 27, avalie os limites das funções de três variáveis.

26)$\displaystyle \lim_{(x,y,z)→(1,2,3)}\frac{xz^2−y^2z}{xyz−1}$

27)$\displaystyle \lim_{(x,y,z)→(0,0,0)}\frac{x^2−y^2−z^2}{x^2+y^2−z^2}$

Responda: O limite não existe.

Nos exercícios 28 a 31, avalie o limite da função determinando o valor que a função se aproxima ao longo dos caminhos indicados. Se o limite não existir, explique por que não.

28)$\displaystyle \lim_{(x,y)→(0,0)}\frac{xy+y^3}{x^2+y^2}$

a. Ao longo do$x$ eixo -$ (y=0)$

b. Ao longo do$y$ eixo -$ (x=0)$

c. Ao longo do caminho$y=2x$

29) Avalie$\displaystyle \lim_{(x,y)→(0,0)}\frac{xy+y^3}{x^2+y^2}$ usando os resultados do problema anterior.

Responda: O limite não existe. A função aborda dois valores diferentes ao longo de caminhos diferentes.

30)$\displaystyle \lim_{(x,y)→(0,0)}\frac{x^2y}{x^4+y^2}$

a. Ao longo do$x$ eixo -$ (y=0)$

b. Ao longo do$y$ eixo -$ (x=0)$

c. Ao longo do caminho$y=x^2$

31) Avalie$\displaystyle \lim_{(x,y)→(0,0)}\frac{x^2y}{x^4+y^2}$ usando os resultados do problema anterior.

Responda: O limite não existe porque a função se aproxima de dois valores diferentes ao longo dos caminhos.

Nos exercícios 32 a 35, discuta a continuidade de cada função. Encontre a maior região no$xy$ plano -na qual cada função é contínua.

32)$ f(x,y)=\sin(xy)$

33)$ f(x,y)=\ln(x+y)$

Responda: A função$ f$ é contínua na região$ y>−x.$

34)$ f(x,y)=e^{3xy}$

35)$ f(x,y)=\dfrac{1}{xy}$

Responda: A função$f$ é contínua em todos os pontos do$xy$ plano -, exceto nos pontos nos$y$ eixos$x$ - e -.

Nos exercícios 36 a 38, determine a região na qual a função é contínua. Explique sua resposta.

36)$ f(x,y)=\dfrac{x^2y}{x^2+y^2}$

37)$ f(x,y)=$$ \begin{cases}\dfrac{x^2y}{x^2+y^2} & if(x,y)≠(0,0)\\0 & if(x,y)=(0,0)\end{cases}$

Dica:: Mostre que a função aborda valores diferentes ao longo de dois caminhos diferentes.

Responda: A função é contínua em,$ (0,0)$ pois o limite da função at$ (0,0)$ é$ 0$, o mesmo valor de$ f(0,0).$

38)$ f(x,y)=\dfrac{\sin(x^2+y^2)}{x^2+y^2}$

39) Determine se$ g(x,y)=\dfrac{x^2−y^2}{x^2+y^2}$ é contínuo em$ (0,0)$.

Responda: A função é descontínua em$ (0,0).$ O limite$ (0,0)$ em não existe e$ g(0,0)$ não existe.

40) Crie um gráfico usando um software gráfico para determinar onde o limite não existe. Determine a região do plano coordenado em que$ f(x,y)=\dfrac{1}{x^2−y}$ é contínuo.

41) Determine a região do$xy$ plano -na qual a função composta$ g(x,y)=\arctan(\frac{xy^2}{x+y})$ é contínua. Use a tecnologia para apoiar sua conclusão.

Responda: Como a função$ \arctan x$ é contínua, o over$ (−∞,∞), g(x,y)=\arctan(\frac{xy^2}{x+y})$ é contínuo, onde$ z=\dfrac{xy^2}{x+y}$ é contínuo. A função interna$ z$ é contínua em todos os pontos do$xy$ plano -, exceto onde$ y=−x.$ Assim,$ g(x,y)=\arctan(\frac{xy^2}{x+y})$ é contínua em todos os pontos do plano coordenado, exceto nos pontos em que$ y=−x.$

42) Determine a região do$xy$ plano -em que$ f(x,y)=\ln(x^2+y^2−1)$ é contínuo. Use a tecnologia para apoiar sua conclusão. (Dica: escolha a faixa de valores para$ x$ e$ y$ com cuidado!)

43) Em quais pontos do espaço é$ g(x,y,z)=x^2+y^2−2z^2$ contínuo?

Responda: Todos os pontos$ P(x,y,z)$ no espaço

44) Em quais pontos do espaço é$ g(x,y,z)=\dfrac{1}{x^2+z^2−1}$ contínuo?

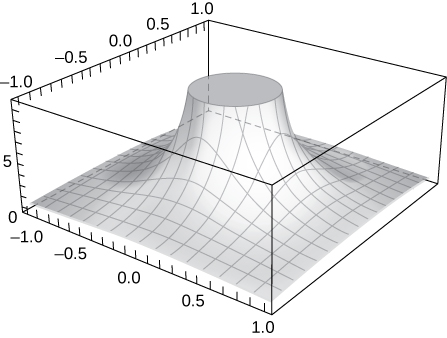
45) Mostre que$\displaystyle \lim_{(x,y)→(0,0)}\frac{1}{x^2+y^2}$ não existe em$ (0,0)$ traçando o gráfico da função.

Responda

O gráfico aumenta sem limite à medida que$ x$$ y$ ambos se aproximam de zero.

$O gráfico de uma superfície em que a coordenada z aumenta sem limite à medida que o ponto de entrada (x, y) se aproxima da origem.$

46) [T] Avalie$\displaystyle \lim_{(x,y)→(0,0)}\frac{−xy^2}{x^2+y^4}$ traçando a função usando um CAS. Determine analiticamente o limite ao longo do caminho$ x=y^2.$

47) [T]

a. Use um CAS para desenhar um mapa de contorno de$ z=\sqrt{9−x^2−y^2}$.

b. Qual é o nome da forma geométrica das curvas de nível?

c. Forneça a equação geral das curvas de nível.

d. Qual é o valor máximo de$ z$?

e. Qual é o domínio da função?

f. Qual é o alcance da função?

Responda

uma.

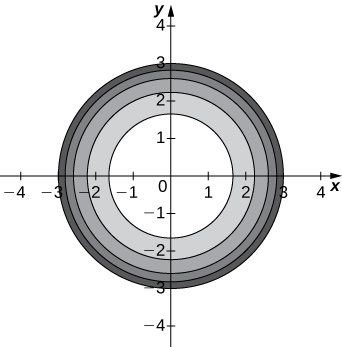
$Mapa de contorno da função z=sqrt {9−x^2−y^2}$

b. As curvas de nível são círculos centrados em$ (0,0)$ com raio$ 9−c$.
c.$ x^2+y^2=9−c$
d.$ z=3$
e.$ \{(x,y)∈R^2∣x^2+y^2≤9\}$
f.$ \{z|0≤z≤3\}$

48) Verdadeiro ou falso: Se avaliarmos$\displaystyle \lim_{(x,y)→(0,0)}f(x)$ ao longo de vários caminhos e cada vez que o limite for$ 1$, podemos concluir que$\displaystyle \lim_{(x,y)→(0,0)}f(x)=1.$

49) Use coordenadas polares para encontrar$\displaystyle \lim_{(x,y)→(0,0)}\frac{\sin\sqrt{x^2+y^2}}{\sqrt{x^2+y^2}}.$ Você também pode encontrar o limite usando a regra de L'Hôpital.

Responda: $\displaystyle \lim_{(x,y)→(0,0)}\frac{\sin\sqrt{x^2+y^2}}{\sqrt{x^2+y^2}} = 1$

50) Use coordenadas polares para encontrar$\displaystyle \lim_{(x,y)→(0,0)}\cos(x^2+y^2).$

51) Discuta a continuidade de$ f(g(x,y))$ onde$ f(t)=1/t$ e$ g(x,y)=2x−5y.$

Responda: $ f(g(x,y))$é contínuo em todos os pontos$ (x,y)$ que não estão na linha$ 2x−5y=0.$

52) Dado o$ f(x,y)=x^2−4y,$ achado$\displaystyle \lim_{h→0}\frac{f(x+h,y)−f(x,y)}{h}.$

53) Dado o$ f(x,y)=x^2−4y,$ achado$\displaystyle \lim_{h→0}\frac{f(1+h,y)−f(1,y)}{h}$.

Responda: $ \displaystyle \lim_{h→0}\frac{f(1+h,y)−f(1,y)}{h} = 2$

Colaboradores

Template:ContribOpenStaxCalc
Paul Seeburger (Monroe Community College) created problem 1.