Skip to main content
Global

14.6E: Exercícios para a Seção 14.6

  1. Last updated
  2. Save as PDF
  • Page ID
    187927

    • Edwin “Jed” Herman & Gilbert Strang
    • OpenStax
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    No exercício 1, encontre a derivada direcional usando somente a definição de limite.

    1) a.\( f(x,y)=5−2x^2−\frac{1}{2}y^2\) em um ponto\( P(3,4)\) na direção de\(\vecs u=(\cos\frac{π}{4})\,\hat{\mathbf i}+(\sin\frac{π}{4})\,\hat{\mathbf j}\)

    Resposta
    uma.\( D_{\vecs u}f(3,4) =−8\sqrt{2}\)

    1) b.\( f(x,y)=y^2\cos(2x)\) em um ponto\( P(\frac{π}{3},2)\) na direção de\(\vecs u=(\cos\frac{π}{4})\,\hat{\mathbf i}+(\sin\frac{π}{4})\,\hat{\mathbf j}\)

    Resposta
    b.\( D_{\vecs u}f(\frac{π}{3},2) =−2\sqrt{6}-\sqrt{2}\)

    2) Encontre a derivada direcional de\( f(x,y)=y^2\sin(2x)\) no ponto\( P(\frac{π}{4},2)\) na direção de\(\vecs u=5\,\hat{\mathbf i}+12\,\hat{\mathbf j}\).

    Nos exercícios 3 a 13, encontre a derivada direcional da função na direção de\(\vecs v\) como uma função de\(x\)\(y\) e. Lembre-se de que primeiro você precisa encontrar um vetor unitário na direção do vetor de direção. Em seguida, encontre o valor da derivada direcional no ponto\(P\).

    3)\( f(x,y)=xy, \quad P(-2,0), \quad \vecs v=\frac{1}{2}\,\hat{\mathbf i}+\frac{\sqrt{3}}{2}\,\hat{\mathbf j}\)

    Resposta
    \(D_{\vecs v}f(x, y) = \frac{1}{2}y + \frac{\sqrt{3}}{2}x \)
    \(D_{\vecs v}f(-2, 0) = −\sqrt{3}\)

    4)\( h(x,y)=e^x\sin y,\quad P(1,\frac{π}{2}),\quad \vecs v=−\,\hat{\mathbf i}\)

    5)\( f(x,y)=x^2y,\quad P(−5,5),\quad \vecs v=3\,\hat{\mathbf i}−4\,\hat{\mathbf j}\)

    Resposta
    \(D_{\vecs v}f(x, y) = \frac{6}{5}xy - \frac{4}{5}x^2 \)
    \(D_{\vecs v}f(-5,5)= -50\)

    6)\( f(x,y)=xy,\quad P(1,1), \quad \vecs u=⟨\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}⟩\)

    7)\( f(x,y)=x^2−y^2, \quad P(1,0), \quad \vecs u=⟨\frac{\sqrt{3}}{2},\frac{1}{2}⟩\)

    Resposta
    \(D_{\vecs u}f(x, y) = x\sqrt{3} - y \)
    \(D_{\vecs u}f(1,0)= \sqrt{3}\)

    8)\( f(x,y)=3x+4y+7,\quad P(0,\frac{π}{2}), \quad \vecs u=⟨\frac{3}{5},\frac{4}{5}⟩\)

    9)\( f(x,y)=e^x\cos y,\quad P=(0,\frac{π}{2}), \quad \vecs u=⟨0,5⟩\)

    Resposta
    \(D_{\vecs u}f(x, y) = -e^x\sin y \)
    \(D_{\vecs u}f(0, \frac{π}{2})= −1\)

    10)\( f(x,y)=y^{10},\quad \vecs u=⟨0,−3⟩,\quad P=(1,−1)\)

    11)\( f(x,y)=\ln(x^2+y^2),\quad \vecs u=⟨2,-5⟩,\quad P(1,2)\)

    Resposta
    \(D_{\vecs u}f(x, y) = \frac{\sqrt{29}}{29}\left( \dfrac{4x-10y}{x^2 +y^2}\right) \)
    \(D_{\vecs u}f(1,2)= -\frac{16\sqrt{29}}{145}\)

    12)\( h(x,y,z)=xyz, \quad P(2,1,1),\quad \vecs v=2\,\hat{\mathbf i}+\,\hat{\mathbf j}−\,\hat{\mathbf k}\)

    Resposta
    \( D_{\vecs v}h(x, y, z) = \frac{\sqrt{6}}{6}(2yz + xz - xy)\)
    \( D_{\vecs v}h(2,1,1) = \frac{2}{\sqrt{6}} = \frac{\sqrt{6}}{3}\)

    13)\( f(x,y,z)=y^2+xz,\quad P(1,2,2),\quad \vecs v=⟨2,−1,2⟩\)

    Responda
    \( D_{\vecs v}f(x, y, z) = \frac{2}{3}(z - y + x)\)
    \(D_{\vecs v}f(1,2,2)= \frac{2}{3}\)

    Nos exercícios 14 a 19, encontre a derivada direcional da função na direção do vetor unitário\(\vecs u=\cos θ \,\hat{\mathbf i}+\sin θ \,\hat{\mathbf j}.\)

    14)\( f(x,y)=x^2+2y^2,\quad θ=\frac{π}{6}\)

    15)\( f(x,y)=\dfrac{y}{x+2y},\quad θ=−\frac{π}{4}\)

    Responda
    \( D_{\vecs u}f(x,y) = \dfrac{−\sqrt{2}(x+y)}{2(x+2y)^2}\)

    16)\( f(x,y)=\cos(3x+y),\quad θ=\frac{π}{4}\)

    17)\( w(x,y)=ye^x,\quad θ=\frac{π}{3}\)

    Responda
    \( D_{\vecs u}f(x,y) = \dfrac{e^x(y+\sqrt{3})}{2}\)

    18)\( f(x,y)=x\arctan(y),\quad θ=\frac{π}{2}\)

    19)\( f(x,y)=\ln(x+2y),\quad θ=\frac{π}{3}\)

    Responda
    \( D_{\vecs u}f(x,y) = \dfrac{1+2\sqrt{3}}{2(x+2y)}\)

    Nos exercícios 20 a 23, encontre o gradiente\(\vecs \nabla f\).

    20) Encontre o gradiente de\( f(x, y) = 3x^2 + y^3 - 3x + y\). Em seguida, encontre seu valor no ponto\(P(2,3)\).

    21) Encontre o gradiente de\( f(x,y)=\dfrac{14−x^2−y^2}{3}\). Em seguida, encontre o gradiente no ponto\( P(1,2)\).

    Responda
    \( \vecs \nabla f(x, y) = -\frac{2}{3}x\,\hat{\mathbf i} -\frac{2}{3}y\,\hat{\mathbf j}\)
    \( \vecs \nabla f(1,2) = -\frac{2}{3}\,\hat{\mathbf i} -\frac{4}{3}\,\hat{\mathbf j}\)

    22) Encontre o gradiente de\( f(x,y)=\ln(4x^3 - 3y)\). Em seguida, encontre o gradiente no ponto\( P(1,1)\).

    23) Encontre o gradiente de\( f(x,y,z)=xy+yz+xz\). Em seguida, encontre o gradiente no ponto\( P(1,2,3).\)

    Responda
    \( \vecs \nabla f(x, y, z) = ⟨y+z, x+z, y + x⟩\)
    \( \vecs \nabla f(1,2,3) = ⟨5,4,3⟩\)

    Nos exercícios 24 a 25, encontre a derivada direcional da função no ponto\( P\) na direção de\( Q\).

    24)\( f(x,y)=x^2+3y^2,\quad P(1,1),\quad Q(4,5)\)

    25)\( f(x,y,z)=\dfrac{y}{x+z},\quad P(2,1,−1),\quad Q(−1,2,0)\)

    Responda
    \( D_{\vecd{PQ}}f(x,y) = \frac{3}{\sqrt{11}}\)

    26) Encontre a derivada direcional de\( f(x,y,z))\) em\( P\) e na direção de\( \vecs u: \quad f(x,y,z)=\ln(x^2+2y^2+3z^2),\quad P(2,1,4),\quad \vecs u=\frac{−3}{13}\,\hat{\mathbf i}−\frac{4}{13}\,\hat{\mathbf j}−\frac{12}{13}\,\hat{\mathbf k}\).

    Nos exercícios 27 a 29, encontre a derivada direcional da função\( P\) na direção de\(\vecs u\).

    27)\( f(x,y)=\ln(5x+4y),\quad P(3,9),\quad \vecs u=6\,\hat{\mathbf i}+8\,\hat{\mathbf j}\)

    Responda
    \( D_{\vecs u}f(3,9) = \frac{31}{255}\)

    28)\( f(x,y)=−7x+2y,\quad P(2,−4),\quad \vecs u=4\,\hat{\mathbf i}−3\,\hat{\mathbf j}\)

    29)\( f(x,y,z)=4x^5y^2z^3,\quad P(2,−1,1),\quad \vecs u=\frac{1}{3}\,\hat{\mathbf i}+\frac{2}{3}\,\hat{\mathbf j}−\frac{2}{3}\,\hat{\mathbf k}\)

    Responda
    \( D_{\vecs u}f(2,-1,1) = -320\)

    30) [T] Use a tecnologia para esboçar a curva de nível\( f(x,y)=4x−2y+3\) que passa\( P(1,2)\) e desenhar o vetor de gradiente em\( P\).

    31) [T] Use a tecnologia para esboçar a curva de nível\( f(x,y)=x^2+4y^2\) que passa\( P(−2,0)\) e desenhar o vetor de gradiente em\(P\).

    Responda
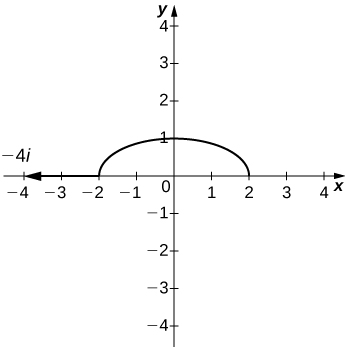
    Esboço da curva de nível de f (x, y) =x^2+4y^2 que passa por P (−2,0) e mostra o vetor de gradiente em P.

    Nos exercícios 32 a 35, encontre o vetor de gradiente no ponto indicado.

    32)\( f(x,y)=xy^2−yx^2,\quad P(−1,1)\)

    33)\( f(x,y)=xe^y−\ln(x),\quad P(−3,0)\)

    Responda
    \(\vecs \nabla f(-3,0) = \frac{4}{3}\,\hat{\mathbf i}−3\,\hat{\mathbf j}\)

    34)\( f(x,y,z)=xy−\ln(z),\quad P(2,−2,2)\)

    35)\( f(x,y,z)=x\sqrt{y^2+z^2}, \quad P(−2,−1,−1)\)

    Responda
    \(\vecs \nabla f(-2,-1,-1) = \sqrt{2}\,\hat{\mathbf i}+\sqrt{2}\,\hat{\mathbf j}+\sqrt{2}\,\hat{\mathbf k}\)

    Nos exercícios 36 a 40, encontre a derivada direcional indicada da função.

    36)\( f(x,y)=x^2+xy+y^2\) em um ponto\( (−5,−4)\) na direção em que a função aumenta mais rapidamente.

    37)\( f(x,y)=e^{xy}\) em um ponto\( (6,7)\) na direção em que a função aumenta mais rapidamente.

    Responda
    \( 1.6(10^{19})\)

    38)\( f(x,y)=\arctan\left(\dfrac{y}{x}\right)\) em um ponto\( (−9,9)\) na direção em que a função aumenta mais rapidamente.

    39)\( f(x,y,z)=\ln(xy+yz+zx)\) em um ponto\( (−9,−18,−27)\) na direção em que a função aumenta mais rapidamente.

    Responda
    \( \frac{5\sqrt{2}}{99}\)

    40)\( f(x,y,z)=\dfrac{x}{y}+\dfrac{y}{z}+\dfrac{z}{x}\) em um ponto\( (5,−5,5)\) na direção em que a função aumenta mais rapidamente.

    Nos exercícios 41 a 43, determine a taxa máxima de variação de\( f\) no ponto determinado e na direção em que ela ocorre.

    41)\( f(x,y)=xe^{−y}, \quad (-2,0)\)

    Responda
    \(\text{max}\big\{D_{\vecs u} f(-2,0)\big\} = \sqrt{5}, \quad ⟨1,2⟩\)
    Solução:
    \( \vecs \nabla f(x, y) = e^{-y} \mathbf{\hat i} - xe^{-y} \mathbf{\hat j}.\)Portanto,\(\text{max}\big\{D_{\vecs u} f(-2,0)\big\} = \|\vecs \nabla f(-2, 0)\| = \sqrt{5}.\)
    a direção em que isso ocorre será apenas a direção do vetor de gradiente:\(\vecs \nabla f(-2, 0) = ⟨1,2⟩.\)

    42)\( f(x,y)=\sqrt{x^2+2y}, \quad (4,10)\)

    43)\( f(x,y)=\cos(3x+2y),\quad (\frac{π}{6},−\frac{π}{8})\)

    Responda
    \( \text{max}\big\{D_{\vecs u} f\left(\frac{π}{6},−\frac{π}{8}\right)\big\} = \sqrt{\frac{13}{2}} = \frac{\sqrt{26}}{2},\quad ⟨−3,−2⟩\)

    Nos exercícios 44 a 47, encontre equações de

    a. o plano tangente e

    b. a linha normal até a superfície dada no ponto dado.

    44) A curva de nível\( f(x,y,z)=12\) para\( f(x,y,z)=4x^2−2y^2+z^2\) no ponto\( (2,2,2).\)

    45)\( f(x,y,z)=xy+yz+xz=3\) no ponto\( (1,1,1)\)

    Responda
    a. equação do plano tangente:\(x+y+z=3\),
    b. equações de linha normal:\(x−1=y−1=z−1\)

    46)\( f(x,y,z)=xyz=6\) no ponto\( (1,2,3)\)

    47)\( f(x,y,z)=xe^y\cos z−z=1\) no ponto\( (1,0,0)\)

    Responda
    a. equação do plano tangente:\(x+y−z=1\),
    b. equações de linha normal:\(x−1=y=−z\)

    Nos exercícios 48 a 51, resolva o problema indicado.

    48) A temperatura\( T\) em uma esfera de metal é inversamente proporcional à distância do centro da esfera (a origem:\( (0,0,0))\). A temperatura no ponto\( (1,2,2)\) é\( 120\) °C.

    a. Encontre a taxa de variação da temperatura no ponto\( (1,2,2)\) na direção do ponto\( (2,1,3).\)

    b. Mostre que, em qualquer ponto da esfera, a direção do maior aumento de temperatura é dada por um vetor que aponta para a origem.

    49) O potencial elétrico (tensão) em uma determinada região do espaço é dado pela função\( V(x,y,z)=5x^2−3xy+xyz.\)

    a. Encontre a taxa de variação da tensão no ponto\( (3,4,5)\) na direção do vetor\( ⟨1,1,−1⟩.\)

    b. Em qual direção a tensão muda mais rapidamente em um ponto\( (3,4,5)\)?

    c. Qual é a taxa máxima de variação da tensão no ponto\( (3,4,5)\)?

    Responda
    a.\(\frac{32}{\sqrt{3}}\),
    b.\(⟨38,6,12⟩\),
    c.\(2\sqrt{406}\)

    50) Se o potencial elétrico em um ponto\( (x,y)\) no\(xy\) plano -é\( V(x,y)=e^{−2x}\cos(2y)\), então o vetor de intensidade elétrica em\( (x,y)\) é\( E=−\vecs \nabla V(x,y).\)

    a. Encontre o vetor de intensidade elétrica em\( (\frac{π}{4},0).\)

    b. Mostre que, em cada ponto do plano, o potencial elétrico diminui mais rapidamente na direção do vetor\( E.\)

    51) Em duas dimensões, o movimento de um fluido ideal é governado por um potencial de velocidade\( φ\). Os componentes de velocidade do fluido\(u\) na direção\(x\) - e\(v\) na\(y\) direção -são dados por\( ⟨u,v⟩=\vecs \nabla φ\). Encontre os componentes de velocidade associados ao potencial de velocidade\( φ(x,y)=\sin πx\sin 2πy.\)

    Responda
    \( ⟨u,v⟩=⟨π\cos(πx)\sin(2πy),2π\sin(πx)\cos(2πy)⟩\)

    Colaboradores