Skip to main content
Global

16.3E: Mazoezi ya Sehemu ya 16.3

  1. Last updated
  2. Save as PDF
  • Page ID
    178920

    • Edwin “Jed” Herman & Gilbert Strang
    • OpenStax
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    1. Kweli au Uongo? Ikiwa uwanja wa vector\(\vecs F\) ni kihafidhina kwenye eneo la wazi na lililounganishwa\(D\), kisha mstari wa integrals wa\(\vecs F\) ni njia ya kujitegemea\(D\), bila kujali sura ya\(D\).

    Jibu
    Kweli

    2. Kweli au Uongo? Kazi\(\vecs r(t)=\vecs a+t(\vecs b−\vecs a)\), wapi\(0≤t≤1\), parameterizes sehemu ya mstari wa moja kwa moja kutoka\(\vecs a\) kwa\(\vecs b\).

    Jibu
    Kweli

    3. Kweli au Uongo? Vector shamba\(\vecs F(x,y,z)=(y\sin z)\,\mathbf{\hat i}+(x\sin z)\,\mathbf{\hat j}+(xy\cos z)\,\mathbf{\hat k}\) ni kihafidhina.

    Jibu
    Kweli

    4. Kweli au Uongo? Vector shamba\(\vecs F(x,y,z)=y\,\mathbf{\hat i}+(x+z)\,\mathbf{\hat j}−y\,\mathbf{\hat k}\) ni kihafidhina.

    5. Kuhalalisha Theorem ya Msingi ya Line Integrals kwa\(\displaystyle \int _C\vecs F·d\vecs r\) katika kesi wakati\(\vecs{F}(x,y)=(2x+2y)\,\mathbf{\hat i}+(2x+2y)\,\mathbf{\hat j}\) na\(C\) ni sehemu ya mduara chanya oriented\(x^2+y^2=25\) kutoka\((5, 0)\) kwa\((3, 4).\)

    Jibu
    \(\displaystyle \int _C \vecs F·d\vecs r=24\)vitengo vya kazi

    6. [T] Kupata\(\displaystyle \int _C\vecs F·d\vecs r,\) wapi\(\vecs{F}(x,y)=(ye^{xy}+\cos x)\,\mathbf{\hat i}+\left(xe^{xy}+\frac{1}{y^2+1}\right)\,\mathbf{\hat j}\) na\(C\) ni sehemu ya Curve\(y=\sin x\) kutoka\(x=0\) kwa\(x=\frac{π}{2}\).

    7. [T] Kutathmini line muhimu\(\displaystyle \int _C\vecs F·d\vecs r\), ambapo\(\vecs{F}(x,y)=(e^x\sin y−y)\,\mathbf{\hat i}+(e^x\cos y−x−2)\,\mathbf{\hat j}\), na\(C\) ni njia iliyotolewa na\(\vecs r(t)=(t^3\sin\frac{πt}{2})\,\mathbf{\hat i}−(\frac{π}{2}\cos(\frac{πt}{2}+\frac{π}{2}))\,\mathbf{\hat j}\) kwa\(0≤t≤1\).

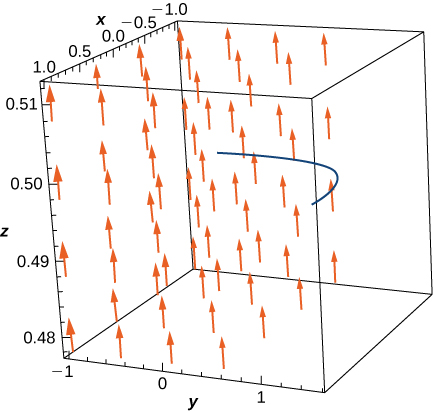
    CNX_Calc_Figure_16_03_201.jpg

    Jibu
    \(\displaystyle \int _C\vecs F·d\vecs r=\left(e−\frac{3π}{2}\right)\)vitengo vya kazi

    Kwa mazoezi yafuatayo, onyesha kama shamba la vector ni kihafidhina na, ikiwa ni, pata kazi inayoweza.

    8. \(\vecs{F}(x,y)=2xy^3\,\mathbf{\hat i}+3y^2x^2\,\mathbf{\hat j}\)

    9. \(\vecs{F}(x,y)=(−y+e^x\sin y)\,\mathbf{\hat i}+((x+2)e^x\cos y)\,\mathbf{\hat j}\)

    Jibu
    Si kihafidhina

    10. \(\vecs{F}(x,y)=(e^{2x}\sin y)\,\mathbf{\hat i}+(e^{2x}\cos y)\,\mathbf{\hat j}\)

    11. \(\vecs{F}(x,y)=(6x+5y)\,\mathbf{\hat i}+(5x+4y)\,\mathbf{\hat j}\)

    Jibu
    Kihafidhina,\(f(x,y)=3x^2+5xy+2y^2+k\)

    12. \(\vecs{F}(x,y)=(2x\cos(y)−y\cos(x))\,\mathbf{\hat i}+(−x^2\sin(y)−\sin(x))\,\mathbf{\hat j}\)

    13. \(\vecs{F}(x,y)=(ye^x+\sin(y))\,\mathbf{\hat i}+(e^x+x\cos(y))\,\mathbf{\hat j}\)

    Jibu
    Kihafidhina,\(f(x,y)=ye^x+x\sin(y)+k\)

    Kwa mazoezi yafuatayo, tathmini integrals line kutumia Theorem ya Msingi ya Line Integrals.

    14. \(\displaystyle ∮_C(y\,\mathbf{\hat i}+x\,\mathbf{\hat j})·d\vecs r,\)\(C\)wapi njia yoyote kutoka\((0, 0)\) kwa\((2, 4)\)

    15. \(\displaystyle ∮_C(2y\,dx+2x\,dy),\)\(C\)wapi sehemu ya mstari kutoka\((0, 0)\) kwa\((4, 4)\)

    Jibu
    \(\displaystyle ∮_C(2y\,dx+2x\,dy)=32\)vitengo vya kazi

    16. [T]\(\displaystyle ∮_C\left[\arctan\dfrac{y}{x}−\dfrac{xy}{x^2+y^2}\right]\,dx+\left[\dfrac{x^2}{x^2+y^2}+e^{−y}(1−y)\right]\,dy\), wapi\(C\) Curve yoyote laini kutoka\((1, 1)\) kwa\((−1,2).\)

    17. Pata shamba la vector la kihafidhina kwa kazi inayoweza\(f(x,y)=5x^2+3xy+10y^2.\)

    Jibu
    \(\vecs{F}(x,y)=(10x+3y)\,\mathbf{\hat i}+(3x+20y)\,\mathbf{\hat j}\)

    Kwa mazoezi yafuatayo, onyesha kama shamba la vector ni kihafidhina na, ikiwa ni hivyo, pata kazi inayoweza.

    18. \(\vecs{F}(x,y)=(12xy)\,\mathbf{\hat i}+6(x^2+y^2)\,\mathbf{\hat j}\)

    19. \(\vecs{F}(x,y)=(e^x\cos y)\,\mathbf{\hat i}+6(e^x\sin y)\,\mathbf{\hat j}\)

    Jibu
    \(\vecs F\)si kihafidhina.

    20. \(\vecs{F}(x,y)=(2xye^{x^2y})\,\mathbf{\hat i}+6(x^2e^{x^2y})\,\mathbf{\hat j}\)

    21. \(\vecs F(x,y,z)=(ye^z)\,\mathbf{\hat i}+(xe^z)\,\mathbf{\hat j}+(xye^z)\,\mathbf{\hat k}\)

    Jibu
    \(\vecs F\)ni kihafidhina na kazi uwezo ni\(f(x,y,z)=xye^z+k\).

    22. \(\vecs F(x,y,z)=(\sin y)\,\mathbf{\hat i}−(x\cos y)\,\mathbf{\hat j}+\,\mathbf{\hat k}\)

    23. \(\vecs F(x,y,z)=\dfrac{1}{y}\,\mathbf{\hat i}-\dfrac{x}{y^2}\,\mathbf{\hat j}+(2z−1)\,\mathbf{\hat k}\)

    Jibu
    \(\vecs F\)ni kihafidhina na kazi uwezo ni\(f(x,y,z)=\dfrac{x}{y}+z^2-z+k.\)

    24. \(\vecs F(x,y,z)=3z^2\,\mathbf{\hat i}−\cos y\,\mathbf{\hat j}+2xz\,\mathbf{\hat k}\)

    25. \(\vecs F(x,y,z)=(2xy)\,\mathbf{\hat i}+(x^2+2yz)\,\mathbf{\hat j}+y^2\,\mathbf{\hat k}\)

    Jibu
    \(\vecs F\)ni kihafidhina na kazi uwezo ni\(f(x,y,z)=x^2y+y^2z+k.\)

    Kwa mazoezi yafuatayo, onyesha kama shamba la vector lililopewa ni kihafidhina na kupata kazi inayoweza.

    26. \(\vecs{F}(x,y)=(e^x\cos y)\,\mathbf{\hat i}+6(e^x\sin y)\,\mathbf{\hat j}\)

    27. \(\vecs{F}(x,y)=(2xye^{x^2y})\,\mathbf{\hat i}+(x^2e^{x^2y})\,\mathbf{\hat j}\)

    Jibu
    \(\vecs F\)ni kihafidhina na kazi uwezo ni\(f(x,y)=e^{x^2y}+k\)

    Kwa mazoezi yafuatayo, tathmini muhimu kwa kutumia Theorem ya Msingi ya Integrals Line.

    28. Tathmini\(\displaystyle \int _C\vecs ∇f·d\vecs r\), wapi\(f(x,y,z)=\cos(πx)+\sin(πy)−xyz\) na\(C\) ni njia yoyote ambayo huanza saa\((1,12,2)\) na kuishia saa\((2,1,−1)\).

    29. [T] Tathmini\(\displaystyle \int _C\vecs ∇f·d\vecs r\), wapi\(f(x,y)=xy+e^x\) na\(C\) ni mstari wa moja kwa moja kutoka\((0,0)\) kwa\((2,1)\).

    Jibu
    \(\displaystyle \int _C\vecs F·d\vecs r=\left(e^2+1\right)\)vitengo vya kazi

    30. [T] Kutathmini\(\displaystyle \int _C\vecs ∇f·d\vecs r,\) wapi\(f(x,y)=x^2y−x\) na\(C\) ni njia yoyote katika ndege kutoka (1, 2) kwa (3, 2).

    31. Tathmini\(\displaystyle \int _C\vecs ∇f·d\vecs r,\) wapi\(f(x,y,z)=xyz^2−yz\) na\(C\) ina hatua ya awali\((1, 2, 3)\) na hatua ya mwisho\((3, 5, 2).\)

    Jibu
    \(\displaystyle \int _C\vecs F·d\vecs r=38\)vitengo vya kazi

    Kwa ajili ya mazoezi yafuatayo, basi\(\vecs{F}(x,y)=2xy^2\,\mathbf{\hat i}+(2yx^2+2y)\,\mathbf{\hat j}\) na\(G(x,y)=(y+x)\,\mathbf{\hat i}+(y−x)\,\mathbf{\hat j}\), na basi\(C_1\) kuwa Curve yenye mduara wa Radius 2, unaozingatia katika asili na oriented kinyume chake, na\(C_2\) kuwa Curve yenye sehemu line kutoka\((0, 0)\) kwa\((1, 1)\) ikifuatiwa na sehemu line kutoka\((1, 1)\) kwa\((3, 1).\)

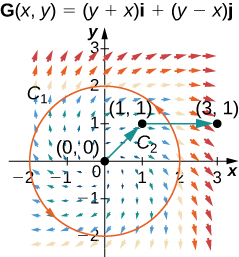
    CNX_Calc_Figure_16_03_203.jpg

    32. Tumia mstari muhimu wa\(\vecs F\) juu\(C_1\).

    33. Tumia mstari muhimu wa\(\vecs G\) juu\(C_1\).

    Jibu
    \(\displaystyle ∮_{C_1}\vecs G·d\vecs r=−8π\)vitengo vya kazi

    34. Tumia mstari muhimu wa\(\vecs F\) juu\(C_2\).

    35. Tumia mstari muhimu wa\(\vecs G\) juu\(C_2\).

    Jibu
    \(\displaystyle ∮_{C_2}\vecs F·d\vecs r=7\)vitengo vya kazi

    36. [T] Hebu\(\vecs F(x,y,z)=x^2\,\mathbf{\hat i}+z\sin(yz)\,\mathbf{\hat j}+y\sin(yz)\,\mathbf{\hat k}\). Tumia\(\displaystyle ∮_C\vecs F·d\vecs{r}\),\(C\) wapi njia kutoka\(A=(0,0,1)\) kwa\(B=(3,1,2)\).

    37. [T] Kupata line muhimu\(\displaystyle ∮_C\vecs F·dr\) ya uwanja vector\(\vecs F(x,y,z)=3x^2z\,\mathbf{\hat i}+z^2\,\mathbf{\hat j}+(x^3+2yz)\,\mathbf{\hat k}\) pamoja Curve\(C\) parameterized na\(\vecs r(t)=(\frac{\ln t}{\ln 2})\,\mathbf{\hat i}+t^{3/2}\,\mathbf{\hat j}+t\cos(πt),1≤t≤4.\)

    Jibu
    \(\displaystyle \int _C\vecs F·d\vecs r=150\)vitengo vya kazi

    Kwa mazoezi 38 - 40, onyesha kwamba mashamba ya vector yafuatayo ni kihafidhina. Kisha uhesabu\(\displaystyle \int _C\vecs F·d\vecs r\) kwa curve iliyotolewa.

    38. \(\vecs{F}(x,y)=(xy^2+3x^2y)\,\mathbf{\hat i}+(x+y)x^2\,\mathbf{\hat j}\);\(C\) ni safu yenye makundi ya mstari kutoka\((1,1)\)\((0,2)\) hadi\((3,0).\)

    39. \(\vecs{F}(x,y)=\dfrac{2x}{y^2+1}\,\mathbf{\hat i}−\dfrac{2y(x^2+1)}{(y^2+1)^2}\,\mathbf{\hat j}\);\(C\) ni parameterized na\(x=t^3−1,\;y=t^6−t\), kwa\(0≤t≤1.\)

    Jibu
    \(\displaystyle \int _C\vecs F·d\vecs r=−1\)vitengo vya kazi

    40. [T]\(\vecs{F}(x,y)=[\cos(xy^2)−xy^2\sin(xy^2)]\,\mathbf{\hat i}−2x^2y\sin(xy^2)\,\mathbf{\hat j}\);\(C\) ni Curve\(\langle e^t,e^{t+1}\rangle,\) kwa\(−1≤t≤0\).

    41. Masi ya Dunia ni takriban\(6×10^{27}g\) na ile ya Jua ni mara 330,000 zaidi. Mara kwa mara ya mvuto ni\(6.7×10^{−8}cm^3/s^2·g\). Umbali wa Dunia kutoka Jua ni karibu\(1.5×10^{12}cm\). Compute, takriban, kazi muhimu ili kuongeza umbali wa Dunia kutoka Jua na\(1\;cm\).

    Jibu
    \(4×10^{31}\)erg

    42. [T] Hebu\(\vecs{F}(x,y,z)=(e^x\sin y)\,\mathbf{\hat i}+(e^x\cos y)\,\mathbf{\hat j}+z^2\,\mathbf{\hat k}\). Tathmini muhimu\(\displaystyle \int _C\vecs F·d\vecs r\), ambapo\(\vecs r(t)=\langle\sqrt{t},t^3,e^{\sqrt{t}}\rangle,\) kwa\(0≤t≤1.\)

    43. [T] Hebu\(C:[1,2]→ℝ^2\) apewe na\(x=e^{t−1},y=\sin\left(\frac{π}{t}\right)\). Tumia kompyuta ili kukokotoa muhimu\(\displaystyle \int _C\vecs F·d\vecs r=\int _C 2x\cos y\,dx−x^2\sin y\,dy\), wapi\(\vecs{F}(x,y)=(2x\cos y)\,\mathbf{\hat i}−(x^2\sin y)\,\mathbf{\hat j}.\)

    Jibu
    \(\displaystyle \int _C\vecs F·d\vecs s=0.4687\)vitengo vya kazi

    44. [T] Tumia mfumo wa algebra ya kompyuta ili kupata wingi wa waya unao kando ya pembe\(\vecs r(t)=(t^2−1)\,\mathbf{\hat j}+2t\,\mathbf{\hat k},\) ambapo\(0≤t≤1\), ikiwa wiani unatolewa na\(d(t) = \dfrac{3}{2}t\).

    45. Pata mzunguko na mzunguko wa shamba\(\vecs{F}(x,y)=−y\,\mathbf{\hat i}+x\,\mathbf{\hat j}\) karibu na njia iliyofungwa iliyofungwa ambayo ina arch ya semicircular\(\vecs r_1(t)=(a\cos t)\,\mathbf{\hat i}+(a\sin t)\,\mathbf{\hat j},\quad 0≤t≤π\), ikifuatiwa na sehemu ya mstari\(\vecs r_2(t)=t\,\mathbf{\hat i},\quad −a≤t≤a.\)

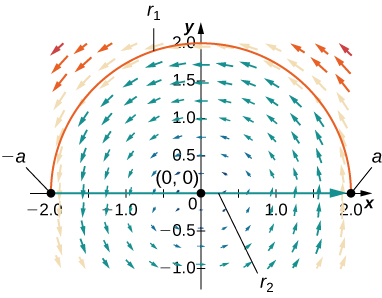
    CNX_Calc_Figure_16_03_204.jpg

    Jibu
    \(\text{circulation}=πa^2\)na\(\text{flux}=0\)

    46. Kokotoa\(\displaystyle \int _C\cos x\cos y\,dx−\sin x\sin y\,dy,\) wapi\(\vecs r(t)=\langle t,t^2 \rangle, \quad 0≤t≤1.\)

    47. Kukamilisha ushahidi wa theorem yenye jina la PATH UHURU MTIHANI KWA FIELDS CONSERVATIV\(f_y=Q(x,y).\)