16.4: Theorem ya Green
- Page ID
- 178928
- Tumia fomu ya mzunguko wa theorem ya Green.
- Tumia fomu ya flux ya theorem ya Green.
- Tumia mzunguko na uingie kwenye mikoa zaidi ya jumla.
Katika sehemu hii, tunachunguza theorem ya Green, ambayo ni ugani wa Theorem ya Msingi ya Calculus kwa vipimo viwili. Theorem ya Green ina aina mbili: fomu ya mzunguko na fomu ya flux, ambayo yote yanahitaji kanda\(D\) katika sehemu mbili ili kushikamana tu. Hata hivyo, tutaongeza theorem ya Green kwa mikoa ambayo haijaunganishwa tu.
Kuweka tu, Theorem Green inahusiana line muhimu karibu tu imefungwa ndege Curve\(C\) na muhimu mara mbili juu ya kanda iliyoambatanishwa na\(C\). Theorem ni muhimu kwa sababu inaruhusu sisi kutafsiri integrals line ngumu katika integrals rahisi zaidi mara mbili, au ngumu integrals mara mbili katika integrals rahisi zaidi line.
Kupanua Theorem ya Msingi ya Calculus
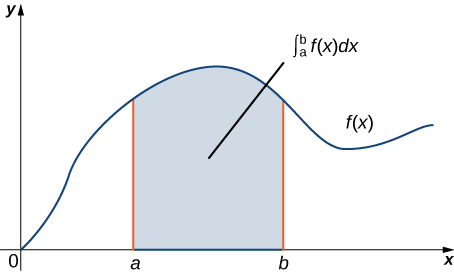
Kukumbuka kwamba Theorem ya Msingi ya Calculus anasema kwamba
\[\int_a^b F′(x)\,dx=F(b)−F(a). \nonumber \]
Kama taarifa ya kijiometri, equation hii inasema kuwa muhimu juu ya kanda chini ya grafu ya\(F′(x)\) na juu ya sehemu ya mstari\([a,b]\) inategemea tu thamani ya\(F\) mwisho\(a\) na\(b\) ya sehemu hiyo. Kwa kuwa idadi\(a\) na\(b\) ni mipaka ya sehemu ya mstari\([a,b]\), theorem inasema tunaweza kuhesabu muhimu\(\int_a^b F′(x)\,dx\) kulingana na habari kuhusu mipaka ya sehemu ya mstari\([a,b]\) (Kielelezo\(\PageIndex{1}\)). Wazo moja ni kweli ya Theorem ya Msingi kwa Line Integrals:
\[\int_C \vecs \nabla f·d\vecs r=f(\vecs r(b))−f(\vecs r(a)). \nonumber \]
Wakati tuna kazi uwezo (“antiderivative”), tunaweza mahesabu line muhimu kulingana tu juu ya taarifa kuhusu mipaka ya Curve\(C\).
Theorem ya Green inachukua wazo hili na inaongeza kwa kuhesabu integrals mara mbili. Theorem Green anasema kwamba tunaweza mahesabu muhimu mara mbili juu ya mkoa\(D\) msingi tu juu ya taarifa kuhusu mipaka ya\(D\). Theorem Green pia anasema tunaweza mahesabu line muhimu juu ya Curve rahisi imefungwa\(C\) msingi tu juu ya taarifa kuhusu kanda kwamba\(C\) encloses. Hasa, Theorem Green ya unajumuisha muhimu mara mbili juu ya kanda\(D\) ya mstari muhimu karibu na mipaka ya\(D\).
Fomu ya mzunguko wa Theorem ya Green
Fomu ya kwanza ya theorem ya Green ambayo tunachunguza ni fomu ya mzunguko. Aina hii ya theorem inahusiana vector line muhimu juu ya rahisi, imefungwa ndege Curve\(C\) kwa muhimu mara mbili juu ya kanda iliyoambatanishwa na\(C\). Kwa hiyo, mzunguko wa shamba la vector pamoja na safu rahisi iliyofungwa inaweza kubadilishwa kuwa muhimu mara mbili na kinyume chake.
Hebu\(D\) kuwa wazi, tu kushikamana kanda na Curve mipaka\(C\) ambayo ni piecewise laini, rahisi kufungwa Curve oriented kinyume (Kielelezo\(\PageIndex{1}\)). Hebu\(\vecs F=⟨P,Q⟩\) kuwa uwanja wa vector na kazi za sehemu ambazo zina derivatives ya sehemu inayoendelea\(D\). Kisha,
\[ \begin{align} \oint_C \vecs F·d\vecs r =\oint_C P\,dx+Q\,dy \\[4pt] =\iint_D (Q_x−P_y)\,dA. \end{align} \nonumber \]
Angalia kwamba theorem ya Green inaweza kutumika tu kwa uwanja wa vector mbili-dimensional\(\vecs F\). Ikiwa\(\vecs F\) ni shamba tatu-dimensional, basi theorem ya Green haitumiki. Tangu
\[\displaystyle \int_C P\,dx+Q\,dy=\int_C \vecs F·\vecs T\,ds \nonumber \]
toleo hili la theorem ya Green wakati mwingine hujulikana kama aina ya tangential ya theorem ya Green.
Ushahidi wa theorem ya Green ni badala ya kiufundi, na zaidi ya upeo wa maandiko haya. Hapa tunachunguza ushahidi wa theorem katika kesi maalum ambayo\(D\) ni mstatili. Kwa sasa, angalia kwamba tunaweza kuthibitisha haraka kwamba theorem ni kweli kwa kesi maalum ambayo\(\vecs F=⟨P,Q⟩\) ni kihafidhina. Katika kesi hiyo,
\[\oint_C P\,dx+Q\,dy=0 \nonumber \]
kwa sababu mzunguko ni sifuri katika mashamba ya kihafidhina vector. \(\vecs F\)satisfies hali ya msalaba-sehemu, hivyo\(P_y=Q_x\). Kwa hiyo,
\[\iint_D (Q_x−P_y)\,dA=\int_D 0\,dA=0=\oint_C P\,dx+Q\,dy \nonumber \]
ambayo inathibitisha Theorem Green katika kesi ya mashamba ya kihafidhina vector.
Hebu sasa tuhakikishe kwamba fomu ya mzunguko wa theorem ya Green ni kweli wakati kanda\(D\) ni mstatili. Hebu\(D\) kuwa mstatili\([a,b]×[c,d]\) oriented kinyume chake. Kisha, mipaka\(C\) ya\(D\) lina vipande vinne vya laini\(C_1\),,\(C_2\)\(C_3\), na\(C_4\) (Kielelezo\(\PageIndex{3}\)). Sisi parameterize kila upande wa\(D\) kama ifuatavyo:
\(C_1: \vecs r_1(t)=⟨t,c⟩\),\(a≤t≤b\)
\(C_2: \vecs r_2(t)=⟨b,t⟩\),\(c≤t≤d\)
\(−C_3: \vecs r_3(t)=⟨t,d⟩\),\(a≤t≤b\)
\(−C_4: \vecs r_4(t)=⟨a,t⟩\),\(c≤t≤d\).
Kisha,
\[\begin{align*} \int_C \vecs F·d \vecs r &=\int_{C_1} \vecs F·d \vecs r+\int_{C_2} \vecs F·d \vecs r+\int_{C_3} \vecs F·d \vecs r+\int_{C_4} \vecs F·d \vecs r \\[4pt] &=\int_{C_1} \vecs F·d \vecs r+\int_{C_2} \vecs F·d \vecs r−\int_{−C_3} \vecs F·d \vecs r−\int_{−C_4} \vecs F·d \vecs r \\[4pt] &=\int_a^b \vecs F( \vecs r_1(t))· \vecs r_1'(t)\,dt+\int_c^d \vecs F( \vecs r_2(t))· \vecs r_2'(t)\,dt−\int_a^b \vecs F( \vecs r_3(t))· \vecs r_3'(t)\,dt−\int_c^d \vecs F( \vecs r_4(t))·\vecs r_4'(t)\,dt\\[4pt] &=\int_a^b P(t,c)\,dt+\int_c^dQ(b,t)\,dt−\int_a^bP(t,d)\,dt−\int_c^dQ(a,t)\,dt \\[4pt] &=\int_a^b(P(t,c)−P(t,d))\,dt+\int_c^d(Q(b,t)−Q(a,t))\,dt\\[4pt] &=−\int_a^b(P(t,d)−P(t,c))\,dt+\int_c^d(Q(b,t)−Q(a,t))\,dt. \end{align*}\]
Kwa Theorem ya Msingi ya Calculus,
\[P(t,d)−P(t,c)=\int_c^d \dfrac{\partial}{\partial y}P(t,y)dy \nonumber \]
na
\[Q(b,t)−Q(a,t)=\int_a^b \dfrac{\partial}{\partial x} Q(x,t)\,dx. \nonumber \]
Kwa hiyo,
\[−\int_a^b(P(t,d)−P(t,c))\,dt+\int_c^d(Q(b,t)−Q(a,t))\,dt=−\int_a^b\int_c^d \dfrac{\partial}{\partial y} P(t,y)\,dy\,dt+\int_c^d\int_a^b \dfrac{\partial}{\partial x}Q(x,t)\,dx\,dt. \nonumber \]
Lakini,
\[\begin{align*} −\int_a^b\int_c^d \dfrac{\partial}{\partial y}P(t,y)\,dy\,dt+\int_c^d\int_a^b \dfrac{\partial}{\partial x}Q(x,t)\,dx\,dt &=−\int_a^b\int_c^d \dfrac{\partial}{\partial y}P(x,y)\,dy\,dx+\int_c^d\int_a^b \dfrac{\partial}{\partial x}Q(x,y)\,dx\,dy \\[4pt] &=\int_a^b\int_c^d(Q_x−P_y)\,dy\,dx\\[4pt] &=\iint_D(Q_x−P_y)\,dA. \end{align*}\]
Kwa hiyo,\(\displaystyle \int_C \vecs F\cdot d\vecs r=\iint_D(Q_x−P_y)\,dA\) na tumeonyesha theorem ya Green katika kesi ya mstatili.
\(\square\)
Ili kuthibitisha theorem ya Green juu ya eneo la jumla\(D\), tunaweza kuharibika\(D\) katika rectangles nyingi vidogo na kutumia ushahidi kwamba theorem inafanya kazi juu ya rectangles. Maelezo ni ya kiufundi, hata hivyo, na zaidi ya upeo wa maandishi haya.
Tumia mstari muhimu
\[\oint_C x^2ydx+(y−3)dy, \nonumber \]
ambapo\(C\) ni mstatili na vertices\((1,1)\),,\((4,1)\)\((4,5)\), na\((1,5)\) oriented counterclockwise.
Suluhisho
Hebu\( \vecs F(x,y)=⟨P(x,y),Q(x,y)⟩=⟨x^2y,y−3⟩\). Kisha,\(Q_x(x,y)=0\) na\(P_y(x,y)=x^2\). Kwa hiyo,\(Q_x−P_y=−x^2\).
Hebu\(D\) kuwa kanda ya mstatili iliyofungwa na\(C\) (Kielelezo\(\PageIndex{4}\)). Kwa theorem ya Green,
\[\begin{align*} \oint_C x^2ydx+(y−3)\,dy &=\iint_D (Q_x−P_y)\,dA \\[4pt] &=\iint_D −x^2 \,dA=\int_1^5\int_1^4−x^2\,dx\,dy \\[4pt] &=\int_1^5−21\,dy=−84.\end{align*}\]

Uchambuzi
Kama tulikuwa na kutathmini mstari huu muhimu bila kutumia theorem Green, tunataka haja parameterize kila upande wa mstatili, kuvunja mstari muhimu katika nne tofauti line integrals, na kutumia mbinu kutoka sehemu yenye jina Line Integrals kutathmini kila muhimu. Zaidi ya hayo, tangu uwanja vector hapa si kihafidhina, hatuwezi kutumia Theorem Msingi kwa Line Integrals. Theorem ya Green inafanya hesabu iwe rahisi zaidi.
Tumia kazi iliyofanyika kwenye chembe kwa shamba la nguvu
\[\vecs F(x,y)=⟨y+\sin x,e^y−x⟩ \nonumber \]
kama chembe hupitia mduara\(x^2+y^2=4\) hasa mara moja katika mwelekeo kinyume, kuanzia na kuishia katika hatua\((2,0)\).
Suluhisho
Hebu\(C\) ueleze mduara na uache\(D\) kuwa disk iliyofungwa na\(C\). Kazi iliyofanywa kwenye chembe ni
\[W=\oint_C (y+\sin x)\,dx+(e^y−x)\,dy. \nonumber \]
Kama ilivyo kwa Mfano\(\PageIndex{1}\), muhimu hii inaweza kuhesabiwa kwa kutumia zana tumejifunza, lakini ni rahisi kutumia muhimu mara mbili iliyotolewa na theorem ya Green (Kielelezo\(\PageIndex{5}\)).
Hebu\(\vecs F(x,y)=⟨P(x,y),Q(x,y)⟩=⟨y+\sin x,e^y−x⟩\). Kisha,\(Q_x=−1\) na\(P_y=1\). Kwa hiyo,\(Q_x−P_y=−2\).
Kwa theorem ya Green,
\[\begin{align*} W &=\oint_C(y+\sin(x))dx+(e^y−x)\,dy \\[4pt] &=\iint_D (Q_x−P_y)\,dA \\[4pt] &=\iint_D−2\,dA \\[4pt] &=−2(area(D))=−2\pi (2^2)=−8\pi. \end{align*}\]
Matumizi Theorem Green ya mahesabu line muhimu
\[\oint_C \sin(x^2)\,dx+(3x−y)\,dy. \nonumber \]
\(C\)wapi pembetatu ya kulia na vipeo\((−1,2)\),\((4,2)\), na\((4,5)\) inaelekezwa kinyume chake.
- Kidokezo
-
Kubadilisha mstari muhimu katika muhimu mara mbili.
- Jibu
-
\(\dfrac{45}{2}\)
Katika mifano miwili iliyotangulia, muhimu mara mbili katika theorem ya Green ilikuwa rahisi kuhesabu kuliko mstari muhimu, kwa hiyo tulitumia theorem kuhesabu mstari muhimu. Katika mfano unaofuata, muhimu mara mbili ni vigumu zaidi kuhesabu kuliko mstari muhimu, kwa hiyo tunatumia theorem ya Green kutafsiri sehemu mbili katika mstari muhimu.
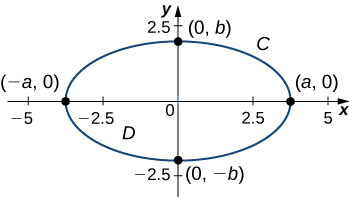
Tumia eneo lililofungwa na ellipse\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\) (Kielelezo\(\PageIndex{6}\)).
Suluhisho
Hebu\(C\) taja duaradufu na uache\(D\) kuwa kanda iliyofungwa na\(C\). Kumbuka kwamba duaradufu\(C\) inaweza parameterized na
- \(x=a\cos t\),
- \(y=b \sin t\),
- \(0≤t≤2\pi\).
Kuhesabu eneo la\(D\) ni sawa na kompyuta mbili muhimu\(\iint_D \,dA\). Ili kuhesabu jambo hili bila theorem ya Green, tunahitaji\(D\) kugawanywa katika mikoa miwili: kanda iliyo juu ya x -axis na kanda hapa chini. Eneo la ellipse ni
\[\int_{−a}^a\int_0^{\sqrt{b^2−{(bx/a)}^2}} \,dy\,dx+\int_{−a}^{a} \int_{−\sqrt{b^2−{(bx/a)}^2}}^{0} \,dy\,dx. \nonumber \]
Integrals hizi mbili si moja kwa moja kuhesabu (ingawa tunapojua thamani ya muhimu ya kwanza, tunajua thamani ya pili kwa ulinganifu). Badala ya kujaribu kuhesabu, tunatumia theorem ya Green ili kubadilisha\(\iint_D \,dA\) kuwa mstari muhimu karibu na mipaka\(C\).
Fikiria uwanja wa vector
\[F(x,y)=⟨P,Q⟩=⟨−\dfrac{y}{2},\dfrac{x}{2}⟩. \nonumber \]
Kisha,\(Q_x=\dfrac{1}{2}\) na\(P_y=−\dfrac{1}{2}\), na kwa hiyo\(Q_x−P_y=1\). Taarifa kwamba\(\vecs F\) alichaguliwa kuwa na mali hiyo\(Q_x−P_y=1\). Kwa kuwa hii ni kesi, Theorem ya Green inabadilisha mstari muhimu wa\(\vecs F\) juu\(C\) katika muhimu mara mbili ya 1 juu\(D\).
Kwa theorem ya Green,
\[\begin{align*} \iint_D \,dA &=\iint_D (Q_x−P_y)\,dA \\[4pt] &=\int_C \vecs F\cdot d\vecs r=\dfrac{1}{2}\int_C −y\,dx+x\,dy \\[4pt] &=\dfrac{1}{2}\int_0^{2\pi}−b \sin t(−a\sin t)+a(\cos t)b\cos t\,dt \\[4pt] &=\dfrac{1}{2}\int_0^{2\pi} ab \cos^2 t+ab \sin^2 t\,dt \\[4pt] &=\dfrac{1}{2}\int_0^{2\pi} ab\,dt =\pi ab. \end{align*}\]
Kwa hiyo, eneo la ellipse ni\(\pi ab\;\text{units}^2\).
Katika Mfano\(\PageIndex{3}\), tulitumia uwanja wa vector\(\vecs F(x,y)=⟨P,Q⟩=⟨−\dfrac{y}{2},\dfrac{x}{2}⟩\) kupata eneo la duaradufu yoyote. Mantiki ya mfano uliopita inaweza kupanuliwa ili kupata formula kwa eneo la eneo lolote\(D\). Hebu\(D\) kuwa mkoa wowote na mipaka ambayo ni rahisi kufungwa Curve\(C\) oriented kinyume chake. Ikiwa\(F(x,y)=⟨P,Q⟩=⟨−\dfrac{y}{2},\dfrac{x}{2}⟩\), basi\(Q_x−P_y=1\). Kwa hiyo, kwa mantiki sawa na katika Mfano\(\PageIndex{3}\),
\[ \text{area of} \; D=\iint_D dA=\dfrac{1}{2}\oint_C−ydx+xdy. \label{greenarea} \]
Ni muhimu kutambua kwamba ikiwa\(F=⟨P,Q⟩\) ni shamba lolote la vector na\(Q_x−P_y=1\), basi mantiki ya aya iliyotangulia inafanya kazi. Hivyo. Equation\ ref {greenarea} sio equation pekee inayotumia sehemu za mchanganyiko wa shamba la vector kupata eneo la kanda.
Pata eneo la kanda lililofungwa na safu na parameterization\(r(t)=⟨\sin t\cos t,\sin t⟩\),\(0≤t≤\pi\).
- Kidokezo
-
Tumia Equation\ ref {eneo la kijani}.
- Jibu
-
\(\dfrac{4}{3}\)
Fomu ya Flux ya Theorem ya Green
Fomu ya mzunguko wa theorem ya Green inahusiana muhimu mara mbili juu ya kanda\(D\) kwa mstari muhimu\(\oint_C \vecs F·\vecs Tds\), wapi\(C\) mipaka ya\(D\). Fomu ya flux ya theorem ya Green inahusiana na muhimu mara mbili juu ya kanda\(D\) kwa kuongezeka kwa mipaka\(C\). Mzunguko wa maji katika pembe inaweza kuwa vigumu kuhesabu kutumia mstari wa flux muhimu. Aina hii ya theorem ya Green inatuwezesha kutafsiri flux ngumu muhimu katika muhimu mara mbili ambayo mara nyingi ni rahisi kuhesabu.
Hebu\(D\) kuwa wazi, tu kushikamana kanda na Curve mipaka\(C\) ambayo ni piecewise laini, rahisi imefungwa Curve kwamba ni oriented kinyume chake (Kielelezo\(\PageIndex{7}\)). Hebu\(\vecs F=⟨P,Q⟩\) kuwa uwanja wa vector na kazi za sehemu ambazo zina derivatives ya sehemu inayoendelea kwenye kanda iliyo wazi iliyo na\(D\). Kisha,
\[\oint_C \vecs F·\vecs N\,ds=\iint_D P_x+Q_y\,dA. \label{GreenN} \]
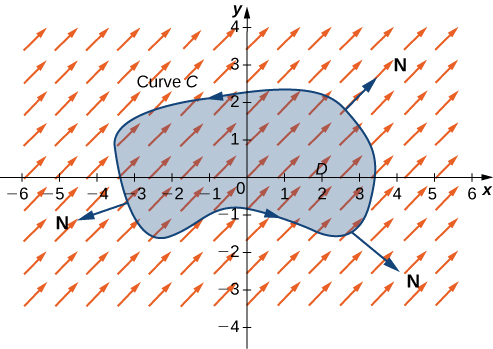
Kwa sababu aina hii ya theorem Green ina kitengo kawaida vector\(\vecs N\), ni wakati mwingine inajulikana kama aina ya kawaida ya Theorem Green ya.
Kumbuka kwamba\(\displaystyle \oint_C \vecs F·\vecs N\,ds=\oint_C −Q\,dx+P\,dy\). Hebu\(M=−Q\) na\(N=P\). Kwa aina ya mzunguko wa theorem ya Green,
\[\begin{align*} \oint_C−Q\,dx+P\,dy &=\oint_C M\,dx+N\,dy\\[4pt] &=\iint_D N_x−M_y \,dA\\[4pt] &=\iint_D P_x−{(−Q)}_y \,dA\\[4pt] &=\iint_D P_x+Q_y \,dA. \end{align*}\]
\(\square\)
Hebu\(C\) kuwa mduara wa radius\(r\) unaozingatia asili (Kielelezo\(\PageIndex{8}\)) na basi\(\vecs F(x,y)=⟨x,y⟩\). Tumia flux kote\(C\).

Suluhisho
Hebu\(D\) kuwa disk iliyofungwa na\(C\). Flux kote\(C\) ni\(\displaystyle \oint_C \vecs F·\vecs N\,ds\). Tunaweza kutathmini hii muhimu kwa kutumia zana tumejifunza, lakini theorem ya Green inafanya hesabu iwe rahisi zaidi. Hebu\(P(x,y)=x\) na\(Q(x,y)=y\) hivyo\(\vecs F=⟨P,Q⟩\). Kumbuka kwamba\(P_x=1=Q_y\), na kwa hiyo\(P_x+Q_y=2\). Kwa theorem ya Green,
\[\int_C \vecs F\cdot\vecs N\,ds=\iint_D 2\,dA=2\iint_D \,dA. \nonumber \]
Tangu\(\displaystyle \iint_D \,dA\) ni eneo la mduara,\(\displaystyle \iint_D \,dA=\pi r^2\). Kwa hiyo, flux kote\(C\) ni\(2\pi r^2\).
Hebu\(S\) kuwa pembetatu na vertices\((0,0)\),\((1,0)\), na\((0,3)\) mwelekeo wa saa moja kwa moja (Kielelezo\(\PageIndex{9}\)). Tumia mzunguko wa\(\vecs F(x,y)=⟨P(x,y),Q(x,y)⟩=⟨x^2+e^y,x+y⟩\) hela\(S\).
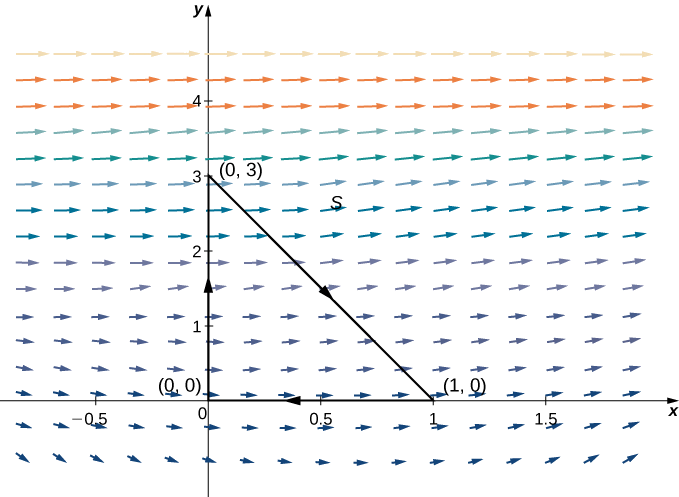
Suluhisho
Ili kuhesabu mtiririko bila theorem ya Green, tunahitaji kuvunja flux muhimu katika integrals tatu mstari, moja muhimu kwa kila upande wa pembetatu. Kutumia theorem ya Green kutafsiri mstari wa flux muhimu katika moja muhimu mara mbili ni rahisi zaidi.
Hebu\(D\) kuwa kanda iliyoambatanishwa na\(S\). Kumbuka kwamba\(P_x=2x\) na\(Q_y=1\); kwa hiyo,\(P_x+Q_y=2x+1\). Theorem Green inatumika tu kwa curves rahisi imefungwa oriented kinyume, lakini bado tunaweza kutumia theorem kwa sababu\(\displaystyle \oint_C \vecs F·\vecs N\,ds=−\oint_{−S} \vecs F·\vecs N\,ds\) na\(−S\) ni oriented kinyume chake. Kwa theorem ya Green, flux ni
\[\begin{align*} \oint_C \vecs F·\vecs N\,ds &= \oint_{−S} \vecs F·\vecs N\,ds\\[4pt] &=−\iint_D (P_x+Q_y)\,dA \\[4pt] &=−\iint_D (2x+1)\,dA.\end{align*}\]
Angalia kwamba makali ya juu ya pembetatu ni mstari\(y=−3x+3\). Kwa hiyo, katika iterated mara mbili muhimu,\(y\) -maadili kukimbia kutoka\(y=0\) kwa\(y=−3x+3\), na tuna
\[\begin{align*} −\iint_D (2x+1)\,dA &= −\int_0^1\int_0^{−3x+3}(2x+1)\,dy\,dx \\[4pt] &=−\int_0^1(2x+1)(−3x+3)\,dx \\[4pt] &=−\int_0^1(−6x^2+3x+3)\,dx\\[4pt] &=−{[−2x^3+\dfrac{3x^2}{2}+3x]}_0^1 \\[4pt] &=−\dfrac{5}{2}. \end{align*}\]
Tumia mzunguko wa\(\vecs F(x,y)=⟨x^3,y^3⟩\) kwenye mduara wa kitengo unaoelekezwa kinyume chake.
- Kidokezo
-
Tumia theorem ya Green na utumie kuratibu za polar.
- Jibu
-
\(\dfrac{3\pi}{2}\)
Maji hutoka kwenye chemchemi iliyo asili. Kasi ya maji inatokana na shamba la vector\(\vecs v(x,y)=⟨5x+y,x+3y⟩\) m/sec. Pata kiasi cha maji kwa pili ambacho kinapita katikati ya mstatili na vipeo\((−1,−2)\),,\((1,−2)\), na\((1,3)\)\((−1,3)\), vinaelekezwa kinyume chake (Kielelezo\(\PageIndex{10}\)).

Suluhisho
Hebu\(C\) kuwakilisha mstatili uliotolewa na\(D\) uwe mkoa wa mstatili uliofungwa na\(C\). Ili kupata kiasi cha maji kinachozunguka kote\(C\), tunahesabu mtiririko\(\int_C \vecs v\cdot d\vecs r\). Hebu\(P(x,y)=5x+y\) na\(Q(x,y)=x+3y\) hivyo\(\vecs v=⟨P,Q⟩\). Kisha,\(P_x=5\) na\(Q_y=3\). Kwa theorem ya Green,
\[\begin{align*} \int_C \vecs v\cdot d\vecs r &=\iint_D (P_x+Q_y)\,dA \\ &=\iint_D 8\,dA \\ &=8(area\space of\space D)=80. \end{align*}\]
Kwa hiyo, mtiririko wa maji ni 80 m 2 /sec.
Kumbuka kwamba kama uwanja\(\vecs F\) wa vector ni kihafidhina, basi\(\vecs F\) haifanyi kazi karibu na curves imefungwa - yaani, mzunguko wa\(\vecs F\) karibu Curve imefungwa ni sifuri. Kwa kweli, kama uwanja wa\(\vecs F\) ni kushikamana tu, basi\(\vecs F\) ni kihafidhina kama na tu kama mzunguko wa\(\vecs F\) karibu yoyote Curve imefungwa ni sifuri. Ikiwa tunachukua nafasi ya “mzunguko wa\(\vecs F\)” na “kuongezeka kwa\(\vecs F\),” basi tunapata ufafanuzi wa uwanja wa vector usio na chanzo. Taarifa zifuatazo ni njia zote sawa za kufafanua uwanja usio na chanzo\(\vecs F=⟨P,Q⟩\) kwenye uwanja unaounganishwa tu (angalia kufanana na mali ya mashamba ya vector ya kihafidhina):
- Flux\( \displaystyle \oint_C \vecs F·\vecs N\,ds\) katika Curve yoyote imefungwa\(C\) ni sifuri.
- Kama\(C_1\) na\(C_2\) ni curves katika uwanja wa\(\vecs F\) na pointi sawa kuanzia na endpoints, basi\(\displaystyle \int_{C_1} \vecs F·\vecs N\,ds=\int_{C_2} \vecs F·\vecs N\,ds\). Kwa maneno mengine, flux ni huru ya njia.
- Kuna mkondo kazi\(g(x,y)\) kwa\(\vecs F\). kazi mkondo kwa\(\vecs F=⟨P,Q⟩\) ni kazi g kama kwamba\(P=g_y\)\(Q=−g_x\) na.Geometrically,\(\vecs F=\langle a,b\rangle\) ni tangential kwa Curve ngazi ya\(g\) saa\((a,b)\). Kwa kuwa gradient ya\(g\) ni perpendicular kwa Curve\(g\) ngazi ya saa\((a,b)\), mkondo kazi\(g\) ina mali\(\vecs F(a,b)\cdot\vecs\nabla g(a,b)=0\) kwa hatua yoyote\((a,b)\) katika uwanja wa\(g\). (Kazi za mkondo zina jukumu sawa kwa mashamba yasiyo ya chanzo ambayo kazi zinazoweza kucheza kwa mashamba ya kihafidhina.)
- \(P_x+Q_y=0\)
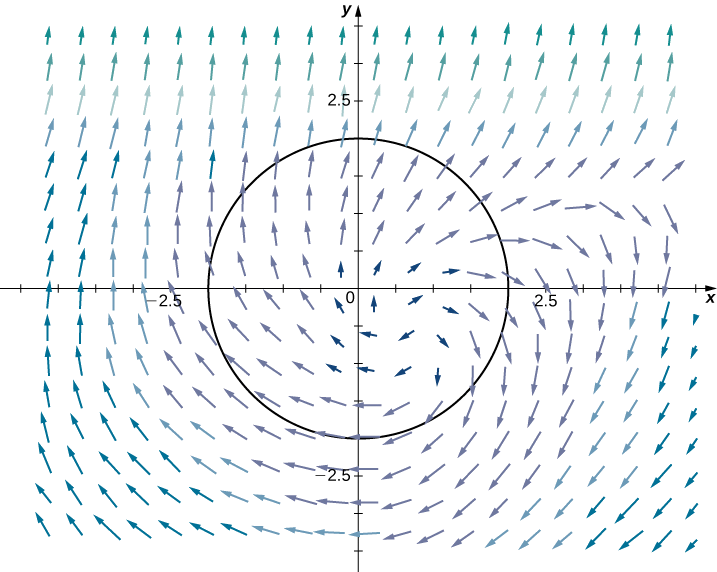
Thibitisha kwamba mzunguko vector shamba\(\vecs F(x,y)=⟨y,−x⟩\) ni chanzo bure, na kupata mkondo kazi kwa\(\vecs F\).
Suluhisho
Kumbuka kuwa uwanja wa\(\vecs F\) ni wote wa\(ℝ^2\), ambayo ni tu kushikamana. Kwa hiyo, kuonyesha kwamba\(\vecs F\) ni chanzo bure, tunaweza kuonyesha yoyote ya vitu 1 hadi 4 kutoka orodha ya awali kuwa kweli. Katika mfano huu, tunaonyesha kwamba kipengee cha 4 ni kweli. Hebu\(P(x,y)=y\) na\(Q(x,y)=−x\). Kisha\(P_x+0=Q_y\), na kwa hiyo\(P_x+Q_y=0\). Hivyo,\(\vecs F\) ni chanzo bure.
Ili kupata kazi ya mkondo\(\vecs F\), endelea kwa njia sawa na kutafuta kazi ya uwezo kwa uwanja wa kihafidhina. Hebu\(g\) kuwa mkondo kazi kwa\(\vecs F\). Kisha\(g_y=y\), ambayo ina maana kwamba
\(g(x,y)=\dfrac{y^2}{2}+h(x)\).
tangu\(−g_x=Q=−x\), tuna\(h′(x)=x\). Kwa hiyo,
\(h(x)=\dfrac{x^2}{2}+C\).
Kuruhusu\(C=0\) anatoa mkondo kazi
\(g(x,y)=\dfrac{x^2}{2}+\dfrac{y^2}{2}\).
Ili kuthibitisha kwamba\(g\) ni mkondo kazi kwa\(\vecs F\), kumbuka kuwa\(g_y=y=P\) na\(−g_x=−x=Q\).
Kumbuka kwamba chanzo bure mzunguko vector shamba\(\vecs F(x,y)=⟨y,−x⟩\) ni perpendicular kihafidhina radial vector shamba\(\vecs \nabla g=⟨x,y⟩\) (Kielelezo\(\PageIndex{11}\)).
Kupata mkondo kazi kwa ajili ya uwanja vector\(\vecs F(x,y)=⟨x \sin y,\cos y⟩\).
- Kidokezo
-
Fuata muhtasari uliotolewa katika mfano uliopita.
- Jibu
-
\(g(x,y)=−x\cos y\)
Mashamba ya vector ambayo ni ya kihafidhina na chanzo bure ni mashamba muhimu ya vector. Kipengele kimoja muhimu cha mashamba ya vector ya kihafidhina na ya chanzo kwenye uwanja unaounganishwa tu ni kwamba kazi yoyote ya uwezo\(f\) wa shamba kama hiyo inatimiza usawa wa Laplace\(f_{xx}+f_{yy}=0\). Equation ya Laplace ni msingi katika uwanja wa equations tofauti ya sehemu kwa sababu inaiga matukio kama uwezo wa mvuto na magnetic katika nafasi, na uwezo wa kasi wa maji bora. kazi kwamba satisfies equation Laplace ya inaitwa kazi harmonic. Kwa hiyo kazi yoyote ya uwezo wa uwanja wa vector wa kihafidhina na usio na chanzo ni harmonic.
Kuona kwamba kazi yoyote ya uwezo wa uwanja wa vector wa kihafidhina na usio na chanzo kwenye uwanja unaounganishwa tu ni harmonic, basi\(f\) iwe kazi kama hiyo ya shamba la vector\(\vecs F=⟨P,Q⟩\). Kisha,\(f_x=P\) na\(f_x=Q\) kwa sababu\(\vecs \nabla f=\vecs F\). Kwa hiyo,\(f_{xx}=P_x\) na\(f_{yy}=Q_y\). Kwa kuwa\(\vecs F\) ni chanzo bure,\(f_{xx}+f_{yy}=P_x+Q_y=0\), na tuna kwamba\(f\) ni harmonic.
Kwa uwanja vector\(\vecs F(x,y)=⟨e^x\sin y,e^x\cos y⟩\), kuthibitisha kwamba shamba ni wote kihafidhina na chanzo bure, kupata kazi uwezo kwa\(\vecs F\), na kuthibitisha kwamba kazi uwezo ni harmonic.
Suluhisho
Hebu\(P(x,y)=e^x\sin y\) na\(Q(x,y)=e^x \cos y\). Angalia kwamba uwanja wa\(\vecs F\) ni wote wa nafasi mbili, ambayo ni tu kushikamana. Kwa hiyo, tunaweza kuangalia sehemu za msalaba wa\(\vecs F\) kuamua kama\(\vecs F\) ni kihafidhina. Kumbuka kwamba\(P_y=e^x \cos y=Q_x\), hivyo\(\vecs F\) ni kihafidhina. Tangu\(P_x=e^x \sin y\) na\(Q_y=e^x \sin y\),\(P_x+Q_y=0\) na shamba ni chanzo bure.
Ili kupata kazi inayoweza\(\vecs F\), basi\(f\) iwe kazi ya uwezo. Kisha\(\vecs \nabla f=\vecs F\), hivyo\(f_x(x,y)=e^x \sin y\). Kuunganisha equation hii kwa heshima na x anatoa\(f(x,y)=e^x \sin y+h(y)\). Tangu\(f_y(x,y)=e^x \cos y\), kutofautisha\(f\) kwa heshima na y anatoa\(e^x\cos y=e^x\cos y+h′(y)\). Kwa hiyo, tunaweza kuchukua\(h(y)=0\), na\(f(x,y)=e^x\sin y\) ni kazi uwezo kwa ajili ya\(f\).
Ili kuthibitisha kuwa\(f\) ni kazi ya harmonic, kumbuka kuwa\(f_{xx}(x,y)=\dfrac{\partial}{\partial x}(e^x\sin y)=e^x \sin y\) na
\(f_{yy}(x,y)=\dfrac{\partial}{\partial x}(e^x\cos y)=−e^x\sin y\). Kwa hiyo,\(f_{xx}+f_{yy}=0\), na\(f\) satisfies equation Laplace ya.
Ni kazi\(f(x,y)=e^{x+5y}\) harmonic?
- Kidokezo
-
Kuamua kama kazi satisfies equation Laplace ya.
- Jibu
-
Hapana
Theorem ya Green juu ya Mikoa Mkuu
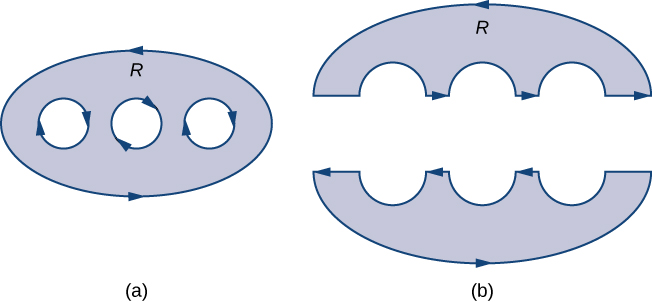
Theorem ya Green, kama ilivyoelezwa, inatumika tu kwa mikoa ambayo ni kushikamana tu-yaani, theorem ya Green kama ilivyoelezwa hadi sasa haiwezi kushughulikia mikoa yenye mashimo. Hapa, tunapanua theorem ya Green ili iweze kufanya kazi kwenye mikoa yenye mashimo mengi (Kielelezo\(\PageIndex{12}\)).
Kabla ya kujadili upanuzi wa theorem ya Green, tunahitaji kwenda juu ya istilahi fulani kuhusu mipaka ya kanda. Hebu\(D\) kuwa kanda na basi\(C\) kuwa sehemu ya mipaka ya\(D\). Tunasema kuwa\(C\) inaelekezwa vizuri ikiwa, tunapotembea pamoja\(C\) katika mwelekeo wa mwelekeo, kanda\(D\) ni daima upande wa kushoto. Kwa hiyo, mwelekeo wa kinyume cha mipaka ya disk ni mwelekeo mzuri, kwa mfano. Curve\(C\) inaelekezwa vibaya ikiwa, tunapotembea pamoja\(C\) katika mwelekeo wa mwelekeo, kanda\(D\) ni daima juu ya haki yetu. Mwelekeo wa saa moja kwa moja wa mipaka ya disk ni mwelekeo hasi, kwa mfano.
Hebu\(D\) kuwa kanda na mashimo finitely wengi (hivyo kwamba\(D\) ina finitely wengi curves mipaka), na kuashiria mipaka ya\(D\) na\(\partial D\) (Kielelezo\(\PageIndex{13}\)). Kupanua theorem ya Green ili iweze kushughulikia\(D\), tunagawanya kanda\(D\) katika mikoa miwili,\(D_1\) na\(D_2\) (pamoja\(\partial D_1\) na mipaka husika na\(\partial D_2\)), kwa namna ambayo\(D=D_1\cup D_2\) na\(D_1\) wala\(D_2\) haina mashimo yoyote (Kielelezo\(\PageIndex{13}\)).
Tuseme mipaka ya\(D\) ni oriented kama katika takwimu, na mashimo ya ndani kutokana mwelekeo hasi na mipaka ya nje kupewa mwelekeo chanya. Mpaka wa kila mkoa unaounganishwa tu\(D_1\) na\(D_2\) unaelekezwa vizuri. Ikiwa\(\vecs F\) ni shamba la vector linaloelezwa\(D\), basi theorem ya Green inasema kuwa
\[\begin{align} \oint_{\partial D} \vecs F·d\vecs{r} &=\oint_{\partial D_1}\vecs F·d\vecs{r}+\oint_{\partial D_2}\vecs F·d\vecs{r} \\ &=\iint_{D_1}Q_x−P_y\,dA+\iint_{D_2}Q_x−P_y\,dA \\ &=\iint_D (Q_x−P_y)\,dA.\end{align} \nonumber \]
Kwa hiyo, theorem ya Green bado inafanya kazi katika kanda yenye mashimo.
Kuona jinsi hii inafanya kazi katika mazoezi, fikiria annulus\(D\) katika Kielelezo\(\PageIndex{14}\) na tuseme kwamba\(F=⟨P,Q⟩\) ni uwanja vector defined juu ya annulus hii. Mkoa\(D\) una shimo, hivyo sio tu kushikamana. Orient mzunguko wa nje wa annulus kinyume na mzunguko wa ndani clockwise (Kielelezo\(\PageIndex{14}\)) ili, tunapogawanya kanda ndani\(D_1\) na\(D_2\), tunaweza kuweka kanda upande wetu wa kushoto tunapotembea njia inayovuka mipaka. Hebu\(D_1\) kuwa nusu ya juu ya annulus na\(D_2\) uwe nusu ya chini. Hakuna mikoa hii ina mashimo, kwa hiyo\(D\) tumegawanywa katika mikoa miwili iliyounganishwa tu.
Sisi studio kila kipande cha mipaka hii mpya kama\(P_i\) kwa baadhi\(i\), kama katika Kielelezo\(\PageIndex{14}\). Ikiwa tunaanza\(P\) na kusafiri kando ya mipaka iliyoelekezwa, sehemu ya kwanza ni\(P_1\)\(P_2\), basi\(P_3\), na\(P_4\). Sasa\(D_1\) tumepitia na kurudi\(P\). Ifuatayo, tunaanza\(P\) tena na tunapita\(D_2\). Kwa kuwa kipande cha kwanza cha mipaka ni sawa na\(P_4\) ndani\(D_1\), lakini inaelekezwa kinyume chake, kipande cha kwanza cha\(D_2\) ni\(−P_4\). Kisha, tuna\(P_5\), basi\(−P_2\), na hatimaye\(P_6\).
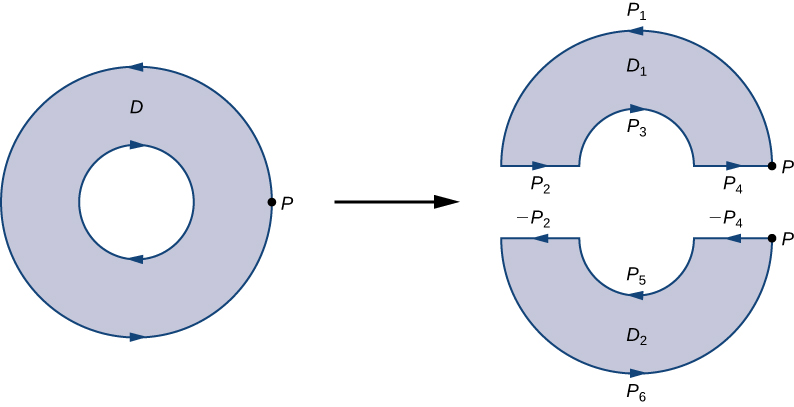
Kielelezo\(\PageIndex{14}\) inaonyesha njia ambayo hupitia mipaka ya\(D\). Angalia kwamba njia hii inapita mipaka ya kanda\(D_1\), inarudi kwenye hatua ya mwanzo, na kisha hupitia mipaka ya kanda\(D_2\). Zaidi ya hayo, tunapotembea njiani, kanda ni daima upande wa kushoto wetu. Angalia kwamba njia hii ya\(P_i\) njia inashughulikia mipaka yote ya kanda\(D\). Kama tulikuwa tu kupita sehemu moja ya mipaka ya\(D\), basi hatuwezi kuomba Theorem Green ya\(D\).
Mpaka wa nusu ya juu ya annulus, kwa hiyo, ni\(P_1\cup P_2\cup P_3\cup P_4\) na mipaka ya nusu ya chini ya annulus ni\(−P_4\cup P_5\cup −P_2\cup P_6\). Kisha, Theorem ya Green ina maana
\[\begin{align} \oint_{\partial D}\vecs F·d\vecs{r} &=\int_{P_1}\vecs F·d\vecs{r}+\int_{P_2}\vecs F·d\vecs{r}+\int_{P_3}\vecs F·d\vecs{r}+\int_{P_4}\vecs F·d\vecs{r}+\int_{−P_4}\vecs F·d\vecs{r}+\int_{P_5}\vecs F·d\vecs{r}+\int_{−P_2}\vecs F·d\vecs{r}+\int_{P_6}\vecs F·d\vecs{r} \\ &=\int_{P_1}\vecs F·d\vecs{r}+\int_{P_2}\vecs F·d\vecs{r}+\int_{P_3}\vecs F·d\vecs{r}+\int_{P_4}\vecs F·d\vecs{r}+\int_{P_4}\vecs F·d\vecs{r}+\int_{P_5}\vecs F·d\vecs{r}+\int_{−P_2}\vecs F·d\vecs{r}+\int_{P_6}\vecs F·d\vecs{r} \\ &=\int_{P_1}\vecs F·d\vecs{r}+\int_{P_3}\vecs F·d\vecs{r}+\int_{P_5}\vecs F·d\vecs{r}+\int_{P_6}\vecs F·d\vecs{r} \\ &=\oint_{\partial D_1}\vecs F·d\vecs{r}+\oint_{\partial D_2}\vecs F·d\vecs{r}\\ &=\iint_{D_1}(Q_x−P_y)\,dA+\iint_{D_2}(Q_x−P_y)\,dA \\ &=\iint_D(Q_x−P_y)\,dA. \end{align} \nonumber \]
Kwa hiyo, sisi kufika katika equation kupatikana katika Theorem Green ya-yaani,
\[\oint_{\partial D}\vecs F·d\vecs{r}=\iint_D (Q_x−P_y)\,dA. \nonumber \]
Mantiki hiyo ina maana kwamba aina ya flux ya theorem ya Green pia inaweza kupanuliwa kwa kanda yenye mashimo mengi sana:
\[\oint_C F·N\,ds=\iint_D (P_x+Q_y)\,dA. \nonumber \]
Tumia hesabu muhimu
\[\oint_{\partial D}(\sin x−\dfrac{y^3}{3})dx+(\dfrac{y^3}{3}+\sin y)dy, \nonumber \]
\(D\)wapi annulus iliyotolewa na kukosekana kwa usawa Polar\(1≤r≤2\),\(0≤\theta≤2\pi\).
Suluhisho
Ingawa\(D\) sio tu kushikamana, tunaweza kutumia fomu iliyopanuliwa ya theorem ya Green ili kuhesabu muhimu. Tangu ushirikiano hutokea juu ya annulus, sisi kubadilisha kwa kuratibu polar:
\[\begin{align*} \oint_{\partial D}(\sin x−\dfrac{y^3}{3})\,dx+(\dfrac{x^3}{3}+\sin y)\,dy &=\iint_D (Q_x−P_y)\,dA \\ &=\iint_D (x^2+y^2)\,dA\\ &=\int_0^{2\pi}\int_1^2 r^3\,drd\theta=\int_0^{2\pi} \dfrac{15}{4}\,d\theta \\ &=\dfrac{15\pi}{2}. \end{align*}\]
Hebu\(\vecs F=⟨P,Q⟩=⟨\dfrac{y}{x^2+y^2},-\dfrac{x}{x^2+y^2}⟩\) na hebu\(C\) kuwa yoyote rahisi imefungwa Curve katika ndege oriented kinyume chake. Je, ni maadili iwezekanavyo ya\(\oint_C \vecs F·d\vecs{r}\)?
Suluhisho
Sisi kutumia fomu kupanuliwa ya theorem Green ya kuonyesha kwamba\(\oint_C \vecs F·d\vecs{r}\) ni aidha\(0\) au\(−2\pi\) - kwamba ni, bila kujali jinsi mambo Curve\(C\) ni, line muhimu ya\(\vecs F\) pamoja\(C\) unaweza kuwa na moja tu ya maadili mawili iwezekanavyo. Tunazingatia kesi mbili: kesi wakati\(C\) inahusisha asili na kesi wakati\(C\) haihusishi asili.
Uchunguzi wa 1: C Haiingii Mwanzo
Katika kesi hiyo, kanda\(C\) iliyoambatanishwa na imeunganishwa tu kwa sababu shimo pekee katika uwanja wa\(\vecs F\) ni asili. Tulionyesha katika majadiliano yetu ya sehemu za msalaba ambazo\(\vecs F\) zinatimiza hali ya msalaba-sehemu. Ikiwa tunazuia kikoa cha\(\vecs F\) tu\(C\) na kanda ambayo inafunga, basi\(\vecs F\) kwa kikoa hiki kilichozuiliwa sasa kinaelezwa kwenye uwanja unaounganishwa tu. Kwa kuwa\(\vecs F\) inatimiza mali ya sehemu ya msalaba kwenye uwanja wake uliozuiliwa, shamba\(\vecs F\) hilo ni kihafidhina kwenye eneo hili lililounganishwa tu na hivyo mzunguko\(\oint_C \vecs F·d\vecs{r}\) ni sifuri.
Uchunguzi wa 2: C Inajumuisha Mwanzo
Katika kesi hiyo, kanda iliyofungwa na\(C\) haijaunganishwa tu kwa sababu eneo hili lina shimo la asili. Hebu\(C_1\) kuwa mduara wa Radius unaozingatia katika asili ili\(C_1\) ni kabisa ndani ya kanda iliyoambatanishwa na\(C\) (Kielelezo\(\PageIndex{15}\)). \(C_1\)Kutoa mwelekeo wa saa.
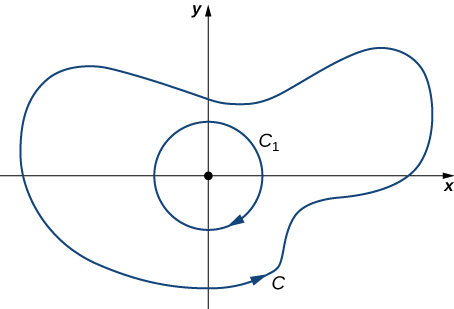
Hebu\(D\) kuwa kanda kati\(C_1\) na\(C\), na\(C\) ni orientated kinyume chake. Kwa toleo la kupanuliwa la theorem ya Green,
\[\begin{align*} \int_C \vecs F·d\vecs{r}+\int_{C_1}\vecs F·d\vecs{r} &=\iint_D Qx_−P_y \,dA \\[4pt] &=\iint_D−\dfrac{y^2−x^2}{{(x^2+y^2)}^2}+\dfrac{y^2−x^2}{{(x^2+y^2)}^2}dA \\[4pt] &=0, \end{align*}\]
na kwa hiyo
\[\int_C \vecs F·d\vecs{r}=−\int_{C_1} \vecs F·d\vecs{r}. \nonumber \]
Kwa kuwa\(C_1\) ni Curve maalum, tunaweza kutathmini\(\int_{C_1}\vecs F·d\vecs{r}\). Hebu
\[ x=a\cos t, \;\; y=a\sin t, \;\; 0≤t≤2\pi \nonumber \]
kuwa parameterization ya\(C_1\). Kisha,
\[\begin{align*} \int_{C_1}\vecs F·d\vecs{r} &=\int_0^{2\pi} F(r(t))·r′(t)dt \\[4pt] &=\int_0^{2\pi} ⟨−\dfrac{\sin(t)}{a},−\dfrac{\cos(t)}{a}⟩·⟨−a\sin(t),−a\cos(t)⟩dt \\[4pt] &=\int_0^{2\pi}{\sin}^2(t)+{\cos}^2(t)dt \\[4pt] &=\int_0^{2\pi}dt=2\pi. \end{align*}\]
Kwa hiyo,\(\int_C F·ds=−2\pi\).
Mahesabu muhimu\(\oint_{\partial D}\vecs F·d\vecs{r}\), wapi\(D\) annulus iliyotolewa na kutofautiana Polar\(2≤r≤5\),\(0≤\theta≤2\pi\), na\(F(x,y)=⟨x^3,5x+e^y\sin y⟩\).
- Kidokezo
-
Tumia toleo la kupanuliwa la theorem ya Green.
- Jibu
-
\(105\pi\)
Fikiria wewe ni daktari ambaye amepokea picha ya resonance ya magnetic ya ubongo wa mgonjwa wako. Ubongo una tumor (Kielelezo\(\PageIndex{16}\)). Je, tumor ni kubwa sana? Ili kuwa sahihi, ni eneo gani la kanda nyekundu? Sehemu nyekundu ya tumor ina sura isiyo ya kawaida, na kwa hiyo haiwezekani kwamba utaweza kupata seti ya equations au kutofautiana kwa kanda na kisha uweze kuhesabu eneo lake kwa njia za kawaida. Unaweza takriban eneo hilo kwa kukata kanda katika viwanja vidogo (mbinu ya jumla ya Riemann), lakini njia hii daima inatoa jibu kwa makosa fulani.
Badala ya kujaribu kupima eneo la kanda moja kwa moja, tunaweza kutumia kifaa kinachoitwa planimeter inayoendelea kuhesabu eneo la kanda hasa, kwa kupima mipaka yake. Katika mradi huu kuchunguza jinsi planimeter kazi, na unatumia Theorem Green ya kuonyesha kifaa huhesabu eneo kwa usahihi.
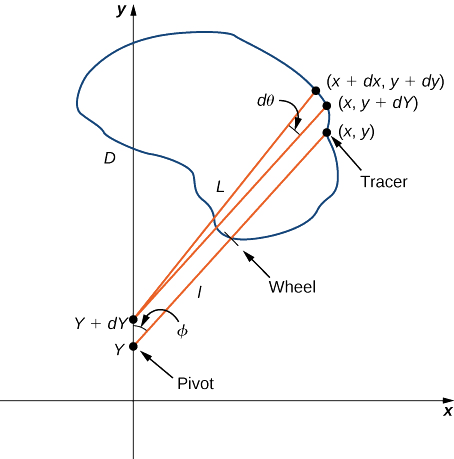
Mpangilio unaozunguka ni kifaa kinachopima eneo la mkoa wa mipango kwa kufuatilia mipaka ya eneo hilo (Kielelezo\(\PageIndex{17}\)). Ili kupima eneo la kanda, tunaendesha tu mchezaji wa planimeter karibu na mipaka ya kanda. Mpangilio hupima idadi ya zamu kwa njia ambayo gurudumu huzunguka tunapofuatilia mipaka; eneo la sura ni sawa na idadi hii ya zamu za gurudumu. Tunaweza hupata sahihi uwiano equation kutumia theorem Green ya. Kama mfuatiliaji anazunguka mipaka ya kanda, mkono wa tracer huzunguka na roller huenda na kurudi (lakini hauzunguki).
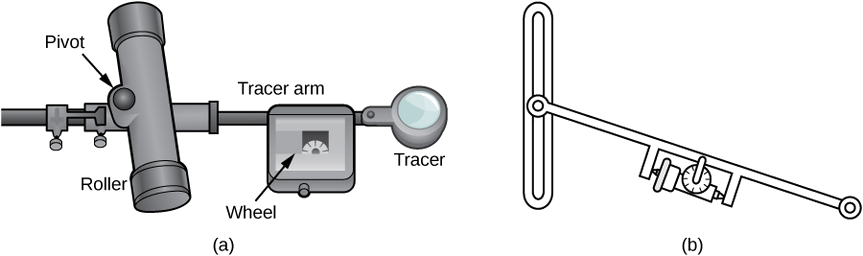
Hebu\(C\) kuashiria mipaka ya kanda\(D\), eneo la kuhesabiwa. Kama tracer inapita curve\(C\), kudhani roller hatua pamoja y -axis (tangu roller haina mzunguko, mtu anaweza kudhani ni hatua pamoja na mstari wa moja kwa moja). Tumia kuratibu\((x,y)\) kuwakilisha pointi kwenye mipaka\(C\), na kuratibu\((0,Y)\) kuwakilisha nafasi ya egemeo. Kama athari planimeter\(C\), egemeo hatua pamoja y -axis wakati mkono tracer huzunguka juu ya egemeo.
Tazama uhuishaji mfupi wa planimeter katika hatua.
Kuanza uchambuzi kwa kuzingatia mwendo wa tracer kama hatua kutoka hatua\((x,y)\) kinyume na uhakika\((x+dx,y+dy)\) kwamba ni karibu na\((x,y)\) (Kielelezo\(\PageIndex{18}\)). Pivot pia huenda, kutoka hatua\((0,Y)\) hadi sehemu ya karibu\((0,Y+dY)\). Je, gurudumu hugeuka kiasi gani kutokana na mwendo huu? Ili kujibu swali hili, piga mwendo katika sehemu mbili. Kwanza, roll egemeo pamoja y -axis kutoka\((0,Y)\) kwenda\((0,Y+dY)\) bila kupokezana mkono tracer. Mkono wa tracer kisha unakaribia\((x,y+dY)\) wakati wa kudumisha angle ya mara kwa mara\(\phi\) na x -axis. Pili, mzunguko mkono wa tracer kwa angle\(d\theta\) bila kusonga roller. Sasa mtafiti ni katika hatua\((x+dx,y+dy)\). Hebu ll kuwa umbali kutoka egemeo kwa gurudumu na basi L kuwa umbali kutoka egemeo kwa tracer (urefu wa mkono tracer).

- Eleza kwa nini umbali jumla kwa njia ambayo gurudumu Rolls mwendo ndogo tu ilivyoelezwa ni\(\sin \phi dY+ld\theta=\dfrac{x}{L}dY+ld\theta\).
- Onyesha hilo\(\oint_C d\theta=0\).
- Matumizi hatua 2 kuonyesha kwamba jumla rolling umbali wa gurudumu kama tracer hupitia Curve\(C\) ni
Jumla gurudumu roll\(=\dfrac{1}{L}\oint_C xdY\).
Sasa kwa kuwa una equation kwa jumla rolling umbali wa gurudumu, kuunganisha equation hii Theorem Green ya mahesabu ya eneo\(D\) iliyoambatanishwa na\(C\). - Onyesha hilo\(x^2+(y−Y)^2=L^2\).
- Fikiria mwelekeo wa planimeter ni kama inavyoonekana katika Kielelezo\(\PageIndex{18}\). Eleza kwa nini\(Y≤y\), na utumie usawa huu ili kuonyesha kuna thamani ya kipekee ya\(Y\) kwa kila hatua\((x,y)\):\(Y=y=\sqrt{L^2−x^2}\).
- Tumia hatua ya 5 ili kuonyesha kwamba\(dY=dy+\dfrac{x}{L^2−x^2}dx.\)
- Tumia theorem ya Green ili kuonyesha hilo\(\displaystyle \oint_C \dfrac{x}{L^2−x^2}dx=0\).
- Matumizi hatua 7 kuonyesha kwamba jumla gurudumu roll ni
\[\text{Total wheel roll}\quad =\quad 1L\oint_C x\,dy. \nonumber \]
Ilichukua kazi kidogo, lakini equation hii inasema kuwa kutofautiana kwa ushirikiano Y katika hatua ya 3 inaweza kubadilishwa na y.
- Tumia theorem ya Green ili kuonyesha kwamba eneo la\(D\) ni\(\oint_C xdy\). mantiki ni sawa na mantiki kutumika kuonyesha kwamba eneo la\(\displaystyle D=12\oint_C −y\,dx+x\,dy\).
- Hitimisha kuwa eneo la\(D\) sawa na urefu wa mkono wa tracer umeongezeka kwa umbali wa jumla wa gurudumu.
Sasa unajua jinsi planimeter inavyofanya kazi na umetumia theorem ya Green ili kuhalalisha kuwa inafanya kazi. Ili kuhesabu eneo la mkoa wa mipango\(D\), tumia planimeter kufuatilia mipaka ya kanda. Eneo la kanda ni urefu wa mkono wa tracer unaoongezeka kwa umbali gurudumu lililovingirishwa.
Dhana muhimu
- Theorem ya Green inahusiana muhimu juu ya kanda iliyounganishwa kwa muhimu juu ya mipaka ya kanda. Theorem ya Green ni toleo la Theorem ya Msingi ya Calculus katika mwelekeo mmoja wa juu.
- Theorem ya Green inakuja katika aina mbili: fomu ya mzunguko na fomu ya flux. Katika fomu ya mzunguko, integrand ni\(\vecs F·\vecs T\). Katika fomu ya flux, integrand ni\(\vecs F·\vecs N\).
- Theorem Green inaweza kutumika kubadilisha mstari mgumu muhimu katika rahisi mara mbili muhimu, au kubadilisha ngumu mara mbili muhimu katika rahisi line muhimu.
- Shamba la vector ni chanzo bure ikiwa ina kazi ya mkondo. Mzunguko wa uwanja wa vector usio na chanzo kwenye safu iliyofungwa ni sifuri, kama mzunguko wa shamba la vector la kihafidhina katika safu iliyofungwa ni sifuri.
Mlinganyo muhimu
- Theorem Green ya, mzunguko fomu
\(\displaystyle ∮_C P\,dx+Q\,dy=∬_D Q_x−P_y\,dA\), ambapo\(C\) ni mipaka ya\(D\) - Theorem ya Green, flux fomu
\(\displaystyle ∮_C\vecs F·\vecs N\,ds=∬_D P_x+Q_y\,dA\),\(C\) wapi mipaka ya\(D\) - Theorem ya Green, toleo la kupanuliwa
\(\displaystyle ∮_{\partial D}\vecs F·d\vecs{r}=∬_D Q_x−P_y\,dA\)
faharasa
- Theorem ya Green
- inahusiana muhimu juu ya mkoa kushikamana na muhimu juu ya mipaka ya kanda
- kazi ya mkondo
- ikiwa\(\vecs F=⟨P,Q⟩\) ni uwanja wa vector usio na chanzo, basi kazi ya mkondo\(g\) ni kazi kama hiyo\(P=g_y\) na\(Q=−g_x\)


