16.3: Kihafidhina Vector Mashamba

Malengo ya kujifunza

• Eleza curves rahisi na imefungwa; kufafanua mikoa iliyounganishwa na iliyounganishwa tu.
• Eleza jinsi ya kupata kazi inayoweza kutumika kwa uwanja wa vector wa kihafidhina.
• Matumizi Theorem Msingi kwa Line Integrals kutathmini line muhimu katika uwanja vector.
• Eleza jinsi ya kupima shamba la vector ili kuamua ikiwa ni kihafidhina.

Katika sehemu hii, tunaendelea utafiti wa mashamba ya vector ya kihafidhina. Sisi kuchunguza Theorem Msingi kwa Line Integrals, ambayo ni generalization muhimu ya Theorem Msingi ya Calculus kwa line integrals ya mashamba kihafidhina vector. Sisi pia kugundua kuonyesha jinsi ya kupima kama kupewa vector shamba ni kihafidhina, na kuamua jinsi ya kujenga kazi uwezo kwa ajili ya uwanja vector inayojulikana kuwa kihafidhina.

Curves na Mikoa

Kabla ya kuendelea na utafiti wetu wa mashamba ya vector kihafidhina, tunahitaji ufafanuzi wa kijiometri Theorems katika sehemu zifuatazo zote hutegemea kuunganisha juu ya aina fulani za curves na mikoa, kwa hiyo tunaendeleza ufafanuzi wa curves hizo na mikoa hapa. Sisi kwanza kufafanua aina mbili maalum ya curves: curves imefungwa na curves rahisi. Kama tulivyojifunza, curve imefungwa ni moja ambayo huanza na kuishia kwa hatua moja. Curve rahisi ni moja ambayo haina kuvuka yenyewe. Curve ambayo imefungwa na rahisi ni rahisi imefungwa Curve (Kielelezo\(\PageIndex{1}\)).

Kielelezo\(\PageIndex{1}\). Aina ya curves ambazo ni rahisi au si rahisi na zimefungwa au hazifungwa.

Ufafanuzi: Curves imefungwa

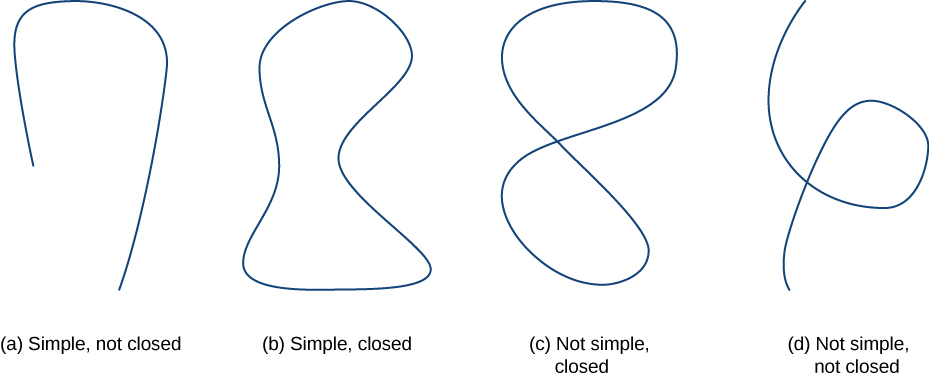
Curve\(C\) ni Curve imefungwa ikiwa kuna parameterization\(\vecs r(t)\),\(a≤t≤b\) ya\(C\) vile kwamba parameterization hupitia Curve hasa mara moja na\(\vecs r(a)=\vecs r(b)\). Curve\(C\) ni Curve rahisi kama\(C\) haina msalaba yenyewe. Hiyo\(C\) ni rahisi ikiwa kuna parameterization\(\vecs r(t)\),\(a≤t≤b\) ya\(C\) vile kwamba\(\vecs r\) ni moja kwa moja juu\((a,b)\). Inawezekana kwa\(\vecs r(a)=\vecs r(b)\), maana yake ni kwamba Curve rahisi pia imefungwa.

Mfano\(\PageIndex{1}\): Determining Whether a Curve Is Simple and Closed

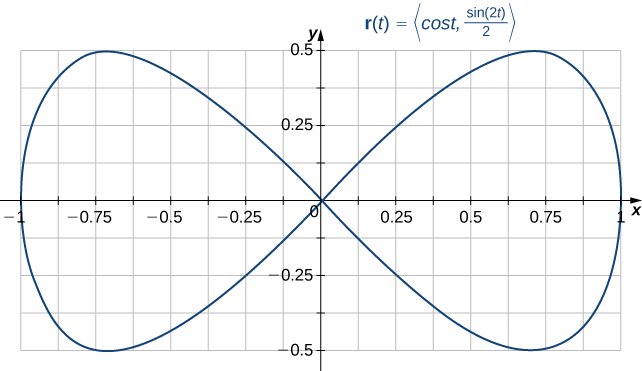
Je, ni safu na parameterization\(\vecs{r}(t)=\left\langle\cos t,\frac{\sin(2t)}{2}\right\rangle\),\(0≤t≤2\pi\) rahisi imefungwa Curve?

Suluhisho

Kumbuka kwamba\(\vecs{r}(0)=⟨1,0⟩=\vecs r(2\pi)\); kwa hiyo, curve imefungwa. Curve si rahisi, hata hivyo. Ili kuona hili, kumbuka kuwa\(\vecs{r}\left(\frac{\pi}{2}\right)=⟨0,0⟩=\vecs{r}\left(\frac{3\pi}{2}\right)\), na kwa hiyo curve huvuka yenyewe katika asili (Kielelezo\(\PageIndex{2}\)).

Kielelezo\(\PageIndex{2}\) . Curve kwamba ni kufungwa lakini si rahisi.

Zoezi\(\PageIndex{1}\)

Je Curve iliyotolewa na parameterization\(\vecs{r}(t)=⟨2\cos t,3\sin t⟩\)\(0≤t≤6\pi\),, rahisi imefungwa Curve?

Kidokezo

Mchoro Curve.

Jibu

Ndio

Wengi wa theorems katika sura hii yanahusiana muhimu juu ya mkoa kwa muhimu juu ya mipaka ya kanda, ambapo mipaka ya kanda ni rahisi kufungwa Curve au muungano wa curves rahisi imefungwa. Ili kuendeleza theorems hizi, tunahitaji ufafanuzi wa kijiometri mbili kwa mikoa: ile ya kanda iliyounganishwa na ile ya kanda iliyounganishwa tu. Eneo lililounganishwa ni moja ambamo kuna njia katika kanda inayounganisha pointi zozote mbili ambazo ziko ndani ya eneo hilo. Eneo lililounganishwa tu ni kanda iliyounganishwa ambayo haina mashimo yoyote ndani yake. Mawazo haya mawili, pamoja na dhana ya safu rahisi iliyofungwa, inatuwezesha kutaja generalizations kadhaa ya Theorem ya Msingi ya Calculus baadaye katika sura. Ufafanuzi huu wawili ni halali kwa mikoa katika idadi yoyote ya vipimo, lakini tunahusika tu na mikoa katika vipimo viwili au vitatu.

Ufafanuzi: mikoa iliyounganishwa

Mkoa D ni kanda iliyounganishwa ikiwa, kwa pointi\(P_1\) zozote mbili na\(P_2\), kuna njia kutoka\(P_1\) kwa\(P_2\) na maelezo yaliyomo ndani ya D. kanda D ni kanda tu kushikamana kama D ni kushikamana kwa yoyote rahisi imefungwa Curve C ambayo ipo ndani ya D, na Curve C inaweza kupunguzwa kuendelea kwa uhakika wakati kukaa kabisa ndani ya D. Katika vipimo viwili, kanda imeunganishwa tu ikiwa imeunganishwa na haina mashimo.

Mikoa yote iliyounganishwa imeunganishwa, lakini sio mikoa yote iliyounganishwa imeunganishwa tu (Kielelezo\(\PageIndex{3}\)).

Kielelezo\(\PageIndex{3}\): Sio mikoa yote iliyounganishwa imeunganishwa tu. (a) Mikoa iliyounganishwa tu haina mashimo. (b) Mikoa iliyounganishwa ambayo haijaunganishwa tu inaweza kuwa na mashimo lakini bado unaweza kupata njia katika eneo kati ya pointi zozote mbili. (c) Eneo ambalo halijaunganishwa lina baadhi ya pointi ambazo haziwezi kushikamana na njia katika kanda.

Zoezi\(\PageIndex{2}\)

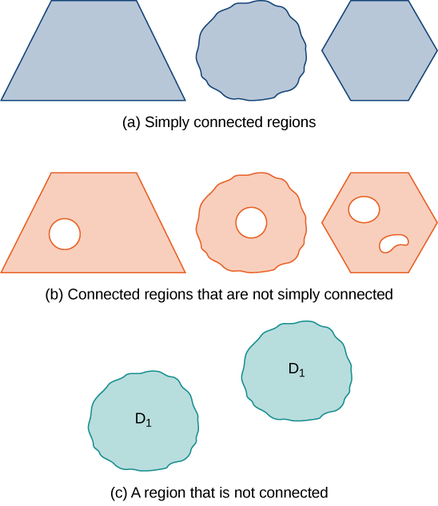
Je, kanda iliyo katika picha iliyo chini imeunganishwa? Je, kanda imeunganishwa tu?

Kidokezo

Fikiria ufafanuzi.

Jibu

Kanda katika takwimu imeunganishwa. Kanda katika takwimu sio tu kushikamana.

Theorem ya msingi kwa ajili ya mstari Integrals

Sasa kwa kuwa tunaelewa baadhi ya curves msingi na mikoa, hebu kuzalisha Theorem ya Msingi ya Calculus kwa mstari integrals. Kumbuka kwamba Theorem ya Msingi ya Calculus inasema kwamba ikiwa kazi\(f\) ina antiderivative\(F\), basi muhimu ya\(f\) kutoka\(a\) kwa\(b\) inategemea tu maadili ya\(F\) saa\(a\) na\(b\) katika-yaani,

\[\int_a^bf(x)\,dx=F(b)−F(a). \nonumber \]

Ikiwa tunadhani ya gradient kama derivative, basi theorem hiyo inashikilia kwa integrals line vector. Tunaonyesha jinsi hii inavyofanya kazi kwa kutumia mfano wa motisha.

Mfano\(\PageIndex{2}\): Evaluating a Line Integral and the Antiderivatives of the Endpoints

Hebu\(\vecs{F}(x,y)=⟨2x,4y⟩\). Tumia\(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}\), ambapo C ni sehemu ya mstari kutoka\((0,0)\) kwa\((2,2)\) (Kielelezo\(\PageIndex{4}\)).

Suluhisho

Tunatumia njia kutoka sehemu iliyopita ili kuhesabu\(\int_C \vecs{F} \cdot d\vecs{r}\). Curve C inaweza parameterized na\(\vecs{r}(t)=⟨2t,2t⟩\),\(0≤t≤1\). Kisha,\(\vecs{F}(\vecs r(t))=⟨4t,8t⟩\) na\(\vecs r′(t)=⟨2,2⟩\), ambayo ina maana kwamba

\[\begin{align*} \int_C \vecs{F}·d\vecs{r} &=\int_0^1⟨4t,8t⟩·⟨2,2⟩dt \\[4pt] &=\int_0^1(8t+16t)dt=\int_0^1 24tdt\\[4pt] &={\big[12t^2\big]}_0^1=12. \end{align*}\]

Kielelezo\(\PageIndex{4}\): Thamani ya mstari muhimu\(\int_C \vecs{F} \cdot d\vecs{r}\) inategemea tu thamani ya kazi ya\(\vecs{F}\) uwezo wa mwisho wa pembe.

Kumbuka kwamba\(\vecs{F}=\vecs \nabla f\), wapi\(f(x,y)=x^2+2y^2\). Ikiwa tunadhani ya gradient kama derivative, basi\(f\) ni “antiderivative” ya\(\vecs{F}\). Katika kesi ya integrals moja-variable\(g(b)−g(a)\), muhimu ya derivative\(g′(x)\) ni, ambapo ni mwanzo wa muda wa ushirikiano na b ni mwisho. Kama vector line integrals kazi kama integrals single-variable, basi\(\vecs{F}\) tunataka kutarajia muhimu kuwa\(f(P_1)−f(P_0)\), ambapo\(P_1\) ni endpoint ya Curve ya ushirikiano na\(P_0\) ni hatua ya mwanzo. Angalia kwamba hii ndiyo kesi kwa mfano huu:

\[\int_C \vecs{F} \cdot d\vecs{r}=\int_C \vecs \nabla f \cdot d\vecs{r}=12 \nonumber \]

na

\[f(2,2)−f(0,0)=4+8−0=12. \nonumber \]

Kwa maneno mengine, muhimu ya “derivative” inaweza kuhesabiwa kwa kutathmini “antiderivative” katika mwisho wa Curve na kutoa, kama vile integrals moja-variable.

Theorem ifuatayo inasema kuwa, chini ya hali fulani, kilichotokea katika mfano uliopita kinashikilia shamba lolote la gradient. Theorem hiyo inashikilia integrals line vector, ambayo tunaita Theorem ya Msingi kwa Line Integrals.

Theorem: THEOREM MSINGI KWA LINE INTEGRALS

Hebu C kuwa piecewise laini Curve na parameterization\(\vecs r(t)\),\(a≤t≤b\). Hebu\(f\) kuwa kazi ya vigezo mbili au tatu na derivatives kwanza ili sehemu ambazo zipo na zinaendelea kwenye C. Kisha,

\[\int_C \vecs \nabla f \cdot d\vecs{r}=f(\vecs r(b))−f(\vecs r(a)). \label{FunTheLine} \]

Ushahidi

Kwanza,

\[\int_C \vecs \nabla f \cdot d \vecs{r}=\int_a^b \vecs \nabla f( \vecs r(t)) \cdot \vecs r′(t)\,dt. \nonumber \]

Kwa utawala wa mnyororo,

\[\dfrac{d}{dt}(f( \vecs r(t))= \vecs \nabla f( \vecs r(t)) \cdot \vecs r′(t) \nonumber \]

Kwa hiyo, kwa Theorem ya Msingi ya Calculus,

\[\begin{align*} \int_C \vecs \nabla f \cdot d \vecs{r} &=\int_a^b \vecs \nabla f( \vecs r(t)) \cdot \vecs r′(t)dt \\[4pt] &=\int_a^b\dfrac{d}{dt}(f( \vecs r(t))dt \\[4pt] &={\big[f( \vecs r(t))\big]}_{t=a}^{t=b}\\[4pt] &=f( \vecs r(b))−f( \vecs r(a)). \end{align*}\]

\(\square\)

Tunajua kwamba kama\(\vecs{F}\) ni kihafidhina vector shamba, kuna kazi uwezo\(f\) kama kwamba\( \vecs \nabla f= \vecs F\). Kwa hiyo

\[\int_C \vecs F·d\vecs r=\int_C\vecs \nabla f·d\vecs{r}=f(\vecs r(b))−f(\vecs r(a)). \nonumber \]

Kwa maneno mengine, kama ilivyo na Theorem ya Msingi ya Calculus, kompyuta ya mstari muhimu\(\int_C \vecs F·d\vecs{r}\), ambapo\(\vecs{F}\) ni kihafidhina, ni mchakato wa hatua mbili:

1. Kupata kazi uwezo (“antiderivative”)\(f\) kwa\(\vecs{F}\) na
2. Compute thamani ya\(f\) katika endpoints ya\(C\) na mahesabu tofauti yao\(f(\vecs r(b))−f(\vecs r(a))\).

Kumbuka, hata hivyo, kuna tofauti moja kubwa kati ya Theorem ya Msingi ya Calculus na Theorem ya Msingi kwa Line Integrals:
kazi ya variable moja kwamba ni kuendelea lazima antiderivative. Hata hivyo, uwanja wa vector, hata kama unaendelea, hauhitaji kuwa na kazi inayoweza.

Mfano\(\PageIndex{3}\): Applying the Fundamental Theorem

Mahesabu muhimu\(\int_C \vecs{F} \cdot d\vecs{r}\), wapi\(\vecs{F}(x,y,z)=⟨2x\ln y,\dfrac{x^2}{y}+z^2,2yz⟩\) na\(C\) ni Curve na parameterization\(\vecs{r}(t)=⟨t^2,t,t⟩\),\(1≤t≤e\)

1. bila kutumia Theorem ya Msingi ya Line Integrals na
2. kutumia Theorem ya Msingi ya Line Integrals.

Suluhisho

1. Kwanza, hebu tuhesabu muhimu bila Theorem ya Msingi kwa Line Integrals na badala yake tumia njia tuliyojifunza katika sehemu iliyopita:

\[\begin{align*} \int_C \vecs{F} \cdot dr &=\int_1^e\vecs F(\vecs r(t)) \cdot \vecs r′(t)\,dt\\[4pt] &=\int_1^e⟨2t^2\ln t,\dfrac{t^4}{t}+t^2,2t^2⟩ \cdot ⟨2t,1,1⟩\,dt\\[4pt] &=\int_1^e(4t^3\ln t+t^3+3t^2)\,dt \\[4pt] &=\int_1^e 4t^3\ln t \,dt+\int_1^e(t^3+3t^2)\,dt \\[4pt] &=\int_1^e 4t^3\ln t\,dt+{\Big[\dfrac{t^4}{4}+t^3\Big]}_1^e \\[4pt] &=\int_1^e 4t^3\ln t\,dt+\dfrac{e^4}{4}+e^3 −\dfrac{1}{4} −1 \\[4pt] &= \int_1^e 4t^3\ln t\,dt+\dfrac{e^4}{4}+e^3 −\dfrac{5}{4}\end{align*}\]

Integral\(\displaystyle \int_1^e t^3\ln t\,dt\) inahitaji ushirikiano na sehemu. Hebu\(u=\ln t\) na\(dv=t^3\). Kisha\(u=\ln t\),\(dv=t^3\)

na

\[du=\dfrac{1}{t}\,dt, \;\;v=\dfrac{t^4}{4}.\nonumber \]

Kwa hiyo,

\[\begin{align*} \int_1^e t^3\ln t\,dt &={\Big[\dfrac{t^4}{4}\ln t\Big]}_1^e−\dfrac{1}{4}\int_1^e t^3\,dt \\[4pt] &=\dfrac{e^4}{4}−\dfrac{1}{4}\left(\dfrac{e^4}{4}−\dfrac{1}{4}\right). \end{align*}\]

Hivyo,

\[\begin{align*} \int_C \vecs F \cdot d\vecs{r} &= 4\int_1^e t^3\ln t\, dt\quad +\quad \dfrac{e^4}{4}+e^3 − \dfrac{5}{4} \\[4pt] &=4\left(\dfrac{e^4}{4}−\dfrac{1}{4}\left(\dfrac{e^4}{4}−\dfrac{1}{4}\right)\right)+\dfrac{e^4}{4}+e^3−\dfrac{5}{4}\\[4pt] &=e^4−\dfrac{e^4}{4}+\dfrac{1}{4}+\dfrac{e^4}{4}+e^3−\dfrac{5}{4} \\[4pt] &=e^4+e^3−1. \end{align*}\]

2. Kutokana na kwamba\(f(x,y,z)=x^2\ln y+yz^2\) ni kazi uwezo kwa\(\vecs F\), hebu kutumia Theorem Msingi kwa Line Integrals kwa mahesabu muhimu. Kumbuka kwamba

\[\begin{align*} \int_C \vecs F \cdot d\vecs{r} &=\int_C \vecs \nabla f \cdot d\vecs{r} \\[4pt] &=f(\vecs r(e))−f(\vecs r(1)) \\[4pt] &=f(e^2,e,e)−f(1,1,1)\\[4pt] &=e^4+e^3−1. \end{align*}\]

Hesabu hii ni moja kwa moja zaidi kuliko hesabu tuliyofanya katika (a). Muda mrefu kama tuna kazi ya uwezo, kuhesabu mstari muhimu kwa kutumia Theorem ya Msingi kwa Line Integrals ni rahisi zaidi kuliko kuhesabu bila theorem.

Mfano\(\PageIndex{3}\) unaeleza kipengele nzuri ya Theorem ya Msingi ya Line Integrals: inaruhusu sisi mahesabu kwa urahisi zaidi wengi vector line integrals. Kwa muda mrefu kama tuna kazi inayoweza, kuhesabu mstari muhimu ni suala la kutathmini kazi inayoweza kufikia mwisho na kuondoa.

Zoezi\(\PageIndex{3}\)

Kutokana na kwamba\(f(x,y)={(x−1)}^2y+{(y+1)}^2x\) ni kazi uwezo kwa\(\vecs F(x,y)=⟨2xy−2y+{(y+1)}^2,{(x−1)}^2+2yx+2x⟩\), mahesabu muhimu\(\int_C \vecs F·d\vecs r\), ambapo\(C\) ni nusu ya chini ya kitengo mduara oriented kinyume chake.

Kidokezo

Theorem Msingi kwa Line Vipindi anasema muhimu hii inategemea tu juu ya thamani ya\(f\) katika endpoints ya\(C\).

Jibu

2

Theorem Msingi kwa Line Integrals ina matokeo mawili muhimu. Matokeo ya kwanza ni kwamba ikiwa\(\vecs{F}\) ni kihafidhina na\(C\) ni safu iliyofungwa, basi mzunguko wa\(\vecs{F}\) pamoja\(C\) ni sifuri-yaani,\(\int_C \vecs F·d\vecs r=0\). Ili kuona kwa nini hii ni kweli, basi\(f\) iwe kazi ya uwezo\(\vecs{F}\). Kwa kuwa\(C\) ni Curve imefungwa, hatua\(\vecs r(b)\) ya mwisho ya\(C\) ni sawa na\(\vecs r(a)\) ya awali ya\(C\) - yaani,\(\vecs r(a)=\vecs r(b)\). Kwa hiyo, kwa Theorem ya Msingi kwa Line Integrals,

\[\begin{align} \oint_C \vecs F·d\vecs r &=\oint_C \vecs \nabla f·d\vecs r\\[4pt] &=f(\vecs r(b))−f(\vecs r(a)) \\[4pt] &=f(\vecs r(b))−f(\vecs r(b)) \\[4pt] &=0. \end{align} \nonumber \]

Kumbuka kwamba sababu shamba la vector la kihafidhina\(\vecs{F}\) linaitwa “kihafidhina” ni kwa sababu vile mashamba ya vector vikosi vya mfano ambavyo nishati huhifadhiwa. Tumeonyesha mvuto kuwa mfano wa nguvu hiyo. Ikiwa tunadhani ya uwanja wa vector\(\vecs{F}\) katika muhimu\(\oint_C \vecs F·d\vecs r\) kama shamba la mvuto, basi equation\(\oint_C \vecs{F}·d\vecs{r}=0\) ifuatavyo. Ikiwa chembe inasafiri kwenye njia inayoanza na kuishia mahali pale pale, basi kazi iliyofanywa kwa mvuto kwenye chembe ni sifuri.

Matokeo ya pili muhimu ya Theorem ya Msingi kwa Line Integrals (Equation\ ref {FunthELine}) ni kwamba mstari integrals ya mashamba ya vector kihafidhina ni huru ya njia-maana, wao hutegemea tu juu ya endpoints ya Curve kupewa, na wala hutegemea njia kati ya endpoints.

Ufafanuzi: Njia ya Uhuru

Hebu\(\vecs{F}\) kuwa uwanja vector na domain\(D\); ni huru ya njia (au njia huru) kama

\[\int_{C_1} \vecs{F}·d\vecs{r}=\int_{C_2} \vecs{F}·d\vecs{r} \nonumber \]

kwa njia yoyote\(C_1\) na\(C_2\) katika\(D\) na pointi sawa ya awali na terminal.

Matokeo ya pili yameelezwa rasmi katika theorem ifuatayo.

Theorem: KIHAFIDHINA

Ikiwa\(\vecs{F}\) ni uwanja wa vector wa kihafidhina, basi\(\vecs{F}\) ni huru ya njia.

Ushahidi

Hebu\(D\) kuashiria uwanja wa\(\vecs{F}\) na kuruhusu\(C_1\) na\(C_2\) kuwa njia mbili katika\(D\) na pointi sawa ya awali na terminal (Kielelezo\(\PageIndex{5}\)). Piga hatua ya awali\(P_1\) na hatua ya mwisho\(P_2\). Kwa kuwa\(\vecs{F}\) ni kihafidhina, kuna kazi ya uwezo\(f\) kwa\(\vecs{F}\). Kwa Theorem ya Msingi ya Line Integrals,

\[\int_{C_1} \vecs{F}·d\vecs{r}=f(P_2)−f(P_1)=\int_{C_2} \vecs{F}·d\vecs{r}. \nonumber \]

Kwa hiyo,\(\int_{C_1}\vecs F·d\vecs r=\int_{C_2}\vecs F·d\vecs r\) na\(\vecs{F}\) ni huru ya njia.

\(\square\)

Ili kutazama nini uhuru wa njia ina maana, fikiria watembezi watatu wanaopanda kutoka kambi ya msingi hadi juu ya mlima. Hiker 1 inachukua njia mwinuko moja kwa moja kutoka kambi hadi juu. Hiker 2 inachukua njia ya vilima ambayo si mwinuko kutoka kambi hadi juu. Hiker 3 anaanza kwa kuchukua njia ya mwinuko lakini nusu hadi juu anaamua ni vigumu sana kwake. Kwa hiyo anarudi kambini na kuchukua njia isiyo ya mwinuko hadi juu. Hikers wote watatu wanasafiri kando ya njia katika uwanja wa mvuto. Kwa kuwa mvuto ni nguvu ambayo nishati huhifadhiwa, uwanja wa mvuto ni kihafidhina. Kwa uhuru wa njia, jumla ya kazi iliyofanywa kwa mvuto kwenye kila moja ya watembea ni sawa kwa sababu wote walianza mahali pale na kumalizika mahali pale. Kazi iliyofanywa na watembeaji hujumuisha mambo mengine kama vile msuguano na mwendo wa misuli, hivyo jumla ya nishati inayotumiwa kila mmoja si sawa, lakini nishati ya wavu inayotumiwa dhidi ya mvuto ni sawa kwa watembea wote watatu.

Kielelezo\(\PageIndex{4}\): Shamba la vector ni kihafidhina, na kwa hiyo huru njia.

Tumeonyesha kwamba ikiwa\(\vecs{F}\) ni kihafidhina, basi\(\vecs{F}\) ni huru ya njia. Inageuka kuwa ikiwa uwanja wa\(\vecs{F}\) wazi na umeunganishwa, basi kuzungumza pia ni kweli. Hiyo ni, ikiwa\(\vecs{F}\) ni huru ya njia na uwanja wa\(\vecs{F}\) ni wazi na kushikamana, basi\(\vecs{F}\) ni kihafidhina. Kwa hiyo, seti ya mashamba ya vector ya kihafidhina kwenye vikoa vya wazi na vilivyounganishwa ni seti ya mashamba ya vector huru ya njia.

Theorem: PATH UHURU MTIHANI KWA FIELDS KI

Kama\(\vecs{F}\) ni kuendelea vector shamba ambayo ni huru ya njia na uwanja\(D\) wa\(\vecs{F}\) ni wazi na kushikamana, basi\(\vecs{F}\) ni kihafidhina.

Ushahidi

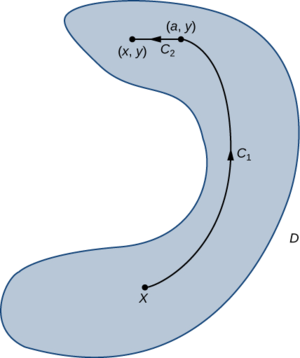
Sisi kuthibitisha theorem kwa mashamba vector katika\(ℝ^2\). Ushahidi wa mashamba ya vector ndani\(ℝ^3\) ni sawa. Kuonyesha kwamba\(\vecs F=⟨P,Q⟩\) ni kihafidhina, ni lazima kupata kazi uwezo\(f\) kwa\(\vecs{F}\). Ili kufikia mwisho huo, hebu\(X\) iwe hatua ya kudumu\(D\). Kwa hatua yoyote\((x,y)\) katika\(D\), basi\(C\) iwe njia kutoka\(X\) kwa\((x,y)\). Eleza\(f(x,y)\) na\(f(x,y)=\int_C \vecs F·d\vecs r\). (Kumbuka kuwa ufafanuzi huu wa\(f\) mantiki tu kwa sababu\(\vecs{F}\) ni huru ya njia. Kama\(\vecs{F}\) haikuwa huru ya njia, basi inaweza kuwa inawezekana kupata njia nyingine\(C′\) kutoka\(X\) kwa\((x,y)\) vile kwamba\(\int_C \vecs F·d\vecs r≠\int_C \vecs F·d\vecs r\), na katika kesi kama hiyo\(f(x,y)\) bila kuwa kazi.) Tunataka kuonyesha kwamba\(f\) ina mali\(\vecs \nabla f=\vecs F\).

Kwa kuwa uwanja\(D\) umefunguliwa, inawezekana kupata disk iliyozingatia\((x,y)\) kama vile disk iko ndani kabisa\(D\). Hebu\(a<x\) iwe\((a,y)\) na uhakika katika diski hiyo. Hebu\(C\) kuwa njia kutoka\(X\) kwa\((x,y)\) kuwa lina vipande viwili:\(C_1\) na\(C_2\). kipande kwanza,\(C_1\), ni njia yoyote kutoka\(C\) kwa\((a,y)\) kwamba anakaa ndani\(D\);\(C_2\) ni usawa line sehemu kutoka\((a,y)\) kwa\((x,y)\) (Kielelezo\(\PageIndex{6}\)). Kisha

\[f(x,y)=\int_{C_1} \vecs F·d\vecs r+\int_{C_2}\vecs F \cdot d\vecs r.\nonumber \]

Muhimu wa kwanza hautegemei\(x\), hivyo

\[f_x(x,y)=\dfrac{∂}{∂x}\int_{C_2} \vecs F \cdot d\vecs r. \nonumber \]

Ikiwa sisi parameterize\(C_2\) na\(\vecs r(t)=⟨t,y⟩\)\(a≤t≤x\), basi

\[\begin{align*} f_x(x,y) &=\dfrac{∂}{∂x}\int_{C_2} \vecs F \cdot d\vecs r \\[4pt] &=\dfrac{∂}{∂x}\int_a^x \vecs F(\vecs r(t)) \cdot \vecs r′(t)\,dt \\[4pt] &=\dfrac{∂}{∂x}\int_a^x \vecs F(\vecs r(t)) \cdot \dfrac{d}{dt}(⟨t,y⟩)\,dt \\[4pt] &=\dfrac{∂}{∂x}\int_a^x \vecs F(\vecs r(t)) \cdot ⟨1,0⟩\,dt \\[4pt] &=\dfrac{∂}{∂x}\int_a^x P(t,y)\,dt.\\[4pt] \end{align*}\]

Kwa Theorem ya Msingi ya Calculus (sehemu ya 1),

\[f_x(x,y)=\dfrac{∂}{∂x}\int_a^x P(t,y)\,dt=P(x,y).\nonumber \]

Kielelezo\(\PageIndex{6}\). Hapa,\(C_1\) ni njia yoyote kutoka\(C\) kwa\((a,y)\) kwamba anakaa ndani\(D\), na\(C_2\) ni usawa line sehemu kutoka\((a,y)\) kwa\((x,y)\).

Hoja sawa kwa kutumia sehemu ya mstari wa wima badala ya sehemu ya mstari wa usawa inaonyesha kwamba\(f_y(x,y)=Q(x,y)\).

Kwa hiyo\(\vecs \nabla f=\vecs F\) na\(\vecs{F}\) ni kihafidhina.

\(\square\)

Tumetumia muda mwingi kujadili na kuthibitisha theorems hapo juu, lakini tunaweza muhtasari wao tu: uwanja wa vector\(\vecs F\) kwenye uwanja wazi na kushikamana ni kihafidhina ikiwa na tu ikiwa ni huru ya njia. Hii ni muhimu kujua kwa sababu mashamba ya vector kihafidhina ni muhimu sana katika maombi, na theorems hizi kutupa njia tofauti ya kuangalia nini maana ya kuwa kihafidhina kutumia njia uhuru.

Mfano\(\PageIndex{4}\): Showing That a Vector Field Is Not Conservative

Kutumia njia uhuru kuonyesha kwamba uwanja vector\(\vecs F(x,y)=⟨x^2y,y+5⟩\) si kihafidhina.

Suluhisho

Tunaweza kuonyesha kwamba\(\vecs{F}\) si kihafidhina kwa kuonyesha kwamba\(\vecs{F}\) si njia huru. Sisi kufanya hivyo kwa kutoa njia mbili tofauti,\(C_1\) na\(C_2\), kwamba wote kuanza saa\((0,0)\) na mwisho katika\((1,1)\), na bado\(\int_{C_1} \vecs F \cdot d\vecs r≠\int_{C_2} \vecs F \cdot d\vecs r\).

Hebu\(C_1\) kuwa curve na parameterization\(\vecs r_1(t)=⟨t,\,t⟩\),\(0≤t≤1\) na hebu\(C_2\) kuwa curve na parameterization\(\vecs r_2(t)=⟨t,\,t^2⟩\),\(0≤t≤1\) (Kielelezo\(\PageIndex{7}\).). Kisha

\[\begin{align*} \int_{C_1} \vecs{F}·d\vecs r &=\int_0^1 \vecs F(\vecs r_1(t))·\vecs r_1′(t)\,dt \\[4pt] &=\int_0^1⟨t^3,t+5⟩·⟨1,1⟩\,dt=\int_0^1(t^3+t+5)\,dt\\[4pt] &={\Big[\dfrac{t^4}{4}+\dfrac{t^2}{2}+5t\Big]}_0^1=\dfrac{23}{4} \end{align*}\]

na

\[\begin{align*} \int_{C_2}\vecs F·d\vecs r &=\int_0^1 \vecs F(\vecs r_2(t))·\vecs r_2′(t)\,dt \\[4pt] &=\int_0^1⟨t^4,t^2+5⟩·⟨1,2t⟩\,dt=\int_0^1(t^4+2t^3+10t)\,dt \\[4pt] &={\Big[\dfrac{t^5}{5}+\dfrac{t^4}{2}+5t^2\Big]}_0^1=\dfrac{57}{10}. \end{align*}\]

Kwa kuwa\(\int_{C_1} \vecs F \cdot d\vecs r≠\int_{C_2} \vecs F \cdot d\vecs r\), thamani ya mstari muhimu ya\(\vecs{F}\) inategemea njia kati ya pointi mbili kutokana. Kwa hiyo,\(\vecs{F}\) si huru ya njia, na\(\vecs{F}\) si kihafidhina.

Kielelezo\(\PageIndex{7}\): Curves\(C_1\) na wote\(C_2\) ni oriented kutoka kushoto kwenda kulia.

Zoezi\(\PageIndex{4}\)

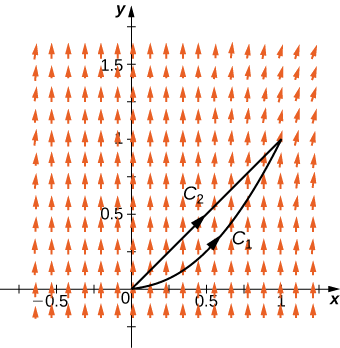
Onyesha kwamba\(\vecs{F}(x,y)=⟨xy,\,x^2y^2⟩\) si njia huru kwa kuzingatia line sehemu kutoka\((0,0)\) kwa\((0,2)\) na kipande cha graph ya\(y=\dfrac{x^2}{2}\) kwamba huenda kutoka\((0,0)\) kwa\((0,2)\).

Kidokezo

Tumia mahesabu ya mstari wa sambamba.

Jibu

Kama\(C_1\) na\(C_2\) kuwakilisha curves mbili, basi\[\int_{C_1} \vecs F \cdot d\vecs r≠\int_{C_2} \vecs F \cdot d\vecs r. \nonumber \]

Mashamba ya Vector ya kihafidhina na Kazi

Kama tulivyojifunza, Theorem ya Msingi kwa Line Integrals inasema kwamba ikiwa\(\vecs{F}\) ni\(\int_C \vecs F·d\vecs r\) kihafidhina, basi kuhesabu ina hatua mbili: kwanza, kupata kazi\(f\) ya uwezo\(\vecs{F}\) na\(f(P_1)−f(P_0)\), pili, kuhesabu, wapi\(P_1\) mwisho wa\(C\) na\(P_0\) ni hatua ya mwanzo. Ili kutumia theorem hii kwa uwanja wa kihafidhina\(\vecs{F}\), lazima tuweze kupata kazi\(f\) inayoweza\(\vecs{F}\). Kwa hiyo, tunapaswa kujibu swali linalofuata: Kutokana na uwanja wa vector wa kihafidhina\(\vecs{F}\), tunawezaje kupata kazi\(f\) kama hiyo\(\vecs \nabla f=\vecs{F}\)? Kabla ya kutoa njia ya jumla ya kutafuta kazi inayoweza, hebu tuhamasishe njia kwa mfano.

Mfano\(\PageIndex{5}\): Finding a Potential Function

Kupata kazi uwezo kwa\(\vecs F(x,y)=⟨2xy^3,3x^2y^2+\cos(y)⟩\), hivyo kuonyesha kwamba\(\vecs{F}\) ni kihafidhina.

Suluhisho

Tuseme kwamba\(f(x,y)\) ni kazi uwezo kwa ajili ya\(\vecs{F}\). Kisha\(\vecs \nabla f=\vecs F\), na kwa hiyo

\[f_x(x,y)=2xy^3 \; \; \text{and} \;\; f_y(x,y)=3x^2y^2+\cos y. \nonumber \]

Kuunganisha equation\(f_x(x,y)=2xy^3\) kwa heshima na\(x\) mavuno equation

\[f(x,y)=x^2y^3+h(y). \nonumber \]

Kumbuka kwamba tangu sisi ni kuunganisha mbili variable kazi kuhusiana na\(x\), ni lazima kuongeza mara kwa mara ya ushirikiano kwamba ni mara kwa mara kuhusiana na\(x\), lakini bado inaweza kuwa kazi ya\(y\). Equation\(f(x,y)=x^2y^3+h(y)\) inaweza kuthibitishwa kwa kuchukua derivative sehemu kwa heshima na\(x\):

\[\dfrac{∂f}{∂x}=\dfrac{∂}{∂x}(x^2y^3)+\dfrac{∂}{∂x}(h(y))=2xy^3+0=2xy^3. \nonumber \]

Kwa kuwa\(f\) ni kazi uwezo kwa ajili ya\(\vecs{F}\),

\[f_y(x,y)=3x^2y^2+\cos(y), \nonumber \]

na kwa hiyo

\[3x^2y^2+g′(y)=3x^2y^2+\cos(y). \nonumber \]

Hii ina maana kwamba\(h′(y)=\cos y\), hivyo\(h(y)=\sin y+C\). Kwa hiyo, kazi yoyote ya fomu\(f(x,y)=x^2y^3+\sin(y)+C\) ni kazi inayoweza. Kuchukua, hasa,\(C=0\) hutoa kazi inayoweza\(f(x,y)=x^2y^3+\sin(y)\).

Ili kuthibitisha kuwa\(f\) ni kazi inayoweza, kumbuka kuwa\(\vecs \nabla f(x,y)=⟨2xy^3,3x^2y^2+\cos y⟩=\vecs F\).

Zoezi\(\PageIndex{5}\)

Kupata kazi uwezo kwa ajili ya\(\vecs{F}(x,y)=⟨e^xy^3+y,3e^xy^2+x⟩\).

Kidokezo

Fuata hatua katika Mfano\(\PageIndex{5}\).

Jibu

\(f(x,y)=e^xy^3+xy\)

Mantiki ya mfano uliopita inaenea kutafuta kazi ya uwezo kwa shamba lolote la vector la kihafidhina\(ℝ^2\). Hivyo, tuna mkakati wafuatayo wa kutatua matatizo ya kutafuta kazi zinazoweza:

MKAKATI WA KUTATUA MATATIZO: KUTAFUTA KAZI YA UWEZO KWA SHAMBA LA VECTOR\(\vecs{F}(x,y)=⟨P(x,y),Q(x,y)⟩\)

1. Unganisha\(P\) kwa heshima na\(x\). Hii inasababisha kazi ya fomu\(g(x,y)+h(y)\), ambapo\(h(y)\) haijulikani.
2. Kuchukua derivative sehemu ya kwa heshima\(g(x,y)+h(y)\) na\(y\), ambayo matokeo katika kazi\(gy(x,y)+h′(y)\).
3. Tumia equation\(gy(x,y)+h′(y)=Q(x,y)\) kupata\(h′(y)\).
4. Unganisha\(h′(y)\) ili upate\(h(y)\).
5. Kazi yoyote ya fomu\(f(x,y)=g(x,y)+h(y)+C\), ambapo\(C\) ni mara kwa mara, ni kazi inayoweza\(\vecs{F}\).

Tunaweza kukabiliana na mkakati huu kupata kazi uwezo kwa ajili ya mashamba vector katika\(ℝ^3\), kama inavyoonekana katika mfano unaofuata.

Mfano\(\PageIndex{6}\): Finding a Potential Function in \(ℝ^3\)

Kupata kazi uwezo kwa\(F(x,y,z)=⟨2xy,x^2+2yz^3,3y^2z^2+2z⟩\), hivyo kuonyesha kwamba\(\vecs{F}\) ni kihafidhina.

Suluhisho

Tuseme kwamba\(f\) ni kazi uwezo. Kisha,\(\vecs \nabla f= \vecs{F}\) na kwa hiyo\(f_x(x,y,z)=2xy\). Kuunganisha equation hii kwa heshima na\(x\) mavuno equation\(f(x,y,z)=x^2y+g(y,z)\) kwa baadhi ya kazi\(g\). Kumbuka kwamba, katika kesi hii, mara kwa mara ya ushirikiano kwa heshima na\(x\) ni kazi ya\(y\) na\(z\).

Tangu\(f\) ni kazi uwezo,

\[x^2+2yz^3=f_y(x,y,z)=x^2+g_y(y,z). \nonumber \]

Kwa hiyo,

\[g_y(y,z)=2yz^3. \nonumber \]

Kuunganisha kazi hii kwa heshima na\(y\) mavuno

\[g(y,z)=y^2z^3+h(z) \nonumber \]

kwa baadhi\(h(z)\) ya kazi ya\(z\) peke yake. (Kumbuka kwamba, kwa sababu tunajua kwamba\(g\) ni kazi ya tu\(y\) na\(z\), hatuna haja ya kuandika\(g(y,z)=y^2z^3+h(x,z)\).) Kwa hiyo,

\[f(x,y,z)=x^2y+g(y,z)=x^2y+y^2z^3+h(z). \nonumber \]

Ili kupata\(f\), sasa tunapaswa kupata tu\(h\). Tangu\(f\) ni kazi uwezo,

\[3y^2z^2+2z=g_z(y,z)=3y^2z^2+h′(z). \nonumber \]

Hii ina maana kwamba\(h′(z)=2z\), hivyo\(h(z)=z^2+C\). Kuruhusu\(C=0\) inatoa kazi ya uwezo

\[f(x,y,z)=x^2y+y^2z^3+z^2. \nonumber \]

Ili kuthibitisha kuwa\(f\) ni kazi inayoweza, kumbuka kuwa\(\vecs \nabla f(x,y,z)=⟨2xy,x^2+2yz^3,3y^2z^2+2z⟩=\vecs F(x,y,z)\).

Zoezi\(\PageIndex{6}\)

Kupata kazi uwezo kwa ajili ya\(\vecs{F}(x,y,z)=⟨12x^2,\cos y\cos z,1−\sin y\sin z⟩\).

Kidokezo

Kufuatia Mfano\(\PageIndex{6}\), kuanza kwa kuunganisha kwa heshima na\(x\).

Jibu

\(f(x,y,z)=4x^3+\sin y\cos z+z\)

Tunaweza kutumia mchakato wa kutafuta kazi ya uwezo kwa nguvu ya mvuto. Kumbuka kwamba, ikiwa kitu kina kitengo cha wingi na iko katika asili, basi nguvu ya mvuto kwa\(ℝ^2\) kuwa kitu kinajumuisha kitu kingine cha wingi wa kitengo wakati huo\((x,y)\) hutolewa na shamba la vector

\(\vecs F(x,y)=−G\left\langle\dfrac{x}{ {(x^2+y^2)}^{3/2} },\dfrac{y}{ {(x^2+y^2)}^{3/2} }\right\rangle\),

ambapo\(G\) ni mara kwa mara ya mvuto wa ulimwengu wote. Katika mfano unaofuata, tunajenga kazi inayoweza\(\vecs{F}\), hivyo kuthibitisha kile tunachojua tayari: mvuto huo ni kihafidhina.

Mfano\(\PageIndex{7}\): Finding a Potential Function

Kupata kazi uwezo\(f\) kwa ajili ya\(\vecs{F}(x,y)=−G\left\langle\dfrac{x}{ {(x^2+y^2)}^{3/2} },\dfrac{y}{ {(x^2+y^2)}^{3/2} }\right\rangle\).

Suluhisho

Tuseme kwamba\(f\) ni kazi uwezo. Basi,\(\vecs \nabla f= \vecs{F}\) na kwa hiyo

\[f_x(x,y)=\dfrac{−Gx}{ {(x^2+y^2)}^{3/2} }.\nonumber \]

Kuunganisha kazi hii kwa heshima na\(x\), tunaweza kutumia\(u\) -badala. Ikiwa\(u=x^2+y^2\), basi\(\dfrac{du}{2}=x\,dx\), hivyo

\[\begin{align*} \int \dfrac{−Gx}{ {(x^2+y^2)}^{3/2} }\,dx &=\int \dfrac{−G}{2u^{3/2}} \,du \\[4pt] &=\dfrac{G}{\sqrt{u}}+h(y) \\[4pt] &=\dfrac{G}{\sqrt{x^2+y^2}}+h(y) \end{align*}\]

kwa baadhi ya kazi\(h(y)\). Kwa hiyo,

\[f(x,y)=\dfrac{G}{ \sqrt{x^2+y^2}}+h(y).\nonumber \]

Kwa kuwa\(f\) ni kazi uwezo kwa ajili ya\(\vecs{F}\),

\[f_y(x,y)=\dfrac{−Gy}{ {(x^2+y^2)}^{3/2} }\nonumber \].

tangu\(f(x,y)=\dfrac{G}{ \sqrt{x^2+y^2}}+h(y)\),\(f_y(x,y)\) pia ni sawa\(\dfrac{−Gy}{ {(x^2+y^2)}^{3/2} }+h′(y)\).

Kwa hiyo,

\[\dfrac{−Gy}{ {(x^2+y^2)}^{3/2} }+h′(y)=\dfrac{−Gy}{ {(x^2+y^2)}^{3/2} }, \nonumber \]

ambayo ina maana kwamba\(h′(y)=0\). Hivyo, tunaweza\(h(y)\) kuchukua kuwa yoyote ya mara kwa mara; hasa, tunaweza basi\(h(y)=0\). Kazi

\[f(x,y)=\dfrac{G}{ \sqrt{x^2+y^2} } \nonumber \]

ni kazi ya uwezo wa shamba la mvuto\(\vecs{F}\). Ili kuthibitisha kuwa\(f\) ni kazi inayoweza, kumbuka kuwa

\[\begin{align*} \vecs\nabla f(x,y) &=⟨−\dfrac{1}{2} \dfrac{G}{ {(x^2+y^2)}^{3/2} } (2x),−\dfrac{1}{2} \dfrac{G}{ {(x^2+y^2)}^{3/2} }(2y)⟩ \\[4pt] &=⟨\dfrac{−Gx}{ {(x^2+y^2)}^{3/2} },\dfrac{−Gy}{ {(x^2+y^2)}^{3/2} }⟩\\[4pt] &=\vecs F(x,y). \end{align*}\]

Zoezi\(\PageIndex{7}\)

Pata kazi\(f\) ya uwezo wa nguvu ya mvuto wa tatu-dimensional\(\vecs{F}(x,y,z)=\left\langle\dfrac{−Gx}{ {(x^2+y^2+z^2)}^{3/2} },\dfrac{−Gy}{ {(x^2+y^2+z^2)}^{3/2} },\dfrac{−Gz}{ {(x^2+y^2+z^2)}^{3/2} }\right\rangle\).

Kidokezo

Fuata Mkakati wa Kutatua Matatizo.

Jibu

\(f(x,y,z)=\dfrac{G}{\sqrt{x^2+y^2+z^2}}\)

Kupima uwanja wa Vector

Hadi sasa, tumefanya kazi na mashamba ya vector ambayo tunajua ni kihafidhina, lakini ikiwa hatuambiwi kuwa uwanja wa vector ni kihafidhina, tunahitaji kuwa na uwezo wa kupima ikiwa ni kihafidhina. Kumbuka kwamba, ikiwa\(\vecs{F}\) ni kihafidhina, basi\(\vecs{F}\) ina mali ya msalaba-sehemu (angalia Mali ya Msalaba wa Mashamba ya Vector Conservative). Hiyo ni, ikiwa\(\vecs F=⟨P,Q,R⟩\) ni kihafidhina\(P_y=Q_x\), basi\(P_z=R_x\), na\(Q_z=R_y\). Kwa hiyo, ikiwa\(\vecs{F}\) ina mali ya msalaba, basi ni\(\vecs{F}\) kihafidhina? Ikiwa uwanja wa\(\vecs{F}\) ni wazi na umeunganishwa tu, basi jibu ni ndiyo.

Theorem: Mtihani wa msalaba-sehemu kwa ajili ya mashamba

Ikiwa\(\vecs{F}=⟨P,Q,R⟩\) ni shamba la vector kwenye eneo la wazi, lililounganishwa tu\(D\) na\(P_y=Q_x\)\(P_z=R_x\), na wakati\(Q_z=R_y\) wote\(D\), basi\(\vecs{F}\) ni kihafidhina.

Ingawa ushahidi wa theorem hii ni zaidi ya upeo wa maandishi, tunaweza kugundua nguvu zake kwa mifano fulani. Baadaye, tunaona kwa nini ni muhimu kwa kanda kuwa tu kushikamana.

Kuchanganya theorem hii na mali ya sehemu ya msalaba, tunaweza kuamua kama shamba la vector lililopewa ni kihafidhina:

Theorem: MSALABA-SEHEMU YA MALI YA MASHAMBA YA

Hebu\(\vecs{F}=⟨P,Q,R⟩\) kuwa uwanja wa vector kwenye eneo la wazi, lililounganishwa tu\(D\). Kisha\(P_y=Q_x\),\(P_z=R_x\), na\(Q_z=R_y\) katika\(D\) ikiwa na tu ikiwa\(\vecs{F}\) ni kihafidhina.

Toleo la theorem hii pia\(ℝ^2\) ni kweli. Ikiwa\(\vecs F(x,y)=⟨P,Q⟩\) ni uwanja wa vector kwenye uwanja wa wazi, unaounganishwa tu\(ℝ^2\), basi\(\vecs F\) ni kihafidhina ikiwa na tu ikiwa\(P_y=Q_x\).

Mfano\(\PageIndex{8}\): Determining Whether a Vector Field Is Conservative

Kuamua kama uwanja wa vector\(\vecs F(x,y,z)=⟨xy^2z,x^2yz,z^2⟩\) ni kihafidhina.

Suluhisho

Kumbuka kuwa uwanja wa\(\vecs{F}\) ni wote\(ℝ^2\) na\(ℝ^3\) ni tu kushikamana. Kwa hiyo, tunaweza kutumia Mali ya Msalaba wa sehemu ya Mashamba ya Vector Conservative kuamua kama\(\vecs{F}\) ni kihafidhina. Hebu

\[P(x,y,z)=xy^2z \nonumber \]

\[Q(x,y,z)=x^2yz \nonumber \]

na

\[R(x,y,z)=z^2.\nonumber \]

Tangu\(Q_z(x,y,z)=x^2y\) na\(R_y(x,y,z)=0\), uwanja wa vector sio kihafidhina.

Mfano\(\PageIndex{9}\): Determining Whether a Vector Field Is Conservative

Kuamua uwanja wa vector\(\vecs{F}(x,y)=⟨x\ln (y), \,\dfrac{x^2}{2y}⟩\) ni kihafidhina.

Suluhisho

Kumbuka kuwa uwanja wa\(\vecs{F}\) ni sehemu\(ℝ^2\) ya ambayo\(y>0\). Hivyo, uwanja wa\(\vecs{F}\) ni sehemu ya ndege juu ya\(x\) -axis, na uwanja huu unaunganishwa tu (hakuna mashimo katika eneo hili na eneo hili linaunganishwa). Kwa hiyo, tunaweza kutumia Mali ya Msalaba wa sehemu ya Mashamba ya Vector Conservative kuamua kama\(\vecs{F}\) ni kihafidhina. Hebu

\[P(x,y)=x\ln (y) \;\; \text{and} \;\;\ Q(x,y)=\dfrac{x^2}{2y}. \nonumber \]

Kisha\(P_y(x,y)=\dfrac{x}{y}=Q_x(x,y)\) na hivyo\(\vecs{F}\) ni kihafidhina.

Zoezi\(\PageIndex{8}\)

Kuamua kama\(\vecs{F}(x,y)=⟨\sin x\cos y,\,\cos x\sin y⟩\) ni kihafidhina.

Kidokezo

Tumia Mali ya Msalaba wa Mashamba ya Vector ya Kihafidhina kutoka sehemu iliyopita.

Jibu

Ni kihafidhina.

Wakati wa kutumia Mali ya Msalaba wa Mashamba ya Vector Conservative, ni muhimu kukumbuka kuwa theorem ni chombo, na kama chombo chochote, inaweza kutumika tu chini ya hali sahihi. Katika kesi ya Mali ya Msalaba wa Mashamba ya Vector ya Kihafidhina, theorem inaweza kutumika tu ikiwa uwanja wa uwanja wa vector unaunganishwa tu.

Ili kuona nini kinachoweza kwenda vibaya wakati unapotumia theorem, fikiria shamba la vector kutoka Mfano\(\PageIndex{4}\):

\[\vecs F(x,y)=\dfrac{y}{x^2+y^2}\,\hat{\mathbf i}+\dfrac{−x}{x^2+y^2}\,\hat{\mathbf j}. \nonumber \]

Hii shamba vector satisfies mali msalaba-sehemu, tangu

\[\dfrac{∂}{∂y}\left(\dfrac{y}{x^2+y^2}\right)=\dfrac{(x^2+y^2)−y(2y)}{ {(x^2+y^2)}^2}=\dfrac{x^2−y^2}{ {(x^2+y^2)}^2} \nonumber \]

na

\[\dfrac{∂}{∂x}\left(\dfrac{−x}{x^2+y^2}\right)=\dfrac{−(x^2+y^2)+x(2x)}{ {(x^2+y^2)}^2}=\dfrac{x^2−y^2}{ {(x^2+y^2)}^2}. \nonumber \]

Kwa kuwa\(\vecs{F}\) satisfies mali msalaba-sehemu, tunaweza kujaribiwa kuhitimisha kwamba\(\vecs{F}\) ni kihafidhina. Hata hivyo,\(\vecs{F}\) si kihafidhina. Ili kuona hili, basi

\[\vecs r(t)=⟨\cos t,\sin t⟩,\;\; 0≤t≤\pi \nonumber \]

kuwa parameterization ya nusu ya juu ya mduara wa kitengo oriented kinyume (kuashiria hii\(C_1\)) na basi

\[\vecs s(t)=⟨\cos t,−\sin t⟩,\;\; 0≤t≤\pi \nonumber \]

kuwa parameterization ya nusu ya chini ya mduara wa kitengo oriented clockwise (kuashiria hii\(C_2\)). Angalia kwamba\(C_1\) na\(C_2\) uwe na hatua sawa ya kuanzia na mwisho. Tangu\({\sin}^2 t+{\cos}^2 t=1\),

\[\vecs F(\vecs r(t)) \cdot \vecs r′(t)=⟨\sin(t),−\cos(t)⟩ \cdot ⟨−\sin(t), \cos(t)⟩=−1 \nonumber \]

na

\[\vecs F(\vecs s(t))·\vecs s′(t)=⟨−\sin t,−\cos t⟩·⟨−\sin t,−\cos t⟩={\sin}^2 t+{\cos}^2t=1. \nonumber \]

Kwa hiyo,

\[\int_{C_1} \vecs F·d\vecs r=\int_0^{\pi}−1\,dt=−\pi \nonumber \]

na

\[\int_{C_2}\vecs F·d\vecs r=\int_0^{\pi} 1\,dt=\pi. \nonumber \]

Hivyo,\(C_1\) na\(C_2\) uwe na hatua sawa ya kuanzia na mwisho, lakini\(\int_{C_1} \vecs F·d\vecs r≠\int_{C_2} \vecs F·d\vecs r\). Kwa hiyo,\(\vecs{F}\) si huru ya njia na\(\vecs{F}\) si kihafidhina.

Kwa muhtasari:\(\vecs{F}\) hutimiza mali ya sehemu ya msalaba na bado\(\vecs{F}\) sio kihafidhina. Nini kosa? Je, hii inakabiliwa na Mali ya Msalaba wa sehemu ya Mashamba ya Vector ya Kihafidhina Suala ni kwamba uwanja wa\(\vecs{F}\) ni wote\(ℝ^2\) isipokuwa kwa asili. Kwa maneno mengine, uwanja wa\(\vecs{F}\) ina shimo katika asili, na kwa hiyo uwanja hauunganishwa tu. Kwa kuwa uwanja haujaunganishwa tu, Mali ya Msalaba wa sehemu ya Mashamba ya Vector ya Kihafidhina hayatumiki\(\vecs{F}\).

Tunakaribia sehemu hii kwa kuangalia mfano wa manufaa ya Theorem ya Msingi kwa Line Integrals. Sasa kwa kuwa tunaweza kupima kama uwanja vector ni kihafidhina, tunaweza daima kuamua kama Theorem Msingi kwa Line Integrals inaweza kutumika kwa mahesabu ya mstari vector muhimu. Ikiwa tunaulizwa kuhesabu sehemu muhimu ya fomu\(\int_C \vecs F·d\vecs r\), basi swali letu la kwanza linapaswa kuwa: Je, ni\(\vecs{F}\) kihafidhina? Ikiwa jibu ni ndiyo, basi tunapaswa kupata kazi inayoweza na kutumia Theorem ya Msingi kwa Line Integrals kuhesabu muhimu. Ikiwa jibu ni hapana, basi Theorem ya Msingi kwa Line Integrals haiwezi kutusaidia na tunapaswa kutumia njia nyingine, kama vile kutumia njia kutoka sehemu ya awali (kutumia\(\vecs F(\vecs r(t))\) na\(\vecs r'(t)\)).

Mfano\(\PageIndex{10}\): Using the Fundamental Theorem for Line Integrals

Mahesabu line muhimu\(\int_C \vecs F·d\vecs r\), wapi\(\vecs F(x,y,z)=⟨2xe^yz+e^xz,\,x^2e^yz,\,x^2e^y+e^x⟩\) na\(C\) ni yoyote Curve laini kwamba huenda kutoka asili ya\((1,1,1)\).

Suluhisho

Kabla ya kujaribu kuhesabu muhimu, tunahitaji kuamua kama\(\vecs{F}\) ni kihafidhina na kama uwanja wa\(\vecs{F}\) ni kushikamana tu. uwanja wa\(\vecs{F}\) ni wote wa\(ℝ^3\), ambayo ni kushikamana na haina mashimo. Kwa hiyo, uwanja wa\(\vecs{F}\) ni kushikamana tu. Hebu

\[P(x,y,z)=2xe^yz+e^xz, \;\; Q(x,y,z)=x^2e^yz, \;\; \text{and} \;\; R(x,y,z)=x^2e^y+e^x \nonumber \]

ili\(\vecs{F}(x,y,z)=⟨P,Q,R⟩\). Kwa kuwa uwanja wa\(\vecs{F}\) ni kushikamana tu, tunaweza kuangalia sehemu msalaba kuamua kama\(\vecs{F}\) ni kihafidhina. Kumbuka kwamba

\[\begin{align*} P_y(x,y,z) &=2xe^yz=Q_x(x,y,z) \\[4pt]P_z(x,y,z) &=2xe^y+e^x=R_x(x,y,z) \\[4pt] Q_z(x,y,z) &=x^2e^y=R_y(x,y,z).\end{align*}\]

Kwa hiyo,\(\vecs{F}\) ni kihafidhina.

Kutathmini\(\int_C \vecs F·d\vecs r\) kutumia Theorem ya Msingi kwa Line Integrals, tunahitaji kupata kazi uwezo\(f\) kwa\(\vecs{F}\). Hebu\(f\) kuwa kazi uwezo kwa ajili ya\(\vecs{F}\). Kisha\(\vecs \nabla f=\vecs F\), na kwa hiyo\(f_x(x,y,z)=2xe^yz+e^xz\). Kuunganisha equation hii kwa heshima na\(x\) anatoa\(f(x,y,z)=x^2e^yz+e^xz+h(y,z)\) kwa baadhi ya kazi\(h\). Kutofautisha equation hii kwa heshima na\(y\) anatoa\(x^2e^yz+h_y(y,z)=Q(x,y,z)=x^2e^yz\), ambayo ina maana kwamba\(h_y(y,z)=0\). Kwa hiyo,\(h\) ni kazi ya\(z\) tu, na\(f(x,y,z)=x^2e^yz+e^xz+h(z)\). Ili kupata\(h\), kumbuka kuwa\(f_z=x^2e^y+e^x+h′(z)=R=x^2e^y+e^x\). Kwa hiyo,\(h′(z)=0\) na tunaweza kuchukua\(h(z)=0\). kazi uwezo kwa ajili ya\(\vecs{F}\) ni\(f(x,y,z)=x^2e^yz+e^xz\).

Sasa kwa kuwa tuna kazi uwezo, tunaweza kutumia Theorem Msingi kwa Line Integrals kutathmini muhimu. Kwa theorem,

\[\begin{align*} \int_C \vecs F·d\vecs r &=\int_C \vecs \nabla f·d\vecs r\\[4pt] &=f(1,1,1)−f(0,0,0)\\[4pt] &=2e. \end{align*}\]

Uchambuzi

Taarifa kwamba kama sisi alikuwa si kutambuliwa kwamba\(\vecs{F}\) ni kihafidhina, sisi ingekuwa alikuwa\(C\) na parameterize na kutumia njia kutoka sehemu ya awali. Kwa kuwa Curve\(C\) haijulikani, kutumia Theorem ya Msingi kwa Line Integrals ni rahisi sana.

Zoezi\(\PageIndex{9}\)

Tumia hesabu muhimu\(\int_C \vecs F·d\vecs r\), wapi\(\vecs{F}(x,y)=⟨\sin x\sin y, 5−\cos x\cos y⟩\) na\(C\) ni semicircle na hatua ya kuanzia\((0,\pi)\) na mwisho\((0,−\pi)\).

Kidokezo

Matumizi Theorem Msingi kwa Line Integrals.

Jibu

\(−10\pi\)

Mfano\(\PageIndex{11}\): Work Done on a Particle

Hebu\(\vecs F(x,y)=⟨2xy^2,2x^2y⟩\) kuwa uwanja wa nguvu. Tuseme kwamba chembe inaanza mwendo wake katika asili na kuishia mwendo wake wakati wowote katika ndege isiyo kwenye\(x\) -axis au\(y\) -axis. Zaidi ya hayo, mwendo wa chembe unaweza kuwa inatokana na parameterization laini. Onyesha kwamba\(\vecs{F}\) anafanya kazi nzuri kwenye chembe.

Suluhisho

Tunaonyesha kwamba\(\vecs{F}\) anafanya kazi chanya juu ya chembe kwa kuonyesha kwamba\(\vecs{F}\) ni kihafidhina na kisha kwa kutumia Theorem Msingi kwa Line Integrals.

Kuonyesha kwamba\(\vecs{F}\) ni kihafidhina, tuseme\(f(x,y)\) walikuwa kazi uwezo kwa\(\vecs{F}\). Kisha,\(\vecs \nabla f(x,y)=\vecs F(x,y)=⟨2xy^2,2x^2y⟩\) na kwa hiyo\(f_x(x,y)=2xy^2\) na\(f_y(x,y)=2x^2y\). Equation\(fx(x,y)=2xy^2\) ina maana kwamba\(f(x,y)=x^2y^2+h(y)\). Kupata pande zote mbili kwa heshima na\(y\) mavuno\(f_y(x,y)=2x^2y+h′(y)\). Kwa hiyo,\(h′(y)=0\) na tunaweza kuchukua\(h(y)=0\).

Ikiwa\(f(x,y)=x^2y^2\), basi kumbuka kuwa\(\vecs \nabla f(x,y)=⟨2xy^2,2x^2y⟩=\vecs F\), na kwa hiyo\(f\) ni kazi inayoweza\(\vecs{F}\).

Hebu\((a,b)\) kuwa hatua ambayo chembe ataacha ni mwendo, na hebu\(C\) kuashiria Curve kwamba mifano ya mwendo wa chembe ya. Kazi iliyofanywa na\(\vecs{F}\) chembe ni\(\int_C \vecs{F}·d\vecs{r}\). Kwa Theorem ya Msingi ya Line Integrals,

\[\begin{align*} \int_C \vecs F·d\vecs r &=\int_C \nabla f·d\vecs r \\[4pt] &=f(a,b)−f(0,0)\\[4pt] &=a^2b^2. \end{align*}\]

Tangu\(a≠0\) na\(b≠0\), kwa dhana,\(a^2b^2>0\). Kwa hiyo,\(\int_C \vecs F·d\vecs r>0\), na\(\vecs{F}\) anafanya kazi nzuri kwenye chembe.

Uchambuzi

Kumbuka kwamba tatizo hili itakuwa vigumu zaidi bila kutumia Theorem ya Msingi kwa Line Integrals. Ili kutumia zana ambazo tumejifunza, tutahitaji kutoa parameterization ya curve na kutumia njia kutoka sehemu iliyopita. Kwa kuwa njia ya mwendo\(C\) inaweza kuwa ya kigeni kama tunavyotaka (kwa muda mrefu kama ni laini), inaweza kuwa vigumu sana kuimarisha mwendo wa chembe.

Zoezi\(\PageIndex{10}\)

Hebu\(\vecs{F}(x,y)=⟨4x^3y^4,4x^4y^3⟩\), na tuseme kwamba chembe hatua kutoka hatua\((4,4)\) kwa\((1,1)\) pamoja Curve yoyote laini. Je, kazi iliyofanywa na\(\vecs{F}\) chembe chanya, hasi, au sifuri?

Kidokezo

Matumizi Theorem Msingi kwa Line Integrals.

Jibu

Hasi

Dhana muhimu

• Theorems katika sehemu hii zinahitaji curves ambazo zimefungwa, rahisi, au zote mbili, na mikoa iliyounganishwa au imeunganishwa tu.
• Mstari muhimu wa uwanja wa vector wa kihafidhina unaweza kuhesabiwa kwa kutumia Theorem ya Msingi kwa Line Integrals. Theorem hii ni generalization ya Theorem ya Msingi ya Calculus katika vipimo vya juu. Kutumia theorem hii kwa kawaida hufanya hesabu ya mstari iwe rahisi.
• Mashamba ya kihafidhina yanajitegemea njia. Mstari muhimu wa uwanja wa kihafidhina unategemea tu thamani ya kazi inayoweza kutokea kwenye mwisho wa safu ya kikoa.
• Kutokana vector shamba\(\vecs{F}\), tunaweza mtihani kama\(\vecs{F}\) ni kihafidhina kwa kutumia msalaba-sehemu mali. Ikiwa\(\vecs{F}\) ina mali ya sehemu ya msalaba na uwanja unaunganishwa tu, basi\(\vecs{F}\) ni kihafidhina (na hivyo ina kazi inayoweza). Ikiwa\(\vecs{F}\) ni kihafidhina, tunaweza kupata kazi inayoweza kutumia Mkakati wa Kutatua Matatizo.
• Mzunguko wa uwanja wa vector kihafidhina kwenye uwanja uliounganishwa tu juu ya safu iliyofungwa ni sifuri.

Mlinganyo muhimu

• Theorem ya msingi kwa ajili ya mstari Integrals
  \(\displaystyle \int_C \vecs \nabla f·d\vecs r=f(\vecs r(b))−f(\vecs r(a))\)
• Mzunguko wa uwanja wa kihafidhina juu ya Curve C ambayo inafunga kanda iliyounganishwa tu
  \(\displaystyle \oint_C \vecs \nabla f·d\vecs r=0\)

faharasa

Curve imefungwa

Curve ambayo huanza na kuishia kwa hatua moja

kanda iliyounganishwa

kanda ambayo pointi mbili zinaweza kushikamana na njia yenye maelezo yaliyomo ndani ya kanda

Theorem ya msingi kwa ajili ya mstari Integrals

thamani ya mstari muhimu\(\displaystyle \int_C\vecs ∇f⋅d\vecs r\) inategemea tu juu ya thamani ya\(f\) katika endpoints ya\(C: \displaystyle \int_C \vecs ∇f⋅d\vecs r=f(\vecs r(b))−f(\vecs r(a))\)

uhuru wa njia

uwanja wa vector\(\vecs{F}\) una njia ya uhuru ikiwa\(\displaystyle \int_{C_1} \vecs F⋅d\vecs r=\displaystyle \int_{C_2} \vecs F⋅d\vecs r\) kwa curves yoyote\(C_1\) na\(C_2\) katika uwanja wa\(\vecs{F}\) na pointi sawa za awali na pointi za terminal

curve rahisi

Curve ambayo haina msalaba yenyewe

kanda iliyounganishwa tu

kanda ambayo imeunganishwa na ina mali ambayo Curve yoyote imefungwa ambayo iko kabisa ndani ya kanda inahusisha pointi ambazo ni kabisa ndani ya kanda