14.6: Derivatives directional na Gr

Malengo ya kujifunza

• Kuamua derivative directional katika mwelekeo fulani kwa ajili ya kazi ya vigezo mbili.
• Kuamua vector gradient ya kupewa halisi thamani kazi.
• Eleza umuhimu wa vector gradient kuhusiana na mwelekeo wa mabadiliko juu ya uso.
• Tumia gradient ili kupata tangent kwenye safu ya kiwango cha kazi iliyotolewa.
• Tumia derivatives ya uongozi na gradients katika vipimo vitatu.

Kazi\(z=f(x,y)\) ina derivatives mbili za sehemu:\(∂z/∂x\) na\(∂z/∂y\). Derivatives hizi zinahusiana na kila moja ya vigezo vya kujitegemea na vinaweza kutafsiriwa kama viwango vya haraka vya mabadiliko (yaani, kama mteremko wa mstari wa tangent). Kwa mfano,\(∂z/∂x\) inawakilisha mteremko wa mstari tangent kupitia hatua fulani juu ya uso inavyoelezwa kwa\(z=f(x,y),\) kuchukua mstari tangent ni sambamba na \(x\)-axis. Vile vile,\(∂z/∂y\) inawakilisha mteremko wa mstari wa tangent sambamba na \(y\)-axis. Sasa tunazingatia uwezekano wa mstari wa tangent sambamba na mhimili wala.

derivatives mwelekeo

Tunaanza na grafu ya uso unaofafanuliwa na equation\(z=f(x,y)\). Kutokana na hatua\((a,b)\) katika uwanja wa\(f\), sisi kuchagua mwelekeo wa kusafiri kutoka hatua hiyo. Tunapima mwelekeo kwa kutumia angle\(θ\), ambayo hupimwa kinyume chake katika\(xy\) -ndege, kuanzia saa sifuri kutoka kwa\(x\) mhimili mzuri (Kielelezo\(\PageIndex{1}\)). Umbali tunayosafiri ni\(h\) na mwelekeo tunayosafiri hutolewa na vector ya kitengo\(\vecs u=(\cos θ)\,\hat{\mathbf i}+(\sin θ)\,\hat{\mathbf j}.\) Kwa hiyo,\(z\) -kuratibu ya hatua ya pili kwenye grafu hutolewa na\(z=f(a+h\cos θ,b+h\sin θ).\)

Kielelezo\(\PageIndex{1}\): Kupata derivative directional katika hatua juu ya graph ya\(z=f(x,y)\). Mteremko wa mshale wa bluu kwenye grafu unaonyesha thamani ya derivative ya uongozi wakati huo.

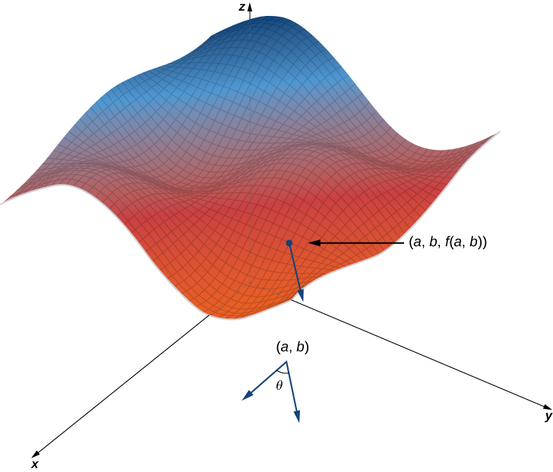
Tunaweza kuhesabu mteremko wa mstari wa secant kwa kugawanya tofauti\(z\) katika-maadili kwa urefu wa sehemu ya mstari kuunganisha pointi mbili katika uwanja. Urefu wa sehemu ya mstari ni\(h\). Kwa hiyo, mteremko wa mstari wa secant ni

\[m_{sec}=\dfrac{f(a+h\cos θ,b+h\sin θ)−f(a,b)}{h} \nonumber \]

Ili kupata mteremko wa mstari wa tangent katika mwelekeo huo, tunachukua kikomo kama\(h\) inakaribia sifuri.

Ufafanuzi: derivatives

Tuseme\(z=f(x,y)\) ni kazi ya vigezo mbili na uwanja wa\(D\). Hebu\((a,b)∈D\) na ufafanue\(\vecs u=(\cos θ)\,\hat{\mathbf i}+(\sin θ)\,\hat{\mathbf j}\). Kisha derivative directional ya\(f\) katika mwelekeo wa\(\vecs u\) ni kutolewa na

\[D_{\vecs u}f(a,b)=\lim_{h→0}\dfrac{f(a+h \cos θ,b+h\sin θ)−f(a,b)}{h} \label{DD} \]

zinazotolewa kikomo ipo.

Equation\ ref {DD} hutoa ufafanuzi rasmi wa derivative directional ambayo inaweza kutumika katika kesi nyingi kwa mahesabu derivative directional.

Kumbuka kuwa tangu hatua\((a, b)\) ni kuchaguliwa nasibu kutoka uwanja\(D\) wa kazi\(f\), tunaweza kutumia ufafanuzi huu kupata derivative directional kama kazi ya\(x\) na\(y\).

Hiyo ni,

\[D_{\vecs u}f(x,y)=\lim_{h→0}\dfrac{f(x+h \cos θ,y+h\sin θ)−f(x,y)}{h} \label{DDxy} \]

Mfano\(\PageIndex{1}\): Finding a Directional Derivative from the Definition

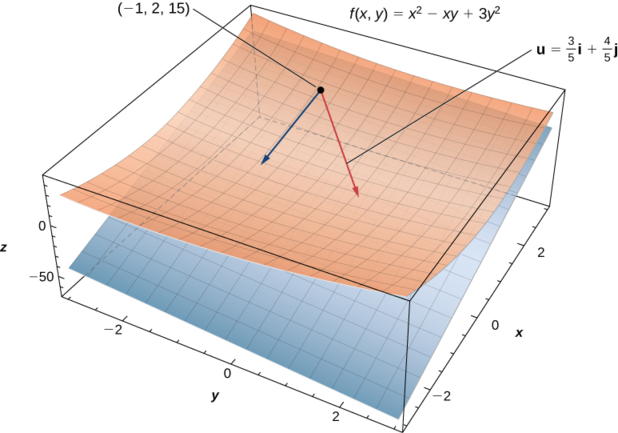
Hebu\(θ=\arccos(3/5).\) Kupata derivative directional\(D_{\vecs u}f(x,y)\) ya\(f(x,y)=x^2−xy+3y^2\) katika mwelekeo wa\(\vecs u=(\cos θ)\,\hat{\mathbf i}+(\sin θ)\,\hat{\mathbf j}\).

Kisha kuamua\(D_{\vecs u}f(−1,2)\).

Suluhisho

Kwanza kabisa, tangu\(\cos θ=3/5\) na\(θ\) ni papo hapo, hii ina maana

\[\sin θ=\sqrt{1−\left(\dfrac{3}{5}\right)^2}=\sqrt{\dfrac{16}{25}}=\dfrac{4}{5}. \nonumber \]

Kutumia\(f(x,y)=x^2−xy+3y^2,\) sisi kwanza kuhesabu\(f(x+h\cos θ,y+h\sin θ)\):

\ [kuanza {kuungana*} f (x+h\ cos γ, y+h\ dhambi γ) &= (x+h\ cos) ^2- (x+h\ cos γ) (y+h\ dhambi) +3 (y+h\ dhambi) ^2\\
&=x ^ 2+2xh\ cos ρ+h\ cos ^2\ cos ^2 κος xy-xy\ dhambi ν\ cos ρ,1h ^ 2\ dhambi γ\ cos ρ+3y ^ 2+6yh\ dhambi ν+3h ^ 2\ dhambi\\
&=x ^ 2+2xh (\ frac {3} {5}) +\ frac {9h ^ 2} {25} -xy\ frac {4xh} {5}\ frac {5} {5}} {5}} {5}} {5} c {12h ^2} {25} +3y ^ 2+6yh (\ frac {4} {5}) +3h ^ 2 (\ frac {16} {25})\\
&=x^2,1xy+3y ^ 2+\ FRAC {2xh} {5} +\ FRAC {5} {5}. \ mwisho {align*}\]

Sisi badala ya maneno haya katika Equation\ ref {DD} na\(a = x\) na\(b = y\):

\ [kuanza {align*} D_ {\ vecs u} f (x, y) &=\ lim_ {h → 0}\ frac {f (x+h\ cos γ, y+h\ dhambi) -f (x, y)} {h}\\
&=\ lim_ {h→ 0}\ frac {(x ^ 2,1+xy+3y ^ 2+\ frac {2xh} {5} {5} +\ frac {9h ^ 2} {5} +\ Frac {21yh} {5}) - (x^2,1xy+3y ^ 2)} {h}\\
&=\ lim_ {h→ 0}\ frac {2xh} {5} {5} +\ Frac {21} yh} {5}} {h}\\
& ; =\ lim_ {h→ 0}\ frac {2x} {5} +\ frac {9h} {5} +\ frac {21y} {5}\\
&=\ Frac {2x+21y} {5}. \ mwisho {align*}\]

Kuhesabu\(D_{\vecs u}f(−1,2),\) sisi badala\(x=−1\) na\(y=2\) katika jibu hili (Kielelezo\(\PageIndex{2}\)):

\[ D_{\vecs u}f(−1,2)=\dfrac{2(−1)+21(2)}{5}=\dfrac{−2+42}{5}=8. \nonumber \]

Kielelezo\(\PageIndex{2}\): Kutafuta derivative directional\(\vecs u\) katika mwelekeo fulani katika hatua fulani juu ya uso. Ndege ni tangent kwa uso katika hatua fulani\((−1,2,15).\)

Njia rahisi ya kuhesabu derivatives directional ambayo inahusisha derivatives sehemu ni ilivyoainishwa katika theorem zifuatazo.

Derivative Directional ya Kazi ya Vigezo mbili

Hebu\(z=f(x,y)\) kuwa kazi ya vigezo mbili\(x\) na\(y\), na kudhani kwamba\(f_x\) na\(f_y\) kuwepo. Kisha derivative directional ya\(f\) katika mwelekeo wa\(\vecs u=(\cos θ)\,\hat{\mathbf i}+(\sin θ)\,\hat{\mathbf j}\) ni kutolewa na

\[D_{\vecs u}f(x,y)=f_x(x,y)\cos θ+f_y(x,y)\sin θ. \label{DD2v} \]

Ushahidi

Kutumia ufafanuzi wa derivative directional ilivyoelezwa hapo juu katika Equation\ ref {DD}, derivative directional ya\(\vecs u=(\cos θ)\,\hat{\mathbf i}+(\sin θ)\,\hat{\mathbf j}\)\((x_0, y_0)\) katika mwelekeo wa katika hatua katika uwanja wa\(f\) inaweza kuandikwa\(f\)

\[D_{\vecs u}f((x_0, y_0))=\lim_{t→0}\dfrac{f(x_0+t \cos θ,y_0+t\sin θ)−f(x_0,y_0)}{t}. \nonumber \]

Hebu\(x=x_0+t\cos θ\)\(y=y_0+t\sin θ,\) na ufafanue\(g(t)=f(x,y)\). Tangu\(f_x\) na\(f_y\) zote mbili zipo, tunaweza kutumia utawala wa mnyororo kwa kazi za vigezo viwili ili kuhesabu\(g′(t)\):

\[g′(t)=\dfrac{∂f}{∂x}\dfrac{dx}{dt}+\dfrac{∂f}{∂y}\dfrac{dy}{dt}=f_x(x,y)\cos θ+f_y(x,y)\sin θ. \nonumber \]

Kama\(t=0,\) basi\(x=x_0\) na\(y=y_0,\) hivyo

\[g′(0)=f_x(x_0,y_0)\cos θ+f_y(x_0,y_0)\sin θ \nonumber \]

Kwa ufafanuzi wa pia\(g′(t),\) ni kweli kwamba

\[g′(0)=\lim_{t→0}\dfrac{g(t)−g(0)}{t}=\lim_{t→0}\dfrac{f(x_0+t\cos θ,y_0+t\sin θ)−f(x_0,y_0)}{t}. \nonumber \]

Kwa hiyo,\(D_{\vecs u}f(x_0,y_0)=f_x(x_0,y_0)\cos θ+f_y(x_0,y_0)\sin θ\).

Kwa kuwa hatua\( (x_0,y_0) \) ni hatua ya kiholela kutoka uwanja wa\(f\), matokeo haya anashikilia kwa pointi zote katika uwanja wa\(f\) ambayo sehemu\(f_x\) na\(f_y\) zipo.

Kwa hiyo,\[D_{\vecs u}f(x,y)=f_x(x,y)\cos θ+f_y(x,y)\sin θ. \nonumber \]

□

Mfano\(\PageIndex{2}\): Finding a Directional Derivative: Alternative Method

Hebu\(θ=\arccos (3/5).\) Kupata derivative directional\(D_{\vecs u}f(x,y)\) ya\(f(x,y)=x^2−xy+3y^2\) katika mwelekeo wa\(\vecs u=(\cos θ)\,\hat{\mathbf i}+(\sin θ)\,\hat{\mathbf j}\).

Kisha kuamua\(D_{\vecs u}f(−1,2)\).

Suluhisho

Kwanza, tunapaswa kuhesabu derivatives ya sehemu ya\(f\):

\[\begin{align*}f_x(x,y) &=2x−y \\ f_y(x,y) &=−x+6y, \end{align*}\]

Kisha sisi kutumia Equation\ ref {DD2v} na\(θ=\arccos (3/5)\):

\ [kuanza {align*} D_ {\ vecs u} f (x, y) &=f_x (x, y)\ cos ρ+f_y (x, y)\ sin γ\\
& =( 2x-y)\ dfrac {3} {5} {5} {5} {3} {5} {3} {5} {3} {5} {3} {5} {3} {5} {5}\\ 6x} {5} -\ dfrac {3y} {5} -\ dfrac {4x} {5} +\ dfrac {24y} {5}\\
&=\ dfrac {2x+21y} {5}.
\ mwisho {align*}\]

Kuhesabu\(D_{\vecs u}f(−1,2),\) basi\(x=−1\) na\(y=2\):

\[D_{\vecs u}f(−1,2)=\dfrac{2(−1)+21(2)}{5}=\dfrac{−2+42}{5}=8.\nonumber \]

Hii ni jibu moja kupatikana katika Mfano\(\PageIndex{1}\).

Zoezi\(\PageIndex{1}\):

Kupata derivative directional\(D_{\vecs u}f(x,y)\) ya\(f(x,y)=3x^2y−4xy^3+3y^2−4x\) katika mwelekeo wa\(\vecs u=(\cos \dfrac{π}{3})\,\hat{\mathbf i}+(\sin \dfrac{π}{3})\,\hat{\mathbf j}\) kutumia Equation\ ref {DD2v}.

Ni nini\(D_{\vecs u} f(3,4)\)?

Kidokezo

Tumia derivatives ya sehemu na ueleze thamani ya\(θ\).

Jibu

\(D_{\vecs u}f(x,y)=\dfrac{(6xy−4y^3−4)(1)}{2}+\dfrac{(3x^2−12xy^2+6y)\sqrt{3}}{2}\)

\(D_{\vecs u}f(3,4)=\dfrac{72−256−4}{2}+\dfrac{(27−576+24)\sqrt{3}}{2}=−94−\dfrac{525\sqrt{3}}{2}\)

Ikiwa vector inayotolewa kwa mwelekeo wa derivative sio vector kitengo, basi ni muhimu tu kugawanya na kawaida ya vector. Kwa mfano, kama tunataka kupata derivative directional ya kazi\(\PageIndex{2}\) katika Mfano katika mwelekeo wa vector\(⟨−5,12⟩\), sisi kwanza kugawanya na ukubwa wake kupata\(\vecs u\). Hii inatupa\(\vecs u=⟨−\frac{5}{13},\frac{12}{13}⟩\).

Kisha

\ [kuanza {align*} D_ {\ vecs u} f (x, y) &=f_x (x, y)\ cos ρ+f_y (x, y)\ sin\\
&=\dfrac {5} {13} (2x-y) +\ dfrac {12} {13} (-x+6y)\\
&=Δ\ dfrac c {22} {13} x+\ dfrac {17} {13} y\ mwisho {align*}\]

Gradient

Upande wa kulia wa Equation\ ref {DD2v} ni sawa na\(f_x(x,y)\cos θ+f_y(x,y)\sin θ\), ambayo inaweza kuandikwa kama bidhaa dot ya wadudu wawili. Kufafanua vector kwanza kama\(\vecs ∇f(x,y)=f_x(x,y)\,\hat{\mathbf i}+f_y(x,y)\,\hat{\mathbf j}\) na vector pili kama\(\vecs u=(\cos θ)\,\hat{\mathbf i}+(\sin θ)\,\hat{\mathbf j}\). Kisha upande wa kulia wa equation unaweza kuandikwa kama bidhaa dot ya wadudu hawa wawili:

\[D_{\vecs u}f(x,y)=\vecs ∇f(x,y)⋅\vecs u. \label{gradDirDer} \]

Vector ya kwanza katika Equation\ ref {GradRidder} ina jina maalum: gradient ya kazi\(f\). Ishara\(∇\) inaitwa nabla na vector\(\vecs ∇f\) inasoma “del\(f\).”

Ufafanuzi: Gradient

Hebu\(z=f(x,y)\) kuwa kazi ya\(x\) na\(y\) vile kwamba\(f_x\) na\(f_y\) kuwepo. Vector\(\vecs ∇f(x,y)\) inaitwa gradient ya\(f\) na inaelezwa kama

\[\vecs ∇f(x,y)=f_x(x,y)\,\hat{\mathbf i}+f_y(x,y)\,\hat{\mathbf j}. \label{grad} \]

Vector pia\(\vecs ∇f(x,y)\) imeandikwa kama “grad\(f\).”

Mfano\(\PageIndex{3}\): Finding Gradients

Pata\(\vecs ∇f(x,y)\) kipengee cha kila kazi zifuatazo:

1. \(f(x,y)=x^2−xy+3y^2\)
2. \(f(x,y)=\sin 3 x \cos 3y\)

Suluhisho

Kwa sehemu zote mbili a. na b., sisi kwanza kuhesabu derivatives sehemu\(f_x\) na\(f_y\), kisha kutumia Equation\ ref {grad}.

a.\( f_x(x,y)=2x−y\) na\(f_y(x,y)=−x+6y\), hivyo

\[\begin{align*} \vecs ∇f(x,y) &=f_x(x,y)\,\hat{\mathbf i}+f_y(x,y)\,\hat{\mathbf j}\\ &=(2x−y)\,\hat{\mathbf i}+(−x+6y)\,\hat{\mathbf j}.\end{align*}\]

b.\( f_x(x,y)=3\cos 3x \cos 3y\) na\(f_y(x,y)=−3\sin 3x \sin 3y\), hivyo

\ [kuanza {align*}\ vecs f (x, y) &=f_x (x, y)\,\ kofia {\ mathbf i} +f_y (x, y)\,\ kofia {\ mathbf j}\\
& =( 3\ cos 3x\ cos 3y)\,\ kofia {\ mathbf i} - (3\ dhambi 3x\ cos 3y)\,\ kofia {\ mathbf i} (3\\ sin 3y)\\ x\ sin 3g)\,\ kofia {\ mathbf j}. \ mwisho {align*}\]

Zoezi\(\PageIndex{2}\)

Kupata gradient\(\vecs ∇f(x,y)\) ya\(f(x,y)=\dfrac{x^2−3y^2}{2x+y}\).

Kidokezo

Tumia derivatives ya sehemu, kisha utumie Equation\ ref {grad}.

Jibu

\(\vecs ∇f(x,y)=\dfrac{2x^2+2xy+6y^2}{(2x+y)^2}\,\hat{\mathbf i}−\dfrac{x^2+12xy+3y^2}{(2x+y)^2}\,\hat{\mathbf j}\)

Gradient ina mali muhimu. Tayari tumeona formula moja ambayo inatumia gradient: formula ya derivative directional. Kumbuka kutoka Dot Bidhaa kwamba kama angle kati ya vectors mbili\(\vecs a\) na\(\vecs b\) ni\(φ\), basi\(\vecs a⋅\vecs b=‖\vecs a‖‖\vecs b‖\cos φ.\) Kwa hiyo, kama angle kati\(\vecs ∇f(x_0,y_0)\) na\(\vecs u=(cosθ)\,\hat{\mathbf i}+(sinθ)\,\hat{\mathbf j}\) ni\(φ\), tuna

\[D_{\vecs u}f(x_0,y_0)=\vecs ∇f(x_0,y_0)⋅\vecs u=\|\vecs ∇f(x_0,y_0)\|‖\vecs u‖\cos φ=\|\vecs ∇f(x_0,y_0)\|\cos φ. \nonumber \]

\(‖\vecs u‖\)kutoweka kwa sababu\(\vecs u\) ni kitengo vector. Kwa hiyo, derivative directional ni sawa na ukubwa wa gradient tathmini katika\((x_0,y_0)\) kuongezeka kwa\(\cos φ\). Kumbuka kuwa\(\cos φ\) ni kati\(−1\) ya hadi\(1\).

Ikiwa\(φ=0,\) basi\(\cos φ=1\)\(\vecs ∇f(x_0,y_0)\) na\(\vecs u\) wote wawili wanasema katika mwelekeo huo.

Ikiwa\(φ=π\), basi\(\cos φ=−1\)\(\vecs ∇f(x_0,y_0)\) na\(\vecs u\) uelekeze kwa njia tofauti.

Katika kesi ya kwanza, thamani ya\(D_{\vecs u}f(x_0,y_0)\) ni maximized; katika kesi ya pili, thamani ya\(D_{\vecs u}f(x_0,y_0)\) ni kupunguzwa.

Tunaweza pia kuona kwamba kama\(\vecs ∇f(x_0,y_0)=\vecs 0\), basi

\[ D_{\vecs u}f(x_0,y_0)=\vecs ∇f(x_0,y_0)⋅\vecs u=0 \nonumber \]

kwa vector yoyote\(\vecs u\). Matukio haya matatu yameelezwa katika theorem ifuatayo.

Mali ya Gradient

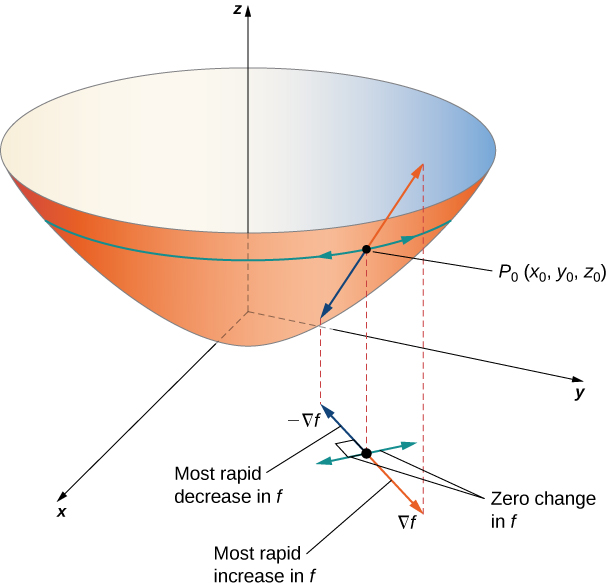
Tuseme kazi\(z=f(x,y)\) ni tofauti katika\((x_0,y_0)\) (Kielelezo\(\PageIndex{3}\)).

1. Ikiwa\(\vecs ∇f(x_0,y_0)=\vecs 0\), basi\(D_{\vecs u}f(x_0,y_0)=0\) kwa vector yoyote ya kitengo\(\vecs u\).
2. Kama\(\vecs ∇f(x_0,y_0)≠ \vecs 0\), basi\(D_{\vecs u}f(x_0,y_0)\) ni maximized wakati\(\vecs u\) pointi katika mwelekeo huo kama\(\vecs ∇f(x_0,y_0)\). Thamani ya juu ya\(D_{\vecs u}f(x_0,y_0)\) ni\(\|\vecs ∇f(x_0,y_0)\|\).
3. Kama\(\vecs ∇f(x_0,y_0)≠\vecs 0\), basi\(D_{\vecs u}f(x_0,y_0)\) ni kupunguzwa wakati\(\vecs u\) pointi katika mwelekeo kinyume na\(\vecs ∇f(x_0,y_0)\). Thamani ya chini ya\(D_{\vecs u}f(x_0,y_0)\) ni\(−\|\vecs ∇f(x_0,y_0)\|\).

Kielelezo\(\PageIndex{3}\): Gradient inaonyesha maadili ya juu na ya chini ya derivative directional kwa uhakika.

Mfano\(\PageIndex{4}\): Finding a Maximum Directional Derivative

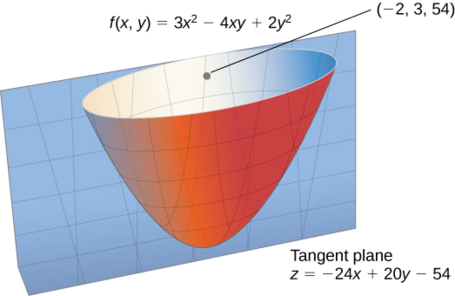
Pata mwelekeo ambao derivative ya uongozi wa\(f(x,y)=3x^2−4xy+2y^2\) saa\((−2,3)\) ni kiwango cha juu. Thamani ya juu ni nini?

Suluhisho

Thamani ya juu ya derivative directional hutokea wakati\(\vecs ∇f\) na kitengo cha vector hatua katika mwelekeo huo. Kwa hiyo, tunaanza kwa kuhesabu\(\vecs ∇f(x,y\)):

\[f_x(x,y)=6x−4y \; \text{and}\; f_y(x,y)=−4x+4y \nonumber \]

kwa hivyo

\[\vecs ∇f(x,y)=f_x(x,y)\,\hat{\mathbf i}+f_y(x,y)\,\hat{\mathbf j}=(6x−4y)\,\hat{\mathbf i}+(−4x+4y)\,\hat{\mathbf j}. \nonumber \]

Kisha, tunatathmini gradient katika\((−2,3)\):

\[\vecs ∇f(−2,3)=(6(−2)−4(3))\,\hat{\mathbf i}+(−4(−2)+4(3))\,\hat{\mathbf j}=−24\,\hat{\mathbf i}+20\,\hat{\mathbf j}. \nonumber \]

Tunahitaji kupata vector kitengo ambacho kinaonyesha katika mwelekeo sawa na\(\vecs ∇f(−2,3),\) hivyo hatua inayofuata ni kugawanya\(\vecs ∇f(−2,3)\) kwa ukubwa wake, ambayo ni\(\sqrt{(−24)^2+(20)^2}=\sqrt{976}=4\sqrt{61}\). Kwa hiyo,

\[\dfrac{\vecs ∇f(−2,3)}{\|\vecs ∇f(−2,3)\|}=\dfrac{−24}{4\sqrt{61}}i+\dfrac{20}{4\sqrt{61}}j=−\dfrac{6\sqrt{61}}{61}\,\hat{\mathbf i}+\dfrac{5\sqrt{61}}{61}\,\hat{\mathbf j}. \nonumber \]

Hii ni vector kitengo kwamba pointi katika mwelekeo sawa na\(\vecs ∇f(−2,3).\) Ili kupata angle sambamba na vector kitengo hiki, sisi kutatua equations

\[\cos θ=\dfrac{−6\sqrt{61}}{61}\; \text{and}\; \sin θ=\dfrac{5\sqrt{61}}{61} \nonumber \]

kwa\(θ\). Kwa kuwa cosine ni hasi na sine ni chanya, angle lazima iwe katika quadrant ya pili. Kwa hiyo,\(θ=π−\arcsin((5\sqrt{61})/61)≈2.45\) rad.

Thamani ya juu ya derivative directional katika\((−2,3)\) ni\(\|\vecs ∇f(−2,3)\|=4\sqrt{61}\) (Kielelezo\(\PageIndex{4}\)).

Kielelezo\(\PageIndex{4}\): Thamani ya juu ya derivative directional katika\((−2,3)\) ni katika mwelekeo wa gradient.

Zoezi\(\PageIndex{3}\)

Pata mwelekeo ambao derivative ya uongozi wa\(g(x,y)=4x−xy+2y^2\) saa\((−2,3)\) ni kiwango cha juu. Thamani ya juu ni nini?

Kidokezo

Tathmini gradient ya\(g\) wakati\((−2,3)\).

Jibu

Gradient ya\(g\) saa\((−2,3)\) ni\(\vecs ∇g(−2,3)=\,\hat{\mathbf i}+14\,\hat{\mathbf j}\). kitengo vector kwamba pointi katika mwelekeo huo kama\(\vecs ∇g(−2,3)\) ni

\[\dfrac{\vecs ∇g(−2,3)}{\|\vecs ∇g(−2,3)\|}=\dfrac{1}{\sqrt{197}}\,\hat{\mathbf i}+\dfrac{14}{\sqrt{197}}\,\hat{\mathbf j}=\dfrac{\sqrt{197}}{197}\,\hat{\mathbf i}+\dfrac{14\sqrt{197}}{197}\,\hat{\mathbf j},\nonumber \]

ambayo inatoa angle ya\(θ=\arcsin ((14\sqrt{197})/197)≈1.499\) rad.

Thamani ya juu ya derivative directional ni\(\|\vecs ∇g(−2,3)\|=\sqrt{197}\).

Kielelezo\(\PageIndex{5}\) kinaonyesha sehemu ya grafu ya kazi\(f(x,y)=3+\sin x \sin y\). Kutokana na hatua\((a,b)\) katika uwanja wa\(f\), thamani ya juu ya derivative directional katika hatua hiyo ni iliyotolewa na\(\|\vecs ∇f(a,b)\|\). Hii ingekuwa sawa na kiwango cha kupaa kubwa kama uso kuwakilishwa ramani topographical. Kama sisi akaenda katika mwelekeo kinyume, itakuwa kiwango cha asili kubwa.

Kielelezo\(\PageIndex{5}\): uso kawaida katika\(\mathbb R^3\). Kutokana na uhakika juu ya uso, derivative directional inaweza kuhesabiwa kwa kutumia gradient.

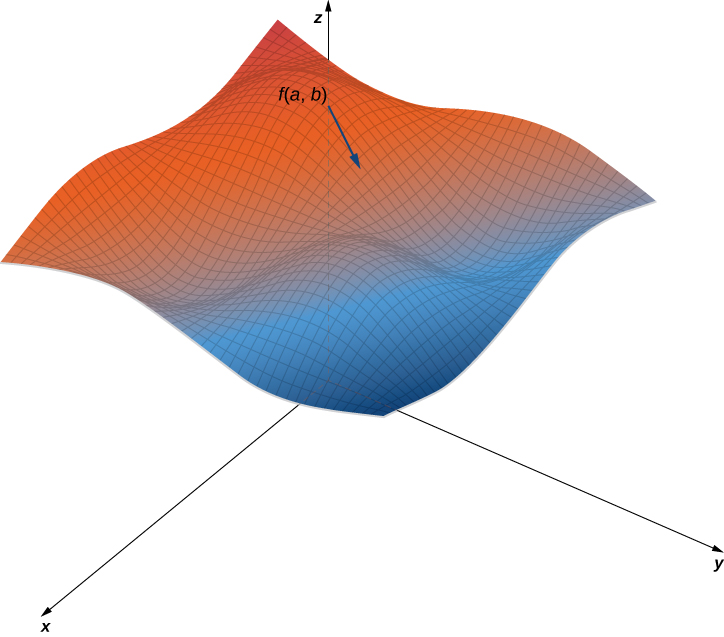
Wakati wa kutumia ramani ya kijiografia, mteremko mwinuko ni daima katika mwelekeo ambapo mistari ya contour iko karibu zaidi (Kielelezo\(\PageIndex{6}\)). Hii ni sawa na ramani contour ya kazi, kuchukua curves ngazi ni kupatikana kwa maadili sawa spaced katika aina mbalimbali ya kazi hiyo.

Kielelezo\(\PageIndex{6}\): Contour ramani kwa ajili ya kazi\(f(x,y)=x^2−y^2\) kwa kutumia maadili ngazi kati\(−5\) na\(5\).

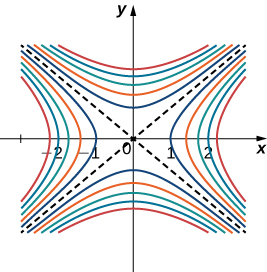
Gradients na Ngazi Curves

Kumbuka kwamba kama Curve inaelezwa parametrically na jozi kazi\((x(t),y(t)),\) basi vector\(x′(t)\,\hat{\mathbf i}+y′(t)\,\hat{\mathbf j}\) ni tangent kwa Curve kwa kila thamani ya\(t\) katika uwanja. Sasa hebu tuchukue\(z=f(x,y)\) ni kazi tofauti ya\(x\) na\(y\), na\((x_0,y_0)\) iko katika uwanja wake. Hebu tuseme zaidi kwamba\(x_0=x(t_0)\) na\(y_0=y(t_0)\) kwa baadhi ya thamani ya\(t\), na kufikiria Curve ngazi\(f(x,y)=k\). Eleza\(g(t)=f(x(t),y(t))\) na uhesabu\(g′(t)\) kwenye safu ya ngazi. Kwa mnyororo Utawala,

\[g′(t)=f_x(x(t),y(t))x′(t)+f_y(x(t),y(t))y′(t). \nonumber \]

Lakini\(g′(t)=0\) kwa sababu\(g(t)=k\) kwa wote\(t\). Kwa hiyo, kwa upande mmoja,

\[f_x(x(t),y(t))x′(t)+f_y(x(t),y(t))y′(t)=0; \nonumber \]

kwa upande mwingine,

\[f_x(x(t),y(t))x′(t)+f_y(x(t),y(t))y′(t)=\vecs ∇f(x,y)⋅⟨x′(t),y′(t)⟩. \nonumber \]

Kwa hiyo,

\[\vecs ∇f(x,y)⋅⟨x′(t),y′(t)⟩=0. \nonumber \]

Hivyo, bidhaa ya dot ya vectors hizi ni sawa na sifuri, ambayo inamaanisha kuwa ni orthogonal. Hata hivyo, vector ya pili ni tangent kwa curve ngazi, ambayo ina maana gradient lazima iwe ya kawaida kwa Curve ngazi, ambayo inatoa kupanda kwa theorem zifuatazo.

Gradient Ni ya kawaida kwa Curve Ngazi

Tuseme kazi\(z=f(x,y)\) ina derivatives ya sehemu ya kwanza ya utaratibu wa kwanza katika diski iliyo wazi inayozingatia wakati\((x_0,y_0)\). Kama\(\vecs ∇f(x_0,y_0)≠0\), basi\(\vecs ∇f(x_0,y_0)\) ni ya kawaida kwa Curve ngazi ya\(f\) saa\((x_0,y_0).\)

Tunaweza kutumia theorem hii kupata wadudu tangent na kawaida kwa curves ngazi ya kazi.

Mfano\(\PageIndex{5}\): Finding Tangents to Level Curves

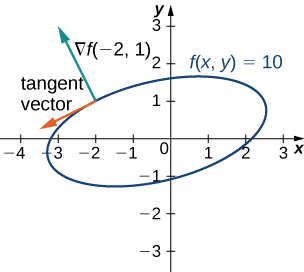
Kwa kazi\(f(x,y)=2x^2−3xy+8y^2+2x−4y+4,\) kupata vector tangent kwa Curve ngazi katika hatua\((−2,1)\). Graph Curve ngazi sambamba\(f(x,y)=18\) na na kuteka katika\(\vecs ∇f(−2,1)\) na vector tangent.

Suluhisho

Kwanza, ni lazima mahesabu\(\vecs ∇f(x,y):\)

\[f_x(x,y)=4x−3y+2 \;\text{and}\; f_y=−3x+16y−4 \;\text{so}\; \vecs ∇f(x,y)=(4x−3y+2)\,\hat{\mathbf i}+(−3x+16y−4)\,\hat{\mathbf j}.\nonumber \]

Kisha, tunatathmini\(\vecs ∇f(x,y)\)\((−2,1):\)

\[\vecs ∇f(−2,1)=(4(−2)−3(1)+2)\,\hat{\mathbf i}+(−3(−2)+16(1)−4)\,\hat{\mathbf j}=−9\,\hat{\mathbf i}+18\,\hat{\mathbf j}.\nonumber \]

Vector hii ni orthogonal kwa Curve katika hatua\((−2,1)\). Tunaweza kupata vector tangent kwa kugeuza vipengele na kuzidisha ama moja kwa\(−1\). Hivyo, kwa mfano,\(−18\,\hat{\mathbf i}−9\,\hat{\mathbf j}\) ni vector tangent (Kielelezo\(\PageIndex{7}\)).

Kielelezo\(\PageIndex{7}\): Vectors Tangent na kawaida kwa\(2x^2−3xy+8y^2+2x−4y+4=18\) wakati\((−2,1)\).

Zoezi\(\PageIndex{4}\)

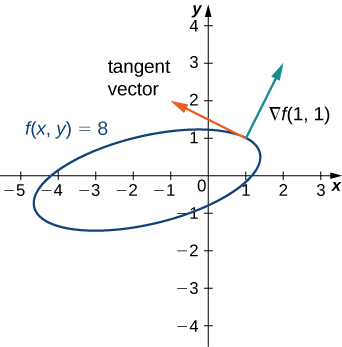
Kwa ajili ya kazi\(f(x,y)=x^2−2xy+5y^2+3x−2y+3\), kupata tangent kwa Curve ngazi katika hatua\((1,1)\). Chora grafu ya safu ya ngazi inayofanana\(f(x,y)=8\) na na kuteka\(\vecs ∇f(1,1)\) na vector tangent.

Kidokezo

Tumia gradient kwa uhakika\((1,1)\).

Jibu

\(\vecs ∇f(x,y)=(2x−2y+3)\,\hat{\mathbf i}+(−2x+10y−2)\,\hat{\mathbf j}\)

\(\vecs ∇f(1,1)=3\,\hat{\mathbf i}+6\,\hat{\mathbf j}\)

Vector tangent:\(6\,\hat{\mathbf i}−3\,\hat{\mathbf j}\) au\(−6\,\hat{\mathbf i}+3\,\hat{\mathbf j}\)

Gradients tatu-dimensional na der

Ufafanuzi wa gradient unaweza kupanuliwa kwa kazi za vigezo zaidi ya mbili.

Ufafanuzi: Gradients katika 3D

Hebu\(w=f(x, y, z)\) kuwa kazi ya vigezo tatu vile kwamba\(f_x, \, f_y\),fx,fy,andfzfx,fy,andfz" role="presentation" tabindex="0"> na\(f_z\) zipo. Vector\(\vecs ∇f(x,y,z)\) inaitwa gradient yaff" role="presentation" tabindex="0">\(f\) na inaelezwa kama

\[\vecs ∇f(x,y,z)=f_x(x,y,z)\,\hat{\mathbf i}+f_y(x,y,z)\,\hat{\mathbf j}+f_z(x,y,z)\,\hat{\mathbf k}.\label{grad3d} \]

\(\vecs ∇f(x,y,z)\)pia inaweza kuandikwa kama grad\(f(x,y,z).\)

Kuhesabu gradient ya kazi katika vigezo vitatu ni sawa na kuhesabu gradient ya kazi katika vigezo viwili. Kwanza, tunahesabu derivatives ya sehemu\(f_x, \, f_y,\) na\(f_z\), na kisha tunatumia Equation\ ref {grad3d}.

Mfano\(\PageIndex{6}\): Finding Gradients in Three Dimensions

Pata\(\vecs ∇f(x,y,z)\) kipengee cha kila kazi zifuatazo:

1. \(f(x,y,z)=5x^2−2xy+y^2−4yz+z^2+3xz\)
2. \(f(x,y,z)=e^{−2z}\sin 2x \cos 2y\)

Suluhisho

Kwa sehemu zote mbili a. na b., sisi kwanza kuhesabu derivatives sehemu\(f_x,f_y,\) na\(f_z\), kisha kutumia Equation\ ref {grad3d}.

a.\(f_x(x,y,z)=10x−2y+3z\),\(f_y(x,y,z)=−2x+2y−4z\), na\( f_z(x,y,z)=3x−4y+2z\), hivyo

\ [kuanza {align*}\ vecs f (x, y, z) &=f_x (x, y, z)\,\ kofia {\ mathbf i} +f_y (x, y, z)\,\ kofia {\ mathbf j} +f_z (x, y, z)\,\ kofia {\ mathbf k}\\
& =( 10x-2y+3z)\,\ kofia {\ mathbf i} + (-2x+2y-4z)\,\ kofia {\ mathbf j} + (3x-4y+2z)\,\ kofia {\ mathbf k}. \ mwisho {align*}\]

b.\(f_x(x,y,z) =2e^{−2z}\cos 2x \cos 2y\),\( f_y(x,y,z)=−2e^{−2z} \sin 2x \sin 2y\), na\(f_z(x,y,z)=−2e^{−2z}\sin 2x \cos 2y\), hivyo

\[\begin{align*} \vecs ∇f(x,y,z) &=f_x(x,y,z)\,\hat{\mathbf i}+f_y(x,y,z)\,\hat{\mathbf j}+f_z(x,y,z)\,\hat{\mathbf k} \\ &=(2e^{−2z}\cos 2x \cos 2y)\,\hat{\mathbf i}+(−2e^{−2z} \sin 2x \sin 2y)\,\hat{\mathbf j}+(−2e^{−2z}\sin 2x \cos 2y)\,\hat{\mathbf k} \\ &=2e^{−2z}(\cos 2x \cos 2y \,\hat{\mathbf i}−\sin 2x \sin 2y\,\hat{\mathbf j}−\sin 2x \cos 2y\,\hat{\mathbf k}). \end{align*}\]

Zoezi\(\PageIndex{5}\):

Kupata gradient\(\vecs ∇f(x,y,z)\) ya\(f(x,y,z)=\dfrac{x^2−3y^2+z^2}{2x+y−4z.}\)

Jibu

\[\vecs ∇f(x,y,z)=\dfrac{2x^2+2xy+6y^2−8xz−2z^2}{(2x+y−4z)^2}\,\hat{\mathbf i}−\dfrac{x^2+12xy+3y^2−24yz+z^2}{(2x+y−4z)^2}\,\hat{\mathbf j}+\dfrac{4x^2−12y^2−4z^2+4xz+2yz}{(2x+y−4z)^2}\,\hat{\mathbf k}\nonumber \]

Derivative ya uongozi pia inaweza kuzalishwa kwa kazi za vigezo vitatu. Kuamua mwelekeo katika vipimo vitatu, vector yenye vipengele vitatu inahitajika. Vector hii ni vector kitengo, na vipengele vya vector kitengo huitwa cosines directional. Kutokana na vector ya kitengo cha tatu-dimensional\(\vecs u\) katika fomu ya kawaida (yaani, hatua ya awali ni asili), vector hii huunda pembe tatu tofauti na chanya\(x\) -,\(y\) -, na\(z\) -axes. Hebu wito pembe hizi\(α,β,\) na\(γ\). Kisha cosines ya uongozi hutolewa na\(\cos α,\cos β,\) na\(\cos γ\). Hizi ni sehemu ya vector kitengo\(\vecs u\); tangu\(\vecs u\) ni kitengo vector, ni kweli kwamba\(\cos^2 α+\cos^2 β+\cos^2 γ=1.\)

Ufafanuzi: Derivative Directional ya Kazi ya vigezo Tatu

Tuseme\(w=f(x,y,z)\) ni kazi ya vigezo tatu na uwanja wa\(D\). Hebu\((x_0,y_0,z_0)∈D\) na basi\(\vecs u=\cos α\,\hat{\mathbf i}+\cos β\,\hat{\mathbf j}+\cos γ\,\hat{\mathbf k}\) iwe vector kitengo. Kisha, derivative directional ya\(f\) katika mwelekeo wa\(u\) ni kutolewa na

\[D_{\vecs u}f(x_0,y_0,z_0)=\lim_{t→0}\dfrac{f(x_0+t \cos α,y_0+t\cos β,z_0+t\cos γ)−f(x_0,y_0,z_0)}{t} \nonumber \]

zinazotolewa kikomo ipo.

Tunaweza kuhesabu derivative directional ya kazi ya vigezo tatu kwa kutumia gradient, na kusababisha formula kwamba ni sawa na Equation\ ref {DD2V}.

Directional derivative ya Kazi ya Vigezo Tatu

Hebu\(f(x,y,z)\) kuwa kazi differentiable ya vigezo tatu na basi\(\vecs u=\cos α\,\hat{\mathbf i}+\cos β\,\hat{\mathbf j}+\cos γ\,\hat{\mathbf k}\) kuwa kitengo vector. Kisha, derivative directional ya\(f\) katika mwelekeo wa\(\vecs u\) ni kutolewa na

\[D_{\vecs u}f(x,y,z)=\vecs ∇f(x,y,z)⋅\vecs u=f_x(x,y,z)\cos α+f_y(x,y,z)\cos β+f_z(x,y,z)\cos γ. \label{DDv3} \]

Pembe tatu\(α,β,\) na\(γ\) kuamua vector kitengo\(\vecs u\). Katika mazoezi, tunaweza kutumia vector ya kiholela (isiyo ya kawaida), kisha ugawanye na ukubwa wake ili kupata vector kitengo katika mwelekeo uliotaka.

Mfano\(\PageIndex{7}\): Finding a Directional Derivative in Three Dimensions

Tumia\(D_{\vecs v}f(1,−2,3)\) kwa uongozi wa\(\vecs v=−\,\hat{\mathbf i}+2\,\hat{\mathbf j}+2\,\hat{\mathbf k}\) kazi

\[ f(x,y,z)=5x^2−2xy+y^2−4yz+z^2+3xz. \nonumber \]

Suluhisho:

Kwanza, tunapata ukubwa wa\(v\):

\[‖\vecs v‖=\sqrt{(−1)^2+(2)^2+(2)^2}=\sqrt{9}=3. \nonumber \]

Kwa hiyo,\(\dfrac{\vecs v}{‖\vecs v‖}=\dfrac{−\hat{\mathbf i}+2\,\hat{\mathbf j}+2\,\hat{\mathbf k}}{3}=−\dfrac{1}{3}\,\hat{\mathbf i}+\dfrac{2}{3}\,\hat{\mathbf j}+\dfrac{2}{3}\,\hat{\mathbf k}\) ni kitengo vector katika mwelekeo wa\(\vecs v\), hivyo\(\cos α=−\dfrac{1}{3},\cos β=\dfrac{2}{3},\) na\(\cos γ=\dfrac{2}{3}\). Kisha, tunahesabu derivatives ya sehemu ya\(f\):

\ [kuanza {align*} f_x (x, y, z) &=10x-2y+3z\\
f_y (x, y, z) &=-2x+2y-4z\\
f_z (x, y, z) &=-4y+2z+3x,\ mwisho {align*}\ nonumber\]

kisha badala yao katika Equation\ ref {dDV3}:

\ [kuanza {align*} D_ {\ vecs v} f (x, y, z) &=f_x (x, y, z)\ cos α+f_y (x, y, z)\ cos β+f_z (x, y, z)\ cos γ\\
& =( 10x-2y+3z) (\\ dfrac {1} {3}) + (-2x+2y-4z) (\ dfrac {2} {3}) + (-4y+2z+3x) (\ dfrac {2} {3})\\
&=-dfrac {10x} {3} {3} +\ dfrac {2y} {3} {3}} {4x}} {3} +\ dfrac {4y} {3} -\ dfrac {8z} {3} -\ dfrac { 8y} {3} +\ dfrac {4z} {3} +\ dfrac {6x} {3}\\
&=\ dfrac {8x} {3}} {2y} {3} {3}} {3}} {3}} {3}} {3}. \ mwisho {align*}\]

Mwisho, kupata\(D_{\vecs v}f(1,−2,3),\) sisi mbadala\(x=1,\, y=−2\), na\(z=3:\)

\ [kuanza {align*} D_ {\ vecs v} f (1, -2,3) &=\ dfrac {8 (1)} {3} -\ dfrac {2)} {3}} {3} {3} {3} {3} {3} {3} {3} {3} {4} {3} {3} {4} {3} {3} {4} {3} {3} {4} {3} {3} {4} {3} {3} {4} {3} {3} {4} {3} {3} {4} {3} {3} {4} {3}}
-\ dfrac {21} {3}\\ &=\ dfrac {25} {3}.
\ mwisho {align*}\]

Zoezi\(\PageIndex{6}\):

Tumia\(D_{\vecs v}f(x,y,z)\) na\(D_{\vecs v}f(0,−2,5)\)\(\vecs v=−3\,\hat{\mathbf i}+12\,\hat{\mathbf j}−4\,\hat{\mathbf k}\) kwa uongozi wa kazi

\[f(x,y,z)=3x^2+xy−2y^2+4yz−z^2+2xz.\nonumber \]

Kidokezo

Kwanza, ugawanye\(\vecs v\) kwa ukubwa wake, uhesabu derivatives ya sehemu ya\(f\), kisha utumie Equation\ ref {dDV3}.

Jibu

\(D_{\vecs v}f(x,y,z)=−\dfrac{3}{13}(6x+y+2z)+\dfrac{12}{13}(x−4y+4z)−\dfrac{4}{13}(2x+4y−2z)\)

\(D_{\vecs v}f(0,−2,5)=\dfrac{384}{13}\)

Muhtasari

• derivative directional inawakilisha kiwango cha mabadiliko ya kazi katika mwelekeo wowote.
• Gradient inaweza kutumika katika formula ili kuhesabu derivative directional.
• Gradient inaonyesha mwelekeo wa mabadiliko makubwa ya kazi ya kutofautiana zaidi ya moja.

Mlinganyo muhimu

• derivative directional (vipimo mbili)\[D_{\vecs u}f(a,b)=\lim_{h→0}\dfrac{f(a+h\cos θ,b+h\sin θ)−f(a,b)}{h} \nonumber \] au\[D_{\vecs u}f(x,y)=f_x(x,y)\cos θ+f_y(x,y)\sin θ\nonumber \]
• gradient (vipimo viwili)\[\vecs ∇f(x,y)=f_x(x,y)\,\hat{\mathbf i}+f_y(x,y)\,\hat{\mathbf j}\nonumber \]
• gradient (vipimo vitatu)\[\vecs ∇f(x,y,z)=f_x(x,y,z)\,\hat{\mathbf i}+f_y(x,y,z)\,\hat{\mathbf j}+f_z(x,y,z)\,\hat{\mathbf k}\nonumber \]
• derivative directional (vipimo tatu)\[D_{\vecs u}f(x,y,z)=\vecs ∇f(x,y,z)⋅\vecs u=f_x(x,y,z)\cos α+f_y(x,y,z)\cos β+f_x(x,y,z)\cos γ\nonumber \]

faharasa

derivative mwelekeo

derivative ya kazi katika mwelekeo wa kutolewa kitengo vector

gradient

gradient ya kazi\(f(x,y)\) inafafanuliwa kuwa\(\vecs ∇f(x,y)=(∂f/∂x)\,\hat{\mathbf i}+(∂f/∂y)\,\hat{\mathbf j},\) ambayo inaweza kuzalishwa kwa kazi ya idadi yoyote ya vigezo vya kujitegemea