Skip to main content
Global

14.6E: Mazoezi ya Sehemu ya 14.6

  1. Last updated
  2. Save as PDF
  • Page ID
    178552

    • Edwin “Jed” Herman & Gilbert Strang
    • OpenStax
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Katika zoezi la 1, pata derivative ya uongozi kwa kutumia ufafanuzi wa kikomo tu.

    1) a.\( f(x,y)=5−2x^2−\frac{1}{2}y^2\) katika hatua\( P(3,4)\) katika mwelekeo wa\(\vecs u=(\cos\frac{π}{4})\,\hat{\mathbf i}+(\sin\frac{π}{4})\,\hat{\mathbf j}\)

    Jibu
    a.\( D_{\vecs u}f(3,4) =−8\sqrt{2}\)

    1) b.\( f(x,y)=y^2\cos(2x)\) kwa uhakika\( P(\frac{π}{3},2)\) katika mwelekeo wa\(\vecs u=(\cos\frac{π}{4})\,\hat{\mathbf i}+(\sin\frac{π}{4})\,\hat{\mathbf j}\)

    Jibu
    b.\( D_{\vecs u}f(\frac{π}{3},2) =−2\sqrt{6}-\sqrt{2}\)

    2) Kupata derivative directional ya\( P(\frac{π}{4},2)\) katika\( f(x,y)=y^2\sin(2x)\) hatua katika mwelekeo wa\(\vecs u=5\,\hat{\mathbf i}+12\,\hat{\mathbf j}\).

    Katika mazoezi 3 - 13, tafuta derivative directional ya kazi katika mwelekeo wa\(\vecs v\) kama kazi ya\(x\) na\(y\). Kumbuka kwamba wewe kwanza unahitaji kupata vector kitengo katika mwelekeo wa vector mwelekeo. Kisha kupata thamani ya derivative directional katika hatua\(P\).

    3)\( f(x,y)=xy, \quad P(-2,0), \quad \vecs v=\frac{1}{2}\,\hat{\mathbf i}+\frac{\sqrt{3}}{2}\,\hat{\mathbf j}\)

    Jibu
    \(D_{\vecs v}f(x, y) = \frac{1}{2}y + \frac{\sqrt{3}}{2}x \)
    \(D_{\vecs v}f(-2, 0) = −\sqrt{3}\)

    4)\( h(x,y)=e^x\sin y,\quad P(1,\frac{π}{2}),\quad \vecs v=−\,\hat{\mathbf i}\)

    5)\( f(x,y)=x^2y,\quad P(−5,5),\quad \vecs v=3\,\hat{\mathbf i}−4\,\hat{\mathbf j}\)

    Jibu
    \(D_{\vecs v}f(x, y) = \frac{6}{5}xy - \frac{4}{5}x^2 \)
    \(D_{\vecs v}f(-5,5)= -50\)

    6)\( f(x,y)=xy,\quad P(1,1), \quad \vecs u=⟨\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}⟩\)

    7)\( f(x,y)=x^2−y^2, \quad P(1,0), \quad \vecs u=⟨\frac{\sqrt{3}}{2},\frac{1}{2}⟩\)

    Jibu
    \(D_{\vecs u}f(x, y) = x\sqrt{3} - y \)
    \(D_{\vecs u}f(1,0)= \sqrt{3}\)

    8)\( f(x,y)=3x+4y+7,\quad P(0,\frac{π}{2}), \quad \vecs u=⟨\frac{3}{5},\frac{4}{5}⟩\)

    9)\( f(x,y)=e^x\cos y,\quad P=(0,\frac{π}{2}), \quad \vecs u=⟨0,5⟩\)

    Jibu
    \(D_{\vecs u}f(x, y) = -e^x\sin y \)
    \(D_{\vecs u}f(0, \frac{π}{2})= −1\)

    10)\( f(x,y)=y^{10},\quad \vecs u=⟨0,−3⟩,\quad P=(1,−1)\)

    11)\( f(x,y)=\ln(x^2+y^2),\quad \vecs u=⟨2,-5⟩,\quad P(1,2)\)

    Jibu
    \(D_{\vecs u}f(x, y) = \frac{\sqrt{29}}{29}\left( \dfrac{4x-10y}{x^2 +y^2}\right) \)
    \(D_{\vecs u}f(1,2)= -\frac{16\sqrt{29}}{145}\)

    12)\( h(x,y,z)=xyz, \quad P(2,1,1),\quad \vecs v=2\,\hat{\mathbf i}+\,\hat{\mathbf j}−\,\hat{\mathbf k}\)

    Jibu
    \( D_{\vecs v}h(x, y, z) = \frac{\sqrt{6}}{6}(2yz + xz - xy)\)
    \( D_{\vecs v}h(2,1,1) = \frac{2}{\sqrt{6}} = \frac{\sqrt{6}}{3}\)

    13)\( f(x,y,z)=y^2+xz,\quad P(1,2,2),\quad \vecs v=⟨2,−1,2⟩\)

    Jibu
    \( D_{\vecs v}f(x, y, z) = \frac{2}{3}(z - y + x)\)
    \(D_{\vecs v}f(1,2,2)= \frac{2}{3}\)

    Katika mazoezi 14 - 19, tafuta derivative directional ya kazi katika mwelekeo wa vector kitengo\(\vecs u=\cos θ \,\hat{\mathbf i}+\sin θ \,\hat{\mathbf j}.\)

    14)\( f(x,y)=x^2+2y^2,\quad θ=\frac{π}{6}\)

    15)\( f(x,y)=\dfrac{y}{x+2y},\quad θ=−\frac{π}{4}\)

    Jibu
    \( D_{\vecs u}f(x,y) = \dfrac{−\sqrt{2}(x+y)}{2(x+2y)^2}\)

    16)\( f(x,y)=\cos(3x+y),\quad θ=\frac{π}{4}\)

    17)\( w(x,y)=ye^x,\quad θ=\frac{π}{3}\)

    Jibu
    \( D_{\vecs u}f(x,y) = \dfrac{e^x(y+\sqrt{3})}{2}\)

    18)\( f(x,y)=x\arctan(y),\quad θ=\frac{π}{2}\)

    19)\( f(x,y)=\ln(x+2y),\quad θ=\frac{π}{3}\)

    Jibu
    \( D_{\vecs u}f(x,y) = \dfrac{1+2\sqrt{3}}{2(x+2y)}\)

    Katika mazoezi 20 - 23, tafuta gradient\(\vecs \nabla f\).

    20) Kupata gradient ya\( f(x, y) = 3x^2 + y^3 - 3x + y\). Kisha kupata thamani yake katika hatua\(P(2,3)\).

    21) Kupata gradient ya\( f(x,y)=\dfrac{14−x^2−y^2}{3}\). Kisha, tafuta gradient kwa uhakika\( P(1,2)\).

    Jibu
    \( \vecs \nabla f(x, y) = -\frac{2}{3}x\,\hat{\mathbf i} -\frac{2}{3}y\,\hat{\mathbf j}\)
    \( \vecs \nabla f(1,2) = -\frac{2}{3}\,\hat{\mathbf i} -\frac{4}{3}\,\hat{\mathbf j}\)

    22) Kupata gradient ya\( f(x,y)=\ln(4x^3 - 3y)\). Kisha, tafuta gradient kwa uhakika\( P(1,1)\).

    23) Kupata gradient ya\( f(x,y,z)=xy+yz+xz\). Kisha kupata gradient katika hatua\( P(1,2,3).\)

    Jibu
    \( \vecs \nabla f(x, y, z) = ⟨y+z, x+z, y + x⟩\)
    \( \vecs \nabla f(1,2,3) = ⟨5,4,3⟩\)

    Katika mazoezi 24 - 25, tafuta derivative directional ya kazi\( P\) katika hatua katika mwelekeo wa\( Q\).

    24)\( f(x,y)=x^2+3y^2,\quad P(1,1),\quad Q(4,5)\)

    25)\( f(x,y,z)=\dfrac{y}{x+z},\quad P(2,1,−1),\quad Q(−1,2,0)\)

    Jibu
    \( D_{\vecd{PQ}}f(x,y) = \frac{3}{\sqrt{11}}\)

    26) Kupata derivative directional ya\( f(x,y,z))\) saa\( P\) na katika mwelekeo wa\( \vecs u: \quad f(x,y,z)=\ln(x^2+2y^2+3z^2),\quad P(2,1,4),\quad \vecs u=\frac{−3}{13}\,\hat{\mathbf i}−\frac{4}{13}\,\hat{\mathbf j}−\frac{12}{13}\,\hat{\mathbf k}\).

    Katika mazoezi 27 - 29, tafuta derivative directional ya kazi\( P\) katika mwelekeo wa\(\vecs u\).

    27)\( f(x,y)=\ln(5x+4y),\quad P(3,9),\quad \vecs u=6\,\hat{\mathbf i}+8\,\hat{\mathbf j}\)

    Jibu
    \( D_{\vecs u}f(3,9) = \frac{31}{255}\)

    28)\( f(x,y)=−7x+2y,\quad P(2,−4),\quad \vecs u=4\,\hat{\mathbf i}−3\,\hat{\mathbf j}\)

    29)\( f(x,y,z)=4x^5y^2z^3,\quad P(2,−1,1),\quad \vecs u=\frac{1}{3}\,\hat{\mathbf i}+\frac{2}{3}\,\hat{\mathbf j}−\frac{2}{3}\,\hat{\mathbf k}\)

    Jibu
    \( D_{\vecs u}f(2,-1,1) = -320\)

    30) [T] Matumizi ya teknolojia ya mchoro Curve ngazi ya\( f(x,y)=4x−2y+3\) kwamba hupita kwa njia\( P(1,2)\) na kuteka gradient vector katika\( P\).

    31) [T] Matumizi ya teknolojia ya mchoro Curve ngazi ya\( f(x,y)=x^2+4y^2\) kwamba hupita kwa njia\( P(−2,0)\) na kuteka gradient vector katika\(P\).

    Jibu
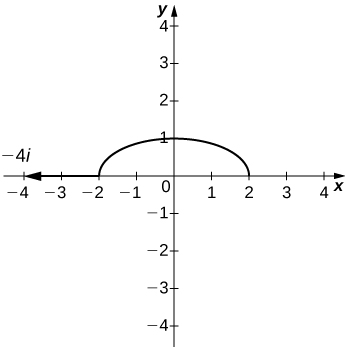
    Mchoro wa safu ya ngazi ya f (x, y) =x ^ 2+4y ^ 2 ambayo hupita kupitia P (-2,0) na kuonyesha vector gradient katika P.

    Katika mazoezi 32 - 35, pata vector gradient katika hatua iliyoonyeshwa.

    32)\( f(x,y)=xy^2−yx^2,\quad P(−1,1)\)

    33)\( f(x,y)=xe^y−\ln(x),\quad P(−3,0)\)

    Jibu
    \(\vecs \nabla f(-3,0) = \frac{4}{3}\,\hat{\mathbf i}−3\,\hat{\mathbf j}\)

    34)\( f(x,y,z)=xy−\ln(z),\quad P(2,−2,2)\)

    35)\( f(x,y,z)=x\sqrt{y^2+z^2}, \quad P(−2,−1,−1)\)

    Jibu
    \(\vecs \nabla f(-2,-1,-1) = \sqrt{2}\,\hat{\mathbf i}+\sqrt{2}\,\hat{\mathbf j}+\sqrt{2}\,\hat{\mathbf k}\)

    Katika mazoezi 36 - 40, tafuta derivative inayoonyeshwa ya kazi.

    36)\( f(x,y)=x^2+xy+y^2\) wakati wa\( (−5,−4)\) mwelekeo kazi huongezeka kwa kasi zaidi.

    37)\( f(x,y)=e^{xy}\) wakati wa\( (6,7)\) mwelekeo kazi huongezeka kwa kasi zaidi.

    Jibu
    \( 1.6(10^{19})\)

    38)\( f(x,y)=\arctan\left(\dfrac{y}{x}\right)\) wakati wa\( (−9,9)\) mwelekeo kazi huongezeka kwa kasi zaidi.

    39)\( f(x,y,z)=\ln(xy+yz+zx)\) wakati wa\( (−9,−18,−27)\) mwelekeo kazi huongezeka kwa kasi zaidi.

    Jibu
    \( \frac{5\sqrt{2}}{99}\)

    40)\( f(x,y,z)=\dfrac{x}{y}+\dfrac{y}{z}+\dfrac{z}{x}\) wakati wa\( (5,−5,5)\) mwelekeo kazi huongezeka kwa kasi zaidi.

    Katika mazoezi 41 - 43, pata kiwango cha juu cha mabadiliko ya\( f\) wakati uliopewa na mwelekeo ambao hutokea.

    41)\( f(x,y)=xe^{−y}, \quad (-2,0)\)

    Jibu
    \(\text{max}\big\{D_{\vecs u} f(-2,0)\big\} = \sqrt{5}, \quad ⟨1,2⟩\)
    Suluhisho:
    \( \vecs \nabla f(x, y) = e^{-y} \mathbf{\hat i} - xe^{-y} \mathbf{\hat j}.\)Hivyo\(\text{max}\big\{D_{\vecs u} f(-2,0)\big\} = \|\vecs \nabla f(-2, 0)\| = \sqrt{5}.\)
    Mwelekeo ambao hutokea utakuwa tu mwelekeo wa vector gradient:\(\vecs \nabla f(-2, 0) = ⟨1,2⟩.\)

    42)\( f(x,y)=\sqrt{x^2+2y}, \quad (4,10)\)

    43)\( f(x,y)=\cos(3x+2y),\quad (\frac{π}{6},−\frac{π}{8})\)

    Jibu
    \( \text{max}\big\{D_{\vecs u} f\left(\frac{π}{6},−\frac{π}{8}\right)\big\} = \sqrt{\frac{13}{2}} = \frac{\sqrt{26}}{2},\quad ⟨−3,−2⟩\)

    Katika mazoezi 44 - 47, kupata equations ya

    a. ndege ya tangent na

    b. mstari wa kawaida kwa uso uliopewa katika hatua iliyotolewa.

    44) Curve\( f(x,y,z)=12\) ya\( f(x,y,z)=4x^2−2y^2+z^2\) ngazi kwa wakati\( (2,2,2).\)

    45)\( f(x,y,z)=xy+yz+xz=3\) katika hatua\( (1,1,1)\)

    Jibu
    a. tangent ndege equation:\(x+y+z=3\),
    b. kawaida line equations:\(x−1=y−1=z−1\)

    46)\( f(x,y,z)=xyz=6\) katika hatua\( (1,2,3)\)

    47)\( f(x,y,z)=xe^y\cos z−z=1\) katika hatua\( (1,0,0)\)

    Jibu
    a. tangent ndege equation:\(x+y−z=1\),
    b. kawaida line equations:\(x−1=y=−z\)

    Katika mazoezi 48 - 51, tatua tatizo lililoelezwa.

    48) Joto\( T\) katika nyanja ya chuma ni inversely sawia na umbali kutoka katikati ya nyanja (asili:\( (0,0,0))\). Joto kwenye hatua\( (1,2,2)\) ni\( 120\) °C.

    Find kiwango cha mabadiliko ya joto katika hatua\( (1,2,2)\) katika mwelekeo kuelekea hatua\( (2,1,3).\)

    b Onyesha kwamba, wakati wowote katika nyanja, mwelekeo wa ongezeko kubwa la joto hutolewa na vector inayoelezea asili.

    49) Uwezo wa umeme (voltage) katika eneo fulani la nafasi hutolewa na kazi\( V(x,y,z)=5x^2−3xy+xyz.\)

    Kupata kiwango cha mabadiliko ya voltage\( (3,4,5)\) katika hatua katika mwelekeo wa vector\( ⟨1,1,−1⟩.\)

    b Katika mwelekeo gani voltage inabadilika kwa kasi zaidi wakati\( (3,4,5)\)?

    c. kiwango cha juu cha mabadiliko ya voltage katika hatua gani\( (3,4,5)\)?

    Jibu
    a.\(\frac{32}{\sqrt{3}}\),
    b.\(⟨38,6,12⟩\),
    c.\(2\sqrt{406}\)

    50) Ikiwa uwezo wa umeme\( (x,y)\) katika hatua katika\(xy\) -ndege ni\( V(x,y)=e^{−2x}\cos(2y)\), basi vector nguvu ya umeme katika\( (x,y)\) ni\( E=−\vecs \nabla V(x,y).\)

    Pata vector ya nguvu ya umeme\( (\frac{π}{4},0).\)

    b Onyesha kwamba, kwa kila hatua katika ndege, uwezo wa umeme hupungua kwa kasi zaidi katika mwelekeo wa vector\( E.\)

    51) Katika vipimo viwili, mwendo wa maji bora huongozwa na uwezo wa kasi\( φ\). Vipengele vya kasi vya maji\(u\) katika mwelekeo na\(v\)\(y\) -mwelekeo, hutolewa na\( ⟨u,v⟩=\vecs \nabla φ\).\(x\) Find vipengele kasi kuhusishwa na uwezo kasi\( φ(x,y)=\sin πx\sin 2πy.\)

    Jibu
    \( ⟨u,v⟩=⟨π\cos(πx)\sin(2πy),2π\sin(πx)\cos(2πy)⟩\)

    Wachangiaji