3.4: Triângulos, retângulos e o teorema de Pitágoras

Last updated
Save as PDF

Page ID: 184320

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de

Ao final desta seção, você poderá:

Resolva aplicativos usando propriedades de triângulos
Use o teorema de Pitágoras
Resolva aplicativos usando propriedades de retângulo

Esteja preparado

Antes de começar, faça este teste de prontidão.

Simplifique:$12(6h)$.
Se você perdeu esse problema, revise o Exercício 1.10.1.
O comprimento de um retângulo é três a menos que a largura. Deixe w representar a largura. Escreva uma expressão para o comprimento do retângulo.
Se você perdeu esse problema, revise o Exercício 1.3.43.
Resolva:$A=\frac{1}{2}bh$ para b quando A=260 e h=52.
Se você perdeu esse problema, revise o Exercício 2.6.10.
Simplifique:$\sqrt{144}$.
Se você perdeu esse problema, revise o Exercício 1.9.10.

Resolva aplicativos usando propriedades de triângulos

Nesta seção, usaremos algumas fórmulas de geometria comuns. Adaptaremos nossa estratégia de resolução de problemas para que possamos resolver aplicações de geometria. A fórmula geométrica nomeará as variáveis e nos dará a equação a ser resolvida. Além disso, como todos esses aplicativos envolvem algum tipo de formato, a maioria das pessoas acha útil desenhar uma figura e rotulá-la com as informações fornecidas. Incluiremos isso na primeira etapa da estratégia de solução de problemas para aplicações de geometria.

RESOLVER APLICAÇÕES DE GEOMETRIA

Leia o problema e certifique-se de que todas as palavras e ideias sejam compreendidas. Desenhe a figura e identifique-a com as informações fornecidas.
Identifique o que estamos procurando.
Identifique o que estamos procurando escolhendo uma variável para representá-la.
Traduza em uma equação escrevendo a fórmula ou modelo apropriado para a situação. Substitua as informações fornecidas.
Resolva a equação usando boas técnicas de álgebra.
Verifique a resposta substituindo-a novamente na equação resolvida na etapa 5 e certificando-se de que ela faça sentido no contexto do problema.
Responda à pergunta com uma frase completa.

Iniciaremos as aplicações de geometria observando as propriedades dos triângulos. Vamos analisar alguns fatos básicos sobre triângulos. Os triângulos têm três lados e três ângulos internos. Normalmente, cada lado é rotulado com uma letra minúscula para coincidir com a letra maiúscula do vértice oposto.

O plural da palavra vértice é vértices. Todos os triângulos têm três vértices. Os triângulos são nomeados por seus vértices: O triângulo na Figura$\PageIndex{1}$ é chamado$\triangle{ABC}$.

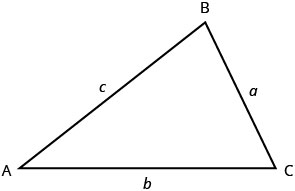
Um triângulo com os vértices A, B e C. Os lados opostos a esses vértices são marcados com a, b e c, respectivamente. — Figura$\PageIndex{1}$: O triângulo ABC tem vértices$A$$B$,$C$ e. Os comprimentos dos lados são$a$$b$,$c$ e.

Os três ângulos de um triângulo estão relacionados de uma forma especial. A soma de suas medidas é$180^{\circ}$. Note que lemos$m\angle{A}$ como “a medida do ângulo A” Então,$\triangle{ABC}$ na Figura$\PageIndex{1}$.

\[m \angle A+m \angle B+m \angle C=180^{\circ} \nonumber\]

Como o perímetro de uma figura é o comprimento de seu limite, o perímetro de$\triangle{ABC}$ é a soma dos comprimentos de seus três lados.

\[P = a + b + c \nonumber\]

Para encontrar a área de um triângulo, precisamos conhecer sua base e altura. A altura é uma linha que conecta a base ao vértice oposto e faz um$90^\circ$ ângulo com a base. Vamos desenhar$\triangle{ABC}$ novamente e agora mostrar a altura$h$. Veja a Figura$\PageIndex{2}$.

PROPRIEDADES DO TRIÂNGULO

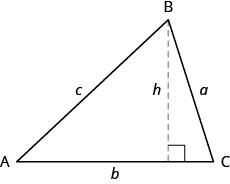
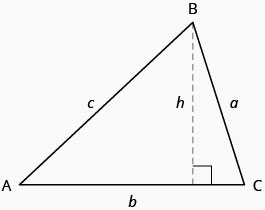
$Um triângulo com os vértices A, B e C. Os lados opostos a esses vértices são marcados com a, b e c, respectivamente. O lado b é paralelo à parte inferior da página e tem uma linha tracejada desenhada do vértice B até ela. Essa linha está marcada com h e forma um ângulo reto com o lado b.$

Para$\triangle{ABC}$

Medidas de ângulo:

\[m \angle A+m \angle B+m \angle C=180^{\circ}\]

A soma das medidas dos ângulos de um triângulo é 180°.

Perímetro:

\[P = a + b + c\]

O perímetro é a soma dos comprimentos dos lados do triângulo.

Área:

$A = \frac{1}{2}bh, b = \text{ base }, h = \text{ height }$

A área de um triângulo é metade da base vezes a altura.

Exemplo$\PageIndex{1}$

As medidas de dois ângulos de um triângulo são 55 e 82 graus. Encontre a medida do terceiro ângulo.

Solução

Etapa 1. Leia o problema. Desenhe a figura e identifique-a com as informações fornecidas.	$.$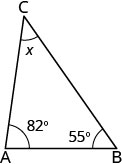
Etapa 2. Identifique o que você está procurando.	a medida do terceiro ângulo em um triângulo
Etapa 3. Nome. Escolha uma variável para representá-la.	Deixe$x=$ a medida do ângulo.
Etapa 4. Traduzir.
Escreva a fórmula apropriada e substitua.	$m \angle A+m \angle B+m \angle C=180^{\circ}$
Etapa 5. Resolva a equação.	$\begin{array} {rll} {55 + 82 + x} &{=} &{180} \\ {137 + x} &{=} &{180} \\ {x} &{=} &{43} \end{array}$
Etapa 6. Verifique. $\begin{array} {rll} {55 + 82 + 43} &{\stackrel{?}{=}} &{180} \\ {180} &{=} &{180\checkmark} \end{array}$
Etapa 7. Responda à pergunta.	A medida do terceiro ângulo é de 43 graus.

Experimente$\PageIndex{1}$

As medidas de dois ângulos de um triângulo são 31 e 128 graus. Encontre a medida do terceiro ângulo.

Responda: 21 graus

Experimente$\PageIndex{2}$

As medidas de dois ângulos de um triângulo são 49 e 75 graus. Encontre a medida do terceiro ângulo.

Responda: 56 graus

Exemplo$\PageIndex{2}$

O perímetro de um jardim triangular é de 24 pés. Os comprimentos dos dois lados são quatro pés e nove pés. Quanto tempo dura o terceiro lado?

Solução

Etapa 1. Leia o problema. Desenhe a figura e identifique-a com as informações fornecidas.	$.$ $.$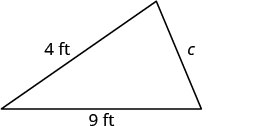
Etapa 2. Identifique o que você está procurando.	comprimento do terceiro lado de um triângulo
Etapa 3. Nome. Escolha uma variável para representá-la.	Deixe$c=$ o terceiro lado.
Etapa 4. Traduzir.
Escreva a fórmula apropriada e substitua.	$.$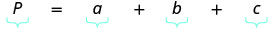
Substitua as informações fornecidas.	$.$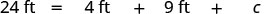
Etapa 5. Resolva a equação.	$.$ $.$
Etapa 6. Verifique. $\begin{array} {rll} {P} &{=} &{a + b +c} \\ {24} &{\stackrel{?}{=}} &{4 + 9+11} \\ {24} &{=} &{24\checkmark} \end{array}$
Etapa 7. Responda à pergunta.	O terceiro lado tem 11 pés de comprimento.

Experimente$\PageIndex{3}$

O perímetro de um jardim triangular é de 48 pés. Os comprimentos dos dois lados são 18 pés e 22 pés. Quanto tempo dura o terceiro lado?

Responda: 8 pés

Experimente$\PageIndex{4}$

O comprimento dos dois lados de uma janela triangular é de sete pés e cinco pés. O perímetro é de 18 pés. Quanto tempo dura o terceiro lado?

Responda: 6 pés

Exemplo$\PageIndex{3}$

A área de uma janela triangular da igreja é de 90 metros quadrados. A base da janela é de 15 metros. Qual é a altura da janela?

Solução

Etapa 1. Leia o problema. Desenhe a figura e identifique-a com as informações fornecidas.	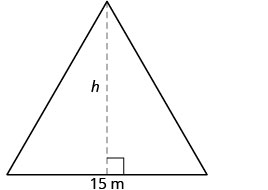$.$ $\text{ Area } = 90m^{2}$
Etapa 2. Identifique o que você está procurando.	altura de um triângulo
Etapa 3. Nome. Escolha uma variável para representá-la.	Deixe$h=$ a altura.
Etapa 4. Traduzir.
Escreva a fórmula apropriada.	$.$
Substitua as informações fornecidas.	$.$
Etapa 5. Resolva a equação.	$90 = \dfrac{15}{2}h$ $12 = h$
Etapa 6. Verifique. $\begin{array} {rll} {A} &{=} &{\frac{1}{2}bh} \\ {90} &{\stackrel{?}{=}} &{\frac{1}{2}\cdot 15\cdot 12} \\ {90} &{=} &{90\checkmark} \end{array}$
Etapa 7. Responda à pergunta.	A altura do triângulo é de 12 metros.

Experimente$\PageIndex{5}$

A área de uma pintura triangular é de 126 polegadas quadradas. A base tem 18 polegadas. Qual é a altura?

Responda: 14 polegadas

Experimente$\PageIndex{6}$

Uma porta de tenda triangular tem uma área de 15 pés quadrados. A altura é de cinco pés. Qual é a base?

Responda: 6 pés

As propriedades do triângulo que usamos até agora se aplicam a todos os triângulos. Agora, veremos um tipo específico de triângulo — um triângulo reto. Um triângulo reto tem um ângulo de 90°, que geralmente marcamos com um pequeno quadrado no canto.

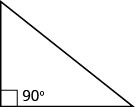
Um triângulo reto com o maior ângulo marcado em 90 graus. — Figura$\PageIndex{3}$

Definição: TRIÂNGULO DIREITO

Um triângulo reto tem um ângulo de 90°, que geralmente é marcado com um quadrado no vértice.

Exemplo$\PageIndex{4}$

Um ângulo de um triângulo reto mede 28°. Qual é a medida do terceiro ângulo?

Solução

Etapa 1. Leia o problema. Desenhe a figura e identifique-a com as informações fornecidas.	$.$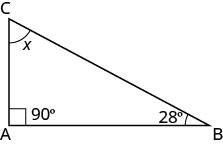
Etapa 2. Identifique o que você está procurando.	a medida de um ângulo
Etapa 3. Nome. Escolha uma variável para representá-la.	Deixe$x=$ a medida de um ângulo.
Etapa 4. Traduzir.	$m\angle{A} + m\angle{B} + m\angle{C} = 180$
Escreva a fórmula apropriada e substitua.	$x+90+28=180$
Etapa 5. Resolva a equação.	$x=62$
Etapa 6. Verifique. $\begin{array} {rll} {180} &{\stackrel{?}{=}} &{90+28+62} \\ {180} &{=} &{180\checkmark} \end{array}$
Etapa 7. Responda à pergunta.	A medida do terceiro ângulo é 62 ^°.

Experimente$\PageIndex{7}$

Um ângulo de um triângulo reto mede 56°. Qual é a medida do outro ângulo pequeno?

Responda: 34°

Experimente$\PageIndex{8}$

Um ângulo de um triângulo reto mede 45°. Qual é a medida do outro ângulo pequeno?

Responda: 45°

Nos exemplos que vimos até agora, poderíamos desenhar uma figura e rotulá-la diretamente após a leitura do problema. No próximo exemplo, teremos que definir um ângulo em termos de outro. Vamos esperar para desenhar a figura até escrevermos expressões para todos os ângulos que estamos procurando.

Exemplo$\PageIndex{5}$

A medida de um ângulo de um triângulo reto é 20 graus a mais do que a medida do menor ângulo. Encontre as medidas dos três ângulos.

Solução

Etapa 1. Leia o problema.
Etapa 2. Identifique o que você está procurando.	as medidas de todos os três ângulos
Etapa 3. Nome. Escolha uma variável para representá-la.	Deixe o$a=1^{st}$ ângulo. $a+20=2^{nd}$ $90=3^{rd}$ângulo angular (o ângulo reto)
Desenhe a figura e identifique-a com as informações fornecidas	$.$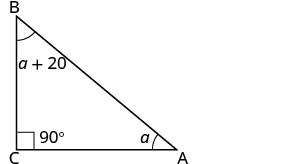
Etapa 4. Traduzir	$.$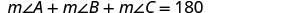
Escreva a fórmula apropriada. Substitua na fórmula.	$a + (a + 20) + 90 = 180$
Etapa 5. Resolva a equação.	\ (\ begin {align} 2a + 110 &= 180\\ [3pt] 2a &= 70\\ [3pt] a &= 35\ texto {primeiro ângulo}\\ [3pt] a &+ 20\ texto {segundo ângulo}\\ [3pt] {\ color {red} {35}} &+ 20 = 55\ end {align}\) E o terceiro ângulo é 90.
Etapa 6. Verifique. $\begin{array} {rll} {35 + 55 + 90} &{\stackrel{?}{=}} &{180} \\ {180} &{=} &{180\checkmark} \end{array}$
Etapa 7. Responda à pergunta.	Os três ângulos medem 35 ^°, 55 ^° e 90 ^°.

Experimente$\PageIndex{9}$

A medida de um ângulo de um triângulo reto é 50° a mais do que a medida do menor ângulo. Encontre as medidas dos três ângulos.

Responda: 20°, 70°, 90°

Experimente$\PageIndex{10}$

A medida de um ângulo de um triângulo reto é 30° a mais do que a medida do menor ângulo. Encontre as medidas dos três ângulos.

Responda: 30°, 60°, 90°

Use o teorema de Pitágoras

Aprendemos como as medidas dos ângulos de um triângulo se relacionam entre si. Agora, aprenderemos como os comprimentos dos lados se relacionam entre si. Uma propriedade importante que descreve a relação entre os comprimentos dos três lados de um triângulo reto é chamada de Teorema de Pitágoras. Esse teorema tem sido usado em todo o mundo desde os tempos antigos. Tem o nome do filósofo e matemático grego Pitágoras, que viveu por volta de 500 aC.

Antes de declararmos o Teorema de Pitágoras, precisamos introduzir alguns termos para os lados de um triângulo. Lembre-se de que um triângulo reto tem um ângulo de 90°, marcado com um pequeno quadrado no canto. O lado do triângulo oposto ao ângulo de 90° 90° é chamado de hipotenusa e cada um dos outros lados é chamado de pernas.

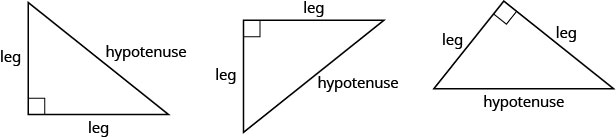
Três triângulos retos com diferentes orientações. Os ângulos retos são marcados com duas pequenas linhas que formam um pequeno quadrado com o ângulo. Em frente a esses ângulos, a hipotenusa é escrita. Os outros lados estão marcados com “perna”. — Figura$\PageIndex{4}$

O Teorema de Pitágoras conta como os comprimentos dos três lados de um triângulo reto se relacionam entre si. Ele afirma que em qualquer triângulo reto, a soma dos quadrados dos comprimentos das duas pernas é igual ao quadrado do comprimento da hipotenusa. Em símbolos, dizemos: em qualquer triângulo reto$a^{2}+b^{2}=c^{2}$,, onde a e b são os comprimentos das pernas e cc é o comprimento da hipotenusa.

Escrever a fórmula em cada exercício e dizê-la em voz alta enquanto a escreve pode ajudá-lo a se lembrar do Teorema de Pitágoras.

O TEOREMA DE PITÁGORAS

Em qualquer triângulo reto, onde$a$ e$b$ estão os comprimentos das pernas,$c$ está o comprimento da hipotenusa.

$Um triângulo reto com os lados marcados com a, b e c. O lado marcado com c é a hipotenusa.$

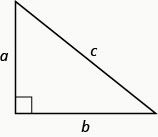
Então

\[a^{2}+b^{2}=c^{2} \label{Ptheorem}\]

Para resolver exercícios que usam o Teorema de Pitágoras (Equação\ ref {Pteorema}), precisaremos encontrar raízes quadradas. Usamos a notação$\sqrt{m}$ e a definição:

E se$m = n^{2}$, então$\sqrt{m} = n$, para$n\geq 0$.

Por exemplo, descobrimos que$\sqrt{25}$ é 5 porque$25=5^{2}$.

Como o Teorema de Pitágoras contém variáveis que são quadradas, para resolver o comprimento de um lado em um triângulo reto, teremos que usar raízes quadradas.

Exemplo$\PageIndex{6}$

Use o Teorema de Pitágoras para encontrar o comprimento da hipotenusa mostrado abaixo.

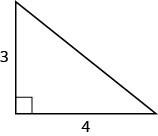
$Um triângulo reto com pernas marcadas com 3 e 4.$

Solução

Etapa 1. Leia o problema.
Etapa 2. Identifique o que você está procurando.	o comprimento da hipotenusa do triângulo
Etapa 3. Nome. Escolha uma variável para representá-la. Etiquete o lado c na figura.	Seja c = o comprimento da hipotenusa. $.$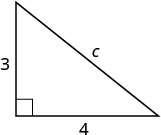
Etapa 4. Traduzir.
Escreva a fórmula apropriada.	$a^{2} + b^{2} = c^{2}$
Substituto.	$3^{2}+4^{2}=c^{2}$
Etapa 5. Resolva a equação.	$9+16=c^{2}$
Simplifique.	$25=c^{2}$
Use a definição de raiz quadrada.	$\sqrt{25} = c$
Simplifique.	$5=c$
Etapa 6. Verifique. $.$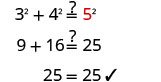
Etapa 7. Responda à pergunta.	O comprimento da hipotenusa é 5.

Experimente$\PageIndex{11}$

Use o Teorema de Pitágoras para encontrar o comprimento da hipotenusa no triângulo mostrado abaixo.

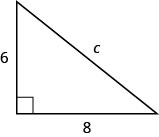
$Um triângulo reto com pernas marcadas com 6 e 8. A hipotenusa está marcada com c.$

Responda: c=10

Experimente$\PageIndex{12}$

Use o Teorema de Pitágoras para encontrar o comprimento da hipotenusa no triângulo mostrado abaixo.

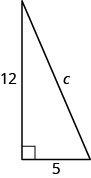
$Sem texto alternativo$

Responda: c=13

Exemplo$\PageIndex{7}$

Use o Teorema de Pitágoras para encontrar o comprimento da perna mostrado abaixo.

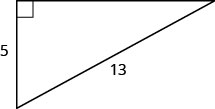
$Um ângulo reto com uma perna marcada com 5. A hipotenusa é rotulada como 13.$

Solução

Etapa 1. Leia o problema.
Etapa 2. Identifique o que você está procurando.	o comprimento da perna do triângulo
Etapa 3. Nome. Escolha uma variável para representá-la.	Deixe$b=$ a perna do triângulo.
Lado da etiqueta$b$.	$.$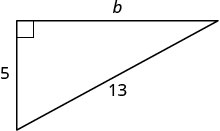
Etapa 4. Traduzir
Escreva a fórmula apropriada.	$a^{2} + b^{2} = c^{2}$
Substituto.	$5^{2}+b^{2}=13^{2}$
Etapa 5. Resolva a equação.	$25+b^{2}=169$
Isole o termo variável.	$b^{2}=144$
Use a definição de raiz quadrada.	$b = \sqrt{144}$
Simplifique.	$b=12$
Etapa 6. Verifique. $.$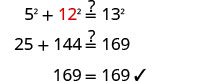
Etapa 7. Responda à pergunta.	O comprimento da perna é 12.

Experimente$\PageIndex{13}$

Use o Teorema de Pitágoras para encontrar o comprimento da perna no triângulo mostrado abaixo.

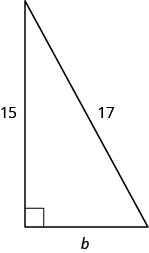
$Um triângulo reto com pernas marcadas com b e 15. A hipotenusa está marcada como 17.$

Responda: 8

Experimente$\PageIndex{14}$

Use o Teorema de Pitágoras para encontrar o comprimento da perna no triângulo mostrado abaixo.

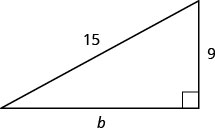
$Um triângulo reto com pernas marcadas com b e 9. A hipotenusa está marcada como 15.$

Responda: 12

Exemplo$\PageIndex{8}$

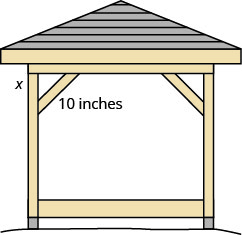
$Um gazebo é mostrado. Em um de seus cantos, um triângulo é feito com a madeira. A hipotenusa está marcada com 10 polegadas e uma das pernas está marcada com x$

Kelvin está construindo um gazebo e quer contornar cada canto colocando um pedaço de madeira de 10 ″ na diagonal, conforme mostrado acima.

Se ele apertar a madeira de forma que as extremidades da cinta fiquem à mesma distância do canto, qual é o comprimento das pernas do triângulo reto formado? Aproximadamente ao décimo de polegada mais próximo.

Solução

$\begin{array} {ll} {\textbf{Step 1. }\text{Read the problem.}} &{} \\\\ {\textbf{Step 2. }\text{Identify what we are looking for.}} &{\text{the distance from the corner that the}} \\ {} &{\text{bracket should be attached}} \\ \\{\textbf{Step 3. }\text{Name. Choose a variable to represent it.}} &{\text{Let x = distance from the corner.}} \\ {\textbf{Step 4.} \text{Translate}} &{} \\ {\text{Write the appropriate formula and substitute.}} &{a^{2} + b^{2} = c^{2}} \\ {} &{x^{2} + x^{2} = 10^{2}} \\ \\ {\textbf{Step 5. Solve the equation.}} &{} \\ {} &{2x^{2} = 100} \\ {\text{Isolate the variable.}} &{x^{2} = 50} \\ {\text{Simplify. Approximate to the nearest tenth.}} &{x \approx 7.1}\\\\ {\textbf{Step 6. }\text{Check.}} &{}\\ {a^{2} + b^{2} = c^{2}} &{} \\ {(7.1)^{2} + (7.1)^{2} \approx 10^{2} \text{ Yes.}} &{} \\\\ {\textbf{Step 7. Answer the question.}} &{\text{Kelven should fasten each piece of}} \\ {} &{\text{wood approximately 7.1'' from the corner.}} \end{array}$

Experimente$\PageIndex{15}$

John coloca a base de uma escada de 13 pés a cinco pés da parede de sua casa, conforme mostrado abaixo. Até que ponto a escada chega na parede?

$Uma casa é mostrada com uma escada encostada nela. A escada está marcada com 13' e a distância da casa até a base da escada está marcada com 5'.$

Responda: 12 pés

Experimente$\PageIndex{16}$

Randy quer colocar um fio de luzes de 17 pés no topo do mastro de 15 pés de seu veleiro, conforme mostrado abaixo. A que distância da base do mastro ele deve prender a extremidade do cordão de luz?

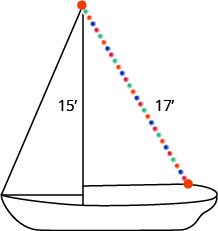
$Um veleiro é mostrado com um mastro de 15 pés (a parte reta e alta). Do topo do mastro, uma série de pontos coloridos se estende até a parte de trás do barco e está marcada com 17'.$

Responda: 8 pés

Resolva aplicativos usando propriedades de retângulo

Talvez você já esteja familiarizado com as propriedades dos retângulos. Os retângulos têm quatro lados e quatro ângulos retos (90°). Os lados opostos de um retângulo têm o mesmo comprimento. Nós nos referimos a um lado do retângulo como o comprimento,$L$, e seu lado adjacente como a largura,$W$.

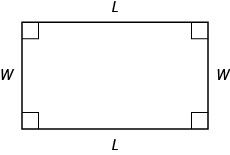
$Um retângulo com lados marcados com W e L.$

A distância ao redor desse retângulo é$L+W+L+W$, ou$2L+2W$. Este é o perímetro$P$,, do retângulo.

\[P=2L+2W\]

E a área de um retângulo? Imagine um tapete retangular com 2 pés de comprimento por 3 pés de largura. Sua área é de 6 pés quadrados. Há seis quadrados na figura.

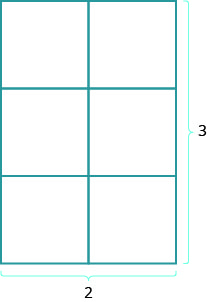
$Um retângulo composto por 6 quadrados com três de altura e dois de largura. A altura está marcada com 3 e a largura é marcada com 2.$

\[\begin{array} {l} {A=6} \\ {A=2\cdot3} \\ {A=L\cdot W} \end{array}\]

A área é o comprimento vezes a largura. A fórmula para a área de um retângulo é

\[A=LW.\]

PROPRIEDADES DOS RETÂNGULOS

Os retângulos têm quatro lados e quatro ângulos retos (90°).

Os comprimentos dos lados opostos são iguais.

O perímetro de um retângulo é a soma do dobro do comprimento e do dobro da largura.

\[P=2L+2W\]

A área de um retângulo é o produto do comprimento e da largura.

\[A=L·W\]

Exemplo$\PageIndex{9}$

O comprimento de um retângulo é de 32 metros e a largura é de 20 metros. Qual é o perímetro?

Solução

Etapa 1. Leia o problema. Desenhe a figura e identifique-a com as informações fornecidas.	$.$
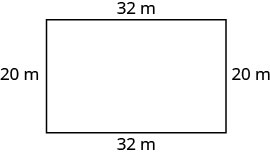Etapa 2. Identifique o que você está procurando.	o perímetro de um retângulo
Etapa 3. Nome. Escolha uma variável para representá-la.	Deixe$P=$ o perímetro.
Etapa 4. Traduzir.
Escreva a fórmula apropriada.	$.$
Substituto.	$.$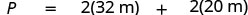
Etapa 5. Resolva a equação.	$P = 64 + 40$ $P = 104$
Etapa 6. Verifique. $\begin{array} {rcl} {P} &{\stackrel{?}{=}} &{104} \\ {20+32+20+32} &{\stackrel{?}{=}} &{104} \\ {104} &{=} &{104\checkmark} \end{array}$
Etapa 7. Responda à pergunta.	O perímetro do retângulo é de 104 metros.

Experimente$\PageIndex{17}$

O comprimento de um retângulo é de 120 jardas e a largura é de 50 jardas. Qual é o perímetro?

Responda: 340 jardas

Experimente$\PageIndex{18}$

O comprimento de um retângulo é 62 pés e a largura é 48 pés. Qual é o perímetro?

Responda: 220 pés

Exemplo$\PageIndex{10}$

A área de uma sala retangular é de 168 pés quadrados. O comprimento é de 14 pés. Qual é a largura?

Solução

Etapa 1. Leia o problema. Desenhe a figura e identifique-a com as informações fornecidas.	$.$
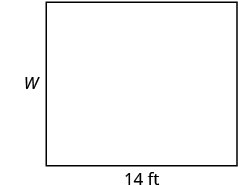Etapa 2. Identifique o que você está procurando.	a largura de uma sala retangular
Etapa 3. Nome. Escolha uma variável para representá-la.	Deixe$W=$ a largura.
Etapa 4. Traduzir.
Escreva a fórmula apropriada.	$A=LW$
Substituto.	$168 = 14W$
Etapa 5. Resolva a equação.	$\frac{168}{14} = \frac{14W}{14}$ $12 = W$
Etapa 6. Verifique. 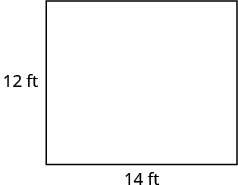$.$ $\begin{array} {rcl} {A} &{=} &{LW} \\ {168} &{\stackrel{?}{=}} &{14\cdot 12} \\ {168} &{=} &{168\checkmark} \end{array}$
Etapa 7. Responda à pergunta.	A largura da sala é de 12 pés.

Experimente$\PageIndex{19}$

A área de um retângulo é de 598 pés quadrados. O comprimento é de 23 pés. Qual é a largura?

Responda: 26 pés

Experimente$\PageIndex{20}$

A largura de um retângulo é de 21 metros. A área é de 609 metros quadrados. Qual é o comprimento?

Responda: 29 metros

Exemplo$\PageIndex{11}$

Encontre o comprimento de um retângulo com perímetro de 50 polegadas e largura de 10 polegadas.

Solução

Etapa 1. Leia o problema. Desenhe a figura e identifique-a com as informações fornecidas.	$.$ $.$
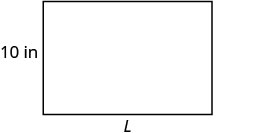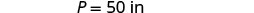Etapa 2. Identifique o que você está procurando.	o comprimento do retângulo
Etapa 3. Nome. Escolha uma variável para representá-la.	Deixe$L=$ o comprimento.
Etapa 4. Traduzir.
Escreva a fórmula apropriada.	$P = 2L + 2W$
Substituto.	$50 = 2L + 2(10)$
Etapa 5. Resolva a equação.	$.$ $.$ $.$ $.$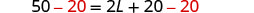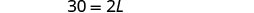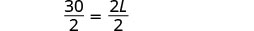
Etapa 6. Verifique. $.$ $\begin{array} {rcl} {P} &{=} &{50} \\ {15+10+15+10} &{\stackrel{?}{=}} &{50} \\ {50} &{=} &{50\checkmark} \end{array}$
Etapa 7. Responda à pergunta.	O comprimento é de 15 polegadas.

Experimente$\PageIndex{21}$

Encontre o comprimento de um retângulo com: perímetro 80 e largura 25.

Responda: 15

Experimente$\PageIndex{22}$

Encontre o comprimento de um retângulo com: perímetro 30 e largura 6.

Responda: 9

Resolvemos problemas em que o comprimento ou a largura foram dados, junto com o perímetro ou a área; agora aprenderemos como resolver problemas nos quais a largura é definida em termos do comprimento. Vamos esperar para desenhar a figura até escrevermos uma expressão para a largura, para que possamos rotular um lado com essa expressão.

Exemplo$\PageIndex{12}$

A largura de um retângulo é dois pés a menos que o comprimento. O perímetro é de 52 pés. Encontre o comprimento e a largura.

Solução

Etapa 1. Leia o problema.
Etapa 2. Identifique o que você está procurando.	o comprimento e a largura de um retângulo
Etapa 3. Nome. Escolha uma variável para representá-la. Como a largura é definida em termos do comprimento, deixamos o$L=$ comprimento. A largura é dois pés a menos que o comprimento, então deixamos a$L-2$ largura.	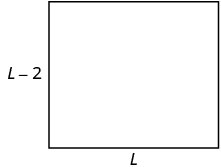$.$ $P=52$pés
Etapa 4. Traduzir.
Escreva a fórmula apropriada. A fórmula para o perímetro de um retângulo relaciona todas as informações.	$P=2L+2W$
Substitua as informações fornecidas.	$52=2L+2(L−2)$
Etapa 5. Resolva a equação.	$52=2L+2L−4$
Combine termos semelhantes.	$52=4L−4$
Adicione 4 em cada lado.	$56 = 4L$
Divida por 4.	$\frac{56}{4} = \frac{4L}{4}$ $14=L$ O comprimento é de 14 pés.
Agora precisamos encontrar a largura.	A largura é$L−2$. $.$ A largura é de 12 pés.
Etapa 6. Verifique. Desde então$14+12+14+12=52$, isso funciona! $.$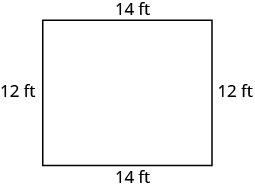
Etapa 7. Responda à pergunta.	O comprimento é de 14 pés e a largura é de 12 pés.

Experimente$\PageIndex{23}$

A largura de um retângulo é sete metros menor que o comprimento. O perímetro é de 58 metros. Encontre o comprimento e a largura.

Responda: 18 metros, 11 metros

Experimente$\PageIndex{24}$

O comprimento de um retângulo é oito pés a mais do que a largura. O perímetro é de 60 pés. Encontre o comprimento e a largura.

Responda: 19 pés, 11 pés

Exemplo$\PageIndex{13}$

O comprimento de um retângulo é quatro centímetros a mais do que o dobro da largura. O perímetro é de 32 centímetros. Encontre o comprimento e a largura.

Solução

Etapa 1. Leia o problema.
Etapa 2. Identifique o que você está procurando.	o comprimento e a largura
Etapa 3. Nome. Escolha uma variável para representar a largura.	$.$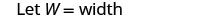
O comprimento é quatro a mais do que o dobro da largura.	$.$ $.$ $.$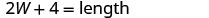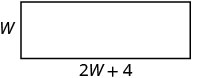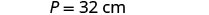
Etapa 4. Traduzir
Escreva a fórmula apropriada.	$\quad P=2L+2W$
Substitua as informações fornecidas.	$.$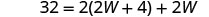
Etapa 5. Resolva a equação.	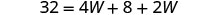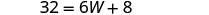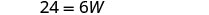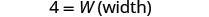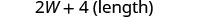$.$ $.$ $.$ $.$ $.$ $.$ 12 O comprimento é 12 cm.
Etapa 6. Verifique. 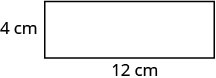$.$ $\begin{array} {rcl} {P} &{=} &{2L + 2W} \\ {32} &{\stackrel{?}{=}} &{2\cdot 12 + 2\cdot 4} \\ {32} &{=} &{32\checkmark} \end{array}$
Etapa 7. Responda à pergunta.	O comprimento é de 12 cm e a largura é de 4 cm.

Experimente$\PageIndex{25}$

O comprimento de um retângulo é oito a mais do que o dobro da largura. O perímetro é 64. Encontre o comprimento e a largura.

Responda: 24, 8

Experimente$\PageIndex{26}$

A largura de um retângulo é seis a menos que o dobro do comprimento. O perímetro é 18. Encontre o comprimento e a largura.

Responda: 5, 4

Exemplo$\PageIndex{14}$

O perímetro de uma piscina retangular é de 150 pés. O comprimento é 15 pés a mais do que a largura. Encontre o comprimento e a largura.

Solução

Etapa 1. Leia o problema. Desenhe a figura e identifique-a com as informações fornecidas.	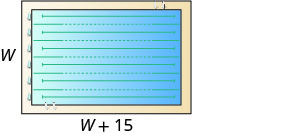$.$ $P=150$pés
Etapa 2. Identifique o que você está procurando.	o comprimento e a largura da piscina
Etapa 3. Nome. Escolha uma variável para representar a largura. O comprimento é 15 pés a mais do que a largura.	$.$ $.$
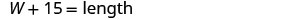Etapa 4. Traduzir
Escreva a fórmula apropriada.	$\quad P=2L+2W$
Substituto.	$.$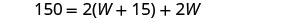
Etapa 5. Resolva a equação.	$.$ $.$ $.$ $.$ $.$ $.$ $.$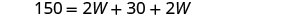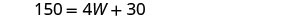
Etapa 6. Verifique. $\begin{array} {rcl} {P} &{=} &{2L + 2W} \\ {150} &{\stackrel{?}{=}} &{2(45) + 2(30)} \\ {150} &{=} &{150\checkmark} \end{array}$
Etapa 7. Responda à pergunta.	O comprimento da piscina é de 45 pés e a largura é de 30 pés.

Experimente$\PageIndex{27}$

O perímetro de uma piscina retangular é de 200 pés. O comprimento é 40 pés a mais do que a largura. Encontre o comprimento e a largura.

Responda: 70 pés, 30 pés

Experimente$\PageIndex{28}$

O comprimento de um jardim retangular é 30 metros a mais do que a largura. O perímetro é de 300 metros. Encontre o comprimento e a largura.

Responda: 90 jardas, 60 jardas

Conceitos chave

Estratégia de resolução de problemas para aplicações de geometria
1. Leia o problema e faça com que todas as palavras e ideias sejam compreendidas. Desenhe a figura e identifique-a com as informações fornecidas.
2. Identifique o que estamos procurando.
3. Nomeie o que estamos procurando escolhendo uma variável para representá-la.
4. Traduza em uma equação escrevendo a fórmula ou modelo apropriado para a situação. Substitua as informações fornecidas.
5. Resolva a equação usando boas técnicas de álgebra.
6. Verifique a resposta do problema e verifique se faz sentido.
7. Responda à pergunta com uma frase completa.
Propriedades do triângulo para △ medidas de
ângulo ABC:
- $m\angle{A}+m\angle{B}+m\angle{C}=180$
Perímetro:
- $P=a+b+c$
Área:
- $A=\frac{1}{2}bh$, b=base, h=altura
Um triângulo reto tem um ângulo de 90°.
O Teorema de Pitágoras Em qualquer triângulo reto,$a^{2} + b^{2} = c^{2}$ onde$c$ está o comprimento da hipotenusa e$a$ e$b$ são os comprimentos das pernas.
Propriedades dos retângulos
- Os retângulos têm quatro lados e quatro ângulos retos (90°).
- Os comprimentos dos lados opostos são iguais.
- O perímetro de um retângulo é a soma do dobro do comprimento e do dobro da largura:$P=2L+2W$.
- A área de um retângulo é o comprimento vezes a largura:$A=LW$.

Etapa 1. Leia o problema. Desenhe a figura e identifique-a com as informações fornecidas.	$.$ \(\text{ Area } = 90m^{2}\)
Etapa 2. Identifique o que você está procurando.	altura de um triângulo
Etapa 3. Nome. Escolha uma variável para representá-la.	Deixe\(h=\) a altura.
Etapa 4. Traduzir.
Escreva a fórmula apropriada.	$.$
Substitua as informações fornecidas.	$.$
Etapa 5. Resolva a equação.	\(90 = \dfrac{15}{2}h\) \(12 = h\)
Etapa 6. Verifique. \(\begin{array} {rll} {A} &{=} &{\frac{1}{2}bh} \\ {90} &{\stackrel{?}{=}} &{\frac{1}{2}\cdot 15\cdot 12} \\ {90} &{=} &{90\checkmark} \end{array}\)
Etapa 7. Responda à pergunta.	A altura do triângulo é de 12 metros.

Etapa 1. Leia o problema. Desenhe a figura e identifique-a com as informações fornecidas.	$.$ \(P=150\)pés
Etapa 2. Identifique o que você está procurando.	o comprimento e a largura da piscina
Etapa 3. Nome. Escolha uma variável para representar a largura. O comprimento é 15 pés a mais do que a largura.	$.$ $.$
Etapa 4. Traduzir
Escreva a fórmula apropriada.	\(\quad P=2L+2W\)
Substituto.	$.$
Etapa 5. Resolva a equação.	$.$ $.$ $.$ $.$ $.$ $.$ $.$
Etapa 6. Verifique. \(\begin{array} {rcl} {P} &{=} &{2L + 2W} \\ {150} &{\stackrel{?}{=}} &{2(45) + 2(30)} \\ {150} &{=} &{150\checkmark} \end{array}\)
Etapa 7. Responda à pergunta.	O comprimento da piscina é de 45 pés e a largura é de 30 pés.

Objetivos de

Esteja preparado

Resolva aplicativos usando propriedades de triângulos

RESOLVER APLICAÇÕES DE GEOMETRIA

PROPRIEDADES DO TRIÂNGULO

Exemplo\(\PageIndex{1}\)

Experimente\(\PageIndex{1}\)

Experimente\(\PageIndex{2}\)

Exemplo\(\PageIndex{2}\)

Experimente\(\PageIndex{3}\)

Experimente\(\PageIndex{4}\)

Exemplo\(\PageIndex{3}\)

Experimente\(\PageIndex{5}\)

Experimente\(\PageIndex{6}\)

Definição: TRIÂNGULO DIREITO

Exemplo\(\PageIndex{4}\)

Experimente\(\PageIndex{7}\)

Experimente\(\PageIndex{8}\)

Exemplo\(\PageIndex{5}\)

Experimente\(\PageIndex{9}\)

Experimente\(\PageIndex{10}\)

Use o teorema de Pitágoras

O TEOREMA DE PITÁGORAS

Exemplo\(\PageIndex{6}\)

Experimente\(\PageIndex{11}\)

Experimente\(\PageIndex{12}\)

Exemplo\(\PageIndex{7}\)

Experimente\(\PageIndex{13}\)

Experimente\(\PageIndex{14}\)

Exemplo\(\PageIndex{8}\)

Experimente\(\PageIndex{15}\)

Experimente\(\PageIndex{16}\)

Resolva aplicativos usando propriedades de retângulo

PROPRIEDADES DOS RETÂNGULOS

Exemplo\(\PageIndex{9}\)

Experimente\(\PageIndex{17}\)

Experimente\(\PageIndex{18}\)

Exemplo\(\PageIndex{10}\)

Experimente\(\PageIndex{19}\)

Experimente\(\PageIndex{20}\)

Exemplo\(\PageIndex{11}\)

Experimente\(\PageIndex{21}\)

Experimente\(\PageIndex{22}\)

Exemplo\(\PageIndex{12}\)

Experimente\(\PageIndex{23}\)

Experimente\(\PageIndex{24}\)

Exemplo\(\PageIndex{13}\)

Experimente\(\PageIndex{25}\)

Experimente\(\PageIndex{26}\)

Exemplo\(\PageIndex{14}\)

Experimente\(\PageIndex{27}\)

Experimente\(\PageIndex{28}\)

Conceitos chave