Skip to main content
Global

15.4E: Exercícios para a Seção 15.4

  1. Last updated
  2. Save as PDF
  • Page ID
    188087

    • Edwin “Jed” Herman & Gilbert Strang
    • OpenStax
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Nos exercícios 1 a 4, avalie as integrais triplas sobre a caixa sólida retangular\(B\).

    1. \(\displaystyle \iiint_B (2x + 3y^2 + 4z^3) \, dV,\)onde\(B = \big\{(x,y,z) \,|\, 0 \leq x \leq 1, \, 0 \leq y \leq 2, \, 0 \leq z \leq 3\big\}\)

    Responda
    \(192\)

    2. \(\displaystyle \iiint_B (xy + yz + xz) \, dV,\)onde\(B = \big\{(x,y,z) \,|\, 1 \leq x \leq 2, \, 0 \leq y \leq 2, \, 1 \leq z \leq 3\big\}\)

    3. \(\displaystyle \iiint_B (x \cos y + z) \, dV,\)onde\(B = \big\{(x,y,z) \,|\, 0 \leq x \leq 1, \, 0 \leq y \leq \pi, \, -1 \leq z \leq 1\big\}\)

    Responda
    \(0\)

    4. \(\displaystyle \iiint_B (z \sin x + y^2) \, dV,\)onde\(B = \big\{(x,y,z) \,|\, 0 \leq x \leq \pi, \, 0 \leq y \leq 1, \, -1 \leq z \leq 2\big\}\)

    Nos exercícios 5 a 8, altere a ordem de integração integrando primeiro em relação a\(z\), depois\(x\), depois\(y\).

    5. \(\displaystyle \int_0^1 \int_1^2 \int_2^3 (x^2 + \ln y + z) \, dx \, dy \, dz\)

    Responda
    \(\displaystyle \int_0^1 \int_1^2 \int_2^3 (x^2 + \ln y + z) \, dx \, dy \, dz = \frac{35}{6} + 2 \ln 2\)

    6. \(\displaystyle \int_0^1 \int_{-1}^1 \int_0^3 (ze^x + 2y) \, dx \, dy \, dz\)

    7. \(\displaystyle \int_{-1}^2 \int_1^3 \int_0^4 \left(x^2z + \frac{1}{y}\right) \, dx \, dy \, dz\)

    Responda
    \(\displaystyle \int_{-1}^2 \int_1^3 \int_0^4 \left(x^2z + \frac{1}{y}\right) \, dx \, dy \, dz = 64 + 12 \ln 3\)

    8. \(\displaystyle \int_1^2 \int_{-2}^{-1} \int_0^1 \frac{x + y}{z} \, dx \, dy \, dz\)

    9. Seja\(F\)\(G\), e\(H\) seja funções contínuas em\([a,b]\)\([c,d]\), e\([e,f]\), respectivamente\(a, \, b, \, c, \, d, \, e\), onde e\(f\) são números reais tais que\(a < b, \, c < d\),\(e < f\) e. Mostre isso

    \[\int_a^b \int_c^d \int_e^f F (x) \, G (y) \, H(z) \, dz \, dy \, dx = \left(\int_a^b F(x) \, dx \right) \left(\int_c^d G(y) \, dy \right) \left(\int_e^f H(z) \, dz \right).\nonumber \]

    10. Sejam\(F\)\(G\), e\(H\) as funções diferenciais em\([a,b]\)\([c,d]\), e\([e,f]\), respectivamente\(a, \, b, \, c, \, d, \, e\), onde e\(f\) são números reais tais que\(a < b, \, c < d\),\(e < f\) e. Mostre isso

    \[\int_a^b \int_c^d \int_e^f F' (x) \, G' (y) \, H'(z) \, dz \, dy \, dx = [F (b) - F (a)] \, [G(d) - G(c)] \, H(f) - H(e)].\nonumber \]

    Nos exercícios 11 a 14, avalie as integrais triplas sobre a região limitada

    \(E = \big\{(x,y,z) \,|\, a \leq x \leq b, \, h_1 (x) \leq y \leq h_2 (x), \, e \leq z \leq f \big\}.\)

    11. \(\displaystyle \iiint_E (2x + 5y + 7z) \, dV, \)onde\(E = \big\{(x,y,z) \,|\, 0 \leq x \leq 1, \, 0 \leq y \leq -x + 1, \, 1 \leq z \leq 2\big\}\)

    Responda
    \(\frac{77}{12}\)

    12. \(\displaystyle \iiint_E (y \ln x + z) \, dV,\)onde\(E = \big\{(x,y,z) \,|\, 1 \leq x \leq e, \, 0 \leq y \ln x, \, 0 \leq z \leq 1\big\}\)

    13. \(\displaystyle \iiint_E (\sin x + \sin y) \, dV,\)onde\(E = \big\{(x,y,z) \,|\, 0 \leq x \leq \frac{\pi}{2}, \, -\cos x \leq y \cos x, \, -1 \leq z \leq 1 \big\}\)

    Responda
    \(2\)

    14. \(\displaystyle \iiint_E (xy + yz + xz ) dV\)onde\(E = \big\{(x,y,z) \,|\, 0 \leq x \leq 1, \, -x^2 \leq y \leq x^2, \, 0 \leq z \leq 1 \big\}\)

    Nos exercícios 15 a 18, avalie as integrais triplas sobre a região limitada indicada\(E\).

    15. \(\displaystyle \iiint_E (x + 2yz) \, dV,\)onde\(E = \big\{(x,y,z) \,|\, 0 \leq x \leq 1, \, 0 \leq y \leq x, \, 0 \leq z \leq 5 - x - y \big\}\)

    Responda
    \(\frac{430}{120}\)

    16. \(\displaystyle \iiint_E (x^3 + y^3 + z^3) \, dV,\)onde\(E = \big\{(x,y,z) \,|\, 0 \leq x \leq 2, \, 0 \leq y \leq 2x, \, 0 \leq z \leq 4 - x - y \big\}\)

    17. \(\displaystyle \iiint_E y \, dV,\)onde\(E = \big\{(x,y,z) \,|\, -1 \leq x \leq 1, \, -\sqrt{1 - x^2} \leq y \leq \sqrt{1 - x^2}, \, 0 \leq z \leq 1 - x^2 - y^2 \big\}\)

    Responda
    \(0\)

    18. \(\displaystyle \iiint_E x \, dV,\)onde\(E = \big\{(x,y,z) \,|\, -2 \leq x \leq 2, \, -4\sqrt{1 - x^2} \leq y \leq \sqrt{4 - x^2}, \, 0 \leq z \leq 4 - x^2 - y^2 \big\}\)

    Nos exercícios 19 a 22, avalie as integrais triplas sobre a região limitada\(E\) da forma

    \(E = \big\{(x,y,z) \,|\, g_1 (y) \leq x \leq g_2(y), \, c \leq y \leq d, \, e \leq z \leq f \big\}\).

    19. \(\displaystyle \iiint_E x^2 \, dV,\)onde\(E = \big\{(x,y,z) \,|\, 1 - y^2 \leq x \leq y^2 - 1, \, -1 \leq y \leq 1, \, 1 \leq z \leq 2 \big\}\)

    Responda
    \(-\frac{64}{105}\)

    20. \(\displaystyle \iiint_E (y + \sin x) \, dV,\)onde\(E = \big\{(x,y,z) \,|\, -y^4 \leq x \leq y^4, \, 0 \leq y \leq 2, \, 0 \leq z \leq 4\big\}\)

    21. \(\displaystyle \iiint_E (x - yz) \, dV,\)onde\(E = \big\{(x,y,z) \,|\, -y^6 \leq x \leq \sqrt{y}, \, 0 \leq y \leq 1x, \, -1 \leq z \leq 1 \big\}\)

    Responda
    \(\frac{11}{26}\)

    22. \(\displaystyle \iiint_E z \, dV,\)onde\(E = \big\{(x,y,z) \,|\, 2 - 2y \leq x \leq 2 + \sqrt{y}, \, 0 \leq y \leq 1x, \, 2 \leq z \leq 3 \big\}\)

    Nos exercícios 23 a 26, avalie as integrais triplas sobre a região limitada

    \(E = \big\{(x,y,z) \,|\, g_1(y) \leq x \leq g_2(y), \, c \leq y \leq d, \, u_1(x,y) \leq z \leq u_2 (x,y) \big\}\)

    23. \(\displaystyle \iiint_E z \, dV,\)onde\(E = \big\{(x,y,z) \,|\, -y \leq x \leq y, \, 0 \leq y \leq 1, \, 0 \leq z \leq 1 - x^4 - y^4 \big\}\)

    Responda
    \(\frac{113}{450}\)

    24. \(\displaystyle \iiint_E (xz + 1) \, dV,\)onde\(E = \big\{(x,y,z) \,|\, 0 \leq x \leq \sqrt{y}, \, 0 \leq y \leq 2, \, 0 \leq z \leq 1 - x^2 - y^2 \big\}\)

    25. \(\displaystyle \iiint_E (x - z) \, dV,\)onde\(E = \big\{(x,y,z) \,|\, - \sqrt{1 - y^2} \leq x \leq y, \, 0 \leq y \leq \frac{1}{2}x, \, 0 \leq z \leq 1 - x^2 - y^2 \big\}\)

    Responda
    \(\frac{1}{160}(6 \sqrt{3} - 41)\)

    26. \(\displaystyle \iiint_E (x + y) \, dV,\)onde\(E = \big\{(x,y,z) \,|\, 0 \leq x \leq \sqrt{1 - y^2}, \, 0 \leq y \leq 1x, \, 0 \leq z \leq 1 - x \big\}\)

    Nos exercícios 27 a 30, avalie as integrais triplas sobre a região limitada

    \(E = \big\{(x,y,z) \,|\, (x,y) \in D, \, u_1 (x,y) x \leq z \leq u_2 (x,y) \big\}\), onde\(D\) está a\(E\) projeção de no\(xy\) plano -.

    27. \(\displaystyle \iint_D \left(\int_1^2 (x + y) \, dz \right) \, dA,\)onde\(D = \big\{(x,y) \,|\, x^2 + y^2 \leq 1\big\}\)

    Responda
    \(\frac{3\pi}{2}\)

    28. \(\displaystyle \iint_D \left(\int_1^3 x (z + 1)\, dz \right) \, dA,\)onde\(D = \big\{(x,y) \,|\, x^2 -y^2 \geq 1, \, x \leq \sqrt{5}\big\}\)

    29. \(\displaystyle \iint_D \left(\int_0^{10-x-y} (x + 2z) \, dz \right) \, dA,\)onde\(D = \big\{(x,y) \,|\, y \geq 0, \, x \geq 0, \, x + y \leq 10\big\}\)

    Responda
    \(1250\)

    30. \(\displaystyle \iint_D \left(\int_0^{4x^2+4y^2} y \, dz \right) \, dA,\)onde\(D = \big\{(x,y) \,|\, x^2 + y^2 \leq 4, \, y \geq 1, \, x \geq 0\big\}\)

    31. O sólido\(E\) delimitado por\(y^2 + z^2 = 9, \, z = 0\), e\(x = 5\) é mostrado na figura a seguir. Avalie a integral\(\displaystyle \iiint_E z \, dV\) integrando primeiro em relação a\(z\)\(y\), depois e depois\(x\).

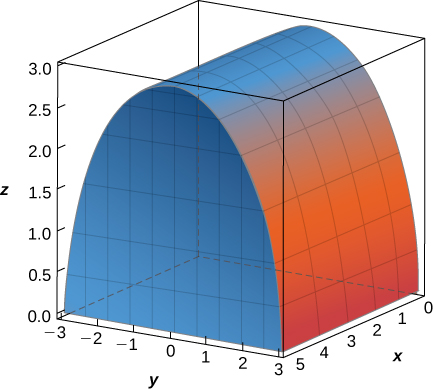
    Uma forma sólida de arco que atinge seu máximo ao longo do eixo y com z = 3. A forma atinge zero em y = mais ou menos 3, e o gráfico é truncado em x = 0 e 5.

    Responda
    \(\displaystyle \int_0^5 \int_{-3}^3 \int_0^{\sqrt{9-y^2}} z \, dz \, dy \, dx = 90\)

    32. The solid \(E\) bounded by \(y = \sqrt{x}, \, x = 4, \, y = 0\), and \(z = 1\) is given in the following figure. Evaluate the integral \(\displaystyle \iiint_E xyz \, dV\) by integrating first with respect to \(x\), then \(y\), and then \(z\).

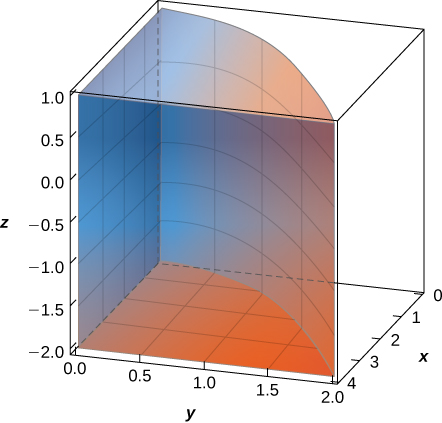
    A quarter section of an oval cylinder with z from negative 2 to positive 1. The solid is bounded by y = 0 and x = 4, and the top of the shape runs from (0, 0, 1) to (4, 2, 1) in a gentle arc.

    33. [T] O volume de um sólido\(E\) é dado pela integral\(\displaystyle \int_{-2}^0 \int_x^0 \int_0^{x^2+y^2} \, dz \, dy \, dx.\) Use um sistema de álgebra computacional (CAS) para representar graficamente\(E\) e encontrar seu volume. Arredonde sua resposta para duas casas decimais.

    Responda
    \(V \approx 5.33 \text{ units}^3\)

    Uma forma complexa que começa na origem e atinge seu máximo em (menos 2, menos 2, 8). A forma é truncada pelo plano x = y, o plano x = 0, o plano y = menos 2, o plano z = 0 e uma forma triangular complexa com bordas e lados curvos (menos 2, menos 2, 8), (0, 0, 0, 0) e (0, menos 2, 4).

    34. [T] O volume de um sólido\(E\) is given by the integral \(\displaystyle \int_{-1}^0 \int_{-x^3}^0 \int_0^{1+\sqrt{x^2+y^2}} \, dz \, dy \, dx.\) Use a CAS to graph \(E\) and find its volume \(V\). Round your answer to two decimal places.

    In exercises 35 - 38, use two circular permutations of the variables \(x, \, y,\) and \(z\) to write new integrals whose values equal the value of the original integral. A circular permutation of \(x, \, y\), and \(z\) is the arrangement of the numbers in one of the following orders: \(y, \, z,\) and \(x\) or \(z, \, x,\) and \(y\).

    35. \(\displaystyle \int_0^1 \int_1^3 \int_2^4 (x^2z^2 + 1) \, dx \, dy \, dz\)

    Answer
    \(\displaystyle \int_0^1 \int_1^3 \int_2^4 (y^2z^2 + 1) \, dz \, dx \, dy;\)
    \(\displaystyle \int_0^1 \int_1^3 \int_2^4 (x^2y^2 + 1) \, dy \, dz \, dx\)

    36. \(\displaystyle \int_0^3 \int_0^1 \int_0^{-x+1} (2x + 5y + 7z) dy \, dx \, dz\)

    37. \(\displaystyle \int_0^1 \int_{-y}^y \int_0^{1-x^4-y^4} \ln x \, dz \, dx \, dy\)

    38. \(\displaystyle \int_{-1}^1 \int_0^1 \int_{-y^6}^{\sqrt{y}} (x + yz) \, dx \, dy \, dz\)

    39. Set up the integral that gives the volume of the solid \(E\) bounded by \(y^2 = x^2 + z^2\) and \(y = a^2\), where \(a > 0\).

    Answer
    \(\displaystyle V = \int_{-a}^a \int_{-\sqrt{a^2-z^2}}^{\sqrt{a^2-z^2}} \int_{\sqrt{x^2+z^2}}^{a^2} \, dy \, dx \, dz\)

    40. Set up the integral that gives the volume of the solid \(E\) bounded by \(x = y^2 + z^2\) and \(x = a^2\), where \(a > 0\).

    Average Value of a Function

    41. Find the average value of the function \(f(x,y,z) = x + y + z\) over the parallelepiped determined by \(x + 0, \, x = 1, \, y = 0, \, y = 3, \, z = 0\), and \(z = 5\).

    Answer
    \(\frac{9}{2}\)

    42. Find the average value of the function \(f(x,y,z) = xyz\) over the solid \(E = [0,1] \times [0,1] \times [0,1]\) situated in the first octant.

    Finding Volumes using Triple Integrals

    43. Find the volume of the solid \(E\) that lies under the plane \(x + y + z = 9\) and whose projection onto the \(xy\)-plane is bounded by \(x = sqrt{y-1}, \, x = 0\), and \(x + y = 7\).

    Answer
    \(\frac{156}{5} \text{ units}^3\)

    44. Find the volume of the solid \(E\) that lies under the plane \(2x+y+z=8\) and whose projection onto the \(xy\)-plane is bounded by \(x = sin^{-1} y, \, y = 0\), and \(x = \frac{\pi}{2}\).

    a. Show that the equations of the planes of the lateral faces of the pyramid are \(4y + z = 8, \, 4y - z = -8, \, 4x + z = 8\), and \(-4x + z = 8\).

    b. Find the volume of the pyramid.

    Answer
    a. Answers may vary;
    b. \(\frac{128}{3} \text{ units}^3\)

    46. Consider the pyramid with the base in the \(xy\)-plane of \([-3,3] \times [-3,3]\) and the vertex at the point \((0,0,9)\).

    a. Show that the equations of the planes of the side faces of the pyramid are \(3y + z = 9, \, 3y + z = 9, \, y = 0\) and \(x = 0\).

    b. Find the volume of the pyramid.

    47. The solid \(E\) bounded by the sphere of equation \(x^2 + y^2 + z^2 = r^2\) with \(r > 0\) and located in the first octant is represented in the following figure.

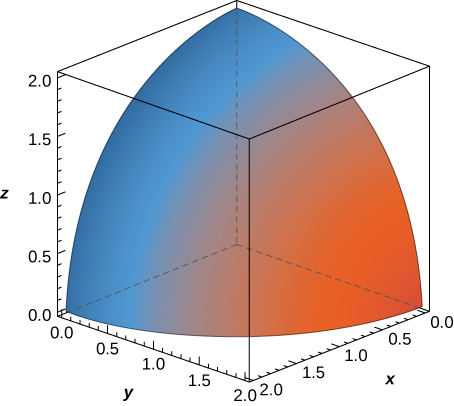
    The eighth of a sphere of radius 2 with center at the origin for positive x, y, and z.

    a. Escreva a integral tripla que fornece o volume de\(E\) integrando primeiro em relação a\(z\), depois com\(y\) e depois com\(x\).

    b. Reescreva a integral na parte a. como uma integral equivalente em outras cinco ordens.

    Responda

    a.\(\displaystyle \int_0^4 \int_0^{\sqrt{r^2-x^2}} \int_0^{\sqrt{r^2-x^2-y^2}} \, dz \, dy \, dx\)
    b.\(\displaystyle \int_0^2 \int_0^{\sqrt{r^2-x^2}} \int_0^{\sqrt{r^2-x^2-y^2}} \, dz \, dx \, dy,\)
    \(\displaystyle \int_0^r \int_0^{\sqrt{r^2-x^2}} \int_0^{\sqrt{r^2-x^2-y^2}} \, dy \, dx \, dz,\)
    \(\displaystyle \int_0^r \int_0^{\sqrt{r^2-x^2}} \int_0^{\sqrt{r^2-x^2-y^2}} dy \, dz \, dx,\)
    \(\displaystyle \int_0^r \int_0^{\sqrt{r^2-x^2}} \int_0^{\sqrt{r^2-x^2-y^2}} dx \, dy \, dz,\)
    \(\displaystyle \int_0^r \int_0^{\sqrt{r^2-x^2}} \int_0^{\sqrt{r^2-x^2-y^2}} dx \, dz \,dy\)

    48. O sólido\(E\) delimitado pela esfera da equação\(9x^2 + 4y^2 + z^2 = 1\) e localizado no primeiro octante é representado na figura a seguir.

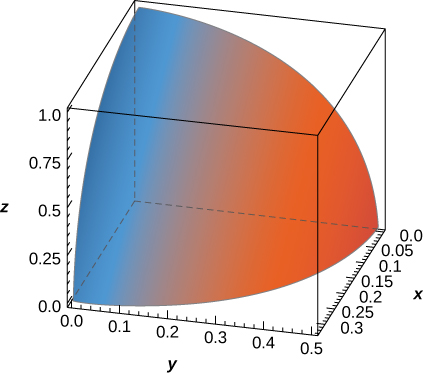
    No primeiro octante, é mostrada uma forma complexa que é aproximadamente um ovóide sólido com centro de origem, altura 1, largura 0,5 e comprimento 0,35.

    a. Escreva a integral tripla que fornece o volume de\(E\) by integrating first with respect to \(z\) then with \(y\) and then with \(x\).

    b. Rewrite the integral in part a. as an equivalent integral in five other orders.

    49. Find the volume of the prism with vertices \((0,0,0), \, (2,0,0), \, (2,3,0), \, (0,3,0), \, (0,0,1)\), and \((2,0,1)\).

    Answer
    \(3 \text{ units}^3\)

    50. Find the volume of the prism with vertices \((0,0,0), \, (4,0,0), \, (4,6,0), \, (0,6,0), \, (0,0,1)\), and \((4,0,1)\).

    51. The solid \(E\) bounded by \(z = 10 - 2x - y\) and situated in the first octant is given in the following figure. Find the volume of the solid.

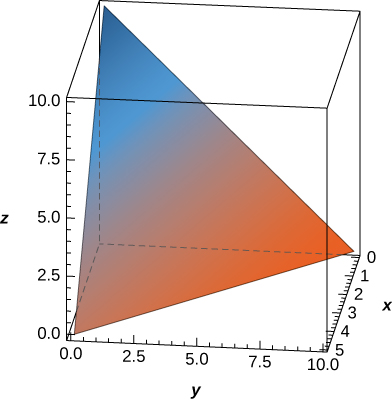
    A tetrahedron bounded by the x y, y z, and x z planes and a triangle with vertices (0, 0, 10), (5, 0, 0), and (0, 10, 0).

    Responda
    \(\frac{250}{3} \text{ units}^3\)

    52. O sólido\(E\) delimitado\(z = 1 - x^2\) e situado no primeiro octante é dado na figura a seguir. Encontre o volume do sólido.

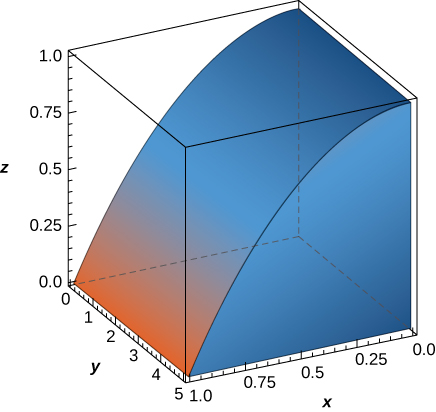
    Uma forma complexa no primeiro octante com altura 1, largura 5 e comprimento 1. A forma parece ser um quarto ligeiramente deformado de um cilindro de raio 1 e largura 5.

    Aproximando integrais triplos

    53. A regra do ponto médio para a integral tripla\(\displaystyle \iiint_B f(x,y,z) \,dV\) over the rectangular solid box \(B\) is a generalization of the midpoint rule for double integrals. The region \(B\) is divided into subboxes of equal sizes and the integral is approximated by the triple Riemann sum \[\sum_{i=1}^l \sum_{j=1}^m \sum_{k=1}^n f(\bar{x_i}, \bar{y_j}, \bar{z_k}) \Delta V,\nonumber \] where \((\bar{x_i}, \bar{y_j}, \bar{z_k})\) is the center of the box \(B_{ijk}\) and \(\Delta V\) is the volume of each subbox. Apply the midpoint rule to approximate \[\iiint_B x^2 \,dV\nonumber \] over the solid \(B = \big\{(x,y,z) \,|\, 0 \leq x \leq 1, \, 0 \leq y \leq 1, \, 0 \leq z \leq 1 \big\}\) by using a partition of eight cubes of equal size. Round your answer to three decimal places.

    Answer
    \(\displaystyle \iiint_B f(x,y,z) \,dV\quad\) \(\approx\quad\frac{5}{16} \approx 0.313 \text{ units}^3\)

    54. [T]

    a. Apply the midpoint rule to approximate \(\displaystyle \iiint_B e^{-x^2} \, dV\) over the solid \(B = \big\{(x,y,z) \,|\, 0 \leq x \leq 1, \, 0 \leq y \leq 1, \, 0 \leq z \leq 1 \big\}\) by using a partition of eight cubes of equal size. Round your answer to three decimal places.

    b. Use a CAS to improve the above integral approximation in the case of a partition of \(n^3\) cubes of equal size, where \(n = 3,\,4,\, ..., \,10\).

    Applications

    55. Suppose that the temperature in degrees Celsius at a point \((x,y,z)\) of a solid \(E\) bounded by the coordinate planes and the plane \(x + y + z = 5\) is given by: \[T (x,y,z) = xz + 5z + 10\nonumber \] Find the average temperature over the solid.

    Answer
    \(17.5^{\circ}\) C

    56. Suppose that the temperature in degrees Fahrenheit at a point \((x,y,z)\) of a solid \(E\) bounded by the coordinate planes and the plane \(x + y + z = 5\) is given by: \[T(x,y,z) = x + y + xy\nonumber \] Find the average temperature over the solid.

    57. Show that the volume of a right square pyramid of height \(h\) and side length \(a\) is \( v = \dfrac{ha^2}{3}\) by using triple integrals.

    58. Show that the volume of a regular right hexagonal prism of edge length \(a\) is \(\dfrac{3a^3 \sqrt{3}}{2}\) by using triple integrals.

    59. Show that the volume of a regular right hexagonal pyramid of edge length \(a\) is \(\dfrac{a^3 \sqrt{3}}{2}\) by using triple integrals.

    60. If the charge density at an arbitrary point \((x,y,z)\) of a solid \(E\) is given by the function \(\rho (x,y,z)\), then the total charge inside the solid is defined as the triple integral \(\displaystyle \iiint_E \rho (x,y,z) \,dV.\) Assume that the charge density of the solid \(E\) enclosed by the paraboloids \(x = 5 - y^2 - z^2\) and \(x = y^2 + z^2 - 5\) is equal to the distance from an arbitrary point of \(E\) to the origin. Set up the integral that gives the total charge inside the solid \(E\).

    Answer
    Total Charge inside the Solid \(E \quad=\quad\) \(\displaystyle \int_{-\sqrt{5}}^{\sqrt{5}}\int_{-\sqrt{5-y^2}}^{\sqrt{5-y^2}}\int_{y^2+z^2-5}^{5 - y^2 - z^2} \sqrt{x^2+y^2+z^2}\,dx\,dz\,dy\)