15.4: Integrais triplos
- Page ID
- 188072
- Reconheça quando uma função de três variáveis é integrável em uma caixa retangular.
- Calcule uma integral tripla expressando-a como uma integral iterada.
- Reconheça quando uma função de três variáveis é integrável em uma região fechada e limitada.
- Simplifique um cálculo alterando a ordem de integração de uma integral tripla.
- Calcule o valor médio de uma função de três variáveis.
Anteriormente, discutimos a integral dupla de uma função\(f(x,y)\) de duas variáveis sobre uma região retangular no plano. Nesta seção, definimos a integral tripla de uma função\(f(x,y,z)\) de três variáveis sobre uma caixa sólida retangular no espaço,\(\mathbb{R}^3\). Posteriormente, nesta seção, estenderemos a definição para regiões mais gerais em\(\mathbb{R}^3\).
Funções integráveis de três variáveis
Podemos definir uma caixa\(B\) retangular\(\mathbb{R}^3\) como
\[B = \big\{(x,y,z)\,|\,a \leq x \leq b, \, c \leq y \leq d, \, e \leq z \leq f \big\}. \nonumber \]
Seguimos um procedimento semelhante ao que fizemos anteriormente. Dividimos o intervalo\([a,b]\) em\(l\) subintervalos\([x_{i-1},x_i]\) de igual comprimento\(\Delta x\) com
\[\Delta x = \dfrac{x_i - x_{i-1}}{l}, \nonumber \]
divida o intervalo\([c,d]\) em\(m\) subintervalos\([y_{i-1}, y_i]\) de igual comprimento\(\Delta y\) com
\[\Delta y = \dfrac{y_j - y_{j-1}}{m}, \nonumber \]
e divida o intervalo\([e,f]\) em\(n\) subintervalos\([z_{i-1},z_i]\) de igual comprimento\(\Delta z\) com
\[\Delta z = \dfrac{z_k - z_{k-1}}{n} \nonumber \]
Em seguida, a caixa retangular\(B\) é subdividida em\(lmn\) subcaixas:
\[B_{ijk} = [x_{i-1}, x_i] \times [y_{i-1}, y_i] \times [z_{i-1},z_i], \nonumber \]
conforme mostrado na Figura\(\PageIndex{1}\).
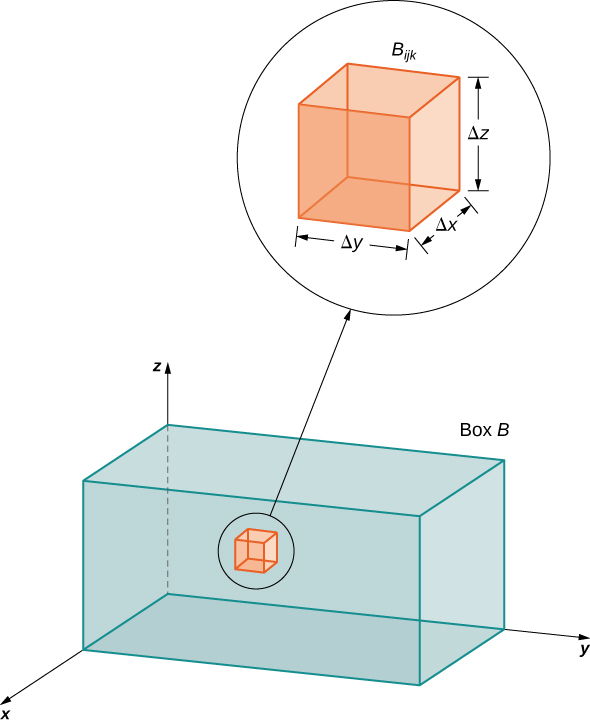
Para cada\(i, \, j,\) e\(k\), considere um ponto de amostra\((x_{ijk}^*, y_{ijk}^*, z_{ijk}^*)\) em cada subcaixa\(B_{ijk}\). Vemos que seu volume é\(\Delta V = \Delta x \Delta y \Delta z\). Forme a soma tripla de Riemann
\[\sum_{i=1}^l \sum_{j=1}^m \sum_{k=1}^n f ( x_{ijk}^*, y_{ijk}^*, z_{ijk}^*)\,\Delta x \Delta y \Delta z. \nonumber \]
Definimos a integral tripla em termos do limite de uma soma tripla de Riemann, como fizemos com a integral dupla em termos de uma soma dupla de Riemann.
A integral tripla de uma função\(f(x,y,z)\) sobre uma caixa retangular\(B\) é definida como
\[\lim_{l,m,n\rightarrow\infty} \sum_{i=1}^l \sum_{j=1}^m \sum_{k=1}^n f ( x_{ijk}^*, y_{ijk}^*, z_{ijk}^*)\,\Delta x \Delta y \Delta z = \iiint_B f(x,y,z) \,dV \nonumber \]se esse limite existir.
Quando a integral tripla existe\(B\) na função, diz-se que\(f(x,y,z)\) é integrável em\(B\). Além disso, a integral tripla\(f(x,y,z)\) existe se for contínua\(B\). Portanto, usaremos funções contínuas em nossos exemplos. No entanto, a continuidade é suficiente, mas não necessária; em outras palavras,\(f\) é limitada\(B\) e contínua, exceto possivelmente na fronteira de\(B\). O ponto de amostra\((x_{ijk}^*, y_{ijk}^*, z_{ijk}^*)\) pode ser qualquer ponto na subcaixa retangular\(B_{ijk}\) e todas as propriedades de uma integral dupla se aplicam a uma integral tripla. Assim como a integral dupla tem muitas aplicações práticas, a integral tripla também tem muitas aplicações, que discutiremos nas seções posteriores.
Agora que desenvolvemos o conceito da integral tripla, precisamos saber como computá-la. Assim como no caso da integral dupla, podemos ter uma integral tripla iterada e, consequentemente, existe uma versão do teorema de Fubini para integrais triplas.
Se\(f(x,y,z)\) for contínuo em uma caixa retangular\(B = [a,b] \times [c,d] \times [e,f]\), então
\[\iint_B f(x,y,z) \,dV = \int_e^f \int_c^d \int_a^b f(x,y,z) \,dx \, dy \, dz. \nonumber \]
Essa integral também é igual a qualquer uma das outras cinco ordens possíveis para a integral tripla iterada.
Para\(a, b, c, d, e\) números\(f\) reais, a integral tripla iterada pode ser expressa em seis ordens diferentes:
\[\begin{align} \int_e^f \int_c^d \int_a^b f(x,y,z)\, dx \, dy \, dz = \int_e^f \left( \int_c^d \left( \int_a^b f(x,y,z) \,dx \right) dy \right) dz \\ = \int_c^d \left( \int_e^f \left( \int_a^b f(x,y,z) \,dx \right)dz \right) dy \\ = \int_a^b \left( \int_e^f \left( \int_c^d f(x,y,z) \,dy \right)dz \right) dx \\ = \int_e^f \left( \int_a^b \left( \int_c^d f(x,y,z) \,dy \right) dx \right) dz \\ = \int_c^d \left( \int_a^b \left( \int_c^d f(x,y,z) \,dz\right)dx \right) dy \\ = \int_a^b \left( \int_c^d \left( \int_e^f f(x,y,z) \,dz \right) dy \right) dx \end{align} \nonumber \]
Para uma caixa retangular, a ordem de integração não faz nenhuma diferença significativa no nível de dificuldade na computação. Nós calculamos integrais triplos usando o Teorema de Fubini em vez de usar a definição da soma de Riemann. Seguimos a ordem de integração da mesma forma que fizemos com integrais duplas (ou seja, de dentro para fora).
Avalie a integral tripla\[\int_{z=0}^{z=1} \int_{y=2}^{y=4} \int_{x=-1}^{x=5} (x + yz^2)\, dx \, dy \, dz. \nonumber \]
Solução
A ordem de integração é especificada no problema, então integre em relação a\(x\) primeiro, depois y e depois\(z\).
\[\begin{align*}&\int_{z=0}^{z=1} \int_{y=2}^{y=4} \int_{x=-1}^{x=5} (x + yz^2) \,dx \,dy \,dz \\ &= \int_{z=0}^{z=1} \int_{y=2}^{y=4} \left. \left[ \dfrac{x^2}{2} + xyz^2\right|_{x=-1}^{x=5}\right]\,dy \,dz &&\text{Integrate with respect to $x$.}\\ &= \int_{z=0}^{z=1} \int_{y=2}^{y=4} \left[12+6yz^2\right] \,dy \,dz &&\text{Evaluate.}\\ &= \int_{z=0}^{z=1} \left[ \left.12y+6\dfrac{y^2}{2}z^2 \right|_{y=2}^{y=4} \right] dz &&\text{Integrate with respect to $y$.} \\ &= \int_{z=0}^{z=1} [24+36z^2] \, dz &&\text{Evaluate.} \\ &= \left[ 24z+36\dfrac{z^3}{3} \right]_{z=0}^{z=1} &&\text{Integrate with respect to $z$.}\\ &=36. &&\text{Evaluate.}\end{align*}\]
Avalie a integral tripla
\[\iiint_B x^2 yz \,dV \nonumber \]
onde\(B = \big\{(x,y,z)\,|\, - 2 \leq x \leq 1, \, 0 \leq y \leq 3, \, 1 \leq z \leq 5 \big\} \), conforme mostrado na Figura\(\PageIndex{2}\).
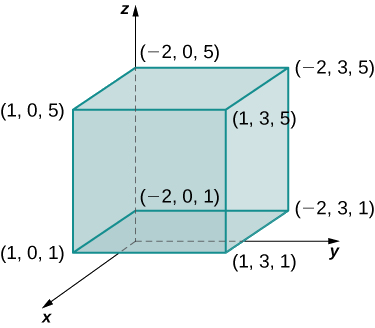
Solução
A ordem não está especificada, mas podemos usar a integral iterada em qualquer ordem sem alterar o nível de dificuldade. Escolha, digamos, integrar\(y\) primeiro\(x\), depois e depois\(z\).
\[\begin{align*}\iiint\limits_{B} x^2 yz \,dV &= \int_1^5 \int_{-2}^1 \int_0^3 [x^2 yz] \,dy \, dx \, dz \\&= \int_1^5 \int_{-2}^1 \left[ \left. x^2 \dfrac{y^3}{3} z\right|_0^3 \right] dx \, dz \\&= \int_1^5 \int_{-2}^1 \dfrac{y}{2} x^2 z \,dx \, dz \\&= \int_1^5 \left[ \left. \dfrac{9}{2} \dfrac{x^3}{3} z \right|_{-2}^1 \right] dz \\&= \int_1^5 \dfrac{27}{2} z \, dz \\&= \left. \dfrac{27}{2} \dfrac{z^2}{2} \right|_1^5 = 162.\end{align*}\]
Agora tente se integrar em uma ordem diferente apenas para ver se obtemos a mesma resposta. Opte por integrar em relação a\(x\) primeiro, depois\(z\), depois\(y\)
\[\begin{align*}\iiint\limits_{B} x^2yz \,dV &= \int_0^3 \int_1^5 \int_{-2}^1 [x^2yz] \,dx\, dz\, dy \\&= \int_0^3 \int_1^5 \left[ \left. \dfrac{x^3}{3} yz \right|_{-2}^1 \right] dz \,dy \\&= \int_0^3 \int_1^5 3yz \; dz \,dy \\&= \int_0^3 \left.\left[ 3y\dfrac{z^2}{2} \right|_1^5 \right] \,dy \\&= \int_0^3 36y \; dy \\&= \left. 36\dfrac{y^2}{2} \right|_0^3 =18(9-0) =162.\end{align*}\]
Avalie a integral tripla
\[\iiint_B z \, \sin \, x \, \cos \, y \, dV\nonumber \]
onde\(B = \big\{(x,y,z)\,|\,0 \leq x \leq \pi, \, \dfrac{3\pi}{2} \leq y \leq 2\pi, \, 1 \leq z \leq 3 \big\}\).
- Dica
-
Siga as etapas no exemplo anterior.
- Responda
-
\[\iiint_B z \, \sin \, x \, \cos \, y \, dV = 8 \nonumber \]
A integral tripla de uma função contínua\(f(x,y,z)\) sobre uma região tridimensional geral
\[E = \big\{(x,y,z)\,|\,(x,y) \in D, \, u_1(x,y) \leq z \leq u_2(x,y) \big\} \nonumber \]
in\(\mathbb{R}^3\), onde\(D\) está a\(E\) projeção de no\(xy\) plano -, é
\[\iiint_E f(x,y,z) \,dV = \iint_D \left[\int_{u_1(x,y)}^{u_2(x,y)} f(x,y,z) \,dz \right] \, dA. \nonumber \]
Da mesma forma, podemos considerar uma região limitada geral\(D\) no\(xy\) plano -e duas funções\(y = u_1(x,z)\) e\(y = u_2(x,z)\) tal que\(u_1(x,z) \leq u_2(x,z)\) para todos\((x,z)\) em\(D\). Em seguida, podemos descrever a\(E\) região sólida\(\mathbb{R}^3\) como
\[E = \big\{(x,y,z)\,|\,(x,z) \in D, \, u_1(x,z) \leq z \leq u_2(x,z) \big\} \nonumber \]onde\(D\) está a\(E\) projeção de no\(xy\) plano -e a integral tripla é
\[\iiint_E f(x,y,z)\,dV = \iint_D \left[\int_{u_1(x,z)}^{u_2(x,z)} f(x,y,z) \,dy \right] \, dA. \nonumber \]
Finalmente, se\(D\) é uma região limitada geral no\(xy\) plano -e temos duas funções\(x = u_1(y,z)\) e\(x = u_2(y,z)\) tal que,\(u_1(y,z) \leq u_2(y,z)\) para todos\((y,z)\) em\(D\), então a região sólida\(E\) em\(\mathbb{R}^3\) pode ser descrita como
\[E = \big\{(x,y,z)\,|\,(y,z) \in D, \, u_1(y,z) \leq z \leq u_2(y,z) \big\} \nonumber \]onde\(D\) está a\(E\) projeção de no\(xy\) plano -e a integral tripla é
\[\iiint_E f(x,y,z)\,dV = \iint_D \left[\int_{u_1(y,z)}^{u_2(y,z)} f(x,y,z) \, dx \right] \, dA. \nonumber \]
Observe que a região\(D\) em qualquer um dos planos pode ser do Tipo I ou do Tipo II, conforme descrito anteriormente. Se\(D\) no\(xy\) plano -for do Tipo I (Figura\(\PageIndex{4}\)), então
\[E = \big\{(x,y,z)\,|\,a \leq x \leq b, \, g_1(x) \leq y \leq g_2(x), \, u_1(x,y) \leq z \leq u_2(x,y) \big\}. \nonumber \]
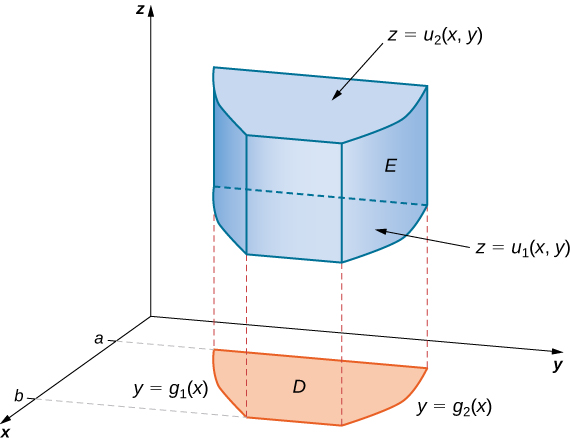
Então, a integral tripla se torna
\[\iiint_E f(x,y,z) \,dV = \int_a^b \int_{g_1(x)}^{g_2(x)} \int_{u_1(x,y)}^{u_2(x,y)} f(x,y,z) \,dz \, dy \, dx. \nonumber \]
Se\(D\) no\(xy\) plano -for do Tipo II (Figura\(\PageIndex{5}\)), então
\[E = \big\{(x,y,z)\,|\,c \leq x \leq d, h_1(x) \leq y \leq h_2(x), \, u_1(x,y) \leq z \leq u_2(x,y) \big\}. \nonumber \]
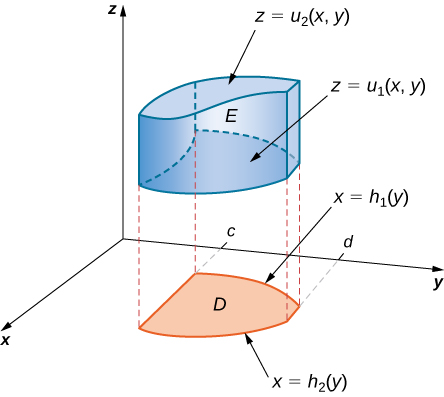
Então, a integral tripla se torna
\[\iiint_E f(x,y,z) \,dV = \int_{y=c}^{y=d} \int_{x=h_1(y)}^{x=h_2(y)} \int_{z=u_1(x,y)}^{z=u_2(x,y)} f(x,y,z)\,dz \, dx \, dy. \nonumber \]
Avalie a integral tripla da função\(f(x,y,z) = 5x - 3y\) sobre o tetraedro sólido limitado pelos planos\(x = 0, \, y = 0, \, z = 0\),\(x + y + z = 1\) e.
Solução
A figura\(\PageIndex{6}\) mostra o tetraedro sólido\(E\) e sua projeção\(D\) no\(xy\) plano.
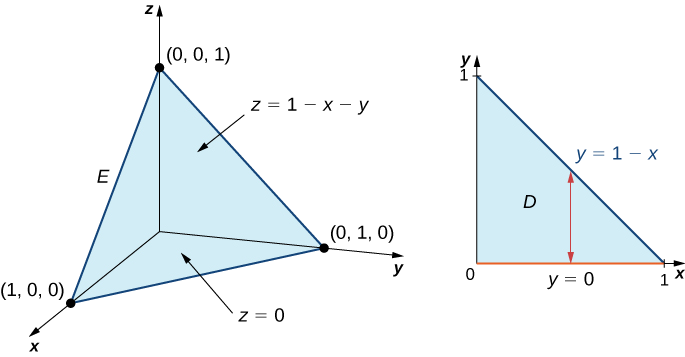
Podemos descrever o tetraedro da região sólida como
\[E = \big\{(x,y,z)\,|\,0 \leq x \leq 1, \, 0 \leq y \leq 1 - x, \, 0 \leq z \leq 1 - x - y \big\}. \nonumber \]
Portanto, a integral tripla é
\[\iiint_E f(x,y,z) \,dV = \int_{x=0}^{x=1} \int_{y=0}^{y=1-x} \int_{z=0}^{z=1-x-y} (5x - 3y) \,dz \, dy \, dx. \nonumber \]
Para simplificar o cálculo, primeiro avalie a integral\(\displaystyle \int_{z=0}^{z=1-x-y} (5x - 3y) \,dz\). Nós temos
\[\int_{z=0}^{z=1-x-y} (5x - 3y) \,dz = (5x - 3y)z \bigg|_{z=0}^{z=1-x-y} = (5x - 3y)(1 - x - y).\nonumber \]
Agora, avalie a integral
\[\int_{y=0}^{y=1-x} (5x - 3y)(1 - x - y) \,dy, \nonumber \]
obtenção
\[\int_{y=0}^{y=1-x} (5x - 3y)(1 - x - y)\,dy = \dfrac{1}{2}(x - 1)^2 (6x - 1).\nonumber \]
Finalmente avalie
\[\int_{x=0}^{x=1} \dfrac{1}{2}(x - 1)^2 (6x - 1)\,dx = \dfrac{1}{12}.\nonumber \]
Juntando tudo, temos
\[\iiint_E f(x,y,z)\,dV = \int_{x=0}^{x=1} \int_{y=0}^{y=1-x} \int_{z=0}^{z=1-x-y}(5x - 3y)\,dz \, dy \, dx = \dfrac{1}{12}.\nonumber \]
Assim como usamos a integral dupla\[\iint_D 1 \,dA \nonumber \] para encontrar a área de uma região limitada geral,\(D\) podemos usar\[\iiint_E 1\,dV \nonumber \] para encontrar o volume de uma região geral limitada sólida\(E\). O exemplo a seguir ilustra o método.
Encontre o volume de uma pirâmide direita que tem a base quadrada no\(xy\) plano\([-1,1] \times [-1,1]\) -e o vértice no ponto,\((0, 0, 1)\) conforme mostrado na figura a seguir.
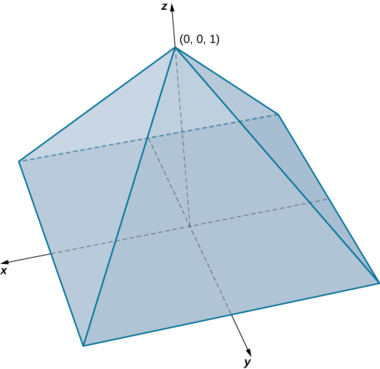
Solução
Nesta pirâmide, o valor de\(z\) muda de 0 para 1 e, em cada altura,\(z\) a seção transversal da pirâmide para qualquer valor de\(z\) é o quadrado.
\[[-1 + z, \, 1 - z] \times [-1 + z, \, 1 - z].\nonumber \]
Portanto, o volume da pirâmide é\[\iiint_E 1\,dV\nonumber \] onde
\[E = \big\{(x,y,z)\,|\,0 \leq z \leq 1, \, -1 + z \leq y \leq 1 - z, \, -1 + z \leq x \leq 1 - z \big\}.\nonumber \]
Assim, temos
\ [\ begin {align*}\ IIint_E 1\, dV &=\ int_ {z=0} ^ {z=1}\ int_ {y=-1+z} ^ {y=1-z}\ int_ {x=-1+z} ^ {x=1-z} 1\, dx\, dy\, dz\\ [5pt]
&=\ int_ {z_ =0} ^ {z=1}\ int_ {y=-1+z} ^ {y=1-z} (2 - 2z)\, dy\, dz\\ [5pt]
&=\ int_ {z=0} ^ {z=1} (2 - 2z) ^2\, dz =\ dfrac {4} {3}. \ end {align*}\]
Portanto, o volume da pirâmide é de unidades\(\dfrac{4}{3}\) cúbicas.
Considere a esfera sólida\(E = \big\{(x,y,z)\,|\,x^2 + y^2 + z^2 = 9 \big\}\). Escreva a integral tripla\[\iiint_E f(x,y,z) \,dV\nonumber \] para uma função arbitrária\(f\) como uma integral iterada. Em seguida, avalie essa integral tripla com\(f(x,y,z) = 1\). Observe que isso fornece o volume de uma esfera usando uma integral tripla.
- Dica
-
Siga as etapas no exemplo anterior. Use simetria.
- Responda
-
\[\begin{align*} \iiint_E 1\,dV = 8 \int_{x=-3}^{x=3} \int_{y=-\sqrt{9-z^2}}^{y=\sqrt{9-z^2}}\int_{z=-\sqrt{9-x^2-y^2}}^{z=\sqrt{9-x^2-y^2}} 1\,dz \, dy \, dx \\ = 36 \pi \,\text{cubic units}. \end{align*}\]
Alterando a ordem da integração
Como já vimos em integrais duplas sobre regiões limitadas gerais, a alteração da ordem da integração é feita com bastante frequência para simplificar o cálculo. Com uma integral tripla sobre uma caixa retangular, a ordem de integração não altera o nível de dificuldade do cálculo. No entanto, com uma integral tripla sobre uma região limitada geral, escolher uma ordem apropriada de integração pode simplificar um pouco o cálculo. Às vezes, fazer a alteração nas coordenadas polares também pode ser muito útil. Demonstramos dois exemplos aqui.
Considere a integral iterada
\[\int_{x=0}^{x=1} \int_{y=0}^{y=x^2} \int_{z=0}^{z=y} f(x,y,z)\,dz \, dy \, dx. \nonumber \]
A ordem de integração aqui é primeiro em relação a z, depois y e depois x. Expresse essa integral alterando a ordem de integração para ser a primeira em relação a\(x\)\(z\), depois e depois\(y\). Verifique se o valor da integral é o mesmo se deixarmos\(f (x,y,z) =xyz\).
Solução
A melhor maneira de fazer isso é esboçar a região\(E\) e suas projeções em cada um dos três planos coordenados. Assim, deixe
\[E = \big\{(x,y,z)\,|\,0 \leq x \leq 1, \, 0 \leq y \leq x^2, \, 0 \leq z \leq y \big\}.\nonumber \]
e
\[\int_{x=0}^{x=1} \int_{y=0}^{y=x^2} \int_{z=0}^{z=x^2} f(x,y,z) \,dz \, dy \, dx = \iiint_E f(x,y,z)\,dV.\nonumber \]
Precisamos expressar essa integral tripla como
\[\int_{y=c}^{y=d} \int_{z=v_1(y)}^{z=v_2(y)} \int_{x=u_1(y,z)}^{x=u_2(y,z)} f(x,y,z)\,dx \, dz \, dy.\nonumber \]
Conhecendo a região,\(E\) podemos desenhar as seguintes projeções (Figura\(\PageIndex{8}\)):
no\(xy\) plano -é\(D_1 = \big\{(x,y)\,|\, 0 \leq x \leq 1, \, 0 \leq y \leq x^2 \big\} = \{ (x,y) \,|\, 0 \leq y \leq 1, \, \sqrt{y} \leq x \leq 1 \big\},\)
no\(yz\) plano -é\(D_2 = \big\{(y,z) \,|\, 0 \leq y \leq 1, \, 0 \leq z \leq y^2 \big\}\), e
no\(xz\) plano -é\(D_3 = \big\{(x,z) \,|\, 0 \leq x \leq 1, \, 0 \leq z \leq x^2 \big\}\).
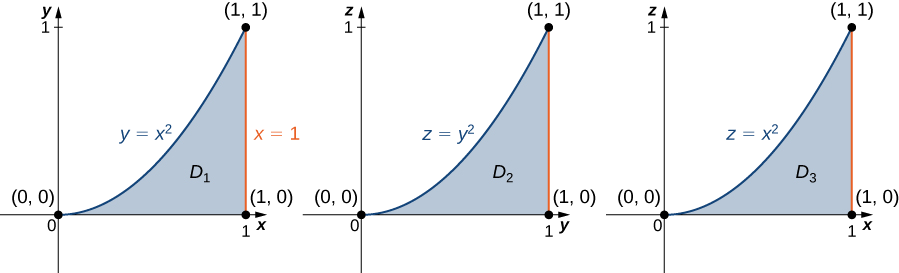
Agora podemos descrever a\(E\) mesma região que\(\big\{(x,y,z) \,|\, 0 \leq y \leq 1, \, 0 \leq z \leq y^2, \, \sqrt{y} \leq x \leq 1 \big\}\), e consequentemente, a integral tripla se torna
\[\int_{y=c}^{y=d} \int_{z=v_1(y)}^{z=v_2(y)} \int_{x=u_1(y,z)}^{x=u_2(y,z)} f(x,y,z)\,dx \, dz \, dy = \int_{y=0}^{y=1} \int_{z=0}^{z=x^2} \int_{x=\sqrt{y}}^{x=1} f(x,y,z)\,dx \, dz \, dy \nonumber \]
Agora, suponha que\(f (x,y,z) = xyz\) em cada uma das integrais. Então nós temos
\ [\ begin {align*}\ int_ {x=0} ^ {x=1}\ int_ {y=0} ^ {y=x^2}\ int_ {z=0} ^ {z=y^2} xyz\, dz\, dy\, dx &=\ int_ {x=0} ^ {x=1}\ int_ {y=0} ^ {x=1}\ int_ {y=0} ^ {y=0} x^2}\ esquerda. \ left [xy\ dfrac {z^2} {2}\ right|_ {z=0} ^ {z=y^2}\ direita]\, dy\, dx\\ [5pt]
&=\ int_ {x=0} ^ {x=1}\ int_ {y=0} ^ {y=x^2}\ esquerda (x\ dfrac {y^5} {2}\ right) dy\, dx\\ [5pt]
&=\ int_ {x=0} ^ {x=1}\ left. \ left [x\ dfrac {y^6} {12}\ right|_ {y=0} ^ {y=x^2}\ direita] dx\\ [5pt]
&=\ int_ {x=0} ^ {x=1}\ dfrac {x^ {13}} {12} dx =\ left. \ dfrac {x^ {14}} {168}\ right|_ {x=0} ^ {x=1}\\ [5pt]
&=\ dfrac {1} {168},\ end {align*}\]
\ [\ begin {align*}\ int_ {y=0} ^ {y=1}\ int_ {z=0} ^ {z=y^2}\ int_ {x=\ sqrt {y}} ^ {x=1} xyz\, dx\, dz\, dy &=\ int_ {y=0} ^ {y=1}\ int_ {z=0} ^ {z=y^2}\ esquerda. \ left [yz\ dfrac {x^2} {2}\ right|_ {\ sqrt {y}} ^ {1}\ direita] dz\, dy\\ [5pt]
&=\ int_ {y=0} ^ {y=1}\ int_ {z=0} ^ {z=y^2}\ left (\ dfrac {yz} {2} -\ dfrac {y^2z} {2}\ direita) dz\, dy\\ [5pt]
&=\ int_ {y=0} ^ {y=1}\ esquerda. \ left [\ dfrac {yz^2} {4} -\ dfrac {y^2z^2} {4}\ right|_ {z=0} ^ {z=y^2}\ direita] dy\\ [5pt]
&=\ int_ {y=0} ^ {y=1}\ left (\ dfrac {y^5} {4} -\ dfrac {y^5} {4} -\ dfrac {y^5} {4} -\ dfrac {y^5} {4} -\ dfrac c {y^6} {4}\ right) dy\\ [5pt]
&=\ left. \ left (\ dfrac {y^6} {24} -\ dfrac {y^7} {28}\ direita)\ right|_ {y=0} ^ {y=1}\\ [5pt]
&=\ dfrac {1} {168}. \ end {align*}\ nonumber\]
As respostas coincidem.
Escreva cinco integrais iteradas diferentes iguais à integral fornecida
\[\int_{z=0}^{z=4} \int_{y=0}^{y=4-z} \int_{x=0}^{x=\sqrt{y}} f(x,y,z) \, dx \, dy \, dz.\nonumber \]
- Dica
-
Siga as etapas do exemplo anterior, usando a região\(E\) como\( \big\{(x,y,z) \,|\, 0 \leq z \leq 4, \, 0 \leq y \leq 4 - z, \, 0 \leq x \leq \sqrt{y} \big\}\), e descreva e esboce as projeções em cada um dos três planos, cinco vezes diferentes.
- Responda
-
\[(i) \, \int_{z=0}^{z=4} \int_{x=0}^{x=\sqrt{4-z}} \int_{y=x^2}^{y=4-z} f(x,y,z) \, dy \, dx \, dz, \, (ii) \, \int_{y=0}^{y=4} \int_{z=0}^{z=4-y} \int_{x=0}^{x=\sqrt{y}} f(x,y,z) \,dx \, dz \, dy, \,(iii) \, \int_{y=0}^{y=4} \int_{x=0}^{x=\sqrt{y}} \int_{z=0}^{Z=4-y} f(x,y,z) \,dz \, dx \, dy, \, \nonumber \]
\[ (iv) \, \int_{x=0}^{x=2} \int_{y=x^2}^{y=4} \int_{z=0}^{z=4-y} f(x,y,z) \,dz \, dy \, dx, \, (v) \int_{x=0}^{x=2} \int_{z=0}^{z=4-x^2} \int_{y=x^2}^{y=4-z} f(x,y,z) \,dy \, dz \, dx \nonumber \]
Avalie a integral tripla
\[\iiint_{E} \sqrt{x^2 + z^2} \,dV, \nonumber \]
onde\(E\) está a região delimitada pelo parabolóide\(y = x^2 + z^2\) (Figura\(\PageIndex{9}\)) e pelo plano\(y = 4\).
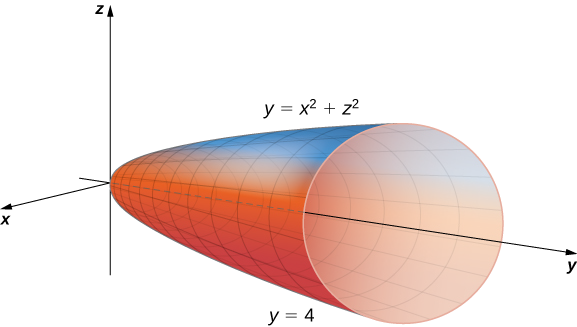
Solução
A projeção da região sólida\(E\) no\(xy\) plano -é a região delimitada acima\(y = 4\) e abaixo pela parábola,\(y = x^2\) conforme mostrado.
Assim, temos
\[E = \big\{(x,y,z) \,|\, -2 \leq x \leq 2, \, x^2 \leq y \leq 4, \, -\sqrt{y - x^2} \leq z \sqrt{y - x^2} \big\}.\nonumber \]
A integral tripla se torna
\[\iiint_E \sqrt{x^2 + z^2} \,dV = \int_{x=-2}^{x=2} \int_{y=x^2}^{y=4} \int_{z=-\sqrt{y-x^2}}^{z=\sqrt{y-x^2}} \sqrt{x^2 + z^2} \,dz \, dy \, dx.\nonumber \]
Essa expressão é difícil de calcular, então considere a\(E\) projeção de no\(xz\) plano -. Este é um disco circular\(x^2 + z^2 \leq 4\). Então, obtemos
\[\iiint_E \sqrt{x^2 + z^2} \,dV = \int_{x=-2}^{x=2} \int_{y=x^2}^{y=4} \int_{z=-\sqrt{y-x^2}}^{z=\sqrt{y-x^2}} \sqrt{x^2 + z^2} \,dz \, dy \, dx = \int_{x=-2}^{x=2} \int_{z=-\sqrt{4-x^2}}^{z=\sqrt{4-x^2}} \int_{y=x^2+z^2}^{y=4} \sqrt{x^2 + z^2} \,dy \, dz \, dx.\nonumber \]
Aqui, a ordem de integração muda de ser primeiro em relação a\(z\) então\(y\) e depois\(x\) para ser primeiro em relação a\(y\) depois para\(z\) e depois para\(x\). Em breve, ficará claro como essa mudança pode ser benéfica para a computação. Nós temos
\[\int_{x=-2}^{x=2} \int_{z=\sqrt{4-x^2}}^{z=\sqrt{4-x^2}} \int_{y=x^2+z^2}^{y=4} \sqrt{x^2 + z^2} \,dy \, dz \, dx = \int_{x=-2}^{x=2} \int_{z=-\sqrt{4-x^2}}^{z=\sqrt{4-x^2}} (4 - x^2 - z^2) \sqrt{x^2 + z^2} \,dz \, dx.\nonumber \]
Agora use a substituição\(x = r \, \cos \, \theta, \, z = r \, \sin \, \theta\) polar e\(dz \, dx = r \, dr \, d\theta\) no\(xz\) plano -. Isso é essencialmente o mesmo de quando usamos coordenadas polares no\(xy\) plano -, exceto que estamos substituindo\(y\) por\(z\). Consequentemente, os limites da integração mudam e temos, ao usar\(r^2 = x^2 + z^2\),
\[\int_{x=-2}^{x=2} \int_{z=-\sqrt{4-x^2}}^{z=\sqrt{4-x^2}} (4 - x^2 - z^2) \sqrt{x^2 + z^2}\,dz \, dx = \int_{\theta=0}^{\theta=2\pi} \int_{r=0}^{r=2} (4 - r^2) rr \, dr \, d\theta = \int_0^{2\pi} \left. \left[ \dfrac{4r^3}{3} - \dfrac{r^5}{5} \right|_0^2 \right] \, d\theta = \int_0^{2\pi} \dfrac{64}{15} \,d\theta = \dfrac{128\pi}{15}\nonumber \]
Valor médio de uma função de três variáveis
Lembre-se de que encontramos o valor médio de uma função de duas variáveis avaliando a integral dupla sobre uma região no plano e depois dividindo pela área da região. Da mesma forma, podemos encontrar o valor médio de uma função em três variáveis avaliando a integral tripla sobre uma região sólida e depois dividindo pelo volume do sólido.
Se\(f(x,y,z)\) for integrável em uma região limitada sólida\(E\) com volume positivo\(V \, (E),\), o valor médio da função é
\[f_{ave} = \dfrac{1}{V \, (E)} \iiint_E f(x,y,z) \, dV. \nonumber \]
Observe que o volume é
\[V \, (E) = \iiint_E 1 \,dV. \nonumber \]
A temperatura em um ponto\((x,y,z)\) de um sólido\(E\) limitado pelos planos de coordenadas e o plano\(x + y + z = 1\) é\(T(x,y,z) = (xy + 8z + 20) \, \text{°}\text{C} \). Encontre a temperatura média sobre o sólido.
Solução
Use o teorema dado acima e a integral tripla para encontrar o numerador e o denominador. Então faça a divisão. Observe que o avião\(x + y + z = 1\) tem interceptações\((1,0,0), \, (0,1,0),\)\((0,0,1)\) e. A região\(E\) parece
\[E = \big\{(x,y,z) \,|\, 0 \leq x \leq 1, \, 0 \leq y \leq 1 - x, \, 0 \leq z \leq 1 - x - y \big\}.\nonumber \]
Portanto, a integral tripla da temperatura é
\[\iiint_E f(x,y,z) \,dV = \int_{x=0}^{x=1} \int_{y=0}^{y=1-x} \int_{z=0}^{z=1-x-y} (xy + 8z + 20) \, dz \, dy \, dx = \dfrac{147}{40}. \nonumber \]
A avaliação do volume é
\[V \, (E) = \iiint_E 1\,dV = \int_{x=0}^{x=1} \int_{y=0}^{y=1-x} \int_{z=0}^{z=1-x-y} 1 \,dz \, dy \, dx = \dfrac{1}{6}. \nonumber \]
Portanto, o valor médio é
\[ T_{ave} = \dfrac{147/40}{1/6} = \dfrac{6(147)}{40} = \dfrac{441}{20} \, \text{°}\text{C} \nonumber \].
Encontre o valor médio da função\(f(x,y,z) = xyz\) sobre o cubo com lados de comprimento de 4 unidades no primeiro octante com um vértice na origem e bordas paralelas aos eixos coordenados.
- Dica
-
Siga as etapas no exemplo anterior.
- Responda
-
\(f_{ave} = 8\)
Conceitos-chave
- Para calcular uma integral tripla, usamos o teorema de Fubini, que afirma que se\(f(x,y,z)\) é contínuo em uma caixa retangular\(B = [a,b] \times [c,d] \times [e,f]\), então\[\iiint_B f(x,y,z) \,dV = \int_e^f \int_c^d \int_a^b f(x,y,z) \, dx \, dy \, dz \nonumber \] e também é igual a qualquer uma das outras cinco ordenações possíveis para a integral tripla iterada.
- Para calcular o volume de uma região limitada sólida geral,\(E\) usamos a integral tripla.\[V \, (E) = \iiint_E 1 \,dV. \nonumber \]
- A troca da ordem das integrais iteradas não altera a resposta. De fato, trocar a ordem de integração pode ajudar a simplificar a computação.
- Para calcular o valor médio de uma função sobre uma região tridimensional geral, usamos\[f_{ave} = \dfrac{1}{V \, (E)} \iiint_E f(x,y,z) \,dV. \nonumber \]
Equações-chave
- Integral triplo
\[\lim_{l,m,n \rightarrow \infty} \sum_{i=1}^l \sum_{j=1}^m \sum_{k=1}^n f(x_{ijk}^*, y_{ijk}^*, z_{ijk}^*) \,\Delta x \Delta y \Delta z = \iiint_B f(x,y,z) \,dV \nonumber \]
Glossário
- integral triplo
- a integral tripla de uma função contínua\(f(x,y,z)\) sobre uma caixa sólida retangular\(B\) é o limite de uma soma de Riemann para uma função de três variáveis, se esse limite existir



Integrais triplos em uma região delimitada geral
Agora expandimos a definição da integral tripla para calcular uma integral tripla sobre uma região limitada mais geral\(E\) em\(\mathbb{R}^3\). As regiões delimitadas gerais que consideraremos são de três tipos. Primeiro,\(D\) seja a região limitada que é uma\(E\) projeção\(xy\) de no plano. Suponha que a região\(E\) em\(\mathbb{R}^3\) tenha a forma
\[E = \big\{(x,y,z)\,|\,(x,y) \in D, u_1(x,y) \leq z \leq u_2(x,y) \big\}. \nonumber \]
Para duas funções\(z = u_1(x,y)\) e\(u_2(x,y)\), de forma que\(u_1(x,y) \leq u_2(x,y)\) para todos\((x,y)\),\(D\) conforme mostrado na figura a seguir.