Skip to main content
Global

15.3E: Exercícios para a Seção 15.3

  1. Last updated
  2. Save as PDF
  • Page ID
    188141

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Termos e conceitos

    1. Ao avaliar\(\displaystyle \int\int_R f(x,y)\,dA\) usando coordenadas polares,\(f(x,y)\) é substituído por _______ e\(dA\) é substituído por _______.

    Responda
    \(f(x,y)\)é substituído por \(f(r\cos \theta, r\sin\theta)\)e\(dA\) é substituído por \(r\,dr\,d\theta\).

    2. Por que alguém estaria interessado em avaliar uma integral dupla com coordenadas polares?

    Definindo regiões polares

    Nos exercícios 3 a 6, expresse a região\(R\) em coordenadas polares.

    3)\(R\) é a região do disco de raio 2 centrada na origem que está no primeiro quadrante.

    Responda
    \(R = \big\{(r, \theta)\,|\,0 \leq r \leq 2, \space 0 \leq \theta \leq \frac{\pi}{2}\big\}\)

    4)\(R\) é a região do disco de raio 3 centrada na origem.

    5)\(R\) é a região entre os círculos do raio 4 e do raio 5 centrada na origem que está no segundo quadrante.

    Responda
    \(R = \big\{(r, \theta)\,|\,4 \leq r \leq 5, \space \frac{\pi}{2} \leq \theta \leq \pi\big\}\)

    6)\(R\) é a região delimitada pelo\(y\) eixo\(x = \sqrt{1 - y^2}\) -e.

    7)\(R\) é a região delimitada pelo\(x\) eixo\(y = \sqrt{2 - x^2}\) -e.

    Responda
    \(R = \big\{(r, \theta)\,|\,0 \leq r \leq \sqrt{2}, \space 0 \leq \theta \leq \pi\big\}\)

    8)\(R = \big\{(x,y)\,|\,x^2 + y^2 \leq 4x\big\}\)

    9)\(R = \big\{(x,y)\,|\,x^2 + y^2 \leq 4y\big\}\)

    Responda
    \(R = \big\{(r, \theta)\,|\,0 \leq r \leq 4 \space \sin \theta, \space 0 \leq \theta \leq \pi\big\}\)

    Nos exercícios 10 a 15, o gráfico da região retangular polar\(D\) é fornecido. Expresse\(D\) em coordenadas polares.

    10)
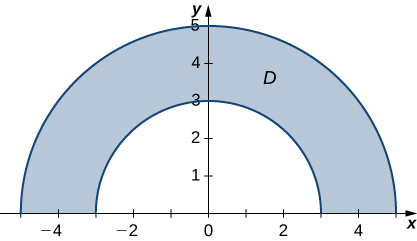
    Meio anel D é desenhado no primeiro e segundo quadrantes com raio interno 3 e raio externo 5.
    11)
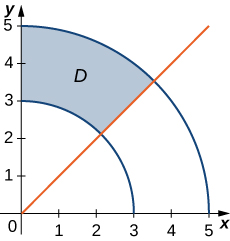
    Um setor de um anel D é traçado entre teta = pi/4 e teta = pi/2 com raio interno 3 e raio externo 5.
    Responda
    \(D = \big\{(r, \theta)\,|\, 3 \leq r \leq 5, \space \frac{\pi}{4} \leq \theta \leq \frac{\pi}{2}\big\}\)

    12)

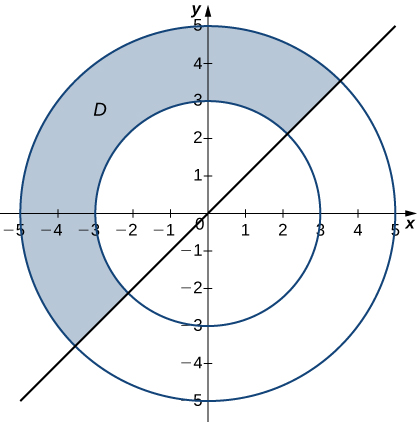
    Half of an annulus D is drawn between theta = pi/4 and theta = 5 pi/4 with inner radius 3 and outer radius 5.

    13)
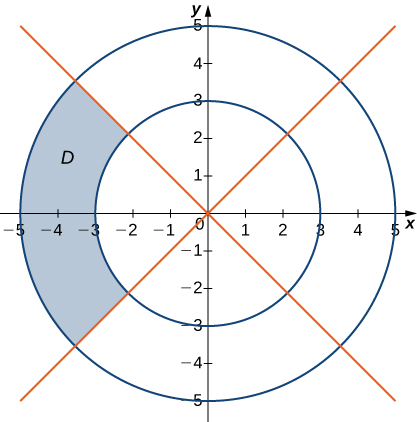
    Um setor de um anel D é traçado entre teta = 3 pi/4 e teta = 5 pi/4 com raio interno 3 e raio externo 5.

    Responda
    \(D = \big\{(r, \theta)\,|\,3 \leq r \leq 5, \space \frac{3\pi}{4} \leq \theta \leq \frac{5\pi}{4}\big\}\)
    14) In the following graph, the region \(D\) is situated below \(y = x\) and is bounded by \(x = 1, \space x = 5\), and \(y = 0\).

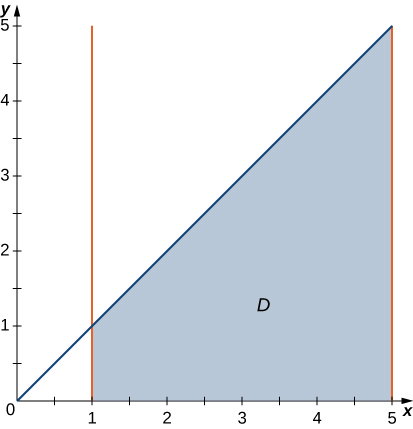
    A region D is given that is bounded by y = 0, x = 1, x = 5, and y = x, that is, a right triangle with a corner cut off.

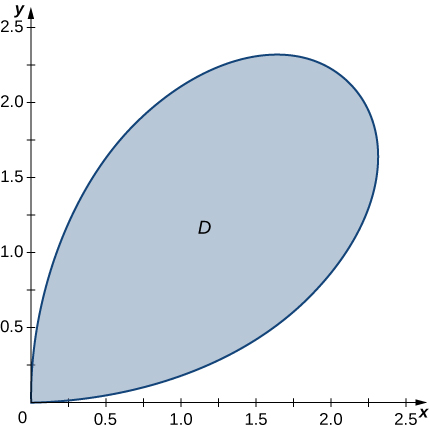
    15) No gráfico a seguir, a região\(D\) é delimitada por\(y = x\)\(y = x^2\) e.

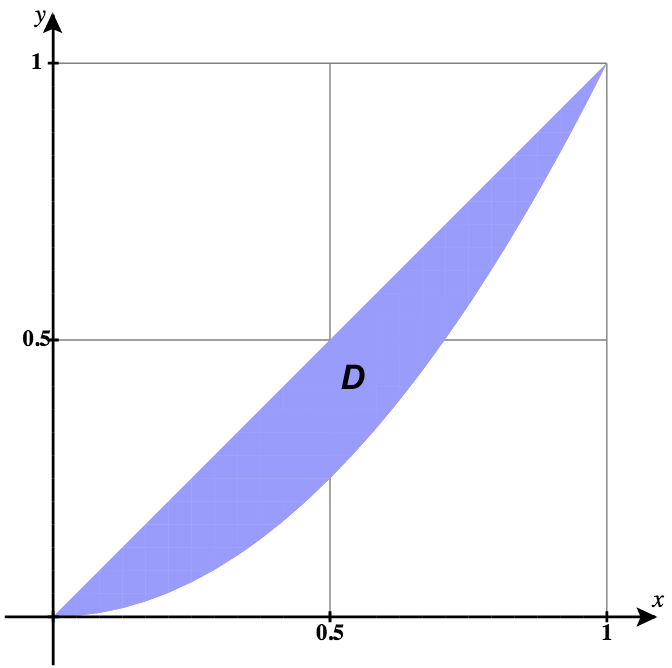
    Uma região D é desenhada entre y = x e y = x ao quadrado, que parece uma lente deformada, com a parte bulbosa abaixo da parte reta.

    Responda
    \(D = \big\{(r, \theta)\,|\,0 \leq r \leq \tan \theta \space \sec \theta, \space 0 \leq \theta \leq \frac{\pi}{4}\big\}\)

    Evaluating Polar Double Integrals

    In exercises 16 - 25, evaluate the double integral \(\displaystyle \iint_R f(x,y) \,dA\) over the polar rectangular region \(R\).

    16) \(f(x,y) = x^2 + y^2\), \(R = \big\{(r, \theta)\,|\,3 \leq r \leq 5, \space 0 \leq \theta \leq 2\pi\big\}\)

    17) \(f(x,y) = x + y\), \(R = \big\{(r, \theta)\,|\,3 \leq r \leq 5, \space 0 \leq \theta \leq 2\pi\big\}\)

    Answer
    \(0\)

    18) \(f(x,y) = x^2 + xy, \space R = \big\{(r, \theta )\,|\,1 \leq r \leq 2, \space \pi \leq \theta \leq 2\pi\big\}\)

    19) \(f(x,y) = x^4 + y^4, \space R = \big\{(r, \theta)\,|\,1 \leq r \leq 2, \space \frac{3\pi}{2} \leq \theta \leq 2\pi\big\}\)

    Answer
    \(\frac{63\pi}{16}\)

    20) \(f(x,y) = \sqrt[3]{x^2 + y^2}\), where \(R = \big\{(r, \theta)\,|\,0 \leq r \leq 1, \space \frac{\pi}{2} \leq \theta \leq \pi\big\}\).

    21) \(f(x,y) = x^4 + 2x^2y^2 + y^4\), where \(R = \big\{(r,\theta)\,|\,3 \leq r \leq 4, \space \frac{\pi}{3} \leq \theta \leq \frac{2\pi}{3}\big\}\).

    Answer
    \(\frac{3367\pi}{18}\)

    22) \(f(x,y) = \sin (\arctan \frac{y}{x})\), where \(R = \big\{(r, \theta)\,|\,1 \leq r \leq 2, \space \frac{\pi}{6} \leq \theta \leq \frac{\pi}{3}\big\}\)

    23) \(f(x,y) = \arctan \left(\frac{y}{x}\right)\), where \(R = \big\{(r, \theta)\,|\,2 \leq r \leq 3, \space \frac{\pi}{4} \leq \theta \leq \frac{\pi}{3}\big\}\)

    Answer
    \(\frac{35\pi^2}{576}\)

    24) \(\displaystyle \iint_R e^{x^2+y^2} \left[1 + 2 \space \arctan \left(\frac{y}{x}\right)\right] \,dA, \space R = \big\{(r,\theta)\,|\,1 \leq r \leq 2, \space \frac{\pi}{6} \leq \theta \frac{\pi}{3}\big\}\)

    25) \(\displaystyle \iint_R \left(e^{x^2+y^2} + x^4 + 2x^2y^2 + y^4 \right) \arctan \left(\frac{y}{x}\right) \,dA, \space R = \big\{(r, \theta )\,|\,1 \leq r \leq 2, \space \frac{\pi}{4} \leq \theta \leq \frac{\pi}{3}\big\}\)

    Answer
    \(\frac{7}{576}\pi^2 (21 - e + e^4)\)

    Converting Double Integrals to Polar Form

    In exercises 26 - 29, the integrals have been converted to polar coordinates. Verify that the identities are true and choose the easiest way to evaluate the integrals, in rectangular or polar coordinates.

    26) \(\displaystyle \int_1^2 \int_0^x (x^2 + y^2)\,dy \space dx = \int_0^{\frac{\pi}{4}} \int_{\sec \theta}^{2 \space \sec \theta}r^3 \,dr \space d\theta\)

    27) \(\displaystyle \int_2^3 \int_0^x \frac{x}{\sqrt{x^2 + y^2}}\,dy \space dx = \int_0^{\pi/4} \int_{2\sec\theta}^{3\sec \theta} \,r \space \cos \theta \space dr \space d\theta\)

    Answer
    \(\frac{5}{2} \ln (1 + \sqrt{2})\)

    28) \(\displaystyle \int_0^1 \int_{x^2}^x \frac{1}{\sqrt{x^2 + y^2}}\,dy \space dx = \int_0^{\pi/4} \displaystyle \int_0^{\tan \theta \space \sec \theta} \space dr \space d\theta\)

    29) \(\displaystyle \int_0^1 \int_{x^2}^x \frac{y}{\sqrt{x^2 + y^2}}\,dy \space dx = \int_0^{\pi/4} \displaystyle \int_0^{\tan \theta \space \sec \theta} \,r \space \sin \theta \space dr \space d\theta\)

    Answer
    \(\frac{1}{6}(2 - \sqrt{2})\)

    In exercises 30 - 37, draw the region of integration, \(R\), labeling all limits of integration, convert the integrals to polar coordinates and evaluate them.

    30) \(\displaystyle \int_0^3 \int_0^{\sqrt{9-y^2}}\left(x^2 + y^2\right)\,dx \space dy\)

    31) \(\displaystyle \int_0^2 \int_{-\sqrt{4-y^2}}^{\sqrt{4-y^2}}\left(x^2 + y^2\right)^2\,dx \space dy\)

    Answer
    \(\displaystyle \int_0^{\pi} \int_0^2 r^5 \,dr \space d\theta \quad = \quad \frac{32\pi}{3}\)

    32) \(\displaystyle \int_0^1 \int_0^{\sqrt{1-x^2}} (x + y) \space dy \space dx\)

    33) \(\displaystyle \int_0^4 \int_{-\sqrt{16-x^2}}^{\sqrt{16-x^2}} \sin (x^2 + y^2) \space dy \space dx\)

    Answer
    \(\displaystyle \int_{-\pi/2}^{\pi/2} \int_0^4 \,r \space \sin (r^2) \space dr \space d\theta \quad = \quad \pi \space \sin^2 8\)

    34) \(\displaystyle \int_0^5 \int_{-\sqrt{25-x^2}}^{\sqrt{25-x^2}}\sqrt{x^2+y^2}\,dy\,dx\)

    35) \(\displaystyle \int_{-4}^4 \int_{-\sqrt{16-y^2}}^{0}(2y-x)\,dx\,dy\)

    Answer
    \(\displaystyle \int_{\frac{\pi}{2}}^{\frac{3\pi}{2}} \int_0^{4} \big( 2r\sin \theta - r\cos\theta\big) \,r\,dr \space d\theta \quad = \quad \frac{128}{3}\)

    36) \(\displaystyle \int_0^2 \int_{y}^{\sqrt{8-y^2}}(x+y)\,dx\,dy\)

    37) \(\displaystyle \int_{-2}^{-1} \int_{0}^{\sqrt{4-x^2}}(x+5)\,dy\,dx+\int_{-1}^1\int_{\sqrt{1-x^2}}^{\sqrt{4-x^2}}(x+5)\,dy\,dx+\int_1^2\int_0^{\sqrt{4-x^2}}(x+5)\,dy\,dx\)

    Answer
    \(\displaystyle \int_{0}^{\pi} \int_1^{2} \big( r\cos \theta + 5\big) \,r\,dr \space d\theta \quad = \quad \frac{15\pi}{2}\)

    38) Evaluate the integral \(\displaystyle \iint_D r \,dA\) where \(D\) is the region bounded by the polar axis and the upper half of the cardioid \(r = 1 + \cos \theta\).

    39) Find the area of the region \(D\) bounded by the polar axis and the upper half of the cardioid \(r = 1 + \cos \theta\).

    Answer
    \(\frac{3\pi}{4}\)

    40) Evaluate the integral \(\displaystyle \iint_D r \,dA,\) where \(D\) is the region bounded by the part of the four-leaved rose \(r = \sin 2\theta\) situated in the first quadrant (see the following figure).

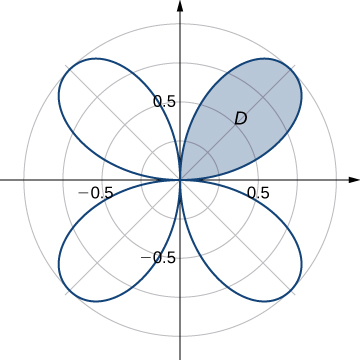
    A region D is drawn in the first quadrant petal of the four petal rose given by r = sin (2 theta).

    41) Encontre a área total da região cercada pela rosa de quatro folhas\(r = \sin 2\theta\) (veja a figura no exercício anterior).

    Responda
    \(\frac{\pi}{2}\)

    42) Encontre a área da região\(D\) que é a região delimitada por\(y = \sqrt{4 - x^2}\)\(x = \sqrt{3}\)\(x = 2\),,\(y = 0\) e.

    43) Encontre a área da região\(D\), que é a região dentro do disco\(x^2 + y^2 \leq 4\) e à direita da linha\(x = 1\).

    Responda
    \(\frac{1}{3}(4\pi - 3\sqrt{3})\)

    44) Determine o valor médio da função\(f(x,y) = x^2 + y^2\) sobre a região\(D\) delimitada pela curva polar\(r = \cos 2\theta\), onde\(-\frac{\pi}{4} \leq \theta \leq \frac{\pi}{4}\) (veja o gráfico a seguir).

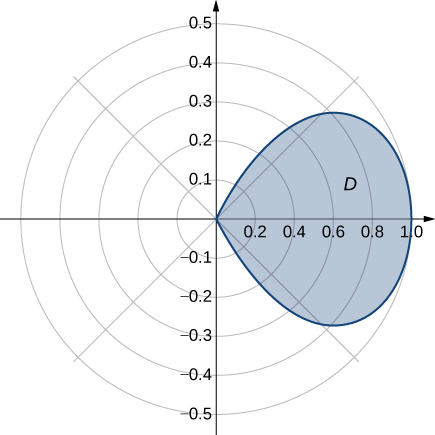
    A pétala do primeiro/quarto quadrante da rosa de quatro pétalas dada por r = cos (2 teta) é mostrada.

    45) Determine o valor médio da função\(f(x,y) = \sqrt{x^2 + y^2}\) over the region \(D\) bounded by the polar curve \(r = 3\sin 2\theta\), where \(0 \leq \theta \leq \frac{\pi}{2}\) (see the following graph).

    The first-quadrant petal of the four-petal rose given by r = 3sin (2 theta) is shown.

    Responda
    \(\frac{16}{3\pi}\)

    46) Encontre o volume do sólido situado no primeiro octante e limitado pelo parabolóide\(z = 1 - 4x^2 - 4y^2\) e pelos planos\(x = 0, \space y = 0\),\(z = 0\) e.

    47) Encontre o volume do sólido delimitado pelo parabolóide\(z = 2 - 9x^2 - 9y^2\) e pelo plano\(z = 1\).

    Responda
    \(\frac{\pi}{18}\)

    48)

    1. Encontre o volume do sólido\(S_1\) delimitado pelo cilindro\(x^2 + y^2 = 1\) e pelos planos\(z = 0\)\(z = 1\) e.
    2. Encontre o volume do sólido\(S_2\) fora do cone duplo\(z^2 = x^2 + y^2\) dentro do cilindro\(x^2 + y^2 = 1\) e acima do plano\(z = 0\).
    3. Encontre o volume do sólido dentro do cone\(z^2 = x^2 + y^2\) e abaixo do plano\(z = 1\) subtraindo os volumes dos sólidos\(S_1\)\(S_2\) e.

    49)

    1. Encontre o volume do sólido\(S_1\) dentro da esfera unitária\(x^2 + y^2 + z^2 = 1\) e acima do plano\(z = 0\).
    2. Encontre o volume do sólido\(S_2\) dentro do cone duplo\((z - 1)^2 = x^2 + y^2\) e acima do plano\(z = 0\).
    3. Encontre o volume do sólido fora do cone duplo\((z - 1)^2 = x^2 + y^2\) e dentro da esfera\(x^2 + y^2 + z^2 = 1\).
    Responda
    a.\(\frac{2\pi}{3}\); b.\(\frac{\pi}{2}\); c.\(\frac{\pi}{6}\)

    Nos exercícios 50-51, são apresentadas integrais duplas especiais que são especialmente adequadas para avaliação em coordenadas polares.

    50) A superfície de um cone circular reto com altura\(h\) e raio base\(a\) pode ser descrita pela equação\(f(x,y)=h-h\sqrt{\frac{x^2}{a^2}+\frac{y^2}{a^2}}\), onde a ponta do cone está\((0,0,h)\) e a base circular está no\(xy\) plano -, centrada na origem.
    Confirme se o volume de um cone circular reto com altura\(h\) e raio base\(a\) é\(V=\frac{1}{3}\pi a^2h\) avaliado\(\displaystyle \int\int_R f(x,y)\,dA\) em coordenadas polares.

    51) Considere\(\displaystyle \int\int_R e^{-(x^2+y^2)}\,dA.\)
    (a) Por que essa integral é difícil de avaliar em coordenadas retangulares, independentemente da região\(R\)?
    (b)\(R\) Seja a região delimitada pelo círculo de raio\(a\) centrado na origem. Avalie a integral dupla usando coordenadas polares.
    (c) Pegue o limite de sua resposta de (b), como\(a\to \infty\). O que isso implica sobre o volume sob a superfície\(xy\) de\(e^{-(x^2+y^2)}\) todo o plano?

    Para os dois exercícios a seguir, considere um anel esférico, que é uma esfera com um orifício cilíndrico cortado de forma que o eixo do cilindro passe pelo centro da esfera (veja a figura a seguir).

    É mostrado um anel esférico, ou seja, uma esfera com um orifício cilíndrico passando por ele.

    52) Se a esfera tiver raio 4 e o cilindro tiver raio 2, encontre o volume do anel esférico.

    53) Um furo cilíndrico de 6 cm de diâmetro é perfurado através de uma esfera de raio de 5 cm, de forma que o eixo do cilindro passe pelo centro da esfera. Encontre o volume do anel esférico resultante.

    Responda
    \(\frac{256\pi}{3} \space \text{cm}^3\)

    54) Find the volume of the solid that lies under the double cone \(z^2 = 4x^2 + 4y^2\), inside the cylinder \(x^2 + y^2 = x\), and above the plane \(z = 0\).

    55) Find the volume of the solid that lies under the paraboloid \(z = x^2 + y^2\), inside the cylinder \(x^2 + y^2 = 1\) and above the plane \(z = 0\).

    Answer
    \(\frac{3\pi}{32}\)

    56) Find the volume of the solid that lies under the plane \(x + y + z = 10\) and above the disk \(x^2 + y^2 = 4x\).

    57) Find the volume of the solid that lies under the plane \(2x + y + 2z = 8\) and above the unit disk \(x^2 + y^2 = 1\).

    Answer
    \(4\pi\)

    58) A radial function \(f\) is a function whose value at each point depends only on the distance between that point and the origin of the system of coordinates; that is, \(f (x,y) = g(r)\), where \(r = \sqrt{x^2 + y^2}\). Show that if \(f\) is a continuous radial function, then

    \[\iint_D f(x,y)dA = (\theta_2 - \theta_1) [G(R_2) - G(R_1)], \space where \space G'(r) = rg(r) \nonumber \] and \((x,y) \in D = \big\{(r, \theta)\,|\,R_1 \leq r \leq R_2, \space 0 \leq \theta \leq 2\pi\big\}\), with \(0 \leq R_1 < R_2\) and \(0 \leq \theta_1 < \theta_2 \leq 2\pi\).

    59) Use the information from the preceding exercise to calculate the integral \(\displaystyle \iint_D (x^2 + y^2)^3 dA,\) where \(D\) is the unit disk.

    Answer
    \(\frac{\pi}{4}\)

    60) Let \(f(x,y) = \dfrac{F'(r)}{r}\) be a continuous radial function defined on the annular region \(D = \big\{(r,\theta)\,|\,R_1 \leq r \leq R_2, \space 0 \leq \theta \leq 2\pi\big\}\), where \(r = \sqrt{x^2 + y^2}\), \(0 < R_1 < R_2\), and \(F\) is a differentiable function.

    Show that \(\displaystyle \iint_D f(x,y)\,dA = 2\pi [F(R_2) - F(R_1)].\)

    61) Apply the preceding exercise to calculate the integral \(\displaystyle \iint_D \frac{e^{\sqrt{x^2+y^2}}}{\sqrt{x^2 + y^2}} \,dx \space dy\) where \(D\) is the annular region between the circles of radii 1 and 2 situated in the third quadrant.

    Answer
    \(\frac{1}{2} \pi e(e - 1)\)

    62) Let \(f\) be a continuous function that can be expressed in polar coordinates as a function of \(\theta\) only; that is, \(f(x,y) = h(\theta)\), where \((x,y) \in D = \big\{(r, \theta)\,|\,R_1 \leq r \leq R_2, \space \theta_1 \leq \theta \leq \theta_2\big\}\), with \(0 \leq R_1 < R_2\) and \(0 \leq \theta_1 < \theta_2 \leq 2\pi\).

    Show that \(\displaystyle \iint_D f(x,y) \,dA = \frac{1}{2} (R_2^2 - R_1^2) [H(\theta_2) - H(\theta_1)]\), where \(H\) is an antiderivative of \(h\).

    63) Apply the preceding exercise to calculate the integral \(\displaystyle \iint_D \frac{y^2}{x^2}\,dA,\) where \(D = \big\{(r, \theta)\,|\, 1 \leq r \leq 2, \space \frac{\pi}{6} \leq \theta \leq \frac{\pi}{3}\big\}.\)

    Answer
    \(\sqrt{3} - \frac{\pi}{4}\)

    64) Let \(f\) be a continuous function that can be expressed in polar coordinates as a function of \(\theta\) only; that is \(f(x,y) = g(r)h(\theta)\), where \((x,y) \in \big\{(r, \theta )\,|\,R_1 \leq r \leq R_2, \space \theta_1 \leq \theta \leq \theta_2\big\}\) with \(0 \leq R_1 < R_2\) and \(0 \leq \theta_1 < \theta_2 \leq 2\pi\). Show that \[\iint_D f(x,y)\,dA = [G(R_2) - G(R_1)] \space [H(\theta_2) - H(\theta_1)], \nonumber \] where \(G\) and \(H\) are antiderivatives of \(g\) and \(h\), respectively.

    65) Evaluate \(\displaystyle \iint_D \arctan \left(\frac{y}{x}\right) \sqrt{x^2 + y^2}\,dA,\) where \(D = \big\{(r,\theta)\,|\, 2 \leq r \leq 3, \space \frac{\pi}{4} \leq \theta \leq \frac{\pi}{3}\big\}\).

    Answer
    \(\frac{133}{864}\pi^2\)

    66) A spherical cap is the region of a sphere that lies above or below a given plane.

    a. Show that the volume of the spherical cap in the figure below is \(\frac{1}{6} \pi h (3a^2 + h^2)\).

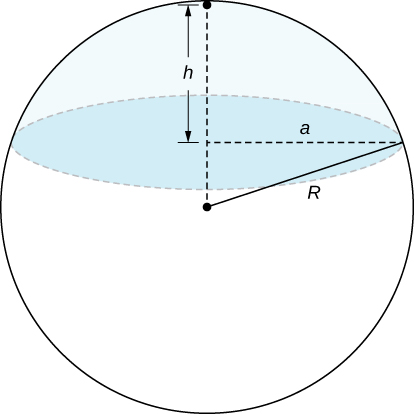
    A sphere of radius R has a circle inside of it h units from the top of the sphere. This circle has radius a, which is less than R.

    b. Um segmento esférico é o sólido definido pela interseção de uma esfera com dois planos paralelos. Se a distância entre os planos for\(h\) mostrada, o volume do segmento esférico na figura abaixo é\(\frac{1}{6}\pi h (3a^2 + 3b^2 + h^2)\).

    b." data-type="media" id="fs-id1167793495515">Uma esfera tem dois círculos paralelos dentro dela com h unidades de distância. O círculo superior tem raio b e o círculo inferior tem raio a. Observe que a b." src="https://math.libretexts.org/@api/dek...15_03_212.jpeg">

    67) Em estatística, a densidade conjunta para dois eventos independentes, normalmente distribuídos, com uma média

    • Template:ContribOpenStaxCalc
    • Problems 1, 2, 34 - 37 and 50 - 51 are from Apex Calculus, Chapter 13.3
    • Edited by Paul Seeburger (Monroe Community College)