15.3: Integrais duplos em coordenadas polares
- Page ID
- 188126
- Reconheça o formato de uma integral dupla sobre uma região retangular polar.
- Calcule uma integral dupla em coordenadas polares usando uma integral iterada.
- Reconheça o formato de uma integral dupla sobre uma região polar geral.
- Use integrais duplos em coordenadas polares para calcular áreas e volumes.
Às vezes, integrais duplos são muito mais fáceis de avaliar se mudarmos as coordenadas retangulares para coordenadas polares. No entanto, antes de descrevermos como fazer essa mudança, precisamos estabelecer o conceito de uma integral dupla em uma região retangular polar.
Regiões polares retangulares de integração
Quando definimos a integral dupla para uma função contínua em coordenadas retangulares — digamos,\(g\) sobre uma região\(R\) no\(xy\) plano\(R\) -—dividimos em sub-retângulos com lados paralelos aos eixos coordenados. Esses lados têm\(x\) valores constantes e/ou\(y\) valores constantes. Nas coordenadas polares, a forma com a qual trabalhamos é um retângulo polar, cujos lados têm\(r\) valores constantes e/ou\(\theta\) valores constantes. Isso significa que podemos descrever um retângulo polar como na Figura\(\PageIndex{1a}\), com\(R = \{(r,\theta)\,|\, a \leq r \leq b, \, \alpha \leq \theta \leq \beta\}\).
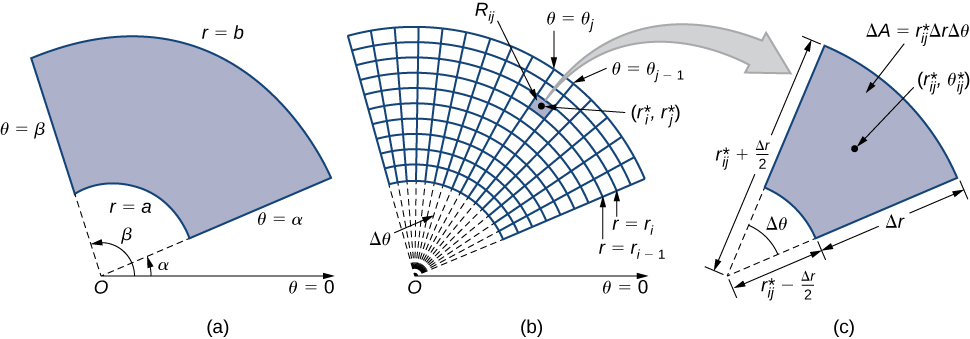
Nesta seção, estamos procurando integrar mais de retângulos polares. Considere uma função\(f(r,\theta)\) sobre um retângulo polar\(R\). Dividimos o intervalo\([a,b]\) em\(m\) subintervalos\([r_{i-1}, r_i]\) de comprimento\(\Delta r = (b - a)/m\) e dividimos o intervalo\([\alpha, \beta]\) em\(n\) subintervalos\([\theta_{i-1}, \theta_i]\) de largura\(\Delta \theta = (\beta - \alpha)/n\). Isso significa que os círculos\(r = r_i\) e\(\theta = \theta_i\) os raios formam\(1 \leq i \leq m\) e\(1 \leq j \leq n\) dividem o retângulo polar\(R\) em subretângulos polares menores\(R_{ij}\) (Figura\(\PageIndex{1b}\)).
Como antes, precisamos encontrar a área\(\Delta A\) do sub-retângulo polar\(R_{ij}\) e o volume “polar” da caixa fina acima\(R_{ij}\). Lembre-se de que, em um círculo de raio,\(r\) o comprimento\(s\) de um arco subtendido por um ângulo central de\(\theta\) radianos é\(s = r\theta\). Observe que o retângulo polar\(R_{ij}\) se parece muito com um trapézio com lados paralelos\(r_{i-1}\Delta \theta\)\(r_i\Delta \theta\) e com uma largura\(\Delta r\). Portanto, a área do sub-retângulo polar\(R_{ij}\) é
\[\Delta A = \frac{1}{2} \Delta r (r_{i-1} \Delta \theta + r_i \Delta \theta ). \nonumber \]
Simplificando e deixando
\[r_{ij}^* = \frac{1}{2}(r_{i-1}+r_i) \nonumber \]
nós temos\(\Delta A = r_{ij}^* \Delta r \Delta \theta\).
Portanto, o volume polar da caixa fina acima\(R_{ij}\) (Figura\(\PageIndex{2}\)) é
\[f(r_{ij}^*, \theta_{ij}^*) \Delta A = f(r_{ij}^*, \theta_{ij}^*)r_{ij}^* \Delta r \Delta \theta. \nonumber \]
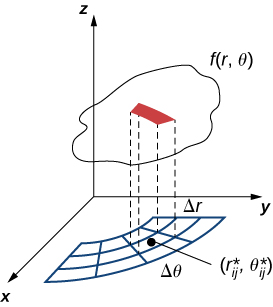
Usando a mesma ideia para todos os sub-retângulos e somando os volumes das caixas retangulares, obtemos uma soma dupla de Riemann como
\[\sum_{i=1}^m \sum_{j=1}^n f(r_{ij}^*, \theta_{ij}^*) r_{ij}^* \Delta r \Delta \theta. \nonumber \]
Como vimos antes, obtemos uma melhor aproximação do volume polar do sólido acima da região\(R\) quando deixamos\(m\) e nos\(n\) tornamos maiores. Portanto, definimos o volume polar como o limite da soma dupla de Riemann,
\[V = \lim_{m,n\rightarrow\infty}\sum_{i=1}^m \sum_{j=1}^n f(r_{ij}^*, \theta_{ij}^*) r_{ij}^* \Delta r \Delta \theta. \nonumber \]
Isso se torna a expressão da integral dupla.
A integral dupla da função\(f(r, \theta)\) sobre a região retangular polar\(R\) no\(r\theta\) plano -é definida como
\[\begin{align} \iint_R f(r, \theta)dA &= \lim_{m,n\rightarrow\infty}\sum_{i=1}^m \sum_{j=1}^n f(r_{ij}^*, \theta_{ij}^*) \Delta A \\[4pt] &= \lim_{m,n\rightarrow \infty} \sum_{i=1}^m \sum_{j=1}^n f(r_{ij}^*,\theta_{ij}^*)r_{ij}^* \Delta r \Delta \theta. \end{align} \nonumber \]
Novamente, assim como na seção sobre Integrais Duplas sobre Regiões Retangulares, a integral dupla sobre uma região retangular polar pode ser expressa como uma integral iterada em coordenadas polares. Conseqüentemente,
\[\iint_R f(r, \theta)\,dA = \iint_R f(r, \theta) \,r \, dr \, d\theta = \int_{\theta=\alpha}^{\theta=\beta} \int_{r=a}^{r=b} f(r,\theta) \,r \, dr \, d\theta. \nonumber \]
Observe que a expressão for\(dA\) é substituída por\(r \, dr \, d\theta\) quando se trabalha em coordenadas polares. Outra forma de observar a integral dupla polar é alterar a integral dupla em coordenadas retangulares por substituição. Quando a função\(f\) é dada em termos de\(x\) e\(y\) uso\(x = r \, \cos \, \theta, \, y = r \, \sin \, \theta\), e a\(dA = r \, dr \, d\theta\) altera para
\[\iint_R f(x,y) \,dA = \iint_R f(r \, \cos \, \theta, \, r \, \sin \, \theta ) \,r \, dr \, d\theta. \nonumber \]
Observe que todas as propriedades listadas na seção Integrais duplas sobre regiões retangulares para a integral dupla em coordenadas retangulares também são válidas para a integral dupla em coordenadas polares, então podemos usá-las sem hesitar.
Desenhe a região retangular polar
\[R = \{(r, \theta)\,|\,1 \leq r \leq 3, 0 \leq \theta \leq \pi \}. \nonumber \]
Solução
Como podemos ver na Figura\(\PageIndex{3}\),\(r = 1\) e\(r = 3\) são círculos de raio 1 e 3 e\(0 \leq \theta \leq \pi\) cobrem toda a metade superior do plano. Portanto, a região\(R\) parece uma faixa semicircular.
Agora que esboçamos uma região retangular polar, vamos demonstrar como calcular uma integral dupla sobre essa região usando coordenadas polares.
Avalie\(\displaystyle \iint_R 3x \, dA\) a integral na região\(R = \{(r, \theta)\,|\,1 \leq r \leq 2, \, 0 \leq \theta \leq \pi \}.\)
Solução
Primeiro, esboçamos uma figura semelhante à Figura\(\PageIndex{3}\), mas com raio externo\(r=2\). A partir da figura, podemos ver que temos
\[\begin{align*} \iint_R 3x \, dA &= \int_{\theta=0}^{\theta=\pi} \int_{r=1}^{r=2} 3r \, \cos \, \theta \,r \, dr \, d\theta \quad\text{Use an integral with correct limits of integration.} \\ &= \int_{\theta=0}^{\theta=\pi} \cos \, \theta \left[\left. r^3\right|_{r=1}^{r=2}\right] d\theta \quad\text{Integrate first with respect to $r$.} \\ &=\int_{\theta=0}^{\theta=\pi} 7 \, \cos \, \theta \, d\theta \\ &= 7 \, \sin \, \theta \bigg|_{\theta=0}^{\theta=\pi} = 0. \end{align*}\]
Esboce a região\(D = \{ (r,\theta) \vert 1\leq r \leq 2, \, -\frac{\pi}{2} \leq \theta \leq \frac{\pi}{2} \}\) e avalie\(\displaystyle \iint_R x \, dA\).
- Dica
-
Siga as etapas em Exemplo\(\PageIndex{1A}\).
- Resposta
-
\(\frac{14}{3}\)
Avalie a integral
\[\iint_R (1 - x^2 - y^2) \,dA \nonumber \]
onde\(R\) está o círculo unitário no\(xy\) plano -.
Solução
A região\(R\) é um círculo unitário, então podemos descrevê-la como\(R = \{(r, \theta )\,|\,0 \leq r \leq 1, \, 0 \leq \theta \leq 2\pi \}\).
Usando a conversão\(x = r \, \cos \, \theta, \, y = r \, \sin \, \theta\), e\(dA = r \, dr \, d\theta\), temos
\[\begin{align*} \iint_R (1 - x^2 - y^2) \,dA &= \int_0^{2\pi} \int_0^1 (1 - r^2) \,r \, dr \, d\theta \\[4pt] &= \int_0^{2\pi} \int_0^1 (r - r^3) \,dr \, d\theta \\ &= \int_0^{2\pi} \left[\frac{r^2}{2} - \frac{r^4}{4}\right]_0^1 \,d\theta \\&= \int_0^{2\pi} \frac{1}{4}\,d\theta = \frac{\pi}{2}. \end{align*}\]
Avalie a integral\[\displaystyle \iint_R (x + y) \,dA \nonumber \] onde\(R = \big\{(x,y)\,|\,1 \leq x^2 + y^2 \leq 4, \, x \leq 0 \big\}.\)
Solução
Podemos ver que\(R\) é uma região anular que pode ser convertida em coordenadas polares e descrita como\(R = \left\{(r, \theta)\,|\,1 \leq r \leq 2, \, \frac{\pi}{2} \leq \theta \leq \frac{3\pi}{2} \right\}\) (veja o gráfico a seguir).

Portanto, usando a conversão\(x = r \, \cos \, \theta, \, y = r \, \sin \, \theta\), e\(dA = r \, dr \, d\theta\), temos
\[\begin{align*} \iint_R (x + y)\,dA &= \int_{\theta=\pi/2}^{\theta=3\pi/2} \int_{r=1}^{r=2} (r \, \cos \, \theta + r \, \sin \, \theta) r \, dr \, d\theta \\ &= \left(\int_{r=1}^{r=2} r^2 \, dr\right)\left(\int_{\pi/2}^{3\pi/2} (\cos \, \theta + \sin \, \theta)\,d\theta\right) \\ &= \left. \left[\frac{r^3}{3}\right]_1^2 [\sin \, \theta - \cos \, \theta] \right|_{\pi/2}^{3\pi/2} \\ &= - \frac{14}{3}. \end{align*}\]
Avalie a integral\[ \displaystyle \iint_R (4 - x^2 - y^2)\,dA \nonumber \] onde\(R\) está o círculo do raio 2 no\(xy\) plano.
- Dica
-
Siga as etapas no exemplo anterior.
- Resposta
-
\(8\pi\)
Regiões polares gerais de integração
Para avaliar a integral dupla de uma função contínua por integrais iteradas sobre regiões polares gerais, consideramos dois tipos de regiões, análogas às do Tipo I e do Tipo II, conforme discutido para coordenadas retangulares na seção sobre Integrais Duplas sobre Regiões Gerais. É mais comum escrever equações polares como\(r = f(\theta)\)\(\theta = f(r)\), então descrevemos uma região polar geral como\(R = \{(r, \theta)\,|\,\alpha \leq \theta \leq \beta, \, h_1 (\theta) \leq r \leq h_2(\theta)\}\) (Figura\(\PageIndex{5}\)).
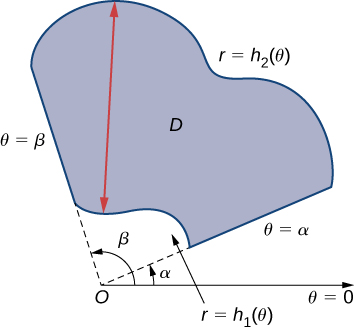
Se\(f(r, \theta)\) for contínuo em uma região polar geral,\(D\) conforme descrito acima, então
\[\iint_D f(r, \theta ) \,r \, dr \, d\theta = \int_{\theta=\alpha}^{\theta=\beta} \int_{r=h_1(\theta)}^{r=h_2(\theta)} f(r,\theta) \, r \, dr \, d\theta. \nonumber \]
Avalie a integral
\[\iint_D r^2 \sin \theta \, r \, dr \, d\theta \nonumber \]
onde\(D\) está a região delimitada pelo eixo polar e pela metade superior do cardióide\(r = 1 + \cos \, \theta\).
Solução
Podemos descrever a região\(D\)\(\{(r, \theta)\,|\,0 \leq \theta \leq \pi, \, 0 \leq r \leq 1 + \cos \, \theta\} \) conforme mostrado na Figura\(\PageIndex{6}\).
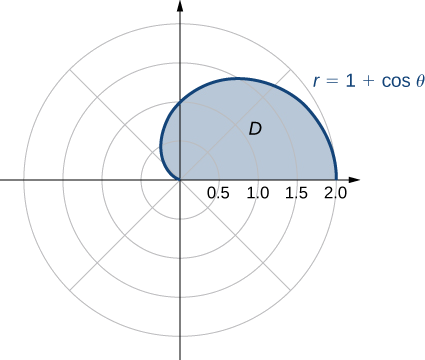
Portanto, temos
\[\begin{align*} \iint_D r^2 \sin \, \theta \, r \, dr \, d\theta &= \int_{\theta=0}^{\theta=\pi} \int_{r=0}^{r=1+\cos \theta} (r^2 \sin \, \theta) \,r \, dr \, d\theta \\ &= \frac{1}{4}\left.\int_{\theta=0}^{\theta=\pi}[r^4] \right|_{r=0}^{r=1+\cos \, \theta} \sin \, \theta \, d\theta \\ &= \frac{1}{4} \int_{\theta=0}^{\theta=\pi} (1 + \cos \, \theta )^4 \sin \, \theta \, d\theta \\ &= - \frac{1}{4} \left[ \frac{(1 + \cos \, \theta)^5}{5}\right]_0^{\pi} = \frac{8}{5}.\end{align*}\]
Avalie a integral
\[\iint_D r^2 \sin^2 2\theta \,r \, dr \, d\theta \nonumber \]
onde\(D = \left\{ (r,\theta)\,|\,0 \leq \theta \leq \pi, \, 0 \leq r \leq 2 \sqrt{\cos \, 2\theta} \right\}\).
- Dica
-
Faça um gráfico da região e siga as etapas no exemplo anterior.
- Resposta
-
\(\frac{\pi}{8}\)
Áreas e volumes polares
Como nas coordenadas retangulares, se um sólido\(S\) é limitado pela superfície\(z = f(r, \theta)\), bem como pelas superfícies\(r = a, \, r = b, \, \theta = \alpha\), e\(\theta = \beta\), podemos encontrar o volume\(V\) de\(S\) por dupla integração, como
\[V = \iint_R f(r, \theta) \,r \, dr \, d\theta = \int_{\theta=\alpha}^{\theta=\beta} \int_{r=a}^{r=b} f(r,\theta)\, r \, dr \, d\theta. \nonumber \]
Se a base do sólido puder ser descrita como\(D = \{(r, \theta)|\alpha \leq \theta \leq \beta, \, h_1 (\theta) \leq r \leq h_2(\theta)\}\), então a integral dupla para o volume se torna
\[V = \iint_D f(r, \theta) \,r \, dr \, d\theta = \int_{\theta=\alpha}^{\theta=\beta} \int_{r=h_1(\theta)}^{r=h_2(\theta)} f(r,\theta) \,r \, dr \, d\theta. \nonumber \]
Ilustramos essa ideia com alguns exemplos.
Encontre o volume do sólido que está abaixo do parabolóide\(z = 1 - x^2 - y^2\) e acima do círculo unitário no\(xy\) plano -( Figura\(\PageIndex{7}\)).
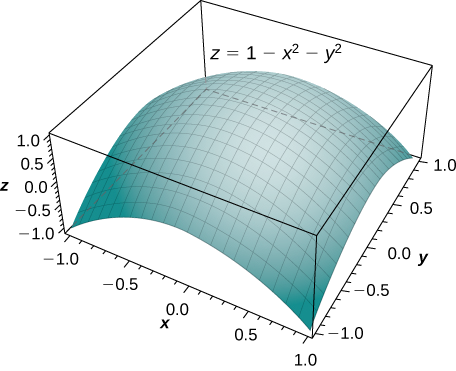
Solução
Pelo método de dupla integração, podemos ver que o volume é a integral iterada da forma
\[\displaystyle \iint_R (1 - x^2 - y^2)\,dA \nonumber \]
onde\(R = \big\{(r, \theta)\,|\,0 \leq r \leq 1, \, 0 \leq \theta \leq 2\pi\big\}\).
Essa integração foi mostrada anteriormente em Exemplo\(\PageIndex{2A}\), então o volume é de unidades\(\frac{\pi}{2}\) cúbicas.
Encontre o volume do sólido que está abaixo do parabolóide\(z = 4 - x^2 - y^2\) e acima do disco\((x - 1)^2 + y^2 = 1\) no\(xy\) plano. Veja o parabolóide na Figura\(\PageIndex{8}\) cruzando o cilindro\((x - 1)^2 + y^2 = 1\) acima do\(xy\) plano.
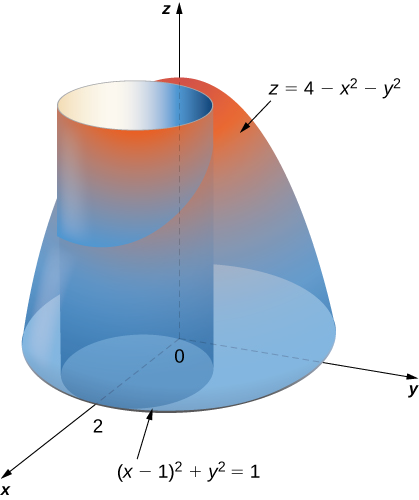
Solução
Primeiro mude o disco\((x - 1)^2 + y^2 = 1\) para coordenadas polares. Expandindo o termo quadrado, temos\(x^2 - 2x + 1 + y^2 = 1\). Em seguida, simplifique para obter\(x^2 + y^2 = 2x\), que em coordenadas polares se torna\(r^2 = 2r \, \cos \, \theta\) e depois\(r = 0\) ou\(r = 2 \, \cos \, \theta\). Da mesma forma, a equação do parabolóide muda para\(z = 4 - r^2\). Portanto, podemos descrever o disco\((x - 1)^2 + y^2 = 1\) no\(xy\) plano -como a região.
\[D = \{(r,\theta)\,|\,0 \leq \theta \leq \pi, \, 0 \leq r \leq 2 \, \cos \theta\}. \nonumber \]
Portanto, o volume do sólido delimitado acima pelo parabolóide\(z = 4 - x^2 - y^2\) e abaixo por\(r = 2 \, \cos \theta\) é
\[\begin{align*} V &= \iint_D f(r, \theta) \,r \, dr \, d\theta \\&= \int_{\theta=0}^{\theta=\pi} \int_{r=0}^{r=2 \, \cos \, \theta} (4 - r^2) \,r \, dr \, d\theta\\ &= \int_{\theta=0}^{\theta=\pi}\left.\left[4\frac{r^2}{2} - \frac{r^4}{4}\right|_0^{2 \, \cos \, \theta}\right]d\theta \\ &= \int_0^{\pi} [8 \, \cos^2\theta - 4 \, \cos^4\theta]\,d\theta \\&= \left[\frac{5}{2}\theta + \frac{5}{2} \sin \, \theta \, \cos \, \theta - \sin \, \theta \cos^3\theta \right]_0^{\pi} = \frac{5}{2}\pi\; \text{units}^3. \end{align*}\]
Observe no próximo exemplo que a integração nem sempre é fácil com coordenadas polares. A complexidade da integração depende da função e também da região na qual precisamos realizar a integração. Se a região tiver uma expressão mais natural nas coordenadas polares ou se\(f\) tiver uma antiderivada mais simples nas coordenadas polares, a mudança nas coordenadas polares é apropriada; caso contrário, use coordenadas retangulares.
Encontre o volume da região que está abaixo do parabolóide\(z = x^2 + y^2\) e acima do triângulo delimitado pelas linhas\(y = x, \, x = 0\) e\(x + y = 2\) no\(xy\) plano -.
Solução
Primeiro, examine a região sobre a qual precisamos configurar a integral dupla e o parabolóide que o acompanha.
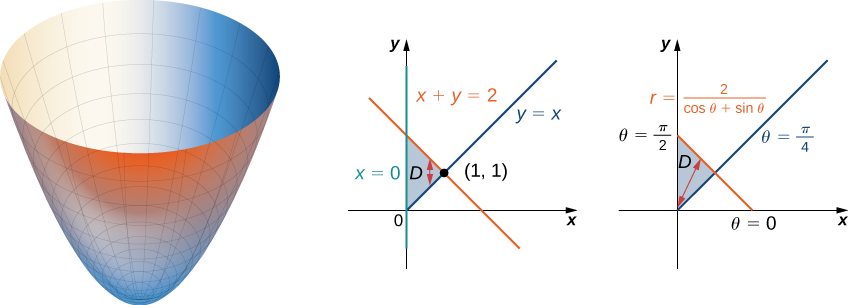
A região\(D\) é\(\{(x,y)\,|\,0 \leq x \leq 1, \, x \leq y \leq 2 - x\}\). Convertendo as linhas\(y = x, \, x = 0\) e\(x + y = 2\) no\(xy\) plano -em funções de\(r\) e\(\theta\) temos\(\theta = \pi/4, \, \theta = \pi/2\), e\(r = 2 / (\cos \, \theta + \sin \, \theta)\), respectivamente. Representando graficamente a região no plano\(xy\) -, vemos que ela se parece\(D = \{(r, \theta)\,|\,\pi/4 \leq \theta \leq \pi/2, \, 0 \leq r \leq 2/(\cos \, \theta + \sin \, \theta)\}\).
Agora, a conversão da equação da superfície dá\(z = x^2 + y^2 = r^2\). Portanto, o volume do sólido é dado pela integral dupla
\[\begin{align*} V &= \iint_D f(r, \theta)\,r \, dr \, d\theta \\&= \int_{\theta=\pi/4}^{\theta=\pi/2} \int_{r=0}^{r=2/ (\cos \, \theta + \sin \, \theta)} r^2 r \, dr d\theta \\ &= \int_{\pi/4}^{\pi/2}\left[\frac{r^4}{4}\right]_0^{2/(\cos \, \theta + \sin \, \theta)} d\theta \\ &=\frac{1}{4}\int_{\pi/4}^{\pi/2} \left(\frac{2}{\cos \, \theta + \sin \, \theta}\right)^4 d\theta \\ &= \frac{16}{4} \int_{\pi/4}^{\pi/2} \left(\frac{1}{\cos \, \theta + \sin \, \theta} \right)^4 d\theta \\&= 4\int_{\pi/4}^{\pi/2} \left(\frac{1}{\cos \, \theta + \sin \, \theta}\right)^4 d\theta. \end{align*}\]
Como você pode ver, essa integral é muito complicada. Então, podemos, em vez disso, calcular essa integral dupla em coordenadas retangulares como
\[V = \int_0^1 \int_x^{2-x} (x^2 + y^2) \,dy \, dx. \nonumber \]
Avaliando doações
\[\begin{align*} V &= \int_0^1 \int_x^{2-x} (x^2 + y^2) \,dy \, dx \\&= \int_0^1 \left.\left[x^2y + \frac{y^3}{3}\right]\right|_x^{2-x} dx\\ &= \int_0^1 \frac{8}{3} - 4x + 4x^2 - \frac{8x^3}{3} \,dx \\ &= \left.\left[\frac{8x}{3} - 2x^2 + \frac{4x^3}{3} - \frac{2x^4}{3}\right]\right|_0^1 \\&= \frac{4}{3} \; \text{units}^3. \end{align*}\]
Para responder à pergunta de como as fórmulas para os volumes de diferentes sólidos padrão, como uma esfera, um cone ou um cilindro, são encontradas, queremos demonstrar um exemplo e determinar o volume de um cone arbitrário.
Use coordenadas polares para encontrar o volume dentro do cone\(z = 2 - \sqrt{x^2 + y^2}\) e acima do\(xy\) plano.
Solução
A região\(D\) para a integração é a base do cone, que parece ser um círculo no\(xy\) plano C (Figura\(\PageIndex{10}\)).
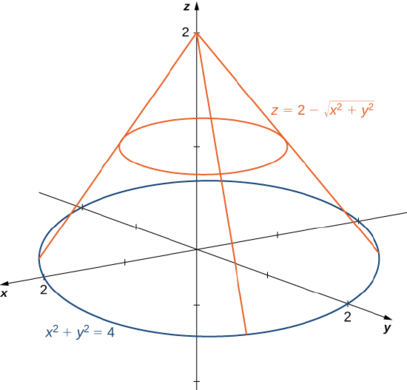
Encontramos a equação da circunferência definindo\(z = 0\):
\[\begin{align*} 0 &= 2 - \sqrt{x^2 + y^2} \\ 2 &= \sqrt{x^2 + y^2} \\ x^2 + y^2 &= 4. \end{align*}\]
Isso significa que o raio do círculo é adequado\(2\) para a integração que temos\(0 \leq \theta \leq 2\pi\)\(0 \leq r \leq 2\) e. Substituindo\(x = r \, \cos \theta\) e\(y = r \, \sin \, \theta\) na equação\(z = 2 - \sqrt{x^2 + y^2}\) que temos\(z = 2 - r\). Portanto, o volume do cone é
\[\int_{\theta=0}^{\theta=2\pi} \int_{r=0}^{r=2} (2 - r)\,r \, dr \, d\theta = 2 \pi \frac{4}{3} = \frac{8\pi}{3}\; \text{cubic units.} \nonumber \]
AnáliseObserve que, se encontrássemos o volume de um cone arbitrário com\(\alpha\) unidades de raio e\(h\) unidades de altura, a equação do cone seria\(z = h - \frac{h}{a}\sqrt{x^2 + y^2}\).
Ainda podemos usar a Figura\(\PageIndex{10}\) e configurar a integral como
\[\int_{\theta=0}^{\theta=2\pi} \int_{r=0}^{r=a} \left(h - \frac{h}{a}r\right) r \, dr \, d\theta. \nonumber \]
Avaliando a integral, obtemos\(\frac{1}{3} \pi a^2 h\).
Use coordenadas polares para encontrar uma integral iterada para encontrar o volume do sólido envolto pelos parabolóides\(z = x^2 + y^2\)\(z = 16 - x^2 - y^2\) e.
- Dica
-
Esboçar os gráficos pode ajudar.
- Resposta
-
\[V = \int_0^{2\pi} \int_0^{2\sqrt{2}} (16 - 2r^2) \,r \, dr \, d\theta = 64 \pi \; \text{cubic units.} \nonumber \]
Encontre a área delimitada pelo círculo\(r = 3 \, \cos \, \theta\) e pelo cardióide\(r = 1 + \cos \, \theta\).
Solução
Em primeiro lugar, esboce os gráficos da região (Figura\(\PageIndex{12}\)).
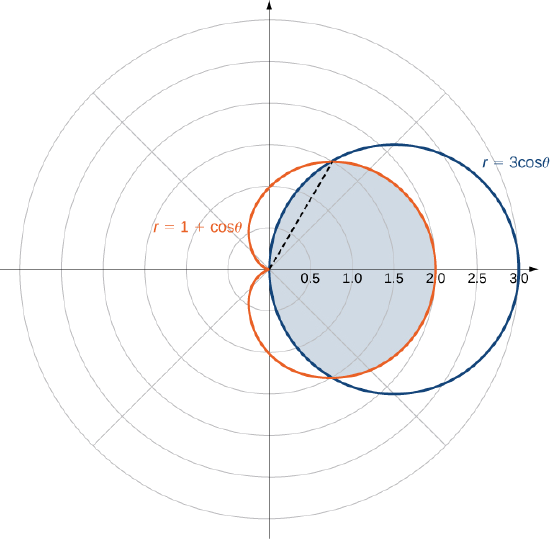
Podemos ver a simetria do gráfico que precisamos encontrar os pontos de interseção. Definir as duas equações iguais uma à outra dá
\[3 \, \cos \, \theta = 1 + \cos \, \theta. \nonumber \]
Um dos pontos de interseção é\(\theta = \pi/3\). A área acima do eixo polar consiste em duas partes, com uma parte definida pelo cardióide de\(\theta = 0\) para\(\theta = \pi/3\) e a outra parte definida pelo círculo de\(\theta = \pi/3\) para\(\theta = \pi/2\). Por simetria, a área total é o dobro da área acima do eixo polar. Assim, temos
\[A = 2 \left[\int_{\theta=0}^{\theta=\pi/3} \int_{r=0}^{r=1+\cos \, \theta} 1 \,r \, dr \, d\theta + \int_{\theta=\pi/3}^{\theta=\pi/2} \int_{r=0}^{r=3 \, \cos \, \theta} 1\,r \, dr \, d\theta \right]. \nonumber \]
Avaliando cada peça separadamente, descobrimos que a área é
\[A = 2 \left(\frac{1}{4}\pi + \frac{9}{16} \sqrt{3} + \frac{3}{8} \pi - \frac{9}{16} \sqrt{3} \right) = 2 \left(\frac{5}{8}\pi\right) = \frac{5}{4}\pi \, \text{square units.} \nonumber \]
Encontre a área dentro do cardióide\(r = 3 - 3 \, \sin \theta\) e fora do cardióide\(r = 1 + \sin \theta\).
- Dica
-
Esboce o gráfico e resolva os pontos de interseção.
- Resposta
-
\[A = 2 \int_{-\pi/2}^{\pi/6} \int_{1+\sin \, \theta}^{3-3\sin \, \theta} \,r \, dr \, d\theta = \left(8 \pi + 9 \sqrt{3}\right) \; \text{units}^2 \nonumber \]
Avalie a integral
\[\iint_{R^2} e^{-10(x^2+y^2)} \,dx \, dy. \nonumber \]
Solução
Essa é uma integral imprópria porque estamos nos integrando em uma região ilimitada\(R^2\). Nas coordenadas polares, o plano inteiro\(R^2\) pode ser visto como\(0 \leq \theta \leq 2\pi, \, 0 \leq r \leq \infty\).
Usando as mudanças de variáveis de coordenadas retangulares para coordenadas polares, temos
\[\begin{align*} \iint_{R^2} e^{-10(x^2+y^2)}\,dx \, dy &= \int_{\theta=0}^{\theta=2\pi} \int_{r=0}^{r=\infty} e^{-10r^2}\,r \, dr \, d\theta = \int_{\theta=0}^{\theta=2\pi} \left(\lim_{a\rightarrow\infty} \int_{r=0}^{r=a} e^{-10r^2}r \, dr \right) d\theta \\ &=\left(\int_{\theta=0}^{\theta=2\pi}\right) d\theta \left(\lim_{a\rightarrow\infty} \int_{r=0}^{r=a} e^{-10r^2}r \, dr \right) \\ &=2\pi \left(\lim_{a\rightarrow\infty} \int_{r=0}^{r=a} e^{-10r^2}r \, dr \right) \\ &=2\pi \lim_{a\rightarrow\infty}\left(-\frac{1}{20}\right)\left(\left. e^{-10r^2}\right|_0^a\right) \\ &=2\pi \left(-\frac{1}{20}\right)\lim_{a\rightarrow\infty}\left(e^{-10a^2} - 1\right) \\ &= \frac{\pi}{10}. \end{align*}\]
Avalie a integral
\[\iint_{R^2} e^{-4(x^2+y^2)}dx \, dy. \nonumber \]
- Dica
-
Converta para o sistema de coordenadas polares.
- Resposta
-
\(\frac{\pi}{4}\)
Conceitos-chave
- Para aplicar uma integral dupla a uma situação com simetria circular, geralmente é conveniente usar uma integral dupla em coordenadas polares. Podemos aplicar essas integrais duplas sobre uma região retangular polar ou uma região polar geral, usando uma integral iterada semelhante às usadas com integrais duplas retangulares.
- A área\(dA\) nas coordenadas polares se torna\(r \, dr \, d\theta\).
- Use\(x = r \, \cos \, \theta, \, y = r \, \sin \, \theta\) e\(dA = r \, dr \, d\theta\) para converter uma integral em coordenadas retangulares em uma integral em coordenadas polares.
- Use\(r^2 = x^2 + y^2\) e\(\theta = tan^{-1} \left(\frac{y}{x}\right)\) para converter uma integral em coordenadas polares em uma integral em coordenadas retangulares, se necessário.
- Para encontrar o volume em coordenadas polares delimitadas acima por uma superfície\(z = f(r, \theta)\) sobre uma região no\(xy\) plano -, use uma integral dupla em coordenadas polares.
Equações-chave
- Integral duplo sobre uma região retangular polar\(R\)
\[\iint_R f(r, \theta) dA = \lim_{m,n\rightarrow\infty}\sum_{i=1}^m \sum_{j=1}^n f(r_{ij}^*, \theta_{ij}^*) \Delta A = \lim_{m,n\rightarrow\infty}\sum_{i=1}^m \sum_{j=1}^nf(r_{ij}^*,\theta_{ij}^*)r_{ij}^*\Delta r \Delta \theta \nonumber \]
- Integral duplo sobre uma região polar geral
\[\iint_D f(r, \theta)\,r \, dr \, d\theta = \int_{\theta=\alpha}^{\theta=\beta} \int_{r=h_1(\theta)}^{r_2(\theta)} f (r,\theta) \,r \, dr \, d\theta \nonumber \]
Glossário
- retângulo polar
- a região entre os círculos\(r = a\) e\(r = b\) e os ângulos\(\theta = \alpha\) e\(\theta = \beta\); é descrita como\(R = \{(r, \theta)\,|\,a \leq r \leq b, \, \alpha \leq \theta \leq \beta\}\)



Assim como nas coordenadas retangulares, também podemos usar coordenadas polares para encontrar áreas de certas regiões usando uma integral dupla. Como antes, precisamos entender a região cuja área queremos calcular. Esboçar um gráfico e identificar a região pode ser útil para perceber os limites da integração. Geralmente, a fórmula da área em dupla integração será semelhante a
\[\text{Area of} \, A = \int_{\alpha}^{\beta} \int_{h_1(\theta)}^{h_2(\theta)} 1 \,r \, dr \, d\theta. \nonumber \]
Exemplo\(\PageIndex{6A}\): Finding an Area Using a Double Integral in Polar Coordinates
Avalie a área delimitada pela curva\(r = \cos \, 4\theta\).
Solução
Esboçar o gráfico da função\(r = \cos \, 4\theta\) revela que ela é uma rosa polar com oito pétalas (veja a figura a seguir).
Usando simetria, podemos ver que precisamos encontrar a área de uma pétala e depois multiplicá-la por 8. Observe que os valores\(\theta\) pelos quais o gráfico passa pela origem são os zeros da função\(\cos \, 4\theta\), e esses são múltiplos ímpares de\(\pi/8\). Assim, uma das pétalas corresponde aos valores de\(\theta\) no intervalo\([-\pi/8, \pi/8]\). Portanto, a área delimitada pela curva\(r = \cos \, 4\theta\) é
\[\begin{align*} A &= 8 \int_{\theta=-\pi/8}^{\theta=\pi/8} \int_{r=0}^{r=\cos \, 4\theta} 1\,r \, dr \, d\theta \\ &= 8 \int_{\theta=-\pi/8}^{\theta=\pi/8}\left.\left[\frac{1}{2}r^2\right|_0^{\cos \, 4\theta}\right] d\theta \\ &= 8 \int_{-\pi/8}^{\pi/8} \frac{1}{2} \cos^24\theta \, d\theta \\&= 8\left. \left[\frac{1}{4} \theta + \frac{1}{16} \sin \, 4\theta \, \cos \, 4\theta \right|_{-\pi/8}^{\pi/8}\right] \\&= 8 \left[\frac{\pi}{16}\right] = \frac{\pi}{2}\; \text{units}^2. \end{align*}\]