15.2E: Exercícios para a Seção 15.2

Last updated
Save as PDF

Page ID: 188061

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

1) A região$D$ delimitada por$y = x^3, \space y = x^3 + 1, \space x = 0,$ e$x = 1$ conforme indicado na figura a seguir.

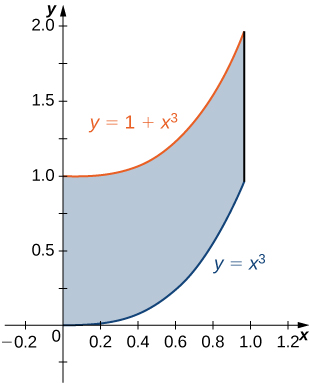
$Uma região é limitada por y = 1 + x ao cubo, y = x ao cubo, x = 0 e x = 1.$

a. Classifique essa região como verticalmente simples (Tipo I) ou horizontalmente simples (Tipo II).

Tipo:: Tipo I, mas não Tipo II

b. Encontre a área da região$D$.

c. Find the average value of the function $f(x,y) = 3xy$ on the region graphed in the previous exercise.

Answer: $\frac{27}{20}$

2) The region $D$ bounded by $y = \sin x, \space y = 1 + \sin x, \space x = 0$, and $x = \frac{\pi}{2}$ as given in the following figure.

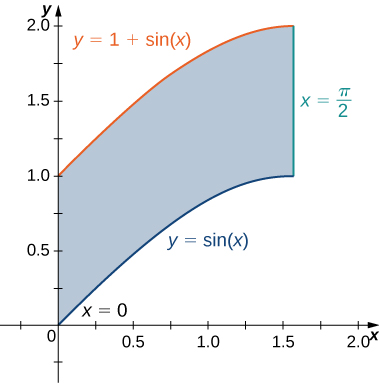
$A region is bounded by y = 1 + sin x, y = sin x, x = 0, and x = pi/2.$

a. Classifique essa região como verticalmente simples (Tipo I) ou horizontalmente simples (Tipo II).

Tipo:: Tipo I, mas não Tipo II

b. Encontre a área da região$D$.

Responda: $\frac{\pi}{2}\, \text{units}^2$

c. Encontre o valor médio da função$f(x,y) = \cos x$ na região$D$.

3) A região$D$ delimitada por$x = y^2 - 1$ e$x = \sqrt{1 - y^2}$ conforme indicado na figura a seguir.

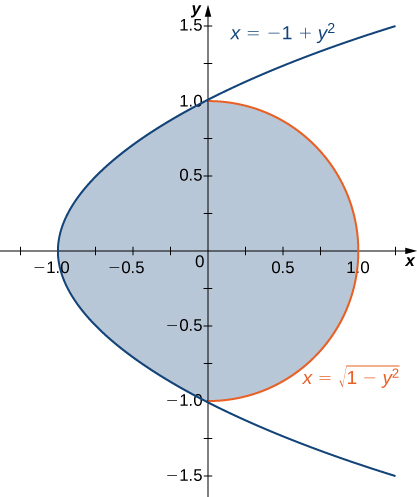
$Uma região é limitada por x = menos 1 + y ao quadrado e x = a raiz quadrada da quantidade (1 menos y ao quadrado).$

a. Classifique essa região como verticalmente simples (Tipo I) ou horizontalmente simples (Tipo II).

Tipo:: Tipo II, mas não Tipo I

b. Encontre o volume do sólido abaixo do gráfico da função$f(x,y) = xy + 1$ and above the region $D$.

Answer: $\frac{1}{6}(8 + 3\pi)\, \text{units}^3$

4) The region $D$ bounded by $y = 0, \space x = -10 + y,$ and $x = 10 - y$ as given in the following figure.

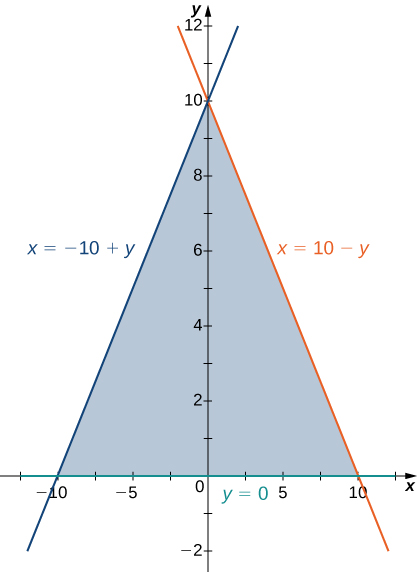
$A region is bounded by x = negative 10 + y, x = 10 minus y, and y = 0.$

a. Classifique essa região como verticalmente simples (Tipo I) ou horizontalmente simples (Tipo II).

Tipo:: Tipo II, mas não Tipo I

b. Encontre o volume do sólido abaixo do gráfico da função$f(x,y) = x + y$ e acima da região na figura do exercício anterior.

Responda: $\frac{1000}{3}\, \text{units}^3$

5) A região$D$ delimitada por$y = 0, \space x = y - 1, \space x = \frac{\pi}{2}$, conforme indicado na figura a seguir.

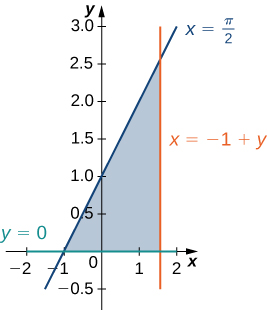
$Uma região é limitada por x = pi/2, y = 0 e x = menos 1 + y.$

Classifique essa região como verticalmente simples (Tipo I) ou horizontalmente simples (Tipo II).

Tipo:: Tipo I e Tipo II

6) A região$D$ bounded by $y = 0$ and $y = x^2 - 1$ as given in the following figure.

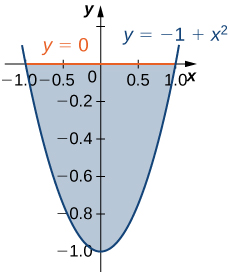
$A region is bounded by y = 0 and y = negative 1 + x squared.$

Classifique essa região como verticalmente simples (Tipo I) ou horizontalmente simples (Tipo II).

Tipo:: Tipo I e Tipo II

7)$D$ Seja a região delimitada pelas curvas das equações$y = \cos x$$y = 4 - x^2$ e e$x$ pelo eixo. Explique por que não$D$ é do Tipo I nem II.

Responda: A região não$D$ é do Tipo I: ela não fica entre duas linhas verticais e os gráficos de duas funções contínuas$g_1(x)$$g_2(x)$ e. A região não é do Tipo II: ela não fica entre duas linhas horizontais e os gráficos de duas funções contínuas$h_1(y)$$h_2(y)$ e.

8)$D$ Seja a região delimitada pelas curvas das equações$y = x, \space y = -x$$y = 2 - x^2$ e. Explique por que não$D$ é do Tipo I nem II.

Nos exercícios 9 a 14, avalie a integral dupla$\displaystyle \iint_D f(x,y) \,dA$ sobre a região$D$.

9)$f(x,y) = 1$ e

$D = \big\{(x,y)| \, 0 \leq x \leq \frac{\pi}{2}, \space \sin x \leq y \leq 1 + \sin x \big\}$

Responda: $\frac{\pi}{2}$

10)$f(x,y) = 2$ e

$D = \big\{(x,y)| \, 0 \leq y \leq 1, \space y - 1 \leq x \leq \arccos y \big\}$

11)$f(x,y) = xy$ e

$D = \big\{(x,y)| \, -1 \leq y \leq 1, \space y^2 - 1 \leq x \leq \sqrt{1 - y^2} \big\}$

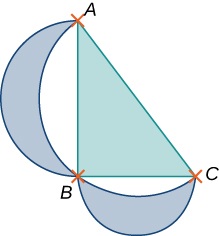
Responda: $0$

12)$f(x,y) = \sin y$ e$D$ é a região triangular com vértices$(0,0), \space (0,3)$, e$(3,0)$

13)$f(x,y) = -x + 1$ e$D$ é a região triangular com vértices$(0,0), \space (0,2)$, e$(2,2)$

Responda: $\frac{2}{3}$

14)$f(x,y) = 2x + 4y$ e

$D = \big\{(x,y)|\, 0 \leq x \leq 1, \space x^3 \leq y \leq x^3 + 1 \big\}$

Nos exercícios 15 a 20, avalie as integrais iteradas.

15)$\displaystyle \int_0^1 \int_{2\sqrt{x}}^{2\sqrt{x}+1} (xy + 1) \,dy \space dx$

Responda: $\frac{41}{20}$

16)$\displaystyle \int_0^3 \int_{2x}^{3x} (x + y^2) \,dy \space dx$

17)$\displaystyle \int_1^2 \int_{-u^2-1}^{-u} (8 uv) \,dv \space du$

Responda: $-63$

18)$\displaystyle \int_e^{e^2} \int_{\ln u}^2 (v + \ln u) \,dv \space du$

19)$\displaystyle \int_0^{1/2} \int_{-\sqrt{1-4y^2}}^{\sqrt{1-4y^2}} 4 \,dx \space dy$

Responda: $\pi$

20)$\displaystyle \int_0^1 \int_{-\sqrt{1-y^2}}^{\sqrt{1-y^2}} (2x + 4y^3) \,dx \space dy$

21)$D$ Seja a região delimitada por$y = 1 - x^2, \space y = 4 - x^2$, e os$y$ eixos$x$ - e -.

a. Mostre isso$\displaystyle \iint_D x\,dA = \int_0^1 \int_{1-x^2}^{4-x^2} x \space dy \space dx + \int_1^2 \int_0^{4-x^2} x \space dy \space dx$ dividindo a região$D$ em duas regiões do Tipo I.

b. Avalie a integral$\displaystyle \iint_D x \,dA.$

22)$D$ Seja a região delimitada por$y = 1, \space y = x, \space y = \ln x$, e o$x$ eixo -.

a. Mostre isso$\displaystyle \iint_D y^2 \,dA = \int_{-1}^0 \int_{-x}^{2-x^2} y^2 dy \space dx + \int_0^1 \int_x^{2-x^2} y^2 dy \space dx$ dividindo a região$D$ em duas regiões do Tipo I, onde$D = \big\{(x,y)\,|\,y \geq x, y \geq -x, \space y \leq 2-x^2\big\}$.

b. Avalie a integral$\displaystyle \iint_D y^2 \,dA.$

23)$D$ Seja a região delimitada por$y = x^2$$y = x + 2$,$y = -x$ e.

a. Mostre isso$\displaystyle \iint_D x \, dA = \int_0^1 \int_{-y}^{\sqrt{y}} x \space dx \space dy + \int_1^4 \int_{y-2}^{\sqrt{y}} x \space dx \space dy$ dividindo a região$D$ em duas regiões do Tipo II, onde$D = \big\{(x,y)\,|\,y \geq x^2, \space y \geq -x, \space y \leq x + 2\big\}$.

b. Avalie a integral$\displaystyle \iint_D x \,dA.$

Responda: a. As respostas podem variar;
b.$\frac{8}{12}$

24) A região$D$ delimitada por$x = 0, y = x^5 + 1$, e$y = 3 - x^2$ é mostrada na figura a seguir. Encontre a área$A(D)$ da região$D$.

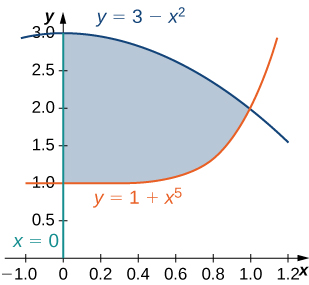
$Uma região é limitada por y = 1 + x elevado à quinta potência, y = 3 menos x ao quadrado e x = 0.$

25) A região$D$ bounded by $y = \cos x, \space y = 4 + \cos x$, and $x = \pm \frac{\pi}{3}$ is shown in the following figure. Find the area $A(D)$ of the region $D$.

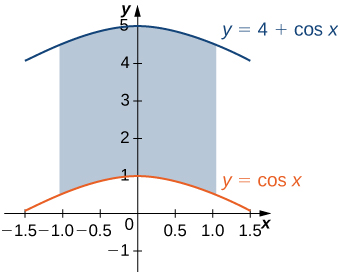
$A region is bounded by y = cos x, y = 4 + cos x, x = negative 1, and x = 1.$

Responda: $\frac{8\pi}{3}$

26) Encontre a área$A(D)$ da região$D = \big\{(x,y)| \, y \geq 1 - x^2, y \leq 4 - x^2, \space y \geq 0, \space x \geq 0 \big\}$.

27)$D$ Seja a região delimitada por$ y = 1, \space y = x, \space y = \ln x$, e o$x$ eixo -. Encontre a área$A(D)$ da região$D$.

Responda: $\left(e - \frac{3}{2}\right)\, \text{units}^2$

28) Encontre o valor médio da função$f(x,y) = \sin y$ na região triangular com vértices$(0,0), \space (0,3)$,$(3,0)$ e.

29) Encontre o valor médio da função$f(x,y) = -x + 1$ na região triangular com vértices$(0,0), \space (0,2)$,$(2,2)$ e.

Resposta: O valor médio de$f$ nesta região triangular é$\frac{1}{3}.$

Nos exercícios 30 a 33, altere a ordem de integração e avalie a integral.

30)$\displaystyle \int_{-1}^{\pi/2} \int_0^{x+1} \sin x \, dy \, dx$

31)$\displaystyle \int_0^1 \int_{x-1}^{1-x} x \, dy \, dx$

Resposta: $\displaystyle \int_0^1 \int_{x-1}^{1-x} x \space dy \space dx = \int_{-1}^0 \int_0^{y+1} x \space dx \space dy + \int_0^1 \int_0^{1-y} x \space dx \space dy = \frac{1}{3}$

32)$\displaystyle \int_{-1}^0 \int_{-\sqrt{y+1}}^{\sqrt{y+1}} y^2 dx \space dy$

33)$\displaystyle \int_{-1/2}^{1/2} \int_{-\sqrt{y^2+1}}^{\sqrt{y^2+1}} y \space dx \space dy$

Resposta: $\displaystyle \int_{-1/2}^{1/2} \int_{-\sqrt{y^2+1}}^{\sqrt{y^2+1}} y \space dx \space dy = \int_1^2 \int_{-\sqrt{x^2-1}}^{\sqrt{x^2-1}} y \space dy \space dx = 0$

34) A região$D$ é mostrada na figura a seguir. Avalie a integral dupla$\displaystyle \iint_D (x^2 + y) \,dA$ usando a ordem mais fácil de integração.

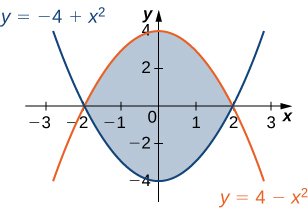
$Uma região é limitada por y = menos 4 + x ao quadrado e y = 4 menos x ao quadrado.$

35) A região$D$ is shown in the following figure. Evaluate the double integral $\displaystyle \iint_D (x^2 - y^2) \,dA$ by using the easier order of integration.

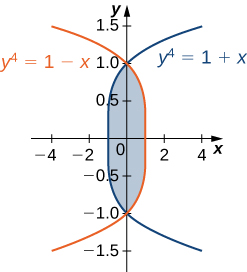
$A region is bounded by y to the fourth power = 1 minus x and y to the fourth power = 1 + x.$

Resposta: $\displaystyle \iint_D (x^2 - y^2) dA = \int_{-1}^1 \int_{y^4-1}^{1-y^4} (x^2 - y^2)dx \space dy = \frac{464}{4095}$

36) Encontre o volume do sólido sob a superfície$z = 2x + y^2$ e acima da região delimitada por$y = x^5$$y = x$ e.

37) Encontre o volume do sólido abaixo do plano$z = 3x + y$ e acima da região determinada por$y = x^7$$y = x$ e.

Resposta: $\frac{4}{5}\, \text{units}^3$

38) Encontre o volume do sólido abaixo do plano$z = 3x + y$ e acima da região delimitada por$x = \tan y, \space x = -\tan y$,$x = 1$ e.

39) Encontre o volume do sólido sob a superfície$z = x^3$ e acima da região plana delimitada por$x = \sin y, \space x = -\sin y$,$x = 1$ e.

Resposta: $\frac{5\pi}{32}\, \text{units}^3$

40)$g$ Seja uma função positiva, crescente e diferenciável no intervalo$[a,b]$. Mostre que o volume do sólido abaixo da superfície$z = g'(x)$ e acima da região delimitada por$y = 0, \space y = g(x), \space x = a$ e$x = b$ é dado por$\frac{1}{2}(g^2 (b) - g^2 (a))$.

41)$g$ Seja uma função positiva, crescente e diferenciável no intervalo$[a,b]$ e$k$ seja um número real positivo. Mostre que o volume do sólido sob a superfície$z = g'(x)$ e acima da região delimitada por$y = g(x), \space y = g(x) + k, \space x = a$ e$x = b$ é dado por$k(g(b) - g(a)).$

42) Encontre o volume do sólido situado no primeiro octante e determinado pelos planos$z = 2$$z = 0, \space x + y = 1, \space x = 0$,,$y = 0$ e.

43) Encontre o volume do sólido situado no primeiro octante e limitado pelos planos$x + 2y = 1$$x = 0, \space z = 4$,,$z = 0$ e.

Resposta: $1\, \text{units}^3$

44) Encontre o volume do sólido delimitado pelos planos$x + y = 1, \space x - y = 1, \space x = 0, \space z = 0$,$z = 10$ e.

45) Encontre o volume do sólido delimitado pelos planos$x + y = 1, \space x - y = 1, \space x + y = -1\space x - y = -1, \space z = 1$ e$z = 0$

Resposta: $2\, \text{units}^3$

46)$S_2$ Seja$S_1$ e seja os sólidos situados no primeiro octante sob os planos$x + y + z = 1$ e$x + y + 2z = 1$ respectivamente, e$S$ seja o sólido situado entre$S_1, \space S_2, \space x = 0$,$y = 0$ e.

Encontre o volume do sólido$S_1$.
Encontre o volume do sólido$S_2$.
Encontre o volume do sólido$S$ subtraindo os volumes dos sólidos$S_1$$S_2$ e.

47)$S_2$ Seja$S_1$ e seja os sólidos situados no primeiro octante sob os planos$2x + 2y + z = 2$ e$x + y + z = 1$ respectivamente, e$S$ seja o sólido situado entre$S_1, \space S_2, \space x = 0$,$y = 0$ e.

Encontre o volume do sólido$S_1$.
Encontre o volume do sólido$S_2$.
Encontre o volume do sólido$S$ subtraindo os volumes dos sólidos$S_1$$S_2$ e.

Resposta: a.$\frac{1}{3}\, \text{units}^3$
b.$\frac{1}{6}\, \text{units}^3$
c.$\frac{1}{6}\, \text{units}^3$

48) Sejam$S_1$ e$S_2$ sejam os sólidos situados no primeiro octante sob o plano$x + y + z = 2$ e sob a esfera$x^2 + y^2 + z^2 = 4$, respectivamente. Se o volume do sólido$S_2$ for,$\frac{4\pi}{3}$ determine o volume do sólido$S$ situado entre$S_1$ e$S_2$ subtraindo os volumes desses sólidos.

49) Sejam$S_1$ e$S_2$ sejam os sólidos situados no primeiro octante abaixo do plano$x + y + z = 2$ e delimitados pelo cilindro$x^2 + y^2 = 4$, respectivamente.

Encontre o volume do sólido$S_1$.
Encontre o volume do sólido$S_2$.
Encontre o volume do sólido$S$ situado entre$S_1$ e$S_2$ subtraindo os volumes dos sólidos$S_1$$S_2$ e.

Resposta: a.$\frac{4}{3}\, \text{units}^3$
b.$2\pi\, \text{units}^3$
c.$\frac{6\pi - 4}{3}\, \text{units}^3$

50) [T] A figura a seguir mostra a região$D$ delimitada pelas curvas$y = \sin x, \space x = 0$,$y = x^4$ e. Use uma calculadora gráfica ou CAS para encontrar as$x$ coordenadas -dos pontos de interseção das curvas e determinar a área da região$D$. Arredonde suas respostas para seis casas decimais.

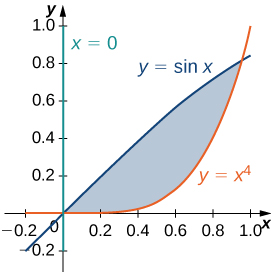
$Uma região é limitada por y = sin x, y = x até a quarta potência e x = 0.$

51) [T] A região$D$ bounded by the curves $y = \cos x, \space x = 0$, and $y = x^3$ is shown in the following figure. Use a graphing calculator or CAS to find the $x$-coordinates of the intersection points of the curves and to determine the area of the region $D$. Round your answers to six decimal places.

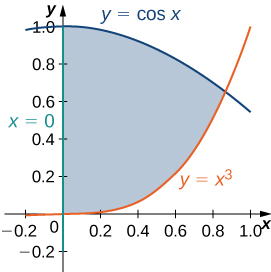
$A region is bounded by y = cos x, y = x cubed, and x = 0.$

Resposta: 0 e 0,865474;$A(D) = 0.621135\, \text{units}^3$

52) Suponha que esse$(X,Y)$ seja o resultado de um experimento que deve ocorrer$S$ em uma região específica no$xy$ plano. Nesse contexto, a região$S$ é chamada de espaço amostral do experimento$X$ e$Y$ são variáveis aleatórias. Se$D$ for uma região incluída em$S$, então a probabilidade de$(X,Y)$ estar em$D$ é definida como$P[(X,Y) \in D] = \iint_D p(x,y)dx \space dy$, onde$p(x,y)$ está a densidade de probabilidade conjunta do experimento. Aqui$p(x,y)$ está uma função não negativa para a qual$\iint_S p(x,y) dx \space dy = 1$. Suponha que um ponto$(X,Y)$ seja escolhido arbitrariamente no quadrado$[0,3] \times [0,3]$ com a densidade de probabilidade

\[p(x,y) = \frac{1}{9} (x,y) \in [0,3] \times [0,3],\nonumber \]

\[p(x,y) = 0 \space \text{otherwise}\nonumber \]

Encontre a probabilidade de que o ponto$(X,Y)$ esteja dentro da unidade quadrada e interprete o resultado.

53) Considere$X$$Y$ duas variáveis aleatórias de densidades de probabilidade$p_1(x)$ e$p_2(x)$, respectivamente. As variáveis$X$ aleatórias$Y$ são consideradas independentes se sua função de densidade articular for dada por$p_(x,y) = p_1(x)p_2(y)$. Em um restaurante drive-thru, os clientes passam, em média, 3 minutos fazendo seus pedidos e mais 5 minutos pagando e retirando suas refeições. Suponha que fazer o pedido e pagar/retirar a refeição sejam dois eventos independentes$X$$Y$ e. Se os tempos de espera forem modelados pelas densidades de probabilidade exponenciais

\[p_1(x) = \frac{1}{3}e^{-x/3} \space x\geq 0,\nonumber \]

\[p_1(x) = 0 \space \text{otherwise}\nonumber \]

\[p_2(y) = \frac{1}{5} e^{-y/5} \space y \geq 0\nonumber \]

\[p_2(y) = 0 \space \text{otherwise}\nonumber \]

respectivamente, a probabilidade de um cliente passar menos de 6 minutos na fila do drive-thru é dada por$P[X + Y \leq 6] = \iint_D p(x,y) dx \space dy$, where$D = {(x,y)|x \geq 0, \space y \geq 0, \space x + y \leq 6}$. Encontre$P[X + Y \leq 6]$ e interprete o resultado.

Resposta: $P[X + Y \leq 6] = 1 + \frac{3}{2e^2} - \frac{5}{e^{6/5}} \approx 0.45$; há uma$45\%$ chance de um cliente passar$6$ minutos na fila do drive-thru.

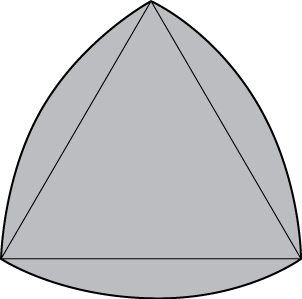
54) [T] O triângulo de Reuleaux consiste em um triângulo equilátero e três regiões, cada uma delas delimitada por um lado do triângulo e um arco de um círculo de raio s centrado no vértice oposto do triângulo. Mostre que a área do triângulo de Reuleaux na figura a seguir de comprimento lateral$s$ é$\frac{s^2}{2}(\pi - \sqrt{3})$.

$Um triângulo equilátero com regiões adicionais consistindo em três arcos de um círculo com raio igual ao comprimento do lado do triângulo. Esses arcos conectam dois vértices adjacentes e o raio é obtido do vértice oposto.$

55) [T] Mostre que a área das lunas de Alhazen, as duas linhas azuis na figura a seguir, é a mesma que a área do triângulo reto$ABC.$ The outer boundaries of the lunes are semicircles of diameters $AB$ and $AC$ respectively, and the inner boundaries are formed by the circumcircle of the triangle $ABC$.

$A right triangle with points A, B, and C. Point B has the right angle. There are two lunes drawn from A to B and from B to C with outer diameters AB and AC, respectively, and with the inner boundaries formed by the circumcircle of the triangle ABC.$