15.5: Integrais triplos em coordenadas cilíndricas e esféricas
- Page ID
- 188124
- Avalie uma integral tripla mudando para coordenadas cilíndricas.
- Avalie uma integral tripla mudando para coordenadas esféricas.
No início deste capítulo, mostramos como converter uma integral dupla em coordenadas retangulares em uma integral dupla em coordenadas polares para lidar de forma mais conveniente com problemas envolvendo simetria circular. Uma situação semelhante ocorre com integrais triplos, mas aqui precisamos distinguir entre simetria cilíndrica e simetria esférica. Nesta seção, convertemos integrais triplos em coordenadas retangulares em uma integral tripla em coordenadas cilíndricas ou esféricas.
Lembre-se também do prelúdio do capítulo, que mostrava a casa de ópera l'Hemisphèric em Valência, Espanha. Tem quatro seções, com uma das seções sendo um teatro em uma esfera (bola) de cinco andares sob um teto oval, do comprimento de um campo de futebol. No interior, há uma tela IMAX que transforma a esfera em um planetário com um céu cheio de estrelas\(9000\) cintilantes. Usando integrais triplos em coordenadas esféricas, podemos encontrar os volumes de diferentes formas geométricas como essas.
Revisão das coordenadas cilíndricas
Como vimos anteriormente, no espaço bidimensional,\(\mathbb{R}^2\) um ponto com coordenadas retangulares\((x,y)\) pode ser identificado\((r,\theta)\) em coordenadas polares e vice-versa\(x = r \, \cos \theta\), onde\(y = r \, \sin \, \theta, \, r^2 = x^2 + y^2\) e\(\tan \, \theta = \left(\frac{y}{x}\right)\) são as relações entre as variáveis.
No espaço tridimensional,\(\mathbb{R}^3\) um ponto com coordenadas retangulares\((x,y,z)\) pode ser identificado com coordenadas cilíndricas\((r, \theta, z)\) e vice-versa. Podemos usar essas mesmas relações de conversão, adicionando\(z\) a distância vertical até o ponto do\((xy\) plano -, conforme mostrado em\(\PageIndex{1}\).
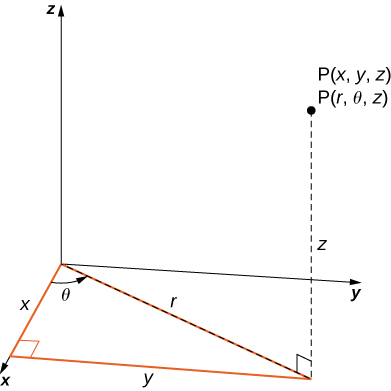
Para converter coordenadas retangulares em cilíndricas, usamos a conversão
- \(x = r \, \cos \theta\)
- \(y = r \, \sin \, \theta\)
- \(z=z\)
Para converter coordenadas cilíndricas em retangulares, usamos
- \(r^2 = x^2 + y^2\)e
- \(\theta = \tan^{-1} \left(\frac{y}{x}\right)\)
- \(z=z\)
Observe que a\(z\) coordenada -permanece a mesma em ambos os casos.
No plano bidimensional com um sistema de coordenadas retangular, quando dizemos\(x = k\) (constante) queremos dizer uma linha vertical ilimitada paralela ao\(y\) eixo -e quando\(y = l\) (constante) queremos dizer uma linha horizontal ilimitada paralela ao\(x\) eixo. Com o sistema de coordenadas polares, quando dizemos\(r = c\) (constante), queremos dizer um círculo de\(c\) unidades de raio e quando\(\theta = \alpha\) (constante) queremos dizer um raio infinito fazendo um ângulo\(\alpha\) com o\(x\) eixo positivo.
Da mesma forma, no espaço tridimensional com coordenadas retangulares,\((x,y,z)\) as equações\(x = k, \, y = l\)\(k, \, l\) e\(z = m\) onde e\(m\) são constantes, representam planos ilimitados paralelos ao\(yz\) plano -,\(xz\) -plano e\(xy\) -plano, respectivamente. Com coordenadas cilíndricas\((r, \theta, z)\)\(r = c, \, \theta = \alpha\), por\(z = m\), e\(c, \alpha\), onde e\(m\) são constantes, queremos dizer um cilindro vertical ilimitado com o eixo z como eixo radial; um plano fazendo um ângulo constante\(\alpha\) com o\(xy\) plano -; e um plano horizontal ilimitado paralelo ao\(xy\) plano -, respectivamente. Isso significa que o cilindro circular\(x^2 + y^2 = c^2\) em coordenadas retangulares pode ser representado simplesmente como\(r = c\) em coordenadas cilíndricas. (Consulte Coordenadas cilíndricas e esféricas para obter mais informações.)
Integração em coordenadas cilíndricas
Integrais triplos geralmente podem ser avaliados mais facilmente usando coordenadas cilíndricas em vez de coordenadas retangulares. Algumas equações comuns de superfícies em coordenadas retangulares junto com equações correspondentes em coordenadas cilíndricas estão listadas na Tabela\(\PageIndex{1}\). Essas equações se tornarão úteis à medida que prosseguirmos com a solução de problemas usando integrais triplos.
| cilindro circular | Cone circular | Esfera | Parabolóide | |
|---|---|---|---|---|
| Retangular | \(x^2 + y^2 = c^2\) | \(z^2 = c^2 (x^2 + y^2)\) | \(x^2 + y^2 + z^2 = c^2\) | \(z = c(x^2 + y^2)\) |
| Cilíndrico | \(r = c\) | \(z = cr\) | \(r^2 + z^2 = c^2\) | \(z = cr^2\) |
Como antes, começamos com a região\(B\) limitada mais simples\(\mathbb{R}^3\) para descrever em coordenadas cilíndricas, na forma de uma caixa cilíndrica\(B = \{(r,\theta,z) | a \leq r \leq b, \, \alpha \leq \theta \leq \beta, \, c \leq z \leq d\}\) (Figura\(\PageIndex{2}\)). Suponha que dividimos cada intervalo em\(l, \, m\), e\(n\) subdivisões de tal forma que\(\Delta r = \frac{b \cdot a}{l}, \, \Delta \theta = \frac{\beta \cdot \alpha}{m}\),\(\Delta z = \frac{d \cdot c}{n}\) e. Então, podemos declarar a seguinte definição para uma integral tripla em coordenadas cilíndricas.
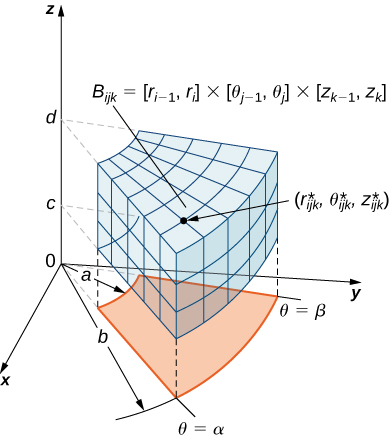
Considere a caixa cilíndrica (expressa em coordenadas cilíndricas)
\[B = \{(r, \theta, z)|a \leq r \leq b, \, \alpha \leq \theta \leq \beta, \, c \leq z \leq d\}. \nonumber \]
Se a função\(f(r, \theta, z)\) for contínua\(B\) e se\((r_{ijk}^*, \theta_{ijk}^*, z_{ijk}^*)\) for qualquer ponto de amostra na subcaixa cilíndrica\(B_{ijk} = |r_{i-1}, r_i| \times |\theta_{j-1}, \theta_j| \times |z_{k-1}, k_i|\) (Figura\(\PageIndex{2}\)), então podemos definir a integral tripla em coordenadas cilíndricas como o limite de uma soma tripla de Riemann, desde que exista o seguinte limite:
\[\lim_{l,m,n \rightarrow \infty} \sum_{i=1}^l \sum_{j=1}^m \sum_{k=1}^n f(r_{ijk}^*, \theta_{ijk}^*, z_{ijk}^*) \Delta r \Delta \theta \Delta z. \nonumber \]
Observe que se\(g(x,y,z)\) for a função em coordenadas retangulares e a caixa\(B\) for expressa em coordenadas retangulares, então a integral tripla
\[\iiint_B g(x,y,z)dV \nonumber \]
é igual à integral tripla
\[\iiint_B g(r \, \cos \theta, \, r \, \sin \, \theta, \, z) r \, dr \, d\theta \, dz \nonumber \]
e nós temos
\[\iiint_B g(x,y,z)dV = \iiint_B g(r \, \cos \theta, \, r \, \sin \, \theta, \, z) r \, dr \, d\theta \, dz = \iiint_B f(r, \theta \, z) r \, dr \, d\theta \, dz. \nonumber \]
Conforme mencionado na seção anterior, todas as propriedades de uma integral dupla funcionam bem em integrais triplas, seja em coordenadas retangulares ou cilíndricas. Eles também são válidos para integrais iterados. Para reiterar, em coordenadas cilíndricas, o teorema de Fubini assume a seguinte forma:
Suponha que\(g(x,y,z)\) seja contínuo em uma caixa retangular\(B\) que, quando descrita em coordenadas cilíndricas, se parece\(B = \{(r,\theta,z) | a \leq r \leq b, \, \alpha \leq \theta \leq \beta, \, c \leq z \leq d\}\).
Então\(g(x,y,z) = g(r \, \cos \theta, r \, \sin \, \theta,z) = f(r, \theta,z)\) e
\[\iiint_B g(x,y,z)dV = \int_c^d \int_{\beta}^{\alpha} \int_a^b f(r, \theta, z) r \, dr \, d\theta \, dz. \nonumber \]
A integral iterada pode ser substituída equivalentemente por qualquer uma das outras cinco integrais iteradas obtidas pela integração em relação às três variáveis em outras ordens.
Os sistemas de coordenadas cilíndricos funcionam bem para sólidos que são simétricos em torno de um eixo, como cilindros e cones. Vejamos alguns exemplos antes de definirmos a integral tripla em coordenadas cilíndricas em regiões cilíndricas gerais.
Avalie a integral tripla
\[\iiint_B (zr \, \sin \, \theta) r \, dr \, d\theta \, dz \nonumber \]
onde está a caixa\(B\) cilíndrica\(B = \{(r,\theta,z) |0 \leq r \leq 2, \, 0 \leq \theta \leq \pi/2, \, 0, \leq z \leq 4\}.\)
Solução
Conforme declarado no teorema de Fubini, podemos escrever a integral tripla como a integral iterada
\[\iiint_B (zr \, \sin \, \theta) r \, dr \, d\theta \, dz = \int_{\theta=0}^{\theta=\pi/2} \int_{r=0}^{r=2} \int_{z=0}^{z=4} (zr \, \sin \, \theta) r \, dz \, dr \, d\theta. \nonumber \]
A avaliação da integral iterada é simples. Cada variável na integral é independente das outras, então podemos integrar cada variável separadamente e multiplicar os resultados juntos. Isso torna o cálculo muito mais fácil:
\[\int_{\theta=0}^{\theta=\pi/2} \int_{r=0}^{r=2} \int_{z=0}^{z=4} (zr \, \sin \, \theta) r \, dz \, dr \, d\theta = \left(\int_0^{\pi/2} \sin \, \theta \, d\theta \right) \left( \int_0^2 r^2 dr\right) \left( \int_0^4 z \, dz\right) = \left(\left. -\cos \theta \right|_0^{\pi/2} \right) \left(\left.\frac{r^3}{3} \right|_0^2 \right) \left( \left. \frac{z^2}{2} \right|_0^4 \right) = \frac{64}{3}. \nonumber \]
Avalie a integral tripla\[\int_{\theta=0}^{\theta=\pi} \int_{r=0}^{r=1} \int_{z=0}^{z=4} rz \, \sin \, \theta r \, dz \, dr \, d\theta. \nonumber \]
- Dica
-
Siga as mesmas etapas do exemplo anterior.
- Resposta
-
\(8\)
Se a região cilíndrica sobre a qual temos que nos integrar é um sólido geral, observamos as projeções nos planos coordenados. Portanto, a integral tripla de uma função contínua\(f(r, \theta, z)\) sobre uma\(E = \{(r, \theta, z)|(r, \theta) \in D, u_1 (r, \theta) \leq z \leq u_2 (r, \theta)\}\) região sólida geral,\(\mathbb{R}^3\) onde\(D\) está a\(E\) projeção de no\(r\theta\) plano -, é
\[\iiint_E f(r, \theta, z) r \, dr \, d\theta \, dz = \iint_D \left[\int_{u_1(r,\theta)}^{u_2(r,\theta)} f(r, \theta, z) dz \right] r \, dr \, d\theta. \nonumber \]
Em particular, se\(D = \{(r, \theta) |G_1 (\theta) \leq r \leq g_2(\theta), \alpha \leq \theta \leq \beta \}\), então temos
\[ \iiint_E f(r,\theta, z) r \, dr \, d\theta = \int_{\theta=\alpha}^{\theta=\beta} \int_{r=g_1(\theta)}^{r=g_2(\theta)} \int_{z=u_1(r,\theta)}^{z=u_2(r,\theta)} f(r,\theta,z) r \, dz \, dr \, d\theta. \nonumber \]
Existem fórmulas similares para projeções em outros planos de coordenadas. Podemos usar coordenadas polares nesses planos, se necessário.
Considere a região\(E\) dentro do cilindro circular direito com a equação\(r = 2 \, \sin \, \theta\), limitada abaixo pelo\(r\theta\) plano -e delimitada acima pela esfera com raio\(4\) centrado na origem (Figura 15.5.3). Configure uma integral tripla sobre essa região com uma função\(f(r, \theta, z)\) em coordenadas cilíndricas.
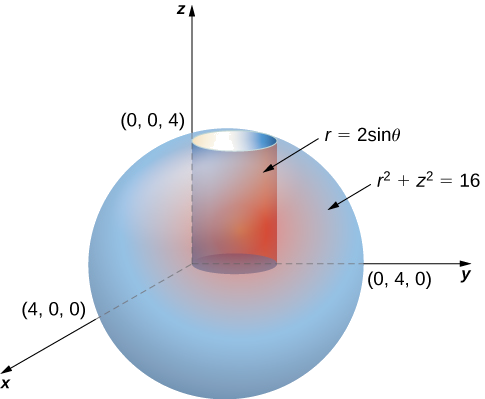
Solução
Primeiro, identifique se a equação da esfera é\(r^2 + z^2 = 16\). Podemos ver que os limites para\(z\) são\(0\) de\(z = \sqrt{16 - r^2}\) a. Então, os limites para\(r\) são\(0\) de\(r = 2 \, \sin \, \theta\) a. Finalmente, os limites para\(\theta\) são\(0\) de\(\pi\) a. Portanto, a região é\(E = \{(r,\theta, z)|0 \leq \theta \leq \pi, \, 0 \leq r \leq 2 \, \sin \, \theta, \, 0 \leq z \leq \sqrt{16 - r^2} \}.\) Portanto, a integral tripla é
\[\iiint_E f(r,\theta, z) r \, dz \, dr \, d\theta = \int_{\theta=0}^{\theta=\pi} \int_{r=0}^{r=2 \, \sin \, \theta} \int_{z=0}^{z=\sqrt{16-r^2}} f(r,\theta,z) r \, dz \, dr \, d\theta. \nonumber \]
Considere a região dentro do cilindro circular direito com a equação\(r=2 \, \sin \, \theta\) limitada abaixo pelo\(r\theta\) plano -e delimitada acima por\(z = 4 - y\). Configure uma integral tripla com uma função\(f(r,\theta,z)\) em coordenadas cilíndricas.
- Dica
-
Analise a região e desenhe um esboço.
- Resposta
-
\[\iiint_E f(r,\theta, z) r \, dz \, dr \, d\theta = \int_{\theta=0}^{\theta=\pi} \int_{r=0}^{r=2 \, \sin \, \theta} \int_{z=0}^{z=4-r \, \sin \, \theta} f(r,\theta,z) r \, dz \, dr \, d\theta. \nonumber \]
\(E\)Seja a região delimitada abaixo pelo cone\(z = \sqrt{x^2 + y^2}\) e acima pelo parabolóide\(z = 2 - x^2 - y^2\). (Figura 15.5.4). Configure uma integral tripla em coordenadas cilíndricas para encontrar o volume da região, usando as seguintes ordens de integração:
uma.\(dz \, dr \, d\theta\)
b.\(dr \, dz \, d\theta\)
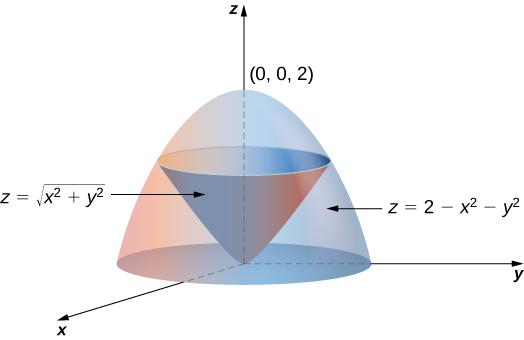
Solução
a. O cone é do raio 1 onde encontra o parabolóide. Como\(z = 2 - x^2 - y^2 = 2 - r^2\) e\(z = \sqrt{x^2 + y^2} = r^2\) (supondo\(r\) que não seja negativo), temos\(2 - r^2 = r\). Resolvendo, nós temos\(r^2 + r - 2 = (r + 2)(r - 1) = 0\). Desde então\(r \geq 0\), nós temos\(r = 1\). Portanto\(z = 1\). Portanto, a interseção dessas duas superfícies é um círculo de raio\(1\) no plano\(z = 1\). O cone é o limite inferior\(z\) e o parabolóide é o limite superior. A projeção da região no\(xy\) plano -é o círculo de raio\(1\) centrado na origem.
Assim, podemos descrever a região como\(E = \{(r, \theta, z) |0 \leq \theta \leq 2\pi, \, 0 \leq r \leq 1, \, r \leq z \leq 2 - r^2 \}\).
Portanto, a integral do volume é
\[V = \int_{\theta=0}^{\theta=2\pi} \int_{r=0}^{r=1} \int_{z=r}^{z=2-r^2} r \, dz \, dr \, d\theta. \nonumber \]
b. Também podemos escrever a superfície do cone como\(r = z\) e o parabolóide como\(r^2 = 2 - z\). O limite inferior para\(r\) é zero, mas o limite superior às vezes é o cone e outras vezes é o parabolóide. O avião\(z = 1\) divide a região em duas regiões. Então, a região pode ser descrita como\[E = \{(r,\theta,z)|0 \leq \theta \leq 2\pi, \, 0 \leq z \leq 1, \, 0 \leq r \leq z\} \cup \{(r,\theta,z)|0 \leq \theta \leq 2\pi, \, 1 \leq z \leq 2, \, 0 \leq r \leq \sqrt{2 - z}\}. \nonumber \]
Agora, a integral do volume se torna
\[V = \int_{\theta=0}^{\theta=2\pi} \int_{z=0}^{z=1} \int_{r=0}^{r=z} r \, dr \, dz \, d\theta + \int_{\theta=0}^{\theta=2\pi} \int_{z=1}^{z=2} \int_{r=0}^{r=\sqrt{2-z}} r \, dr \, dz \, d\theta. \nonumber \]
Refaça o exemplo anterior com a ordem de integração\(d\theta \, dz \, dr\).
- Dica
-
Observe que\(\theta\) é independente de\(r\)\(z\) e.
- Resposta
-
\(E = \{(r,\theta,z)|0 \leq \theta \leq 2\pi, \, 0 \leq z \leq 1, \, 0 \leq r \leq 2 - z^2\}\)e\[V = \int_{r=0}^{r=1} \int_{z=0}^{z=2 - r^2} \int_{\theta=0}^{\theta=2\pi} r \, d\theta \, dz \, dr. \nonumber \]
Solução
a. Observe que a equação para a esfera é
\[x^2 + y^2 + z^2 = 4 \, \text{or} \, r^2 + z^2 = 4 \nonumber \]
e a equação para o cilindro é
\[x^2 + y^2 = 1 \, \text{or} \, r^2 = 1. \nonumber \]
Assim, temos para a região\(E\)
\[E = \{(r,\theta,z)|0 \leq z \leq \sqrt{4 - r^2}, \, 0 \leq r \leq 1, \, 0 \leq \theta \leq 2\pi\} \nonumber \]
Portanto, a integral do volume é
\[\begin{align} V (E) = \int_{\theta=0}^{\theta=2\pi} \int_{r=0}^{r=1} \int_{z=0}^{z=\sqrt{4-r^2}} r \, dz \, dr \, d\theta \\ = \int_{\theta=0}^{\theta=2\pi} \int_{r=0}^{r=1} \left[ \left>rz\right|_{z=0}^{z=\sqrt{4-r^2}}\right] dr \, d\theta = \int_{\theta=0}^{\theta=2\pi} \int_{r=0}^{r=1} \left(r\sqrt{4 - r^2}\right) dr \, d\theta\\ = \int_0^{2\pi} \left(\frac{8}{3} - \sqrt{3} \right) d\theta = 2\pi \left(\frac{8}{3} - \sqrt{3} \right) \, \text{cubic units.} \end{align} \nonumber \]
b. Uma vez que a esfera é\(x^2 + y^2 + z^2 = 4\), que é\(r^2 + z^2 = 4\), e o cilindro é\(x^2 + y^2 = 1\), que é\(r^2 = 1\), nós temos\(1 + z^2 = 4\), isto é,\(z^2 = 3\). Assim, temos duas regiões, já que a esfera e o cilindro se cruzam\((1,\sqrt{3})\) no\(rz\) plano -
\[E_1 = \{ (r,\theta,z) | 0 \leq r \leq \sqrt{4 - r^2}, \, \sqrt{3} \leq z \leq 2, \, 0 \leq \theta \leq 2\pi\} \nonumber \]e
\[E_2 = \{(r,\theta,z) | 0 \leq r \leq 1, \, 0 \leq z \leq \sqrt{3}, \, 0 \leq \theta \leq 2\pi\}. \nonumber \]
Portanto, a integral do volume é
\[\begin{align} V(E) = \int_{\theta=0}^{\theta=2\pi} \int_{z=\sqrt{3}}^{z=2} \int_{r=0}^{r=\sqrt{4-r^2}} r \, dr \, dz \, d\theta + \int_{\theta=0}^{\theta=2\pi} \int_{z=0}^{z=\sqrt{3}} \int_{r=0}^{r=1} r \, dr \, dz \, d\theta\\ = \sqrt{3} \pi + \left( \dfrac{16}{3} - 3 \sqrt{3} \right) \pi = 2\pi \left( \frac{8}{3} - \sqrt{3} \right) \, \text{cubic units.} \end{align} \nonumber \]
Refaça o exemplo anterior com a ordem de integração\(d\theta \, dz \, dr\).
- Dica
-
Uma figura pode ser útil. Observe que\(\theta\) é independente de\(r\)\(z\) e.
- Resposta
-
\(E_2 = \{(r,\theta,z) | 0 \leq \theta \leq 2\pi, \, 0 \leq r \leq 1, \, r \leq z \leq \sqrt{4 - r^2}\}\)e
\[V = \int_{r=0}^{r=1} \int_{z=r}^{z=\sqrt{4-r^2}} \int_{\theta=0}^{\theta=2\pi} r \, d\theta \, dz \, dr. \nonumber \]
Revisão das coordenadas esféricas
No espaço tridimensional\(\mathbb{R}^3\) no sistema de coordenadas esféricas, especificamos um ponto\(P\) por sua\(\rho\) distância da origem, o ângulo polar\(\theta\) do\(x\) eixo positivo (o mesmo que no sistema de coordenadas cilíndricas) e o ângulo\(\varphi\) do positivo \(z\)-eixo e a linha\(OP\) (Figura\(\PageIndex{6}\)). Observe isso\(\rho > 0\)\(0 \leq \varphi \leq \pi\) e. (Consulte Coordenadas cilíndricas e esféricas para uma revisão.) As coordenadas esféricas são úteis para integrais triplas sobre regiões que são simétricas em relação à origem.
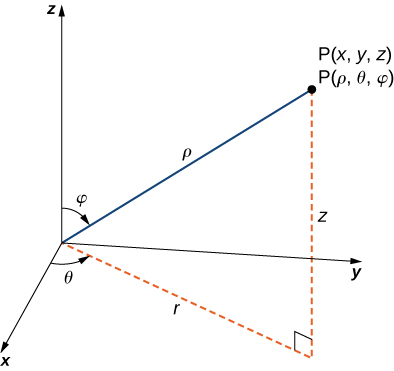
Lembre-se das relações que conectam coordenadas retangulares com coordenadas esféricas.
De coordenadas esféricas a coordenadas retangulares:
\[x = \rho \, \sin \, \varphi \, \cos \theta, \, y = \rho \, \sin \, \varphi \, \sin \, \theta, \, and \, z = \rho \, \cos \, \varphi. \nonumber \]
De coordenadas retangulares a coordenadas esféricas:
\[\rho^2 = x^2 + y^2 + z^2, \, \tan \, \theta = \frac{y}{x}, \, \varphi = \arccos \left( \frac{z}{\sqrt{x^2 + y^2 + z^2}}\right). \nonumber \]
Outros relacionamentos que é importante conhecer para conversões são
- \(r = \rho \, \sin \, \varphi\)
- \(\theta = \theta\)Essas equações são usadas para converter coordenadas esféricas em coordenadas cilíndricas.
- \(z = \rho \, \cos \, \varphi\)
e
- \(\rho = \sqrt{r^2 + z^2}\)
- \(\theta = \theta\)Essas equações são usadas para converter coordenadas cilíndricas em coordenadas esféricas.
- \(\varphi = \arccos \left(\frac{z}{\sqrt{r^2 + z^2}}\right)\)
\(\PageIndex{7}\)mostra algumas regiões sólidas que são convenientes para expressar em coordenadas esféricas.
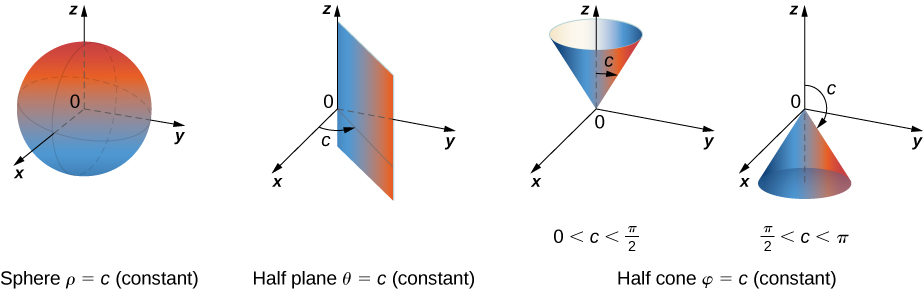
Integração em coordenadas esféricas
Agora estabelecemos uma integral tripla no sistema de coordenadas esféricas, como fizemos antes no sistema de coordenadas cilíndricas. Deixe a função\(f(\rho,\theta,\varphi)\) ser contínua em uma caixa esférica limitada,\(B = \{(\rho,\theta,\varphi) | a \leq \rho \leq b, \, \alpha \leq \theta \leq \beta, \, \gamma \leq \varphi \leq \psi \}\). Em seguida, dividimos cada intervalo em\(l,m,n\) e\(n\) subdivisões de forma que\(\Delta \rho = \frac{b - a}{l}, \, \Delta \theta = \frac{\beta - \alpha}{m}. \, \Delta \varphi = \frac{\psi - \gamma}{n}\). Agora podemos ilustrar o seguinte teorema para integrais triplas em coordenadas esféricas\((\rho_{ijk}^*, \theta_{ijk}^*, \varphi_{ijk}^*)\) como sendo qualquer ponto de amostra na subcaixa esférica\(B_{ijk}\). Para o elemento de volume da subcaixa\(\Delta V\) em coordenadas esféricas, temos\(\Delta V = (\Delta \rho)\, (\rho \Delta \varphi)\, (\rho \, \sin \, \varphi \, \Delta \theta)\), conforme mostrado na figura a seguir.
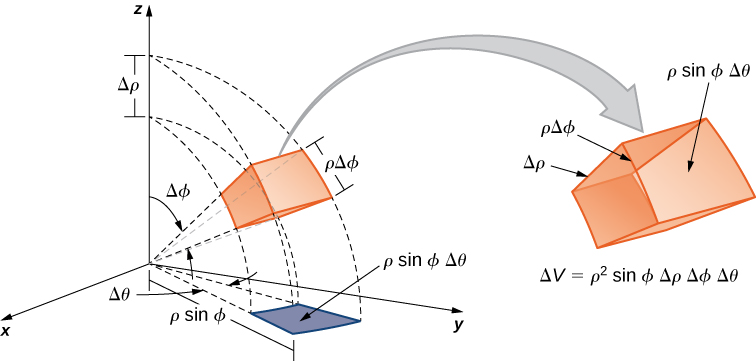
A integral tripla em coordenadas esféricas é o limite de uma soma tripla de Riemann,
\[\lim_{l,m,n \rightarrow \infty} \sum_{i=1}^l \sum_{j=1}^m \sum_{k=1}^n f ( \rho_{ijk}^*, \theta_{ijk}^*, \varphi_{ijk}^*) (\rho_{ijk}^*)^2 \sin \, \varphi \Delta \rho \Delta \theta \Delta \varphi \nonumber \]
desde que o limite exista.
Assim como as outras integrais múltiplas que examinamos, todas as propriedades funcionam de forma semelhante para uma integral tripla no sistema de coordenadas esféricas, assim como as integrais iteradas. O teorema de Fubini assume a seguinte forma.
Se\(f(\rho,\theta, \varphi)\) for contínuo em uma caixa sólida esférica\(B = [a,b] \times [\alpha,\beta] \times [\gamma , \psi]\), então
\[\iiint_B f(\rho,\theta,\varphi ) \, \rho^2 \sin \, \varphi d\rho \, d\varphi \, d\theta = \int_{\varphi=\gamma}^{\varphi=\psi} \int_{\theta=\alpha}^{\theta=\beta} \int_{\rho=a}^{\rho=b} f(\rho,\theta,\varphi) \, \rho^2 \sin \, \varphi \, d\rho \, d\varphi \, d\theta. \nonumber \]
Essa integral iterada pode ser substituída por outras integrais iteradas integrando em relação às três variáveis em outras ordens.
Como dito anteriormente, os sistemas de coordenadas esféricas funcionam bem para sólidos que são simétricos em torno de um ponto, como esferas e cones. Vejamos alguns exemplos antes de considerarmos integrais triplas em coordenadas esféricas em regiões esféricas gerais.
Avalie a integral tripla iterada
\[\int_{\theta=0}^{\theta=2\pi} \int_{\varphi=0}^{\varphi=\pi/2} \int_{\rho=0}^{\rho=1} \rho^2 \sin \, \varphi \, d\rho \, d\varphi \, d\theta. \nonumber \]
Solução
Como antes, neste caso, as variáveis na integral iterada são na verdade independentes umas das outras e, portanto, podemos integrar cada peça e multiplicar:
\[\int_0^{2\pi} \int_0^{\pi/2} \int_0^1 \rho^2 \sin \, \varphi \, d\rho \, d\varphi \, d\theta = \int_0^{2\pi} d\theta \int_0^{\pi/2} \sin \, \varphi \, d\varphi \int_0^1 \rho^2 d\rho = (2\pi) \, (1) \, \left(\frac{1}{3}\right) = \frac{2\pi}{3} \nonumber \]
O conceito de integração tripla em coordenadas esféricas pode ser estendido para a integração sobre um sólido geral, usando as projeções nos planos coordenados. Observe isso\(dV\) e\(dA\) signifique os incrementos em volume e área, respectivamente. As variáveis\(V\) e\(A\) são usadas como variáveis de integração para expressar as integrais.
A integral tripla de uma função contínua\(f(\rho,\theta,\varphi)\) sobre uma região sólida geral
\[E = \{(\rho,\theta,\varphi) |(\rho,\theta) \in D, u_1 (\rho, \theta) \leq \varphi \leq u_2 (\rho,\theta)\} \nonumber \]
in\(\mathbb{R}^3\), onde\(D\) está a\(E\) projeção de no\(\rho \theta\) plano -, é
\[\iiint_E f(\rho, \theta,\varphi) dV = \iint_D \left[ \int_{u_1(\rho,\theta)}^{u_2(\rho,\theta)} f(\rho,\theta,\varphi) \, d\varphi \right] \, dA. \nonumber \]
Em particular, se\(D = \{(\rho,\theta) | g_1 (\theta) \leq \rho \leq g_2 (\theta), \, \alpha \leq \theta \leq \beta\}\), o nós temos
\[\iiint_E f(\rho,\theta,\varphi) dV = \int_{\alpha}^{\beta} \int_{g_1(\theta)}^{g_2(\theta)} \int_{u_1(\rho,\theta)}^{u_2(\rho,\theta)} f(\rho,\theta,\varphi ) \rho^2 \sin \, \varphi \, d\varphi \, d\rho \, d\theta. \nonumber \]
Fórmulas similares ocorrem para projeções em outros planos coordenados.
Configure uma integral para o volume da região delimitada pelo cone\(z = \sqrt{3(x^2 + y^2)}\) e pelo hemisfério\(z = \sqrt{4 - x^2 - y^2}\) (veja a figura abaixo).
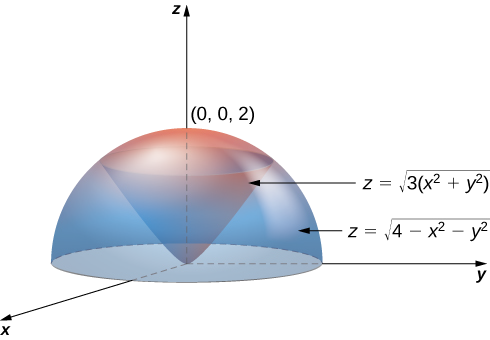
Solução
Usando as fórmulas de conversão de coordenadas retangulares para coordenadas esféricas, temos:
Para o cone:\(z = \sqrt{3(x^2 + y^2)}\) ou\(\rho \, \cos \, \varphi = \sqrt{3} \rho \, \sin \, \varphi\) ou\(\tan \, \varphi = \frac{1}{\sqrt{3}}\) ou\(\varphi = \frac{\pi}{6}\).
Para a esfera:\(z = \sqrt{4 - x^2 - y^2}\) ou\(z^2 + x^2 + y^2 = 4\) ou\(\rho^2 = 4\) ou\(\rho = 2\).
Assim, a integral tripla para o volume é
\[V(E) = \int_{\theta=0}^{\theta=2\pi} \int_{\varphi=0}^{\varphi+\pi/6} \int_{\rho=0}^{\rho=2} \rho^2 \sin \, \varphi \, d\rho \, d\varphi \, d\theta. \nonumber \]
Configure uma integral tripla para o volume da região sólida limitada acima pela esfera\(\rho = 2\) e delimitada abaixo pelo cone\(\varphi = \pi/3\).
- Dica
-
Siga as etapas do exemplo anterior.
- Resposta
-
\[V(E) = \int_{\theta=0}^{\theta=2\pi} \int_{\varphi=0}^{\varphi=\pi/3} \int_{\rho=0}^{\rho=2} \rho^2 \sin \, \varphi \, d\rho \, d\varphi \, d\theta \nonumber \]
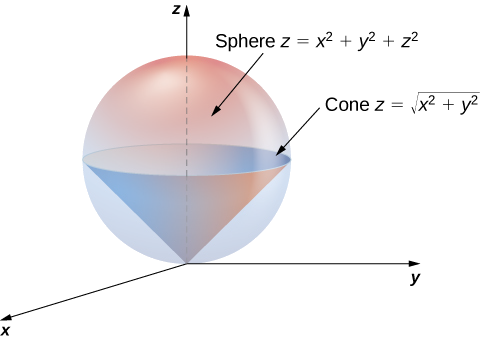
\(E\)Seja a região delimitada abaixo pelo cone\(z = \sqrt{x^2 + y^2}\) e acima pela esfera\(z = x^2 + y^2 + z^2\) (Figura 15.5.10). Configure uma integral tripla em coordenadas esféricas e encontre o volume da região usando as seguintes ordens de integração:
- \(d\rho \, d\phi \, d\theta\)
- \(d\varphi \, d\rho \, d\theta\)
Solução
a. Use as fórmulas de conversão para escrever as equações da esfera e do cone em coordenadas esféricas.
Para a esfera:
\[\begin{align} x^2 + y^2 + z^2 = z \\\rho^2 = \rho \, \cos \, \varphi \\\rho = \cos \, \varphi. \end{align} \nonumber \]
Para o cone:
\[\begin{align} z = \sqrt{x^2 + y^2}\\\rho \, \cos \, \varphi = \sqrt{\rho^2 \sin^2 \, \varphi \, \cos^2 \phi } \\ \rho \, \cos \, \varphi = \sqrt{\rho^2 \sin^2 \varphi \, (\cos^2\phi + \sin^2 \phi)}\\ \rho \, \cos \, \varphi = \rho \, \sin \, \varphi\\ \cos \, \varphi = \sin \, \varphi\\ \varphi = \pi/4. \end{align} \nonumber \]
Portanto, a integral para o volume da região sólida\(E\) se torna
\[V(E) = \int_{\theta=0}^{\theta=2\pi} \int_{\varphi=0}^{\varphi=\pi/4} \int_{\rho=0}^{\rho=\cos \, \varphi} \rho^2 \sin \, \varphi \, d\rho \, d\varphi \, d\theta. \nonumber \]
b. Considere o\(\varphi\rho\) plano X. Observe que os intervalos para\(\varphi\) e\(\rho\) (da parte a.) são
\[\begin{align} 0\leq \rho \sqrt{2}/2 \text{and}\, \sqrt{2} \leq \rho 1 \\ 0 \leq \varphi \leq \pi/4 0 \leq \rho \leq \cos \, \varphi \end{align} \nonumber \]
A curva\(\rho = \cos \, \varphi\) encontra a linha\(\varphi = \pi/4\) no ponto\((\pi/4,\sqrt{2}/2)\). Assim, para mudar a ordem de integração, precisamos usar duas partes:
\[0 \leq \rho \leq \sqrt{2}/2, \, 0 \leq \varphi \leq \pi/4 \nonumber \]e
\[\sqrt{2}/2 \leq \rho \leq 1, \, 0 \leq \varphi \leq \cos^{-1} \rho. \nonumber \]
Portanto, a integral para o volume da região sólida\(E\) se torna
\[V(E) = \int_{\theta=0}^{\theta=2\pi} \int_{\rho=0}^{\rho=\sqrt{2}/2} \int_{\varphi=0}^{\varphi=\pi/4} \rho^2 \sin \, \varphi \, d\varphi \, d\rho \, d\theta + \int_{\theta=0}^{\theta=2\pi} \int_{\rho=\sqrt{2}/2}^{\rho=1} \int_{\varphi=0}^{\varphi=\cos^{-1}\rho} \rho^2 \sin \, \varphi \, d\varphi \, d\rho \, d\theta \nonumber \]
Em cada caso, a integração resulta em\(V(E) = \frac{\pi}{8}\).
Antes de terminarmos esta seção, apresentamos alguns exemplos que podem ilustrar a conversão de coordenadas retangulares em coordenadas cilíndricas e de coordenadas retangulares em coordenadas esféricas.
Converta a seguinte integral em coordenadas cilíndricas:
\[\int_{y=-1}^{y=1} \int_{x=0}^{x=\sqrt{1-y^2}} \int_{z=x^2+y^2}^{z=\sqrt{x^2+y^2}} xyz \, dz \, dx \, dy. \nonumber \]
Solução
Os intervalos das variáveis são
\[\begin{align} -1 \leq y \leq y \\ 0 \leq x \leq \sqrt{1 - y^2} \\x^2 + y^2 \leq z \leq \sqrt{x^2 + y^2}. \end{align} \nonumber \]
As duas primeiras desigualdades descrevem a metade direita de um círculo de raio\(1\). Portanto, os intervalos para\(\theta\) e\(r\) são
\[-\frac{\pi}{2} \leq \theta \leq \frac{\pi}{2} \, \text{and} \, 0 \leq r \leq 1. \nonumber \]
Os limites do\(z\) são\(r^2 \leq z \leq r\), portanto
\[\int_{y=-1}^{y=1} \int_{x=0}^{x=\sqrt{1-y^2}} \int_{z=x^2+y^2}^{z=\sqrt{x^2+y^2}} xyz \, dz \, dx \, dy = \int_{\theta=-\pi/2}^{\theta=\pi/2} \int_{r=0}^{r=1} \int_{z=r^2}^{z=r} r(r \, \cos \theta) \, (r \, \sin \, \theta) \, z \, dz \, dr \, d\theta. \nonumber \]
Converta a seguinte integral em coordenadas esféricas:
\[\int_{y=0}^{y=3} \int_{x=0}^{x=\sqrt{9-y^2}} \int_{z=\sqrt{x^2+y^2}}^{z=\sqrt{18-x^2-y^2}} (x^2 + y^2 + z^2) dz \, dx \, dy. \nonumber \]
Solução
Os intervalos das variáveis são
\[\begin{align} 0 \leq y \leq 3\\ 0 \leq x \leq \sqrt{9 - y^2} \\ \sqrt{x^2 + y^2} \leq z \leq \sqrt{18 - x^2 - y^2}. \end{align} \nonumber \]
Os dois primeiros intervalos de variáveis descrevem um quarto de disco no primeiro\(xy\) quadrante do plano. Portanto, o intervalo para\(\theta\) é\(0 \leq \theta \leq \frac{\pi}{2}\).
O limite inferior\(z = \sqrt{x^2 + y^2}\) é a metade superior de um cone e o limite superior\(z = \sqrt{18 - x^2 - y^2}\) é a metade superior de uma esfera. Portanto, nós temos\(0 \leq \rho \leq \sqrt{18}\), o que é\(0 \leq \rho \leq 3\sqrt{2}\).
Para os intervalos de,\(\varphi\) precisamos descobrir onde o cone e a esfera se cruzam, então resolva a equação
\[\begin{align} r^2 + z^2 = 18\\(\sqrt{x^2 + y^2})^2 + z^2 = 18 \\z^2 + z^2 = 18 \\2z^2 = 18 \\z^2 = 9 \\z = 3. \end{align} \nonumber \]
Isso dá
\[\begin{align} 3\sqrt{2} \, \cos \, \varphi = 3 \\\cos \, \varphi = \frac{1}{\sqrt{2}} \\\varphi = \frac{\pi}{4}. \end{align} \nonumber \]
Juntando isso, obtemos
\[\int_{y=0}^{y=3} \int_{x=0}^{x=\sqrt{9-y^2}} \int_{z=\sqrt{x^2+y^2}}^{z=\sqrt{18-x^2-y^2}} (x^2 + y^2 + z^2) dz \, dx \, dy = \int_{\varphi=0}^{\varphi=\pi/4} \int_{\theta=0}^{\theta=\pi/2} \int_{\rho=0}^{\rho=3\sqrt{2}} \rho^4 \sin \, \varphi \, d\rho \, d\theta \, d\varphi. \nonumber \]
Use coordenadas retangulares, cilíndricas e esféricas para configurar integrais triplos para encontrar o volume da região dentro da esfera,\(x^2 + y^2 + z^2 = 4\) mas fora do cilindro\(x^2 + y^2 = 1\).
- Resposta: Retangular
-
\[\int_{x=-2}^{x=2} \int_{y=-\sqrt{4-x^2}}^{y=\sqrt{4-x^2}} \int_{z=-\sqrt{4-x^2-y^2}}^{z=\sqrt{4-x^2-y^2}} dz \, dy \, dx - \int_{x=-1}^{x=1} \int_{y=-\sqrt{1-x^2}}^{y=\sqrt{1-x^2}} \int_{z=-\sqrt{4-x^2-y^2}}^{z=\sqrt{4-x^2-y^2}} dz \, dy \, dx. \nonumber \]
- Resposta: Cilíndrico
-
\[\int_{\theta=0}^{\theta=2\pi} \int_{r=1}^{r=2} \int_{z=-\sqrt{4-r^2}}^{z=\sqrt{4-r^2}} r \, dz \, dr \, d\theta. \nonumber \]
- Resposta: Esférico
-
\[\int_{\varphi=\pi/6}^{\varphi=5\pi/6} \int_{\theta=0}^{\theta=2\pi} \int_{\rho=\csc \, \varphi}^{\rho=2} \rho^2 \sin \, \varphi \, d\rho \, d\theta \, d\varphi. \nonumber \]
Agora que estamos familiarizados com o sistema de coordenadas esféricas, vamos encontrar o volume de algumas figuras geométricas conhecidas, como esferas e elipsoides.
Encontre o volume do planetário esférico em l'Hemisphèric em Valência, Espanha, que tem cinco andares de altura e um raio de aproximadamente\(50\) pés, usando a equação\(x^2 + y^2 + z^2 = r^2\).

Solução
Calculamos o volume da bola no primeiro octante, onde\(x \leq 0, \, y \leq 0\), e\(z \leq 0\), usando coordenadas esféricas, e depois multiplicamos o resultado por\(8\) para simetria. Como consideramos a região\(D\) como a primeira octante na integral, os intervalos das variáveis são
\[0 \leq \varphi \leq \frac{\pi}{2}, \, 0 \leq \rho \leq r, \, 0 \leq \theta \leq \frac{\pi}{2}. \nonumber \]
Portanto,
\[\begin{align} V = \iiint_D dx \, dy \, dz = 8 \int_{\theta=0}^{\theta=\pi/2} \int_{\rho=0}^{\rho=\pi} \int_{\varphi=0}^{\varphi=\pi/2} \rho^2 \sin \, \theta \, d\varphi \, d\rho \, d\varphi \\ =8 \int_{\varphi=0}^{\varphi=\pi/2} d\varphi \int_{\rho=0}^{\rho=r} \rho^2 d\rho \int_{\theta=0}^{\theta=\pi/2} \sin \, \theta \, d\theta \\ = 8 \, \left(\frac{\pi}{2}\right) \, \left( \frac{r^3}{3} \right) \, (1) \\ =\dfrac{4}{3} \pi r^3.\end{align} \nonumber \]
Isso combina exatamente com o que sabíamos. Portanto, para uma esfera com um raio de aproximadamente\(50\) pés, o volume é\(\frac{4}{3} \pi (50)^3 \approx 523,600 \, ft^3\).
Para o próximo exemplo, encontramos o volume de um elipsóide.
Encontre o volume do elipsoide\(\frac{x^2}{a^2} + \frac{y^2}{b^2} + \frac{z^2}{c^2} = 1\).
Solução
Novamente, usamos a simetria e avaliamos o volume do elipsóide usando coordenadas esféricas. Como antes, usamos o primeiro octante\(x \leq 0, \, y \leq 0\)\(z \leq 0\) e depois multiplicamos o resultado por\(8\).
Nesse caso, os intervalos das variáveis são
\[0 \leq \varphi \leq \frac{\pi}{2} \, 0 \leq \rho \leq 1, \, \text{and} \, 0 \leq \theta \leq \frac{\pi}{2}. \nonumber \]
Além disso, precisamos mudar as coordenadas retangulares para esféricas desta forma:
\[x = a \rho \, \cos \, \varphi \, \sin \, \theta, \, y = b\rho \, \sin \, \varphi \, \sin \, \theta, \, \text{and} \, z = cp \, \cos \theta. \nonumber \]
Em seguida, o volume do elipsóide se torna
\[\begin{align} V = \iiint_D dx \, dy \, dz \\ = 8 \int_{\theta=0}^{\theta=\pi/2} \int_{\rho=0}^{\rho=1} \int_{\varphi=0}^{\varphi=\pi/2} abc \, \rho^2 \sin \, \theta \, d\varphi \, d\rho \, d\theta \\ \\ = 8abc \int_{\varphi=0}^{\varphi=\pi/2} d\varphi \int_{\rho=0}^{\rho=1} \rho^2 d\rho \int_{\theta=0}^{\theta=\pi/2} \sin \, \theta \, d\theta \\ = 8abc \left(\frac{\pi}{2}\right) \left( \frac{1}{3}\right) (1) \\ = \frac{4}{3} \pi abc. \end{align} \nonumber \]
Encontre o volume do espaço dentro do elipsóide\(\frac{x^2}{75^2} + \frac{y^2}{80^2} + \frac{z^2}{90^2} = 1\) e fora da esfera\(x^2 + y^2 + z^2 = 50^2\).
Solução
Esse problema está diretamente relacionado à estrutura hemisférica. O volume de espaço dentro do elipsóide e fora da esfera pode ser útil para calcular a despesa de aquecer ou resfriar esse espaço. Podemos usar os dois exemplos anteriores para o volume da esfera e do elipsoide e depois do substrato.
Primeiro, encontramos o volume do elipsóide usando\(a = 75\) ft,\(b = 80\) ft e\(c = 90\) ft no resultado do Example. Portanto, o volume do elipsóide é
\[V_{ellipsoid} = \frac{4}{3} \pi (75)(80)(90) \approx 2,262,000 \, ft^3. \nonumber \]
Do exemplo, o volume da esfera é
\[V_{sphere} \approx 523,600 \, ft^3. \nonumber \]
Portanto, o volume do espaço dentro do elipsóide\(\frac{x^2}{75^2} + \frac{y^2}{80^2} + \frac{z^2}{90^2} = 1\) e fora da esfera\(x^2 + y^2 + z^2 = 50^2\) é de aproximadamente
\[V_{Hemispheric} = V_{ellipsoid} - V_{sphere} = 1,738,400 \, ft^3. \nonumber \]
Andar de balão é um passatempo relaxante e tranquilo que muitas pessoas gostam. Muitas reuniões de balonistas acontecem em todo o mundo, como a Festa Internacional de Balões de Albuquerque. O evento de Albuquerque é o maior festival de balões de ar quente do mundo, com mais de\(500\) balões participando a cada ano.

Como o nome indica, os balões de ar quente usam ar quente para gerar sustentação. (O ar quente é menos denso do que o ar mais frio, então o balão flutua enquanto o ar quente permanece quente.) O calor é gerado por um queimador de propano suspenso abaixo da abertura da cesta. Depois que o balão decola, o piloto controla a altitude do balão, usando o queimador para aquecer o ar e subir ou usando uma abertura próxima ao topo do balão para liberar ar aquecido e descer. No entanto, o piloto tem muito pouco controle sobre para onde o balão vai — os balões estão à mercê dos ventos. A incerteza sobre onde vamos parar é uma das razões pelas quais os balonistas se sentem atraídos pelo esporte.
Neste projeto, usamos integrais triplos para aprender mais sobre balões de ar quente. Modelamos o balão em duas peças. O topo do balão é modelado por uma meia esfera de raio 28
pés. O fundo do balão é modelado por um tronco de cone (pense em uma casquinha de sorvete com a ponta pontiaguda cortada). O raio da extremidade maior do tronco é\(28\) pés e o raio da extremidade pequena do tronco é\(28\) pés. Um gráfico do nosso modelo de balão e um diagrama transversal mostrando as dimensões são mostrados na figura a seguir.
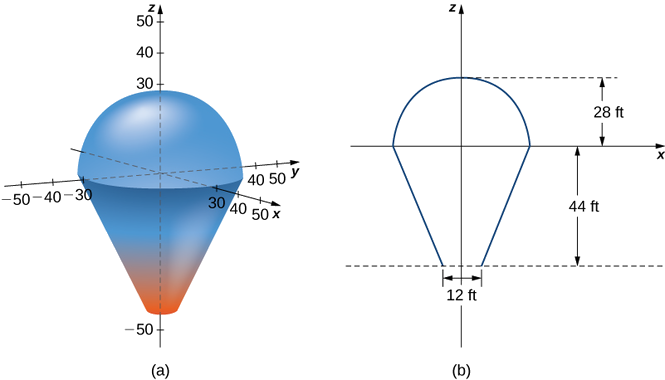
Primeiro, queremos encontrar o volume do balão. Se olharmos separadamente para a parte superior e inferior do balão, veremos que são sólidos geométricos com fórmulas de volume conhecidas. No entanto, ainda vale a pena configurar e avaliar as integrais que precisaríamos para encontrar o volume. Se calcularmos o volume usando a integração, podemos usar as fórmulas de volume conhecidas para verificar nossas respostas. Isso ajudará a garantir que as integrais sejam configuradas corretamente para os estágios posteriores e mais complicados do projeto.
1. Encontre o volume do balão de duas maneiras.
a. Use integrais triplos para calcular o volume. Considere cada parte do balão separadamente. (Considere o uso de coordenadas esféricas para a parte superior e coordenadas cilíndricas para a parte inferior.)
b. Verifique a resposta usando as fórmulas para o volume de uma esfera e para o volume de um cone,\(V = \frac{1}{3} \pi r^2 h\).\(V = \frac{4}{3}\pi r^3\)
Na realidade, calcular a temperatura em um ponto dentro do balão é uma tarefa extremamente complicada. Na verdade, um ramo inteiro da física (termodinâmica) é dedicado ao estudo do calor e da temperatura. Para os propósitos deste projeto, no entanto, faremos algumas suposições simplificadoras sobre como a temperatura varia de ponto a ponto dentro do balão. Suponha que, pouco antes da decolagem, a temperatura (em graus Fahrenheit) do ar dentro do balão varie de acordo com a função\[T_0 (r,\theta,z) = \frac{z - r}{10} + 210. \nonumber \]
2. Qual é a temperatura média do ar no balão logo antes da decolagem? (Novamente, observe cada parte do balão separadamente e não se esqueça de converter a função em coordenadas esféricas ao olhar para a parte superior do balão.)
Agora, o piloto ativa o gravador por\(10\) segundos. Essa ação afeta a temperatura em uma coluna\(12\) de pés de largura com\(20\) pés de altura, diretamente acima do queimador. Uma seção transversal do balão representando esta coluna é mostrada na figura a seguir
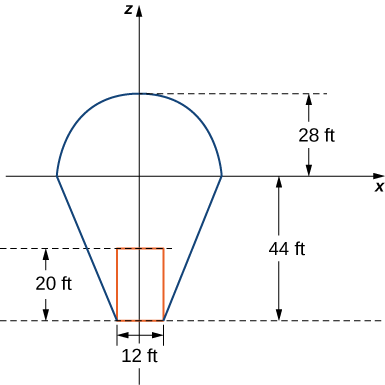
Suponha que após o piloto ativar o queimador por\(10\) segundos, a temperatura do ar na coluna descrita acima aumente de acordo com a fórmula
\[H(r,\theta,z) = -2z - 48. \nonumber \]
Em seguida, a temperatura do ar na coluna é dada por\[T_1(r,\theta,z) = \frac{z - r}{10} + 210 + (-2z - 48), \nonumber \]
enquanto a temperatura no restante do balão ainda é dada por\[T_0(r,\theta,z) = \frac{z - r}{10} + 210. \nonumber \]
3. Encontre a temperatura média do ar no balão após o piloto ter ativado o queimador por\(10\) segundos.
Conceitos chave
- Para calcular uma integral tripla em coordenadas cilíndricas, use a integral iterada\[\int_{\theta=\alpha}^{\theta=\beta} \int_{r=g_1(\theta)}^{r=g_2(\theta)} \int_{z=u_1(r,\theta)}^{u_2(r,\theta)} f(r,\theta,z)r \, dz \, dr \, d\theta. \nonumber \nonumber \]
- Para calcular uma integral tripla em coordenadas esféricas, use a integral iterada\[\int_{\theta=\alpha}^{\theta=\beta} \int_{\rho=g_1(\theta)}^{\rho=g_2(\theta)} \int_{\varphi=u_1(r,\theta)}^{u_2(r,\theta)} f(\rho,\theta,\varphi) \, \rho^2 \sin \varphi \, d\varphi \, d\rho \, d\theta. \nonumber \nonumber \]
Equações chave
- Integral tripla em coordenadas cilíndricas\[\iiint_B g(s,y,z)dV = \iiint_B g(r \, \cos \theta, \, r \, \sin \, \theta, \, z) r \, dr \, d\theta \, dz = \iiint_B f(r,\theta,z) r \, dr \, d\theta \, dz \nonumber \]
- Integral tripla em coordenadas esféricas\[\iiint_B f(\rho,\theta,\varphi) \rho^2 \sin \varphi \, d\rho \, d\varphi \, d\theta = \int_{\varphi=\gamma}^{\varphi=\psi} \int_{\theta=\alpha}^{\theta=\beta} \int_{\rho=a}^{\rho=b} f(\rho, \theta, \varphi) \rho^2 \sin \, \varphi \, d\rho \, d\varphi \, d\theta\nonumber \]
Glossário
- integral tripla em coordenadas cilíndricas
-
o limite de uma soma tripla de Riemann, desde que exista o seguinte limite:
\[lim_{l,m,n\rightarrow\infty} \sum_{i=1}^l \sum_{j=1}^m \sum_{k=1}^n f(r_{ijk}^*, \theta_{ijk}^*, s_{ijk}^*) r_{ijk}^* \Delta r \Delta \theta \Delta z \nonumber \]
- integral tripla em coordenadas esféricas
-
o limite de uma soma tripla de Riemann, desde que exista o seguinte limite:
\[lim_{l,m,n\rightarrow\infty} \sum_{i=1}^l \sum_{j=1}^m \sum_{k=1}^n f(\rho_{ijk}^*, \theta_{ijk}^*, \varphi_{ijk}^*) (\rho_{ijk}^*)^2 \sin \, \varphi \Delta \rho \Delta \theta \Delta \varphi \nonumber \]



Seja E a região delimitada abaixo pelo\(r\theta\) plano -, acima pela esfera\(x^2 + y^2 + z^2 = 4\) e nas laterais pelo cilindro\(x^2 + y^2 = 1\) (Figura 15.5.5). Configure uma integral tripla em coordenadas cilíndricas para encontrar o volume da região usando as seguintes ordens de integração e, em cada caso, encontre o volume e verifique se as respostas são as mesmas: