Skip to main content
Global

15.5E: Exercícios para a Seção 15.5

  1. Last updated
  2. Save as PDF
  • Page ID
    188137

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Nos exercícios 1 a 8, avalie as integrais triplas\(\displaystyle \iiint_E f(x,y,z) \, dV\) sobre o sólido\(E\).

    1. \(f(x,y,z) = z, \quad B = \big\{(x,y,z)\, | \,x^2 + y^2 \leq 9, \quad x \leq 0, \quad y \leq 0, \quad 0 \leq z \leq 1\big\}\)

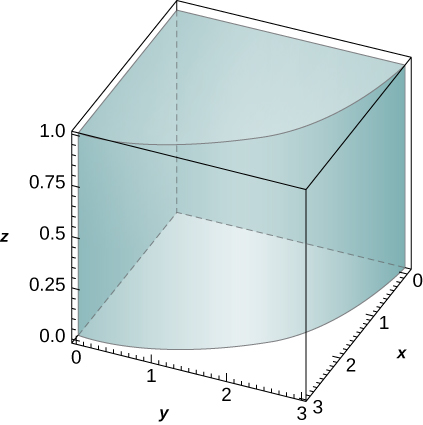
    Um quarto de seção de um cilindro com altura 1 e raio 3.

    Resposta
    \(\frac{9\pi}{8}\)

    2. \(f(x,y,z) = xz^2, \space B = \big\{(x,y,z)\, | \,x^2 + y^2 \leq 16, \space x \geq 0, \space y \leq 0, \space -1 \leq z \leq 1\big\}\)

    3. \(f(x,y,z) = xy, \space B = \big\{(x,y,z)\, | \,x^2 + y^2 \leq 1, \space x \geq 0, \space x \geq y, \space -1 \leq z \leq 1\big\}\)

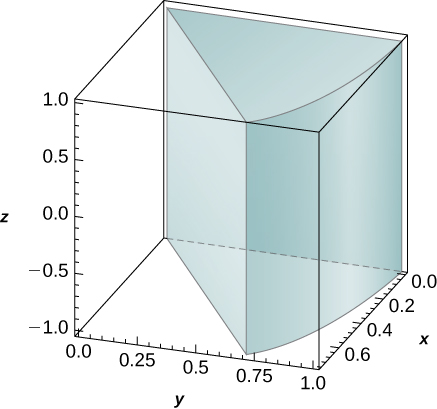
    A wedge with radius 1, height 1, and angle pi/4.

    Resposta
    \(\frac{1}{8}\)

    4. \(f(x,y,z) = x^2 + y^2, \space B = \big\{(x,y,z)\, | \,x^2 + y^2 \leq 4, \space x \geq 0, \space x \leq y, \space 0 \leq z \leq 3\big\}\)

    5. \(f(x,y,z) = e^{\sqrt{x^2+y^2}}, \space B = \big\{(x,y,z)\, | \,1 \leq x^2 + y^2 \leq 4, \space y \leq 0, \space x \leq y\sqrt{3}, \space 2 \leq z \leq 3 \big\}\)

    Resposta
    \(\frac{\pi e^2}{6}\)

    6. \(f(x,y,z) = \sqrt{x^2 + y^2}, \space B = \big\{(x,y,z)\, | \,1 \leq x^2 + y^2 \leq 9, \space y \leq 0, \space 0 \leq z \leq 1\big\}\)

    7. a.\(B\) Seja uma concha cilíndrica com raio interno\(b\), raio\(a\) externo e altura\(c\) onde\(0 < a < b\)\(c>0\) e. Suponha que uma função\(F\) definida em\(B\) possa ser expressa em coordenadas cilíndricas como\(F(x,y,z) = f(r) + h(z)\), onde\(f\) e\(h\) são funções diferenciáveis. Se\(\displaystyle \int_a^b \bar{f} (r) \,dr = 0\) e\(\bar{h}(0) = 0\), onde\(\bar{f}\) e\(\bar{h}\) são antiderivadas de\(f\) e\(h\), respectivamente, mostram que\(\displaystyle \iiint_B F(x,y,z) \,dV = 2\pi c (b\bar{f} (b) - a \bar{f}(a)) + \pi(b^2 - a^2) \bar{h} (c).\)

    b. Use o resultado anterior para mostrar\( \displaystyle \iiint_B \left(z + \sin \sqrt{x^2 + y^2}\right) \,dx \space dy \space dz = 6 \pi^2 ( \pi - 2),\) onde\(B\) está uma concha cilíndrica com raio interno\(2\pi\), raio\(\pi\) externo e altura\(2\).

    8. a.\(B\) Seja uma concha cilíndrica com raio interno, raio\(a\) externo\(b\) e altura\(c\) onde\(0 < a < b\)\(c > 0\) e. Suponha que uma função\(F\) definida em\(B\) possa ser expressa em coordenadas cilíndricas como\(F(x,y,z) = f(r) g(\theta) f(z)\), onde\(f, \space g,\) e\(h\) são funções diferenciáveis. Se\(\displaystyle\int_a^b \tilde{f} (r) \, dr = 0,\) onde\(\tilde{f}\) é uma antiderivada de\(f\), mostre que\(\displaystyle\iiint_B F (x,y,z)\,dV = [b\tilde{f}(b) - a\tilde{f}(a)] [\tilde{g}(2\pi) - \tilde{g}(0)] [\tilde{h}(c) - \tilde{h}(0)],\) onde\(\tilde{g}\) e\(\tilde{h}\) são antiderivadas de\(g\) e\(h\), respectivamente.

    b. Use o resultado anterior para mostrar\(\displaystyle\iiint_B z \sin \sqrt{x^2 + y^2} \,dx \space dy \space dz = - 12 \pi^2,\) onde\(B\) está uma concha cilíndrica com raio interno\(2\pi\), raio\(\pi\) externo e altura\(2\).

    Nos exercícios 9 a 12, os limites do sólido\(E\) são dados em coordenadas cilíndricas.

    a. Expresse a região\(E\) em coordenadas cilíndricas.

    b. Converta\(\displaystyle \iiint_E f(x,y,z) \,dV\) a integral em coordenadas cilíndricas.

    9. \(E\)é limitado pelo cilindro circular direito\(r = 4 \sin \theta\), pelo\(r\theta\) plano -e pela esfera\(r^2 + z^2 = 16\).

    Resposta

    uma.\(E = \big\{(r,\theta,z)\, | \,0 \leq \theta \leq \pi, \space 0 \leq r \leq 4 \sin \theta, \space 0 \leq z \leq \sqrt{16 - r^2}\big\}\)

    b.\(\displaystyle\int_0^{\pi} \int_0^{4 \sin \theta} \int_0^{\sqrt{16-r^2}} f(r,\theta, z) r \, dz \space dr \space d\theta\)

    10. \(E\)é limitado pelo cilindro circular direito\(r = \cos \theta\), pelo\(r\theta\) plano -e pela esfera\(r^2 + z^2 = 9\).

    11. \(E\)está localizado no primeiro octante e é limitado pelo parabolóide circular\(z = 9 - 3r^2\), pelo cilindro\(r = \sqrt{3}\) e pelo plano\(r(\cos \theta + \sin \theta) = 20 - z\).

    Resposta

    uma.\(E = \big\{(r,\theta,z) \, | \, 0 \leq \theta \leq \frac{\pi}{2}, \space 0 \leq r \leq \sqrt{3}, \space 9 - r^2 \leq z \leq 10 - r(\cos \theta + \sin \theta)\big\}\)

    b.\(\displaystyle\int_0^{\pi/2} \int_0^{\sqrt{3}} \int_{9-r^2}^{10-r(\cos \theta + \sin \theta)} f(r,\theta,z) r \space dz \space dr \space d\theta\)

    12. \(E\)está localizado no primeiro octante fora do parabolóide circular\(z = 10 - 2r^2\) e dentro do cilindro\(r = \sqrt{5}\) e é limitado também pelos planos\(z = 20\)\(\theta = \frac{\pi}{4}\) e.

    Nos exercícios 13 a 16, a função\(f\) e a região\(E\) são dadas.

    a. Expresse a região\(E\) e a função\(f\) em coordenadas cilíndricas.

    b. Converta a integral\(\displaystyle \iiint_B f(x,y,z) \,dV\) em coordenadas cilíndricas e avalie-a.

    13. \(f(x,y,z) = x^2 + y^2\),\(E = \big\{(x,y,z)\, | \,0 \leq x^2 + y^2 \leq 9, \space x \geq 0, \space y \geq 0, \space 0 \leq z \leq x + 3\big\}\)

    Resposta

    uma.\(E = \big\{(r,\theta,z)\, | \,0 \leq r \leq 3, \space 0 \leq \theta \leq \frac{\pi}{2}, \space 0 \leq z \leq r \space \cos \theta + 3\big\},\)
    \(f(r,\theta,z) = \frac{1}{r \space \cos \theta + 3}\)

    b.\(\displaystyle \int_0^3 \int_0^{\pi/2} \int_0^{r \space \cos \theta+3} \frac{r}{r \space \cos \theta + 3} \, dz \space d\theta \space dr = \frac{9\pi}{4}\)

    14. \(f(x,y,z) = x^2 + y^2, \space E = \big\{(x,y,z) |0 \leq x^2 + y^2 \leq 4, \space y \geq 0, \space 0 \leq z \leq 3 - x \big\}\)

    15. \(f(x,y,z) = x, \space E = \big\{(x,y,z)\, | \,1 \leq y^2 + z^2 \leq 9, \space 0 \leq x \leq 1 - y^2 - z^2\big\}\)

    Resposta

    uma\(y = r \space \cos \theta, \space z = r \space \sin \theta, \space x = z,\space E = \big\{(r,\theta,z)\, | \,1 \leq r \leq 3, \space 0 \leq \theta \leq 2\pi, \space 0 \leq z \leq 1 - r^2\big\}, \space f(r,\theta,z) = z\);.

    b.\(\displaystyle \int_1^3 \int_0^{2\pi} \int_0^{1-r^2} z r \space dz \space d\theta \space dr = \frac{356 \pi}{3}\)

    16. \(f(x,y,z) = y, \space E = \big\{(x,y,z)\, | \,1 \leq x^2 + z^2 \leq 9, \space 0 \leq y \leq 1 - x^2 - z^2 \big\}\)

    Nos exercícios 17 a 24, determine o volume do sólido\(E\) cujos limites são dados em coordenadas retangulares.

    17. \(E\)está acima do\(xy\) plano -, dentro do cilindro\(x^2 + y^2 = 1\) e abaixo do plano\(z = 1\).

    Resposta
    \(\pi\)

    18. \(E\)está abaixo do plano\(z = 1\) e dentro do parabolóide\(z = x^2 + y^2\).

    19. \(E\)é limitado pelo cone circular\(z = \sqrt{x^2 + y^2}\)\(z = 1\) e.

    Resposta
    \(\frac{\pi}{3}\)

    20. \(E\)está localizado acima do\(xy\) plano -, abaixo\(z = 1\), fora do hiperbolóide\(x^2 + y^2 - z^2 = 1\) de uma folha e dentro do cilindro\(x^2 + y^2 = 2\).

    21. \(E\)está localizado dentro do cilindro\(x^2 + y^2 = 1\) e entre os parabolóides circulares\(z = 1 - x^2 - y^2\)\(z = x^2 + y^2\) e.

    Resposta
    \(\pi\)

    22. \(E\)está localizado dentro da esfera\(x^2 + y^2 + z^2 = 1\), acima do\(xy\) plano -e dentro do cone circular\(z = \sqrt{x^2 + y^2}\).

    23. \(E\)está localizado fora do cone circular\(x^2 + y^2 = (z - 1)^2\) e entre os planos\(z = 0\)\(z = 2\) e.

    Resposta
    \(\frac{4\pi}{3}\)

    24. \(E\)está localizado fora do cone circular\(z = 1 - \sqrt{x^2 + y^2}\), acima do\(xy\) plano -, abaixo do parabolóide circular e entre os planos\(z = 0\)\(z = 2\) e.

    25. [T] Use um sistema computacional de álgebra (CAS) para representar graficamente o sólido cujo volume é dado pela integral iterada em coordenadas cilíndricas.\(\displaystyle \int_{-\pi/2}^{\pi/2} \int_0^1 \int_{r^2}^r r \, dz \, dr \, d\theta.\) Encontre o volume\(V\) do sólido. Arredonde sua resposta para quatro casas decimais.

    Resposta

    \(V = \frac{pi}{12} \approx 0.2618\)

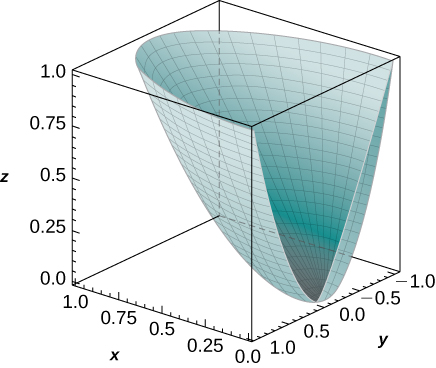
    Um quarto de seção de um elipsóide com largura 2, altura 1 e profundidade 1.

    26. [T] Use um CAS para representar graficamente o sólido cujo volume é dado pela integral iterada em coordenadas cilíndricas\(\displaystyle \int_0^{\pi/2} \int_0^1 \int_{r^4}^r r \, dz \, dr \, d\theta.\) Find the volume \(E\) of the solid. Round your answer to four decimal places.

    27. Convert the integral \(\displaystyle\int_0^1 \int_{-\sqrt{1-y^2}}^{\sqrt{1-y^2}} \int_{x^2+y^2}^{\sqrt{x^2+y^2}} xz \space dz \space dx \space dy\) into an integral in cylindrical coordinates.

    Answer
    \(\displaystyle\int_0^1 \int_0^{\pi} \int_{r^2}^r zr^2 \space \cos \theta \, dz \space d\theta \space dr\)

    28. Convert the integral \(\displaystyle \int_0^2 \int_0^y \int_0^1 (xy + z) \, dz \space dx \space dy\) into an integral in cylindrical coordinates.

    In exercises 29 - 32, evaluate the triple integral \(\displaystyle \iiint_B f(x,y,z) \,dV\) over the solid \(B\).

    29. \(f(x,y,z) = 1, \space B = \big\{(x,y,z)\, | \,x^2 + y^2 + z^2 \leq 90, \space z \geq 0\big\}\)

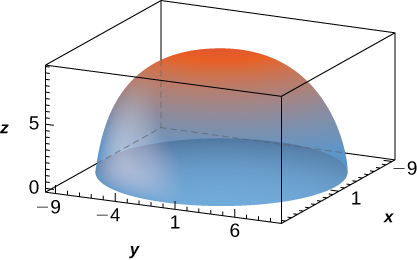
    A filled-in half-sphere with radius 3 times the square root of 10.

    [Ocultar solução]

    Resposta
    \(180 \pi \sqrt{10}\)

    30. \(f(x,y,z) = 1 - \sqrt{x^2 + y^2 + z^2}, \space B = \big\{(x,y,z)\, | \,x^2 + y^2 + z^2 \leq 9, \space y \geq 0, \space z \geq 0\big\}\)

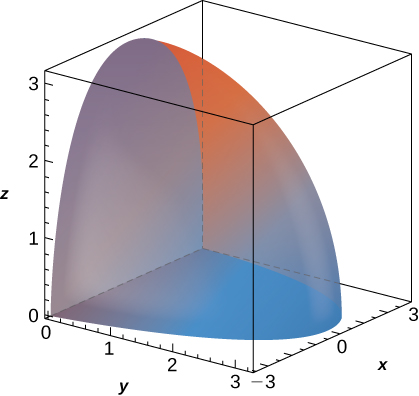
    Um quarto de seção de um ovóide com altura 8, largura 8 e comprimento 18.

    31. \(f(x,y,z) = \sqrt{x^2 + y^2}, \space B \) is bounded above by the half-sphere \(x^2 + y^2 + z^2 = 9\) with \(z \geq 0\) and below by the cone \(2z^2 = x^2 + y^2\).

    Answer
    \(\frac{81\pi(\pi - 2)}{16}\)

    32. \(f(x,y,z) = \sqrt{x^2 + y^2}, \space B \) is bounded above by the half-sphere \(x^2 + y^2 + z^2 = 16\) with \(z \geq 0\) and below by the cone \(2z^2 = x^2 + y^2\).

    33. Show that if \(F ( \rho,\theta,\varphi) = f(\rho)g(\theta)h(\varphi)\) is a continuous function on the spherical box \(B = \big\{(\rho,\theta,\varphi)\, | \,a \leq \rho \leq b, \space \alpha \leq \theta \leq \beta, \space \gamma \leq \varphi \leq \psi\big\}\), then \(\displaystyle\iiint_B F \space dV = \left(\int_a^b \rho^2 f(\rho) \space dr \right) \left( \int_{\alpha}^{\beta} g (\theta) \space d\theta \right)\left( \int_{\gamma}^{\psi} h (\varphi) \space \sin \varphi \space d\varphi \right).\)

    34. A function \(F\) is said to have spherical symmetry if it depends on the distance to the origin only, that is, it can be expressed in spherical coordinates as \(F(x,y,z) = f(\rho)\), where \(\rho = \sqrt{x^2 + y^2 + z^2}\). Show that \(\displaystyle\iiint_B F(x,y,z) \,dV = 2\pi \int_a^b \rho^2 f(\rho) \,d\rho,\) where \(B\) is the region between the upper concentric hemispheres of radii \(a\) and \(b\) centered at the origin, with \(0 < a < b\) and \(F\) a spherical function defined on \(B\).

    Use the previous result to show that \(\displaystyle\iiint_B (x^2 + y^2 + z^2) \sqrt{x^2 + y^2 + z^2} dV = 21 \pi,\) where \(B = \big\{(x,y,z)\, | \,1 \leq x^2 + y^2 + z^2 \leq 2, \space z \geq 0\big\}\).

    35. Let \(B\) be the region between the upper concentric hemispheres of radii a and b centered at the origin and situated in the first octant, where \(0 < a < b\). Consider F a function defined on B whose form in spherical coordinates \((\rho,\theta,\varphi)\) is \(F(x,y,z) = f(\rho)\cos \varphi\). Show that if \(g(a) = g(b) = 0\) and \(\displaystyle\int_a^b h (\rho) \, d\rho = 0,\) then \(\displaystyle\iiint_B F(x,y,z)\,dV = \frac{\pi^2}{4} [ah(a) - bh(b)],\) where \(g\) is an antiderivative of \(f\) and \(h\) is an antiderivative of \(g\).

    Use the previous result to show that \(\displaystyle \iiint_B = \frac{z \cos \sqrt{x^2 + y^2 + z^2}}{\sqrt{x^2 + y^2 + z^2}} \, dV = \frac{3\pi^2}{2},\) where \(B\) is the region between the upper concentric hemispheres of radii \(\pi\) and \(2\pi\) centered at the origin and situated in the first octant.

    In exercises 36 - 39, the function \(f\) and region \(E\) are given.

    a. Express the region \(E\) and function \(f\) in cylindrical coordinates.

    b. Convert the integral \(\displaystyle \iiint_B f(x,y,z)\, dV\) into cylindrical coordinates and evaluate it.

    36. \(f(x,y,z) = z; \space E = \big\{(x,y,z)\, | \,0 \leq x^2 + y^2 + z^2 \leq 1, \space z \geq 0\big\}\)

    37. \(f(x,y,z) = x + y; \space E = \big\{(x,y,z)\, | \,1 \leq x^2 + y^2 + z^2 \leq 2, \space z \geq 0, \space y \geq 0\big\}\)

    Answer

    a. \(f(\rho,\theta, \varphi) = \rho \space \sin \varphi \space (\cos \theta + \sin \theta), \space E = \big\{(\rho,\theta,\varphi)\, | \,1 \leq \rho \leq 2, \space 0 \leq \theta \leq \pi, \space 0 \leq \varphi \leq \frac{\pi}{2}\big\}\);

    b. \(\displaystyle \int_0^{\pi} \int_0^{\pi/2} \int_1^2 \rho^3 \cos \varphi \space \sin \varphi \space d\rho \space d\varphi \space d\theta = \frac{15\pi}{8}\)

    38. \(f(x,y,z) = 2xy; \space E = \big\{(x,y,z)\, | \,\sqrt{x^2 + y^2} \leq z \leq \sqrt{1 - x^2 - y^2}, \space x \geq 0, \space y \geq 0\big\}\)

    39. \(f(x,y,z) = z; \space E = \big\{(x,y,z)\, | \,x^2 + y^2 + z^2 - 2x \leq 0, \space \sqrt{x^2 + y^2} \leq z\big\}\)

    Answer

    a. \(f(\rho,\theta,\varphi) = \rho \space \cos \varphi; \space E = \big\{(\rho,\theta,\varphi)\, | \,0 \leq \rho \leq 2 \space \cos \varphi, \space 0 \leq \theta \leq \frac{\pi}{2}, \space 0 \leq \varphi \leq \frac{\pi}{4}\big\}\);

    b. \(\displaystyle\int_0^{\pi/2} \int_0^{\pi/4} \int_0^{2 \space \cos \varphi} \rho^3 \sin \varphi \space \cos \varphi \space d\rho \space d\varphi \space d\theta = \frac{7\pi}{24}\)

    In exercises 40 - 41, find the volume of the solid \(E\) whose boundaries are given in rectangular coordinates.

    40. \(E = \big\{ (x,y,z)\, | \,\sqrt{x^2 + y^2} \leq z \leq \sqrt{16 - x^2 - y^2}, \space x \geq 0, \space y \geq 0\big\}\)

    41. \(E = \big\{ (x,y,z)\, | \,x^2 + y^2 + z^2 - 2z \leq 0, \space \sqrt{x^2 + y^2} \leq z\big\}\)

    Answer
    \(\frac{\pi}{4}\)

    42. Use spherical coordinates to find the volume of the solid situated outside the sphere \(\rho = 1\) and inside the sphere \(\rho = \cos \varphi\), with \(\varphi \in [0,\frac{\pi}{2}]\).

    43. Use spherical coordinates to find the volume of the ball \(\rho \leq 3\) that is situated between the cones \(\varphi = \frac{\pi}{4}\) and \(\varphi = \frac{\pi}{3}\).

    Answer
    \(9\pi (\sqrt{2} - 1)\)

    44. Convert the integral \(\displaystyle \int_{-4}^4 \int_{-\sqrt{16-y^2}}^{\sqrt{16-y^2}} \int_{-\sqrt{16-x^2-y^2}}^{\sqrt{16-x^2-y^2}} (x^2 + y^2 + z^2) \, dz \, dx \, dy\) into an integral in spherical coordinates.

    45. Convert the integral \(\displaystyle \int_0^4 \int_0^{\sqrt{16-x^2}} \int_{-\sqrt{16-x^2-y^2}}^{\sqrt{16-x^2-y^2}} (x^2 + y^2 + z^2)^2 \, dz \space dy \space dx\) into an integral in spherical coordinates.

    Answer
    \(\displaystyle\int_0^{\pi/2} \int_0^{\pi/2} \int_0^4 \rho^6 \sin \varphi \, d\rho \, d\phi \, d\theta\)

    47. [T] Use a CAS to graph the solid whose volume is given by the iterated integral in spherical coordinates \(\displaystyle \int_{\pi/2}^{\pi} \int_{5\pi}^{\pi/6} \int_0^2 \rho^2 \sin \varphi \space d\rho \space d\varphi \space d\theta.\) Find the volume \(V\) of the solid. Round your answer to three decimal places.

    Answer

    \(V = \frac{4\pi\sqrt{3}}{3} \approx 7.255\)

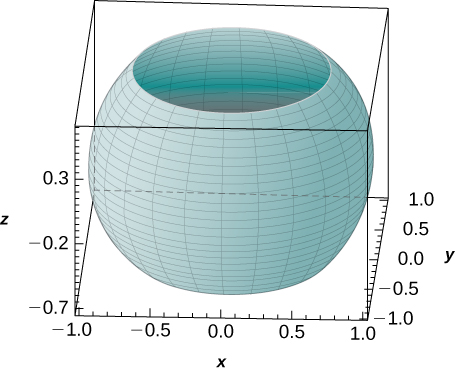
    A sphere of radius 1 with a hole drilled into it of radius 0.5.

    48. [T] Use um CAS para representar graficamente o sólido cujo volume é dado pela integral iterada em coordenadas esféricas como\(\displaystyle \int_0^{2\pi} \int_{3\pi/4}^{\pi/4} \int_0^1 \rho^2 \sin \varphi \space d\rho \space d\varphi \space d\theta.\) Encontre o volume\(V\) do sólido. Arredonde sua resposta para três casas decimais.

    49. [T] Use um CAS para avaliar a integral\(\displaystyle \iiint_E (x^2 + y^2) \, dV\) onde\(E\) está acima do parabolóide\(z = x^2 + y^2\) e abaixo do plano\(z = 3y\).

    Resposta
    \(\frac{343\pi}{32}\)

    50. [T]

    a. Avalie a integral\(\displaystyle \iiint_E e^{\sqrt{x^2+y^2+z^2}}\, dV,\) onde\(E\) é delimitada por esferas\(4x^2 + 4y^2 + 4z^2 = 1\)\(x^2 + y^2 + z^2 = 1\) e.

    b. Use um CAS para encontrar uma aproximação da integral anterior. Arredonde sua resposta para duas casas decimais.

    51. Expresse o volume do sólido dentro da esfera\(x^2 + y^2 + z^2 = 16\) e fora do cilindro\(x^2 + y^2 = 4\) como integrais triplos em coordenadas cilíndricas e coordenadas esféricas, respectivamente.

    Resposta
    \(\displaystyle \int_0^{2\pi}\int_2^4\int_{−\sqrt{16−r^2}}^{\sqrt{16−r^2}}r\,dz\,dr\,dθ\)e\(\displaystyle \int_{\pi/6}^{5\pi/6}\int_0^{2\pi}\int_{2\csc \phi}^{4}\rho^2\sin \rho \, d\rho \, d\theta \, d\phi\)

    52. Expresse o volume do sólido dentro da esfera\(x^2 + y^2 + z^2 = 16\) e fora do cilindro\(x^2 + y^2 = 4\) que está localizado no primeiro octante como integrais triplos em coordenadas cilíndricas e coordenadas esféricas, respectivamente.

    53. A potência emitida por uma antena tem uma densidade de potência por unidade de volume dada em coordenadas esféricas por\(p(\rho,\theta,\varphi) = \frac{P_0}{\rho^2} \cos^2 \theta \space \sin^4 \varphi\), onde\(P_0\) é uma constante com unidades em watts. A potência total dentro de uma esfera\(B\) de\(r\) metros de raio é definida como\(\displaystyle P = \iiint_B p(\rho,\theta,\varphi) \, dV.\) Encontre a potência total\(P\).

    Resposta
    \(P = \frac{32P_0 \pi}{3}\)watts

    54. Use o exercício anterior para encontrar a potência total dentro de uma esfera\(B\) de raio de 5 metros quando a densidade de potência por unidade de volume é dada por\(p(\rho, \theta,\varphi) = \frac{30}{\rho^2} \cos^2 \theta \sin^4 \varphi\).

    55. Uma nuvem de carga contida em uma esfera\(B\) de\(r\) centímetros de raio centrada na origem tem sua densidade de carga dada por\(q(x,y,z) = k\sqrt{x^2 + y^2 + z^2}\frac{\mu C}{cm^3}\), onde\(k > 0\). A cobrança total contida em\(B\) é fornecida por\(\displaystyle Q = \iiint_B q(x,y,z) \, dV.\) Encontre a cobrança total\(Q\).

    Resposta
    \(Q = kr^4 \pi \mu C\)

    56. Use o exercício anterior para encontrar a nuvem de carga total contida na esfera unitária se a densidade de carga for\(q(x,y,z) = 20 \sqrt{x^2 + y^2 + z^2} \frac{\mu C}{cm^3}\).