15.6: Calculando centros de massa e momentos de inércia
- Page ID
- 188099
- Use integrais duplas para localizar o centro de massa de um objeto bidimensional.
- Use integrais duplas para encontrar o momento de inércia de um objeto bidimensional.
- Use integrais triplos para localizar o centro de massa de um objeto tridimensional.
Já discutimos algumas aplicações de várias integrais, como encontrar áreas, volumes e o valor médio de uma função em uma região limitada. Nesta seção, desenvolvemos técnicas computacionais para encontrar o centro de massa e os momentos de inércia de vários tipos de objetos físicos, usando integrais duplas para uma lâmina (placa plana) e integrais triplas para um objeto tridimensional com densidade variável. A densidade geralmente é considerada um número constante quando a lâmina ou o objeto é homogêneo; ou seja, o objeto tem densidade uniforme.
Centro de massa em duas dimensões
O centro de massa também é conhecido como centro de gravidade se o objeto estiver em um campo gravitacional uniforme. Se o objeto tiver densidade uniforme, o centro de massa é o centro geométrico do objeto, que é chamado de centróide. A figura\(\PageIndex{1}\) mostra um ponto\(P\) como o centro de massa de uma lâmina. A lâmina está perfeitamente equilibrada em relação ao seu centro de massa.
Para encontrar as coordenadas do centro de massa\(P(\bar{x},\bar{y})\) de uma lâmina, precisamos encontrar o momento\(M_x\) da lâmina em torno do\(x\) eixo -e o momento\(M_y\) sobre o\(y\) eixo -. Também precisamos encontrar a massa\(m\) da lâmina. Então
\[\bar{x} = \dfrac{M_y}{m} \nonumber \]
e
\[\bar{y} = \dfrac{M_x}{m}. \nonumber \]
Consulte Momentos e Centros de Massa para obter as definições e os métodos de integração única para encontrar o centro de massa de um objeto unidimensional (por exemplo, uma haste fina). Vamos usar uma ideia semelhante aqui, exceto que o objeto é uma lâmina bidimensional e usamos uma integral dupla.
Se permitirmos uma função de densidade constante, então\(\bar{x} = \dfrac{M_y}{m}\)\(\bar{y} = \dfrac{M_x}{m}\) forneça o centróide da lâmina.
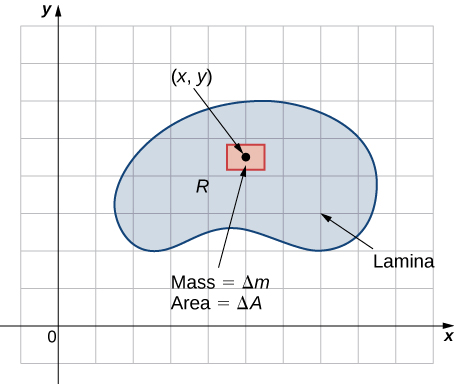
Suponha que a lâmina ocupe uma região\(R\) no\(xy\) plano -e\(\rho (x,y)\) seja sua densidade (em unidades de massa por unidade de área) em qualquer ponto\((x,y)\). Conseqüentemente,
\[\rho(x,y) = \lim_{\Delta A \rightarrow 0} \dfrac{\Delta m}{\Delta A} \nonumber \]
onde\(\Delta m\) e\(\Delta A\) são a massa e a área de um pequeno retângulo contendo o ponto\((x,y)\) e o limite é tomado conforme as dimensões do retângulo vão até\(0\) (veja a figura a seguir).
Assim como antes, dividimos a região\(R\) em pequenos retângulos\(R_{ij}\) com área\(\Delta A\) e escolhemos\((x_{ij}^*, y_{ij}^*)\) como pontos de amostra. Então, a massa\(m_{ij}\) de cada um\(R_{ij}\) é igual a\(\rho (x_{ij}^*, y_{ij}^*) \Delta A\) (Figura\(\PageIndex{2}\)). Seja\(k\) e\(l\) seja o número de subintervalos em\(x\) e\(y\) respectivamente. Além disso, observe que a forma nem sempre é retangular, mas o limite funciona de qualquer maneira, como visto nas seções anteriores.
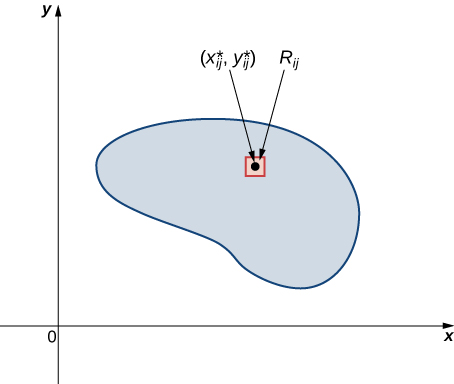
Portanto, a massa da lâmina é
\[m =\lim_{k,l \rightarrow \infty} \sum_{i=1}^k \sum_{j=1}^l m_{ij} = \lim_{k,l \rightarrow \infty} \sum_{i=1}^k \sum_{j=1}^l \rho(x_{ij}^*,y_{ij}^*) \Delta A = \iint_R \rho(x,y) dA. \nonumber \]
Vamos ver agora um exemplo de como encontrar a massa total de uma lâmina triangular.
Considere uma lâmina triangular\(R\) com vértices\((0,0), \, (0,3), \, (3,0)\) e densidade\(\rho(x,y) = xy \, kg/m^2\). Encontre a massa total.
Solução
Um esboço da região\(R\) é sempre útil, conforme mostrado na figura a seguir.
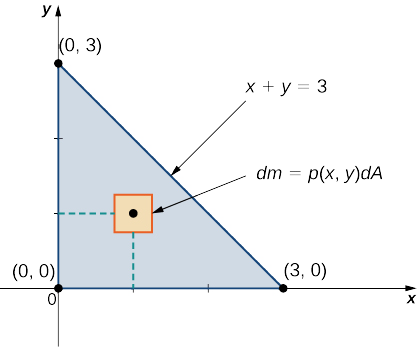
Usando a expressão desenvolvida para massa, vemos que
\[m = \iint_R \, dm = \iint_R \rho (x,y) dA = \int_{x=0}^{x=3} \int_{y=0}^{y=3-x} xy \, dy \, dx = \int_{x=0}^{x=3} \left[ \left. x \dfrac{y^2}{2} \right|_{y=0}^{y=3} \right] \, dx = \int_{x=0}^{x=3} \dfrac{1}{2} x (3 - x)^2 dx = \left.\left[ \dfrac{9x^2}{4} - x^3 + \dfrac{x^4}{8} \right]\right|_{x=0}^{x=3} = \dfrac{27}{8}. \nonumber \]
O cálculo é simples, dando a resposta\(m = \dfrac{27}{8} \, kg\).
Considere a\(R\) mesma região do exemplo anterior e use a função densidade\(\rho (x,y) = \sqrt{xy}\). Encontre a massa total.
- Responda
-
\(\dfrac{9\pi}{8} \, kg\)
Agora que estabelecemos a expressão de massa, temos as ferramentas de que precisamos para calcular momentos e centros de massa. O momento\(M_z\) sobre o\(x\) eixo -para\(R\) é o limite da soma dos momentos das regiões em\(R_{ij}\) torno do\(x\) eixo -. Conseqüentemente
\[M_x = \lim_{k,l \rightarrow \infty} \sum_{i=1}^k \sum_{j=1}^l (y_{ij}^*)m_{ij} = \lim_{k,l \rightarrow \infty} \sum_{i=1}^k \sum_{j=1}^l (y_{ij}^*) \rho(x_{ij}^*,y_{ij}^*) \,\Delta A = \iint_R y\rho (x,y) \,dA \nonumber \]
Da mesma forma, o momento\(M_y\) sobre o\(y\) eixo -para\(R\) é o limite da soma dos momentos das regiões em\(R_{ij}\) torno do\(y\) eixo -. Conseqüentemente
\[M_y = \lim_{k,l \rightarrow \infty} \sum_{i=1}^k \sum_{j=1}^l (x_{ij}^*)m_{ij} = \lim_{k,l \rightarrow \infty} \sum_{i=1}^k \sum_{j=1}^l (x_{ij}^*) \rho(x_{ij}^*,y_{ij}^*) \,\Delta A = \iint_R x\rho (x,y) \,dA \nonumber \]
Considere a mesma lâmina triangular\(R\) com vértices\((0,0), \, (0,3), \, (3,0)\) e densidade\(\rho (x,y) = xy\). Encontre os momentos\(M_x\)\(M_y\) e.
Solução
Use integrais duplas para cada momento e calcule seus valores:
\[M_x = \iint_R y\rho (x,y) \,dA = \int_{x=0}^{x=3} \int_{y=0}^{y=3-x} x y^2 \, dy \, dx = \dfrac{81}{20}, \nonumber \]
\[M_y = \iint_R x\rho (x,y) \,dA = \int_{x=0}^{x=3} \int_{y=0}^{y=3-x} x^2 y \, dy \, dx = \dfrac{81}{20}, \nonumber \]
O cálculo é bastante simples.
Considere a mesma lâmina\(R\) acima e use a função de densidade\(\rho (x,y) = \sqrt{xy}\). Encontre os momentos\(M_x\)\(M_y\) e.
- Responda
-
\(M_x = \dfrac{81\pi}{64}\)e\(M_y = \dfrac{81\pi}{64}\)
Finalmente, estamos prontos para reafirmar as expressões para o centro de massa em termos de integrais. Nós denotamos a coordenada x do centro de massa y\(\bar{x}\) e a coordenada y por\(\bar{y}\). Especificamente,
\[\bar{x} = \dfrac{M_y}{m} = \dfrac{\iint_R x\rho (x,y) \,dA}{\iint_R \rho (x,y)\,dA} \nonumber \]
e
\[\bar{y} = \dfrac{M_x}{m} = \dfrac{\iint_R y\rho (x,y) \,dA}{\iint_R \rho (x,y)\,dA} \nonumber \]
Novamente, considere a mesma região triangular\(R\) com vértices\((0,0), \, (0,3), \, (3,0)\) e com função de densidade\(\rho (x,y) = xy\). Encontre o centro de massa.
Solução
Usando as fórmulas que desenvolvemos, temos
\[\bar{x} = \dfrac{M_y}{m} = \dfrac{\iint_R x\rho (x,y) \,dA}{\iint_R \rho (x,y)\,dA} = \dfrac{81/20}{27/8} = \dfrac{6}{5}, \nonumber \]
\[\bar{y} = \dfrac{M_x}{m} = \dfrac{\iint_R y\rho (x,y) \,dA}{\iint_R \rho (x,y)\,dA} = \dfrac{81/20}{27/8} = \dfrac{6}{5}. \nonumber \]
Portanto, o centro de massa é o ponto\(\left(\dfrac{6}{5},\dfrac{6}{5}\right).\)
AnáliseSe escolhermos que\(\rho(x,y)\) a densidade seja uniforme em toda a região (ou seja, constante), como o valor 1 (qualquer constante serve), então podemos calcular o centróide,
\[x_c = \dfrac{M_y}{m} = \dfrac{\iint_R x \, dA}{\iint_R \,dA} = \dfrac{9/2}{9/2} = 1, \nonumber \]
\[y_c = \dfrac{M_x}{m} = \dfrac{\iint_R y \, dA}{\iint_R \,dA} = \dfrac{9/2}{9/2} = 1. \nonumber \]
Observe que o centro de massa não\(\left(\dfrac{6}{5},\dfrac{6}{5}\right)\) é exatamente o mesmo que o centróide\((1,1)\) da região triangular. Isso se deve à densidade variável de\(R\) Se a densidade for constante, então usamos apenas\(\rho(x,y) = c\) (constante). Esse valor é cancelado das fórmulas, portanto, para uma densidade constante, o centro de massa coincide com o centróide da lâmina.
Novamente, use a\(R\) mesma região acima e use a função de densidade\(\rho (x,y) = \sqrt{xy}\). Encontre o centro de massa.
- Responda
-
\(\bar{x} = \dfrac{M_y}{m} = \dfrac{81\pi/64}{9\pi/8} = \dfrac{9}{8}\)\(\bar{y} = \dfrac{M_x}{m} = \dfrac{81\pi}{9\pi/8} = \dfrac{0}{8}\)e.
Mais uma vez, com base nos comentários no final do Example \(\PageIndex{3}\), temos expressões para o centróide de uma região no plano:
\[x_c = \dfrac{M_y}{m} = \dfrac{\iint_R x \, dA}{\iint_R \,dA} \, \text{and} \, y_c = \dfrac{M_x}{m} = \dfrac{\iint_R y \, dA}{\iint_R \,dA}. \nonumber \]
Devemos usar essas fórmulas e verificar o centróide da região triangular
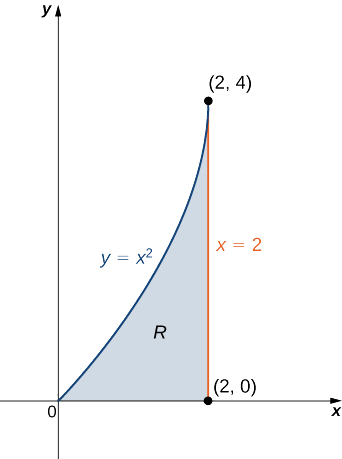
Encontre a massa, os momentos e o centro de massa da lâmina de densidade que\(\rho(x,y) = x + y\) ocupa a região\(R\) abaixo da curva\(y = x^2\) no intervalo\(0 \leq x \leq 2\) (veja a figura a seguir).
Solução
Primeiro, calculamos a massa\(m\). Precisamos descrever a região entre o gráfico de\(y = x^2\) e as linhas verticais\(x = 0\) e\(x = 2\):
\[m = \iint_R \,dm = \iint_R \rho (x,y) \,dA = \int_{x=0}{x=2} \int_{y=0}^{y=x^2} (x + y) dy \, dx = \int_{x=0}^{x=2} \left[\left. xy + \dfrac{y^2}{2}\right|_{y=0}^{y=x^2} \right] \,dx \nonumber \]
\[= \int_{x=0}^{x=2} \left[ x^3 + \dfrac{x^4}{2} \right] dx = \left.\left[ \dfrac{x^4}{4} + \dfrac{x^5}{10}\right] \right|_{x=0}^{x=2} = \dfrac{36}{5}. \nonumber \]
Agora calcule os momentos\(M_x\) e\(M_y\):
\[M_x = \iint_R y \rho (x,y) \,dA = \int_{x=0}^{x=2} \int_{y=0}^{y=x^2} y(x + y) \,dy \, dx = \dfrac{80}{7}, \nonumber \]
\[M_y = \iint_R x \rho (x,y) \,dA = \int_{x=0}^{x=2} \int_{y=0}^{y=x^2} x(x + y) \,dy \, dx = \dfrac{176}{15}. \nonumber \]
Finalmente, avalie o centro de massa,
\[\bar{x} = \dfrac{M_y}{m} = \dfrac{\iint_R x \rho (x,y) \,dA}{\iint_R \rho (x,y)\,dA} = \dfrac{176/15}{36/5} = \dfrac{44}{27}, \nonumber \]
\[\bar{y} = \dfrac{M_x}{m} = \dfrac{\iint_R y \rho (x,y) \,dA}{\iint_R \rho (x,y)\,dA} = \dfrac{80/7}{36/5} = \dfrac{100}{63}. \nonumber \]
Portanto, o centro de massa é\((\bar{x},\bar{y}) = \left(\dfrac{44}{27}, \dfrac{100}{63} \right)\).
Calcule a massa, os momentos e o centro de massa da região entre as curvas\(y = x\) e\(y = x^2\) com a função de densidade\(\rho(x,y) = x\) no intervalo\(0 \leq x \leq 1\).
- Responda
-
\(\bar{x} = \dfrac{M_y}{m} = \dfrac{1/20}{1/12} = \dfrac{3}{5}\)e\(\bar{y} = \dfrac{M_x}{m} = \dfrac{1/24}{1/12} = \dfrac{1}{2}\)
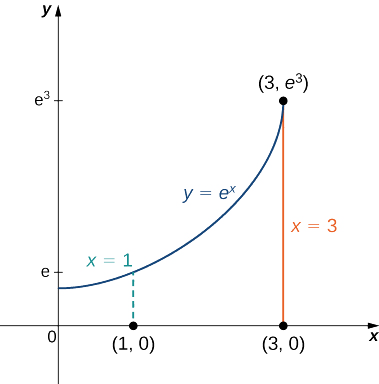
Encontre o centróide da região abaixo da curva ao\(y = e^x\) longo do intervalo\(1 \leq x \leq 3\) (Figura\(\PageIndex{6}\)).
Solução
Para calcular o centróide, assumimos que a função de densidade é constante e, portanto, ela cancela:
\[x_c = \dfrac{M_y}{m} = \dfrac{\iint_R x \, dA}{\iint_R dA} \, and \, y_c = \dfrac{M_x}{m} = \dfrac{\iint_R y \, dA}{\iint_R dA}, \nonumber \]
\[x_c = \dfrac{M_y}{m} = \dfrac{\iint_R x \, dA}{\iint_R dA} = \dfrac{\int_{x=1}^{x=3} \int_{y=0}^{y=e^x} x \, dy \, dx}{\int_{x=1}^{x=3} \int_{y=0}^{y=e^x} \,dy \, dx} = \dfrac{\int_{x=1}^{x=3} xe^x dx}{\int_{x=1}^{x=3} e^x dx} = \dfrac{2e^3}{e^3 - e} = \dfrac{2e^2}{e^2 - 1}, \nonumber \]
\[y_c = \dfrac{M_x}{m} = \dfrac{\iint_R y \, dA}{\iint_R dA} = \dfrac{\int_{x=1}^{x=3} \int_{y=0}^{y=e^x} y \, dy \, dx}{\int_{x=1}^{x=3} \int_{y=0}^{y=e^x} \,dy \, dx} = \dfrac{\int_{x=1}^{x=3} \dfrac{e^{2x}}{2} dx}{\int_{x=1}^{x=3} e^x dx} =\dfrac{\dfrac{1}{4} e^2 (e^4 - 1)}{e(e^2 - 1)} = \dfrac{1}{4} e(e^2 + 1). \nonumber \]
Assim, o centróide da região é
\[(x_c,y_c) = \left( \dfrac{2e^2}{e^2 - 1}, \dfrac{1}{4} e(e^2 + 1)\right). \nonumber \]
Calcule o centróide da região entre as curvas\(y = x\) e\(y = \sqrt{x}\) com densidade uniforme no intervalo\(0 \leq x \leq 1\).
- Responda
-
\(x_c = \dfrac{M_y}{m} = \dfrac{1/15}{1/6} = \dfrac{2}{5}\)e\( y_c = \dfrac{M_x}{m} = \dfrac{1/12}{1/6} = \dfrac{1}{2}\)
Momentos de inércia
Para uma compreensão clara de como calcular momentos de inércia usando integrais duplas, precisamos voltar à definição geral na Seção\(6.6\). O momento de inércia de uma partícula de massa em\(m\) torno de um eixo\(r\) é\(mr^2\) onde está a distância da partícula do eixo. Podemos ver na Figura\(\PageIndex{3}\) que o momento de inércia do sub-retângulo em\(R_{ij}\) torno do\(x\) eixo -é\((y_{ij}^*)^2 \rho(x_{ij}^*,y_{ij}^*) \Delta A\). Da mesma forma, o momento de inércia do sub-retângulo em\(R_{ij}\) torno do\(y\) eixo -é\((x_{ij}^*)^2 \rho(x_{ij}^*,y_{ij}^*) \Delta A\). O momento de inércia está relacionado à rotação da massa; especificamente, ele mede a tendência da massa de resistir a uma mudança no movimento rotacional em torno de um eixo.
O momento de inércia\(I_x\) sobre o\(x\) eixo -para a região\(R\) é o limite da soma dos momentos de inércia das regiões ao\(R_{ij}\) redor do\(x\) eixo -. Conseqüentemente
\[I_x = \lim_{k,l\rightarrow \infty} \sum_{i=1}^k \sum_{j=1}^l (y_{ij}^*)^2 m_{ij} = \lim_{k,l\rightarrow \infty} \sum_{i=1}^k \sum_{j=1}^l (y_{ij}^*)^2 \rho (x_{ij}^*, y_{ij}^*) \,\Delta A = \iint_R y^2 \rho(x,y)\,dA. \nonumber \]
Da mesma forma, o momento de inércia\(I_y\) sobre o\(y\) eixo -para\(R\) é o limite da soma dos momentos de inércia das regiões ao\(R_{ij}\) redor do\(y\) eixo -. Conseqüentemente
\[I_y = \lim_{k,l\rightarrow \infty} \sum_{i=1}^k \sum_{j=1}^l (x_{ij}^*)^2 m_{ij} = \lim_{k,l\rightarrow \infty} \sum_{i=1}^k \sum_{j=1}^l (x_{ij}^*)^2 \rho (x_{ij}^*, y_{ij}^*) \,\Delta A = \iint_R x^2 \rho(x,y)\,dA. \nonumber \]
Às vezes, precisamos encontrar o momento de inércia de um objeto sobre a origem, que é conhecido como momento polar de inércia. Nós denotamos isso por\(I_0\) e o obtemos adicionando os momentos de inércia\(I_x\)\(I_y\) e. Conseqüentemente
\[I_0 = I_x + I_y = \iint_R (x^2 + y^2) \rho (x,y) \,dA. \nonumber \]
Todas essas expressões podem ser escritas em coordenadas polares substituindo\(x = r \, \cos \, \theta, \, y = r \, \sin \, \theta\),\(dA = r \, dr \, d\theta\) e. Por exemplo,\(I_0 = \iint_R r^2 \rho (r \, \cos \, \theta, \, r \, \sin \, \theta)\,dA\).
Use a região triangular\(R\) com vértices e\((2,0)\) e com densidade\((0,0), \, (2,2)\),\(\rho (x,y) = xy\) como nos exemplos anteriores. Encontre os momentos de inércia.
Solução
Usando as expressões estabelecidas acima para os momentos de inércia, temos
\[I_x = \iint_R y^2 \rho(x,y) \,dA = \int_{x=0}^{x=2} \int_{y=0}^{y=x} xy^3 \,dy \, dx = \dfrac{8}{3}, \nonumber \]
\[I_y = \iint_R x^2 \rho(x,y) \,dA = \int_{x=0}^{x=2} \int_{y=0}^{y=x} x^3y \,dy \, dx = \dfrac{16}{3}, \nonumber \]
\[I_0 = \iint_R (x^2 + y^2) \rho(x,y) \,dA = \int_0^2 \int_0^x (x^2 + y^2) xy \, dy \, dx = I_x + I_y = 8 \nonumber \]
Novamente, use a\(R\) mesma região acima e a função de densidade\(\rho (x,y) = \sqrt{xy}\). Encontre os momentos de inércia.
- Responda
-
\[I_x = \int_{x=0}^{x=2} \int_{y=0}^{y=x} y^2 \sqrt{xy} \, dy \, dx = \dfrac{64}{35} \nonumber \]e
\[I_y = \int_{x=0}^{x=2} \int_{y=0}^{y=x} x^2 \sqrt{xy} \, dy \, dx = \dfrac{64}{35}. \nonumber \]Além disso,
\[I_0 = \int_{x=0}^{x=2} \int_{y=0}^{y=x} (x^2 + y^2) \sqrt{xy} \, dy \, dx = \dfrac{128}{21} \nonumber \]
Conforme mencionado anteriormente, o momento de inércia de uma partícula de massa em\(m\) torno de um eixo\(r\) é\(mr^2\) onde está a distância da partícula do eixo, também conhecido como raio de rotação.
Portanto, os raios de rotação em relação ao\(x\) eixo -, ao\(y\) eixo -e à origem são
\[R_x = \sqrt{\dfrac{I_x}{m}}, \, R_y = \sqrt{\dfrac{I_y}{m}}, \, and \, R_0 = \sqrt{\dfrac{I_0}{m}}, \nonumber \]
respectivamente. Em cada caso, o raio de rotação nos diz a que distância (distância perpendicular) do eixo de rotação toda a massa de um objeto pode estar concentrada. Os momentos de um objeto são úteis para encontrar informações sobre o equilíbrio e o torque do objeto em torno de um eixo, mas os raios de rotação são usados para descrever a distribuição da massa em torno de seu eixo centróide. Existem muitas aplicações em engenharia e física. Às vezes, é necessário encontrar o raio de rotação, como no exemplo a seguir.
Considere a mesma lâmina triangular\(R\) com vértices\((0,0), \, (2,2)\) e\((2,0)\) e com densidade\(\rho(x,y) = xy\) como nos exemplos anteriores. Encontre os raios de rotação em relação ao\(x\) eixo -, ao\(y\) eixo -e à origem.
Solução
Se calcularmos a massa dessa região, descobrimos isso\(m = 2\). Encontramos os momentos de inércia dessa lâmina em Example\(\PageIndex{4}\). A partir desses dados, os raios de rotação em relação ao\(x\) eixo -,\(y\) eixo -e a origem são, respectivamente,
\[\begin{align} R_x = \sqrt{\dfrac{I_x}{m}} = \sqrt{\dfrac{8/3}{2}} = \sqrt{\dfrac{8}{6}} = \dfrac{2\sqrt{3}}{3},\\R_y = \sqrt{\dfrac{I_y}{m}} = \sqrt{\dfrac{16/3}{2}} = \sqrt{\dfrac{8}{3}} = \dfrac{2\sqrt{6}}{3}, \\R_0 = \sqrt{\dfrac{I_0}{m}} = \sqrt{\dfrac{8}{2}} = \sqrt{4} = 2.\end{align} \nonumber \]
Use a mesma região\(R\) de Example\(\PageIndex{7}\) e a função de densidade\(\rho (x,y) = \sqrt{xy}\). Encontre os raios de rotação em relação ao\(x\) eixo -, ao\(y\) eixo -e à origem.
- Dica
-
Siga as etapas mostradas no exemplo anterior.
- Responda
-
\(R_x = \dfrac{6\sqrt{35}}{35}, \, R_y = \dfrac{6\sqrt{15}}{15},\)\(R_0 = \dfrac{4\sqrt{42}}{7}\)e.
Suponha que\(Q\) seja uma região sólida limitada pelo plano\(x + 2y + 3z = 6\) e pelos planos coordenados com densidade\(\rho (x,y,z) = x^2yz\) (veja a Figura\(\PageIndex{7}\)). Encontre o centro de massa usando a aproximação decimal.
Solução
Já usamos esse tetraedro antes e conhecemos os limites da integração, para que possamos prosseguir com os cálculos imediatamente. Primeiro, precisamos encontrar os momentos sobre o\(xy\) -plane, o\(xz\) -plane e o\(yz\) -plane:
\[M_{xy} = \iiint_Q z\rho (x,y,z) \,dV = \int_{x=0}^{x=6} \int_{y=0}^{y=\frac{1}{2}(6-x)} \int_{z=0}^{z=\frac{1}{3}(6-x-2y)} x^2 yz^2 \,dz \, dy \, dx = \dfrac{54}{35} \approx 1.543, \nonumber \]
\[M_{xz} = \iiint_Q y\rho (x,y,z) \,dV = \int_{x=0}^{x=6} \int_{y=0}^{y=\frac{1}{2}(6-x)} \int_{z=0}^{z=\frac{1}{3}(6-x-2y)} x^2 y^2z \, dz \, dy \, dx = \dfrac{81}{35} \approx 2.314, \nonumber \]
\[M_{yz} = \iiint_Q x\rho (x,y,z) \,dV = \int_{x=0}^{x=6} \int_{y=0}^{y=\frac{1}{2}(6-x)} \int_{z=0}^{z=\frac{1}{3}(6-x-2y)} x^3 yz \, dz \, dy \, dx = \dfrac{243}{35} \approx 6.943. \nonumber \]
Portanto, o centro de massa é
\[\bar{x} = \dfrac{M_{yz}}{m}, \, \bar{y} = \dfrac{M_{xz}}{m}, \, \bar{z} = \dfrac{M_{xy}}{m}, \nonumber \]
\[\bar{x} = \dfrac{M_{yz}}{m} = \dfrac{243/35}{108/35} = \dfrac{243}{108} = 2.25, \nonumber \]
\[\bar{y} = \dfrac{M_{xz}}{m} = \dfrac{81/35}{108/35} = \dfrac{81}{108} = 0.75, \nonumber \]
\[\bar{z} = \dfrac{M_{xy}}{m} = \dfrac{54/35}{108/35} = \dfrac{54}{108} = 0.5 \nonumber \]
O centro de massa do tetraedro\(Q\) é o ponto\((2.25, 0.75, 0.5)\).
Considere a mesma região\(Q\) (Figura\(\PageIndex{7}\)) e use a função de densidade\(\rho (x,y,z) = xy^2z\). Encontre o centro de massa.
- Dica
-
Verifique isso\(M_{xy} = \dfrac{27}{35}, \, M_{xz} = \dfrac{243}{140},\)\(M_{yz} = \dfrac{81}{35}\) e. Em seguida, use uma pergunta anterior\(m\) do ponto de verificação.
- Responda
-
\(\left(\dfrac{3}{2}, \dfrac{9}{8}, \dfrac{1}{2}\right)\)
Concluímos esta seção com um exemplo de como encontrar momentos de inércia\(I_x, \, I_y\),\(I_z\) e.
Suponha que\(Q\) seja uma região sólida e seja delimitada pelos\(x + 2y + 3z = 6\) planos coordenados com densidade\(\rho (x,y,z) = x^2 yz\) (veja a Figura\(\PageIndex{7}\)). Encontre os momentos de inércia do tetraedro\(Q\) sobre o\(yz\) plano -, o\(xz\) plano -e o\(xy\) plano -.
Solução
Mais uma vez, podemos escrever quase imediatamente os limites da integração e, portanto, podemos rapidamente avaliar os momentos de inércia. Usando a fórmula declarada anteriormente, os momentos de inércia do tetraedro\(Q\) sobre o\(yz\) plano -, o\(xz\) plano -e o\(xy\) plano -são
\[I_x = \iiint_Q (y^2 + z^2) \rho(x,y,z) \,dV, \nonumber \]
\[I_y = \iiint_Q (x^2 + z^2) \rho(x,y,z) \,dV, \nonumber \]e
\[I_z = \iiint_Q (x^2 + y^2) \rho(x,y,z) \,dV \, with \, \rho(x,y,z) = x^2yz. \nonumber \]
Prosseguindo com os cálculos, temos
\[\begin{align*} I_x = \iiint_Q (y^2 + z^2) x^2 \rho(x,y,z) \,dV \\[4pt] = \int_{x=0}^{x=6} \int_{y=0}^{y=\frac{1}{2}(6-x)} \int_{z=0}^{z=\frac{1}{3}(6-x-2y)} (y^2 + z^2) x^2 yz \, dz \, dy \, dx = \dfrac{117}{35} \approx 3.343,\end{align*}\]
\[\begin{align*} I_y = \iiint_Q (x^2 + z^2) x^2 \rho(x,y,z) \,dV \\[4pt] = \int_{x=0}^{x=6} \int_{y=0}^{y=\frac{1}{2}(6-x)} \int_{z=0}^{z=\frac{1}{3}(6-x-2y)} (x^2 + z^2) x^2 yz \, dz \, dy \, dx = \dfrac{684}{35} \approx 19.543, \end{align*}\]
\[\begin{align*} I_z = \iiint_Q (x^2 + y^2) x^2 \rho(x,y,z) \,dV \\[4pt] = \int_{x=0}^{x=6} \int_{y=0}^{y=\frac{1}{2}(6-x)} \int_{z=0}^{z=\frac{1}{3}(6-x-2y)} (x^2 + y^2) x^2 yz \, dz \, dy \, dx = \dfrac{729}{35} \approx 20.829. \end{align*}\]
Assim, os momentos de inércia do tetraedro\(Q\) sobre o\(yz\) plano -, o\(xz\) plano -e o\(xy\) plano -são\(117/35, \, 684/35\), e\(729/35\), respectivamente.
Considere a mesma região\(Q\) (Figura\(\PageIndex{7}\)) e use a função densidade\(\rho(x,y,z) = xy^2z\). Encontre os momentos de inércia sobre os três planos de coordenadas.
- Responda
-
Os momentos de inércia do tetraedro\(Q\) sobre o\(yz\) plano -, o\(xz\) plano -e o\(xy\) plano -são\(99/35, \, 36/7\) e\(243/35\), respectivamente.
Conceitos-chave
Encontrando a massa, o centro de massa, os momentos e os momentos de inércia em integrais duplas:
- Para uma lâmina\(R\) com função de densidade\(\rho (x,y)\) em qualquer ponto\((x,y)\) do plano, a massa é\[m = \iint_R \rho (x,y) \,dA. \nonumber \]
- Os momentos sobre o\(x\) eixo -e o\(y\) eixo -são\[M_x = \iint_R y\rho(x,y) \,dA \, and \, M_y = \iint_R x\rho(x,y) \,dA. \nonumber \]
- O centro de massa é dado por\(\bar{x} = \dfrac{M_y}{m}, \, \bar{y} = \dfrac{M_x}{m}\).
- O centro de massa se torna o centróide do plano quando a densidade é constante.
- Os momentos de inércia sobre o\(x\) eixo\(y\) -, o eixo -e a origem são\[I_x = \iint_R y^2 \rho(x,y) \,dA, \, I_y = \iint_R x^2 \rho(x,y) \,dA, \, and \, I_0 = I_x + I_y = \iint_R (x^2 + y^2) \rho(x,y) \,dA. \nonumber \]
Encontrando a massa, o centro de massa, os momentos e os momentos de inércia em integrais triplos:
- Para um objeto sólido\(Q\) com uma função de densidade\(\rho(x,y,z)\) em qualquer ponto\((x,y,z)\) do espaço, a massa é\[m = \iiint_Q \rho (x,y,z) \,dV. \nonumber \]
- Os momentos sobre o\(xy\) -plane, o\(xz\) -plane e o\(yz\) -plane são\[M_{xy} = \iiint_Q z\rho (x,y,z)\,dV, \, M_{xz} = \iiint_Q y\rho (x,y,z)\,dV, \, M_{yz} = \iiint_Q x\rho (x,y,z)\,dV \nonumber \]
- O centro de massa é dado por\(\bar{x} = \dfrac{M_{yz}}{m}, \, \bar{y} = \dfrac{M_{xz}}{m}, \, \bar{z} = \dfrac{M_{xy}}{m}.\)
- O centro de massa se torna o centróide do sólido quando a densidade é constante.
- Os momentos de inércia sobre o\(yz\) plano -, o\(xz\) plano -e o\(xy\) plano -são\[I_x = \iiint_Q (y^2 + z^2) \, \rho (x,y,z) \, dV, \, I_y = \iiint_Q (x^2 + z^2) \, \rho (x,y,z) \, dV, \, I_z = \iiint_Q (x^2 + y^2) \, \rho (x,y,z) \, dV. \nonumber \]
Equações-chave
- Massa de uma lâmina\[m = \lim_{k,l \rightarrow\infty} \sum_{i=1}^k \sum_{j=1}^l m_{ij} = \lim_{k,l \rightarrow\infty} \sum_{i=1}^k \sum_{j=1}^l \rho (x_{ij}^*, y_{ij}^*) \,\Delta A = \iint_R \rho(x,y) \,dA \nonumber \]
- Momento sobre o eixo x\[M_x = \lim_{k,l \rightarrow\infty} \sum_{i=1}^k \sum_{j=1}^l (y_{ij}^*) m_{ij} = \lim_{k,l \rightarrow\infty} \sum_{i=1}^k \sum_{j=1}^l (y_{ij}^*) \rho (x_{ij}^*, y_{ij}^*) \,\Delta A = \iint_R y\rho(x,y)\,dA \nonumber \]
- Momento sobre o eixo y\[M_y = \lim_{k,l \rightarrow\infty} \sum_{i=1}^k \sum_{j=1}^l (x_{ij}^*) m_{ij} = \lim_{k,l \rightarrow\infty} \sum_{i=1}^k \sum_{j=1}^l (x_{ij}^*) \rho (x_{ij}^*, y_{ij}^*) \,\Delta A = \iint_R x\rho(x,y)\,dA \nonumber \]
- Centro de massa de uma lâmina\[\bar{x} = \dfrac{M_y}{m} = \dfrac{\iint_R x\rho (x,y) \,dA}{\iint_R \rho (x,y) \,dA} \, and \, \bar{y} = \dfrac{M_x}{m} = \dfrac{\iint_R y\rho (x,y) \,dA}{\iint_R \rho (x,y) \,dA} \nonumber \]
Glossário
- raio de rotação
- a distância do centro de massa de um objeto até seu eixo de rotação



Centro de massa e momentos de inércia em três dimensões
Todas as expressões de integrais duplas discutidas até agora podem ser modificadas para se tornarem integrais triplas.
Definição
Se tivermos um objeto sólido\(Q\) com uma função de densidade\(\rho(x,y,z)\)\((x,y,z)\) em qualquer ponto do espaço, então sua massa é
\[m = \iiint_Q \rho(x,y,z) \,dV. \nonumber \]
Seus momentos sobre o\(xy\) plano -, o\(xz\) -plane e o\(yz\) -plane são
\[M_{xy} = \iiint_Q z\rho (x,y,z) \,dV, \, M_{xz} = \iiint_Q y\rho(x,y,z) \,dV, \, M_{yz} = \iiint_Q x\rho(x,y,z) \,dV. \nonumber \]
Se o centro de massa do objeto for o ponto\((\bar{x}, \bar{y}, \bar{z})\), então
\[\bar{x} = \dfrac{M_{yz}}{m}, \, \bar{y} = \dfrac{M_{xz}}{m}, \, \bar{z} = \dfrac{M_{xy}}{m}. \nonumber \]
Além disso, se o objeto sólido for homogêneo (com densidade constante), o centro de massa se tornará o centróide do sólido. Finalmente, os momentos de inércia sobre o\(yz\) plano\(xz\) -, -plane e o\(xy\) -plane são
\[I_x = \iiint_Q (y^2 + z^2) \, \rho (x,y,z) \, dV, \nonumber \]
\[I_y = \iiint_Q (x^2 + z^2) \, \rho (x,y,z) \, dV, \nonumber \]
\[I_z = \iiint_Q (x^2 + y^2) \, \rho (x,y,z) \, dV. \nonumber \]
Exemplo\(\PageIndex{8}\): Finding the Mass of a Solid
Suponha que\(Q\) seja uma região sólida delimitada pelos\(x + 2y + 3z = 6\) planos coordenados e tenha densidade\(\rho (x,y,z) = x^2 yz\). Encontre a massa total.
Solução
A região\(Q\) é um tetraedro (Figura\(\PageIndex{7}\)) encontrando os eixos nos pontos\((6,0,0), \, (0,3,0),\)\((0,0,2)\) e. Para encontrar os limites da integração, deixe\(z = 0\) entrar o plano inclinado\(z = \dfrac{1}{3} (6 - x - 2y)\). Em seguida, procure\(x\) e\(y\) encontre a\(Q\) projeção de no\(xy\) plano -, que é limitado pelos eixos e pela linha\(x + 2y = 6\). Portanto, a massa é
\[m = \iiint_Q \rho (x,y,z) \,dV = \int_{x=0}^{x=6} \int_{y=0}^{y=1/2(6-x)} \int_{z=0}^{z=1/3(6-x-2y)} x^2 yz \, dz \, dy \, dx = \dfrac{108}{35} \nonumber \]
Exercício\(\PageIndex{8}\)
Considere a mesma região\(Q\) (Figura\(\PageIndex{7}\)) e use a função densidade\(\rho (x,y,z) = xy^2z\). Encontre a massa.
Siga as etapas no exemplo anterior.
\(\dfrac{54}{35} = 1.543\)