Skip to main content
Global

15.6E: Exercícios para a Seção 15.6

  1. Last updated
  2. Save as PDF
  • Page ID
    188112

    • Edwin “Jed” Herman & Gilbert Strang
    • OpenStax
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Nos exercícios 1 a 12, a região\(R\) ocupada por uma lâmina é mostrada em um gráfico. Encontre a massa de\(R\) com a função densidade\(\rho\).

    1. \(R\)é a região triangular com vértices\((0,0), \space (0,3)\)\((6,0); \space \rho (x,y) = xy\) e.

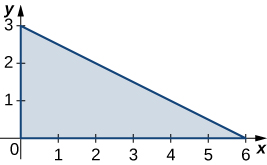
    Um triângulo reto limitado pelos eixos x e y e a linha y = menos x/2 + 3.

    Resposta
    \(\frac{27}{2}\)

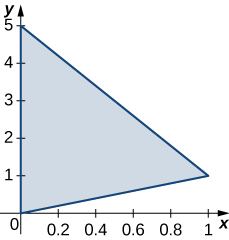
    2. \(R\) is the triangular region with vertices \((0,0), \space (1,1)\), and \((0,5); \space \rho (x,y) = x + y\).

    A triangle bounded by the y axis, the line x = y, and the line y = negative 4x + 5.

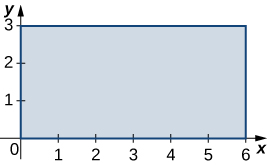
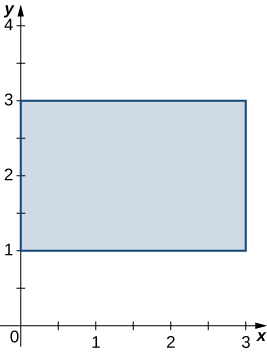
    3. \(R\)é a região retangular com vértices\((0,0), \space (0,3), \space (6,3) \)\((6,0); \space \rho (x,y) = \sqrt{xy}\) e.

    Um retângulo limitado pelos eixos x e y e pelas linhas x = 6 e y = 3.

    Resposta
    \(24\sqrt{2}\)

    4. \(R\) is the rectangular region with vertices \((0,1), \space (0,3), \space (3,3)\) and \( (3,1); \space \rho (x,y) = x^2y\).

    A rectangle bounded by the y axis, the lines y = 1 and 3, and the line x = 3.

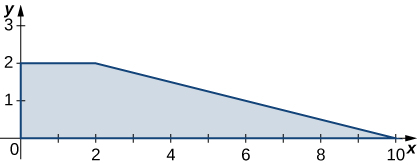
    5. \(R\)é a região trapezoidal determinada pelas linhas\(y = - \frac{1}{4}x + \frac{5}{2}, \space y = 0, \space y = 2\),\(x = 0; \space \rho (x,y) = 3xy\) e.

    Um trapézio limitado pelos eixos x e y, a linha y = 2 e a linha y = negativo x/4 + 2,5.

    Resposta
    \(76\)

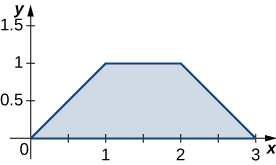
    6. \(R\) is the trapezoidal region determined by the lines \(y = 0, \space y = 1, \space y = x\) and \(y = -x + 3; \space \rho (x,y) = 2x + y\).

    A trapezoid bounded by the x axis, the line y = 1, the line y = x, and the line y = negative x + 3.

    7. \(R\)é o disco de raio\(2\) centrado em\((1,2); \space \rho(x,y) = x^2 + y^2 - 2x - 4y + 5\).

    Resposta
    \(8\pi\)

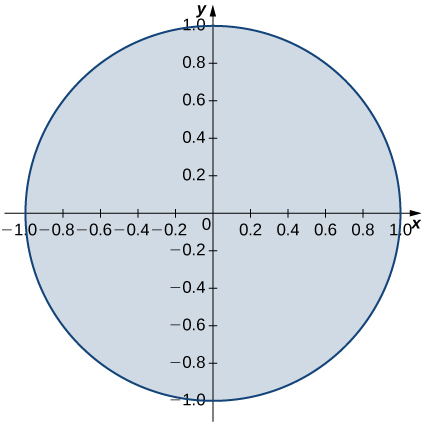
    8. \(R\)é o disco da unidade;\(\rho (x,y) = 3x^4 + 6x^2y^2 + 3y^4\).

    Um círculo com raio 1 e centro da origem.

    9. \(R\) is the region enclosed by the ellipse \(x^2 + 4y^2 = 1; \space \rho(x,y) = 1\).

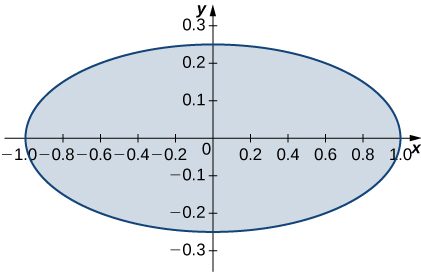
    An ellipse with center the origin, major axis 2, and minor axis 0.5.

    Resposta
    \(\frac{\pi}{2}\)

    10. \(R = \big\{(x,y) \,|\, 9x^2 + y^2 \leq 1, \space x \geq 0, \space y \geq 0\big\} ; \space \rho (x,y) = \sqrt{9x^2 + y^2}\).

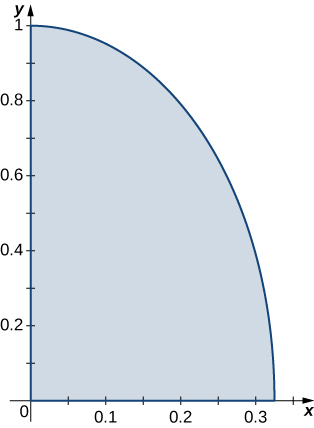
    O quarto de seção de uma elipse no primeiro quadrante com centro na origem, eixo maior 2 e eixo menor aproximadamente 0,64.

    11. \(R\) is the region bounded by \(y = x, \space y = -x, \space y = x + 2, \space y = -x + 2; \space \rho(x,y) = 1\).

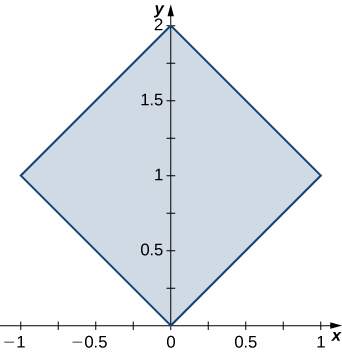
    A square with side length square root of 2 rotated 45 degrees, with corners at the origin, (2, 0), (1, 1), and (negative 1, 1).

    Resposta
    \(2\)

    12. \(R\)é a região delimitada por\(y = \frac{1}{x}, \space y = \frac{2}{x}, \space y = 1\),\(y = 2; \space \rho (x,y) = 4(x + y)\) e.

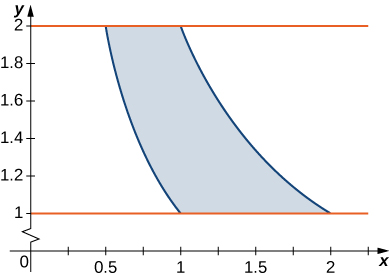
    Uma região complexa entre 2 e 1 que se arrasta para baixo e para a direita com limites y = 1/x e y = 2/x.

    Nos exercícios 13 a 24, considere uma lâmina ocupando a região\(R\) e tendo a função de densidade\(\rho\) dada no grupo anterior de exercícios. Use um sistema computacional de álgebra (CAS) para responder às seguintes perguntas.

    a. Encontre os momentos\(M_x\) e\(M_y\) sobre o\(x\) eixo -e o\(y\) eixo -, respectivamente.

    b. Calcule e plote o centro de massa da lâmina.

    c. [T] Use um CAS para localizar o centro de massa no gráfico de\(R\).

    13. [T]\(R\) is the triangular region with vertices \((0,0), \space (0,3)\), and \((6,0); \space \rho (x,y) = xy\).

    Answer

    a. \(M_x = \frac{81}{5}, \space M_y = \frac{162}{5}\);
    b. \(\bar{x} = \frac{12}{5}, \space \bar{y} = \frac{6}{5}\);
    c.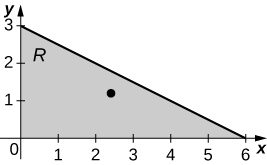

    A triangular region R bounded by the x and y axes and the line y = negative x/2 + 3, with a point marked at (12/5, 6/5).

    14. [T]\(R\) é a região triangular com vértices\((0,0), \space (1,1)\),\((0,5); \space \rho (x,y) = x + y\) e.

    15. [T]\(R\) é a região retangular com vértices\((0,0), \space (0,3), \space (6,3)\)\((6,0); \space \rho (x,y) = \sqrt{xy}\) e.

    Resposta

    a.\(M_x = \frac{216\sqrt{2}}{5}, \space M_y = \frac{432\sqrt{2}}{5}\);
    b.\(\bar{x} = \frac{18}{5}, \space \bar{y} = \frac{9}{5}\);
    c.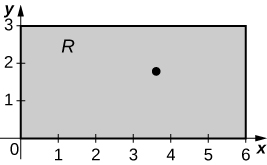

    Um retângulo R limitado pelos eixos x e y e pelas linhas x = 6 e y = 3 com ponto marcado (18/5, 9/5).

    16. [T]\(R\) is the rectangular region with vertices \((0,1), \space (0,3), \space (3,3)\), and \((3,1); \space \rho (x,y) = x^2y\).

    17. [T] \(R\) is the trapezoidal region determined by the lines \(y = - \frac{1}{4}x + \frac{5}{2}, \space y = 0, \space y = 2\), and \(x = 0; \space \rho (x,y) = 3xy\).

    Answer

    a. \(M_x = \frac{368}{5}, \space M_y = \frac{1552}{5}\);
    b. \(\bar{x} = \frac{92}{95}, \space \bar{y} = \frac{388}{95}\);
    c.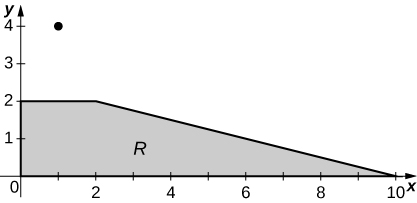

    A trapezoid R bounded by the x and y axes, the line y = 2, and the line y = negative x/4 + 2.5 with the point marked (92/95, 388/95).

    18. [T]\(R\) é a região trapezoidal determinada pelas linhas\(y = 0, \space y = 1, \space y = x,\)\(y = -x + 3; \space \rho (x,y) = 2x + y\) e.

    19. [T]\(R\) é o disco de raio\(2\) centrado em\((1,2); \space \rho(x,y) = x^2 + y^2 - 2x - 4y + 5\).

    Resposta

    a.\(M_x = 16\pi, \space M_y = 8\pi\);
    b.\(\bar{x} = 1, \space \bar{y} = 2\);
    c.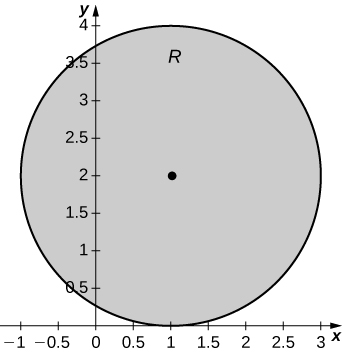

    Um círculo com raio 2 centrado em (1, 2), tangente ao eixo x em (1, 0) e apontado para o centro (1, 2).

    20. [T]\(R\) is the unit disk; \(\rho (x,y) = 3x^4 + 6x^2y^2 + 3y^4\).

    21. [T] \(R\) is the region enclosed by the ellipse \(x^2 + 4y^2 = 1; \space \rho(x,y) = 1\).

    Answer

    a. \(M_x = 0, \space M_y = 0)\);
    b. \(\bar{x} = 0, \space \bar{y} = 0\);
    c.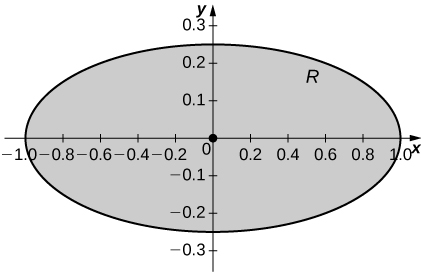

    An ellipse R with center the origin, major axis 2, and minor axis 0.5, with point marked at the origin.

    22. [T]\(R = \big\{(x,y) \,|\, 9x^2 + y^2 \leq 1, \space x \geq 0, \space y \geq 0\big\} ; \space \rho (x,y) = \sqrt{9x^2 + y^2}\).

    23. [T]\(R\) is the region bounded by \(y = x, \space y = -x, \space y = x + 2\), and \(y = -x + 2; \space \rho (x,y) = 1\).

    Resposta

    a.\(M_x = 2, \space M_y = 0)\);
    b.\(\bar{x} = 0, \space \bar{y} = 1\);
    c.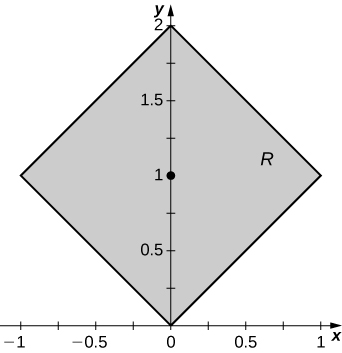

    Um quadrado R com raiz quadrada de comprimento lateral de 2 girado em 45 graus, com cantos na origem, (2, 0), (1, 1) e (menos 1, 1). Um ponto é marcado em (0, 1).

    24. [T]\(R\) is the region bounded by \(y = \frac{1}{x}, \space y = \frac{2}{x}, \space y = 1\), and \(y = 2; \space \rho (x,y) = 4(x + y)\).

    In exercises 25 - 36, consider a lamina occupying the region \(R\) and having the density function \(\rho\) given in the first two groups of Exercises.

    a. Find the moments of inertia \(I_x, \space I_y\) and \(I_0\) about the \(x\)-axis, \(y\)-axis, and origin, respectively.

    b. Find the radii of gyration with respect to the \(x\)-axis, \(y\)-axis, and origin, respectively.

    25. \(R\) is the triangular region with vertices \((0,0), \space (0,3)\), and \((6,0); \space \rho (x,y) = xy\).

    Answer
    a. \(I_x = \frac{243}{10}, \space I_y = \frac{486}{5}\), and \(I_0 = \frac{243}{2}\);
    b. \(R_x = \frac{3\sqrt{5}}{5}, \space R_y = \frac{6\sqrt{5}}{5}\), and \(R_0 = 3\)

    26. \(R\) is the triangular region with vertices \((0,0), \space (1,1)\), and \((0,5); \space \rho (x,y) = x + y\).

    27. \(R\) is the rectangular region with vertices \((0,0), \space (0,3), \space (6,3)\), and \((6,0); \space \rho (x,y) = \sqrt{xy}\).

    Answer
    a. \(I_x = \frac{2592\sqrt{2}}{7}, \space I_y = \frac{648\sqrt{2}}{7}\), and \(I_0 = \frac{3240\sqrt{2}}{7}\);
    b. \(R_x = \frac{6\sqrt{21}}{7}, \space R_y = \frac{3\sqrt{21}}{7}\), and \(R_0 = \frac{3\sqrt{106}}{7}\)

    28. \(R\) is the rectangular region with vertices \((0,1), \space (0,3), \space (3,3)\), and \((3,1); \space \rho (x,y) = x^2y\).

    29. \(R\) is the trapezoidal region determined by the lines \(y = - \frac{1}{4}x + \frac{5}{2}, \space y = 0, \space y = 2\), and x = 0; \space \rho (x,y) = 3xy\).

    Answer
    a. \(I_x = 88, \space I_y = 1560\), and \(I_0 = 1648\);
    b. \(R_x = \frac{\sqrt{418}}{19}, \space R_y = \frac{\sqrt{7410}}{10}\), and \(R_0 = \frac{2\sqrt{1957}}{19}\)

    30. \(R\) is the trapezoidal region determined by the lines \(y = 0, \space y = 1, \space y = x\), and y = -x + 3; \space \rho (x,y) = 2x + y\).

    31. \(R\) is the disk of radius \(2\) centered at \((1,2); \space \rho(x,y) = x^2 + y^2 - 2x - 4y + 5\).

    Answer
    a. \(I_x = \frac{128\pi}{3}, \space I_y = \frac{56\pi}{3}\), and \(I_0 = \frac{184\pi}{3}\);
    b. \(R_x = \frac{4\sqrt{3}}{3}, \space R_y = \frac{\sqrt{21}}{2}\), and \(R_0 = \frac{\sqrt{69}}{3}\)

    32. \(R\) is the unit disk; \(\rho (x,y) = 3x^4 + 6x^2y^2 + 3y^4\).

    33. \(R\) is the region enclosed by the ellipse \(x^2 + 4y^2 = 1; \space \rho(x,y) = 1\).

    Answer
    a. \(I_x = \frac{\pi}{32}, \space I_y = \frac{\pi}{8}\), and \(I_0 = \frac{5\pi}{32}\);
    b. \(R_x = \frac{1}{4}, \space R_y = \frac{1}{2}\), and \(R_0 = \frac{\sqrt{5}}{4}\)

    34. \(R = \big\{(x,y) \,|\, 9x^2 + y^2 \leq 1, \space x \geq 0, \space y \geq 0\big\} ; \space \rho (x,y) = \sqrt{9x^2 + y^2}\).

    35. \(R\) is the region bounded by \(y = x, \space y = -x, \space y = x + 2\), and \(y = -x + 2; \space \rho (x,y) = 1\).

    Answer
    a. \(I_x = \frac{7}{3}, \space I_y = \frac{1}{3}\), and \(I_0 = \frac{8}{3}\);
    b. \(R_x = \frac{\sqrt{42}}{6}, \space R_y = \frac{\sqrt{6}}{6}\), and \(R_0 = \frac{2\sqrt{3}}{3}\)

    36. \(R\) is the region bounded by \(y = \frac{1}{x}, \space y = \frac{2}{x}, \space y = 1\), and \(y = 2; \space \rho (x,y) = 4(x + y)\).

    37. Let \(Q\) be the solid unit cube. Find the mass of the solid if its density \(\rho\) is equal to the square of the distance of an arbitrary point of \(Q\) to the \(xy\)-plane.

    Answer
    \(m = \frac{1}{3}\)

    38. Let \(Q\) be the solid unit hemisphere. Find the mass of the solid if its density \(\rho\) is proportional to the distance of an arbitrary point of \(Q\) to the origin.

    39. The solid \(Q\) of constant density \(1\) is situated inside the sphere \(x^2 + y^2 + z^2 = 16\) and outside the sphere \(x^2 + y^2 + z^2 = 1\). Show that the center of mass of the solid is not located within the solid.

    40. Find the mass of the solid \(Q = \big\{ (x,y,z) \,|\, 1 \leq x^2 + z^2 \leq 25, \space y \leq 1 - x^2 - z^2 \big\}\) whose density is \(\rho (x,y,z) = k\), where \(k > 0\).

    41. [T] The solid \(Q = \big\{ (x,y,z) \,|\, x^2 + y^2 \leq 9, \space 0 \leq z \leq 1, \space x \geq 0, \space y \geq 0\big\}\) has density equal to the distance to the \(xy\)-plane. Use a CAS to answer the following questions.

    a. Find the mass of \(Q\).

    b. Find the moments \(M_{xy}, \space M_{xz}\) and \(M_{yz}\) about the \(xy\)-plane, \(xz\)-plane, and \(yz\)-plane, respectively.

    c. Find the center of mass of \(Q\).

    d. Graph \(Q\) and locate its center of mass.

    Answer

    a. \(m = \frac{9\pi}{4}\);
    b. \(M_{xy} = \frac{3\pi}{2}, \space M_{xz} = \frac{81}{8}, \space M_{yz} = \frac{81}{8}\);
    c. \(\bar{x} = \frac{9}{2\pi}, \space \bar{y} = \frac{9}{2\pi}, \space \bar{z} = \frac{2}{3}\);
    d.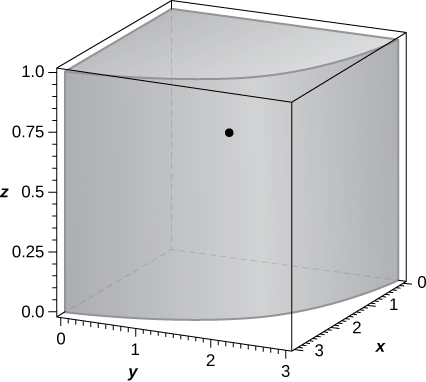

    A quarter cylinder in the first quadrant with height 1 and radius 3. A point is marked at (9/(2 pi), 9/(2 pi), 2/3).

    42. Considere o sólido\(Q = \big\{ (x,y,z) \,|\, 0 \leq x \leq 1, \space 0 \leq y \leq 2, \space 0 \leq z \leq 3\big\}\) com a função de densidade\(\rho(x,y,z) = x + y + 1\).

    a. Encontre a massa de\(Q\).

    b. Encontre os momentos\(M_{xy}, \space M_{xz}\) e\(M_{yz}\) sobre o\(xy\) -plane,\(xz\) -plane e\(yz\) -plane, respectivamente.

    c. Encontre o centro de massa de\(Q\).

    43. [T] O sólido\(Q\) tem a massa dada pela integral tripla\(\displaystyle \int_{-1}^1 \int_0^{\pi/4} \int_0^1 r^2 \, dr \space d\theta \space dz.\)

    Use um CAS para responder às seguintes perguntas.

    • Mostre que o centro de massa de\(Q\) está localizado no\(xy\) plano -.
    • Faça um gráfico\(Q\) e localize seu centro de massa.
    Resposta

    \(\bar{x} = \frac{3\sqrt{2}}{2\pi}\),\(\bar{y} = \frac{3(2-\sqrt{2})}{2\pi}, \space \bar{z} = 0\); 2. o sólido\(Q\) e seu centro de massa são mostrados na figura a seguir.

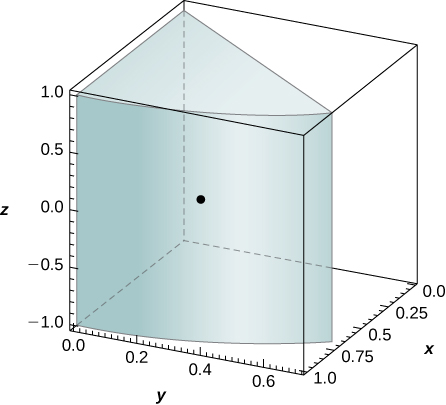
    Uma cunha de um cilindro no primeiro quadrante com altura 2, raio 1 e ângulo de aproximadamente 45 graus. Um ponto é marcado em (3 vezes a raiz quadrada de 2/ (2 pi), 3 vezes (2 menos a raiz quadrada de 2)/(2 pi), 0).

    44. O sólido

    Template:ContribOpenStaxCalc