Skip to main content
Global

13.3E: Exercícios para a Seção 13.3

  1. Last updated
  2. Save as PDF
  • Page ID
    187844

    • Edwin “Jed” Herman & Gilbert Strang
    • OpenStax
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Determine o comprimento do arco

    Nas questões de 1 a 5, determine o comprimento do arco da curva no intervalo dado.

    1)\(\vecs r(t)=t^2 \,\hat{\mathbf{i}}+(2t^2+1)\,\hat{\mathbf{j}}, \quad 1≤t≤3\)

    Responda
    \(8\sqrt{5}\)unidades

    2)\(\vecs r(t)=t^2 \,\hat{\mathbf{i}}+14t \,\hat{\mathbf{j}},\quad 0≤t≤7\). Essa parte do gráfico é mostrada aqui:

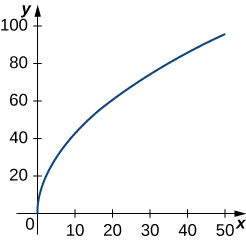
    3)\(\vecs r(t)=⟨t^2+1,4t^3+3⟩, \quad −1≤t≤0\)

    Responda
    \(\frac{1}{54}(37^{3/2}−1)\)unidades

    4)\(\vecs r(t)=⟨2 \sin t,5t,2 \cos t⟩,\quad 0≤t≤π\). Essa parte do gráfico é mostrada aqui:

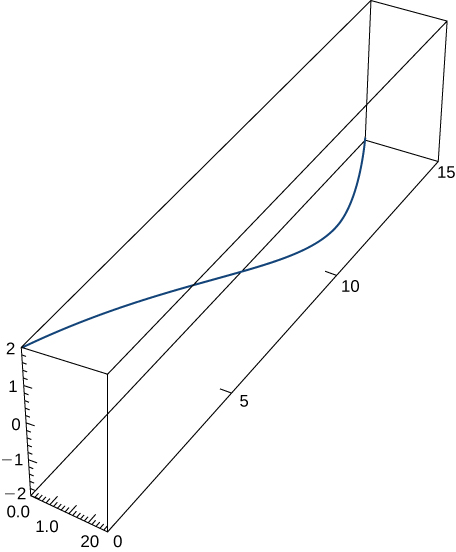
    5)\(\vecs r(t)=⟨e^{−t \cos t},e^{−t \sin t}⟩\) ao longo do intervalo\([0,\frac{π}{2}]\). Aqui está a parte do gráfico no intervalo indicado:

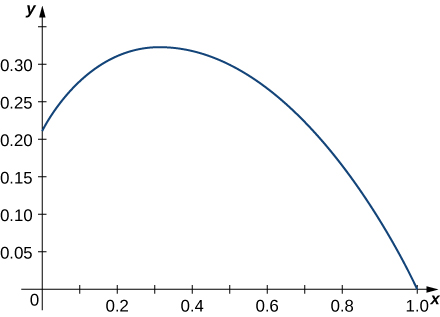
    6) Configure uma integral para representar o comprimento do arco de até\(t = 0\) ao\(t = 2\) longo da curva traçada por\(\vecs r(t) = \langle t, \, t^4\rangle.\) Em seguida, use a tecnologia para aproximar esse comprimento ao milésimo mais próximo de uma unidade.

    7) Encontre o comprimento de uma volta da hélice dada por\(\vecs r(t)= \frac{1}{2} \cos t \,\hat{\mathbf{i}}+\frac{1}{2} \sin t \,\hat{\mathbf{j}}+\frac{\sqrt{3}}{2}\,t \,\hat{\mathbf{k}}\).

    Responda
    \(=2π\)Unidades de comprimento

    8) Encontre o comprimento do arco da função com valor vetorial\(\vecs r(t)=−t \,\hat{\mathbf{i}}+4t \,\hat{\mathbf{j}}+3t \,\hat{\mathbf{k}}\) acima\([0,1]\).

    9) Uma partícula viaja em um círculo com a equação do movimento\(\vecs r(t)=3 \cos t \,\hat{\mathbf{i}}+3 \sin t \,\hat{\mathbf{j}} +0 \,\hat{\mathbf{k}}\). Encontre a distância percorrida ao redor do círculo pela partícula.

    Responda
    \(6π\)unidades

    10) Configure uma integral para encontrar a circunferência da elipse com a equação\(\vecs r(t)= \cos t \,\hat{\mathbf{i}}+2 \sin t \,\hat{\mathbf{j}}+0\,\hat{\mathbf{k}}\).

    11) Encontre o comprimento da curva\(\vecs r(t)=⟨\sqrt{2}t,\, e^t, \, e^{−t}⟩\) ao longo do intervalo\(0≤t≤1\). O gráfico é mostrado aqui:

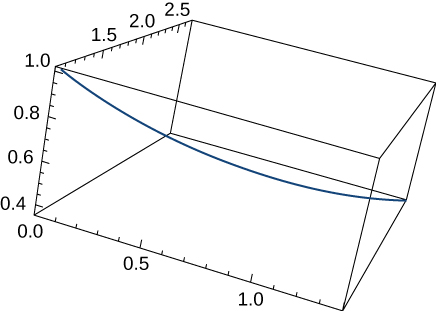
    Responda
    \(\left(e−\frac{1}{e}\right)\)unidades

    12) Encontre o comprimento da curva\(\vecs r(t)=⟨2 \sin t, \, 5t, \, 2 \cos t⟩\) para\(t∈[−10,10]\).

    Vetores tangentes unitários e vetores normais unitários

    13) A função de posição de uma partícula é\(\vecs r(t)=a \cos( ωt) \,\hat{\mathbf{i}}+b \sin (ωt) \,\hat{\mathbf{j}}\). Encontre o vetor tangente unitário e o vetor normal unitário em\(t=0\).

    Solução:
    \ (\ begin {align*}\ vecs r' (t) &= -aω\ sin (ω t)\,\ hat {\ mathbf {i}} +bω\ cos (ω t)\,\ hat {\ mathbf {j}}\\ [5pt]
    \ |\ vecs r' (t)\ | &=\ sqrt {a^2 ω\ 2 sin^2 (ω t) +b^2ω ^2\ cos^2 (ω t)}\\ [5pt]
    \ vecs T (t) &=\ dfrac {\ vecs r' (t)} {\ |\ vecs r' (t)\ |} =\ dfrac {-aω\ sin (ω t)\,\ hat {\ mathbf {i}} +bω\ cos (ω t)\,\ hat {\ mathbf {j}}} {\ sqrt {a^2 ω ^2\ sin^2 (ω t) +b^2ω ^2\ cos^2 (ω t)}}\\ [5pt]
    \ vecs T (0) &=\ dfrac {bω\,\ hat {\ mathbf {j}}} {\ sqrt {(bω) ^2}} =\ dfrac {bω\,\ hat {\ mathbf {j}}} {|bω |}\ end {align*}\)

    Se\(bω > 0, \; \vecs T(0) = \hat{\mathbf{j}},\) e se\( bω < 0, \; T(0)= -\hat{\mathbf{j}}\)
    Responda
    Se\(bω > 0, \; \vecs T(0)= \hat{\mathbf{j}},\) e se\( bω < 0, \; \vecs T(0)= -\hat{\mathbf{j}}\)

    Se\(a > 0, \; \vecs N(0)= -\hat{\mathbf{i}},\) e se\( a < 0, \; \vecs N(0)= \hat{\mathbf{i}}\)

    14) Dado\(\vecs r(t)=a \cos (ωt) \,\hat{\mathbf{i}} +b \sin (ωt) \,\hat{\mathbf{j}}\), encontre o vetor binormal\(\vecs B(0)\).

    15) Dado\(\vecs r(t)=⟨2e^t,e^t \cos t,e^t \sin t⟩\), determine o vetor tangente unitário\(\vecs T(t)\).

    Responda
    \ (\ begin {align*}\ vecs T (t) &=\ left\ langle\ frac {2} {\ sqrt {6}},\,\ frac {\ cos t−\ sin t} {\ sqrt {6}},\,\ frac {\ cos t+\ sin t} {\ sqrt {6}}\ right\ rangle\\ [4pt]
    &=\ left\ langle\ frac {\ sqrt {6}} {3},\,\ frac {\ sqrt {6}} {6} (\ cos t−\ sin t),\,\ frac {\ sqrt {6}} {6} (\ cos t+\ sin t)\ right\ rangle\ end { alinhamento*}\)

    16) Dado\(\vecs r(t)=⟨2e^t,\, e^t \cos t,\, e^t \sin t⟩\), encontre o vetor tangente unitário\(\vecs T(t)\) avaliado em\(t=0\),\(\vecs T(0)\).

    17) Dado\(\vecs r(t)=⟨2e^t,\, e^t \cos t,\, e^t \sin t⟩\), determine o vetor normal unitário\(\vecs N(t)\).

    Responda
    \(\vecs N(t)=⟨0,\, -\frac{\sqrt{2}}{2} (\sin t + \cos t), \, \frac{\sqrt{2}}{2} (\cos t- \sin t)⟩\)

    18) Dado\(\vecs r(t)=⟨2e^t,\, e^t \cos t,\, e^t \sin t⟩\), encontre o vetor normal unitário\(\vecs N(t)\) avaliado em\(t=0\),\(\vecs N(0)\).

    Responda
    \(\vecs N(0)=⟨0, \;-\frac{\sqrt{2}}{2},\;\frac{\sqrt{2}}{2}⟩\)

    19) Dado\(\vecs r(t)=t \,\hat{\mathbf{i}}+t^2 \,\hat{\mathbf{j}}+t \,\hat{\mathbf{k}}\), encontre o vetor tangente unitário\(\vecs T(t)\). O gráfico é mostrado aqui:

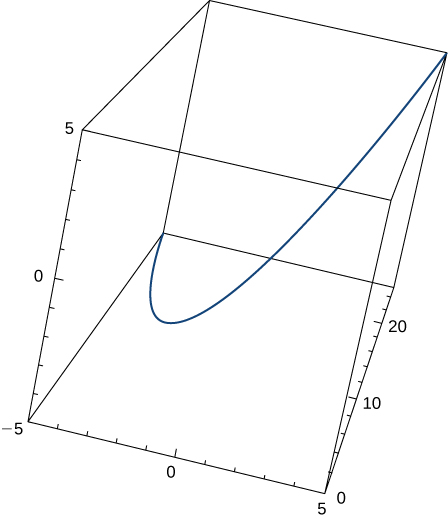
    Responda
    \(\vecs T(t)=\dfrac{1}{\sqrt{4t^2+2}}<1,2t,1>\)

    20) Encontre o vetor tangente unitário\(\vecs T(t)\) e o vetor normal unitário\(\vecs N(t)\) em\(t=0\) para a curva plana\(\vecs r(t)=⟨t^3−4t,5t^2−2⟩\). O gráfico é mostrado aqui:

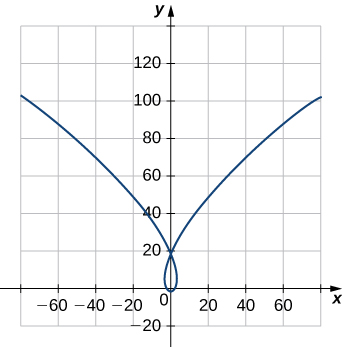
    21) Encontre o vetor tangente unitário\(\vecs T(t)\) para\(\vecs r(t)=3t \,\hat{\mathbf{i}}+5t^2 \,\hat{\mathbf{j}}+2t \,\hat{\mathbf{k}}\).

    Responda
    \(\vecs T(t)=\dfrac{1}{\sqrt{100t^2+13}}(3 \,\hat{\mathbf{i}}+10t \,\hat{\mathbf{j}}+2 \,\hat{\mathbf{k}})\)

    22) Encontre o vetor normal principal da curva\(\vecs r(t)=⟨6 \cos t,6 \sin t⟩\) no ponto determinado por\(t=\frac{π}{3}\).

    23) Encontre\(\vecs T(t)\) a curva\(\vecs r(t)=(t^3−4t) \,\hat{\mathbf{i}}+(5t^2−2) \,\hat{\mathbf{j}}\).

    Responda
    \(\vecs T(t)=\dfrac{1}{\sqrt{9t^4+76t^2+16}}\big((3t^2−4)\,\hat{\mathbf{i}}+10t \,\hat{\mathbf{j}}\big)\)

    24) Encontre\(\vecs N(t)\) a curva\(\vecs r(t)=(t^3−4t)\,\hat{\mathbf{i}}+(5t^2−2)\,\hat{\mathbf{j}}\).

    25) Encontre o vetor tangente unitário\(\vecs T(t)\) para\(\vecs r(t)=⟨2 \sin t,\, 5t,\, 2 \cos t⟩\).

    Responda
    \(\vecs T(t)=⟨\frac{2\sqrt{29}}{29}\cos t,\, \frac{5\sqrt{29}}{29},\,−\frac{2\sqrt{29}}{29}\sin t⟩\)

    26) Encontre o vetor normal unitário\(\vecs N(t)\) para\(\vecs r(t)=⟨2\sin t,\,5t,\,2\cos t⟩\).

    Responda
    \(\vecs N(t)=⟨−\sin t,\, 0,\, −\cos t⟩\)

    Parametrizações do comprimento do arco

    27) Encontre a função de comprimento de arco\(\vecs s(t)\) para o segmento de linha dado por\(\vecs r(t)=⟨3−3t,\, 4t⟩\). Em seguida, escreva a parametrização do comprimento do arco de\(r\) with\(s\) como parâmetro.

    Responda
    Função de comprimento de arco:\(s(t)=5t\); A parametrização do comprimento do arco de\(\vecs r(t)\):\(\vecs r(s)=\left(3−\dfrac{3s}{5}\right)\,\hat{\mathbf{i}}+\dfrac{4s}{5}\,\hat{\mathbf{j}}\)

    28) Parametrize a hélice\(\vecs r(t)= \cos t \,\hat{\mathbf{i}}+ \sin t \,\hat{\mathbf{j}}+t \,\hat{\mathbf{k}}\) usando o parâmetro arc-length\(s\), from\(t=0\).

    29) Parametrize a curva usando o parâmetro de comprimento do arco\(s\), no ponto em que\(t=0\)\(\vecs r(t)=e^t \sin t \,\hat{\mathbf{i}} + e^t \cos t \,\hat{\mathbf{j}}\)

    Responda
    \(\vecs r(s)=\left(1+\dfrac{s}{\sqrt{2}}\right) \sin \left( \ln \left(1+ \dfrac{s}{\sqrt{2}}\right)\right)\,\hat{\mathbf{i}} +\left(1+ \dfrac{s}{\sqrt{2}}\right) \cos \left( \ln \left(1+\dfrac{s}{\sqrt{2}}\right)\right)\,\hat{\mathbf{j}}\)

    Curvatura e o círculo osculante

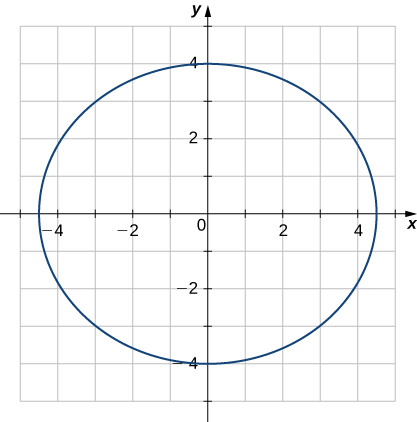
    30) Encontre a curvatura da curva\(\vecs r(t)=5 \cos t \,\hat{\mathbf{i}}+4 \sin t \,\hat{\mathbf{j}}\) em\(t=π/3\). (Nota: O gráfico é uma elipse.)

    31) Encontre a\(x\) coordenada -na qual a curvatura da curva\(y=1/x\) é um valor máximo.

    Responda
    O valor máximo da curvatura ocorre em\(x=1\).

    32) Encontre a curvatura da curva\(\vecs r(t)=5 \cos t \,\hat{\mathbf{i}}+5 \sin t \,\hat{\mathbf{j}}\). A curvatura depende do parâmetro\(t\)?

    33) Encontre a curvatura\(κ\) da curva\(y=x−\frac{1}{4}x^2\) no ponto\(x=2\).

    Responda
    \(\frac{1}{2}\)

    34) Encontre a curvatura\(κ\) da curva\(y=\frac{1}{3}x^3\) no ponto\(x=1\).

    35) Encontre a curvatura\(κ\) da curva\(\vecs r(t)=t \,\hat{\mathbf{i}}+6t^2 \,\hat{\mathbf{j}}+4t \,\hat{\mathbf{k}}\). O gráfico é mostrado aqui:

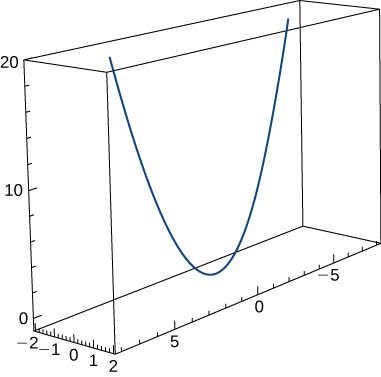
    Responda
    \(κ≈\dfrac{49.477}{(17+144t^2)^{3/2}}\)

    36) Encontre a curvatura de\(\vecs r(t)=⟨2 \sin t,5t,2 \cos t⟩\).

    37) Encontre a curvatura de\(\vecs r(t)=\sqrt{2}t \,\hat{\mathbf{i}}+e^t \,\hat{\mathbf{j}}+e^{−t} \,\hat{\mathbf{k}}\) no ponto\(P(0,1,1)\).

    Responda
    \(\frac{1}{2\sqrt{2}}\)

    38) Em que ponto a curva\(y=e^x\) tem curvatura máxima?

    39) O que acontece com a curvatura e com a curva\(y=e^x\)?\(x→∞\)

    Responda
    A curvatura se aproxima de zero.

    40) Encontre o ponto de curvatura máxima na curva\(y=\ln x\).

    41) Encontre as equações do plano normal e do plano osculante da curva\(\vecs r(t)=⟨2 \sin (3t),t,2 \cos (3t)⟩\) no ponto\((0,π,−2)\).

    Responda
    \(y=6x+π\)e\(x+6y=6π\)

    42) Encontre equações dos círculos osculantes da elipse\(4y^2+9x^2=36\) nos pontos\((2,0)\)\((0,3)\) e.

    43) Encontre a equação para o plano osculante\(t=π/4\) no ponto da curva\(\vecs r(t)=\cos (2t) \,\hat{\mathbf{i}}+ \sin (2t) \,\hat{\mathbf{j}}+t\,\hat{\mathbf{k}}\).

    Responda
    \(x+2z=\frac{π}{2}\)

    44) Encontre o raio de curvatura de\(6y=x^3\) no ponto\((2,\frac{4}{3}).\)

    45) Encontre a curvatura em cada ponto\((x,y)\) da hipérbole\(\vecs r(t)=⟨a \cosh( t),b \sinh (t)⟩\).

    Responda
    \(\dfrac{a^4b^4}{(b^4x^2+a^4y^2)^{3/2}}\)

    46) Calcule a curvatura da hélice circular\(\vecs r(t)=r \sin (t) \,\hat{\mathbf{i}}+r \cos (t) \,\hat{\mathbf{j}}+t \,\hat{\mathbf{k}}\).

    47) Encontre o raio de curvatura de\(y= \ln (x+1)\) no ponto\((2,\ln 3)\).

    Responda
    \(\frac{10\sqrt{10}}{3}\)

    48) Encontre o raio de curvatura da hipérbole\(xy=1\) no ponto\((1,1)\).

    Uma partícula se move ao longo da curva plana\(C\) descrita por\(\vecs r(t)=t \,\hat{\mathbf{i}}+t^2 \,\hat{\mathbf{j}}\). Use essa parametrização para responder às perguntas 49 a 51.

    49) Encontre o comprimento da curva ao longo do intervalo\([0,2]\).

    Responda
    \(\frac{1}{4}\big[ 4\sqrt{17} + \ln\left(4+\sqrt{17}\right)\big]\text{ units }\approx 4.64678 \text{ units}\)

    50) Encontre a curvatura da curva plana em\(t=0,1,2\).

    51) Descreva a curvatura à medida que ela aumenta de\(t=0\) para\(t=2\).

    Responda
    A curvatura está diminuindo nesse intervalo.

    A superfície de um copo grande é formada girando o gráfico da função\(y=0.25x^{1.6}\) de\(x=0\) até\(x=5\) cerca do\(y\) eixo -( medido em centímetros).

    52) [T] Use a tecnologia para representar graficamente a superfície.

    53) Encontre a curvatura\(κ\) da curva geradora em função de\(x\).

    Responda
    \(κ=\dfrac{30}{x^{2/5}\left(25+4x^{6/5}\right)^{3/2}}\)

    Observe que inicialmente sua resposta pode ser:
    \(\dfrac{6}{25x^{2/5}\left(1+\frac{4}{25}x^{6/5}\right)^{3/2}}\)

    Podemos simplificá-la da seguinte forma:
    \ (\ begin {align*}\ dfrac {6} {25x^ {2/5}\ left (1+\ frac {4} {25} x^ {6/5}\ right) ^ {3/2}} &=\ dfrac {6} {25x^ {2/ 5}\ big [\ frac {1} {25}\ left (25+4x^ {6/5}\ right)\ big] ^ {3/2}}\\ [4pt]
    &=\ dfrac {6} {25x^ {2/5}\ left (\ frac {1} {25}\ direita) ^ {3/2}\ big [25+4x^ {6/5}\ big] ^ {3/2}}\\ [4pt]
    &=\ dfrac {6} {\ frac {25} {125} x^ {2/5}\ grande [25+4x^ {6/5}\ big] ^ {3/2}}\\ [4pt]
    &=\ dfrac {30} {x^ {2/ 5}\ esquerda (25+4x^ {6/5}\ direita) ^ {3/2}}\ end {align*}\)

    54) [T] Use a tecnologia para representar graficamente a função de curvatura.

    Colaboradores: