13.4: Movimento no espaço
- Page ID
- 187827
- Descreva os vetores de velocidade e aceleração de uma partícula se movendo no espaço.
- Explique os componentes tangenciais e normais da aceleração.
- Declare as leis do movimento planetário de Kepler.
Agora vimos como descrever curvas no plano e no espaço e como determinar suas propriedades, como comprimento e curvatura do arco. Tudo isso leva ao objetivo principal deste capítulo, que é a descrição do movimento ao longo de curvas planas e curvas espaciais. Agora temos todas as ferramentas de que precisamos; nesta seção, reunimos essas ideias e veremos como usá-las.
Vetores de movimento no plano e no espaço
Nosso ponto de partida é usar funções com valores vetoriais para representar a posição de um objeto em função do tempo. Todo o material a seguir pode ser aplicado em curvas no plano ou em curvas espaciais. Por exemplo, quando observamos a órbita dos planetas, as curvas que definem essas órbitas estão todas em um plano porque são elípticas. No entanto, uma partícula viajando ao longo de uma hélice se move em uma curva em três dimensões.
\(\vecs r(t)\)Seja uma função com valor vetorial duas vezes diferenciável do parâmetro\(t\) que representa a posição de um objeto em função do tempo.
O vetor\(\vecs v(t)\) de velocidade do objeto é dado por
\[\text{Velocity}\,=\vecs v(t)=\vecs r′(t). \label{Eq1} \]
O vetor de aceleração\(\vecs a(t)\) é definido como
\[\text{Acceleration}\,=\vecs a(t)=\vecs v′(t)=\vecs r″(t). \label{Eq2} \]
A velocidade é definida como
\[\mathrm{Speed}\,=v(t)=‖\vecs v(t)‖=‖\vecs r′(t)‖=\dfrac{ds}{dt}. \label{Eq3} \]
Como\(\vecs{r}(t)\) podem estar em duas ou três dimensões, essas funções com valores vetoriais podem ter dois ou três componentes. Em duas dimensões, definimos\(\vecs{r}(t)=x(t) \hat{\mathbf i}+y(t) \hat{\mathbf j}\) e em três dimensões\(\vecs r(t)=x(t) \hat{\mathbf i}+y(t) \hat{\mathbf j}+z(t) \hat{\mathbf k}\). Em seguida, a velocidade, a aceleração e a velocidade podem ser escritas conforme mostrado na tabela a seguir.
| Quantidade | Duas dimensões | Três dimensões |
|---|---|---|
| Posição | \(\vecs{r}(t)=x(t) \hat{\mathbf i}+y(t) \hat{\mathbf j}\) | \(\vecs{r}(t)=x(t) \hat{\mathbf i}+y(t) \hat{\mathbf j}+z(t) \hat{\mathbf k}\) |
| Velocidade | \(\vecs{v}(t)=x′(t) \hat{\mathbf i}+y′(t) \hat{\mathbf j}\) | \(\vecs{v}(t)=x′(t) \hat{\mathbf i}+y′(t) \hat{\mathbf j}+z′(t) \hat{\mathbf k}\) |
| Aceleração | \(\vecs{a}(t)=x″(t) \hat{\mathbf i}+y″(t) \hat{\mathbf j}\) | \(\vecs{a}(t)=x″(t) \hat{\mathbf i}+y″(t) \hat{\mathbf j}+z″(t) \hat{\mathbf k}\) |
| Rapidez | \(\|\vecs{v}(t)\|= \sqrt{(x′(t))^2+(y′(t))^2}\) | \(\|\vecs{v}(t)\|=\sqrt{(x′(t))^2+(y′(t))^2+(z′(t))^2}\) |
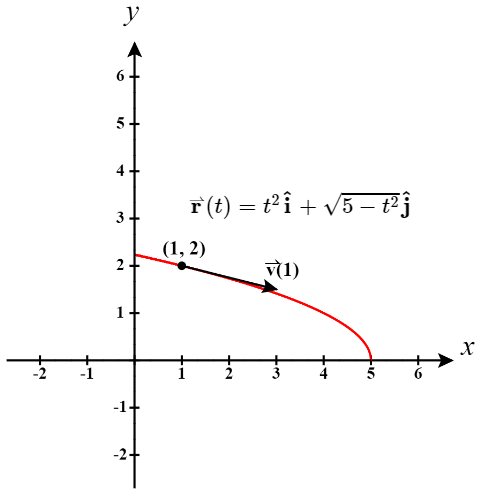
Uma partícula se move em um caminho parabólico definido pela função de valor vetorial\(\vecs{r}(t)=t^2 \hat{\mathbf i}+ \sqrt{5−t^2} \hat{\mathbf j}\), onde\(t\) mede o tempo em segundos.
- Encontre a velocidade, a aceleração e a velocidade como funções do tempo.
- Desenhe a curva junto com o vetor de velocidade no momento\(t=1\).
Solução
- Usamos as Equações\ ref {Eq1},\ ref {Eq2} e\ ref {Eq3}:
\[ \begin{align*} \vecs{v}(t) &= \vecs{r}′(t)=2t\hat{\mathbf i}−\dfrac{t}{\sqrt{5-t^2}}\hat{\mathbf j} \\[4pt] \vecs{a}(t) &=\vecs{v}′(t)=2\hat{\mathbf i}−5(5−t^2)^{-\frac{3}{2}}\hat{\mathbf j} \\[4pt] ||\vecs{v}(t)|| &=||\vecs{r}′(t)|| \\[4pt] &=\sqrt{(2t)^2+\left(-\dfrac{t}{\sqrt{5-t^2}}\right)^2} \\[4pt] &=\sqrt{4t^2+\dfrac{t^2}{5-t^2}} \\[4pt] &=\sqrt{\dfrac{21t^2-4t^4}{5-t^2}}. \end{align*}\]
- O gráfico de\(\vecs{r}(t)=t^2 \hat{\mathbf i}+ \sqrt{5−t^2} \hat{\mathbf j}\) é uma parte de uma parábola (Figura\(\PageIndex{1}\)).
Quando\(t=1\),\(\vecs r(1) = (1)^2 \mathbf{\hat i} + \sqrt{5-(1)^2} \mathbf{\hat j} \quad = \quad \mathbf{\hat i} + \sqrt{4} \mathbf{\hat j} \quad = \quad \mathbf{\hat i} + 2 \mathbf{\hat j}\).
Assim, a partícula estaria localizada no ponto em\((1, 2)\) que\(t =1\).
O vetor de velocidade em\(t=1\) é\[ \begin{align*} \vecs{v}(1) &=\vecs{r}′(1)=2(1)\hat{\mathbf i}−\frac{1}{\sqrt{5-1^2}} \hat{\mathbf j}\quad \\[4pt] &= \quad 2\hat{\mathbf i}−\frac{1}{2}\hat{\mathbf j} \end{align*}\]
e o vetor de aceleração em\(t=1\) é\[\vecs{a}(1)=\vecs{v}′(1)=2\hat{\mathbf i}−5(5 - 1^2)^{-3/2}\hat{\mathbf j}\quad = \quad 2\hat{\mathbf i}−\frac{5}{8}\hat{\mathbf j}. \nonumber \]
Observe que o vetor de velocidade é tangente ao caminho, como sempre acontece.
Uma partícula se move em um caminho definido pela função de valor vetorial\(\vecs r(t)=(t^2−3t)\,\hat{\mathbf i}+(2t−4)\,\hat{\mathbf j}+(t+2)\,\hat{\mathbf k}\), onde\(t\) mede o tempo em segundos e onde a distância é medida em pés. Encontre a velocidade, a aceleração e a velocidade como funções do tempo.
- Dica
-
Use as equações\ ref {Eq1},\ ref {Eq2} e\ ref {Eq3}.
- Responda
-
\[\begin{align*}\vecs v(t) &=\vecs{r}'(t) =(2t-3)\,\hat{\mathbf i}+2\,\hat{\mathbf j}+\,\hat{\mathbf k}\\[4pt] \vecs a(t) &=\vecs v′(t) =2\,\hat{\mathbf i} \end{align*}\]
\[ ||\vecs{r}′(t)||=\sqrt{(2t-3)^2+2^2+1^2} =\sqrt{4t^2-12t+14} \nonumber \]
As unidades de velocidade e velocidade são pés por segundo, e as unidades de aceleração são pés por segundo ao quadrado.
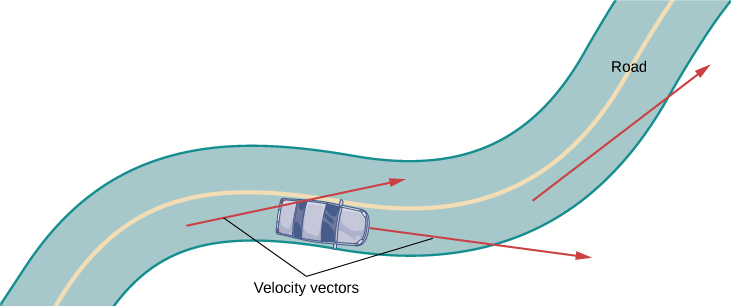
Para entender melhor os vetores de velocidade e aceleração, imagine que você está dirigindo por uma estrada cheia de curvas. Se você não girar o volante, você continuaria em linha reta e sairia correndo da estrada. A velocidade com que você está viajando quando sai da estrada, juntamente com a direção, fornece um vetor representando sua velocidade, conforme ilustrado na Figura\(\PageIndex{2}\).
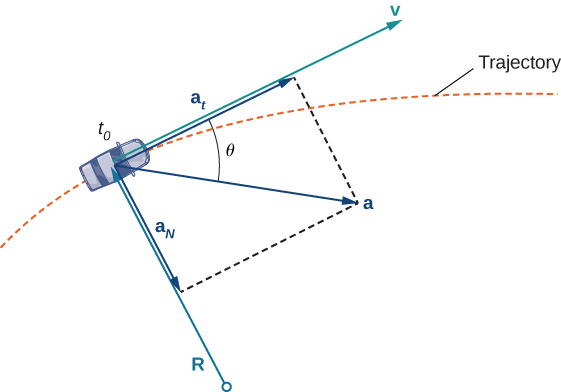
No entanto, o fato de você precisar girar o volante para permanecer na estrada indica que sua velocidade está sempre mudando (mesmo que não esteja) porque sua direção está mudando constantemente para mantê-lo na estrada. Ao virar para a direita, seu vetor de aceleração também aponta para a direita. Quando você vira para a esquerda, seu vetor de aceleração aponta para a esquerda. Isso indica que seus vetores de velocidade e aceleração estão mudando constantemente, independentemente de sua velocidade real variar (Figura\(\PageIndex{3}\)).
Componentes do vetor de aceleração
Podemos combinar alguns dos conceitos discutidos em Comprimento e Curvatura do Arco com o vetor de aceleração para obter uma compreensão mais profunda de como esse vetor se relaciona com o movimento no plano e no espaço. Lembre-se de que o vetor tangente unitário\(\vecs T\) e o vetor normal unitário\(\vecs N\) formam um plano osculante em qualquer ponto\(P\) da curva definido por uma função com valor vetorial\(\vecs{r}(t)\). O teorema a seguir mostra que o vetor de aceleração\(\vecs{a}(t)\) está no plano osculante e pode ser escrito como uma combinação linear da tangente unitária e dos vetores normais unitários.
O vetor\(\vecs{a}(t)\) de aceleração de um objeto se movendo ao longo de uma curva traçada por uma função duas vezes diferenciável\(\vecs{r}(t)\) está no plano formado pelo vetor tangente unitário\(\vecs T(t)\) e pelo vetor\(\vecs N(t)\) normal unitário principal\(C\) a. Além disso,
\[\vecs{a}(t) = v'(t)\vecs{T}(t) + [v(t)]^2 \kappa \vecs{N}(t) \nonumber \]
Aqui,\(v(t) = \|\vecs v(t)\|\) está a velocidade do objeto e\(\kappa\) a curvatura do\(C\) traçado por\(\vecs{r}(t)\).
Porque\(\vecs{v}(t)=\vecs{r}′(t)\) e\(\vecs{T}(t)=\dfrac{\vecs{r}′(t)}{||\vecs{r}′(t)||}\), nós temos\(\vecs v(t)=||\vecs{r}′(t)||\vecs{T}(t)=v(t)\vecs{T}(t)\).
Agora diferenciamos essa equação:
\[\vecs{a}(t)=\vecs{v}′(t)=\dfrac{d}{dt}\left(v(t)\vecs{T}(t)\right)=v′(t)\vecs{T}(t)+v(t)\vecs{T}′(t) \nonumber \]
Uma vez que\(\vecs{N}(t)=\dfrac{\vecs{T}′(t)}{||\vecs{T}′(t)||}\), nós sabemos\(\vecs{T}′(t)=||\vecs{T}′(t)||\vecs{N}(t)\), então
\[\vecs{a}(t)=v′(t)\vecs{T}(t)+v(t)||\vecs{T}′(t)||\vecs{N}(t). \nonumber \]
Uma fórmula para curvatura é\(\kappa=\dfrac{||\vecs{T}'(t)||}{||\vecs{r}'(t)||}\), então\(\vecs{T}'(t) = \kappa ||\vecs{r}'(t) || = \kappa v(t) \).
Isso dá\(\vecs{a}(t)=v′(t)\vecs{T}(t)+\kappa (v(t))^2 \vecs{N}(t).\)
\(\square\)
Os coeficientes de\(\vecs{T}(t)\) e\(\vecs{N}(t)\) são chamados de componente tangencial da aceleração e componente normal da aceleração, respectivamente. Escrevemos\(a_\vecs{T}\) para denotar o componente tangencial e\(a_\vecs{N}\) para denotar o componente normal.
\(\vecs{r}(t)\)Seja uma função com valor vetorial que denota a posição de um objeto em função do tempo. Então\(\vecs{a}(t)=\vecs{r}′′(t)\) é o vetor de aceleração. Os componentes tangenciais e normais da aceleração\(a_\vecs{T}\) e\(a_\vecs{N}\) são dados pelas fórmulas
\[a_{\vecs{T}}=\vecs a \cdot\vecs{T}=\dfrac{\vecs{v}\cdot\vecs{a}}{||\vecs{v}||} \label{Eq1B} \]
e
\[a_\vecs{N}=\vecs a\cdot \vecs N=\dfrac{||\vecs v \times \vecs a||}{||\vecs v||}=\sqrt{||\vecs a||^2−{\left(a_{\vecs{T}}\right)^2}}. \label{Eq2B} \]
Esses componentes estão relacionados pela fórmula
\[\vecs{a}(t)=a_\vecs{T} \vecs{T}(t)+a_\vecs{N}\vecs{N}(t). \label{Eq3B} \]
Aqui\(\vecs{T}(t)\) está o vetor tangente unitário à curva definida por\(\vecs{r}(t)\), e\(\vecs{N}(t)\) é o vetor normal unitário à curva definida por\(\vecs{r}(t)\).
O componente normal da aceleração também é chamado de componente centrípeto da aceleração ou, às vezes, componente radial da aceleração. Para entender a aceleração centrípeta, suponha que você esteja viajando em um carro em uma pista circular a uma velocidade constante. Então, como vimos anteriormente, o vetor de aceleração sempre aponta para o centro da pista. Como piloto no carro, você sente um puxão para fora da pista porque está constantemente virando. Essa sensação age na direção oposta à aceleração centrípeta. O mesmo vale para caminhos não circulares. O motivo é que seu corpo tende a se deslocar em linha reta e resiste à força resultante da aceleração que o empurra para o lado. Observe que,\(B\) no ponto\(\PageIndex{4}\) da Figura, o vetor de aceleração está apontando para trás. Isso ocorre porque o carro está desacelerando à medida que entra na curva.
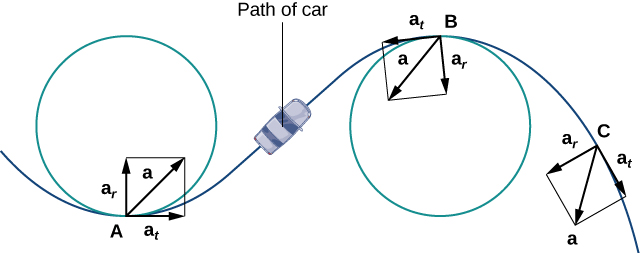
Os vetores unitários tangenciais e normais em qualquer ponto da curva fornecem um quadro de referência nesse ponto. Os componentes tangenciais e normais da aceleração são as projeções do vetor de aceleração em\(\vecs T\) e\(\vecs N\), respectivamente.
Uma partícula se move em um caminho definido pela função de valor vetorial\(\vecs{r}(t)=t^2\,\hat{\mathbf i}+(2t−3)\,\hat{\mathbf j}+(3t^2−3t)\,\hat{\mathbf k}\), onde\(t\) mede o tempo em segundos e a distância é medida em pés.
- Encontre\(a_\vecs{T}\) e\(a_\vecs{N}\) como funções de\(t\).
- Encontre\(a_\vecs{T}\) e\(a_\vecs{N}\) no momento certo\(t=2\).
Solução
- Vamos começar a derivar as funções de velocidade e aceleração:
\[\begin{align*} \vecs{v}(t) &= \vecs{r}'(t) \\[4pt] &= 2t\,\hat{\mathbf i}+2\,\hat{\mathbf j}+(6t-3)\,\hat{\mathbf k} \\[4pt] \vecs{a}(t) &= \vecs{v}'(t) \\[4pt] &=2\,\hat{\mathbf i}+6\,\hat{\mathbf k} \end{align*}\]Agora aplicamos a Equação\ ref {Eq1B}:\[\begin{align*}a_{\vecs{T}} &=\dfrac{\vecs{v}\cdot \vecs{a}}{||\vecs{v} ||} \\[4pt] &= \dfrac{ (2t \,\hat{\mathbf i} +2\,\hat{\mathbf j} +(6t-3)\,\hat{\mathbf k})\cdot(2\,\hat{\mathbf i}+6\,\hat{\mathbf k}) }{|| 2t\,\hat{\mathbf i} + 2\,\hat{\mathbf j} + (6t-3)\,\hat{\mathbf k} ||} \\[4pt] &= \dfrac{4t + 6(6t-3)}{\sqrt{(2t)^2 +2^2 + (6t-3)^2}} \\[4pt] &= \dfrac{40t-18}{40t^2 - 36t+13} \end{align*}\] Agora podemos aplicar a Equação\ ref {Eq2B}:
\[\begin{align*} a_\vecs{N} &=\sqrt{||\vecs{a}||^2-\left(a_{\vecs{T}}\right)^2} \\[4pt] &= \sqrt{||2\,\hat{\mathbf i}+6\,\hat{\mathbf k}||^2 - \left( \dfrac{ 40t-18 }{\sqrt{40t^2-36t+13}} \right)^2} \\[4pt] &= \sqrt{ 4+36-\dfrac{(40t-18)^2}{40t^2-36t+13} } \\[4pt] &= \sqrt{\dfrac{ 40(40t^2-36t+13)-(1600t^2-1440t+324) }{40t^2-36t+13} } \\[4pt] &= \sqrt{ \dfrac{196}{ 40t^2-36t+13} } \\[4pt] &= \dfrac{14}{\sqrt{40t^2-36t+13}} \end{align*}\]
- Devemos avaliar cada uma das respostas da parte a em\(t=2\):
\[\begin{align*} a_{\vecs{T}}(2) &= \dfrac{ 40(2)-18 }{\sqrt{40(2)^2 - 36(2)+13 }} \\[4pt] &= \dfrac{80-18 }{\sqrt{160-72+13}} \\[4pt] &= \dfrac{62}{\sqrt{101}} \\[4pt] a_{\vecs{N}}(2) &= \dfrac{14}{\sqrt{40(2)^2 -36(2)+13 }} \\[4pt] &= \dfrac{14}{\sqrt{160-72+13}} = \dfrac{14}{\sqrt{101}}. \end{align*}\]
As unidades de aceleração são pés por segundo ao quadrado, assim como as unidades dos componentes normal e tangencial da aceleração.
Um objeto se move em um caminho definido pela função de valor vetorial\(\vecs r(t)=4t\,\hat{\mathbf i}+t^2\,\hat{\mathbf j}\), que\(t\) mede o tempo em segundos.
- Encontre\(a_\vecs{T}\) e\(a_\vecs{N}\) como funções de\(t\).
- Encontre\(a_\vecs{T}\) e\(a_\vecs{N}\) no momento certo\(t=−3\).
- Dica
-
Use as equações\ ref {Eq1B} e\ ref {Eq2B}
- Responda
-
uma.\[\begin{align*} a_\vecs{T} =\dfrac{\vecs v(t) \cdot \vecs a(t)}{||\vecs v(t)||}= \dfrac{\vecs r'(t) \cdot \vecs r''(t) }{||\vecs r'(t)||} \\ = \dfrac{ (4\,\hat{\mathbf i} + 2t \,\hat{\mathbf j}) \cdot (2\,\hat{\mathbf j}) }{||4\,\hat{\mathbf i} + 2t \,\hat{\mathbf j} ||} \\ = \dfrac{4t}{\sqrt{4^2 + (2t)^2}}\\ = \dfrac{2t}{\sqrt{2+t^2}} \end{align*}\]
\[\begin{align*} a_\vecs{N} = \sqrt{||\vecs a||^2-a_\vecs{T}^2}\\ =\sqrt{||2\,\hat{\mathbf j} ||^2 - \left(\dfrac{2t}{\sqrt{2+t^2}}\right)^2} \\ =\sqrt{ 4 - \dfrac{4t^2 }{2+t^2} } \end{align*}\]b.\[\begin{align*} a_\vecs{T}(−3) = \dfrac{2(-3)}{\sqrt{2+(-3)^2}} \\ = \dfrac{-6}{\sqrt{11}}\end{align*}\]
\[\begin{align*}a_\vecs{N}(−3) = \sqrt{ 4 - \dfrac{4(-3)^2 }{2+(-3)^2} } \\ = \sqrt{4- \dfrac{36}{11}} \\ = \sqrt{\dfrac{8}{11} }\\ =\dfrac{2\sqrt{2}}{\sqrt{11}} \end{align*}\]
Movimento de projé
Agora vamos ver uma aplicação de funções vetoriais. Em particular, vamos considerar o efeito da gravidade no movimento de um objeto à medida que ele viaja pelo ar e como ela determina a trajetória resultante desse objeto. A seguir, ignoramos o efeito da resistência do ar. Essa situação, com um objeto se movendo com uma velocidade inicial, mas sem forças atuando sobre ele além da gravidade, é conhecida como movimento de projétil. Ele descreve o movimento de objetos de bolas de golfe a bolas de beisebol e de flechas a balas de canhão.
Primeiro, precisamos escolher um sistema de coordenadas. Se estivermos na origem desse sistema de coordenadas, escolhemos o\(y\) eixo positivo para cima, o eixo negativo\(y\) para baixo e o eixo positivo\(x\) para frente (ou seja, longe do lançador do objeto). O efeito da gravidade está na direção descendente, então a segunda lei de Newton nos diz que a força sobre o objeto resultante da gravidade é igual à massa do objeto vezes a aceleração resultante da gravidade, ou\(\vecs F_g=m\vecs a\), onde\(\vecs F_g\) representa a força da gravidade e\(\vecs a = -g\,\hat{\mathbf j}\) representa a aceleração resultante da gravidade na superfície da Terra. O valor de\(g\) no sistema de medição em inglês é de aproximadamente 32 pés/seg 2 e é de aproximadamente 9,8 m/seg 2 no sistema métrico. Essa é a única força atuando sobre o objeto. Como a gravidade atua na direção descendente, podemos escrever a força resultante da gravidade na forma\(\vecs F_g=−mg\,\hat{\mathbf j}\), conforme mostrado na Figura\(\PageIndex{5}\).
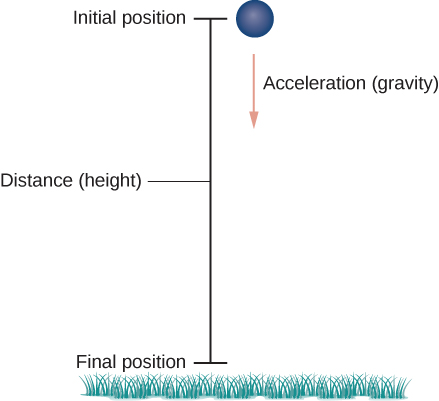
A segunda lei de Newton também nos diz que\(F=m\vecs{a}\), onde\(\vecs a\) representa o vetor de aceleração do objeto. Essa força deve ser igual à força da gravidade em todos os momentos, então sabemos que
\[\begin{align*} \vecs F =\vecs F_g \\ m\vecs{a} = -mg \,\hat{\mathbf j} \\ \vecs{a} = -g\,\hat{\mathbf j}. \end{align*}\]
Agora usamos o fato de que o vetor de aceleração é a primeira derivada do vetor de velocidade. Portanto, podemos reescrever a última equação na forma
\[\vecs v'(t) = -g\,\hat{\mathbf j} \nonumber \]
Ao tomar a antiderivada de cada lado dessa equação, obtemos
\[ \vecs v(t) = \int -g \,\hat{\mathbf j}\; dt = -gt\,\hat{\mathbf j} + \vecs C_1 \nonumber \]
para algum vetor constante\(\vecs C_1\). Para determinar o valor desse vetor, podemos usar a velocidade do objeto em um tempo fixo, digamos, no momento\(t=0\). Chamamos essa velocidade de velocidade inicial:\(\vecs v(0)=\vecs v_0\). Portanto,\(\vecs v(0)=−g(0)\,\hat{\mathbf j}+\vecs C_1=\vecs v_0\)\(\vecs C_1= \vecs v_0\) e. Isso fornece o vetor de velocidade como\(\vecs v(t)=−gt\,\hat{\mathbf j}+\vecs v_0\).
Em seguida, usamos o fato de que a velocidade\(\vecs{v}(t)\) é a derivada da posição\(\vecs{s}(t)\). Isso dá a equação
\[\vecs s'(t)=-gt\,\hat{\mathbf j}+\vecs{v}_0. \nonumber \]
Tomar a antiderivada de ambos os lados dessa equação leva a
\[\begin{align*} \vecs s(t) &= \int -gt\,\hat{\mathbf j} + \vecs{v}_0 \;dt \\[4pt] &= -\dfrac{1}{2}gt^2 \,\hat{\mathbf j} + \vecs{v}_0 t + \vecs{C}_2 \end{align*}\]
com outro vetor constante desconhecido\(\vecs{C}_2\). Para determinar o valor de\(\vecs{C}_2\), podemos usar a posição do objeto em um determinado momento, digamos, no momento\(t=0\). Chamamos essa posição de posição inicial:\(\vecs{s}(0)=\vecs{s}_0\). Portanto,\(\vecs{s}(0)=−(1/2)g(0)^2\,\hat{\mathbf j}+\vecs{v}_0(0)+\vecs{C}_2=\vecs{s}_0\). Isso fornece a posição do objeto a qualquer momento como
\[ \vecs{s}(t)=−\dfrac{1}{2}gt^2 \,\hat{\mathbf j}+\vecs{v}_0 t+\vecs{s}_0. \nonumber \]
Vamos examinar mais de perto a velocidade inicial e a posição inicial. Em particular, suponha que o objeto seja lançado para cima a partir da origem em um ângulo com\(\theta\) a horizontal, com velocidade inicial\(\vecs{v}_0\). Como podemos modificar o resultado anterior para refletir esse cenário? Primeiro, podemos supor que foi retirado da origem. Caso contrário, podemos mover a origem até o ponto de onde ela é lançada. Portanto\(\vecs{s}_0=\vecs{0}\), conforme mostrado na Figura\(\PageIndex{6}\).
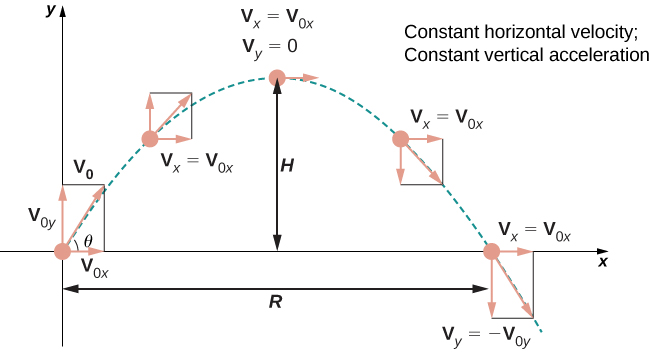
Podemos reescrever o vetor de velocidade inicial no formulário\(\vecs{v}_0= v_0 \cos \theta \,\hat{\mathbf i} + v_0 \sin \theta \,\hat{\mathbf j}\). Em seguida, a equação para a função de posição\(\vecs{s}(t)\) se torna
\[\begin{align*} \vecs{s}(t) &=-\dfrac{1}{2} gt^2\,\hat{\mathbf j} + v_0 t \cos\theta \,\hat{\mathbf i} + v_0 t \sin\theta \,\hat{\mathbf j} \\[4pt] &= v_0 t \cos\theta\,\hat{\mathbf i} + v_0 t \sin\theta \,\hat{\mathbf j} - \dfrac{1}{2} gt^2\,\hat{\mathbf j} \\[4pt] &= v_0 t \cos\theta \,\hat{\mathbf i} + \left(v_0 t \sin\theta - \dfrac{1}{2} gt^2\right)\,\hat{\mathbf j}. \end{align*}\]
O coeficiente de\(\hat{\mathbf i}\) representa o componente horizontal de\(\vecs{s}(t)\) e é a distância horizontal do objeto da origem no momento\(t\). O valor máximo da distância horizontal (medida na mesma altitude inicial e final) é chamado de alcance\(R\). O coeficiente de\(\hat{\mathbf j}\) representa o componente vertical de\(\vecs{s}(t)\) e é a altitude do objeto no momento\(t\). O valor máximo da distância vertical é a altura\(H\).
Durante a celebração do Dia da Independência, uma bala de canhão é disparada de um canhão em um penhasco em direção à água. O canhão é direcionado para um ângulo de 30° acima da horizontal e a velocidade inicial da bala de canhão é de 600 pés/seg. O penhasco está a 100 pés acima da água (Figura\(\PageIndex{7}\)).
- Encontre a altura máxima da bala de canhão.
- Quanto tempo vai demorar para a bala de canhão cair no mar?
- A que distância do mar a bala de canhão atingirá a água?
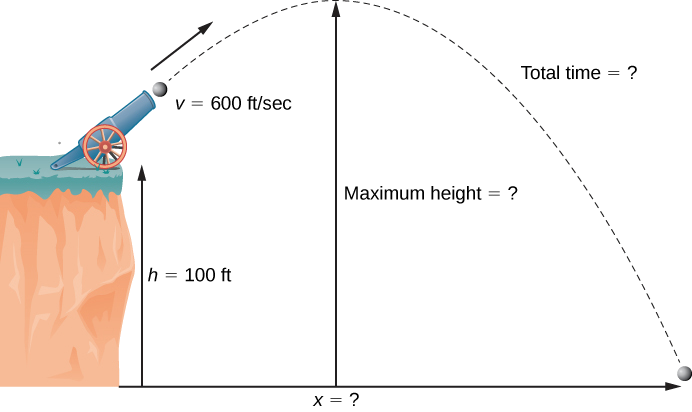
Solução
Usamos a equação
\[\vecs{s}(t) = v_0 t \cos\theta \,\hat{\mathbf i} + \left(v_0 t \sin\theta - \dfrac{1}{2}gt^2 \right)\,\hat{\mathbf j} \nonumber \]
com\(\theta=30^\circ \)\(g=32 \dfrac{\text{ft}}{\text{sec}^2}\),\(v_0=600 \dfrac{\text{ft}}{\text{sec}^2}\) e. Em seguida, a equação de posição se torna
\[\begin{align*} \vecs{s}(t) &= 600 t ( \cos 30^\circ)\,\hat{\mathbf i} + \left(600t \sin30^\circ - \dfrac{1}{2}(32)t^2 \right)\,\hat{\mathbf j} \\[4pt] &= 300t\sqrt{3} \,\hat{\mathbf i} + \left( 300t - 16t^2 \right)\,\hat{\mathbf j} \end{align*}\]
- A bala de canhão atinge sua altura máxima quando o componente vertical de sua velocidade é zero, porque a bala de canhão não está subindo nem descendo nesse ponto. O vetor de velocidade é
\[\begin{align*} \vecs{v}(t) &=\vecs s'(t)\\[4pt] &= 300 \sqrt{3} \,\hat{\mathbf i} + (300-32t)\,\hat{\mathbf j} \end{align*} \nonumber \]
Portanto, o componente vertical da velocidade é dado pela expressão\(300−32t\). Definir essa expressão igual a zero e resolver para t dá\(t=9.375\) segundos. A altura da bala de canhão neste momento é dada pelo componente vertical do vetor de posição, avaliado em\(t=9.375\).\[\begin{align*} \vecs{s}(9.375) &=300(9.375)\sqrt{3}\,\hat{\mathbf i}+(300(9.375)−16(9.375)^2)\,\hat{\mathbf j} \\[4pt] &=4871.39 \,\hat{\mathbf i}+1406.25\,\hat{\mathbf j} \end{align*}\]
Portanto, a altura máxima da bala de canhão é 1406,39 pés acima do canhão ou 1506,39 pés acima do nível do mar. - Quando a bala de canhão cai na água, ela está 100 pés abaixo do canhão. Portanto, o componente vertical do vetor de posição é igual a −100. Definindo o componente vertical de\(\vecs s(t)\) igual a −100 e resolvendo, obtemos
\[\begin{align*} 300t-16t^2 &= -100 \\ 16t^2-300t-100 =0 \\4t^2-75-25 =0 \\[4pt] t &= \dfrac{75\pm \sqrt{(-75)^2}-4(4)(-25) }{2(4)} \\[4pt] &= \dfrac{75 \pm \sqrt{6025}}{8} \\[4pt] &= \dfrac{75 \pm 5\sqrt{241}}{8} \end{align*}\]
O valor positivo\(t\) que resolve essa equação é aproximadamente 19,08. Portanto, a bala de canhão atinge a água após aproximadamente 19,08 s. - Para descobrir a distância até o mar, simplesmente substituímos a resposta da parte (b) por\(\vecs{s}(t)\):
\[\begin{align*} \vecs s(19.08) &=300(19.08)\sqrt{3} \,\hat{\mathbf i}+\left(300(19.08)−16(19.08)^2\right)\,\hat{\mathbf j}\\[4pt] &=9914.26\,\hat{\mathbf i}−100.7424\,\hat{\mathbf j} \end{align*}\]
Portanto, a bola atinge a água a cerca de 9914,26 pés de distância da base do penhasco. Observe que o componente vertical do vetor de posição está muito próximo de −100, o que nos diz que a bola acabou de bater na água. Observe que 9914,26 pés não é o alcance real do canhão, já que a bala de canhão pousa no oceano em um local abaixo do canhão. O alcance do canhão seria determinado pela descoberta da distância da bala de canhão quando sua altura está 100 pés acima da água (a mesma que a altitude do canhão).
Um arqueiro dispara uma flecha em um ângulo de 40° acima da horizontal com uma velocidade inicial de 98 m/seg. A altura do arqueiro é de 171,5 cm. Encontre a distância horizontal que a flecha percorre antes de atingir o chão.
- Dica
-
A equação para o vetor de posição precisa levar em conta a altura do arqueiro em metros.
- Responda
-
967,15 km
Uma última pergunta permanece: Em geral, qual é a distância máxima que um projétil pode percorrer, dada sua velocidade inicial? Para determinar essa distância, assumimos que o projétil foi disparado do nível do solo e desejamos que ele retorne ao nível do solo. Em outras palavras, queremos determinar uma equação para o intervalo. Nesse caso, a equação do movimento do projétil é
\[\vecs{s}=v_0 t \cos\theta \,\hat{\mathbf i} + \left(v_0t\sin\theta - \dfrac{1}{2}gt^2 \right)\,\hat{\mathbf j}. \nonumber \]
Definindo o segundo componente como igual a zero e resolvendo\(t\) os rendimentos
\[\begin{align*} v_0 t \sin\theta - \dfrac{1}{2}gt^2 =0\\ t\left(v_0 \sin\theta - \dfrac{1}{2}gt\right) =0 \end{align*}\]
Portanto, ou\(t=0\) ou\(t=\dfrac{2v_0\sin\theta}{g}\). Estamos interessados no segundo valor de\(t\), então substituímos isso por\(\vecs{s}(t)\), o que dá
\[\begin{align*} \vecs{s}\left(\dfrac{2v_0\sin\theta}{g} \right) = v_0 \left(\dfrac{2v_0\sin\theta}{g} \right) \cos\theta \,\hat{\mathbf i} + \left( v_0\left(\dfrac{2v_0\sin\theta}{g} \right)\sin\theta - \dfrac{1}{2}g\left(\dfrac{2v_0\sin\theta}{g} \right)^2 \right)\,\hat{\mathbf j} \\ = \left(\dfrac{2v_0^2\sin\theta\cos\theta}{g} \right)\,\hat{\mathbf i} \\ = \dfrac{v_0^2 \sin2\theta}{g}\,\hat{\mathbf i}. \end{align*}\]
Assim, a expressão para o alcance de um projétil disparado em ângulo\(\theta\) é
\[R=\dfrac{v_0^2 \sin2\theta}{g}\,\hat{\mathbf i} . \nonumber \]
A única variável nessa expressão é\( \theta\). Para maximizar a distância percorrida, pegue a derivada do coeficiente de i em relação a\(\theta\) e defina-a como igual a zero:
\[\begin{align*} \dfrac{d}{d\theta} \left( \dfrac{v_0^2 \sin2\theta}{g} \right) =0\\ \dfrac{2v_0^2\cos2\theta}{g} =0\\ \theta=45^\circ \end{align*}\]
Esse valor de\(\theta)\) é o menor valor positivo que torna a derivada igual a zero. Portanto, na ausência de resistência do ar, o melhor ângulo para disparar um projétil (para maximizar o alcance) é em um ângulo de 45°. A distância percorrida é dada por
\[\vecs{s}\left(\dfrac{2v_0 \sin 45^\circ}{g} \right)= \dfrac{v_0^2 \sin 90^\circ}{g} \,\hat{\mathbf i} = \dfrac{v_0^2}{g}\,\hat{\mathbf i} \nonumber \]
Portanto, o alcance para um ângulo de 45° é de\(\frac{v_0^2}{g}\) unidades.
Leis de Kepler
Durante o início dos anos 1600, Johannes Kepler conseguiu usar os dados incrivelmente precisos de seu mentor Tycho Brahe para formular suas três leis do movimento planetário, agora conhecidas como leis do movimento planetário de Kepler. Essas leis também se aplicam a outros objetos no sistema solar em órbita ao redor do Sol, como cometas (por exemplo, o cometa Halley) e asteróides. Variações dessas leis se aplicam aos satélites em órbita ao redor da Terra.
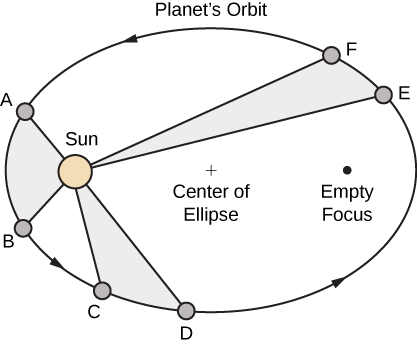
- O caminho de qualquer planeta ao redor do Sol é elíptico, com o centro do Sol localizado em um foco da elipse (a lei das elipses).
- Uma linha traçada do centro do Sol até o centro de um planeta varre áreas iguais em intervalos de tempo iguais (a lei das áreas iguais) (Figura\(\PageIndex{8}\)).
- A proporção dos quadrados dos períodos de quaisquer dois planetas é igual à razão entre os cubos e os comprimentos de seus eixos orbitais semi-maiores (a Lei das Harmonias).
A terceira lei de Kepler é especialmente útil ao usar unidades apropriadas. Em particular, 1 unidade astronômica é definida como sendo a distância média da Terra ao Sol e agora é reconhecida como sendo 149.597.870.700 m ou aproximadamente 93.000.000 milhas. Portanto, escrevemos 1 A.U. = 93.000.000 mi. Como o tempo que a Terra leva para orbitar o Sol é de 1 ano, usamos os anos terrestres como unidades de tempo. Então, substituindo 1 ano pelo período da Terra e 1 A.U. pela distância média ao Sol, a terceira lei de Kepler pode ser escrita como
\[ T_p^2=D_p^3 \nonumber \]
para qualquer planeta do sistema solar, onde\(T_P\) é o período desse planeta medido em anos terrestres e\(D_P\) é a distância média desse planeta ao Sol medida em unidades astronômicas. Portanto, se soubermos a distância média de um planeta ao Sol (em unidades astronômicas), podemos então calcular a duração de seu ano (em anos terrestres) e vice-versa.
As leis de Kepler foram formuladas com base nas observações de Brahe; no entanto, elas não foram provadas formalmente até que Sir Isaac Newton fosse capaz de aplicar o cálculo. Além disso, Newton foi capaz de generalizar a terceira lei de Kepler para outros sistemas orbitais, como uma lua orbitando ao redor de um planeta. A terceira lei original de Kepler só se aplica a objetos que orbitam o Sol.
Vamos agora provar a primeira lei de Kepler usando o cálculo de funções com valores vetoriais. Primeiro, precisamos de um sistema de coordenadas. Vamos colocar o Sol na origem do sistema de coordenadas e deixar que a função vetorial\(\vecs{r}(t)\) represente a localização de um planeta em função do tempo. Newton provou a lei de Kepler usando sua segunda lei do movimento e sua lei da gravitação universal. A segunda lei do movimento de Newton pode ser escrita como\(\vecs{F}=m\vecs{a}\), onde\(\vecs{F}\) representa a força líquida atuando no planeta. Sua lei da gravitação universal pode ser escrita na forma\(\vecs{F}=−\dfrac{GmM}{||\vecs{r}||^2}\cdot \dfrac{\vecs{r}}{||\vecs{r} ||}\), que indica que a força resultante da atração gravitacional do Sol aponta de volta para o Sol e tem magnitude\(\dfrac{GmM}{||\vecs{r}||^2} \) (Figura\(\PageIndex{9}\)).
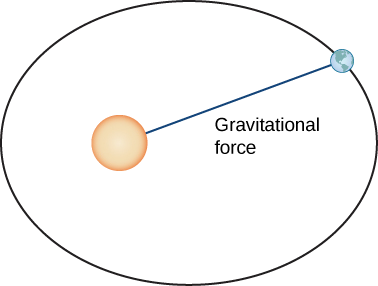
Definindo essas duas forças iguais uma à outra, e usando o fato de que\(\vecs a(t)=\vecs v′(t)\), obtemos
\[ m\vecs v′(t)=−\frac{GmM}{‖\vecs r‖^2}⋅\frac{\vecs r}{‖\vecs r‖}, \nonumber \]
que pode ser reescrito como
\[ \dfrac{d\vecs v}{dt}=−\dfrac{GM}{||\vecs r||^3}\vecs{r}. \nonumber \]
Essa equação mostra que os\(d\vecs{v}/dt\) vetores\(\vecs r\) são paralelos entre si, então\(d\vecs {v}/dt \times \vecs {r}=\vecs 0\). A seguir, vamos diferenciar em\(\vecs{r} \times \vecs{v}\) relação ao tempo:
\[\dfrac{d}{dt}(\vecs{r}\times \vecs{v})=\dfrac{d\vecs{r}}{dt}\times \vecs v+\vecs{r} \times \dfrac{d\vecs{v}}{dt}=\vecs{v}\times \vecs{v}+\vecs{0}=\vecs{0}. \label{Eq10} \]
Isso prova que\(\vecs{r}\times\vecs{v}\) é um vetor constante, que chamamos\(\vecs C\). Como\(\vecs r\) e\(\vecs v\) são perpendiculares\(\vecs C\) para todos os valores de\(t\), eles devem estar em um plano perpendicular\(\vecs C\) a. Portanto, o movimento do planeta está em um plano.
Em seguida, calculamos a expressão\(d\vecs{v}/dt\times \vecs C\):
\[\dfrac{d\vecs{v}}{dt} \times \vecs{C}=−\dfrac{GM}{||\vecs{r}||^3}\vecs{r}\times (\vecs{r}\times\vecs{v})=−\dfrac{GM}{||\vecs r||^3}[(\vecs{r} \cdot \vecs{v})\vecs{r} - (\vecs{r} \cdot \vecs{r})\vecs{v}]. \label{Eq11} \]
A última igualdade na Equação\ ref {Eq10} vem da fórmula do produto cruzado triplo (Introdução aos vetores no espaço). Precisamos de uma expressão para\(\vecs{r}\cdot \vecs{v}\). Para calcular isso, diferenciamos em\(\vecs{r}\cdot \vecs{r}\) relação ao tempo:
\[ \dfrac{d}{dt}(\vecs{r}\cdot \vecs{r})=\dfrac{d\vecs{r}}{dt}\cdot \vecs{r}+\vecs{r}\cdot \dfrac{d\vecs{r}}{dt}=2\vecs{r}\cdot \dfrac{d\vecs{r}}{dt}=2\vecs{r}\cdot \vecs{v}. \label{Eq12} \]
Desde então\(\vecs{r}\cdot\vecs{r}=||\vecs r||^2\), também temos
\[\dfrac{d}{dt}(\vecs{r}\cdot \vecs{r})=\dfrac{d}{dt}||\vecs{r}||^2=2||\vecs{r}|| \dfrac{d}{dt}||\vecs{r}||. \label{Eq13} \]
Combinando a Equação\ ref {Eq12} e a Equação\ ref {Eq13}, obtemos
\[\begin{align*} 2\vecs{r}\cdot \vecs{v} =2||\vecs{r}||\dfrac{d}{dt}||\vecs{r}|| \\ \vecs{r} \cdot \vecs{v} =||\vecs{r}‖\dfrac{d}{dt}||\vecs{r}||. \end{align*} \label{Eq14} \]
Substituir isso na Equação\ ref {Eq11} nos dá
\[\begin{align} \dfrac{d\vecs{v}}{dt} \times \vecs{C} = - \dfrac{GM}{||\vecs{r}||^3} [(\vecs{r}\cdot \vecs{v})\vecs{r} - (\vecs{r}\cdot \vecs{r})\vecs{v}] \nonumber \\ = -\dfrac{GM}{||\vecs{r}||^3}\left[ ||\vecs{r} \left(\dfrac{d}{dt} ||\vecs{r}||\right)\vecs{r} - ||\vecs{r}||^2\vecs{v} \right] \nonumber \\ = -GM\left[ \dfrac{1}{||\vecs{r}||^2}\left( \dfrac{d}{dt} ||\vecs{r}|| \right)\vecs{r} - \dfrac{1}{||\vecs{r}||}\vecs{v} \right] \nonumber \\ = GM\left[ \dfrac{\vecs{v}}{||\vecs{r}||} -\dfrac{\vecs{r}}{||\vecs{r}||^2}\left( \dfrac{d}{dt} ||\vecs{r}|| \right) \right]. \label{Eq15} \end{align} \]
No entanto,
\[ \begin{align*} \dfrac{d}{dt} \dfrac{\vecs{r}}{||\vecs{r}||} = \dfrac{ \frac{d}{dt}(\vecs{r})||\vecs{r}||- \vecs{r}\frac{d}{dt}||\vecs{r}|| }{||\vecs{r}||^2} \\ = \dfrac{ \frac{d\vecs{r}}{dt} }{||\vecs{r}||} - \dfrac{\vecs{r}}{||\vecs{r}||^2}\dfrac{d}{dt}||\vecs{r} || \\ = \dfrac{\vecs{v}}{||\vecs{r}||} - \dfrac{\vecs{r}}{||\vecs{r}||^2} \dfrac{d}{dt}||\vecs{r}||. \end{align*}\]
Portanto, a Equação\ ref {Eq15} se torna
\[\dfrac{d \vecs{v}}{dt}\times \vecs{C}=GM\left( \dfrac{d}{dt}\dfrac{ \vecs{r}}{ || \vecs{r} ||} \right).\nonumber \]
Como\(\vecs{C}\) é um vetor constante, podemos integrar os dois lados e obter
\[ \vecs{v}\times\vecs{C} = GM \dfrac{ \vecs{r} }{|| \vecs{r} ||} + \vecs{D}, \nonumber \]
onde\(\vecs D\) é um vetor constante. Nosso objetivo é resolver\(|| \vecs{r} ||\). Vamos começar calculando\( \vecs{r} \cdot ( \vecs{v}\times \vecs{C}\):
\[\vecs{r} \cdot ( \vecs{v}\times \vecs{C} =GM\dfrac{||\vecs{r}||^2}{||\vecs{r}||}+ \vecs{r}\cdot\vecs{D} =GM||\vecs{r}||+\vecs{r}\cdot \vecs{D}. \nonumber \]
No entanto\( \vecs{r} \cdot ( \vecs{v}\times \vecs{C})= ( \vecs{r} \times \vecs{v})\cdot \vecs{C} \), então
\[ ( \vecs{r} \times \vecs{v})\cdot \vecs{C} =GM||\vecs{r}|| + \vecs{r}\cdot \vecs{D}.\nonumber \]
Desde então\(\vecs{r}\times \vecs{v}=\vecs{C}\), temos
\[ ||\vecs{C}||^2 =GM||\vecs{r}|| +\vecs{r}\cdot \vecs{D}.\nonumber \]
Observe que\( \vecs{r} \cdot \vecs{D}=||\vecs{r}|| ||\vecs{D}||\cos \theta \), onde\(\theta\) está o ângulo entre\(\vecs{r}\)\(\vecs{D}\) e. Portanto,
\[ ||\vecs{C}||^2=GM||\vecs{r}||+||\vecs{r}|| ||\vecs{D}|| \cos\theta \nonumber \]
Resolvendo para\(||\vecs{r}||\),
\[ ||\vecs{r}|| = \dfrac{||\vecs{C}||^2 }{GM+||\vecs{D}||\cos\theta} = \dfrac{||\vecs{C}||^2}{GM}\left( \dfrac{1}{1+e\cos\theta} \right). \nonumber \]
onde\(e=||\vecs{D}||/GM\). Essa é a equação polar de uma cônica com foco na origem, que configuramos para ser o Sol. É uma hipérbole se\(e>1\), uma parábola se\(e=1\), ou uma elipse se\(e<1\). Como os planetas têm órbitas fechadas, a única possibilidade é uma elipse. No entanto, neste momento, deve-se mencionar que existem cometas hiperbólicos. São objetos que estão simplesmente passando pelo sistema solar a velocidades muito altas para ficarem presos em órbita ao redor do Sol. À medida que passam perto o suficiente do Sol, o campo gravitacional do Sol desvia a trajetória o suficiente para que o caminho se torne hiperbólico.
\(\square\)
A terceira lei do movimento planetário de Kepler pode ser modificada para o caso de um objeto em órbita ao redor de um objeto diferente do Sol, como a Lua ao redor da Terra. Nesse caso, a terceira lei de Kepler se torna
\[P^2 = \dfrac{4\pi^2 a^3}{G(m+M)}, \label{Eq30} \]
onde m é a massa da Lua e M é a massa da Terra, a representa o comprimento do eixo principal da órbita elíptica e P representa o período.
Dado que a massa da Lua é\(7.35\times 10^{22}\) kg, a massa da Terra é\(5.97\times 10^{24}\) kg e o período da lua é de 27,3 dias, vamos encontrar o comprimento do eixo principal da órbita da Lua ao redor da Terra.\(G=6.67\times 10^{−11} \text{m} / \text{kg} \cdot \text{sec}^2\)
Solução
É importante ser consistente com as unidades. Como a constante gravitacional universal contém segundos nas unidades, precisamos usar segundos também para o período da Lua:
\[27.3 \; \text{days} \times \dfrac{24 \; \text{hr}}{1 \; \text{day}} \times \dfrac{3600 \; \text{esc}}{1 \; \text{hour}} =2,358,720\; \text{sec}\nonumber \]
Substitua todos os dados na Equação\ ref {Eq30} e resolva por\(a\):
\[\begin{align*} (2,358,720sec)^2 = \dfrac{4\pi^2a^3}{\left( 6.67\times 10^{-11} \frac{m}{\text{kg}\times \text{sec}^2}\right) (7.35\times 10^{22}\text{kg} + 5.97 \times 10^{24}\text{kg})} \\ 5.563 \times 10^{12} = \dfrac{ 4\pi^2a^3}{(6.67 \times 10^{-11}\text{m}^3)(6.04 \times 10^{24})} \\ (5.563 \times 10^{12})(6.67 \times 10^{-11} \text{m}^3)(6.04 \times 10^{24}) = 4\pi^2 a^3 \\ a^3 = \dfrac{2.241 \times 10^{27}}{4\pi^2}\text{m}^3 \\ a = 3.84 \times 10^8 \text{m} \\ \approx 384,000 \,\text{km}. \end{align*}\]
Análise
De acordo com solarsystem.nasa.gov, a distância média real da Lua à Terra é de 384.400 km. Isso é calculado usando refletores deixados na Lua pelos astronautas da Apollo na década de 1960.
Titã é a maior lua de Saturno. A massa de Titã é de aproximadamente\(1.35 \times 10^{23} kg\). A massa de Saturno é de aproximadamente\( 5.68 \times 10^{26}\) kg. Titã leva aproximadamente 16 dias para orbitar Saturno. Use essas informações, junto com a constante de gravitação universal,\(G=6.67×10^{−11} \text{m}/\text{kg} \cdot \text{sec}^2\) para estimar a distância de Titã a Saturno.
- Dica
-
Certifique-se de que suas unidades estejam de acordo e, em seguida, use a Equação\ ref {Eq30}.
- Responda
-
\[a\approx 1.224 \times 10^9 \text{m}= 1,224,000 \text{km} \nonumber \]
Agora voltamos à abertura do capítulo, que discute o movimento do cometa Halley em torno do Sol. A primeira lei de Kepler afirma que o cometa Halley segue um caminho elíptico ao redor do Sol, com o Sol como um foco da elipse. O período do cometa Halley é de aproximadamente 76,1 anos, dependendo de quão perto ele passa por Júpiter e Saturno ao passar pelo sistema solar externo. Vamos usar\(T=76.1\) anos. Qual é a distância média entre o cometa Halley e o Sol?

Solução
Usando a equação\(T^2=D^3\) com\(T=76.1\), obtemos\(D^3=5791.21\), então\(D\approx 17.96\) A.U. Isso resulta em aproximadamente\(1.67\times 10^9\) mi.
Uma pergunta natural a ser feita é: Quais são as distâncias máxima (afélio) e mínima (periélio) do Cometa Halley ao Sol? A excentricidade da órbita do cometa Halley é de 0,967 (Fonte: http://nssdc.gsfc.nasa.gov/planetary...cometfact.html). Lembre-se de que a fórmula para a excentricidade de uma elipse é\(e=c/a\), onde a é o comprimento do semi-eixo maior e c é a distância do centro até qualquer foco. Portanto,\(0.967=c/17.96\) e\(c\approx 17.37\) A.U. Subtraindo isso de a dá a distância do periélio\(p=a−c=17.96−17.37=0.59\) A.U. De acordo com o National Space Science Data Center (Fonte: http://nssdc.gsfc.nasa.gov/planetary...cometfact.html), a distância do periélio para o cometa Halley é 0,587 A.U. Para calcular a distância do afélio, adicionamos
\[ P=a+c=17.96+17.37=35.33 \; \text{A.U.} \nonumber \]
Isso é aproximadamente\(3.3\times 10^9\) mi. A distância média de Plutão ao Sol é de 39,5 A.U. (Fonte: http://www.oarval.org/furthest.htm), então parece que o cometa Halley permanece dentro da órbita de Plutão.
Com que rapidez um carro de corrida pode percorrer uma curva circular sem derrapar e bater na parede? A resposta pode depender de vários fatores:
- O peso do carro;
- O atrito entre os pneus e a estrada;
- O raio do círculo;
- A “inclinação” da curva.
Neste projeto, investigamos essa questão para carros de corrida da NASCAR no Bristol Motor Speedway, no Tennessee. Antes de considerar essa trilha em particular, usamos funções vetoriais para desenvolver a matemática e a física necessárias para responder perguntas como essa.
Um carro de massa\(m\) se move com velocidade angular constante\(\omega\) em torno de uma curva circular de raio\(R\) (Figura\(\PageIndex{9}\)). A curva está inclinada em um ângulo\(\theta\). Se a altura do carro em relação ao solo for\(h\), a posição do carro no momento\(t\) é dada pela função\(\vecs r(t)=< R\cos(\omega t),R\sin(\omega t),h>\).

- Encontre a função\(\vecs{v}(t)\) de velocidade do carro. Mostre que\(\vecs{v}\) é tangente à curva circular. Isso significa que, sem uma força para manter o carro na curva, o carro disparará para fora dele.
- Mostre que a velocidade do carro é\(\omega R\). Use isso para mostrar isso\((2\pi 4)/\|\vecs{v}\|=(2\pi)/\omega \).
- Encontre a aceleração\(\vecs{a}\). Mostre que esse vetor aponta para o centro do círculo e isso\(\|\vecs{a}\|=R\omega ^2\).
- A força necessária para produzir esse movimento circular é chamada de força centrípeta e é denotada\( \vecs{F}_{cent} \). Essa força aponta para o centro do círculo (não para o chão). Mostre isso\(\|\vecs{F}_{cent}\|=\left(m|\vecs{v}|^2 \right)/R\).
Conforme o carro se move ao redor da curva, três forças atuam sobre ela: a gravidade, a força exercida pela estrada (essa força é perpendicular ao solo) e a força de atrito (Figura\(\PageIndex{10}\)). Como descrever a força de atrito gerada pelos pneus e pela estrada é complexo, usamos uma aproximação padrão para a força de atrito. Suponha que\(\vecs{f}=\mu \vecs{N}\) para alguma constante positiva\(\mu \). A constante\(\mu\) é chamada de coeficiente de atrito.
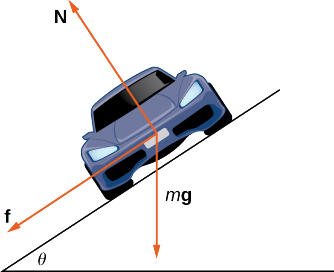
Vamos\(v_{max}\) indicar a velocidade máxima que o carro pode atingir na curva sem derrapar. Em outras palavras,\(v_{max}\) é a velocidade mais rápida na qual o carro pode navegar na curva. Quando o carro está viajando nessa velocidade, a magnitude da força centrípeta é
\[\| \vecs{F}_{cent} \| = \dfrac{m(v_{max})^2}{R}. \nonumber \]
As próximas três perguntas tratam do desenvolvimento de uma fórmula que relaciona\(v_{max}\) a velocidade com o ângulo bancário\(\theta\).
- Mostre isso\(\vecs{N} \cos\theta=m\vecs g+\vecs{f} \sin\theta\). Conclua isso\(\vecs{N}=(m\vecs g)/(\cos\theta−\mu \sin\theta)\).
- A força centrípeta é a soma das forças na direção horizontal, já que a força centrípeta aponta para o centro da curva circular. Mostre isso
\[\vecs{F}_{cent}=\vecs{N} \sin\theta+\vecs{f}\cos\theta. \nonumber \]
Conclua que\[\vecs{F}_{cent}=\dfrac{\sin\theta+\mu \cos\theta}{cos\theta−\mu \sin\theta} m\vecs g. \nonumber \]
- Mostre isso\((v_{\text{max}})^2=((\sin\theta+\mu\ cos\theta)/(\cos\theta−\mu \sin\theta))gR\). Conclua que a velocidade máxima não depende realmente da massa do carro.
Agora que temos uma fórmula que relaciona a velocidade máxima do carro e o ângulo de inclinação, estamos em condições de responder a perguntas como a que foi feita no início do projeto.
O Bristol Motor Speedway é uma pista curta da NASCAR em Bristol, Tennessee. A trilha tem a forma aproximada mostrada na Figura\(\PageIndex{11}\). Cada extremidade da pista é aproximadamente semicircular, então, quando os carros fazem curvas, eles viajam ao longo de uma curva aproximadamente circular. Se um carro pegar a pista interna e acelerar ao longo da parte inferior da curva 1, o carro percorre um semicírculo de raio de aproximadamente 211 pés com um ângulo de inclinação de 24°. Se o carro decidir pegar a pista externa e acelerar no topo da curva 1, o carro percorre um semicírculo com um ângulo de inclinação de 28°. (A pista tem inclinação angular variável.)

O coeficiente de atrito para um pneu normal em condições secas é de aproximadamente 0,7. Portanto, assumimos que o coeficiente para um pneu NASCAR em condições secas é de aproximadamente 0,98.
Antes de responder às perguntas a seguir, observe que é mais fácil fazer cálculos em termos de pés e segundos e, em seguida, converter as respostas em milhas por hora como etapa final.
- Em condições de seca, com que rapidez o carro pode percorrer a parte inferior da curva sem derrapar?
- Em condições de seca, com que rapidez o carro pode percorrer a parte superior da curva sem derrapar?
- Em condições úmidas, o coeficiente de atrito pode chegar a 0,1. Se for esse o caso, com que rapidez o carro pode percorrer a parte inferior da curva sem derrapar?
- Suponha que a velocidade medida de um carro ao longo da borda externa da curva seja 105 mph. Estime o coeficiente de atrito dos pneus do carro.
Conceitos-chave
- Se\(\vecs{r}(t)\) representa a posição de um objeto no tempo t, então\(\vecs{r}'(t)\) representa a velocidade e\(\vecs{r}′′(t)\) representa a aceleração do objeto no tempo t. A magnitude do vetor de velocidade é a velocidade.
- O vetor de aceleração sempre aponta para o lado côncavo da curva definida por\(\vecs{r}(t)\). Os componentes tangenciais e normais da aceleração\(a_\vecs{T}\) e\(a_\vecs{N}\) são as projeções do vetor de aceleração na tangente unitária e os vetores normais unitários na curva.
- As três leis do movimento planetário de Kepler descrevem o movimento de objetos em órbita ao redor do Sol. Sua terceira lei também pode ser modificada para descrever o movimento de objetos em órbita ao redor de outros objetos celestes.
- Newton foi capaz de usar sua lei da gravitação universal em conjunto com sua segunda lei do movimento e do cálculo para provar as três leis de Kepler.
Equações-chave
- Velocidade\[\vecs{v}(t)=\vecs{r}′(t) \nonumber \]
- Aceleração\[\vecs{a}(t)=\vecs{v}′(t)=\vecs{r}′′(t) \nonumber \]
- Velocidade\[v(t)=||\vecs{v}(t)||=||\vecs{r}′(t)||=\dfrac{ds}{dt} \nonumber \]
- Componente tangencial da aceleração\[a_{\vecs{T}} =\vecs{a}\cdot \vecs{T}=\dfrac{\vecs{v}\cdot \vecs{a}}{||\vecs v||} \nonumber \]
- Componente normal da aceleração\[a_{\vecs{N}}=\vecs{a}\cdot \vecs{N} = \dfrac{|| \vecs{v} \times \vecs{a} ||}{||\vecs{v}||} = \sqrt{||\vecs{a}||^2 - a_{\vecs{T}}} \nonumber \]
Glossário
- vetor de aceleração
- a segunda derivada do vetor de posição
- Leis do movimento planetário de Kepler
- três leis que regem o movimento de planetas, asteróides e cometas em órbita ao redor do Sol
- componente normal da aceleração
- o coeficiente do vetor normal unitário\(\vecs N\) quando o vetor de aceleração é escrito como uma combinação linear de\(\vecs T\) e\(\vecs N\)
- movimento do projétil
- movimento de um objeto com uma velocidade inicial, mas nenhuma força atuando sobre ele além da gravidade
- componente tangencial da aceleração
- o coeficiente do vetor tangente unitário\(\vecs T\) quando o vetor de aceleração é escrito como uma combinação linear de\(\vecs T\) e\(\vecs N\)
- vetor de velocidade
- a derivada do vetor de posição
Contribuidores e atribuições
- Template:ContribOpenStaxCalc
- Edited by Paul Seeburger
Paul Seeburger added finding point \((1, 2)\) when \(t=1\) in Example \(\PageIndex{1}\).
He also created Figure \(\PageIndex{1}\).


