13.3: Comprimento e curvatura do arco

Last updated
Save as PDF

Page ID: 187835

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de

Determine o comprimento do caminho de uma partícula no espaço usando a função de comprimento de arco.
Explique o significado da curvatura de uma curva no espaço e indique sua fórmula.
Descreva o significado dos vetores normais e binormais de uma curva no espaço.

Nesta seção, estudamos fórmulas relacionadas a curvas em duas e três dimensões e vemos como elas estão relacionadas a várias propriedades da mesma curva. Por exemplo, suponha que uma função com valor vetorial descreva o movimento de uma partícula no espaço. Gostaríamos de determinar até onde a partícula viajou em um determinado intervalo de tempo, o que pode ser descrito pelo comprimento do arco do caminho que ela segue. Ou suponha que a função vetorial descreva uma estrada que estamos construindo e queremos determinar com que nitidez a estrada se curva em um determinado ponto. Isso é descrito pela curvatura da função nesse ponto. Exploramos cada um desses conceitos nesta seção.

Comprimento do arco para funções vetoriais

Vimos como uma função com valor vetorial descreve uma curva em duas ou três dimensões. Lembre-se de que a fórmula para o comprimento do arco de uma curva definida pelas funções paramétricas$x=x(t),y=y(t),t_1≤t≤t_2$ é dada por

\[s=\int^{t_2}_{t_1} \sqrt{(x′(t))^2+(y′(t))^2}dt. \nonumber \]

De forma semelhante, se definirmos uma curva suave usando uma função com valor vetorial$\vecs r(t)=f(t) \,\hat{\mathbf{i}}+g(t) \,\hat{\mathbf{j}}$, onde$a≤t≤b$, o comprimento do arco é dado pela fórmula

\[s=\int^{b}_{a} \sqrt{(f′(t))^2+(g′(t))^2}dt. \nonumber \]

Em três dimensões, se a função com valor vetorial for descrita$\vecs r(t)=f(t) \,\hat{\mathbf{i}}+g(t) \,\hat{\mathbf{j}}+h(t) \,\hat{\mathbf{k}}$ por no mesmo intervalo$a≤t≤b$, o comprimento do arco será dado por

\[s=\int^{b}_{a} \sqrt{(f′(t))^2+(g′(t))^2+(h′(t))^2}dt. \nonumber \]

Teorema: fórmulas de comprimento de arco para curvas planas e espaciais

Curva plana: Dada uma curva suave$C$ definida pela função$\vecs r(t)=f(t) \,\hat{\mathbf{i}}+g(t) \, \hat{\mathbf{j}}$, onde$t$ está dentro do intervalo$[a,b]$, o comprimento do arco$C$ acima do intervalo é

\[\begin{align} s &=\int^{b}_{a} \sqrt{[f′(t)]^2+[g′(t)]^2}dt \\[4pt] &=\int^{b}_{a} \|\vecs r′(t)\|dt . \label{Arc2D}\end{align} \]

Curva de espaço: dada uma curva suave$C$ definida pela função$\vecs r(t)=f(t) \,\hat{\mathbf{i}}+g(t) \,\hat{\mathbf{j}}+h(t) \,\hat{\mathbf{k}}$, onde$t$ está dentro do intervalo$[a,b]$, o comprimento do arco$C$ acima do intervalo é

\[\begin{align} s &=\int^{b}_{a} \sqrt{[f′(t)]^2+[g′(t)]^2+[h′(t)]^2}dt \\[4pt] &=\int^{b}_{a} \|\vecs r′(t)\|dt . \label{Arc3D} \end{align} \]

As duas fórmulas são muito semelhantes; elas diferem apenas no fato de que uma curva espacial tem três funções componentes em vez de duas. Observe que as fórmulas são definidas para curvas suaves: curvas em que a função com valor vetorial$\vecs r(t)$ é diferenciável com uma derivada diferente de zero. A condição de suavidade garante que a curva não tenha cúspides (ou cantos) que possam tornar a fórmula problemática.

Exemplo$\PageIndex{1}$: Finding the Arc Length

Calcule o comprimento do arco para cada uma das seguintes funções com valores vetoriais:

$\vecs r(t)=(3t−2) \,\hat{\mathbf{i}}+(4t+5) \,\hat{\mathbf{j}},\quad 1≤t≤5$
$\vecs r(t)=⟨t\cos t,t\sin t,2t⟩,0≤t≤2 \pi $

Solução

Usando a Equação\ ref {Arc2D}$\vecs r′(t)=3 \,\hat{\mathbf{i}}+4 \,\hat{\mathbf{j}}$, então
\[\begin{align*} s &=\int^{b}_{a} \|\vecs r′(t)\|dt \\[4pt] &=\int^{5}_{1} \sqrt{3^2 + 4^2} dt \\[4pt] &=\int^{5}_{1} 5 dt = 5t\big|^{5}_{1} = 20. \end{align*}\]
Usando Equation\ ref {Arc3D}$\vecs r′(t)=⟨ \cos t−t \sin t, \sin t+t \cos t,2⟩ $, então
\[\begin{align*} s &=\int^{b}_{a} ∥\vecs r′(t)∥dt \\[4pt] &=\int^{2 \pi}_{0} \sqrt{(\cos t−t \sin t)^2+( \sin t+t \cos t)^2+2^2} dt \\[4pt] &=\int^{2 \pi}_{0} \sqrt{( \cos ^2 t−2t \sin t \cos t+t^2 \sin ^2 t)+( \sin^2 t+2t \sin t \cos t+t^2 \cos ^2 t)+4} dt \\[4pt] &=\int^{2 \pi}_{0} \sqrt{\cos ^2 t+ \sin^2 t+t^2( \cos ^2 t+ \sin ^2 t)+4} dt \\[4pt] &=\int^{2 \pi}_{0} \sqrt{t^2+5} dt\end{align*}\]

Aqui podemos usar uma fórmula de integração de tabelas

\[\int \sqrt{u^2+a^2}du = \dfrac{u}{2}\sqrt{u^2+a^2} + \dfrac{a^2}{2} \ln \,\left|\, u + \sqrt{u^2+a^2} \,\right| + C, \nonumber \]

então obtemos

\[\begin{align*} \int^{2 \pi}_{0} \sqrt{t^2+5} dt \; &= \frac{1}{2} \bigg( t \sqrt{t^2+5}+5 \ln \,\left|t+\sqrt{t^2+5}\right| \bigg) _0^{2π} \\[4pt] &= \frac{1}{2} \bigg( 2π \sqrt{4π^2+5}+5 \ln \bigg( 2π+ \sqrt{4π^2+5} \bigg) \bigg)−\frac{5}{2} \ln \sqrt{5} \\[4pt] &≈25.343 \,\text{units}. \end{align*}\]

Exercício$\PageIndex{1}$

Calcule o comprimento do arco da curva parametrizada

\[\vecs r(t)=⟨2t^2+1,2t^2−1,t^3⟩,\quad 0≤t≤3. \nonumber \]

Dica: Use a Equação\ ref {Arc3D}.
Resposta: $\vecs r′(t)=⟨4t,4t,3t^2⟩,$então$s= \frac{1}{27}(113^{3/2}−32^{3/2})≈37.785$ unidades

Agora retornamos à hélice apresentada anteriormente neste capítulo. Uma função com valor vetorial que descreve uma hélice pode ser escrita na forma

\[\vecs r(t)=R \cos \left(\dfrac{2πNt}{h}\right) \,\hat{\mathbf{i}} +R \sin \left(\dfrac{2πNt}{h}\right) \,\hat{\mathbf{j}}+t \,\hat{\mathbf{k}},0≤t≤h, \nonumber \]

onde$R$ representa o raio da hélice,$h$ representa a altura (distância entre duas voltas consecutivas) e a hélice completa as$N$ curvas. Vamos derivar uma fórmula para o comprimento do arco dessa hélice usando Equation\ ref {Arc3D}. Primeiro de tudo,

\[\vecs r′(t)=−\dfrac{2πNR}{h} \sin \left(\dfrac{2πNt}{h}\right) \,\hat{\mathbf{i}}+ \dfrac{2πNR}{h} \cos \left(\dfrac{2πNt}{h} \right) \,\hat{\mathbf{j}}+\,\hat{\mathbf{k}}. \nonumber \]

Portanto,

\[\begin{align*} s & =\int_a^b ‖\vecs r′(t)‖dt \\[4pt] &=\int_0^h\sqrt{ \bigg(−\dfrac{2πNR}{h} \sin \bigg(\dfrac{2πNt}{h} \bigg) \bigg)^2+ \bigg( \dfrac{2πNR}{h} \cos \bigg( \dfrac{2πNt}{h} \bigg) \bigg)^2+1^2}dt \\[4pt] &=\int_0^h\sqrt{ \dfrac{4π^2N^2R^2}{h^2} \bigg( \sin ^2 \bigg(\dfrac{2πNt}{h} \bigg) + \cos ^2 \bigg( \dfrac{2πNt}{h} \bigg) \bigg)+1}dt \\[4pt] &=\int_0^h\sqrt{ \dfrac{4π^2N^2R^2}{h^2} +1}dt \\[4pt] &=\bigg[ t\sqrt{ \dfrac{4π^2N^2R^2}{h^2} +1}\bigg]^h_0 \\[4pt] &=h \sqrt{ \dfrac{4π^2N^2R^2 + h^2}{h^2}} \\[4pt] &=\sqrt{ 4π^2N^2R^2 + h^2}.\end{align*}\]

Isso fornece uma fórmula para o comprimento de um fio necessário para formar uma hélice com$N$ curvas com raio$R$ e altura$h$.

Parametrização do comprimento do arco

Agora temos uma fórmula para o comprimento do arco de uma curva definida por uma função com valor vetorial. Vamos dar um passo adiante e examinar o que é uma função de comprimento de arco.

Se uma função com valor vetorial representa a posição de uma partícula no espaço em função do tempo, a função de comprimento do arco mede a distância que a partícula viaja em função do tempo. A fórmula para a função de comprimento do arco segue diretamente da fórmula do comprimento do arco:

\[s=\int^{t}_{a} \sqrt{(f′(u))^2+(g′(u))^2+(h′(u))^2}du. \label{arclength2} \]

Se a curva estiver em duas dimensões, somente dois termos aparecerão abaixo da raiz quadrada dentro da integral. A razão para usar a variável independente u é distinguir entre o tempo e a variável de integração. Como$s(t)$ mede a distância percorrida em função do tempo,$s′(t)$ mede a velocidade da partícula a qualquer momento. Como temos uma fórmula para$s(t)$ na Equação\ ref {arclength2}, podemos diferenciar os dois lados da equação:

\[ \begin{align*} s′(t) &=\dfrac{d}{dt} \bigg[ \int^{t}_{a} \sqrt{(f′(u))^2+(g′(u))^2+(h′(u))^2}du \bigg] \\[4pt] &=\dfrac{d}{dt} \bigg[ \int^{t}_{a} ‖\vecs r′(u)‖du \bigg] \\[4pt] &=\|\vecs r′(t)\|.\end{align*}\]

Se assumirmos que isso$\vecs r(t)$ define uma curva suave, então o comprimento do arco está sempre aumentando, então$s′(t)>0$ por diante$t>a$. Por último, se$\vecs r(t)$ for uma curva na qual,$\|\vecs r′(t)\|=1 $ para todos$t$, então

\[s(t)=\int^{t}_{a} ‖\vecs r′(u)‖\,du=\int^{t}_{a} 1\,du=t−a, \nonumber \]

o que significa que$t$ representa o comprimento do arco tão longo quanto$a=0$.

Teorema: função de comprimento de arco

Vamos$\vecs r(t)$ descrever uma curva suave para$t≥a$. Em seguida, a função de comprimento de arco é dada por

\[s(t)=\int^{t}_{a} ‖\vecs r′(u)‖\,du \nonumber \]

Além disso,

\[\dfrac{ds}{dt}=‖\vecs r′(t)‖>0. \nonumber \]

Se for$‖\vecs r′(t)‖=1$ para todos$t≥a$, o parâmetro$t$ representa o comprimento do arco a partir do ponto inicial em$t=a$.

Uma aplicação útil desse teorema é encontrar uma parametrização alternativa de uma determinada curva, chamada de parametrização do comprimento do arco. Lembre-se de que qualquer função com valor vetorial pode ser reparametrizada por meio de uma mudança de variáveis. Por exemplo, se tivermos uma função$\vecs r(t)=⟨3 \cos t,3 \sin t⟩,0≤t≤2π$ que parametriza um círculo de raio 3, podemos alterar o parâmetro de$t$ para$4t$, obtendo uma nova parametrização$\vecs r(t)=⟨3 \cos 4t,3 \sin 4t⟩$. A nova parametrização ainda define um círculo de raio 3, mas agora só precisamos usar os valores$0≤t≤π/2$ para atravessar o círculo uma vez.

Suponha que encontremos a função de comprimento de arco$s(t)$ e sejamos capazes de resolver essa função$t$ como uma função de$s$. Podemos então reparametrizar a função original$\vecs r(t)$ substituindo a expressão por$t$ back into$\vecs r(t)$. A função com valor vetorial agora está escrita em termos do parâmetro$s$. Como a variável$s$ representa o comprimento do arco, chamamos isso de parametrização do comprimento do arco da função original$\vecs r(t)$. Uma vantagem de encontrar a parametrização do comprimento do arco é que a distância percorrida ao longo da curva a partir de agora$s=0$ é igual ao parâmetro$s$. A parametrização do comprimento do arco também aparece no contexto da curvatura (que examinaremos posteriormente nesta seção) e integrais de linha.

Exemplo$\PageIndex{2}$: Finding an Arc-Length Parameterization

Encontre a parametrização do comprimento do arco para cada uma das seguintes curvas:

$\vecs r(t)=4 \cos t \,\hat{\mathbf{i}}+ 4 \sin t \,\hat{\mathbf{j}},\quad t≥0$
$\vecs r(t)=⟨t+3,2t−4,2t⟩,\quad t≥3$

Solução

Primeiro, encontramos a função de comprimento de arco usando a Equação\ ref {arclength2}:
\[\begin{align*} s(t) &= \int_a^t ‖\vecs r′(u)‖ \,du \\[4pt] &= \int_0^t ‖⟨−4 \sin u,4 \cos u⟩‖ \,du \\[4pt] &= \int_0^t \sqrt{(−4 \sin u)^2+(4 \cos u)^2} \,du \\[4pt] &= \int_0^t \sqrt{16 \sin ^2 u+16 \cos ^2 u} \,du \\[4pt] &= \int_0^t 4\,du = 4t, \end{align*}\]
que fornece a relação entre o comprimento do arco$s$ e o parâmetro,$s=4t;$ assim$t$ como,$t=s/4$. Em seguida, substituímos a variável$t$ na função$\vecs r(t)=4 \cos t \,\hat{\mathbf{i}}+4 \sin t \,\hat{\mathbf{j}}$ original pela expressão$s/4$ a ser obtida
\[\vecs r(s)=4 \cos \left(\frac{s}{4}\right) \,\hat{\mathbf{i}} + 4 \sin \left( \frac{s}{4}\right) \,\hat{\mathbf{j}}. \nonumber \]
Essa é a parametrização do comprimento do arco de$\vecs r(t)$. Uma vez que a restrição original$t$ foi dada por$t≥0$, a restrição a s se torna$s/4≥0$, ou$s≥0$.
A função arc-length é dada pela Equação\ ref {arclength2}:
\[\begin{align*} s(t) & = \int_a^t ‖\vecs r′(u)‖ \,du \\[4pt] &= \int_3^t ‖⟨1,2,2⟩‖ \,du \\[4pt] &= \int_3^t \sqrt{1^2+2^2+2^2} \,du \\[4pt] &= \int_3^t 3 \,du \\[4pt] &= 3t - 9. \end{align*}\]
Portanto, a relação entre o comprimento do arco$s$ e o parâmetro$t$ é$s=3t−9$, então$t= \frac{s}{3}+3$. Substituir isso na função original$\vecs r(t)=⟨t+3,2t−4,2t⟩ $ gera
\[\vecs r(s)=⟨\left(\frac{s}{3}+3\right)+3,\,2\left(\frac{s}{3}+3\right)−4,\,2\left(\frac{s}{3}+3\right)⟩=⟨\frac{s}{3}+6, \frac{2s}{3}+2,\frac{2s}{3}+6⟩.\nonumber \]
Essa é uma parametrização de comprimento de arco de$\vecs r(t)$. A restrição original no parâmetro$t$ era$t≥3$, então a restrição em$s$ é$(s/3)+3≥3$, ou$s≥0$.

Exercício$\PageIndex{2}$

Encontre a função de comprimento de arco para a hélice

\[\vecs r(t)=⟨3 \cos t, 3 \sin t,4t⟩,\quad t≥0. \nonumber \]

Em seguida, use a relação entre o comprimento do arco e o parâmetro$t$ para encontrar uma parametrização do comprimento do arco de$\vecs r(t)$.

Dica

Comece encontrando a função de comprimento do arco.

Resposta

$s=5t$, ou$t=s/5$. Substituindo isso em$\vecs r(t)=⟨3 \cos t,3 \sin t,4t⟩$ dá

\[\vecs r(s)=⟨3 \cos \left(\frac{s}{5}\right),3 \sin \left(\frac{s}{5}\right),\frac{4s}{5}⟩,\quad s≥0 \nonumber \]

Curvatura

Um tópico importante relacionado ao comprimento do arco é a curvatura. O conceito de curvatura fornece uma maneira de medir a intensidade com que uma curva suave gira. Um círculo tem curvatura constante. Quanto menor o raio do círculo, maior a curvatura.

Pense em dirigir por uma estrada. Suponha que a estrada esteja em um arco de um círculo grande. Nesse caso, você mal precisaria girar o volante para ficar na estrada. Agora, suponha que o raio seja menor. Nesse caso, você precisaria virar mais bruscamente para permanecer na estrada. No caso de uma curva diferente de um círculo, geralmente é útil primeiro inscrever um círculo na curva em um determinado ponto para que fique tangente à curva nesse ponto e “abraça” a curva o mais próximo possível em uma vizinhança do ponto (Figura$\PageIndex{1}$). A curvatura do gráfico nesse ponto é então definida como a mesma que a curvatura do círculo inscrito.

Essa figura é o gráfico de uma curva. A curva sobe e desce no primeiro quadrante. Ao longo da curva, onde a curva muda de decrescente para crescente, há um círculo. A parte inferior do círculo se curva da mesma forma que o gráfico da curva. Há também um segundo círculo menor em que a curva vai de aumentar para diminuir. Parte do círculo cai na curva. Ambos os círculos têm o raio r representado. — Figura$\PageIndex{1}$: O gráfico representa a curvatura de uma função$y=f(x).$ Quanto mais nítida a curva no gráfico, maior a curvatura e menor o raio do círculo inscrito.

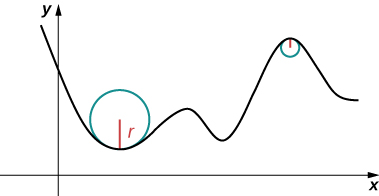
Definição: Curvatura

$C$Seja uma curva suave no plano ou no espaço dado por$\vecs r(s)$, onde$s$ está o parâmetro de comprimento do arco. A curvatura$κ$ em$s$ é

\[κ =\bigg{\|}\dfrac{d\vecs{T}}{ds}\bigg{\|}=‖\vecs T′(s)‖. \nonumber \]

Visite este vídeo para obter mais informações sobre a curvatura de uma curva espacial.

A fórmula na definição de curvatura não é muito útil em termos de cálculo. Em particular, lembre-se de que$\vecs T(t)$ representa o vetor tangente unitário a uma determinada função$\vecs r(t)$ com valor vetorial e a fórmula para$\vecs T(t)$ é

\[\vecs T(t)=\frac{\vecs r′(t)}{∥\vecs r′(t)∥}. \nonumber \]

Para usar a fórmula da curvatura, primeiro é necessário expressar$\vecs r(t)$ em termos do parâmetro de comprimento do arco$s$, depois encontrar o vetor tangente unitário$\vecs T(s)$ para a função e$\vecs r(s)$, em seguida, tomar a derivada de em$\vecs T(s)$ relação$s$ a. Esse é um processo tedioso. Felizmente, existem fórmulas equivalentes para curvatura.

Teorema: Fórmulas alternativas de curvatura

Se$C$ for uma curva suave dada por$\vecs r(t)$, então a curvatura$κ$ de$C$ at$t$ é dada por

\[κ =\dfrac{‖\vecs T′(t)‖}{‖\vecs r′(t)‖}. \label{EqK2} \]

Se$C$ for uma curva tridimensional, a curvatura pode ser dada pela fórmula

\[κ =\dfrac{‖\vecs r′(t)×\vecs r′′(t)‖}{‖\vecs r′(t)‖^3}.\label{EqK3} \]

Se$C$ for o gráfico de uma função$y=f(x)$$y′$ e ambas$y''$ existirem, então a curvatura$κ$ no ponto$(x,y)$ é dada por

\[κ =\dfrac{|y''|}{[1+(y′)^2]^{3/2}}.\label{EqK4} \]

Prova

A primeira fórmula segue diretamente da regra da cadeia:

\[\dfrac{d\vecs{T}}{dt} = \dfrac{d\vecs{T}}{ds} \dfrac{ds}{dt}, \nonumber \]

onde$s$ é o comprimento do arco ao longo da curva$C$. Dividindo os dois lados por$ds/dt$, e considerando a magnitude de ambos os lados, obtém-se

\[\bigg{\|}\dfrac{d\vecs{T}}{ds}\bigg{\|}= \left\lVert\frac{\vecs T′(t)}{\dfrac{ds}{dt}}\right\rVert.\nonumber \]

Uma vez que$ds/dt=‖\vecs r′(t)‖$, isso fornece a fórmula para a curvatura$κ$ de uma curva$C$ em termos de qualquer parametrização de$C$:

\[κ =\dfrac{‖\vecs T′(t)‖}{‖\vecs r′(t)‖}.\nonumber \]

No caso de uma curva tridimensional, começamos com as fórmulas$\vecs T(t)=(\vecs r′(t))/‖\vecs r′(t)‖$$ds/dt=‖\vecs r′(t)‖$ e. Portanto,$\vecs r′(t)=(ds/dt)\vecs T(t)$. Podemos pegar a derivada dessa função usando a fórmula escalar do produto:

\[\vecs r″(t)=\dfrac{d^2s}{dt^2}\vecs T(t)+\dfrac{ds}{dt}\vecs T′(t).\nonumber \]

Usando essas duas últimas equações, obtemos

\[\begin{align*} \vecs r′(t)×\vecs r″(t) &=\dfrac{ds}{dt}\vecs T(t)× \bigg( \dfrac{d^2s}{dt^2}\vecs T(t)+\dfrac{ds}{dt}\vecs T′(t) \bigg) \\[4pt] &=\dfrac{ds}{dt} \dfrac{d^2s}{dt^2}\vecs T(t)×\vecs T(t)+(\dfrac{ds}{dt})^2\vecs T(t)×\vecs T′(t). \end{align*}\]

Uma vez que$\vecs T(t)×\vecs T(t)=0$, isso se reduz a

\[\vecs r′(t)×\vecs r′′(t)=\left(\dfrac{ds}{dt}\right)^2\vecs T(t)×\vecs T′(t).\nonumber \]

Como$\vecs T′$ é paralelo e$\vecs T$ é ortogonal$\vecs N$, segue isso$\vecs T$ e$\vecs T′$ é ortogonal.$\vecs N$ Isso significa que$‖\vecs T×\vecs T′‖=‖\vecs T‖‖\vecs T′‖ \sin (π/2)=‖\vecs T′‖$, então

\[\|\vecs r′(t)×\vecs r″(t)\|=\left(\dfrac{ds}{dt}\right)^2‖\vecs T′(t)‖.\nonumber \]

Agora resolvemos essa equação$‖\vecs T′(t)‖$ e usamos o fato de que$ds/dt=‖\vecs r′(t)‖$:

\[‖\vecs T′(t)‖=\dfrac{‖\vecs r′(t)×\vecs r″(t)‖}{‖\vecs r′(t)‖^2}.\nonumber \]

Em seguida, dividimos os dois lados por$‖\vecs r′(t)‖$. Isso dá

\[κ =\dfrac{‖\vecs T′(t)‖}{‖\vecs r′(t)‖}=\dfrac{‖\vecs r′(t)×\vecs r″(t)‖}{‖\vecs r′(t)‖^3}.\nonumber \]

Isso prova$\ref{EqK3}$. Para provar$\ref{EqK4}$, começamos com a suposição de que a curva$C$ é definida pela função$y=f(x)$. Então, podemos definir$\vecs r(t)=x \,\hat{\mathbf{i}}+f(x) \,\hat{\mathbf{j}}+0 \,\hat{\mathbf{k}}$. Usando a fórmula anterior para curvatura:

\[\begin{align*} \vecs r′(t) &=\,\hat{\mathbf{i}}+f′(x)\,\hat{\mathbf{j}} \\[4pt] \vecs r″(t) &=f″(x)\,\hat{\mathbf{j}} \\[4pt] \vecs r′(t)×\vecs r″(t) &= \begin{vmatrix} \hat{\mathbf{i}} & \hat{\mathbf{j}} & \hat{\mathbf{k}} \\ 1 & f′(x) & 0 \\ 0 & f″(x) & 0 \end{vmatrix} =f″(x)\,\hat{\mathbf{k}}. \end{align*}\]

Portanto,

\[κ= \dfrac{‖\vecs r′(t)×\vecs r″(t)‖}{‖\vecs r′(t)‖^3}=\dfrac{|f″(x)|}{(1+[f′(x)]^2)^{3/2}} \nonumber \]

Exemplo$\PageIndex{3}$: Finding Curvature

Encontre a curvatura para cada uma das seguintes curvas em um determinado ponto:

$\vecs r(t)=4 \cos t\,\hat{\mathbf{i}}+4 \sin t\,\hat{\mathbf{j}}+3t\,\hat{\mathbf{k}},\quad t=\dfrac{4π}{3}$
$\mathrm{f(x)= \sqrt{4x−x^2},x=2}$

Solução

Essa função descreve uma hélice.

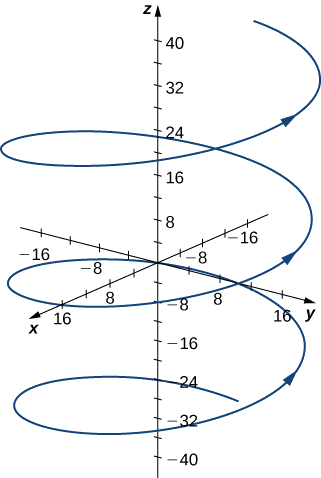
$Esta figura é o gráfico de uma curva em 3 dimensões. A curva é uma hélice que gira em torno do eixo z. Ele começa abaixo do plano xy e sobe em espiral com a orientação.$

A curvatura da hélice em$t=(4π)/3$ pode ser encontrada usando$\ref{EqK2}$. Primeiro, calcule$\vecs T(t)$:

\[\begin{align*} \vecs T(t) &=\dfrac{\vecs r′(t)}{‖\vecs r′(t)‖} \\[4pt] &=\dfrac{⟨−4 \sin t,4 \cos t,3⟩}{\sqrt{(−4 \sin t)^2+(4 \cos t)^2+3^2}}\\[4pt] &=⟨−\dfrac{4}{5} \sin t,\dfrac{4}{5} \cos t, \dfrac{3}{5}⟩. \end{align*}\]

Em seguida, calcule$\vecs T′(t):$

\[\vecs T′(t)=⟨−\dfrac{4}{5} \cos t,− \dfrac{4}{5} \sin t,0⟩. \nonumber \]

Por último, aplique$\ref{EqK2}$:

\[ \begin{align*} κ &=\dfrac{‖\vecs T′(t)‖}{‖\vecs r′(t)‖} = \dfrac{‖⟨−\dfrac{4}{5} \cos t,−\dfrac{4}{5} \sin t,0⟩‖}{‖⟨−4 \sin t,4 \cos t,3⟩‖} \\[4pt] &=\dfrac{\sqrt{(−\dfrac{4}{5} \cos t)^2+(−\dfrac{4}{5} \sin t)^2+0^2}}{\sqrt{(−4 \sin t)^2+(4 \cos t)^2+ 3^2}} \\[4pt] &=\dfrac{4/5}{5}=\dfrac{4}{25}. \end{align*}\]

A curvatura dessa hélice é constante em todos os pontos da hélice.

Essa função descreve um semicírculo.

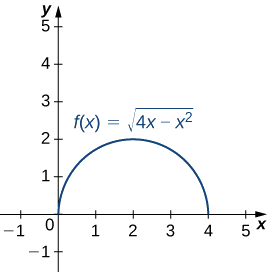
$Essa figura é o gráfico de um semicírculo. Está no primeiro quadrante. O semicírculo começa na origem e para em 4 no eixo x. O semicírculo representa a função f (x) = a raiz quadrada de (4x-x^2).$

Para encontrar a curvatura desse gráfico, devemos usar$\ref{EqK4}$. Primeiro, calculamos$y′$ e$y″:$

\[\begin{align*}y &=\sqrt{4x−x^2}=(4x−x^2)^{1/2} \\[4pt] y′ &=\dfrac{1}{2}(4x−x^2)^{−1/2}(4−2x)=(2−x)(4x−x^2)^{−1/2} \\[4pt] y″ &=−(4x−x^2)^{−1/2}+(2−x)(−\dfrac{1}{2})(4x−x^2)^{−3/2}(4−2x) \\[4pt] & =−\dfrac{4x−x^2}{(4x−x^2)^{3/2}}− \dfrac{(2−x)^2}{(4x−x^2)^{3/2}} \\[4pt] &=\dfrac{x^2−4x−(4−4x+x^2)}{(4x−x^2)^{3/2}} \\[4pt] &=−\dfrac{4}{(4x−x^2)^{3/2}}. \end{align*} \nonumber \]

Em seguida, aplicamos$\ref{EqK4}$:

\[ \begin{align*} κ &=\dfrac{|y''|}{[1+(y′)^2]^{3/2}} \\[4pt] &= \dfrac{\bigg| −\dfrac{4}{(4x−x^2)^{3/2}}\bigg|}{\bigg[1+((2−x)(4x−x^2)^{−1/2})^2 \bigg]^{3/2}} = \dfrac{\bigg| \dfrac{4}{(4x−x^2)^{3/2}} \bigg|}{\bigg[ 1+\dfrac{(2−x)^2}{4x−x^2} \bigg]^ {3/2}} \\[4pt] &= \dfrac{\bigg| \dfrac{4}{(4x−x^2)^{3/2}} \bigg|}{ \bigg[ \dfrac{4x−x^2+x^2−4x+4}{4x−x^2} \bigg]^{3/2}}=\bigg| \dfrac{4}{(4x−x^2)^{3/2}} \bigg| ⋅\dfrac{(4x−x^2)^{3/2}}{8} \\[4pt] &=\dfrac{1}{2}. \end{align*}\]

A curvatura desse círculo é igual à recíproca de seu raio. Há um pequeno problema com o valor absoluto em$\ref{EqK4}$; no entanto, uma análise mais detalhada do cálculo revela que o denominador é positivo para qualquer valor de$x$.

Exercício$\PageIndex{3}$

Encontre a curvatura da curva definida pela função

\[y=3x^2−2x+4 \nonumber \]

no ponto$x=2$.

Dica: Use$\ref{EqK4}$.
Resposta: $κ \; =\frac{6}{101^{3/2}}≈0.0059$

Os vetores normais e binormais

Vimos que a derivada$\vecs r′(t)$ de uma função com valor vetorial é um vetor tangente à curva definida por$\vecs r(t)$, e o vetor tangente unitário$\vecs T(t)$ pode ser calculado dividindo-se$\vecs r′(t)$ por sua magnitude. Ao estudar o movimento em três dimensões, dois outros vetores são úteis para descrever o movimento de uma partícula ao longo de um caminho no espaço: o vetor normal unitário principal e o vetor binormal.

Definição: Vetores binormais

$C$Seja uma curva suave tridimensional representada por$\vecs r$ mais de um intervalo aberto$I$. Se$\vecs T′(t)≠\vecs 0$, então o vetor normal unitário principal at$t$ é definido como

\[\vecs N(t)=\dfrac{\vecs T′(t)}{‖\vecs T′(t)‖}. \label{EqNormal} \]

O vetor binormal em$t$ é definido como

\[\vecs B(t)=\vecs T(t)×\vecs N(t),\label{EqBinormal} \]

onde$\vecs T(t)$ é o vetor tangente unitário.

Observe que, por definição, o vetor binormal é ortogonal ao vetor tangente unitário e ao vetor normal. Além disso,$\vecs B(t)$ é sempre um vetor unitário. Isso pode ser mostrado usando a fórmula para a magnitude de um produto cruzado.

\[‖\vecs B(t)‖=‖\vecs T(t)×\vecs N(t)‖=‖\vecs T(t)‖‖\vecs N(t)‖ \sin \theta, \nonumber \]

onde$\theta$ está o ângulo entre$\vecs T(t)$$\vecs N(t)$ e. Como$\vecs N(t)$ é a derivada de um vetor unitário, a propriedade (vii) da derivada de uma função com valor vetorial nos diz isso$\vecs T(t)$ e$\vecs N(t)$ são ortogonais entre si, então$\theta=π/2$. Além disso, ambos são vetores unitários, então sua magnitude é 1. Portanto,$‖\vecs T(t)‖‖\vecs N(t)‖ \sin \theta=(1)(1) \sin (π/2)=1$ e$\vecs B(t)$ é um vetor unitário.

O vetor normal unitário principal pode ser difícil de calcular porque o vetor tangente unitário envolve um quociente, e esse quociente geralmente tem uma raiz quadrada no denominador. No caso tridimensional, encontrar o produto cruzado do vetor tangente unitário e do vetor normal unitário pode ser ainda mais complicado. Felizmente, temos fórmulas alternativas para encontrar esses dois vetores, e elas são apresentadas em Motion in Space.

Exemplo$\PageIndex{4}$: Finding the Principal Unit Normal Vector and Binormal Vector

Para cada uma das seguintes funções com valores vetoriais, encontre o vetor normal unitário principal. Então, se possível, encontre o vetor binormal.

$\vecs r(t)=4 \cos t\,\hat{\mathbf{i}}− 4 \sin t\,\hat{\mathbf{j}}$
$\vecs r(t)=(6t+2)\,\hat{\mathbf{i}}+5t^2\,\hat{\mathbf{j}}−8t\,\hat{\mathbf{k}}$

Solução

Essa função descreve um círculo.

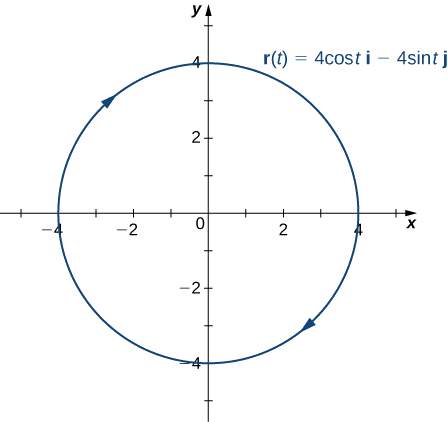
$Esta figura é o gráfico de um círculo centrado na origem com raio de 2. A orientação do círculo é no sentido horário. Representa a função com valor vetorial r (t) = 4costi — 4 sintj.$

Para encontrar o vetor normal unitário principal, primeiro precisamos encontrar o vetor tangente unitário$\vecs T(t):$

\ [\ begin {align*}\ vecs T (t) &=\ dfrac {\ vecs r′( t)} {‖\ vecs r′s (t) ‖}\\ [4pt]
&=\ dfrac {−4\ sin t\,\ hat {\ mathbf {i}} −4\ cos t\,\ hat {\ mathbf {j}} {\ sqrt {(−4\ sin t) ^2+ (−4\ cos t) ^2}}\\ [4pt]
&=\ dfrac {−4\ sin t\,\ hat {\ mathbf {i}} −4\ cos t\,\ hat {\ mathbf {j}}} {\ sqrt {16\ sin ^2 t+16\ cos ^2 t}}\\ [4pt]
&=\ dfrac {−4\ sin t\,\ hat {\ mathbf {i}} −4\ cos t\,\ hat {\ mathbf {j}} {\ sqrt {16 (\ sin ^2 t+\ cos ^2 t)}}\\ [4pt]
&=\ dfrac {−4\ sin t\,\ hat {\ mathbf {i}} −4\ cos t\,\ hat {\ mathbf {j}}} {4}\\[4pt] &=− \sin t\,\hat{\mathbf{i}}− \cos t\,\hat{\mathbf{j}}.\end{align*}\]

Em seguida, usamos$\ref{EqNormal}$:

\ [\ begin {align*}\ vecs N (t) &=\ dfrac {\ vecs T′( t)} {‖\ vecs T′s (t) ‖}\\ [4pt] &=\ dfrac {−\ cos t\,\ hat {\ mathbf {i}} +\ sin t\,\ hat {\ mathbf {j}}} {sqrt {(−\ cos t) ^2+ (\ sin t) ^2}}\\ [4pt]
&=\ dfrac {−\ cos t\,\ hat {\ mathbf {i}} +\ sin t\,\ hat {\ mathbf {j}}} {\ sqrt {\ cos ^2 t+\ sin ^2 t}}\\ [4pt]
&=−\ cos t\,\ hat {\ mathbf {i}} +\ sin t\,\ hat {\ mathbf {j}}. \ end {align*}\]

Observe que o vetor tangente unitário e o vetor normal unitário principal são ortogonais entre si para todos os valores de$t$:

\[\begin{align*} \vecs T(t)·\vecs N(t) &=⟨− \sin t,− \cos t⟩·⟨− \cos t, \sin t⟩ \\[4pt] &= \sin t \cos t−\cos t \sin t \\[4pt] &=0. \end{align*}\]

Além disso, o vetor normal unitário principal aponta para o centro do círculo a partir de cada ponto do círculo. Como$\vecs r(t)$ define uma curva em duas dimensões, não podemos calcular o vetor binormal.

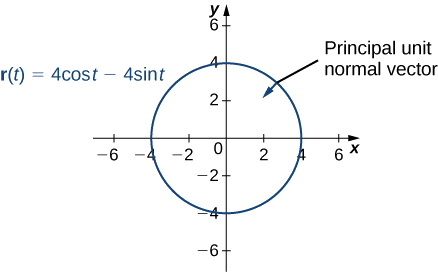
$Esta figura é o gráfico de um círculo centrado na origem com raio de 2. A orientação do círculo é no sentido horário. Representa a função com valor vetorial r (t) = 4costi — 4 sintj. No círculo no primeiro quadrante há um vetor apontando para dentro. É rotulado como “vetor normal da unidade principal”.$

Essa função tem a seguinte aparência:

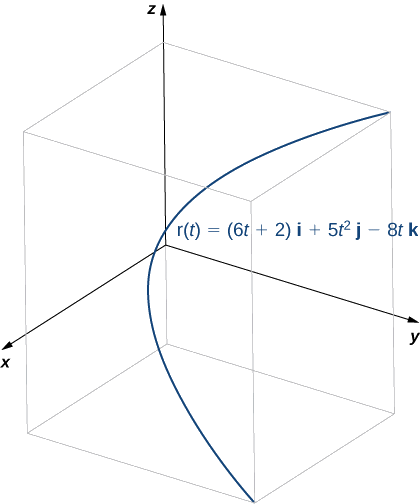
$Esta figura é uma curva em 3 dimensões. Está dentro de uma caixa. A caixa representa o primeiro octante. A curva começa na parte inferior direita da caixa e se curva pela caixa em uma curva parabólica até o topo.$

Para encontrar o vetor normal unitário principal, primeiro encontramos o vetor tangente unitário$\vecs T(t):$

\ [\ begin {align*}\ vecs T (t) &=\ dfrac {\ vecs r′( t)} {‖\ vecs r′s (t) ‖}\\ [4pt]
&=\ dfrac {6\,\ hat {\ mathbf {i}} +10t\,\ hat {\ mathbf {j}} −8\,\ hat {\ mathbf {k}}} {\ sqrt {6^2+ (10t) ^2+ (−8) ^2}}\\ [4pt]
&=\ dfrac {6\,\ hat {\ mathbf {i}} +10t\,\ hat {\ mathbf {j}} −8\,\ hat {\ mathbf {k}} {\ sqrt {36+100t^2+64 }}\\ [4pt]
&=\ dfrac {6\,\ hat {\ mathbf {i}} +10t\,\ hat {\ mathbf {j}} −8\,\ hat {\ mathbf {k}}} {\ sqrt {100 (t^2+1)}}\\ [4pt]
&=\ dfrac {3\, hat {\ mathbf {i}} −5t\,\ hat {\ mathbf {j}} −4\,\ hat {\ mathbf {k}}} {5\ sqrt {t^2+1}}\\ [4pt]
&=\ dfrac {3} {5} (t^2+1) ^ {−1/2}\,\ hat {\ mathbf f {i}} −t (t^2) +1) ^ {−1/2}\,\ hat {\ mathbf {j}} −\ dfrac {4} {5} (t^2+1) ^ {−1/2}\,\ hat {\ mathbf {k}}. \ end {align*}\]

Em seguida, calculamos$\vecs T′(t)$ e$‖\vecs T′(t)‖$:

\ [\ begin {align*}\ vecs T′( t) &=\ dfrac {3} {5} (−\ dfrac {1} {2}) (t^2+1) ^ {−3/2} (2t)\,\ hat {\ mathbf {i}} − (t^2+1) ^ {−1/2} −t (\ dfrac {1} 2}) (t^2+1) ^ {−3/2} (2t))\,\ hat {\ mathbf {j}} −\ dfrac {4} {5} (−\ dfrac {1} {2}) (t^2+1) ^ {−3/2} (2t)\,\ hat {\ mathbf {k}}\\ [4pt]
=−\ dfrac {3t} {5 (t^2+1) ^ {3/2}}\,\ hat {\ mathbf {i}} −\ dfrac { 1} {(t^2+1) ^ {3/2}}\,\ hat {\ mathbf {j}} +\ dfrac {4t} {5 (t^2+1) ^ {3/2}}\,\ hat {\ mathbf {k}}\\ [4pt] ‖\ vecs T′( t) ‖ &=\ sqrt {\ bigg (\ − frac {3t} {5 (t^2+1) ^ {3/2}}\ bigg) ^2+\ bigg (−\ dfrac {1} {(t^2+1) ^ {3/2}}\ bigg) ^2+\ bigg (\ dfrac {4t} {5 (t^2+1) ^ {3/2}}\ bigg) ^2}\\ [4pt]
&=\ sqrt {\ dfrac {9t^2} {25 (t^2+1) ^3} +\ dfrac {1} {(t^2+1) ^3} +\ dfrac {16t^2} {25 (t^2+1) ^3}\\ [4pt]
&=\ sqrt {\ dfrac {25t^2+25} {25 (t^2+1) ^3}}\\ [4pt]
&=\ sqrt {\ dfrac {1} {(t^2+1) ^2}}\\ [4pt]
&=\ dfrac {1} {t^2+1}. \ end {align*}\]

Portanto, de acordo com$\ref{EqNormal}$:

\ [\ begin {align*}\ vecs N (t) &=\ dfrac {\ vecs T′( t)} {‖\ vecs T′( t) ‖}\\ [4pt]
&=\ bigg (−\ dfrac {3t} {5 (t^2+1) ^ {3/2}}\,\ hat {\ mathbf {i}}\ − dfrac {1} {(t^2+1) ^ {3/2}}\,\ hat {\ mathbf {j}} +\ dfrac {4t} {5 (t^2+1) ^ {3/2}}\,\ hat {\ mathbf {k}}\ bigg) (t^2+1)\\ [4pt]
&=−\ dfrac {3t} {5 (t^2+1) ^ {1/2}}\,\ hat {\ mathbf {i}} −\ dfrac {5} {5 (t^2+1) ^ {1/2}}\,\ hat {\ mathbf {j}} +\ dfrac {4t} {5 (t^2+1) ^ {1/2}}\,\ hat {\ mathbf {k}}\\ [4pt]
&=−\ dfrac {3t\,\ hat {\ mathbf {i}} +5\,\ hat {\ mathbf {j}} −4t\,\ hat {\ mathbf {k}}} {5\ sqrt {t^2+1}}. \ end {align*}\]

Mais uma vez, o vetor tangente unitário e o vetor normal unitário principal são ortogonais entre si para todos os valores de$t$:

\ [\ begin {align*}\ vecs T (t) ·\ vecs N (t) &=\ bigg (\ dfrac {3\,\ hat {\ mathbf {i}} −5t\,\ hat {\ mathbf {j}} −4\,\ hat {\ mathbf {k}}} {5\ sqrt {t^2+1}}\ bigg) ·\ bigg (−\ dfrac {3t\,\ hat {\ mathbf {i}} +5\,\ hat {\ mathbf {j}} −4t\,\ hat {\ mathbf {k}}} {5\ sqrt {t^2+1}}\ bigg)\\ [4pt]
&=\ dfrac {3 (−3t) −5t (−5) −4 (4t)} {25 (t^2+1)} \\ [4pt]
&=\ dfrac {−9t+25t−16t} {25 (t^2+1)}\\ [4pt]
&=0. \ end {align*}\ nonumber\]

Por último, como$\vecs r(t)$ representa uma curva tridimensional, podemos calcular o vetor binormal usando$\ref{EqBinormal}$:

\ [\ begin {align*}\ vecs B (t) &=\;\ vecs T (t) ×\ vecs N (t)\\ [4pt]
&=\ begin {vmatrix}\ hat {\ mathbf {i}} &\ hat {\ mathbf {j}} &\ hat {\ mathbf {k}}\\\ dfrac {3} {5\ sqrt {t^2+1}} & −\ dfrac {5t} {5\ sqrt {t^2+1}} & −\ dfrac {4} {5\ sqrt {t^2+1}}\\ −\ −\ dfrac {3t} {5\ sqrt {t^2+1}} e −\ dfrac {5} {5\ sqrt {t^2+1}} &\ dfrac {4t} {5\ sqrt {t^2+1}}\ end {vmatrix}\\ [4pt]
&=\ bigg (\ bigg (−\ dfrac {5t} {5\ sqrt {t^2+1}}\ bigg)\ bigg (\ dfrac {4t} {5\ sqrt {t^2+1}}\ bigg) −\ bigg (−\ dfrac {4} {5\ sqrt {t^2+1}}\ bigg)\ bigg (−\ dfrac {5} {5\ sqrt {t^2+1}}\ bigg)\,\ hat {\ mathbf {i}}\\
& -\ bigg (\ bigg (\ dfrac {3} {5\ sqrt {t^2+1}}\ bigg)\ bigg (\ dfrac {4t} {5\ sqrt {t^2+1}}\ bigg) −\ bigg (−\ dfrac {4} {5\ sqrt {t^2+1}}\ bigg)\ bigg (−\ dfrac {3t} {5\ sqrt {t^2+1}}\ bigg)\ bigg)\,\ hat {\ mathbf {j}}\\
& +\ bigg (\ dfrac {3} {5\ sqrt {t^2+1}}\ bigg)\ bigg (-\ dfrac {5} {5\ sqrt {5} {5\ sqrt {t^2+1}}\ bigg) −\ bigg (−\ dfrac {5t} {5\ sqrt {t^2+1}}\ bigg)\ bigg (−\ dfrac {3t} {5\ sqrt {t^2+1}}\ bigg)\ bigg)\,\ hat {\ mathbf {k}}\\ [4pt] &=\ bigg (\ dfrac {k}}\\ [4pt]
&=\ bigg (\ dfrac {k}}\ [4pt] &=\ bigg (\ dfrac {k}}\\ [4pt] &= c {−20t^2−20} {25 (t^2+1)}\ bigg)\,\ hat {\ mathbf {i}} +\ bigg (\ dfrac {−15−15t^2} {25 (t^2+1)}\ bigg)\,\ hat {\ mathbf {k}}\\ [4pt]
&= −20\ bigg (\ dfrac {t^2+1} {25 (t^2+1)}\ bigg)\,\ hat {\ mathbf {i}} −15\ bigg (\ dfrac {t^2+1} {25 (t^2+1)}\ bigg)\,\ hat {\ mathbf {k}}\\ [4pt]
&= −\ dfrac {4} {5}\,\ hat {\ mathbf {i}} −\ dfrac {3} {5}\,\ hat {\ mathbf {k}}. \ end {align*}\ nonumber\]

Exercício$\PageIndex{4}$

Encontre o vetor normal unitário para a função com valor vetorial$\vecs r(t)=(t^2−3t)\,\hat{\mathbf{i}}+(4t+1)\,\hat{\mathbf{j}}$ e avalie-o em$t=2$.

Dica: Primeiro$\vecs T(t)$, encontre e depois use$\ref{EqNormal}$.
Resposta: $\vecs N(2)=\dfrac{\sqrt{2}}{2}(\,\hat{\mathbf{i}}−\,\hat{\mathbf{j}})$

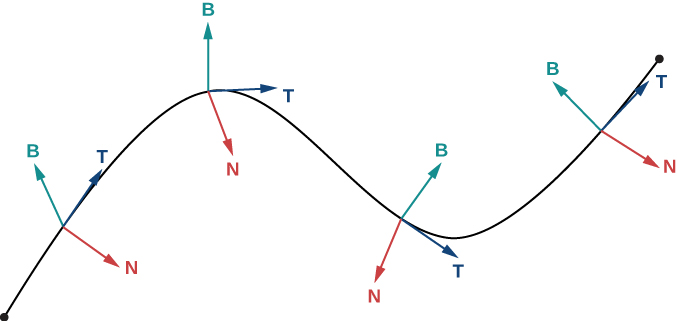
Para qualquer curva suave em três dimensões definida por uma função com valor vetorial, agora temos fórmulas para o vetor tangente unitário$\vecs T$, o vetor$\vecs N$ normal unitário e o vetor binormal$\vecs B$. O vetor normal unitário e o vetor binormal formam um plano que é perpendicular à curva em qualquer ponto da curva, chamado de plano normal. Além disso, esses três vetores formam um quadro de referência no espaço tridimensional chamado quadro de referência Frenet (também chamado de quadro TNB) (Figura$\PageIndex{2}$). Por último, o plano determinado pelos vetores$\vecs T$ e$\vecs N$ forma o plano osculante de$C$ em qualquer ponto$P$ da curva.

Esta figura é o gráfico de uma curva que aumenta e diminui. Ao longo da curva em 4 pontos diferentes, há 3 vetores em cada ponto. O primeiro vetor é rotulado como “T” e é tangente à curva no ponto. O segundo vetor é rotulado como “N” e é normal à curva no ponto. O terceiro vetor é rotulado como “B” e é ortogonal a T e N. — Figura$\PageIndex{2}$: Esta figura mostra um quadro de referência da Frenet. Em cada ponto *$P$*de *uma curva tridimensional, a tangente unitária, a unidade normal e os vetores binormais formam um quadro de referência tridimensional.*

Suponha que formamos um círculo no plano osculante de um$C$ ponto$P$ na curva. Suponha que o círculo tenha a mesma curvatura da curva no ponto$P$ e deixe o círculo ter raio$r$. Então, a curvatura do círculo é dada por$\frac{1}{r}$. Chamamos$r$ o raio de curvatura da curva e é igual ao recíproco da curvatura. Se esse círculo estiver no lado côncavo da curva e for tangente à curva no ponto$P$, esse círculo será chamado de círculo osculante de$C$ at$P$, conforme mostrado na Figura$\PageIndex{3}$.

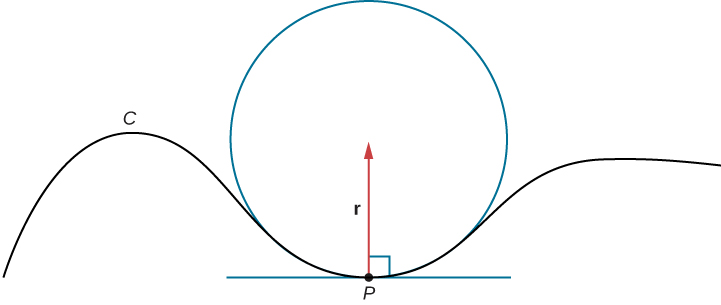
Esta figura é o gráfico de uma curva com um círculo no meio. A parte inferior do círculo é a mesma que parte da curva. Dentro do círculo há um vetor chamado “r”. Começa no ponto “P” do círculo e aponta para o raio. Há também um segmento de linha perpendicular ao raio e tangente ao ponto P. — Figura$\PageIndex{3}$: Neste círculo osculante, o círculo é tangente à curva$C$ no ponto$P$ *e compartilha a mesma curvatura.*

Para obter mais informações sobre círculos osculantes, veja esta demonstração sobre curvatura e torção, este artigo sobre círculos osculantes e esta discussão sobre fórmulas de Serret.

Para encontrar a equação de um círculo osculante em duas dimensões, precisamos encontrar apenas o centro e o raio do círculo.

Exemplo$\PageIndex{5}$: Finding the Equation of an Osculating Circle

Encontre a equação do círculo osculante da curva definida pela função$y=x^3−3x+1$ at$x=1$.

Solução

A figura$\PageIndex{4}$ mostra o gráfico de$y=x^3−3x+1$.

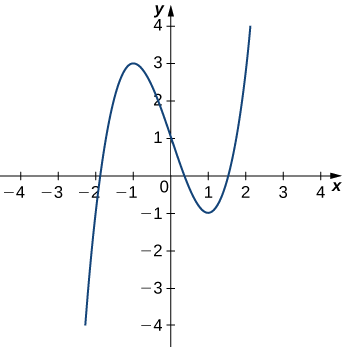
Esta figura é o gráfico de uma função cúbica y = x^3-3x+1. A curva aumenta, atinge um máximo em x=-1, diminui passando pelo eixo y em 1 e, em seguida, atingindo um mínimo em x =1 antes de aumentar novamente. — Figura$\PageIndex{4}$: Queremos encontrar o círculo osculante deste gráfico no ponto em que$x=1$.

Primeiro, vamos calcular a curvatura em$x=1$:

\[κ =\dfrac{|f″(x)|}{\bigg( 1+[f′(x)]^2 \bigg) ^{3/2}} = \dfrac{|6x|}{(1+[3x^2−3]^2)^{3/2}}. \nonumber \]

Isso dá$κ=6$. Portanto, o raio do círculo osculante é dado por$R=\frac{1}{κ}=\dfrac{1}{6}$. Em seguida, calculamos as coordenadas do centro do círculo. Quando$x=1$, a inclinação da reta tangente é zero. Portanto, o centro do círculo osculante está diretamente acima do ponto no gráfico com coordenadas$(1,−1)$. O centro está localizado em$(1,−\frac{5}{6})$. A fórmula para um círculo com raio$r$ e centro$(h,k)$ é dada por$(x−h)^2+(y−k)^2=r^2$. Portanto, a equação do círculo osculante é$(x−1)^2+(y+\frac{5}{6})^2=\frac{1}{36}$. O gráfico e seu círculo osculante aparecem no gráfico a seguir.

Exercício$\PageIndex{5}$

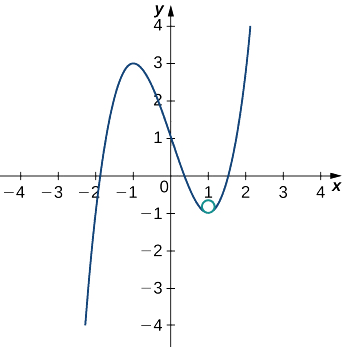
Encontre a equação do círculo osculante da curva definida pela função vetorial$y=2x^2−4x+5$ em$x=1$.

Dica: Use$\ref{EqK4}$ para encontrar a curvatura do gráfico e, em seguida, desenhe um gráfico da função$x=1$ ao redor para ajudar a visualizar o círculo em relação ao gráfico.

Resposta

$κ =\frac{4}{[1+(4x−4)^2]^{3/2}}$

No ponto$x=1$, a curvatura é igual$4$ a. Portanto, o raio do círculo osculante é$\frac{1}{4}$.

Um gráfico dessa função aparece a seguir:

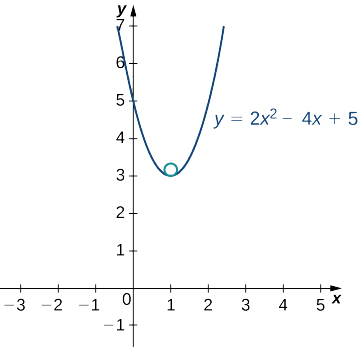
$Esta figura é o gráfico da função y = 2x^2-4x+5. A curva é uma parábola que se abre com o vértice em (1, 3).$

O vértice dessa parábola está localizado no ponto$(1,3)$. Além disso, o centro do círculo osculante está diretamente acima do vértice. Portanto, as coordenadas do centro são$(1,\frac{13}{4})$. A equação do círculo osculante é

$(x−1)^2+(y−\frac{13}{4})^2=\frac{1}{16}$.

Conceitos-chave

A função de comprimento de arco para uma função com valor vetorial é calculada usando a fórmula integral$\displaystyle s(t)=\int_a^b ‖\vecs r′(t)‖\,dt $. Essa fórmula é válida em duas e três dimensões.
A curvatura de uma curva em um ponto em duas ou três dimensões é definida como a curvatura do círculo inscrito nesse ponto. A parametrização do comprimento do arco é usada na definição de curvatura.
Existem várias fórmulas diferentes para curvatura. A curvatura de uma circunferência é igual à recíproca de seu raio.
O vetor normal unitário principal at$t$ é definido como
\[\vecs N(t)=\dfrac{\vecs T′(t)}{‖\vecs T′(t)‖}. \nonumber \]
O vetor binormal em$t$ é definido como$\vecs B(t)=\vecs T(t)×\vecs N(t)$, onde$\vecs T(t)$ é o vetor tangente unitário.
O quadro de referência de Frenet é formado pelo vetor tangente unitário, pelo vetor normal unitário principal e pelo vetor binormal.
O círculo osculante é tangente a uma curva em um ponto e tem a mesma curvatura da curva tangente nesse ponto.

Equações-chave

Comprimento do arco da curva espacial
$s= {\displaystyle \int _a^b} \sqrt{[f′(t)]^2+[g′(t)]^2+[h′(t)]^2} \,dt= {\displaystyle \int _a^b} ‖\vecs r′(t)‖\,dt$
Função de comprimento de arco
$s(t)={\displaystyle \int _a^t} \sqrt{f′(u))^2+(g′(u))^2+(h′(u))^2} \,du \; or \; s(t)={\displaystyle \int _a^t}‖\vecs r′(u)‖\,du$
$κ=\frac{‖\vecs T′(t)‖}{‖\vecs r′(t)‖} \; or \; κ=\frac{‖\vecs r′(t)×\vecs r″(t)‖}{‖\vecs r′(t)‖^3} \; or \; κ=\frac{|y″|}{[1+(y′)^2]^{3/2}}$
Vetor normal da unidade principal
$\vecs N(t)=\frac{\vecs T′(t)}{‖\vecs T′(t)‖}$
Vetor binormal
$\vecs B(t)=\vecs T(t)×\vecs N(t)$

Glossário

função de comprimento de arco: uma função$s(t)$ que descreve o comprimento do arco da curva$C$ como uma função de$t$

parametrização de comprimento de arco: uma reparametrização de uma função com valor vetorial na qual o parâmetro é igual ao comprimento do arco

vetor binormal: um vetor unitário ortogonal ao vetor tangente unitário e ao vetor normal unitário

curvatura: a derivada do vetor tangente unitário em relação ao parâmetro de comprimento do arco

Quadro de referência Frenet: (quadro TNB) um quadro de referência no espaço tridimensional formado pelo vetor tangente unitário, o vetor normal unitário e o vetor binormal

plano normal: um plano que é perpendicular a uma curva em qualquer ponto da curva

círculo osculante: um círculo que é tangente a uma curva$C$ em um ponto$P$ e que compartilha a mesma curvatura

plano oscilante: o plano determinado pela tangente unitária e pelo vetor normal unitário

vetor normal da unidade principal: um vetor ortogonal ao vetor tangente unitário, dado pela fórmula$\frac{\vecs T′(t)}{‖\vecs T′(t)‖}$

raio de curvatura: o recíproco da curvatura

suave: curvas em que a função com valor vetorial$\vecs r(t)$ é diferenciável com uma derivada diferente de zero

Teorema: fórmulas de comprimento de arco para curvas planas e espaciais

Exemplo\(\PageIndex{1}\): Finding the Arc Length

Exercício\(\PageIndex{1}\)

Teorema: função de comprimento de arco

Exemplo\(\PageIndex{2}\): Finding an Arc-Length Parameterization

Exercício\(\PageIndex{2}\)

Teorema: Fórmulas alternativas de curvatura

Prova

Exemplo\(\PageIndex{3}\): Finding Curvature

Exercício\(\PageIndex{3}\)

Exemplo\(\PageIndex{4}\): Finding the Principal Unit Normal Vector and Binormal Vector

Exercício\(\PageIndex{4}\)

Exemplo\(\PageIndex{5}\): Finding the Equation of an Osculating Circle

Exercício\(\PageIndex{5}\)