13.1E: Exercícios para a Seção 13.1

Last updated
Save as PDF

Page ID: 187851

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Introdução às funções com valores vetoriais

1) Forneça as funções do componente$x=f(t)$ e$y=g(t)$ para a função com valor vetorial$\vecs r(t)=3 \sec t \, \hat{\mathbf{i}}+2 \tan t \,\hat{\mathbf{j}}$.

Responda: Aqui podemos dizer isso$f(t)=3 \sec t, \quad g(t)=2 \tan t$

, então temos$x(t)=3 \sec t, \quad y(t)=2 \tan t$.

2) Dado$\vecs r(t)=3 \sec t \hat{\mathbf{i}}+2 \tan t \hat{\mathbf{j}}$, encontre os seguintes valores (se possível).

$\vecs r(\frac{\pi}{4})$
$\vecs r(\pi)$
$\vecs r(\frac{\pi}{2})$

3) Esboce a curva da função com valor vetorial$ \vecs r(t)=3 \sec t \hat{\mathbf{i}}+2 \tan t \hat{\mathbf{j}}$ e forneça a orientação da curva. Esboce assíntotas como guia para o gráfico.

Responda: $Caminho hiperbólico ao longo de uma hipérbole orientada horizontalmente.$

Limites de funções com valores vetoriais

4) Avalie$\lim \limits_{t \to 0}\left(e^t \hat{\mathbf{i}}+\frac{\sin t}{t} \hat{\mathbf{j}}+e^{−t} \hat{\mathbf{k}}\right)$

5) Dada a função com valor vetorial,$\vecs r(t)=⟨\cos t,\sin t⟩$ encontre os seguintes valores:

$\lim \limits_{t \to \frac{\pi}{4}} \vecs r(t)$
$\vecs r(\frac{\pi}{3})$
É$\vecs r(t)$ contínuo em$t=\frac{\pi}{3}$?
Gráfico$\vecs r(t)$.

Responda

a.$⟨\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}⟩$,
b.$⟨\frac{1}{2},\frac{\sqrt{3}}{2}⟩$,
c. Sim, o limite quando t se aproxima$\mathrm{\frac{\pi}{3}}$ é igual a$\mathrm{r(\frac{\pi}{3})}$
d.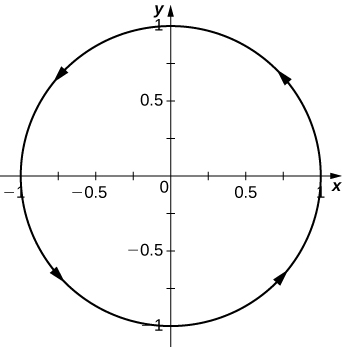

$Caminho orientado no sentido anti-horário no círculo unitário.$

6) Dada a função com valor vetorial$\vecs r(t)=⟨t,t^2+1⟩$, encontre os seguintes valores:

$\lim \limits_{t \to -3} \vecs r(t)$
$\vecs r(−3)$
É$\vecs r(t)$ contínuo em$x=−3$?
$\vecs r(t+2)−\vecs r(t)$

7) Deixe$\vecs r(t)=e^t \hat{\mathbf{i}}+\sin t \hat{\mathbf{j}}+\ln t \hat{\mathbf{k}}$. Encontre os seguintes valores:

$\vecs r(\frac{\pi}{4})$
$\lim \limits_{t \to \frac{\pi}{4} } \vecs r(t)$
É$\vecs r(t)$ contínuo em$t=\frac{\pi}{4}$?

Responda: a.$e^{\frac{\pi}{4}},\frac{\sqrt{2}}{2},\ln (\frac{\pi}{4})$ ⟩;
b.$e^{\frac{\pi}{4}},\frac{\sqrt{2}}{2},\ln (\frac{\pi}{4})$ ⟩;
c. Sim

Para os exercícios 8 a 13, encontre o limite das seguintes funções com valores vetoriais no valor indicado de$t$.

8)$\lim \limits_{t \to 4}⟨\sqrt{t−3},\frac{\sqrt{t}−2}{t−4},\tan(\frac{\pi}{t})⟩$

9)$\lim \limits_{t \to \frac{\pi}{2}} \vecs r(t)$ para$\vecs r(t)=e^t \hat{\mathbf{i}}+\sin t \hat{\mathbf{j}}+\ln t \hat{\mathbf{k}}$

Responda: $⟨e^{\frac{\pi}{2}},1,\ln(\frac{\pi}{2})⟩$

10)$\lim \limits_{t \to \infty}⟨e^{−2t},\frac{2t+3}{3t−1},\arctan(2t)⟩$

11)$\lim \limits_{t \to e^2}⟨t \ln (t),\frac{\ln t}{t^2},\sqrt{\ln(t^2)⟩}$

Responda: $2e^2 \hat{\mathbf{i}}+\frac{2}{e^4}\hat{\mathbf{j}}+2\hat{\mathbf{k}}$

12)$\lim \limits_{t \to \frac{\pi}{6}}⟨\cos 2t,\sin 2t,1⟩$

13)$\lim \limits_{t \to \infty} \vecs r(t)$ para$\vecs r(t)=2e^{−t} \mathbf{ i}+e^{−t} \hat{\mathbf{j}}+\ln(t−1) \hat{\mathbf{k}}$

Responda: O limite não existe porque o limite de$\ln(t−1)$ quando$t$ se aproxima do infinito não existe.

Domínio de uma função com valor vetorial

Para os problemas 14 a 17, encontre o domínio das funções com valor vetorial.

14) Domínio:$\vecs r(t)=⟨t^2,t,\sin t⟩$

15) Domínio:$\vecs r(t)=⟨t^2,\tan t,\ln t⟩$

Responda: $\text{D}_{\vecs r} = \left \{ t \,|\, t>0,t≠(2k+1)\frac{\pi}{2}, \, \text{where} \, k \,\text{is any integer} \right \}$

16) Domínio:$\vecs r(t)=⟨t^2,\sqrt{t−3},\frac{3}{2t+1}⟩$

17) Domínio:$\vecs r(t)=⟨\csc(t),\frac{1}{\sqrt{t−3}}, \ln(t−2)⟩$

Responda: $\text{D}_{\vecs r} = \left \{ t \,|\, t>3,t≠n\pi, \, \text{where} \, n \,\text{is any integer} \right \}$

18) a. Encontre o domínio de$\vecs r(t)=2e^{-t} \hat{\mathbf{i}}+e^{−t}\hat{\mathbf{j}}+\ln(t−1)\hat{\mathbf{k}}$.

b. Para quais valores de$t$ é$\vecs r(t)=2e^{-t} \hat{\mathbf{i}}+e^{−t}\hat{\mathbf{j}}+\ln(t−1)\hat{\mathbf{k}}$ contínuo?

Responda: a.$\text{D}_{\vecs r}: ( 1, \infty )$
b. Tudo$t$ isso$t∈(1,\infty)$

19) Domínio:$\vecs r(t)=(\arccos t) \, \hat{\mathbf{i}} + \sqrt{2t−1} \, \hat{\mathbf{j}}+\ln(t) \, \hat{\mathbf{k}}$

Responda: $\text{D}_{\vecs r}: \big[ \frac{1}{2}, 1 \big]$

Visualizando funções com valores vetoriais

20) Descreva a curva definida pela função vetorial$\vecs r(t)=(1+t)\hat{\mathbf{i}}+(2+5t)\hat{\mathbf{j}}+(−1+6t)\hat{\mathbf{k}}$.

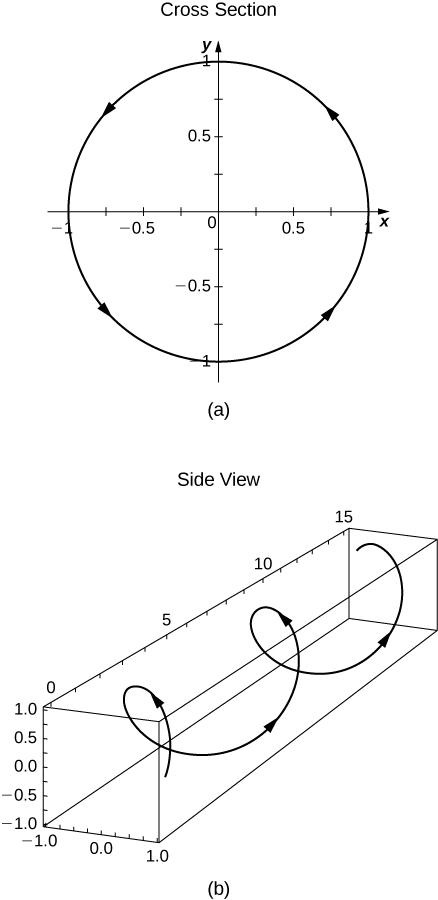
21) Deixe-o$\vecs r(t)=⟨\cos t,t,\sin t⟩$ e use-o para responder às seguintes perguntas.

Para quais valores de$t$ é$\vecs r(t)$ contínuo?
Esboce o gráfico de$\vecs r(t)$.

Responda: a.$\vecs r$ é contínuo para todos os números reais, ou seja, para$t \in \mathbb{R}$.
b. Observe que deve haver um$z$ no eixo vertical na seção transversal na imagem (a) abaixo em vez do$y$.

$A imagem superior mostra o caminho orientado no sentido anti-horário no círculo unitário. A imagem inferior mostra o caminho do saca-rolhas com a coordenada z variando à medida que o movimento circular continua, como na imagem acima.$

22) Produza um esboço cuidadoso do gráfico de$\vecs r(t) = t^2 \, \hat{\mathbf{i}} + t \, \hat{\mathbf{j}}$.

Nas perguntas 23 a 25, use um utilitário gráfico para esboçar cada uma das funções com valor vetorial:

23) [T]$\vecs r(t)=2 \cos^2 t \hat{\mathbf{i}}+(2−\sqrt{t})\hat{\mathbf{j}}$

Responda

24) [T]$\vecs r(t)=⟨e^{\cos (3t)},e^{−\sin(t)}⟩$

25) [T]$\vecs r(t)=⟨2−\sin (2t),3+2 \cos t⟩$

Responda: $Um caminho orientado em figura oito.$

Encontrando equações dentro$x$ e$y$ para o caminho traçado por funções com valores vetoriais

Para as perguntas 26-33, elimine o parâmetro$t$, escreva a equação em coordenadas cartesianas e, em seguida, esboce o gráfico das funções com valores vetoriais.

26)$\vecs r(t)=2t\hat{\mathbf{i}}+t^2 \hat{\mathbf{j}}$
(Dica: Deixe$x=2t$$y=t^2$ e. Resolva a primeira equação$t$ em termos de$x$ e substitua esse resultado pela segunda equação.)

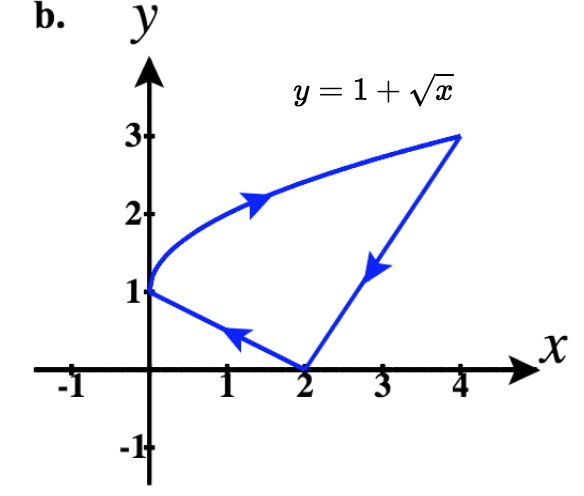
27)$\vecs r(t)=t^3 \hat{\mathbf{i}}+2t \hat{\mathbf{j}}$

Responda

$y=2\sqrt[3]{x}$, uma variação da função de raiz cúbica

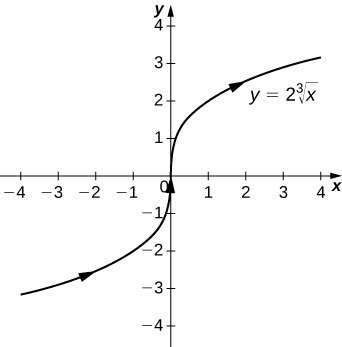
$O caminho orientado ao longo do gráfico de y é igual a 2 vezes a raiz cúbica de x. O movimento ao longo do caminho é orientado da esquerda para a direita.$

28)$\vecs r(t)=\sin t\,\hat{\mathbf{i}}+\cos t\,\hat{\mathbf{j}}$

29)$\vecs r(t)=3\cos t\,\hat{\mathbf{i}}+3\sin t\,\hat{\mathbf{j}}$

Responda

$x^2+y^2=9$, um círculo$(0,0)$ centrado no raio 3 e uma orientação no sentido anti-horário

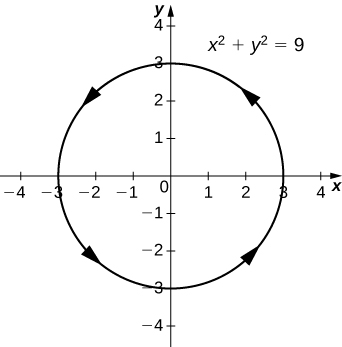
$Movimento no sentido anti-horário ao longo do círculo de raio 3, centrado na origem.$

30)$\vecs r(t)=⟨ \sin t,4 \cos t⟩$

31)$\vecs r(t)=2\sin t\,\hat{\mathbf{i}}-3\cos t\,\hat{\mathbf{j}}$

Responda

$\frac{x^2}{4}+\frac{y^2}{9}=1$, uma elipse centrada em$(0,0)$ com interceptações em$x = \pm2$ e e$y =\pm3$ e uma orientação no sentido horário

$Elipse com orientação no sentido horário passando por (-2,0), (0, 3), (2, 0), (0, -3)$

32)$\vecs r(t)=\tan t\,\hat{\mathbf{i}}-2\sec t\,\hat{\mathbf{j}}$

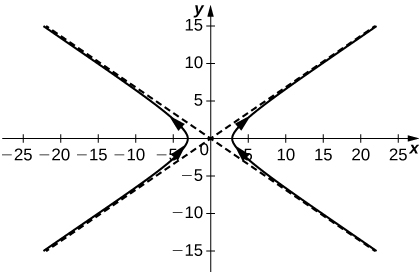
33)$\vecs r(t)=3\sec t\,\hat{\mathbf{i}}+4\tan t\,\hat{\mathbf{j}}$

Responda

$\frac{x^2}{9}-\frac{y^2}{16}=1$, uma hipérbole centrada em$(0,0)$ com$x$ -intercepta$(3, 0)$ e$(-3, 0)$, com orientação mostrada

$Hyperbole orientada$

Encontrando uma função com valor vetorial para traçar o gráfico de uma equação em$x$ e$y$

Para as questões 34 a 40, encontre uma função com valor vetorial que traça a curva dada na direção indicada.

34)$4x^2+9y^2=36$; no sentido horário e anti-horário

35)$y=x^2$; da esquerda para a direita

Responda: $\vecs r(t)=⟨t,t^2⟩$, onde$t$ aumenta

36) A linha que passa$P$ e$Q$ onde$P$ está$(1,4,−2)$ e$Q$ é$(3,9,6)$

37) O círculo$x^2 + y^2 = 36$, orientado no sentido horário, com posição$(-6, 0)$ no momento$t = 0$.

Responda: $\vecs r(t)=-6\cos t\,\hat{\mathbf{i}}+6\sin t\,\hat{\mathbf{j}}$

38) A elipse$x^2 + \dfrac{y^2}{36} = 1$, orientada no sentido anti-horário

Responda: $\vecs r(t)=\cos t\,\hat{\mathbf{i}}+6\sin t\,\hat{\mathbf{j}}$

39) A hipérbole$\dfrac{y^2}{36} - x^2 = 1$, a peça superior é orientada da esquerda para a direita

Responda: $\vecs r(t)=\tan t\,\hat{\mathbf{i}}+6\sec t\,\hat{\mathbf{j}}$

40) A hipérbole$\dfrac{x^2}{49} - \dfrac{y^2}{64} = 1$, peça direita, é orientada de baixo para cima

Responda: $\vecs r(t)=7\sec t\,\hat{\mathbf{i}}+8\tan t\,\hat{\mathbf{j}}$

Parametrizando um caminho por partes

Para as perguntas 41 a 44, forneça uma parametrização para cada caminho por partes. Tente escrever uma parametrização que comece com$t = 0$ e progrida através de valores de à$t$ medida que você passa de uma peça para outra.

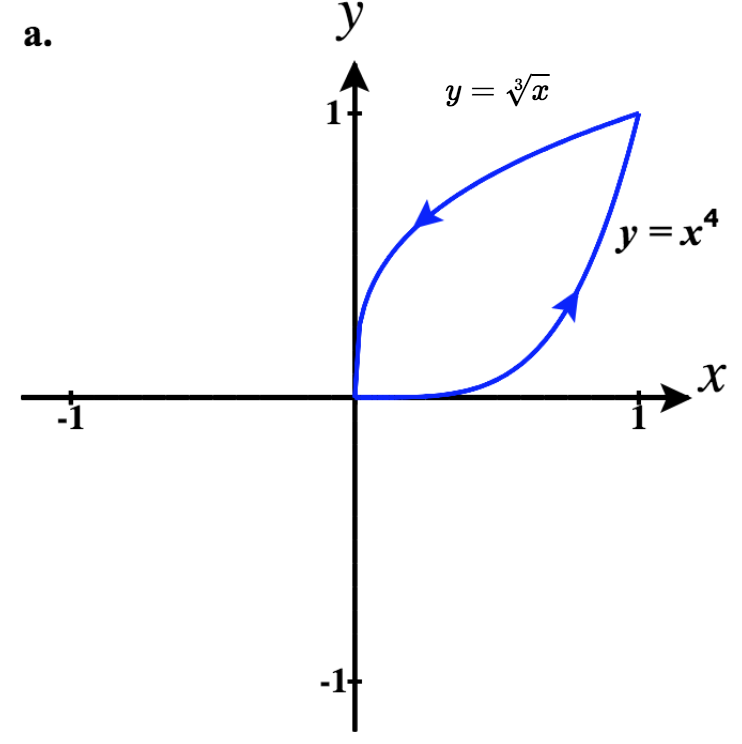
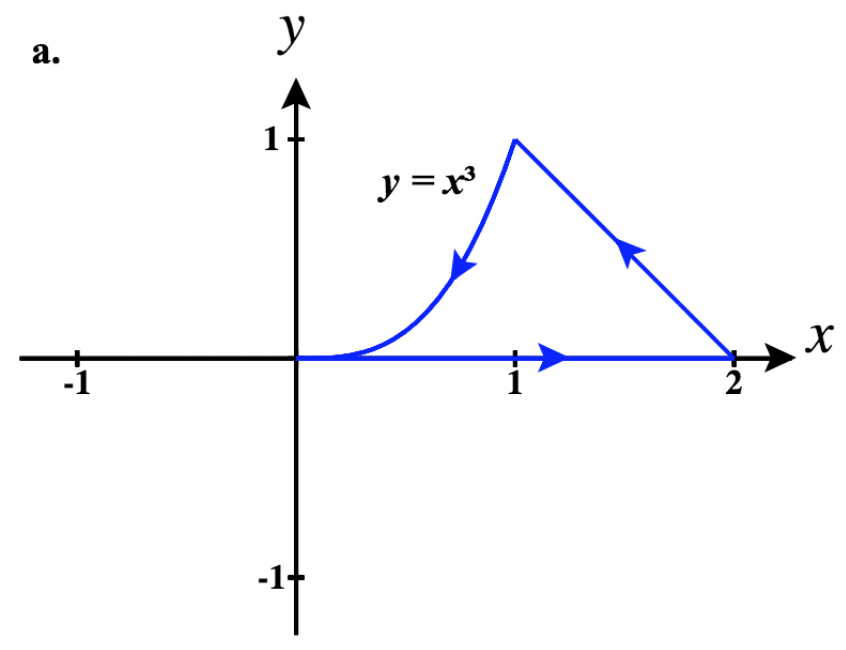
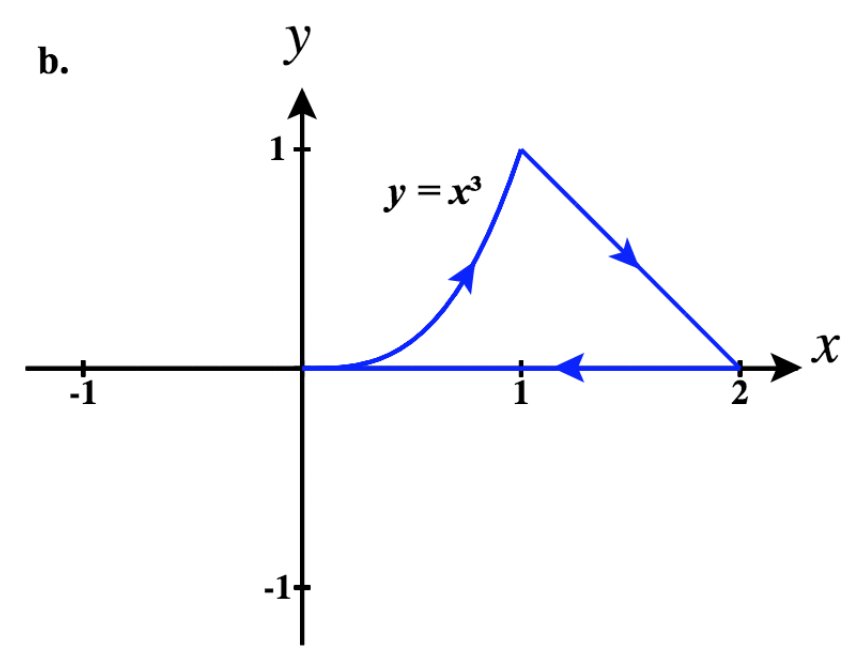
41)

$Limite orientado no sentido anti-horário de uma região fechada formada por y = x^4 e y é igual à raiz cúbica de x.$ $Limite orientado no sentido horário de uma região fechada formada por y = x^4 e y é igual à raiz cúbica de x.$

Responda: a.$\vecs r_1(t)= t\,\hat{\mathbf{i}} + t^4 \,\hat{\mathbf{j}}$ for$0 \le t \le 1$
$\vecs r_2(t)= -t\,\hat{\mathbf{i}} + \sqrt[3]{-t} \,\hat{\mathbf{j}}$ for$-1 \le t \le 0$

Então, uma parametrização fragmentada desse caminho é:
\ (\ vecs r (t) =\ begin {cases}
t\,\ hat {\ mathbf {i}} + t^4\,\ hat {\ mathbf {j}}, & 0\ le t\ le 1\\
\ left (2-t\ right)\,\ hat {\ mathbf {i}} +\ sqrt [3] {2-t}\,\ hat {\ mathbf {j}}, & 1\ lt t
\ le 2\ end {cases}\)

b.$\vecs r_1(t)= t\,\hat{\mathbf{i}} + \sqrt[3]{t} \,\hat{\mathbf{j}}$$0 \le t \le 1$
$\vecs r_2(t)= -t\,\hat{\mathbf{i}} + (-t)^4 \,\hat{\mathbf{j}}$ para$-1 \le t \le 0$

Então, por partes a parametrização desse caminho é:
\ (\ vecs r (t) =\ begin {cases}
t\,\ hat {\ mathbf {i}} +\ sqrt [3] {t}\,\ hat {\ mathbf {j}}, & 0\ le t\ le 1\
\\ left (2-t\ right)\,\ hat {\ mathbf {i}} +\ left (2-t\ right) ^4\,\ hat {\ mathbf {j}} e 1\ lt t\ le 2
\ end {casos}\)

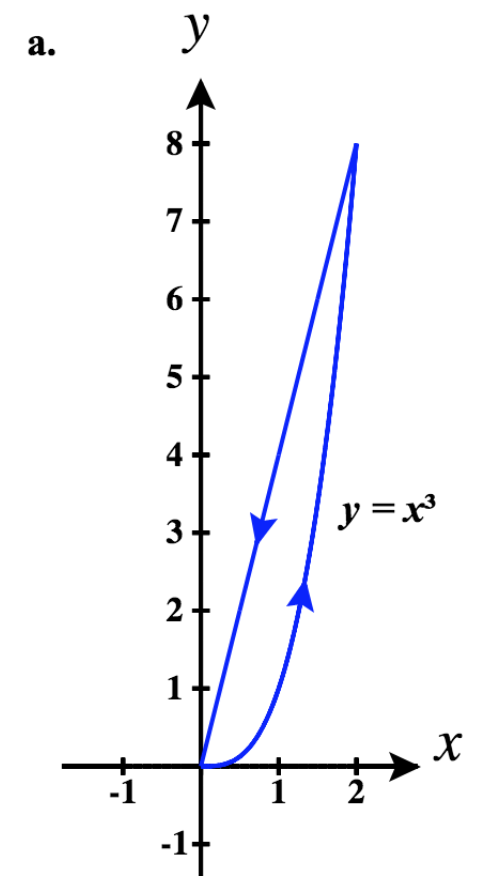
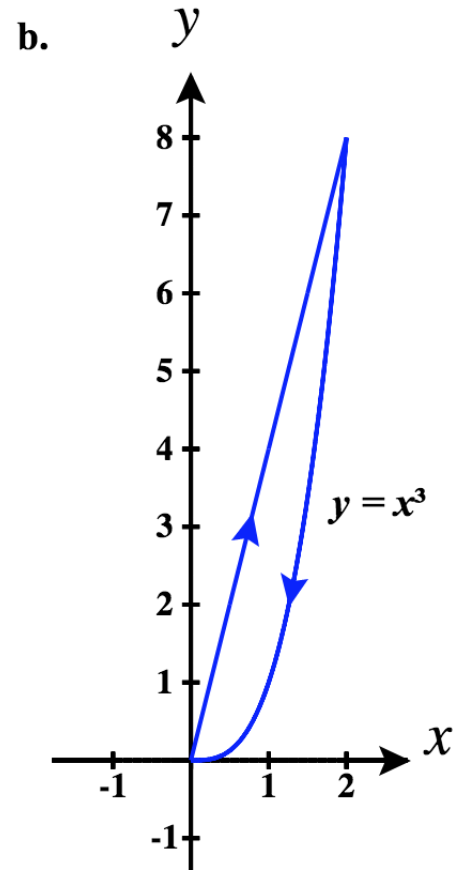
(42)

$Limite orientado no sentido anti-horário de uma região fechada formada por y = x^3 e y = 4x.$ $Limite orientado no sentido horário de uma região fechada formada por y = x^3 e y = 4x.$

43)

$Limite orientado no sentido anti-horário de uma região fechada formada por y = x^3 e y = 2 - x e o eixo x.$ $Limite orientado no sentido horário de uma região fechada formada por y = x^3 e y = 2 - x e o eixo x.$

Responda: a.$\vecs r_1(t)= t\,\hat{\mathbf{i}} +0 \,\hat{\mathbf{j}}$ for$0 \le t \le 2$
$\vecs r_2(t)= -t\,\hat{\mathbf{i}} + \left(2 + t\right) \,\hat{\mathbf{j}}$$-2 \le t \le -1$
$\vecs r_3(t)= -t\,\hat{\mathbf{i}} + \left(-t\right)^3 \,\hat{\mathbf{j}}$ for$-1 \le t \le 0$

Portanto, uma parametrização fragmentada desse caminho é:
\ (\ vecs r (t) =\ begin {cases}
t\,\ hat {\ mathbf {i}}, & 0\ le t\ le 2\\
\ left (4-t\ right)\,\ hat {\ mathbf {i}} +\ left (t-2\ right)\,\ hat {\ mathbf {j}}, & 2\ lt t\ le 3\
\\ left (4-t\ right)\,\ hat {\ mathbf {i}} +\ left (4-t\ right) ^3\,\ hat {\ mathbf {j}} e 3\ lt t\ le 4
\ end {casos}\)

b.$\vecs r_1(t)= t\,\hat{\mathbf{i}} + t^3 \,\hat{\mathbf{j}}$ for$0 \le t \le 1$
$\vecs r_2(t)= t\,\hat{\mathbf{i}} + \left(2 - t\right) \,\hat{\mathbf{j}}$$1 \le t \le 2$
$\vecs r_3(t)= -t\,\hat{\mathbf{i}} + 0 \,\hat{\mathbf{j}}$ for$-2 \le t \le 0$

Portanto, uma parametrização fragmentada desse caminho é:
\ (\ vecs r (t) =\ begin {cases}
t\,\ hat {\ mathbf {i}} + t^3\,\ hat {\ mathbf {j}}, & 0\ le t\ le 1\\
t\,\ hat {\ mathbf {i}} +\ left (2 - t\ right)\,\ hat {\ mathbf {j}}, & 1\ lt t\ le 2\\
\ left (4-t\ direita)\,\ hat {\ mathbf {i}}, & 2\ lt t\ le 4
\ end {casos}\)

44)

$Limite orientado no sentido anti-horário de uma região fechada formada por y = 1-x/2 e y = 3x/2 - 3 e y = 1 mais a raiz quadrada de x.$ $Limite orientado no sentido horário de uma região fechada formada por y = 1-x/2 e y = 3x/2 - 3 e y = 1 mais a raiz quadrada de x.$

Perguntas adicionais sobre funções com valores vetoriais

Para as questões 45 a 48, considere a curva descrita pela função com valor vetorial$\vecs r(t)=(50e^{−t}\cos t)\hat{\mathbf{i}}+(50e^{−t}\sin t)\hat{\mathbf{j}}+(5−5e^{−t})\hat{\mathbf{k}}$.

45) A que corresponde o ponto inicial do caminho$\vecs r(0)$?

Responda: $(50,0,0)$

46) O que é$\lim \limits_{t \to \infty} \vecs r(t) $?

47) [T] Use a tecnologia para esboçar a curva.

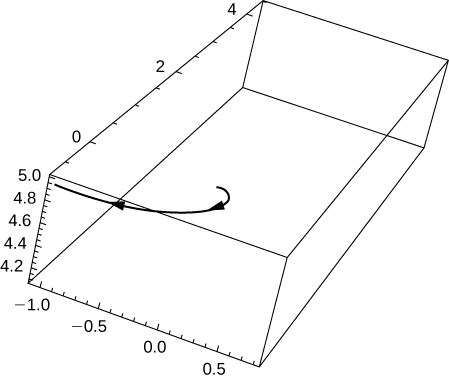
Responda: $Caminho parcial para r (t) = (50e^ (−t) cos t) i+ (50e^ (−t) sin t) j+ (5−5e^ (−t)) k.$

48) Elimine o parâmetro t para mostrar$z=5−\dfrac{r}{10}$ onde$r^2=x^2+y^2$.

49) [T] Deixe$\vecs r(t)=\cos t \hat{\mathbf{i}}+\sin t\hat{\mathbf{j}}+0.3 \sin (2t)\hat{\mathbf{k}}$. Use a tecnologia para representar graficamente a curva (chamada de curva da montanha-russa) ao longo do intervalo$[0,2\pi)$. Escolha pelo menos duas vistas para determinar os picos e vales.

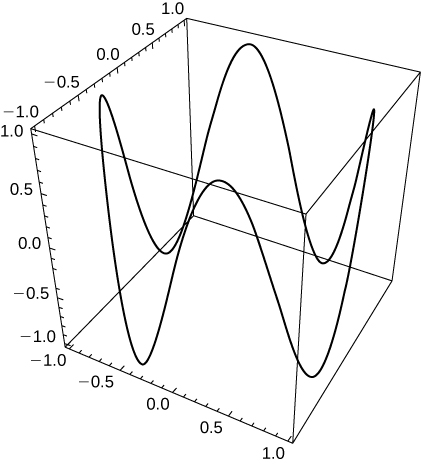
Responda: $Duas vistas do caminho traçado por r (t) = (cos t) i + (sin t) j + (0,3 sin 2t) k.$

50) [T] Use o resultado do problema anterior para construir uma equação de uma montanha-russa com uma queda acentuada do pico e uma inclinação íngreme do “vale”. Em seguida, use a tecnologia para representar graficamente a equação.

51) Use os resultados dos dois problemas anteriores para construir uma equação de um caminho de uma montanha-russa com mais de dois pontos de inflexão (picos e vales).

Responda

Uma possibilidade é$\vecs r(t)=\cos t \hat{\mathbf{i}}+\sin t\hat{\mathbf{j}}+\sin (4t)\hat{\mathbf{k}}$. Ao aumentar o coeficiente de$t$ no terceiro componente, o número de pontos de inflexão aumentará.

$Caminho traçado por r (t) = (cos t) i + (sin t) j + (sin 4t) k.$

52) Conclua a investigação a seguir.

Faça um gráfico da curva$\vecs r(t)=(4+\cos(18t))\cos(t)\hat{\mathbf{i}}+(4+\cos (18t)\sin (t))\hat{\mathbf{j}}+0.3 \sin(18t)\hat{\mathbf{k}}$ usando dois ângulos de visão de sua escolha para ver a forma geral da curva.
A curva se assemelha a um “slinky”?
Quais mudanças na equação devem ser feitas para aumentar o número de bobinas do slinky?

Colaboradores

Template:ContribOpenStaxCalc

Paul Seeburger (Monroe Community College) criou os problemas 12, 14, 19, 22, 30-33, 37- 44.