13.2: Cálculo de funções com valor vetorial

objetivos de aprendizagem

• Escreva uma expressão para a derivada de uma função com valor vetorial.
• Encontre o vetor tangente em um ponto para um determinado vetor de posição.
• Encontre o vetor tangente unitário em um ponto para um determinado vetor de posição e explique seu significado.
• Calcule a integral definida de uma função com valor vetorial.

Para estudar o cálculo de funções com valores vetoriais, seguimos um caminho semelhante ao que seguimos ao estudar funções com valor real. Primeiro, definimos a derivada, depois examinamos as aplicações da derivada e, em seguida, passamos à definição de integrais. No entanto, encontraremos algumas novas ideias interessantes ao longo do caminho, como resultado da natureza vetorial dessas funções e das propriedades das curvas espaciais.

Derivadas de funções com valores vetoriais

Agora que vimos o que é uma função com valor vetorial e como calcular seu limite, a próxima etapa é aprender como diferenciar uma função com valor vetorial. A definição da derivada de uma função com valor vetorial é quase idêntica à definição de uma função de valor real de uma variável. No entanto, como o intervalo de uma função com valor vetorial consiste em vetores, o mesmo vale para o intervalo da derivada de uma função com valor vetorial.

Definição: Derivada de funções com valor vetorial

A derivada de uma função com valor vetorial\(\vecs{r}(t)\) é

\[\vecs{r}′(t) = \lim \limits_{\Delta t \to 0} \dfrac{\vecs{r}(t+\Delta t)−\vecs{r}(t)}{ \Delta t} \label{eq1} \]

desde que o limite exista. Se\(\vecs{r}'(t)\) existe, então\(\vecs{r}(t)\) é diferenciável em\(t\). Se\(\vecs{r}′(t)\) existe para todos\(t\) em um intervalo aberto\((a,b)\), então\(\vecs{r}(t)\) é diferenciável ao longo do intervalo\((a,b)\). Para que a função seja diferenciável no intervalo fechado\([a,b]\), os dois limites a seguir também devem existir:

\[\vecs{r}′(a) = \lim \limits_{\Delta t \to 0^+} \dfrac{\vecs{r}(a+\Delta t)−\vecs{r}(a)}{ \Delta t} \nonumber \]

e

\[\vecs{r}′(b) = \lim \limits_{\Delta t \to 0^-} \dfrac{\vecs{r}(b+\Delta t)−\vecs{r}(b)}{ \Delta t} \nonumber \]

Muitas das regras para calcular derivadas de funções de valor real também podem ser aplicadas ao cálculo das derivadas de funções com valor vetorial. Lembre-se de que a derivada de uma função de valor real pode ser interpretada como a inclinação de uma reta tangente ou a taxa instantânea de mudança da função. A derivada de uma função com valor vetorial também pode ser entendida como uma taxa de mudança instantânea; por exemplo, quando a função representa a posição de um objeto em um determinado ponto no tempo, a derivada representa sua velocidade nesse mesmo ponto no tempo.

Agora demonstramos a derivada de uma função com valor vetorial.

Exemplo\(\PageIndex{1}\): Finding the Derivative of a Vector-Valued Function

Use a definição para calcular a derivada da função

\[\vecs{r}(t)=(3t+4) \,\mathbf{\hat{i}}+(t^2−4t+3) \,\mathbf{\hat{j}} .\nonumber \]

Solução

Vamos usar a Equação\ ref {eq1}:

\ [\ begin {align*}\ vecs {r} ′( t) &=\ lim\ limits_ {\ Delta t\ to 0}\ dfrac {\ vecs {r} (T+Δt) −\ vecs {r} (t)} {Δt}\\ [4pt]
&=\ lim\ limits_ {\ Delta t\ to 0}\ dfrac {[3 (T+δT) +4)\,\ hat {\ mathbf {i}} + ((T+δT) ^2−4 (T+Δt) +3)\,\ hat {\ mathbf {j}}] − [(3t+4)\,\ hat {\ mathbf {i}} + (t^2−4t+3)\,\ hat {\ mathbf {j}}]} {Δt}\\ [4 pt]
&=\ lim\ limits_ {\ Delta t\ to 0}\ dfrac {(3T+3δT+4)\,\ hat {\ mathbf {i}} − (3t+4)\,\ hat {\ mathbf {i}} + (T^2+2TδT+ (Δt) ^2−4T−4ΔT+3)\,\ hat {\ mathbf {j}} − (t^2−4t+3)\,\ hat {\ mathbf {j}} {Δt}\\ [4pt]
&=\ lim\ limits_ {\ Delta t\ a 0}\ dfrac {(3Δt)\,\ hat {\ mathbf {i}} + (2tΔt) T+ (Δt) ^2−4Δt)\,\ hat {\ mathbf {j}} {Δt}\\ [4pt]
&=\ lim\ limits_ {\ Delta t\ to 0} (3\,\ hat {\ mathbf {i}} + (2T+ΔT−4)\,\ hat {\ mathbf {j}})\\ [4pt]
&=3\,\ hat {\ mathbf {i}} + (2t−4)\,\ hat {\ mathbf {j}}\ end {align*}\ nonumber\]

Exercício\(\PageIndex{1}\)

Use a definição para calcular a derivada da função\(\vecs{r}(t)=(2t^2+3) \,\mathbf{\hat{i}}+(5t−6) \,\mathbf{\hat{j}}\).

Dica

Use a Equação\ ref {eq1}.

Resposta

\[\vecs{r}′(t)=4t \,\mathbf{\hat{i}}+5 \,\mathbf{\hat{j}} \nonumber \]

Observe que nos cálculos em Exemplo\(\PageIndex{1}\), também poderíamos obter a resposta calculando primeiro a derivada de cada função componente e, em seguida, colocando essas derivadas de volta na função com valor vetorial. Isso é sempre verdadeiro para calcular a derivada de uma função com valor vetorial, seja em duas ou três dimensões. Nós afirmamos isso no seguinte teorema. A prova desse teorema segue diretamente das definições do limite de uma função com valor vetorial e da derivada de uma função com valor vetorial.

Teorema\(\PageIndex{1}\): Differentiation of Vector-Valued Functions

Sejam\(f\)\(g\), e\(h\) sejam funções diferenciáveis de\(t\).

1. Se\(\vecs{r}(t)=f(t) \,\mathbf{\hat{i}}+g(t) \,\mathbf{\hat{j}}\) então\[\vecs{r}′(t)=f′(t) \,\mathbf{\hat{i}}+g′(t) \,\mathbf{\hat{j}}. \nonumber \]
2. Se\(\vecs{r}(t)=f(t) \,\mathbf{\hat{i}}+g(t) \,\mathbf{\hat{j}} + h(t) \,\mathbf{\hat{k}}\) então\[\vecs{r}′(t)=f′(t) \,\mathbf{\hat{i}}+g′(t) \,\mathbf{\hat{j}} + h′(t) \,\mathbf{\hat{k}}. \nonumber \]

Exemplo\(\PageIndex{2}\): Calculating the Derivative of Vector-Valued Functions

Use o Teorema\(\PageIndex{1}\) para calcular a derivada de cada uma das seguintes funções.

1. \(\vecs{r}(t)=(6t+8) \,\mathbf{\hat{i}}+(4t^2+2t−3) \,\mathbf{\hat{j}}\)
2. \(\vecs{r}(t)=3 \cos t \,\mathbf{\hat{i}}+4 \sin t \,\mathbf{\hat{j}}\)
3. \(\vecs{r}(t)=e^t \sin t \,\mathbf{\hat{i}}+e^t \cos t \,\mathbf{\hat{j}}−e^{2t} \,\mathbf{\hat{k}}\)

Solução

Usamos o Teorema\(\PageIndex{1}\) e o que sabemos sobre a diferenciação de funções de uma variável.

1. O primeiro componente do\[\vecs r(t)=(6t+8) \,\mathbf{\hat{i}}+(4t^2+2t−3) \,\mathbf{\hat{j}} \nonumber \] é\(f(t)=6t+8\). O segundo componente é\(g(t)=4t^2+2t−3\). Nós temos\(f′(t)=6\) e\(g′(t)=8t+2\), é o que o Teorema\(\PageIndex{1}\) dá\(\vecs r′(t)=6 \,\mathbf{\hat{i}}+(8t+2)\,\mathbf{\hat{j}}\).
2. O primeiro componente é\(f(t)=3 \cos t\) e o segundo componente é\(g(t)=4 \sin t\). Nós temos\(f′(t)=−3 \sin t\) e\(g′(t)=4 \cos t\), então, obtemos\(\vecs r′(t)=−3 \sin t \,\mathbf{\hat{i}}+4 \cos t \,\mathbf{\hat{j}}\).
3. O primeiro componente de\(\vecs r(t)=e^t \sin t \,\mathbf{\hat{i}}+e^t \cos t \,\mathbf{\hat{j}}−e^{2t} \,\mathbf{\hat{k}}\) é\(f(t)=e^t \sin t\), o segundo componente é\(g(t)=e^t \cos t\) e o terceiro componente é\(h(t)=−e^{2t}\). Nós temos\(f′(t)=e^t(\sin t+\cos t)\),\(g′(t)=e^t (\cos t−\sin t)\), e\(h′(t)=−2e^{2t}\), é o que o teorema dá\(\vecs r′(t)=e^t(\sin t+\cos t)\,\mathbf{\hat{i}}+e^t(\cos t−\sin t)\,\mathbf{\hat{j}}−2e^{2t} \,\mathbf{\hat{k}}\).

Exercício\(\PageIndex{2}\)

Calcule a derivada da função

\[\vecs{r}(t)=(t \ln t)\,\mathbf{\hat{i}}+(5e^t) \,\mathbf{\hat{j}}+(\cos t−\sin t) \,\mathbf{\hat{k}}. \nonumber \]

Dica

Identifique as funções dos componentes e use o Teorema\(\PageIndex{1}\).

Resposta

\[\vecs{r}′(t)=(1+ \ln t) \,\mathbf{\hat{i}}+5e^t \,\mathbf{\hat{j}}−(\sin t+\cos t)\,\mathbf{\hat{k}} \nonumber \]

Podemos estender às funções com valores vetoriais as propriedades da derivada que apresentamos anteriormente. Em particular, a regra múltipla constante, as regras de soma e diferença, a regra do produto e a regra da cadeia se estendem às funções com valor vetorial. No entanto, no caso da regra do produto, na verdade existem três extensões:

1. para uma função de valor real multiplicada por uma função com valor vetorial,
2. para o produto escalar de duas funções com valores vetoriais, e
3. para o produto cruzado de duas funções com valores vetoriais.

Teorema: Propriedades da derivada de funções com valor vetorial

\(\vecs{u}\)Seja\(\vecs{r}\) e seja funções diferenciáveis com valor vetorial de\(t\),\(f\) seja uma função diferenciável de valor real de\(t\) e\(c\) seja um escalar.

\[\begin{array}{lrcll} \mathrm{i.} & \dfrac{d}{\,dt}[c\vecs r(t)] & = & c\vecs r′(t) & \text{Scalar multiple} \nonumber\\ \mathrm{ii.} & \dfrac{d}{\,dt}[\vecs r(t)±\vecs u(t)] & = & \vecs r′(t)±\vecs u′(t) & \text{Sum and difference} \nonumber\\ \mathrm{iii.} & \dfrac{d}{\,dt}[f(t)\vecs u(t)] & = & f′(t)\vecs u(t)+f(t)\vecs u′(t) & \text{Scalar product} \nonumber\\ \mathrm{iv.} & \dfrac{d}{\,dt}[\vecs r(t)⋅\vecs u(t)] & = & \vecs r′(t)⋅\vecs u(t)+\vecs r(t)⋅\vecs u′(t) & \text{Dot product} \nonumber\\ \mathrm{v.} & \dfrac{d}{\,dt}[\vecs r(t)×\vecs u(t)] & = & \vecs r′(t)×\vecs u(t)+\vecs r(t)×\vecs u′(t) & \text{Cross product} \nonumber\\ \mathrm{vi.} & \dfrac{d}{\,dt}[\vecs r(f(t))] & = & \vecs r′(f(t))⋅f′(t) & \text{Chain rule} \nonumber\\ \mathrm{vii.} & \text{If} \; \vecs r(t)·\vecs r(t) & = & c, \text{then} \; \vecs r(t)⋅\vecs r′(t) \; =0 \; . & \mathrm{} \nonumber \end{array} \nonumber \]

Prova

As provas das duas primeiras propriedades seguem diretamente da definição da derivada de uma função com valor vetorial. A terceira propriedade pode ser derivada das duas primeiras propriedades, junto com a regra do produto. Deixe\(\vecs u(t)=g(t)\,\mathbf{\hat{i}}+h(t)\,\mathbf{\hat{j}}\). Então

\ [\ begin {align*}\ dfrac {d} {\, dt} [f (t)\ vecs u (t)] &=\ dfrac {d} {\, dt} [f (t) (g (t)\,\ mathbf {\ hat {i}} +h (t)\,\ mathbf {\ hat {j}}))\\ [4pt]
&=\ dfrac {d} {\, dt} [f (t) g (t)\,\ mathbf {\ hat {i}} +f (t) h (t)\,\ mathbf {\ hat {j}}]\ [4pt]
&=\ dfrac {d} {\, dt} [f (t) g (t)],\ mathbf {\ hat {i}} +\ dfrac {d} {\, dt} [f (t) h (t)]\,\ mathbf {\ hat {j}}\\ [4pt]
&= (f′( t) g (t) +f (t) g′( t))\,\ mathbf {\ hat {i}} + (f′( t) h (t) +f (t) h′n (t))\,\ mathbf {\ hat {i}} + (f′( t) h (t) +f (t) h′n (t))\ thbf {\ hat {j}}\\ [4pt]
&=f′( t)\ vecs u (t) +f (t)\ vecs u′( t). \ end {align*}\ nonumber\]

Para provar a propriedade iv.\(\vecs r(t)=f_1(t) \,\mathbf{\hat{i}}+g_1(t) \,\mathbf{\hat{j}}\) arrendar\(\vecs u(t)=f_2(t) \,\mathbf{\hat{i}}+g_2(t) \,\mathbf{\hat{j}}\) e. Então

\ [\ begin {align*}\ dfrac {d} {\, dt} [\ vecs r (t) ‣\ vecs u (t)] &=\ dfrac {d} {\, dt} [f_1 (t) f_2 (t) +g_1 (t) g_2 (t)]\\ [4pt]
&=f_1′( t) f_f_1 (t) g_2 (t) g_2 (t) 2 (t) +f_1 (t) f_2′( t) +g_1′( t) g_2 (t) +g_1 (t) g_2′( t) =f_1′( t) f_2 (t) +g_1′( t) g_2 (t) +f_1 (t) f_2′( t) +g_1 (t) g_2′( t)\\ [4pt]
& =( f_1′\,\ mathbf {\ hat {i}} +g_1′\,\ mathbf {\ hat {j}}) ‣ (f_2\,\ mathbf {\ hat {i}} +g_2\,\ mathbf {\ hat {j}}) + (f_1\,\ mathbf {\ hat {i}} +g_1\,\ mathbf {\ hat {j}}) □ (f_2′\,\ mathbf {\ hat {j}}) □ (f_2′\,\ mathbf {\ hat {j}}) □ (f_2′\,\ mathbf {\ hat {j}}) bf {\ hat {i}} +g_2′\,\ mathbf {\ hat {j}})\\ [4pt]
&=\ vecs r′( t) ‣\ vecs u (t) +\ vecs r (t) ‣\ vecs u′n (t). \ end {align*}\ nonumber\]

A prova de propriedade v. é semelhante à da propriedade iv. A propriedade vi. pode ser comprovada usando a regra da cadeia. Por último, a propriedade vii. segue da propriedade iv:

\ [\ begin {align*}\ dfrac {d} {\, dt} [\ vecs r (t) ·\ vecs r (t)] &=\ dfrac {d} {\, dt} [c]\\ [4pt]
\ vecs r (t) ·\ vecs r (t) +\ vecs r (t) ·\ vecs r′r (t) &= 0\\ [4pt]
2\ vecs r (t) ·\ vecs r′( t) &= 0\\ [4pt]
\ vecs r (t) ·\ vecs r (t) &= 0\ end {align*}\ nonumber\]

Agora, alguns exemplos de uso dessas propriedades.

Exemplo\(\PageIndex{3}\): Using the Properties of Derivatives of Vector-Valued Functions

Dadas as funções com valor vetorial

\[\vecs{r}(t)=(6t+8)\,\mathbf{\hat{i}}+(4t^2+2t−3)\,\mathbf{\hat{j}}+5t \,\mathbf{\hat{k}} \nonumber \]

e

\[\vecs{u}(t)=(t^2−3)\,\mathbf{\hat{i}}+(2t+4)\,\mathbf{\hat{j}}+(t^3−3t)\,\mathbf{\hat{k}}, \nonumber \]

calcule cada uma das seguintes derivadas usando as propriedades da derivada de funções com valor vetorial.

1. \(\dfrac{d}{\,dt}[\vecs{r}(t)⋅ \vecs{u}(t)]\)
2. \(\dfrac{d}{\,dt}[ \vecs{u} (t) \times \vecs{u}′(t)]\)

Solução

Nós temos\(\vecs{r}′(t)=6 \,\mathbf{\hat{i}}+(8t+2) \,\mathbf{\hat{j}}+5 \,\mathbf{\hat{k}}\)\(\vecs{u}′(t)=2t \,\mathbf{\hat{i}}+2 \,\mathbf{\hat{j}}+(3t^2−3) \,\mathbf{\hat{k}}\) e. Portanto, de acordo com a propriedade iv:

1. \ [\ begin {align*}\ dfrac {d} {\, dt} [\ vecs r (t) ‣\ vecs u (t)] &=\ vecs r′( t) □\ vecs u (t) +\ vecs r (t) ‣\ vecs u (t)\ vecs u (t)\\ [4pt]
   &= (6\,\ mathbf {\ hat {i}} + (8t+2)\,\ mathbf {\ hat {j}} +5\,\ mathbf {\ hat {k}}) ‣ (t^2−3)\,\ mathbf {\ hat {i}} + (2t+4)\,\ mathbf {\ hat {j}} + (t^3−3t)\,\ mathbf {\ hat {k}})\\ [4 pt]
   &\; + (6t+8)\,\ mathbf {\ hat {i}} + (4t^2+2t−3)\,\ mathbf {\ hat {j}} +5t\,\ mathbf {\ hat {k}}) (2t\,\ mathbf {\ hat {i}} +2\,\ mathbf {\ hat {i}} +2\,\ mathbf {\ hat {i}} +2\,\ mathbf {\ hat {i}} +2\,\ mathbf f {\ hat {j}} + (3t^2−3)\,\ mathbf {\ hat {k}})\ [4pt]
   &= 6 (t^2−3) + (8t+2) (2t+4) +5 (t^3−3t)\\ [4pt]
   &\; +2t (6t+8) +2 (4t^3t) 2+2t−3) +5t (3t^2−3)\\ [4pt ]
   &= 20t^3+42t^2+26t−16. \ end {align*}\]
2. Primeiro, precisamos adaptar a propriedade v para esse problema:

   \[\dfrac{d}{\,dt}[ \vecs{u}(t) \times \vecs{u}′(t)]=\vecs{u}′(t)\times \vecs{u}′(t)+ \vecs{u}(t) \times \vecs{u}′′(t). \nonumber \]

   Lembre-se de que o produto cruzado de qualquer vetor consigo mesmo é zero. Além disso,\(\vecs u′′(t)\) representa a segunda derivada de\(\vecs u(t):\)

   \[\vecs u′′(t)=\dfrac{d}{\,dt}[\vecs u′(t)]=\dfrac{d}{\,dt}[2t \,\mathbf{\hat{i}}+2 \,\mathbf{\hat{j}}+(3t^2−3) \,\mathbf{\hat{k}}]=2 \,\mathbf{\hat{i}}+6t \,\mathbf{\hat{k}}. \nonumber \]

   Portanto,

   \ [\ begin {align*}\ dfrac {d} {\, dt} [\ vecs u (t)\ times\ vecs u′( t)] &=0+ (t^2−3)\,\ hat {\ mathbf {i}} + (2t+4)\,\ hat {\ mathbf {j}} + (t^3−3t)\,\ hat {\ mathbf {k}})\ times (2\,\ hat {\ mathbf {i}} +6t\,\ hat {\ mathbf {k}})\\ [4pt]
   &=\ begin {vmatrix}\,\ hat {\ mathbf {i}} &\,\ hat {\ mathbf {j}} e\,\ hat {\ mathbf {k}}\\ t^2-3 e 2t+4 e t^3 -3t\\ 2 e 0 e 6t\ end {vmatrix}\\ [4pt]
   & =6t (2t+4)\,\ hat {\ mathbf {i}} − (6t (t^2−3) −2 (t^3−3t))\, chapéu {\ mathbf {j}} −2 (2t+4)\,\ hat {\ mathbf {k}}\\ [4pt]
   & =( 12t^2+24t)\,\ hat {\ mathbf {i}} + (12t−4t^3)\,\ hat {\ mathbf {j}} − (4t+8)\, \ hat {\ mathbf {k}}. \ end {align*}\]

Exercício\(\PageIndex{3}\)

\(\dfrac{d}{\,dt}[\vecs{r}(t)⋅ \vecs{r}′(t)]\)Calcule e\( \dfrac{d}{\,dt}[\vecs{u}(t) \times \vecs{r}(t)]\) para as funções com valores vetoriais:

• \(\vecs{r}(t)=\cos t \,\mathbf{\hat{i}}+ \sin t \,\mathbf{\hat{j}}−e^{2t} \,\mathbf{\hat{k}}\)
• \(\vecs{u}(t)=t \,\mathbf{\hat{i}}+ \sin t \,\mathbf{\hat{j}}+ \cos t \,\mathbf{\hat{k}}\),

Dica

Siga as mesmas etapas do exemplo\(\PageIndex{3}\).

Resposta

\(\dfrac{d}{\,dt}[\vecs{r}(t)⋅ \vecs{r}′(t)]=8e^{4t}\)

\( \dfrac{d}{\,dt}[ \vecs{u}(t) \times \vecs{r}(t)] =−(e^{2t}(\cos t+2 \sin t)+ \cos 2t) \,\mathbf{\hat{i}}+(e^{2t}(2t+1)− \sin 2t) \,\mathbf{\hat{j}}+(t \cos t+ \sin t− \cos 2t) \,\mathbf{\hat{k}}\)

Vetores tangentes e vetores tangentes unitários

Lembre-se de que a derivada em um ponto pode ser interpretada como a inclinação da reta tangente ao gráfico nesse ponto. No caso de uma função com valor vetorial, a derivada fornece um vetor tangente à curva representada pela função. Considere a função com valor vetorial

\[\vecs{r}(t)=\cos t \,\mathbf{\hat{i}} + \sin t \,\mathbf{\hat{j}} \label{eq10} \]

A derivada dessa função é

\[\vecs{r}′(t)=−\sin t \,\mathbf{\hat{i}} + \cos t \,\mathbf{\hat{j}} \nonumber \]

Se substituirmos o valor\(t=π/6\) em ambas as funções, obtemos

\[\vecs{r} \left(\dfrac{π}{6}\right)=\dfrac{\sqrt{3}}{2} \,\mathbf{\hat{i}}+\dfrac{1}{2}\,\mathbf{\hat{j}} \nonumber \]

e

\[ \vecs{r}′ \left(\dfrac{π}{6} \right)=−\dfrac{1}{2}\,\mathbf{\hat{i}}+\dfrac{\sqrt{3}}{2}\,\mathbf{\hat{j}}. \nonumber \]

O gráfico dessa função aparece na Figura\(\PageIndex{1}\), junto com os vetores\(\vecs{r}\left(\dfrac{π}{6}\right)\)\(\vecs{r}' \left(\dfrac{π}{6}\right)\) e.

Figura\(\PageIndex{1}\): A reta tangente em um ponto é calculada a partir da derivada da função com valor vetorial\(\vecs{r}(t)\).

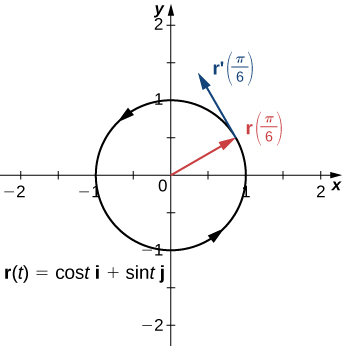
Observe que o vetor\(\vecs{r}′\left(\dfrac{π}{6}\right)\) é tangente ao círculo no ponto correspondente\(t=\dfrac{π}{6}\) a. Este é um exemplo de vetor tangente à curva plana definida pela Equação\ ref {eq10}.

Definição: vetor tangente unitário principal

\(C\)Seja uma curva definida por uma função com valor vetorial\(\vecs{r}\), e suponha que\(\vecs{r}′(t)\) exista quando\(\mathrm{t=t_0}\) um vetor tangente\(\vecs{r}\) em\(t=t_0\) é qualquer vetor tal que, quando a cauda do vetor é colocada em um ponto\(\vecs r(t_0)\) no gráfico, o vetor\(\vecs{r}\) é tangente à curva \(C\). Vector\(\vecs{r}′(t_0)\) é um exemplo de vetor tangente em um ponto\(t=t_0\). Além disso, suponha que\(\vecs{r}′(t)≠0\). O vetor tangente unitário principal at\(t\) é definido como

\[\vecs{T}(t)=\dfrac{ \vecs{r}′(t)}{‖\vecs{r}′(t)‖}, \nonumber \]

fornecido\(‖\vecs{r}′(t)‖≠0\).

O vetor tangente unitário é exatamente o que parece: um vetor unitário tangente à curva. Para calcular um vetor tangente unitário, primeiro encontre a derivada\(\vecs{r}′(t)\). Em segundo lugar, calcule a magnitude da derivada. O terceiro passo é dividir a derivada por sua magnitude.

Exemplo\(\PageIndex{4}\): Finding a Unit Tangent Vector

Encontre o vetor tangente unitário para cada uma das seguintes funções com valor vetorial:

1. \(\vecs{r}(t)=\cos t \,\mathbf{\hat{i}}+\sin t \,\mathbf{\hat{j}}\)
2. \(\vecs{u}(t)=(3t^2+2t) \,\mathbf{\hat{i}}+(2−4t^3)\,\mathbf{\hat{j}}+(6t+5)\,\mathbf{\hat{k}}\)

Solução

1. \(\begin{array}{lrcl} \text{First step:} & \vecs r′(t) & = & − \sin t \,\hat{\mathbf{i}}+ \cos t \,\hat{\mathbf{j}} \\ \text{Second step:} & ‖\vecs r′(t)‖ & = & \sqrt{(− \sin t)^2+( \cos t)^2} = 1 \\ \text{Third step:} & \vecs T(t) & = & \dfrac{\vecs r′(t)}{‖\vecs r′(t)‖}=\dfrac{− \sin t \,\hat{\mathbf{i}}+ \cos t \,\hat{\mathbf{j}}}{1}=− \sin t \,\hat{\mathbf{i}}+ \cos t \,\hat{\mathbf{j}} \end{array}\)
2. \(\begin{array}{lrcl} \text{First step:} & \vecs r′(t) & = & (6t+2) \,\hat{\mathbf{i}}−12t^2 \,\hat{\mathbf{j}}+6 \,\hat{\mathbf{k}} \\ \text{Second step:} & ‖\vecs r′(t)‖ & = & \sqrt{(6t+2)^2+(−12t^2)^2+6^2} \\ \text{} & \text{} & = & \sqrt{144t^4+36t^2+24t+40} \\ \text{} & \text{} & = & 2 \sqrt{36t^4+9t^2+6t+10} \\ \text{Third step:} & \vecs T(t) & = & \dfrac{\vecs r′(t)}{‖\vecs r′(t)‖}=\dfrac{(6t+2) \,\hat{\mathbf{i}}−12t^2 \,\hat{\mathbf{j}}+6 \,\hat{\mathbf{k}}}{2 \sqrt{36t^4+9t^2+6t+10}} \\ \text{} & \text{} & = & \dfrac{3t+1}{\sqrt{36t^4+9t^2+6t+10}} \,\hat{\mathbf{i}} - \dfrac{6t^2}{\sqrt{36t^4+9t^2+6t+10}} \,\hat{\mathbf{j}} + \dfrac{3}{\sqrt{36t^4+9t^2+6t+10}} \,\hat{\mathbf{k}} \end{array}\)

Exercício\(\PageIndex{4}\)

Encontre o vetor tangente unitário para a função com valor vetorial

\[\vecs r(t)=(t^2−3)\,\mathbf{\hat{i}}+(2t+1) \,\mathbf{\hat{j}}+(t−2) \,\mathbf{\hat{k}}. \nonumber \]

Dica

Siga as mesmas etapas do exemplo\(\PageIndex{4}\).

Resposta

\[\vecs T(t)=\dfrac{2t}{\sqrt{4t^2+5}}\,\mathbf{\hat{i}}+\dfrac{2}{\sqrt{4t^2+5}}\,\mathbf{\hat{j}}+\dfrac{1}{\sqrt{4t^2+5}}\,\mathbf{\hat{k}} \nonumber \]

Integrais de funções com valores vetoriais

Introduzimos antiderivadas de funções de valor real em Antiderivadas e integrais definidas de funções de valor real em The Definite Integral. Cada um desses conceitos pode ser estendido para funções com valores vetoriais. Além disso, assim como podemos calcular a derivada de uma função com valor vetorial diferenciando as funções dos componentes separadamente, podemos calcular a antiderivada da mesma maneira. Além disso, o Teorema Fundamental do Cálculo também se aplica a funções com valores vetoriais.

A antiderivada de uma função com valor vetorial aparece nas aplicações. Por exemplo, se uma função com valor vetorial representa a velocidade de um objeto no tempo t, sua antiderivada representa a posição. Ou, se a função representa a aceleração do objeto em um determinado momento, a antiderivada representa sua velocidade.

Definição: Integrais definidas e indefinidas de funções com valor vetorial

Seja\(f\)\(g\), e\(h\) seja funções de valor real integráveis no intervalo fechado\([a,b].\)

1. A integral indefinida de uma função com valor vetorial\(\vecs{r}(t)=f(t) \,\hat{\mathbf{i}}+g(t) \,\hat{\mathbf{j}}\) é

   \[\int [f(t) \,\hat{\mathbf{i}}+g(t) \,\hat{\mathbf{j}}]\,dt= \left[ \int f(t)\,dt \right] \,\hat{\mathbf{i}}+ \left[ \int g(t)\,dt \right] \,\hat{\mathbf{j}}. \nonumber \]

   A integral definida de uma função com valor vetorial é

   \[\int_a^b [f(t) \,\hat{\mathbf{i}}+g(t) \,\hat{\mathbf{j}}]\,dt = \left[ \int_a^b f(t)\,dt \right] \,\hat{\mathbf{i}}+ \left[ \int_a^b g(t)\,dt \right] \,\hat{\mathbf{j}}. \nonumber \]

2. A integral indefinida de uma função com valor vetorial\(\vecs r(t)=f(t) \,\hat{\mathbf{i}}+g(t) \,\hat{\mathbf{j}}+h(t) \,\hat{\mathbf{k}}\) é

   \[\int [f(t) \,\hat{\mathbf{i}}+g(t)\,\hat{\mathbf{j}} + h(t) \,\hat{\mathbf{k}}]\,dt= \left[ \int f(t)\,dt \right] \,\hat{\mathbf{i}}+ \left[ \int g(t)\,dt \right] \,\hat{\mathbf{j}} + \left[ \int h(t)\,dt \right] \,\hat{\mathbf{k}}. \nonumber \]

   A integral definitiva da função com valor vetorial é

   \[\int_a^b [f(t) \,\hat{\mathbf{i}}+g(t) \,\hat{\mathbf{j}} + h(t) \,\hat{\mathbf{k}}]\,dt= \left[ \int_a^b f(t)\,dt \right] \,\hat{\mathbf{i}}+ \left[ \int_a^b g(t)\,dt \right] \,\hat{\mathbf{j}} + \left[ \int_a^b h(t)\,dt \right] \,\hat{\mathbf{k}}. \nonumber \]

Como a integral indefinida de uma função com valor vetorial envolve integrais indefinidas das funções componentes, cada uma dessas integrais de componentes contém uma constante de integração. Todos eles podem ser diferentes. Por exemplo, no caso bidimensional, podemos ter

\[\int f(t)\,dt=F(t)+C_1 \; and \; \int g(t)\,dt=G(t)+C_2, \nonumber \]

onde\(F\) e\(G\) são antiderivadas de\(f\) e\(g\), respectivamente. Então

\ [\ begin {align*}\ int [f (t)\,\ hat {\ mathbf {i}} +g (t)\,\ hat {\ mathbf {j}}]\, dt &=\ left [\ int f (t)\, dt\ direita]\,\ hat {\ mathbf {i}} +\ left [\ int g (t)\, dt\ right]\,\ hat {\ mathbf {j}}\\ [4pt]
&= (F (t) +C_1)\,\ hat {\ mathbf {i}} + (G (t) +C_2)\,\ hat {\ mathbf {j}}\\ [4pt]
&=F (t)\,\ hat {\ mathbf {i}} +G (t)\,\ hat {\ mathbf {j}} +C_1\,\ hat {\ mathbf {i}} +C_2\,\ hat {\ mathbf {j}}\\ [4pt]
&= F (t)\,\ hat {\ mathbf {i}} +G (t)\,\ hat {\ mathbf {j}} +\ vecs {C}\ end {align*}\]

onde\(\vecs{C}=C_1 \,\hat{\mathbf{i}}+C_2 \,\hat{\mathbf{j}}\). Portanto, as constantes de integração se tornam um vetor constante.

Exemplo\(\PageIndex{5}\): Integrating Vector-Valued Functions

Calcule cada uma das seguintes integrais:

1. \( \displaystyle \int [(3t^2+2t) \,\hat{\mathbf{i}}+(3t−6) \,\hat{\mathbf{j}}+(6t^3+5t^2−4) \,\hat{\mathbf{k}}]\,dt\)
2. \( \displaystyle \int [⟨t,t^2,t^3⟩ \times ⟨t^3,t^2,t⟩] \,dt\)
3. \( \displaystyle \int_{0}^{\frac{\pi}{3}} [\sin 2t \,\hat{\mathbf{i}}+ \tan t \,\hat{\mathbf{j}}+e^{−2t} \,\hat{\mathbf{k}}]\,dt\)

Solução

1. Usamos a primeira parte da definição da integral de uma curva espacial:
2. \ [\ begin {align*}\ int [(3t^2+2t)\,\ hat {\ mathbf {i}} + (3t−6)\,\ hat {\ mathbf {j}} + (6t^3+5t^2−4)\,\ hat {\ mathbf {k}}]\, dt &=\ left [\ int 3" t^2+2t\, dt\ right]\,\ hat {\ mathbf {i}} +\ left [\ int 3t−6\, dt\ right]\,\ hat {\ mathbf {j}} +\ left [\ int 6t^3+5t^2−4\, dt\ direita]\,\ hat {\ mathbf {k}}\ [4pt]
   & =( t^3+t^2) \,\ hat {\ mathbf {i}} +\ left (\ frac {3} {2} t^2−6t\ direita)\,\ hat {\ mathbf {j}} +\ left (\ frac {3} {2} t^4+\ frac {5} {3} t^3−4t\ direita)\,\ hat {\ mathbf {k}} +\ vecs C.\ end {align*}\]
3. Primeiro calcule\(⟨t,t^2,t^3⟩ \times ⟨t^3,t^2,t⟩:\)

   \ [\ begin {align*} ⟨t, t^2, t^3⟩\ times ⟨t^3, t^2, t⟩ &=\ begin {vmatrix}\ hat {\ mathbf {i}} &\,\ hat {\ mathbf {j}} &\,\ hat {\ mathbf {k}}\\ t & t^2 & t^3\ t^3 e t^2 & t\ end {vmatrix}\\ [4pt]
   &= (t^2 (t) −t^3 (t^2))\,\ hat {\ mathbf {i}} − (t^2−t^3 (t^3))\,\ hat {\ mathbf {j}} + (t (t^2) −t ^2 (t^3))\,\ hat {\ mathbf {k}}\\ [4pt]
   & =( t^3−t^5)\,\ hat {\ mathbf {i}} + (t^6−t^2)\,\ hat {\ mathbf {j}} + (t^3−t^5)\,\ hat {\ mathbf {bf {k}}. \ end {align*}\ nonumber\]

   Em seguida, substitua isso de volta na integral e integre:

   \ [\ begin {align*}\ int [⟨t, t^2, t^3⟩\ times ⟨t^3, t^2, t⟩]\, dt &=\ int (t^3−t^5)\,\ hat {\ mathbf {i}} + (t^6−t^2)\,\ hat {\ mathbf {j}} + (t^3−t^2)\,\ hat {\ mathbf {j}} + (t^3−t^2) −t^5)\,\ hat {\ mathbf {k}}\, dt\\ [4pt]
   &=\ left (\ frac {t^4} {4} −\ frac {t^6} {6}\ direita)\,\ hat {\ mathbf {i}} +\ left (\ frac {t^7} {7} −\ frac {t^7} {7} −\ frac {t^5} 3} {3}\ direita)\,\ hat {\ mathbf {j}} +\ left (\ frac {t^4} {4} −\ frac {t^6} {6}\ direita)\,\ hat {\ mathbf {k}} +\ vecs C.\ end {align*}\]

4. Use a segunda parte da definição da integral de uma curva espacial:

   \ [\ begin {align*}\ int_0^ {\ frac {\ pi} {3}} [\ sin 2t\,\ hat {\ mathbf {i}} +\ tan t\,\ hat {\ mathbf {j}} +e^ {−2t}\,\ hat {\ mathbf {k}}]\, dt &=\ left [int\ _0^ {\ frac {π} {3}}\ sin 2t\, dt\ right]\,\ hat {\ mathbf {i}} +\ left [\ int_0^ {\ frac {π} {3}}\ tan t\, dt\ direita]\,\ hat {\ mathbf {j}} +\ left [\ int_0^ {\ frac {\ frac {π} {3}} e^ {−2t}\, dt\ right] \,\ hat {\ mathbf {k}}\\ [4pt]
   &= (-\ tfrac {1} {2}\ cos 2t)\ Big\ vert_ {0} ^ {π /3}\,\ hat {\ mathbf {i}} − (\ ln |\ cos t|)\ Big\ vert_ {0} ^ {π /3}\,\ hat {\ mathbf {j}} −\ left (\ tfrac {1} {2} e^ {−2t}\ direita)\ Big\ vert_ {0} ^ {π /3}\,\ hat {\ mathbf {k}}\\ [4pt]
   &=\ left (−\ tfrac {1} {2} cos\\ tfrac {2} cos\\ tfrac {2} π} {3} +\ tfrac {1} {2}\ cos 0\ right)\,\ hat {\ mathbf {i}} −\ left (\ ln\ left (\ cos\ tfrac {π} {3}\ direita) −\ ln (\ cos 0)\ direita)\,\ hat {\ mathbf {j}} −\ left (\ tfrac {1} {2} e^ −2π /3} −\ tfrac {1} {2} e^ {−2 (0)}\ direita)\,\ hat {\ mathbf {k}}\ [4pt]
   & =\ left (\ tfrac {1} {4} +\ tfrac {1} {2}\ direita)\,\ hat {\ mathbf {i}} − (−\ ln 2)\,\ hat {\ mathbf {j}} −\ left (\ tfrac {1} {2} e^ {−2π /3} −\ tfrac {1} {2}\ direita)\,\ hat {\ mathbf {k}}\\ [4pt]
   &=\ tfrac {3} {4}\,\ hat {\ mathbf {i}} +\ ln 2)\,\ hat {\ mathbf {j}} +\ left (\ tfrac {1} {2} −\ tfrac {1} {2} e^ {−2π /3}\ direita)\,\ hat {\ mathbf {k}}. \ end {align*}\]

Exercício\(\PageIndex{5}\)

Calcule a seguinte integral:

\[\int_1^3 [(2t+4) \,\mathbf{\hat{i}}+(3t^2−4t) \,\mathbf{\hat{j}}]\,dt \nonumber \]

Dica

Use a definição da integral definida de uma curva plana.

Resposta

\[\int_1^3 [(2t+4) \,\mathbf{\hat{i}}+(3t^2−4t) \,\mathbf{\hat{j}}]\,dt = 16 \,\mathbf{\hat{i}}+10 \,\mathbf{\hat{j}} \nonumber \]

Resumo

• Para calcular a derivada de uma função com valor vetorial, calcule as derivadas das funções do componente e coloque-as novamente em uma nova função com valor vetorial.
• Muitas das propriedades de diferenciação de funções escalares também se aplicam a funções com valores vetoriais.
• A derivada de uma função com valor vetorial também\(\vecs r(t)\) é um vetor tangente à curva. O vetor tangente unitário\(\vecs T(t)\) é calculado dividindo a derivada de uma função com valor vetorial por sua magnitude.
• A antiderivada de uma função com valor vetorial é encontrada encontrando as antiderivadas das funções componentes e, em seguida, juntando-as novamente em uma função com valor vetorial.
• A integral definida de uma função com valor vetorial é encontrada encontrando as integrais definidas das funções do componente e, em seguida, juntando-as novamente em uma função com valor vetorial.

Equações chave

• Derivada de uma função com valor vetorial\[\vecs r′(t) = \lim \limits_{\Delta t \to 0} \dfrac{\vecs r(t+\Delta t)−\vecs r(t)}{ \Delta t} \nonumber \]
• Vetor tangente unitário principal\[\vecs T(t)=\frac{\vecs r′(t)}{‖\vecs r′(t)‖} \nonumber \]
• Integral indefinida de uma função com valor vetorial\[\int [f(t) \,\mathbf{\hat{i}}+g(t)\,\mathbf{\hat{j}} + h(t) \,\mathbf{\hat{k}}]\,dt= \left[ \int f(t)\,dt \right] \,\mathbf{\hat{i}}+ \left[ \int g(t)\,dt \right] \,\mathbf{\hat{j}} + \left[ \int h(t)\,dt \right] \,\mathbf{\hat{k}}\nonumber \]
• Integral definida de uma função com valor vetorial\[\int_a^b [f(t) \,\mathbf{\hat{i}}+g(t) \,\mathbf{\hat{j}} + h(t) \,\mathbf{\hat{k}}]\,dt= \left[\int_a^b f(t)\,dt \right] \,\mathbf{\hat{i}}+ \left[ \int _a^b g(t)\,dt \right] \,\mathbf{\hat{j}} + \left[ \int _a^b h(t)\,dt \right] \,\mathbf{\hat{k}}\nonumber \]

Glossário

integral definida de uma função com valor vetorial

o vetor obtido calculando a integral definida de cada uma das funções componentes de uma determinada função com valor vetorial e, em seguida, usando os resultados como componentes da função resultante

derivada de uma função com valor vetorial

a derivada de uma função com valor vetorial\(\vecs{r}(t)\) é\(\vecs{r}′(t) = \lim \limits_{\Delta t \to 0} \frac{\vecs r(t+\Delta t)−\vecs r(t)}{ \Delta t}\), desde que o limite exista

integral indefinida de uma função com valor vetorial

uma função com valor vetorial com uma derivada que é igual a uma determinada função com valor vetorial

vetor tangente unitário principal

um vetor unitário tangente a uma curva C

vetor tangente

a\(\vecs{r}(t)\)\(t=t_0\) qualquer vetor de\(\vecs v\) forma que, quando a cauda do vetor é colocada\(\vecs r(t_0)\) no ponto do gráfico, o vetor\(\vecs{v}\) seja tangente à curva C