13.1: Funções com valores vetoriais e curvas espaciais
- Page ID
- 187843
- Escreva a equação geral de uma função com valor vetorial na forma de componente e na forma de vetor unitário.
- Reconheça equações paramétricas para uma curva espacial.
- Descreva a forma de uma hélice e escreva sua equação.
- Defina o limite de uma função com valor vetorial.
Nosso estudo de funções com valores vetoriais combina ideias de nosso exame anterior de cálculo de variável única com nossa descrição de vetores em três dimensões do capítulo anterior. Nesta seção, estendemos os conceitos dos capítulos anteriores e também examinamos novas ideias sobre curvas no espaço tridimensional. Essas definições e teoremas apoiam a apresentação do material no restante deste capítulo e também nos capítulos restantes do texto.
Definição de uma função com valor vetorial
Nosso primeiro passo no estudo do cálculo de funções com valor vetorial é definir o que exatamente é uma função com valor vetorial. Em seguida, podemos ver gráficos de funções com valores vetoriais e ver como eles definem curvas em duas e três dimensões.
Uma função com valor vetorial é uma função da forma
\[\vecs r(t)=f(t)\,\hat{\mathbf{i}}+g(t)\,\hat{\mathbf{j}} \; \; \text{or} \; \;\vecs r(t)=f(t)\,\hat{\mathbf{i}}+g(t)\,\hat{\mathbf{j}}+h(t)\,\hat{\mathbf{k}}, \nonumber \]
onde as funções do componente\(f\)\(g\), e\(h\), são funções de valor real do parâmetro\(t\). Funções com valores vetoriais também são escritas na forma
\[\vecs r(t)=⟨f(t),\,g(t)⟩ \; \; \text{or} \; \; \vecs r(t)=⟨f(t),\,g(t),\,h(t)⟩. \nonumber \]
Em ambos os casos, a primeira forma da função define uma função bidimensional com valor vetorial; a segunda forma descreve uma função tridimensional com valor vetorial.
O parâmetro\(t\) pode estar entre dois números reais:\(a≤t≤b\). Outra possibilidade é que o valor de\(t\) possa assumir todos os números reais. Por último, as próprias funções do componente podem ter restrições de domínio que impõem restrições ao valor de\(t\). Costumamos usar\(t\) como parâmetro porque\(t\) pode representar o tempo.
Para cada uma das seguintes funções com valores vetoriais\(\vecs r(0)\), avalie\(\vecs r(\frac{\pi}{2})\),\(\vecs r(\frac{2\pi}{3})\) e. Alguma dessas funções tem restrições de domínio?
- \(\vecs r(t)=4\cos t\,\hat{\mathbf{i}}+3\sin t\,\hat{\mathbf{j}}\)
- \(\vecs r(t)=3\tan t\,\hat{\mathbf{i}}+4 \sec t\,\hat{\mathbf{j}}+5t\,\hat{\mathbf{k}}\)
Solução
- Para calcular cada um dos valores da função, substitua o valor apropriado de\(t\) na função:
\ begin {align*}\ vecs r (0)\; = 4\ cos (0)\ hat {\ mathbf {i}} +3\ sin (0)\ hat {\ mathbf {j}}\ [4pt] =4\ hat {\ mathbf {i}} +0\ hat {\ mathbf {j}} =4\ hat {\ mathbf {j}} =4\ hat {\ mathbf {\ mathbf {j}} bf {i}}\\ [4pt]\ vecs r\ left (\ frac {\ pi} {2}\ right)\; = 4\ cos\ left (\ frac {π} {2}\ direita)\ hat {\ mathbf {i}} +3\ sin\ left (\ frac {π} {2}\ direita)\ hat {\ mathbf {j}}\\ [4pt] = 0\ hat {\ mathbf {i}} + 3\ hat {\ mathbf {j}} =3\ hat {\ mathbf {j}}\\ [4pt]\ vecs r\ left (\ frac {2\ pi} {3}\ direita)\; =4\ cos\ left (\ frac {2π} {3}\ direita)\ hat {\ mathbf {i}} +3\ sin\ left (\ frac {2π} {3}\ direita)\ hat {\ mathbf {j}}\\ [4pt] =4\ left (−\ tfrac {1} {2}\ direita)\ hat {\ mathbf {i}} +3\ left (\ tfrac {\ sqrt {3}} {2}\ direita)\ hat {\ mathbf {j}} =−2\ hat {\ mathbf {i}} +\ tfrac {3\ sqrt {3}} {2}\ hat {\ mathbf {j}}\ end {align*}
Para determinar se essa função tem alguma restrição de domínio, considere as funções do componente separadamente. A primeira função do componente é\(f(t)=4 \cos t\) e a segunda função do componente é\(g(t)=3\sin t\). Nenhuma dessas funções tem uma restrição de domínio, então o domínio de\(\vecs r(t)=4\cos t\,\hat{\mathbf{i}}+3 \sin t \,\hat{\mathbf{j}}\) é todo números reais. - Para calcular cada um dos valores da função, substitua o valor apropriado de t na função:\[\begin{align*}\vecs r(0) \; = 3\tan(0)\hat{\mathbf{i}}+4\sec(0) \hat{\mathbf{j}}+5(0) \hat{\mathbf{k}} \\[4pt] = 0\hat{\mathbf{i}}+4j+0 \hat{\mathbf{k}}=4 \hat{\mathbf{j}} \\[4pt] \vecs r\left(\frac{\pi}{2}\right) \; = 3\tan\left(\frac{\pi}{2}\right)\hat{\mathbf{i}}+4\sec\left(\frac{\pi}{2}\right) \hat{\mathbf{j}}+5\left(\frac{\pi}{2}\right) \hat{\mathbf{k}},\,\text{which does not exist} \\[4pt] \vecs r\left(\frac{2\pi}{3}\right) \; =3\tan\left(\frac{2 \pi}{3}\right)\hat{\mathbf{i}}+4\sec\left(\frac{2\pi}{3}\right) \hat{\mathbf{j}}+5\left(\frac{2\pi}{ 3}\right) \hat{\mathbf{k}} \\[4pt] =3(−\sqrt{3})\hat{\mathbf{i}}+4(−2)\hat{\mathbf{j}}+\frac{10π}{3} \hat{\mathbf{k}} \\[4pt] =(-3\sqrt{3})\hat{\mathbf{i}}−8\hat{\mathbf{j}}+\frac{10π}{3} \hat{\mathbf{k}}\end{align*}\] Para determinar se essa função tem alguma restrição de domínio, considere as funções do componente separadamente. A primeira função do componente é\(f(t)=3\tan t\), a segunda função do componente é\(g(t)=4\sec t\) e a função do terceiro componente é\(h(t)=5t\). As duas primeiras funções não estão definidas para múltiplos ímpares de\(\frac{\pi}{2}\), então a função não está definida para múltiplos ímpares de\(\frac{\pi}{2}\). Portanto,\[\text{D}_{\vecs r}=\Big\{t\,|\,t≠ \frac{(2n+1)\pi}{2}\Big\},\nonumber \] onde\(n\) está qualquer número inteiro.
Para a função com valor vetorial\(\vecs r(t)=(t^2−3t) \,\hat{\mathbf{i}}+(4t+1) \,\hat{\mathbf{j}}\)\(\vecs r(0),\, \vecs r(1)\), avalie\(\vecs r(−4)\) e. Essa função tem alguma restrição de domínio?
- Dica
-
Substitua os valores apropriados de\(t\) na função.
- Resposta
-
\(\vecs r(0) = \hat{\mathbf{j}},\, \vecs r(1)=−2 \hat{\mathbf{i}}+5 \hat{\mathbf{j}},\, \vecs r(−4)=28 \hat{\mathbf{i}}−15 \hat{\mathbf{j}}\)
O domínio de\(\vecs r(t)=(t^2−3t)\hat{\mathbf{i}}+(4t+1)\hat{\mathbf{j}}\) são todos números reais.
O exemplo\(\PageIndex{1}\) ilustra um conceito importante. O domínio de uma função com valor vetorial consiste em números reais. O domínio pode ser todos números reais ou um subconjunto dos números reais. O intervalo de uma função com valor vetorial consiste em vetores. Cada número real no domínio de uma função com valor vetorial é mapeado para um vetor bidimensional ou tridimensional.
Representação gráfica de funções com valores vetoriais
Lembre-se de que um vetor plano consiste em duas quantidades: direção e magnitude. Dado qualquer ponto no plano (o ponto inicial), se nos movermos em uma direção específica por uma distância específica, chegaremos a um segundo ponto. Isso representa o ponto terminal do vetor. Calculamos os componentes do vetor subtraindo as coordenadas do ponto inicial das coordenadas do ponto terminal.
Um vetor é considerado na posição padrão se o ponto inicial estiver localizado na origem. Ao representar graficamente uma função com valor vetorial, normalmente representamos graficamente os vetores no domínio da função na posição padrão, porque isso garante a exclusividade do gráfico. Essa convenção também se aplica aos gráficos de funções tridimensionais com valores vetoriais. O gráfico de uma função vetorial da forma
\[\vecs r(t)=f(t)\, \hat{\mathbf{i}}+g(t)\,\hat{\mathbf{j}} \nonumber \]
consiste no conjunto de todos os pontos\((f(t),\,g(t))\), e o caminho que ele traça é chamado de curva plana. O gráfico de uma função vetorial da forma
\[\vecs r(t)=f(t) \,\hat{\mathbf{i}}+g(t) \,\hat{\mathbf{j}}+h(t) \,\hat{\mathbf{k}} \nonumber \]
consiste no conjunto de todos os pontos\((f(t),\,g(t),\,h(t))\), e o caminho que ele traça é chamado de curva espacial. Qualquer representação de uma curva plana ou curva espacial usando uma função com valor vetorial é chamada de parametrização vetorial da curva.
Cada curva plana e curva espacial tem uma orientação, indicada pelas setas desenhadas na curva, que mostra a direção do movimento ao longo da curva à medida que o valor do parâmetro\(t\) aumenta.
Crie um gráfico de cada uma das seguintes funções com valores vetoriais:
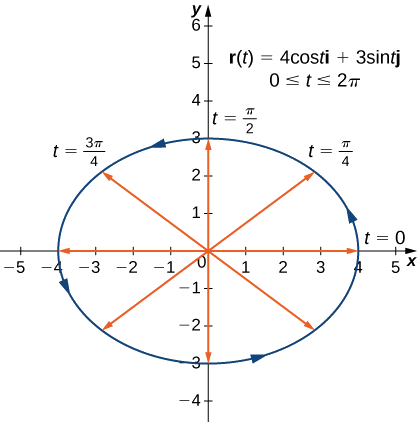
- A curva plana representada por\(\vecs r(t)=4 \cos t \,\hat{\mathbf{i}}+3 \sin t \,\hat{\mathbf{j}}\),\(0≤t≤2\pi\)
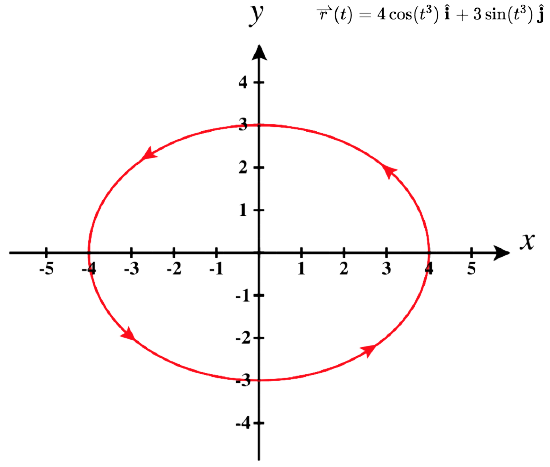
- A curva plana representada por\(\vecs r(t)=4 \cos(t^3) \,\hat{\mathbf{i}}+3 \sin(t^3) \,\hat{\mathbf{j}}\),\(0≤t≤\sqrt[3]{2\pi}\)
- A curva espacial representada por\(\vecs r(t)=4 \cos t \,\hat{\mathbf{i}}+4 \sin t \,\hat{\mathbf{j}}+t \,\hat{\mathbf{k}}\),\(0≤t≤4\pi\)
Solução
1. Como em qualquer gráfico, começamos com uma tabela de valores. Em seguida, representamos graficamente cada um dos vetores na segunda coluna da tabela na posição padrão e conectamos os pontos terminais de cada vetor para formar uma curva (Figura\(\PageIndex{1}\)). Essa curva acaba sendo uma elipse centrada na origem.
| \(t\) | \(\vecs r(t)\) | \(t\) | \(\vecs r(t)\) |
|---|---|---|---|
| \ (t\)” style="alinhamento vertical: médio; ">\(0\) | \ (\ vecs r (t)\)” style="alinhamento vertical: meio; ">\(4\hat{\mathbf{i}}\) | \ (t\)” style="alinhamento vertical: médio; ">\(\pi\) | \ (\ vecs r (t)\)” style="alinhamento vertical: meio; ">\(-4\hat{\mathbf{i}}\) |
| \ (t\)” style="alinhamento vertical: médio; ">\(\dfrac{\pi}{4}\) | \ (\ vecs r (t)\)” style="alinhamento vertical: meio; ">\(2 \sqrt{2} \hat{\mathbf{i}} + \frac{3 \sqrt{2}}{2}\hat{\mathbf{j}}\) | \ (t\)” style="alinhamento vertical: médio; ">\(\dfrac{5\pi}{4}\) | \ (\ vecs r (t)\)” style="alinhamento vertical: meio; ">\(-2 \sqrt{2} \hat{\mathbf{i}} - \frac{3 \sqrt{2}}{2}\hat{\mathbf{j}}\) |
| \ (t\)” style="alinhamento vertical: médio; ">\(\dfrac{\pi}{2}\) | \ (\ vecs r (t)\)” style="alinhamento vertical: meio; ">\(\mathrm{3\hat{\mathbf{j}}}\) | \ (t\)” style="alinhamento vertical: médio; ">\(\dfrac{3\pi}{2}\) | \ (\ vecs r (t)\)” style="alinhamento vertical: meio; ">\(\mathrm{-3\hat{\mathbf{j}}}\) |
| \ (t\)” style="alinhamento vertical: médio; ">\(\dfrac{3\pi}{4}\) | \ (\ vecs r (t)\)” style="alinhamento vertical: meio; ">\( -2 \sqrt{2} \hat{\mathbf{i}} + \frac{3 \sqrt{2}}{2}\hat{\mathbf{j}}\) | \ (t\)” style="alinhamento vertical: médio; ">\(\dfrac{7\pi}{4}\) | \ (\ vecs r (t)\)” style="alinhamento vertical: meio; ">\( 2 \sqrt{2} \hat{\mathbf{i}} - \frac{3 \sqrt{2}}{2}\hat{\mathbf{j}}\) |
| \ (t\)” style="alinhamento vertical: médio; ">\(2\pi\) | \ (\ vecs r (t)\)” style="alinhamento vertical: meio; ">\(4\hat{\mathbf{i}}\) | \ (t\)” style="alinhamento vertical: médio; "> | \ (\ vecs r (t)\)” style="alinhamento vertical: meio; "> |
2. A tabela de valores para\(\vecs r(t)=4 \cos(t^3) \,\hat{\mathbf{i}}+3 \sin(t^3) \,\hat{\mathbf{j}}\),\(0≤t≤\sqrt[3]{2\pi}\) é a seguinte:
| \(t\) | \(\vecs r(t)\) | \(t\) | \(\vecs r(t)\) |
|---|---|---|---|
| \ (t\)” style="alinhamento vertical: médio; ">\(0\) | \ (\ vecs r (t)\)” style="alinhamento vertical: meio; ">\(\mathrm{4\hat{\mathbf{i}}}\) | \ (t\)” style="alinhamento vertical: médio; ">\(\displaystyle\sqrt[3]{\pi}\) | \ (\ vecs r (t)\)” style="alinhamento vertical: meio; ">\(\mathrm{-4\hat{\mathbf{i}}}\) |
| \ (t\)” style="alinhamento vertical: médio; ">\(\displaystyle \sqrt[3]{\dfrac{\pi}{4}}\) | \ (\ vecs r (t)\)” style="alinhamento vertical: meio; ">\(\mathrm{ 2 \sqrt{2} \hat{\mathbf{i}} + \frac{3 \sqrt{2}}{2}\hat{\mathbf{j}}}\) | \ (t\)” style="alinhamento vertical: médio; ">\(\displaystyle \sqrt[3]{\dfrac{5\pi}{4}}\) | \ (\ vecs r (t)\)” style="alinhamento vertical: meio; ">\(\mathrm{ -2 \sqrt{2} \hat{\mathbf{i}} - \frac{3 \sqrt{2}}{2}\hat{\mathbf{j}}}\) |
| \ (t\)” style="alinhamento vertical: médio; ">\(\displaystyle \sqrt[3]{\dfrac{\pi}{2}}\) | \ (\ vecs r (t)\)” style="alinhamento vertical: meio; ">\(\mathrm{3\hat{\mathbf{j}}}\) | \ (t\)” style="alinhamento vertical: médio; ">\(\displaystyle \sqrt[3]{\dfrac{3\pi}{2}}\) | \ (\ vecs r (t)\)” style="alinhamento vertical: meio; ">\(\mathrm{-3\hat{\mathbf{j}}}\) |
| \ (t\)” style="alinhamento vertical: médio; ">\(\displaystyle \sqrt[3]{\dfrac{3\pi}{4}}\) | \ (\ vecs r (t)\)” style="alinhamento vertical: meio; ">\(\mathrm{ -2 \sqrt{2} \hat{\mathbf{i}} + \frac{3 \sqrt{2}}{2}\hat{\mathbf{j}}}\) | \ (t\)” style="alinhamento vertical: médio; ">\(\displaystyle \sqrt[3]{\dfrac{7\pi}{4}}\) | \ (\ vecs r (t)\)” style="alinhamento vertical: meio; ">\(\mathrm{ 2 \sqrt{2} \hat{\mathbf{i}} - \frac{3 \sqrt{2}}{2}\hat{\mathbf{j}}}\) |
| \ (t\)” style="alinhamento vertical: médio; ">\( \displaystyle\sqrt[3]{2\pi}\) | \ (\ vecs r (t)\)” style="alinhamento vertical: meio; ">\(\mathrm{4\hat{\mathbf{i}}}\) | \ (t\)” style="alinhamento vertical: médio; "> | \ (\ vecs r (t)\)” style="alinhamento vertical: meio; "> |
O gráfico dessa curva também é uma elipse centrada na origem.
3. Passamos pelo mesmo procedimento para uma função vetorial tridimensional.
| \(t\) | \(\vecs r(t)\) | \(t\) | \(\vecs r(t)\) |
|---|---|---|---|
| \ (t\)” style="alinhamento vertical: médio; ">\(\mathrm{0}\) | \ (\ vecs r (t)\)” style="alinhamento vertical: meio; ">\(\mathrm{4\hat{\mathbf{i}}}\) | \ (t\)” style="alinhamento vertical: médio; ">\(\mathrm{\pi}\) | \ (\ vecs r (t)\)” style="alinhamento vertical: meio; ">\(\mathrm{-4\hat{\mathbf{i}}}+ \pi \hat{\mathbf{k}}\) |
| \ (t\)” style="alinhamento vertical: médio; ">\(\dfrac{\pi}{4}\) | \ (\ vecs r (t)\)” style="alinhamento vertical: meio; ">\(\mathrm{2 \sqrt{2} \hat{\mathbf{i}} + 2\sqrt{2} \hat{\mathbf{j}} + \frac{\pi}{4} \hat{\mathbf{k}}}\) | \ (t\)” style="alinhamento vertical: médio; ">\(\dfrac{5\pi}{4}\) | \ (\ vecs r (t)\)” style="alinhamento vertical: meio; ">\(\mathrm{ -2 \sqrt{2} \hat{\mathbf{i}} - 2\sqrt{2} \hat{\mathbf{j}} + \frac{5\pi}{4} \hat{\mathbf{k}}}\) |
| \ (t\)” style="alinhamento vertical: médio; ">\(\dfrac{\pi}{2}\) | \ (\ vecs r (t)\)” style="alinhamento vertical: meio; ">\(\mathrm{4\hat{\mathbf{j}} +\frac{\pi}{2} \hat{\mathbf{k}}}\) | \ (t\)” style="alinhamento vertical: médio; ">\(\dfrac{3\pi}{2}\) | \ (\ vecs r (t)\)” style="alinhamento vertical: meio; ">\(\mathrm{-4\hat{\mathbf{j}} +\frac{3\pi}{2} \hat{\mathbf{k}}}\) |
| \ (t\)” style="alinhamento vertical: médio; ">\(\dfrac{3\pi}{4}\) | \ (\ vecs r (t)\)” style="alinhamento vertical: meio; ">\(\mathrm{ -2 \sqrt{2} \hat{\mathbf{i}} + 2\sqrt{2} \hat{\mathbf{j}} + \frac{3\pi}{4} \hat{\mathbf{k}}}\) | \ (t\)” style="alinhamento vertical: médio; ">\(\dfrac{7\pi}{4}\) | \ (\ vecs r (t)\)” style="alinhamento vertical: meio; ">\(\mathrm{ 2 \sqrt{2} \hat{\mathbf{i}} - 2\sqrt{2} \hat{\mathbf{j}} + \frac{7\pi}{4} \hat{\mathbf{k}}}\) |
| \ (t\)” style="alinhamento vertical: médio; ">\(\mathrm{2\pi}\) | \ (\ vecs r (t)\)” style="alinhamento vertical: meio; ">\(\mathrm{4\hat{\mathbf{j}} + 2\pi \hat{\mathbf{k}}}\) | \ (t\)” style="alinhamento vertical: médio; "> | \ (\ vecs r (t)\)” style="alinhamento vertical: meio; "> |
Os valores então se repetem, exceto pelo fato de que o coeficiente de\(\hat{\mathbf{k}}\) está sempre aumentando (\(\PageIndex{3}\)). Essa curva é chamada de hélice. Observe que, se o\(\hat{\mathbf{k}}\) componente for eliminado, a função se torna\(\vecs r(t)=4\cos t \hat{\mathbf{i}}+ 4\sin t \hat{\mathbf{j}}\), que é um círculo de raio 4 centrado na origem.

Você pode notar que os gráficos nas partes a. e b. são idênticos. Isso acontece porque a função que descreve a curva b é a chamada reparametrização da função que descreve a curva a. Na verdade, qualquer curva tem um número infinito de reparametrizações; por exemplo, podemos\(t\) substituir por\(2t\) em qualquer uma das três curvas anteriores sem alterar a forma de a curva. O intervalo no qual\(t\) é definido pode mudar, mas isso é tudo. Retornaremos a essa ideia mais adiante neste capítulo, quando estudamos a parametrização do comprimento do arco. Conforme mencionado, o nome da forma da curva do gráfico em\(\PageIndex{3}\) é uma hélice. A curva se assemelha a uma mola, com uma seção transversal circular voltada para baixo ao\(z\) longo do eixo. Também é possível que uma hélice seja elíptica na seção transversal. Por exemplo, a função com valor vetorial\(\vecs r(t)=4 \cos t \,\hat{\mathbf{i}}+3 \sin t \,\hat{\mathbf{j}}+t \,\hat{\mathbf{k}}\) descreve uma hélice elíptica. A projeção dessa hélice no\(xy\) plano -é uma elipse. Por último, as setas no gráfico dessa hélice indicam a orientação da curva à\(t\) medida que avança de\(0\) para\(4π\).
Crie um gráfico da função com valor vetorial\(\vecs r(t)=(t^2−1)\hat{\mathbf{i}}+(2t−3) \hat{\mathbf{j}}\),\(0≤t≤3\).
- Dica
-
Comece fazendo uma tabela de valores e, em seguida, represente graficamente os vetores para cada valor de\(t\).
- Resposta
-
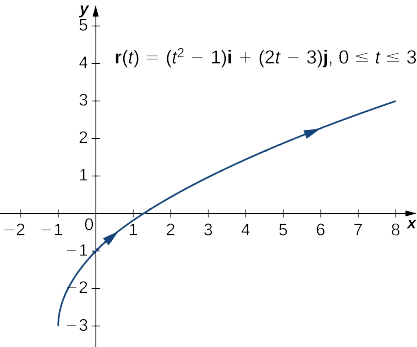
Nesse ponto, você pode notar uma semelhança entre funções com valores vetoriais e curvas parametrizadas. De fato, dada uma função com valor vetorial,\(\vecs r(t)=f(t)\,\hat{\mathbf{i}}+g(t)\,\hat{\mathbf{j}}\) podemos definir\(x=f(t)\)\(y=g(t)\) e. Se existir uma restrição nos valores de\(t\) (por exemplo,\(t\) estiver restrita ao intervalo\([a,b]\) de algumas constantes)\(a<b\), essa restrição será aplicada ao parâmetro. O gráfico da função parametrizada então concordaria com o gráfico da função com valor vetorial, exceto que o gráfico com valor vetorial representaria vetores em vez de pontos. Como podemos parametrizar uma curva definida por uma função\(y=f(x)\), também é possível representar uma curva plana arbitrária por uma função com valor vetorial.
Limites e continuidade de uma função com valor vetorial
Agora vamos dar uma olhada no limite de uma função com valor vetorial. É importante entender isso para estudar o cálculo de funções com valores vetoriais.
Uma função com valor vetorial\(\vecs r\) se aproxima do limite à\(\vecs L\) medida que\(t\) se aproxima\(a\), escrita
\[\lim \limits_{t \to a} \vecs r(t) = \vecs L, \nonumber \]
fornecido
\[\lim \limits_{t \to a} \big\| \vecs r(t) - \vecs L \big\| = 0. \nonumber \]
Essa é uma definição rigorosa do limite de uma função com valor vetorial. Na prática, usamos o seguinte teorema:
Seja\(f\)\(g\), e\(h\) seja funções de\(t\). Então, o limite da função com valor vetorial\(\vecs r(t)=f(t) \hat{\mathbf{i}}+g(t) \hat{\mathbf{j}}\) quando t se aproxima de a é dado por
\[\lim \limits_{t \to a} \vecs r(t) = [\lim \limits_{t \to a} f(t)] \hat{\mathbf{i}} + [\lim \limits_{t \to a} g(t)] \hat{\mathbf{j}} , \label{Th1} \]
forneceu os limites\(\lim \limits_{t \to a} f(t)\) e\(\lim \limits_{t \to a} g(t)\) existe.
Da mesma forma, o limite da função com valor vetorial\(\vecs r(t)=f(t) \hat{\mathbf{i}}+g(t) \hat{\mathbf{j}}+h(t) \hat{\mathbf{k}}\) como\(t\) abordagens\(a\) é dado por
\[\lim \limits_{t \to a} \vecs r(t) = [\lim \limits_{t \to a} f(t)] \hat{\mathbf{i}} + [\lim \limits_{t \to a} g(t)] \hat{\mathbf{j}} +[\lim \limits_{t \to a} h(t)] \hat{\mathbf{k}} , \label{Th2} \]
forneceu os limites\(\lim \limits_{t \to a} f(t)\)\(\lim \limits_{t \to a} g(t)\) e\(\lim \limits_{t \to a} h(t)\) existe.
No exemplo a seguir, mostramos como calcular o limite de uma função com valor vetorial.
Para cada uma das seguintes funções com valores vetoriais, calcule\(\lim \limits_{t \to 3}\vecs r(t)\) para
- \(\vecs r(t)=(t^2−3t+4) \hat{\mathbf{i}}+(4t+3)\hat{\mathbf{j}}\)
- \(\vecs r(t)=\frac{2t−4}{t+1}\hat{\mathbf{i}}+\frac{t}{t^2+1} \hat{\mathbf{j}}+(4t−3) \hat{\mathbf{k}}\)
Solução
- Use Equation\ ref {Th1} e substitua o valor\(t=3\) nas duas expressões do componente:
\[ \begin{align*} \lim \limits_{t \to 3} \vecs r(t) \; = \lim \limits_{t \to 3} \left[(t^2−3t+4) \hat{\mathbf{i}} + (4t+3) \hat{\mathbf{j}}\right] \\[4pt] = \left[\lim \limits_{t \to 3} (t^2−3t+4)\right]\hat{\mathbf{i}}+\left[\lim \limits_{t \to 3} (4t+3)\right] \hat{\mathbf{j}} \\[4pt] = 4 \hat{\mathbf{i}}+15 \hat{\mathbf{j}} \end{align*}\]
- Use Equation\ ref {Th2} e substitua o valor\(t=3\) nas três expressões componentes:
\[ \begin{align*} \lim \limits_{t \to 3} \vecs r(t) \; = \lim \limits_{t \to 3}\left(\dfrac{2t−4}{t+1}\hat{\mathbf{i}}+\dfrac{t}{t^2+1}\hat{\mathbf{j}}+(4t−3) \hat{\mathbf{k}}\right) \\[4pt] = \left[\lim \limits_{t \to 3} \left(\dfrac{2t−4}{t+1}\right)\right]\hat{\mathbf{i}}+\left[\lim \limits_{t \to 3} \left(\dfrac{t}{t^2+1}\right)\right] \hat{\mathbf{j}} +\left[\lim \limits_{t \to 3} (4t−3)\right] \hat{\mathbf{k}} \\[4pt] = \tfrac{1}{2} \hat{\mathbf{i}}+\tfrac{3}{10}\hat{\mathbf{j}}+9 \hat{\mathbf{k}} \end{align*}\]
Calcule\(\lim \limits_{t \to 2} \vecs r(t)\) para a função\(\vecs r(t) = \sqrt{t^2 + 3t - 1}\,\hat{\mathbf{i}}−(4t-3)\hat{\mathbf{j}}− \sin \frac{(t+1)\pi}{2}\hat{\mathbf{k}}\)
- Dica
-
Use a Equação\ ref {Th2} do teorema anterior.
- Resposta
-
\[\lim \limits_{t \to 2} \vecs r(t) = 3\hat{\mathbf{i}}−5\hat{\mathbf{j}}+\hat{\mathbf{k}} \nonumber \]
Agora que sabemos como calcular o limite de uma função com valor vetorial, podemos definir a continuidade em um ponto para essa função.
Seja\(f\)\(g\), e\(h\) seja funções de\(t\). Então, a função com valor vetorial\(\vecs r(t)=f(t) \hat{\mathbf{i}}+g(t)\hat{\mathbf{j}}\) é contínua no ponto\(t=a\) se as três condições a seguir forem válidas:
- \(\vecs r(a)\)existe
- \(\lim \limits_{t \to a} \vecs r(t)\)existe
- \(\lim \limits_{t \to a} \vecs r(t) = \vecs r(a)\)
Da mesma forma, a função com valor vetorial\(\vecs r(t)=f(t) \hat{\mathbf{i}}+g(t)\hat{\mathbf{j}}+h(t)\hat{\mathbf{k}}\) é contínua no ponto\(t=a\) se as três condições a seguir forem válidas:
- \(\vecs r(a)\)existe
- \(\lim \limits_{t \to a} \vecs r(t)\)existe
- \(\lim \limits_{t \to a} \vecs r(t) = \vecs r(a)\)
Resumo
- Uma função com valor vetorial é uma função da forma\(\vecs r(t)=f(t) \hat{\mathbf{i}}+ g(t) \hat{\mathbf{j}}\) ou\(\vecs r(t)=f(t) \hat{\mathbf{i}}+g(t) \hat{\mathbf{j}}+h(t) \hat{\mathbf{k}}\), onde o componente funciona\(f\)\(g\), e\(h\) são funções de valor real do parâmetro\(t\).
- O gráfico de uma função vetorial da forma\(\vecs r(t)=f(t) \hat{\mathbf{i}}+g(t) \hat{\mathbf{j}}\) é chamado de curva plana. O gráfico de uma função vetorial da forma\(\vecs r(t)=f(t)\hat{\mathbf{i}}+g(t)\hat{\mathbf{j}}+h(t) \hat{\mathbf{k}}\) é chamado de curva espacial.
- É possível representar uma curva plana arbitrária por meio de uma função com valor vetorial.
- Para calcular o limite de uma função com valor vetorial, calcule os limites das funções do componente separadamente.
Equações chave
- Função com valor vetorial
\(\vecs r(t)=f(t) \hat{\mathbf{i}}+g(t) \hat{\mathbf{j}}\) ou\(\vecs r(t)=f(t) \hat{\mathbf{i}}+g(t) \hat{\mathbf{j}}+h(t) \hat{\mathbf{k}}\), ou\(\vecs r(t)=⟨f(t),g(t)⟩\) ou\(\vecs r(t)=⟨f(t),g(t),h(t)⟩\) - Limite de uma função com valor vetorial
\(\lim \limits_{t \to a} \vecs r(t) = [\lim \limits_{t \to a} f(t)] \hat{\mathbf{i}} + [\lim \limits_{t \to a} g(t)] \hat{\mathbf{j}}\) ou\(\lim \limits_{t \to a} \vecs r(t) = [\lim \limits_{t \to a} f(t)] \hat{\mathbf{i}} + [\lim \limits_{t \to a} g(t)] \hat{\mathbf{j}} + [\lim \limits_{t \to a} h(t)] \hat{\mathbf{k}}\)
Glossário
- funções do componente
- as funções componentes da função com valor vetorial\(\vecs r(t)=f(t)\hat{\mathbf{i}}+g(t)\hat{\mathbf{j}}\) são\(f(t)\) e\(g(t)\), e as funções componentes da função com valor vetorial\(\vecs r(t)=f(t)\hat{\mathbf{i}}+g(t)\hat{\mathbf{j}}+h(t)\hat{\mathbf{k}}\) são\(f(t)\),\(g(t)\) e\(h(t)\)
- hélice
- uma curva tridimensional em forma de espiral
- limite de uma função com valor vetorial
- uma função com valor vetorial\(\vecs r(t)\) tem um limite à\(\vecs L\) medida que\(a\) se\(t\) aproxima se\(\lim \limits{t \to a} \left| \vecs r(t) - \vecs L \right| = 0\)
- curva plana
- o conjunto de pares ordenados\((f(t),g(t))\) junto com suas equações paramétricas definidoras\(x=f(t)\) e\(y=g(t)\)
- reparametrização
- uma parametrização alternativa de uma determinada função com valor vetorial
- curva de espaço
- o conjunto de triplos ordenados\((f(t),g(t),h(t))\) junto com suas equações paramétricas definidoras\(x=f(t)\),\(y=g(t)\) e\(z=h(t)\)
- parametrização vetorial
- qualquer representação de um plano ou curva espacial usando uma função com valor vetorial
- função com valor vetorial
- uma função da forma\(\vecs r(t)=f(t)\hat{\mathbf{i}}+g(t)\hat{\mathbf{j}}\) ou\(\vecs r(t)=f(t)\hat{\mathbf{i}}+g(t)\hat{\mathbf{j}}+h(t)\hat{\mathbf{k}}\), onde o componente funciona\(f\)\(g\), e\(h\) são funções de valor real do parâmetro\(t\).
Contribuidores e atribuições
- Template:ContribOpenStaxCalc
- Edited by Paul Seeburger (Monroe Community College)


