12.6: Superfícies quádricas

Last updated
Save as PDF

Page ID: 187798

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

objetivos de aprendizagem

Identifique um cilindro como um tipo de superfície tridimensional.
Reconheça as principais características dos elipsoides, parabolóides e hiperbolóides.
Use traços para desenhar as interseções das superfícies quádricas com os planos coordenados.

Estamos explorando vetores e operações vetoriais no espaço tridimensional e desenvolvemos equações para descrever linhas, planos e esferas. Nesta seção, usamos nosso conhecimento de planos e esferas, que são exemplos de figuras tridimensionais chamadas superfícies, para explorar uma variedade de outras superfícies que podem ser representadas graficamente em um sistema de coordenadas tridimensional.

Identificando cilindros

A primeira superfície que examinaremos é o cilindro. Embora a maioria das pessoas pense imediatamente em um cachimbo oco ou em um canudo de refrigerante ao ouvir a palavra cilindro, aqui usamos o amplo significado matemático do termo. Como vimos, as superfícies cilíndricas não precisam ser circulares. Um duto de aquecimento retangular é um cilindro, assim como um tapete de ioga enrolado, cuja seção transversal é em forma de espiral.

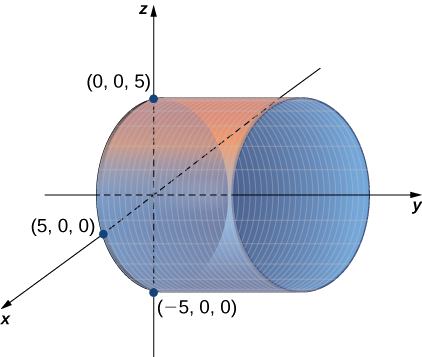
No plano de coordenadas bidimensional, a equação$ x^2+y^2=9$ descreve um círculo centrado na origem com raio$ 3$. No espaço tridimensional, essa mesma equação representa uma superfície. Imagine cópias de um círculo empilhado um sobre o outro centrado no$z$ eixo -( Figura$\PageIndex{1}$), formando um tubo oco. Podemos então construir um cilindro a partir do conjunto de linhas paralelas ao$z$ eixo -que passa pelo círculo$ x^2+y^2=9$ no$xy$ plano -, conforme mostrado na figura. Dessa forma, qualquer curva em um dos planos coordenados pode ser estendida para se tornar uma superfície.

Esta figura é um sistema de coordenadas tridimensional. Tem um centro circular reto com o eixo z passando pelo centro. O cilindro também tem pontos rotulados nos eixos x e y em (3, 0, 0) e (0, 3, 0). — Figura$\PageIndex{1}$: No espaço tridimensional, o gráfico da equação$ x^2+y^2=9$ é um cilindro com raio$ 3$$z$ centrado no eixo. Ele continua indefinidamente nas direções positiva e negativa.

Definição: cilindros e réguas

Um conjunto de linhas paralelas a uma determinada linha passando por uma determinada curva é conhecido como superfície cilíndrica ou cilindro. As linhas paralelas são chamadas de decisões.

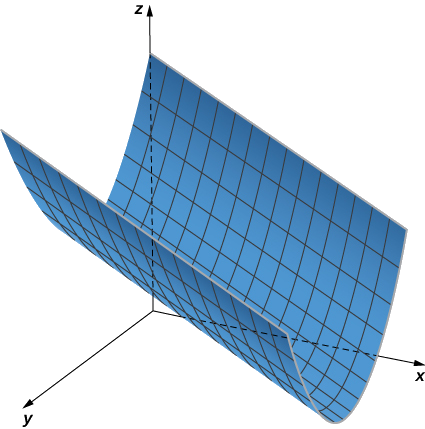
A partir dessa definição, podemos ver que ainda temos um cilindro no espaço tridimensional, mesmo que a curva não seja um círculo. Qualquer curva pode formar um cilindro, e as réguas que compõem o cilindro podem ser paralelas a qualquer linha dada (Figura$\PageIndex{2}$).

Esta figura tem uma superfície tridimensional que começa no eixo y e se curva para cima. Há também os eixos x e z rotulados. — Figura$\PageIndex{2}$: No espaço tridimensional, o gráfico da equação$ z=x^3$ é um cilindro ou uma superfície cilíndrica com réguas paralelas ao$y$ eixo.

Exemplo$ \PageIndex{1}$: Graphing Cylindrical Surfaces

Esboce os gráficos das seguintes superfícies cilíndricas.

$ x^2+z^2=25$
$ z=2x^2−y$
$ y=\sin x$

Solução

a. A variável$ y$ pode assumir qualquer valor sem limite. Portanto, as linhas que governam essa superfície são paralelas ao$y$ eixo y. A interseção dessa superfície com o$xz$ plano -forma um círculo centrado na origem com o raio$ 5$ (veja a Figura$\PageIndex{3}$).

Esta figura é o sistema de coordenadas tridimensional. Ele tem um cilindro circular reto em seu lado com o eixo y no centro. O cilindro cruza o eixo x em (5, 0, 0). Ele também tem dois pontos de interseção rotulados no eixo z em (0, 0, 5) e (0, 0, -5). — Figura$\PageIndex{3}$: O gráfico da equação$ x^2+z^2=25$ é um cilindro com raio$ 5$$y$ centrado no eixo.

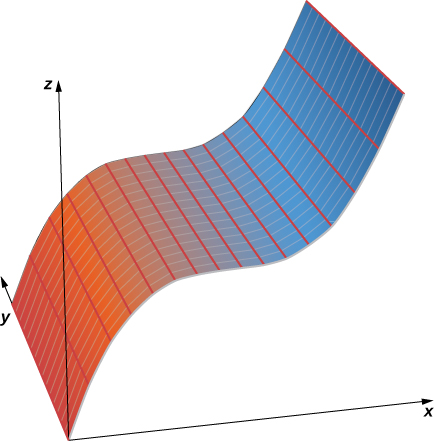
b. Nesse caso, a equação contém todas as três variáveis —$ x,y,$ e$ z$ — portanto, nenhuma das variáveis pode variar arbitrariamente. A maneira mais fácil de visualizar essa superfície é usar um utilitário de computação gráfica (Figura$\PageIndex{4}$).

Esta figura tem uma superfície no primeiro octante. A seção transversal do sólido é uma parábola. — Figura$\PageIndex{4}$

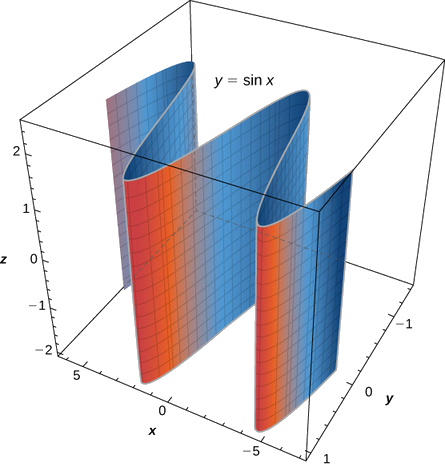
c. Nessa equação, a variável$ z$ pode assumir qualquer valor sem limite. Portanto, as linhas que compõem essa superfície são paralelas ao$z$ eixo y. A interseção dessa superfície com o plano xy contorna a curva$ y=\sin x$ (Figura$\PageIndex{5}$).

Esta figura é uma superfície tridimensional. Uma seção transversal da superfície paralela ao plano x y seria a curva senoidal. — Figura$\PageIndex{5}$: O gráfico da equação$ y=\sin x$ é formado por um conjunto de linhas paralelas ao$z$ eixo -passando pela curva$ y=\sin x$ no$xy$ plano.

Exercício$ \PageIndex{1}$:

Desenhe ou use uma ferramenta gráfica para visualizar o gráfico da superfície cilíndrica definida pela equação$ z=y^2$.

Dica: A variável$ x$ pode assumir qualquer valor sem limite.
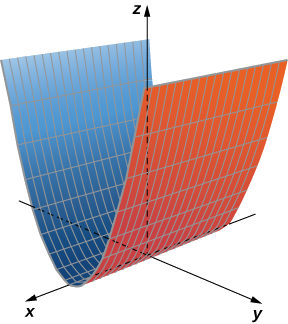
Responda: $Esta figura é uma superfície acima do plano x y. Uma seção transversal dessa superfície paralela ao plano y z seria uma parábola. A superfície fica no topo do plano x y.$

Ao desenhar superfícies, vimos que é útil esboçar a interseção da superfície com um plano paralelo a um dos planos coordenados. Essas curvas são chamadas de traços. Podemos vê-los no gráfico do cilindro na Figura$\PageIndex{6}$.

Definição: traços

Os traços de uma superfície são as seções transversais criadas quando a superfície cruza um plano paralelo a um dos planos coordenados.

Os traços são úteis para desenhar superfícies cilíndricas. Para um cilindro em três dimensões, porém, apenas um conjunto de traços é útil. Observe, na Figura$\PageIndex{6}$, que o traço do gráfico de$ z=\sin x$ no plano xz é útil na construção do gráfico. O traço no plano xy, no entanto, é apenas uma série de linhas paralelas, e o traço no plano yz é simplesmente uma linha.

Esta figura tem duas imagens. A primeira imagem é uma superfície. Uma seção transversal da superfície paralela ao plano x z seria uma curva senoidal. A segunda imagem é a curva senoidal no plano x y. — Figura$\PageIndex{6}$: (a) Essa é uma visão do gráfico da equação$ z=\sin x$. (b) Para encontrar o traço do gráfico no$xz$ plano -, defina$ y=0$. O traço é simplesmente uma onda senoidal bidimensional.

As superfícies cilíndricas são formadas por um conjunto de linhas paralelas. No entanto, nem todas as superfícies em três dimensões são construídas de forma tão simples. Agora exploramos superfícies mais complexas, e os traços são uma ferramenta importante nesta investigação.

Superfícies quadricas

Aprendemos sobre superfícies em três dimensões descritas por equações de primeira ordem; esses são planos. Alguns outros tipos comuns de superfícies podem ser descritos por equações de segunda ordem. Podemos ver essas superfícies como extensões tridimensionais das seções cônicas que discutimos anteriormente: a elipse, a parábola e a hipérbole. Chamamos esses gráficos de superfícies quádricas.

Definição: Superfícies quádricas e seções cônicas

Superfícies quádricas são os gráficos de equações que podem ser expressos na forma

\[Ax^2+By^2+Cz^2+Dxy+Exz+Fyz+Gx+Hy+Jz+K=0. \nonumber \]

Quando uma superfície quádrica cruza um plano coordenado, o traçado é uma seção cônica.

Um elipsóide é uma superfície descrita por uma equação da forma$ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}=1.$ Definida$ x=0$ para ver o traço do elipsóide no plano yz. Para ver os traços nos$xz$ planos$xy$ - e -, defina$ z=0$ e$ y=0$, respectivamente. Observe que, se$ a=b$, o traço no$xy$ plano -é um círculo. Da mesma forma$ a=c$, se, o traço no$xz$ plano -é um círculo e, se$ b=c$, então o traço no$yz$ plano -é um círculo. Uma esfera, então, é um elipsoide com$ a=b=c.$

Exemplo$ \PageIndex{2}$: Sketching an Ellipsoid

Esboce o elipsoide

\[ \dfrac{x^2}{2^2}+\dfrac{y^2}{3^2}+\dfrac{z^2}{5^2}=1. \nonumber \]

Solução

Comece desenhando os traços. Para encontrar o traço no plano xy, defina$ z=0: \dfrac{x^2}{2^2}+\dfrac{y^2}{3^2}=1$ (Figura$\PageIndex{7}$). Para encontrar os outros traços, primeiro defina$ y=0$ e depois defina$ x=0.$

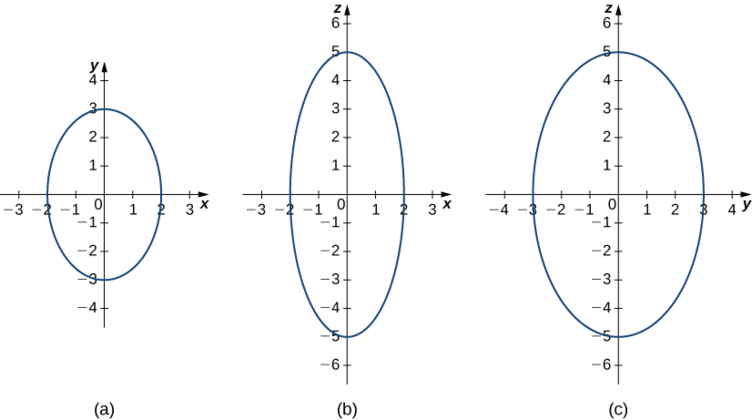
Esta figura tem três imagens. A primeira imagem é uma forma oval centrada em torno da origem do sistema de coordenadas retangulares. Ele cruza o eixo x em -2 e 2. Ele cruza o eixo y em -3 e 3. A segunda imagem é uma forma oval centrada em torno da origem do sistema de coordenadas retangulares. Ele cruza o eixo x em -2 e 2 e o eixo y em -5 e 5. A terceira imagem é uma forma oval centrada em torno da origem do sistema de coordenadas retangulares. Ele cruza o eixo x em -3 e 3 e o eixo y em -5 e 5. — Figura$\PageIndex{7}$: (a) Este gráfico representa o traço da equação$ \dfrac{x^2}{2^2}+\dfrac{y^2}{3^2}+\dfrac{z^2}{5^2}=1$ no$xy$ plano -, quando definimos$ z=0$. (b) Quando definimos$ y=0$, obtemos o traço do elipsóide no$xz$ plano -, que é uma elipse. (c) Quando definimos$ x=0$, obtemos o traço do elipsóide no$yz$ plano C, que também é uma elipse.

Agora que sabemos como são os traços desse sólido, podemos esboçar a superfície em três dimensões (Figura$\PageIndex{8}$).

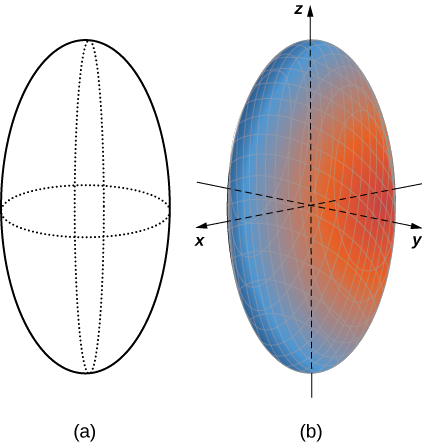
Esta figura tem duas imagens. A primeira imagem é uma elipse vertical. Há duas curvas desenhadas com linhas tracejadas ao redor do centro horizontal e verticalmente para dar à imagem uma forma tridimensional. A segunda imagem é uma forma elíptica sólida com o centro na origem do sistema de coordenadas tridimensional. — Figura$\PageIndex{8}$: (a) Os traços fornecem uma estrutura para a superfície. (b) O centro desse elipsoide é a origem.

O traço de um elipsoide é uma elipse em cada um dos planos coordenados. No entanto, isso não precisa ser o caso de todas as superfícies quádricas. Muitas superfícies quádricas têm traços que são diferentes tipos de seções cônicas, e isso geralmente é indicado pelo nome da superfície. Por exemplo, se uma superfície pode ser descrita por uma equação da forma

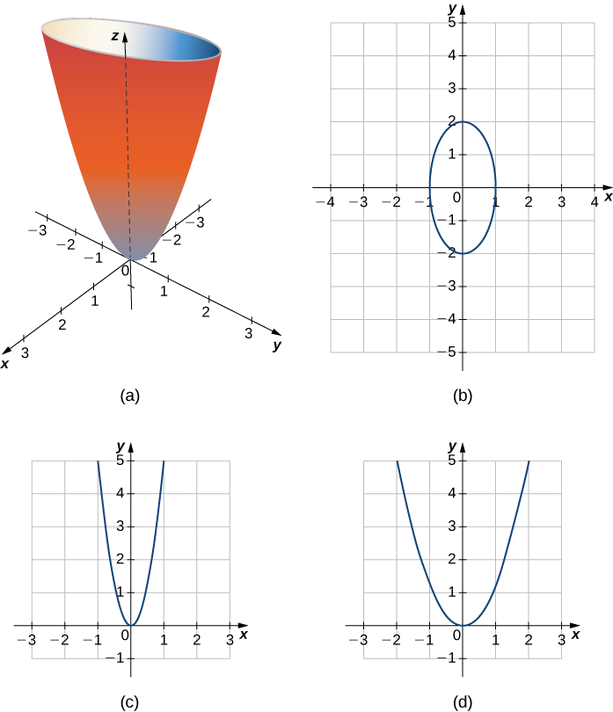
\[ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=\dfrac{z}{c} \nonumber \]

então chamamos essa superfície de parabolóide elíptico. O traço no plano xy é uma elipse, mas os traços no plano xz e no plano yz são parábolas (Figura$\PageIndex{9}$). Outros parabolóides elípticos podem ter outras orientações simplesmente trocando as variáveis para nos dar uma variável diferente no termo linear da equação$ \dfrac{x^2}{a^2}+\dfrac{z^2}{c^2}=\dfrac{y}{b}$ ou$ \dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}=\dfrac{x}{a}$.

Esta figura é a imagem de uma superfície. Está no sistema de coordenadas tridimensional no topo da origem. Uma seção transversal dessa superfície paralela ao plano x y seria uma elipse. — Figura$\PageIndex{9}$: Essa superfície quádrica é chamada de parabolóide elíptico.

Exemplo$ \PageIndex{3}$: Identifying Traces of Quadric Surfaces

Descreva os traços do parabolóide elíptico$ x^2+\dfrac{y^2}{2^2}=\dfrac{z}{5}$.

Solução

Para encontrar o traço no$xy$ plano -,$ z=0: x^2+\dfrac{y^2}{2^2}=0.$ defina O traço no plano$ z=0$ é simplesmente um ponto, a origem. Como um único ponto não nos diz qual é a forma, podemos subir o$z$ eixo -até um plano arbitrário para encontrar a forma de outros traços da figura.

O traço no plano$ z=5$ é o gráfico da equação$ x^2+\dfrac{y^2}{2^2}=1$, que é uma elipse. No$xz$ plano -, a equação se torna$ z=5x^2$. O traço é uma parábola nesse plano e em qualquer plano com a equação$ y=b$.

Em planos paralelos ao$yz$ plano -, os traços também são parábolas, como podemos ver na Figura$\PageIndex{10}$.

Esta figura tem quatro imagens. A primeira imagem é a imagem de uma superfície. Está no sistema de coordenadas tridimensional no topo da origem. Uma seção transversal dessa superfície paralela ao plano x y seria uma elipse. Uma seção transversal paralela ao plano x z seria uma parábola. Uma seção transversal da superfície paralela ao plano y z seria uma parábola. A segunda imagem é a seção transversal paralela ao plano x y e é uma elipse. A terceira imagem é a seção transversal paralela ao plano x z e é uma parábola. A quarta imagem é a seção transversal paralela ao plano y z e é uma parábola. — Figura$\PageIndex{10}$: (a) O parabolóide$ x^2+\dfrac{y^2}{2^2}=\dfrac{z}{5}$. (b) O traço no avião$ z=5$. (c) O traço no$xz$ plano. (d) O traço no$yz$ plano.

Exercício$ \PageIndex{2}$:

Um hiperbolóide de uma folha é qualquer superfície que possa ser descrita com uma equação da forma$ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=1$. Descreva os traços do hiperbolóide de uma folha dada pela equação$ \dfrac{x^2}{3^2}+\dfrac{y^2}{2^2}−\dfrac{z^2}{5^2}=1.$

Dica

Para encontrar os traços nos planos de coordenadas, defina cada variável como zero individualmente.

Responda

Os traços paralelos ao$xy$ plano -são elipses e os traços paralelos aos$yz$ planos$xz$ - e -são hipérboles. Especificamente, o traço no$xy$ plano -é elipse,$ \dfrac{x^2}{3^2}+\dfrac{y^2}{2^2}=1,$ o traço no$xz$ plano -é hipérbole$ \dfrac{x^2}{3^2}−\dfrac{z^2}{5^2}=1,$ e o traço no$yz$ plano -é hipérbole$ \dfrac{y^2}{2^2}−\dfrac{z^2}{5^2}=1$ (veja a figura a seguir).

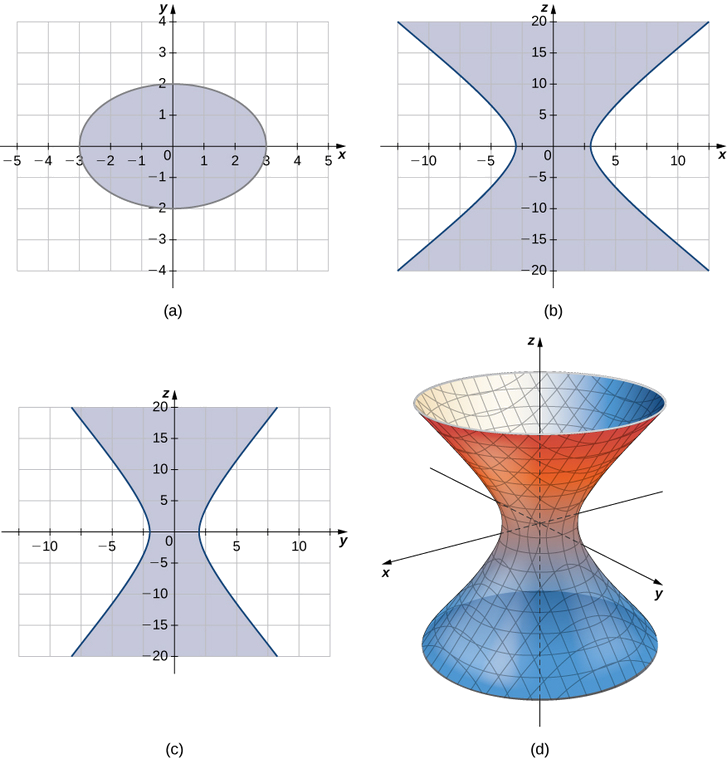
$Esta figura tem quatro imagens. A primeira imagem é uma elipse centrada na origem de um sistema de coordenadas retangulares. Ele cruza o eixo x em -3 e 3. Ele cruza o eixo y em -2 e 2. A segunda imagem é o gráfico de uma hipérbole. São duas curvas, uma abertura na direção x negativa e uma simétrica na direção x positiva. A terceira imagem é o gráfico de uma hipérbole no plano y z. Está abrindo na direção y negativa e uma curva simétrica se abrindo na direção y positiva. A quarta imagem é uma superfície tridimensional. Suas seções transversais superior e inferior seriam circulares. Uma interseção vertical seria uma hipérbole.$

Os hiperbolóides de uma folha têm algumas propriedades fascinantes. Por exemplo, eles podem ser construídos usando linhas retas, como na escultura na Figura$\PageIndex{11a}$. Na verdade, as torres de resfriamento de usinas nucleares geralmente são construídas na forma de um hiperbolóide. Os construtores são capazes de usar vigas de aço retas na construção, o que torna as torres muito fortes e usam relativamente pouco material (Figura$\PageIndex{11b}$).

Esta figura tem duas imagens. A primeira imagem é uma escultura feita de bastões paralelos, curvados juntos em um círculo com uma seção transversal hiperbólica. A segunda imagem é uma usina nuclear. As torres têm formato hiperbólico. — Figura$\PageIndex{11}$: (a) Uma escultura em forma de hiperbolóide pode ser construída com linhas retas. (b) As torres de resfriamento para usinas nucleares geralmente são construídas na forma de um hiperbolóide.

Exemplo$ \PageIndex{4}$: Chapter Opener: Finding the Focus of a Parabolic Reflector

A energia que atinge a superfície de um refletor parabólico é concentrada no ponto focal do refletor (Figura$\PageIndex{12}$). Se a superfície de um refletor parabólico for descrita pela equação,$ \dfrac{x^2}{100}+\dfrac{y^2}{100}=\dfrac{z}{4},$ onde está o ponto focal do refletor?

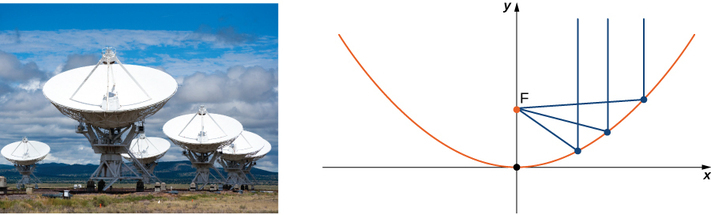
Esta figura tem duas imagens. A primeira imagem é uma foto de antenas parabólicas com refletores parabólicos. A segunda imagem é uma curva parabólica em um segmento de linha. A parte inferior da curva está no ponto V. Há um segmento de linha perpendicular ao outro segmento de linha até V. Há um ponto neste segmento de linha chamado F. Há 3 linhas de F à parábola, que se cruzam em P sub 1, P sub 2 e P sub 3. Há também três linhas verticais de P sub 1 a Q sub 1, de P sub 2 a Q sub 2 e de P sub 3 a Q sub 3. — Figura$\PageIndex{12}$: A energia reflete no refletor parabólico e é coletada no ponto focal. (crédito: modificação da CGP Grey, Wikimedia Commons)

Solução

Como z é a primeira variável de potência, o eixo do refletor corresponde ao$z$ eixo -. Os coeficientes do$ x^2$ and $ y^2$ are equal, so the cross-section of the paraboloid perpendicular to the $z$ eixo -são um círculo. Podemos considerar um traço no plano xz ou no plano yz; o resultado é o mesmo. Configuração$ y=0$, the trace is a parabola opening up along the $z$ do eixo -, com equação padrão$ x^2=4pz$, where $ p$ is the focal length of the parabola. In this case, this equation becomes $ x^2=100⋅\dfrac{z}{4}=4pz$ or $ 25=4p$. So p is $ 6.25$ m, which tells us that the focus of the paraboloid is $ 6.25$ m up the axis from the vertex. Because the vertex of this surface is the origin, the focal point is $ (0,0,6.25).$

Dezessete superfícies quádricas padrão podem ser derivadas da equação geral

\[Ax^2+By^2+Cz^2+Dxy+Exz+Fyz+Gx+Hy+Jz+K=0. \nonumber \]

As figuras a seguir resumem as mais importantes.

Esta figura é de uma tabela com duas colunas e três linhas. As três linhas representam as primeiras 6 superfícies quádricas: elipsoide, hiperbolóide de uma folha e hiperbolóide de duas folhas. As equações e traços estão na primeira coluna. A segunda coluna tem os gráficos das superfícies. O gráfico elipsoide é uma forma redonda oblonga vertical. O hiperbolóide de uma folha é circular na parte superior e inferior e estreito no meio. O hiperbolóide em duas folhas tem duas cúpulas parabólicas opostas uma à outra. — Figura$\PageIndex{13}$: Características das superfícies quádricas comuns: elipsoide, hiperbolóide de uma folha, hiperbolóide de duas folhas.

Esta figura é de uma tabela com duas colunas e três linhas. As três fileiras representam as segundas 6 superfícies quádricas: cone elíptico, parabolóide elíptico e parabolóide hiperbólico. As equações e traços estão na primeira coluna. A segunda coluna tem os gráficos das superfícies. O cone elíptico tem dois cones se tocando nas pontas. O parabolóide elíptico é semelhante a um cone, mas oblongo. O parabolóide hiperbólico tem uma curva no meio semelhante a uma sela. — Figura$\PageIndex{14}$: Características das superfícies quádricas comuns: cone elíptico, parabolóide elíptico, parabolóide hiperbólico.

Exemplo$ \PageIndex{5}$: Identifying Equations of Quadric Surfaces

Identifique as superfícies representadas pelas equações dadas.

$ 16x^2+9y^2+16z^2=144$
$ 9x^2−18x+4y^2+16y−36z+25=0$

Solução

a. Os$ z$ termos$ x,y,$ e estão todos ao quadrado e são todos positivos, então isso provavelmente é um elipsoide. No entanto, vamos colocar a equação na forma padrão de um elipsóide só para ter certeza. Nós temos

\[ 16x^2+9y^2+16z^2=144. \nonumber \]

Dividindo por 144 dá

\[ \dfrac{x^2}{9}+\dfrac{y^2}{16}+\dfrac{z^2}{9}=1. \nonumber \]

Então, isso é, na verdade, um elipsoide, centrado na origem.

b. Primeiro notamos que o$ z$ termo é elevado apenas à primeira potência, então este é um parabolóide elíptico ou um parabolóide hiperbólico. Também observamos que existem$ x$ termos e$ y$ termos que não são quadrados, portanto, essa superfície quádrica não está centrada na origem. Precisamos completar o quadrado para colocar essa equação em uma das formas padrão. Nós temos

\[ \begin{align*} 9x^2−18x+4y^2+16y−36z+25 =0 \\[4pt] 9x^2−18x+4y^2+16y+25 =36z \\[4pt] 9(x^2−2x)+4(y^2+4y)+25 =36z \\[4pt] 9(x^2−2x+1−1)+4(y^2+4y+4−4)+25 =36z \\[4pt] 9(x−1)^2−9+4(y+2)^2−16+25 =36z \\[4pt] 9(x−1)^2+4(y+2)^2 =36z \\[4pt] \dfrac{(x−1)^2}{4}+\dfrac{(y−2)^2}{9} =z. \end{align*}\]

Este é um parabolóide elíptico centrado em$ (1,2,0).$

Exercício$ \PageIndex{3}$

Identifique a superfície representada pela equação$ 9x^2+y^2−z^2+2z−10=0.$

Dica: Veja os sinais e poderes do$ x,y$, e$ z$ os termos
Responda: Hiperbolóide de uma folha, centrado em$ (0,0,1)$.

Conceitos-chave

Um conjunto de linhas paralelas a uma determinada linha passando por uma determinada curva é chamado de cilindro ou superfície cilíndrica. As linhas paralelas são chamadas de decisões.
A interseção de uma superfície tridimensional e um plano é chamada de traço. Para encontrar o traço nos planos $xy$$yz$-, - ou$xz$ -, defina$ z=0,x=0,$ ou$ y=0,$ respectivamente.
As superfícies quádricas são superfícies tridimensionais com traços compostos por seções cônicas. Cada superfície quádrica pode ser expressa com uma equação da forma

\[Ax^2+By^2+Cz^2+Dxy+Exz+Fyz+Gx+Hy+Jz+K=0. \nonumber \]

Para esboçar o gráfico de uma superfície quádrica, comece desenhando os traços para entender a estrutura da superfície.
Superfícies quádricas importantes estão resumidas nas figuras$\PageIndex{13}$$\PageIndex{14}$ e.

Glossário

cilindro: um conjunto de linhas paralelas a uma determinada linha passando por uma determinada curva

elipsoide: uma superfície tridimensional descrita por uma equação da forma$ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}=1$; todos os traços dessa superfície são elipses

cone elíptico: uma superfície tridimensional descrita por uma equação da forma$ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=0$; traços dessa superfície incluem elipses e linhas que se cruzam

parabolóide elíptico: uma superfície tridimensional descrita por uma equação da forma$ z=\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}$; traços dessa superfície incluem elipses e parábolas

hiperbolóide de uma folha: uma superfície tridimensional descrita por uma equação da forma,$ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=1;$ os traços dessa superfície incluem elipses e hipérboles.

hiperbolóide de duas folhas: uma superfície tridimensional descrita por uma equação da forma$ \dfrac{z^2}{c^2}−\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1$; traços dessa superfície incluem elipses e hipérboles

superfícies quádricas: superfícies em três dimensões com a propriedade de que os traços da superfície sejam seções cônicas (elipses, hipérboles e parábolas)

decisões: linhas paralelas que compõem uma superfície cilíndrica

vestígio: a interseção de uma superfície tridimensional com um plano coordenado

Definição: cilindros e réguas

Exemplo\( \PageIndex{1}\): Graphing Cylindrical Surfaces

Exercício\( \PageIndex{1}\):

Definição: traços

Definição: Superfícies quádricas e seções cônicas

Exemplo\( \PageIndex{2}\): Sketching an Ellipsoid

Exemplo\( \PageIndex{3}\): Identifying Traces of Quadric Surfaces

Exercício\( \PageIndex{2}\):

Exemplo\( \PageIndex{4}\): Chapter Opener: Finding the Focus of a Parabolic Reflector

Exemplo\( \PageIndex{5}\): Identifying Equations of Quadric Surfaces

Exercício\( \PageIndex{3}\)