12.5E: Exercícios para a Seção 12.5

Last updated
Save as PDF

Page ID: 187803

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Nos exercícios 1 a 4, pontos$ P$ e$ Q$ são dados. $ L$Seja a linha passando por pontos$ P$$ Q$ e.

a. Encontre a equação vetorial da linha$ L$.

b. Encontre equações paramétricas de linha$ L$.

c. Encontre equações simétricas de linha$ L$.

d. Encontre equações paramétricas do segmento de linha determinado por$ P$$ Q$ e.

1)$ P(−3,5,9), \quad Q(4,−7,2)$

Resposta: a.$\vecs r=⟨−3,5,9⟩+t⟨7,−12,−7⟩, \quad t∈R;$
b.$ x=−3+7t, \quad y=5−12t, \quad z=9−7t, \quad t∈R;$
c.$\dfrac{x+3}{7}=\dfrac{y−5}{−12}=\dfrac{z−9}{−7};$
d.$x=−3+7t, \quad y=5−12t, \quad z=9−7t, \quad 0 \le t \le 1$

2)$ P(4,0,5), \quad Q(2,3,1)$

3)$ P(−1,0,5), \quad Q(4,0,3)$

Resposta: a.$\vecs r=⟨−1,0,5⟩+t⟨5,0,−2⟩, \quad t∈R;$
b.$ x=−1+5t,y=0,z=5−2t, \quad t∈R;$
c.$\dfrac{x+1}{5}=\dfrac{z−5}{−2}, \quad y=0;$
d.$x=−1+5t, \quad y=0, \quad z=5−2t, \quad t∈[0,1]$

4)$ P(7,−2,6), \quad Q(−3,0,6)$

Para os exercícios 5 a 8, pontos$ P$ e vetores$\vecs v$ são fornecidos. $ L$Seja a linha que passa pelo ponto$ P$ com direção$\vecs v$.

a. Encontre equações paramétricas de linha$ L$.

b. Encontre equações simétricas de linha$ L$.

c. Encontre a interseção da linha com o$xy$ plano -.

5)$ P(1,−2,3),\,\vecs v=⟨1,2,3⟩$

Resposta: a.$x=1+t, \quad y=−2+2t, \quad z=3+3t, \quad t∈R;$
b.$ \dfrac{x−1}{1}=\dfrac{y+2}{2}=\dfrac{z−3}{3};$
c.$(0,−4,0)$

6)$ P(3,1,5), \,\vecs v=⟨1,1,1⟩$

7)$ P(3,1,5), \,\vecs v=\vecd{QR},$ onde$ Q(2,2,3)$ e$ R(3,2,3)$

Resposta: a.$x=3+t, \quad y=1, \quad z=5, \quad t∈R;$
b.$ y=1, \quad z=5;$
c. A linha não cruza o$xy$ plano.

8)$ P(2,3,0), \,\vecs v=\vecd{QR},$ onde$ Q(0,4,5)$ e$ R(0,4,6)$

Para os exercícios 9 e 10, a linha$ L$ é dada.

a. Encontre um ponto$ P$ que pertença à linha e um vetor$\vecs v$ de direção da linha. Expresse$\vecs v$ em forma de componente.

b. Encontre a distância da origem até a linha$ L$.

9)$ x=1+t, \quad y=3+t, \quad z=5+4t, \quad t∈R$

Resposta: a. Um possível vetor de ponto e direção é$P(1,3,5)$ e$\vecs v=⟨1,1,4⟩$, mas essas respostas não são únicas.
b.$ \sqrt{3} $ unidades

10)$ −x=y+1, \quad z=2$

11) Encontre a distância entre o ponto$ A(−3,1,1)$ e a linha das equações simétricas

$ x=−y=−z.$

Resposta: $ \frac{2\sqrt{2}}{\sqrt{3}} = \frac{2\sqrt{6}}{3} $unidades

12) Encontre a distância entre o ponto$ A(4,2,5)$ e a linha das equações paramétricas

$ x=−1−t, \; y=−t, \; z=2, \; t∈R.$

Para os exercícios 13 a 14, linhas$ L_1$ e 4$ L_2$ são dadas.

a. Verifique se as linhas$ L_1$ e B$ L_2$ são paralelas.

b. Se as linhas$ L_1$$ L_2$ forem paralelas, determine a distância entre elas.

13)$ L_1:x=1+t, \quad y=t, \quad z=2+t, \quad t∈R$ e$L_2:x−3=y−1=z−3$

Resposta: a. Paralelo;
b.$ \frac{\sqrt{2}}{\sqrt{3}} = \frac{\sqrt{6}}{3} $ unidades

14)$ L_1:x=2, \quad y=1, \quad z=t, \quad t∈R$ e$ L_2:x=1, \quad y=1, \quad z=2−3t, \quad t∈R$

15) Mostre que a linha que passa por pontos$ P(3,1,0)$ e$ Q(1,4,−3)$ é perpendicular à linha com a equação$ x=3t, \quad y=-32+8t, \quad z=−9+6t, \quad t∈R.$

Resposta: $ \vecd{PQ} = \langle -2, 3, -3 \rangle$é o vetor de direção da linha através de pontos$P$ e$Q$, e o vetor de direção da linha definido pelas equações paramétricas acima é$\vecs v = \langle 3, 8, 6 \rangle.$
Since$\vecs v \cdot \vecd{PQ} = -6 + 24 - 18 = 0$, os dois vetores de direção são ortogonais.
Agora, tudo o que precisamos mostrar é que as duas linhas se cruzam.
A linha passa por pontos$ P(3,1,0)$ e$ Q(1,4,−3)$ tem equações paramétricas:$x = 3 - 2u$$y = 1 + 3u$,,$z = -3u$ e.
Definindo as$z$ coordenadas$x$ - e -das duas linhas iguais, obtemos o sistema de equações:
\[3t = 3 - 2u \quad\text{and}\quad -9 + 6t = -3u \nonumber \]
Resolver esse sistema usando substituição nos dá,$u = -3$$t = 3$ e. Conectar esses valores$t$ e$u$ voltar às equações paramétricas dessas duas linhas nos dá o ponto de interseção com as coordenadas$\left(9, -8, 9\right)$ em ambas as linhas.
Portanto, as linhas se cruzam e a linha através de pontos$P$ e$Q$ com vetor de direção$\vecd{PQ} $ é perpendicular à outra linha.

16) As linhas das equações$ x=−2+2t, \quad y=−6, \quad z=2+6t, \quad t∈R$ são$ x=−1+t, \quad y=1+t, \quad z=t, \quad t∈R,$ perpendiculares entre si?

17) Encontre o ponto de interseção das linhas das equações$ x=−2y=3z$ e$ x=−5−t, \quad y=−1+t, \quad z=t−11, \quad t∈R.$

Resposta: $ (−12,6,−4)$

18) Encontre o ponto de interseção do$x$ eixo -com a linha das equações paramétricas$ x=10+t, \quad y=2−2t, \quad z=−3+3t, \quad t∈R.$

Para os exercícios 19 a 22, linhas$ L_1$ e 2$ L_2$ são dadas. Determine se as linhas são iguais, paralelas, mas não iguais, inclinadas ou se cruzam.

19)$ L_1:x=y−1=−z$ e$ L_2:x−2=−y=\dfrac{z}{2}$

Resposta: As linhas estão inclinadas.

20)$ L_1:x=2t, \quad y=0, \quad z=3, \quad t∈R$ e$ L_2:x=0, \quad y=8+s, \quad z=7+s, \quad s∈R$

21)$ L_1:x=−1+2t, \quad y=1+3t, \quad z=7t, \quad t∈R$ e$ L_2:x−1=\frac{2}{3}(y−4)=\frac{2}{7}z−2$

Resposta: As linhas são iguais.

22)$ L_1:3x=y+1=2z$ e$ L_2:x=6+2t, \quad y=17+6t, \quad z=9+3t, \quad t∈R$

23) Considere a linha$ L$ de equações simétricas$ x−2=−y=\dfrac{z}{2}$ e o ponto$ A(1,1,1).$

a. Encontre equações paramétricas para uma reta paralela à$ L$ que passa pelo ponto$ A$.

b. Encontre equações simétricas de uma reta inclinada para$ L$ e que passa pelo ponto$ A$.

c. Encontre equações simétricas de uma reta que se cruza$ L$ e passa pelo ponto$ A$.

Resposta: a.$x=1+t, \quad y=1−t, \quad z=1+2t, \quad t∈R$
b. Por exemplo, a linha que passa$ A$ com o vetor de direção$ j:x=1,z=1$
c. Por exemplo, a linha que passa por$ A$ um ponto$ (2,0,0)$ que pertence$ L$ é uma linha que se cruza;$ L:\frac{x−1}{−1}=y−1=z−1$

24) Considere a linha$ L$ de equações paramétricas$ x=t, \quad y=2t, \quad z=3, \quad t∈R.$

a. Encontre equações paramétricas para uma linha paralela à$ L$ que passa pela origem.

b. Encontre equações paramétricas de uma linha inclinada em relação à$ L$ que passa pela origem.

c. Encontre equações simétricas de uma linha que se cruza$ L$ e passa pela origem.

Para os exercícios 25 a 28, pontos$ P$ e vetores$\vecs n$ são fornecidos.

a. Encontre a equação escalar do plano que passa$ P$ e tem vetor normal$\vecs n$.

b. Encontre a forma geral da equação do plano que passa$ P$ e tem vetor normal$\vecs n$.

25)$ P(0,0,0), \quad \vecs n=3\mathbf{\hat i}−2\mathbf{\hat j}+4\mathbf{\hat k}$

Resposta: a.$3x−2y+4z=0$
b.$3x−2y+4z=0$

26)$ P(3,2,2), \quad \vecs n=2\mathbf{\hat i}+3\mathbf{\hat j}−\mathbf{\hat k}$

27)$ P(1,2,3), \quad \vecs n=⟨1,2,3⟩$

Resposta: a.$(x−1)+2(y−2)+3(z−3)=0$
b.$x+2y+3z−14=0$

28)$ P(0,0,0), \quad \vecs n=⟨−3,2,−1⟩$

Para os exercícios 29 a 32, a equação de um plano é dada.

a. Encontre o vetor$\vecs n$ normal do plano. Expresse$\vecs n$ usando vetores unitários padrão.

b. Encontre as interseções do plano com cada um dos eixos coordenados (suas interceptações).

c. Desenhe o avião.

29) [T]$ 4x+5y+10z−20=0$

Resposta

a.$\vecs n=4\mathbf{\hat i}+5\mathbf{\hat j}+10\mathbf{\hat k}$
b.$(5,0,0), \,(0,4,0),$ e$ (0,0,2)$

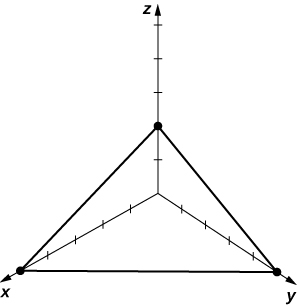
30)$ 3x+4y−12=0$

31)$ 3x−2y+4z=0$

Resposta

a.$\vecs n=3\mathbf{\hat i}−2\mathbf{\hat j}+4\mathbf{\hat k}$
b.$(0,0,0)$

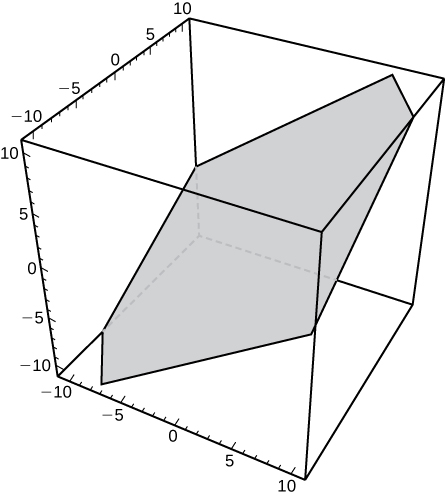
32)$ x+z=0$

33) Dado ponto$ P(1,2,3)$ e vetor$\vecs n=\mathbf{\hat i}+\mathbf{\hat j}$, encontre o ponto$ Q$ no$x$ eixo -de forma que$ \vecd{PQ}$ e$\vecs n$ sejam ortogonais.

Resposta: $ (3,0,0)$

34) Mostre que não há nenhum plano perpendicular ao$\vecs n=\mathbf{\hat i}+\mathbf{\hat j}$ que passe pelos pontos$ P(1,2,3)$$ Q(2,3,4)$ e.

35) Encontre equações paramétricas da reta que passa pelo ponto$ P(−2,1,3)$ que é perpendicular ao plano da equação$ 2x−3y+z=7.$

Resposta: $ x=−2+2t, \quad y=1−3t, \quad z=3+t, \quad t∈R$

36) Encontre equações simétricas da reta que passa pelo ponto$ P(2,5,4)$ que é perpendicular ao plano da equação$ 2x+3y−5z=0.$

37) Mostre que a linha$ \dfrac{x−1}{2}=\dfrac{y+1}{3}=\dfrac{z−2}{4}$ é paralela ao plano$ x−2y+z=6$.

38) Encontre o número real de$ α$ forma que a linha das equações paramétricas$ x=t, \quad y=2−t, \quad z=3+t, \quad t∈R$ seja paralela ao plano da equação$ αx+5y+z−10=0.$

Para os exercícios 39 a 42, as equações de dois planos são dadas.

a. Determine se os planos são paralelos, ortogonais ou nenhum deles.

b. Se os planos não forem paralelos nem ortogonais, então encontre a medida do ângulo entre os planos. Expresse a resposta em graus arredondados para o número inteiro mais próximo.

c. Se os planos se cruzarem, encontre a linha de interseção dos planos, fornecendo as equações paramétricas dessa linha.

39) [T]$ x+y+z=0, \quad 2x−y+z−7=0$

Resposta: a. Os planos não são nem paralelos nem ortogonais.
b.$62°$
c.$x = -1 + 2t$
$y = -4 + t$
$z = 5 - 3t$

40)$ 5x−3y+z=4, \quad x+4y+7z=1$

41)$ x−5y−z=1, \quad 5x−25y−5z=−3$

Resposta: a. Os planos são paralelos.

42) [T]$ x−3y+6z=4, \quad 5x+y−z=4$

Para os exercícios 43 a 46, determine se a linha dada se cruza com o plano dado. Se eles se cruzarem, indique o ponto de interseção.

43) Avião:$2x + y - z = 11$ Linha:$x = 1 + t, \quad y = 3 - 2t, \quad z = 2 +4t$

Resposta: Eles se cruzam no ponto$ (-1, 7, -6) $.

44) Avião:$-x + 2y + z = 2$ Linha:$x = 1 + 2t, \quad y = -2 + t, \quad z = 5 - 3t$

Resposta: Eles se cruzam no ponto$ \left(-\frac{1}{3}, \, -\frac{8}{3}, \, 7\right) $.

45) Avião:$x - 3y + 2z = 4$ Linha:$x = 2 - t, \quad y = t, \quad z = 4 +2t$

Resposta: A linha não se cruza com esse plano.

46) Avião:$x - 3y + 2z = 10$ Linha:$x = 2 - t, \quad y = t, \quad z = 4 +2t$

Resposta: A linha está, na verdade, totalmente contida nesse plano, então cada ponto da linha está no plano. Por exemplo, quando$t = 0$ temos o ponto,$(2, 0, 4)$.

47) Mostre que as linhas das equações$ \dfrac{x}{2}=\dfrac{y−1}{3}=z−3$ estão inclinadas$ x=t, \quad y=1+t, \quad z=2+t, \quad t∈R,$ e encontre a distância entre elas.

Resposta: $ \frac{1}{\sqrt{6}} = \frac{\sqrt{6}}{6}$unidades

48) Mostre que as linhas das equações$ x=5+s, \quad y=−8+2s, \quad z=7s, \quad s∈R$ estão inclinadas$ x=−1+t, \quad y=−2+t, \quad z=3t, \quad t∈R,$ e encontre a distância entre elas.

49) Considere o ponto$ C(−3,2,4)$ e o plano da equação$ 2x+4y−3z=8$.

a. Encontre o raio da esfera com o centro$C$ tangente ao plano dado.

b. Encontre o ponto$P$ de tangência.

Resposta: a.$r = \frac{18}{\sqrt{29}} = \frac{18\sqrt{29}}{29}$
b.$P\left(−\frac{51}{29},\frac{130}{29},\frac{62}{29}\right)$

50) Considere o plano da equação$ x−y−z−8=0.$

a. Encontre a equação da esfera com o centro$C$ na origem que é tangente ao plano dado.

b. Encontre equações paramétricas da reta que passa pela origem e pelo ponto de tangência.

51) Duas crianças estão brincando com uma bola. A garota joga a bola para o garoto. A bola viaja no ar, curva os$ 3$ pés para a direita e cai a$ 5$ pés de distância da garota (veja a figura a seguir). Se o plano que contém a trajetória da bola for perpendicular ao solo, encontre sua equação.

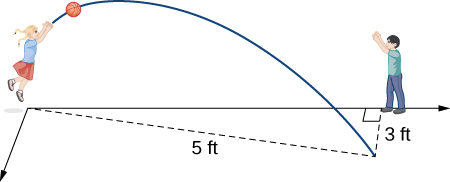
Resposta: $ 4x−3y=0$

52) [T] John aloca$ d$ dólares para consumir mensalmente três bens de preços$ a,b$,$ c$ e. Nesse contexto, a equação orçamentária é definida como$ ax+by+cz=d,$ onde$ x≥0,\, y≥0$ e$ z≥0$ representa o número de itens comprados de cada um dos bens. O orçamento definido é dado por$ \big\{(x,y,z)\,|\,ax+by+cz≤d,\;x≥0,\;y≥0,\;z≥0\big\},$ e o plano de orçamento é a parte do plano de equação$ ax+by+cz=d$ para o qual$ x≥0,\,y≥0$,$ z≥0$ e. Considere$ a=$8, \,b=$5, \,c=$10,$ e$ d=$500.$

a. Use um CAS para representar graficamente o conjunto de orçamento e o plano de orçamento.

b. Para$ z=25,$ encontrar a nova equação orçamentária e representar graficamente o orçamento definido no mesmo sistema de coordenadas.

53) [T] Considere$\vecs r(t)=⟨\sin t,\cos t,2t⟩$ o vetor de posição de uma partícula no momento$ t∈[0,3]$, onde os componentes de$\vecs r$ são expressos em centímetros e o tempo é medido em segundos. $ \vecd{OP}$Seja o vetor de posição da partícula após o$ 1$ segundo.

a. Determine o vetor$\vecs v(1)$ de velocidade da partícula após o$ 1$ segundo.

b. Encontre a equação escalar do plano que é perpendicular$ v(1)$ e passa pelo ponto$ P$. Esse plano é chamado de plano normal até o caminho da partícula no ponto$ P$.

c. Use um CAS para visualizar o caminho da partícula junto com o vetor de velocidade e o plano normal no ponto$ P$.

Resposta: a.$\vecs v(1)=⟨\cos 1,−\sin 1, 2⟩$
b.$ (\cos 1)(x−\sin 1)−(\sin 1)(y−\cos 1)+2(z−2)=0$
c.

54) [T] Um painel solar é montado no telhado de uma casa. O painel pode ser considerado posicionado nos pontos de coordenadas (em metros)$ A(8,0,0), \, B(8,18,0), \, C(0,18,8),$ e$ D(0,0,8)$ (veja a figura a seguir).

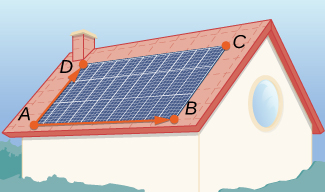
a. Encontre a forma geral da equação do plano que contém o painel solar usando pontos$ A, \, B,$ e$ C$, e mostre que seu vetor normal é equivalente a$ \vecd{AB}×\vecd{AD}.$

b. Encontre equações paramétricas da linha$ L_1$ que passa pelo centro do painel solar e tem um vetor de direção$\vecs s=\frac{1}{\sqrt{3}}\mathbf{\hat i}+\frac{1}{\sqrt{3}}\mathbf{\hat j}+\frac{1}{\sqrt{3}}\mathbf{\hat k},$ que aponta para a posição do Sol em uma determinada hora do dia.

c. Encontre equações simétricas de linha$ L_2$ que passam pelo centro do painel solar e são perpendiculares a ele.

d. Determine o ângulo de elevação do Sol acima do painel solar usando o ângulo entre as linhas$ L_1$$ L_2$ e.

Colaboradores

Template:ContribOpenStaxCalc

Problemas 15 e 43 - 46 criados por Paul Seeburger