12.5: Equações de retas e planos no espaço
- Page ID
- 187799
- Escreva as equações vetoriais, paramétricas e simétricas de uma linha através de um determinado ponto em uma determinada direção e uma linha através de dois pontos dados.
- Encontre a distância de um ponto até uma determinada linha.
- Escreva as equações vetoriais e escalares de um plano através de um determinado ponto com um determinado normal.
- Encontre a distância de um ponto até um determinado plano.
- Encontre o ângulo entre dois planos.
Agora, estamos familiarizados com a escrita de equações que descrevem uma linha em duas dimensões. Para escrever uma equação para uma reta, precisamos conhecer dois pontos na linha, ou devemos saber a direção da reta e pelo menos um ponto pelo qual a linha passa. Em duas dimensões, usamos o conceito de inclinação para descrever a orientação, ou direção, de uma linha. Em três dimensões, descrevemos a direção de uma linha usando um vetor paralelo à linha. Nesta seção, examinamos como usar equações para descrever linhas e planos no espaço.
Equações para uma reta no espaço
Primeiro, vamos explorar o que significa dois vetores serem paralelos. Lembre-se de que os vetores paralelos devem ter direções iguais ou opostas. Se dois vetores diferentes de zero,\( \vecs{u}\) e\( \vecs{v}\), forem paralelos, afirmamos que deve haver um escalar\( k\), tal que\( \vecs{u}=k\vecs{v}\). Se\( \vecs{u}\) e\( \vecs{v}\) tiver a mesma direção, basta escolher
\[ k=\dfrac{‖\vecs{u}‖}{‖\vecs{v}‖}. \nonumber \]
Se\( \vecs{u}\) e\( \vecs{v}\) tiver direções opostas, escolha
\[ k=−\dfrac{‖\vecs{u}‖}{‖\vecs{v}‖}. \nonumber \]
Observe que o inverso também vale. Se for\( \vecs{u}=k \vecs{v}\) para algum escalar\( k\), então\( \vecs{u}\) e\(\vecs{ v}\) ter a mesma direção\( (k>0)\) ou direções opostas\( (k<0)\), então\( \vecs{u}\) e\( \vecs{v}\) são paralelos. Portanto, dois vetores diferentes de zero\( \vecs{u}\) e\(\vecs{ v}\) são paralelos se e somente se\( \vecs{u}=k\vecs{v}\) para algum escalar\( k\). Por convenção, o vetor zero\( \vecs{0}\) é considerado paralelo a todos os vetores.
Figura\(\PageIndex{1}\): O vetor\(\vecs{v}\) é o vetor de direção para\( \vecd{PQ}\).
Como em duas dimensões, podemos descrever uma linha no espaço usando um ponto na linha e a direção da linha, ou um vetor paralelo, que chamamos de vetor de direção (Figura\(\PageIndex{1}\)). \( L\)Seja uma linha no espaço passando pelo ponto\( P(x_0,y_0,z_0)\). \( \vecs{v}=⟨a,b,c⟩\)Seja um vetor paralelo\( L\) a. Então, para qualquer ponto na linha\( Q(x,y,z)\), sabemos que\( \vecd{PQ}\) é paralelo\( \vecs{v}\) a. Assim, como acabamos de discutir, existe um escalar\( t\), tal que\( \vecd{PQ}=t\vecs{v}\), que dá
\ [\ begin {align}\ vecd {PQ} &=t\ vecs {v}\ nonumber\\ [4pt]
⟨x−x_0, y−y_0, z−z_0⟩ &=t⟨a, b, c⟩\ nonumber\\ [4pt]
⟨x−x_0, y−y_0, z−z_0⟩ &=⟨ta, tb, tc⟩. \ label {eq1}\ end {align}\]
Usando operações vetoriais, podemos reescrever Equation\ ref {eq1}
\ [\ begin {align*} ⟨x−x_0, y−y_0, z−z_0⟩ &=⟨ta, tb, tc⟩\\ [4pt]
⟨x, y, z−⟨x_0, y_0, z_0⟩ &=t⟨a, b, c⟩\\ [4pt]
\ underbrace {⟨x, y, z⟩} _\ vecs {r}} &=\ suporte inferior {⟨x_0, y_0, z_0⟩} _ {\ vecs {r} _o} +t\ suporte inferior {⟨a, b, c⟩} _ {\ vecs {v}}. \ end {align*}\]
Definindo\( \vecs{r}=⟨x,y,z⟩\) e\( \vecs{r}_0=⟨x_0,y_0,z_0⟩\), agora temos a equação vetorial de uma linha:
\[ \vecs{r}=\vecs{r}_0+t\vecs{v}. \label{vector} \]
Equacionando componentes, Equation\ ref {vector} mostra que as seguintes equações são simultaneamente verdadeiras:\( x−x_0=ta, y−y_0=tb,\) e\( z−z_0=tc.\) se resolvermos cada uma dessas equações para as variáveis do componente\( x,y,\) e\( z\) obteremos um conjunto de equações em que cada variável é definida em termos do parâmetro \(t\)e que, juntos, descrevem a linha. Esse conjunto de três equações forma um conjunto de equações paramétricas de uma linha:
\[ x=x_0+ta \nonumber \]
\[ y=y_0+tb \nonumber \]
\[ z=z_0+tc.\nonumber \]
Se resolvermos cada uma das equações para\( t\) supor\( a,b\), e\( c\) forem diferentes de zero, obteremos uma descrição diferente da mesma linha:
\[ \begin{align*} \dfrac{x−x_0}{a} =t \\[4pt] \dfrac{y−y_0}{b} =t \\[4pt] \dfrac{z−z_0}{c} =t.\end{align*}\]
Como cada expressão é igual\(t\), todas elas têm o mesmo valor. Podemos defini-los iguais um ao outro para criar equações simétricas de uma linha:
\[\dfrac{x−x_0}{a}=\dfrac{y−y_0}{b}=\dfrac{z−z_0}{c}. \nonumber \]
Resumimos os resultados no seguinte teorema.
Uma linha\( L\) paralela ao vetor\( \vecs{v}=⟨a,b,c⟩\) e passando pelo ponto\( P(x_0,y_0,z_0)\) pode ser descrita pelas seguintes equações paramétricas:
\[ x=x_0+ta, y=y_0+tb, \nonumber \]
e
\[ z=z_0+tc. \nonumber \]
Se as constantes\( a,b,\) e\( c\) forem todas diferentes de zero, então\( L\) podem ser descritas pela equação simétrica da linha:
\[\dfrac{x−x_0}{a}=\dfrac{y−y_0}{b}=\dfrac{z−z_0}{c}. \nonumber \]
As equações paramétricas de uma linha não são exclusivas. Usar um vetor paralelo diferente ou um ponto diferente na linha leva a uma representação diferente e equivalente. Cada conjunto de equações paramétricas leva a um conjunto relacionado de equações simétricas, portanto, uma equação simétrica de uma linha também não é exclusiva.
Encontre equações paramétricas e simétricas da linha que passa por pontos\( (1,4,−2)\) e\( (−3,5,0).\)
Solução
Primeiro, identifique um vetor paralelo à linha:
\[ \vecs v=⟨−3−1,5−4,0−(−2)⟩=⟨−4,1,2⟩. \nonumber \]
Use qualquer um dos pontos fornecidos na linha para completar as equações paramétricas:
\[\begin{align*} x =1−4t \\[4pt] y =4+t, \end{align*}\]
e
\[ z=−2+2t. \nonumber \]
Resolva cada equação\( t\) para criar a equação simétrica da linha:
\[ \dfrac{x−1}{−4}=y−4=\dfrac{z+2}{2}. \nonumber \]
Encontre equações paramétricas e simétricas da linha que passa por pontos\( (1,−3,2)\) e\( (5,−2,8).\)
- Dica:
-
Comece encontrando um vetor paralelo à linha.
- Responda
-
Conjunto possível de equações paramétricas: conjunto\( x=1+4t,\; y=−3+t,\; z=2+6t;\) relacionado de equações simétricas:\[ \dfrac{x−1}{4}=y+3=\dfrac{z−2}{6} \nonumber \]
Às vezes, não queremos a equação de uma linha inteira, apenas um segmento de linha. Nesse caso, limitamos os valores do nosso parâmetro\( t\). Por exemplo, deixe\( P(x_0,y_0,z_0)\) e\( Q(x_1,y_1,z_1)\) seja pontos em uma linha e deixe\( \vecs p=⟨x_0,y_0,z_0⟩\) e\( \vecs q=⟨x_1,y_1,z_1⟩\) seja os vetores de posição associados. Além disso, deixe\(\vecs r=⟨x,y,z⟩\). Queremos encontrar uma equação vetorial para o segmento de linha entre\( P\)\( Q\) e. Usando\( P\) como nosso ponto conhecido na linha e\( \vecd{PQ}=⟨x_1−x_0,y_1−y_0,z_1−z_0⟩\) como equação do vetor de direção, a Equação\ ref {vector} fornece
\[\vecs{r}=\vecs{p}+t(\vecd{PQ}). \label{eq10} \]
A equação\ ref {eq10} pode ser expandida usando propriedades de vetores:
\ [\ begin {align*}\ vecs {r} &=\ vecs {p} +t (\ vecd {PQ})\\ [4pt]
&=⟨x_0, y_0, z_0+t⟨x_1−x_0, y_1−y_0, z_1−z_0⟩\\ [4pt]
&=⟨x_0, y _0, z_0+t (⟨x_1, y_1, z_1−⟨x_0, y_0, z_0⟩)\\ [4pt]
&=⟨x_0, y_0, z_0+t⟨x_1, y_1, z_1−t⟨x_0, y_0, z_0⟩\\ [4pt]
& =( 1−t) ⟨x_0, y_0 , z_0+t⟨x_1, y_1, z_1⟩\\ [4pt]
& =( 1−t)\ vecs {p} +t\ vecs {q}. \ end {align*}\]
Assim, a equação vetorial da linha que passa por\( P\) e\( Q\) é
\[\vecs{r}=(1−t)\vecs{p}+t\vecs{q}. \nonumber \]
Lembre-se de que não queríamos a equação de toda a linha, apenas o segmento de linha entre\( P\)\( Q\) e. Observe que quando\( t=0\)\(\vecs{r}=\vecs{p}\), temos e quando\( t=1\) temos\( \vecs r=\vecs q\). Portanto, a equação vetorial do segmento de linha entre\( P\) e\( Q\) é
\[\vecs{r}=(1−t)\vecs{p}+t\vecs{q},0≤t≤1. \nonumber \]
Voltando à Equação\ ref {vector}, também podemos encontrar equações paramétricas para esse segmento de linha. Nós temos
\ [\ begin {align*}\ vecs {r} &=\ vecs {p} +t (\ vecd {PQ})\\ [4pt]
⟨x, y, z⟩ &=⟨x_0, y_0, z_0+t⟨x_1−x_0, y_1−y_0, z_1−z_0⟩\\ [4pt]
=⟨x_0+t (x_1−x_0), y_0+t (y_1−y_0), z_0+t (z_1−z_0) ⟩. \ end {align*}\]
Então, as equações paramétricas são
\[ \begin{align*} x &=x_0+t(x_1−x_0) \\[4pt] y &=y_0+t(y_1−y_0) \\[4pt] z &=z_0+t(z_1−z_0), \quad 0≤t≤1. \end{align*} \label{para} \]
Encontre equações paramétricas do segmento de linha entre os pontos\( P(2,1,4)\) e\( Q(3,−1,3).\)
Solução
Comece com as equações paramétricas de uma linha (Equations\ ref {para}) e trabalhe com cada componente separadamente:
\[ \begin{align*} x &=x_0+t(x_1−x_0)\\[4pt] &=2+t(3−2)\\[4pt] &=2+t, \end{align*}\]
\[ \begin{align*} y &=y_0+t(y_1−y_0)\\[4pt] &=1+t(−1−1)\\[4pt] &=1−2t, \end{align*}\]
e
\[ \begin{align*} z &=z_0+t(z_1−z_0)\\[4pt] &=4+t(3−4)\\[4pt] &=4−t. \end{align*}\]
Portanto, as equações paramétricas para o segmento de linha são
\[ \begin{align*} x &=2+t\\[4pt] y &=1−2t\\[4pt] z &=4−t,\quad 0≤t≤1.\end{align*}\]
Encontre equações paramétricas do segmento de linha entre os pontos\( P(−1,3,6)\)\( Q(−8,2,4)\) e.
- Responda
-
\( x=−1−7t,\; y=3−t,\; z=6−2t, \quad 0≤t≤1 \)
Distância entre um ponto e uma linha
Já sabemos como calcular a distância entre dois pontos no espaço. Agora expandimos essa definição para descrever a distância entre um ponto e uma linha no espaço. Existem vários contextos do mundo real quando é importante poder calcular essas distâncias. Ao construir uma casa, por exemplo, os construtores devem considerar os requisitos de “retrocesso”, quando as estruturas ou acessórios devem estar a uma certa distância da linha da propriedade. As viagens aéreas oferecem outro exemplo. As companhias aéreas estão preocupadas com as distâncias entre as áreas povoadas e as rotas de voo propostas.
\( L\)Seja uma linha no avião e\( M\) seja qualquer ponto que não esteja na linha. Em seguida, definimos\( M\) a\( d\) distância de até\( L\) como o comprimento do segmento de linha\( \overline{MP}\), onde\( P\) está um ponto em\( L\) tal que\( \overline{MP}\) é perpendicular a\( L\) (Figura\(\PageIndex{2}\)).
Quando procuramos a distância entre uma linha e um ponto no espaço, a Figura\(\PageIndex{2}\) ainda se aplica. Ainda definimos a distância como o comprimento do segmento da linha perpendicular conectando o ponto à linha. No espaço, no entanto, não há uma maneira clara de saber qual ponto na linha cria esse segmento de linha perpendicular, então selecionamos um ponto arbitrário na linha e usamos as propriedades dos vetores para calcular a distância. Portanto,\( P\) seja um ponto arbitrário na linha\( L\) e\(\vecs{v}\) seja um vetor de direção para\( L\) (Figura\(\PageIndex{3}\)).
Vetores\( \vecd{PM}\) e\(\vecs{v}\) formam dois lados de um paralelogramo com área\( ‖\vecd{PM}×\vecs{v}‖\). Usando uma fórmula da geometria, a área desse paralelogramo também pode ser calculada como o produto de sua base e altura:
\[‖\vecd{PM}×\vecs{v}‖=‖\vecs v‖d. \nonumber \]
Podemos usar essa fórmula para encontrar uma fórmula geral para a distância entre uma linha no espaço e qualquer ponto que não esteja na linha.
\( L\)Seja uma linha no espaço passando pelo ponto\( P\) com vetor de direção\(\vecs{v}\). Se\( M\) for algum ponto que não esteja ligado\( L\), então a distância de\( M\) para\( L\) é
\[d=\dfrac{‖\vecd{PM}×\vecs{v}‖}{‖\vecs{v}‖}. \nonumber \]
Encontre a distância entre o ponto\( M=(1,1,3)\) e a linha\( \dfrac{x−3}{4}=\dfrac{y+1}{2}=z−3.\)
Solução:
A partir das equações simétricas da linha, sabemos que o vetor\( \vecs{v}=⟨4,2,1⟩\) é um vetor de direção para a linha. Definindo as equações simétricas da linha iguais a zero, vemos que o ponto\( P(3,−1,3)\) está na linha. Então,
\[\begin{align*} \vecd{PM} =⟨1−3,1−(−1),3−3⟩\\[4pt] =⟨−2,2,0⟩. \end{align*}\]
Para calcular a distância, precisamos encontrar\( \vecd{PM}×\vecs v:\)
\ [\ begin {align*}\ vecd {PM} ×\ vecs {v} &=\ begin {vmatrix}\ mathbf {\ hat i} &\ mathbf {\ hat j} &\ mathbf {\ hat k}\\ −2 e 2 e 0\\ 4 e 2 e 2 e 1\ end {vmatrix}\\ [4pt] &= (2−0)\ mathbf {\ hat i} − (−2−0)\ mathbf {\ hat j} + (−4−8)\ mathbf {\ hat k}\\ [4pt]
&=2\ mathbf {\ hat i} +2\ mathbf {\ hat j} −12\ mathbf {\ hat k}. \ end {align*}\]
Portanto, a distância entre o ponto e a linha é (Figura\(\PageIndex{4}\))
\ [\ begin {align*} d &=\ dfrac {‖\ vecd {PM} ×\ vecs {v} ‖} {‖\ vecs {v} ‖}\\ [4pt]
&=\ dfrac {\ sqrt {2^2+2^2+12^2}} {\ sqrt {4^2+2^2+1^2}}\\ [4pt]
&=\ dfrac {2\ sqrt {38}} {\ sqrt {21}}\\ [4pt]
&=\ dfrac {2\ sqrt {798}} {21}\,\ texto {unidades}\ end {align*}\]

Encontre a distância entre o ponto\( (0,3,6)\) e a linha com equações paramétricas\( x=1−t,\; y=1+2t,\; z=5+3t.\)
- Dica
-
Encontre um vetor com o ponto inicial\( (0,3,6)\) e um ponto terminal na linha e, em seguida, encontre um vetor de direção para a linha.
- Responda
-
\( \sqrt{\dfrac{10}{7}} = \dfrac{\sqrt{70}}{7} \,\text{units} \)
Relações entre linhas
Dadas duas linhas no plano bidimensional, as linhas são iguais, são paralelas, mas não iguais, ou se cruzam em um único ponto. Em três dimensões, um quarto caso é possível. Se duas linhas no espaço não são paralelas, mas não se cruzam, então as linhas são consideradas linhas inclinadas (Figura\(\PageIndex{5}\)).
Figura\(\PageIndex{5}\): Em três dimensões, é possível que duas linhas não se cruzem, mesmo quando têm direções diferentes.
Para classificar as linhas como paralelas, mas não iguais, iguais, que se cruzam ou inclinadas, precisamos saber duas coisas: se os vetores de direção são paralelos e se as linhas compartilham um ponto (Figura\(\PageIndex{6}\)).
Para cada par de linhas, determine se as linhas são iguais, paralelas, mas não iguais, inclinadas ou se cruzam.
uma.
- \( L_1:\; x=2s−1, \; y=s−1, \; z=s−4\)
- \( L_2: \; x=t−3, \; y=3t+8, \; z=5−2t\)
b.
- \( L_1: \; x=−y=z\)
- \( L_2:\; \dfrac{x−3}{2}=y=z−2\)
c.
- \( L_1:\; x=6s−1,\; y=−2s,\; z=3s+1\)
- \( L_2:\; \dfrac{x−4}{6}=\dfrac{y+3}{−2}=\dfrac{z−1}{3}\)
Solução
a. A linha\( L_1\) tem vetor de direção\( \vecs v_1=⟨2,1,1⟩\); a linha\( L_2\) tem vetor de direção\( \vecs v_2=⟨1,3,−2⟩\). Como os vetores de direção não são vetores paralelos, as linhas estão se cruzando ou inclinadas. Para determinar se as linhas se cruzam, vemos se há um ponto,\( (x,y,z)\), que está nas duas linhas. Para encontrar esse ponto, usamos as equações paramétricas para criar um sistema de igualdades:
\[ 2s−1=t−3; \nonumber \]
\[ s−1=3t+8; \nonumber \]
\[ s−4=5−2t. \nonumber \]
Pela primeira equação, a\( t=2s+2.\) substituição pela segunda equação produz
\( s−1=3(2s+2)+8\)
\( s−1=6s+6+8\)
\( 5s=−15\)
\( s=−3.\)
A substituição na terceira equação, no entanto, produz uma contradição:
\( s−4=5−2(2s+2)\)
\( s−4=5−4s−4\)
\( 5s=5\)
\( s=1.\)
Não há um único ponto que satisfaça as equações paramétricas para\( L_1\) e\( L_2\) simultaneamente. Essas linhas não se cruzam, então elas estão inclinadas (veja a figura a seguir).
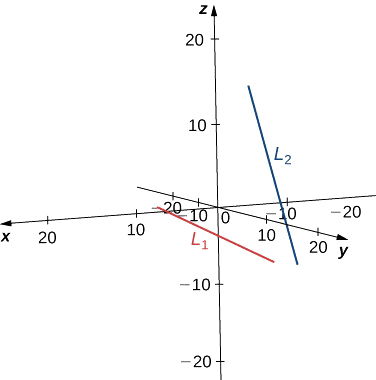
b.\( L_1\) A linha tem vetor de direção\( \vecs v_1=⟨1,−1,1⟩\) e passa pela origem,\( (0,0,0)\). \( L_2\)A linha tem um vetor de direção diferente\( \vecs v_2=⟨2,1,1⟩\), então essas linhas não são paralelas ou iguais. Vamos\( r\) representar o parâmetro para a linha\( L_1\) e vamos\(s\) representar o parâmetro para\( L_2\):
\[\begin{align*} &\text{Line }L_1: & & \text{Line }L_2:\\[4pt] &x = r & & x = 2s + 3\\[4pt] &y = -r & & y = s \\[4pt] &z = r & & z = s + 2 \end{align*}\]
Resolva o sistema de equações para encontrar\( r=1\)\( s=−1\) e. Se precisarmos encontrar o ponto de interseção, podemos substituir esses parâmetros nas equações originais para obter\( (1,−1,1)\) (veja a figura a seguir).

c. Linhas\( L_1\) e\( L_2\) vetores de direção equivalentes:\( \vecs v=⟨6,−2,3⟩.\) Essas duas linhas são paralelas (veja a figura a seguir).

Descreva a relação entre as linhas com as seguintes equações paramétricas:
\[ x=1−4t, \; y=3+t, \; z=8−6t \nonumber \]
\[x=2+3s,\; y=2s,\; z=−1−3s. \nonumber \]
- Dica
-
Comece identificando vetores de direção para cada linha. Um é múltiplo do outro?
- Responda
-
Essas linhas são inclinadas porque seus vetores de direção não são paralelos e não há nenhum ponto\( (x,y,z)\) nas duas linhas.
Equações para um plano
Sabemos que uma linha é determinada por dois pontos. Em outras palavras, para quaisquer dois pontos distintos, há exatamente uma linha que passa por esses pontos, seja em duas dimensões ou três. Da mesma forma, considerando quaisquer três pontos que não estejam todos na mesma linha, existe um plano único que passa por esses pontos. Assim como uma linha é determinada por dois pontos, um plano é determinado por três.
Essa pode ser a maneira mais simples de caracterizar um avião, mas também podemos usar outras descrições. Por exemplo, dadas duas linhas distintas que se cruzam, há exatamente um plano contendo as duas linhas. Um plano também é determinado por uma linha e por qualquer ponto que não esteja na linha. Essas caracterizações surgem naturalmente da ideia de que um plano é determinado por três pontos. Talvez a caracterização mais surpreendente de um avião seja, na verdade, a mais útil.
Imagine um par de vetores ortogonais que compartilham um ponto inicial. Visualize pegar um dos vetores e torcê-lo. Conforme você gira, o outro vetor gira e varre um avião. Aqui, descrevemos esse conceito matematicamente. \(\vecs{n}=⟨a,b,c⟩\)Seja um vetor e\(P=(x_0,y_0,z_0)\) um ponto. Em seguida, o conjunto de todos os pontos\(Q=(x,y,z)\), de forma ortogonal,\(\vecs{n}\) forma um plano (Figura\(\PageIndex{7}\)).\(\vecd{PQ}\) Dizemos que\(\vecs{n}\) é um vetor normal, ou perpendicular ao plano. Lembre-se de que o produto escalar dos vetores ortogonais é zero. Esse fato gera a equação vetorial de um plano:
\[\vecs{n}⋅\vecd{PQ}=0. \nonumber \]
Reescrever essa equação fornece formas adicionais de descrever o plano:
\[ \begin{align*} \vecs{n}⋅\vecd{PQ} &=0 \\[4pt] ⟨a,b,c⟩⋅⟨x−x_0,y−y_0,z−z_0⟩ &=0 \\[4pt] a(x−x_0)+b(y−y_0)+c(z−z_0) &=0. \end{align*}\]
Dado um ponto\(P\) e um vetor\(\vecs n\), o conjunto de todos os pontos\(Q\) que satisfazem a equação\(\vecs n⋅\vecd{PQ}=0\) forma um plano. A equação
\[\vecs{n}⋅\vecd{PQ}=0 \nonumber \]
é conhecida como a equação vetorial de um plano.
A equação escalar de um plano (às vezes também chamada de equação padrão de um plano) contendo ponto\(P=(x_0,y_0,z_0)\) com vetor normal\(\vec{n}=⟨a,b,c⟩\) é
\[a(x−x_0)+b(y−y_0)+c(z−z_0)=0. \nonumber \]
Essa equação pode ser expressa como\(ax+by+cz+d=0,\) onde\(d=−ax_0−by_0−cz_0.\) Essa forma da equação às vezes é chamada de forma geral da equação de um plano.
Conforme descrito anteriormente nesta seção, quaisquer três pontos que não estejam todos na mesma linha determinam um plano. Dados três desses pontos, podemos encontrar uma equação para o plano que contém esses pontos.
Escreva uma equação para o plano contendo pontos\(P=(1,1,−2), Q=(0,2,1),\) e\(R=(−1,−1,0)\) nas formas padrão e geral.
Solução
Para escrever uma equação para um plano, precisamos encontrar um vetor normal para o plano. Começamos identificando dois vetores no plano:
\[ \begin{align*} \vecd{PQ} &=⟨0−1,2−1,1−(−2)⟩\\[4pt] &=⟨−1,1,3⟩ \\[4pt] \vecd{QR} &=⟨−1−0,−1−2,0−1⟩\\[4pt] &=⟨−1,−3,−1⟩.\end{align*}\]
O produto cruzado\(\vecd{PQ}×\vecd{QR}\) é ortogonal a ambos\(\vecd{PQ}\) e\(\vecd{QR}\), portanto, é normal ao plano que contém esses dois vetores:
\[ \begin{align*} \vecs n &=\vecd{PQ}×\vecd{QR} \\[4pt] &=\begin{vmatrix}\mathbf{\hat i} & \mathbf{\hat j} & \mathbf{\hat k}\\−1 & 1 & 3\\−1 & −3 & −1\end{vmatrix} \\[4pt] &=(−1+9)\mathbf{\hat i}−(1+3)\mathbf{\hat j}+(3+1)\mathbf{\hat k} \\[4pt] &= 8\mathbf{\hat i}−4\mathbf{\hat j}+4\mathbf{\hat k}.\end{align*}\]
Assim,\(\vecs n=⟨8,−4,4⟩,\) podemos escolher qualquer um dos três pontos dados para escrever uma equação do plano:
\[ \begin{align*} 8(x−1)−4(y−1)+4(z+2) &=0 \\[4pt] 8x−4y+4z+4 &=0. \end{align*}\]
As equações escalares de um plano variam dependendo do vetor normal e do ponto escolhido.
Encontre uma equação do plano que passa pelo ponto\((1,4,3)\) e contém a linha dada por\(x=\dfrac{y−1}{2}=z+1.\)
Solução
As equações simétricas descrevem a linha que passa pelo ponto\((0,1,−1)\) paralelo ao vetor\(\vecs v_1=⟨1,2,1⟩\) (veja a figura a seguir). Use esse ponto e o ponto dado\((1,4,3),\) para identificar um segundo vetor paralelo ao plano:
\[ \vecs v_2=⟨1−0,4−1,3−(−1)⟩=⟨1,3,4⟩. \nonumber \]
Use o produto cruzado desses vetores para identificar um vetor normal para o plano:
\[ \begin{align*} \vecs n &=\vecs v_1×\vecs v_2 \nonumber \\[4pt] &=\begin{vmatrix}\mathbf{\hat i} & \mathbf{\hat j} & \mathbf{\hat k}\\1 & 2 & 1\\1 & 3 & 4\end{vmatrix} \nonumber \\[4pt] &=(8−3)\mathbf{\hat i}−(4−1)\mathbf{\hat j}+(3−2)\mathbf{\hat k} \\[4pt] &=5\mathbf{\hat i}−3\mathbf{\hat j}+\mathbf{\hat k}. \nonumber\end{align*}\]
As equações escalares para o plano são\(5x−3(y−1)+(z+1)=0\) e\(5x−3y+z+4=0.\)
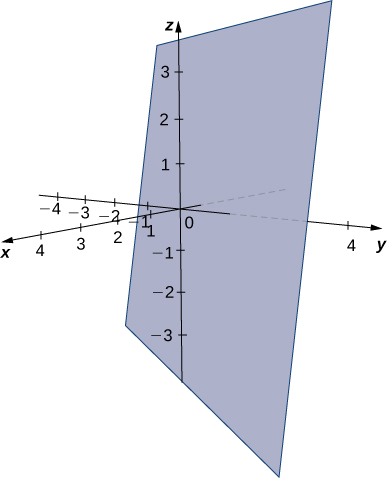
Encontre uma equação do plano contendo as linhas\(L_1\) e\(L_2\):
\[ L_1: \; x=−y=z \nonumber \]
\[ L_2:\; \dfrac{x−3}{2}=y=z−2. \nonumber \]
- Dica
-
Dica: O produto cruzado dos vetores de direção das linhas fornece um vetor normal para o plano.
- Responda
-
\[ −2(x−1)+(y+1)+3(z−1)=0 \nonumber \]
ou
\[ −2x+y+3z=0 \nonumber \]
Agora que podemos escrever uma equação para um plano, podemos usar a equação para encontrar a distância\(d\) entre um ponto\(P\) e o plano. É definido como a menor distância possível de\(P\) até um ponto no plano.
Assim como encontramos a distância bidimensional entre um ponto e uma linha calculando o comprimento de um segmento de linha perpendicular à linha, encontramos a distância tridimensional entre um ponto e um plano calculando o comprimento de um segmento de linha perpendicular ao plano. \(R\)Seja o ponto no plano tal que\(\vecd{RP}\) seja ortogonal ao plano, e\(Q\) seja um ponto arbitrário no plano. Em seguida, a projeção do vetor\(\vecd{QP}\) no vetor normal descreve o vetor\(\vecd{RP}\), conforme mostrado na Figura\(\PageIndex{8}\).
Suponha que um plano com vetor normal\(\vecs{n}\) passe pelo ponto\(Q\). A distância\(d\) do plano a um ponto que\(P\) não está no plano é dada por
\[d=‖\text{proj}_\vecs{n}\,\vecd{QP}‖=∣\text{comp}_\vecs{n}\, \vecd{QP}∣=\dfrac{∣\vecd{QP}⋅\vecs{n}∣}{‖\vecs{n}‖}. \label{distanceplanepoint} \]
Encontre a distância entre o ponto\(P=(3,1,2)\) e o plano dado por\(x−2y+z=5\) (veja a figura a seguir).
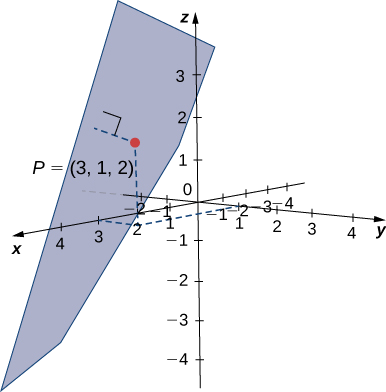
Solução
Os coeficientes da equação do plano fornecem um vetor normal para o plano:\(\vecs{n}=⟨1,−2,1⟩\). Para encontrar o vetor\(\vecd{QP}\), precisamos de um ponto no plano. Qualquer ponto funcionará, então\(y=z=0\) defina para ver que esse ponto\(Q=(5,0,0)\) está no plano. Encontre a forma do componente do vetor de\(Q\) até\(P\):
\[ \vecd{QP}=⟨3−5,1−0,2−0⟩=⟨−2,1,2⟩. \nonumber \]
Aplique a fórmula de distância da Equação\ ref {distanceplanepoint}:
\[\begin{align*} d &=\dfrac{∣\vecd{QP}⋅\vecs n|}{‖\vecs n‖} \\[4pt] &=\dfrac{|⟨−2,1,2⟩⋅⟨1,−2,1⟩|}{\sqrt{1^2+(−2)^2+1^2}} \\[4pt] &=\dfrac{|−2−2+2|}{\sqrt{6}} \\[4pt] &=\dfrac{2}{\sqrt{6}} = \dfrac{\sqrt{6}}{3}\,\text{units}. \end{align*}\]
Encontre a distância entre o ponto\(P=(5,−1,0)\) e o plano dado por\(4x+2y−z=3\).
- Dica
-
O ponto\((0,0,−3)\) está no avião.
- Responda
-
\[ \dfrac{15}{\sqrt{21}} = \dfrac{5\sqrt{21}}{7}\,\text{units} \nonumber \]
Planos paralelos e de interseção
Discutimos as várias relações possíveis entre duas linhas em duas dimensões e três dimensões. Quando descrevemos a relação entre dois planos no espaço, temos apenas duas possibilidades: os dois planos distintos são paralelos ou se cruzam. Quando dois planos são paralelos, seus vetores normais são paralelos. Quando dois planos se cruzam, a interseção é uma linha (Figura\(\PageIndex{9}\)).
Podemos usar as equações dos dois planos para encontrar equações paramétricas para a linha de interseção.
Encontre equações paramétricas e simétricas para a linha formada pela interseção dos planos dados por\(x+y+z=0\) e\(2x−y+z=0\) (veja a figura a seguir).
Solução
Observe que os dois planos têm normais não paralelos, então os planos se cruzam. Além disso, a origem satisfaz cada equação, então sabemos que a linha de interseção passa pela origem. Adicione as equações planas para que possamos eliminar uma das variáveis, neste caso,\(y\):
\(x+y+z=0\)
\(2x−y+z=0\)
________________
\(3x+2z=0\).
Isso nos\(x=−\dfrac{2}{3}z.\) dá Substituímos esse valor na primeira equação para expressar\(y\) em termos de\(z\):
\[ \begin{align*} x+y+z =0 \\[4pt] −\dfrac{2}{3}z+y+z =0 \\[4pt] y+\dfrac{1}{3}z =0 \\[4pt] y =−\dfrac{1}{3}z \end{align*}. \nonumber \]
Agora temos as duas primeiras variáveis\(x\) e\(y\), em termos da terceira variável,\(z\). Agora definimos\(z\) em termos de\(t\). Para eliminar a necessidade de frações, optamos por definir o parâmetro\(t\) como\(t=−\dfrac{1}{3}z\). Então,\(z=−3t\). Substituindo a representação paramétrica de\(z\) back nas outras duas equações, vemos que as equações paramétricas para a linha de interseção são\(x=2t, \; y=t, \; z=−3t.\) As equações simétricas da linha são\(\dfrac{x}{2}=y=\dfrac{z}{−3}\).
Encontre equações paramétricas para a reta formada pela interseção de planos\(x+y−z=3\) e\(3x−y+3z=5.\)
- Dica
-
Adicione as duas equações e, em seguida, expresse\(z\) em termos de\(x\). Então, expresse\(y\) em termos de\(x\).
- Responda
-
\( x=t, \; y=7−3t,\; z=4−2t\)
Além de encontrar a equação da linha de interseção entre dois planos, talvez precisemos encontrar o ângulo formado pela interseção de dois planos. Por exemplo, os construtores que constroem uma casa precisam saber o ângulo em que diferentes seções do telhado se encontram para saber se o telhado ficará bem e drenará adequadamente. Podemos usar vetores normais para calcular o ângulo entre os dois planos. Podemos fazer isso porque o ângulo entre os vetores normais é o mesmo que o ângulo entre os planos. A figura\(\PageIndex{10}\) mostra por que isso é verdade.
Podemos encontrar a medida do ângulo\(θ\) entre dois planos que se cruzam encontrando primeiro o cosseno do ângulo, usando a seguinte equação:
\[\cos θ=\dfrac{|\vecs{n}_1⋅\vecs{n}_2|}{‖\vecs{n}_1‖‖\vecs{n}_2‖}. \nonumber \]
Podemos então usar o ângulo para determinar se dois planos são paralelos ou ortogonais ou se eles se cruzam em algum outro ângulo.
Determine se cada par de planos é paralelo, ortogonal ou nenhum deles. Se os planos estiverem se cruzando, mas não ortogonais, encontre a medida do ângulo entre eles. Dê a resposta em radianos e arredonde para duas casas decimais.
- \(x+2y−z=8\)e\(2x+4y−2z=10\)
- \(2x−3y+2z=3\)e\(6x+2y−3z=1\)
- \(x+y+z=4\)e\(x−3y+5z=1\)
Solução:
- Os vetores normais para esses planos são\(\vecs{n}_1=⟨1,2,−1⟩\) e\(\vecs{n}_2=⟨2,4,−2⟩.\) Esses dois vetores são múltiplos escalares um do outro. Os vetores normais são paralelos, então os planos são paralelos.
- Os vetores normais para esses planos são\(\vecs{n}_1=⟨2,−3,2⟩\)\(\vecs{n}_2=⟨6,2,−3⟩\) e. Tomando o produto escalar desses vetores, temos\[\begin{align*} \vecs{n}_1⋅\vecs{n}_2 =⟨2,−3,2⟩⋅⟨6,2,−3⟩\\[4pt] =2(6)−3(2)+2(−3)=0.\end{align*} \nonumber \] Os vetores normais são ortogonais, então os planos correspondentes também são ortogonais.
- Os vetores normais para esses planos são\(\vecs n_1=⟨1,1,1⟩\) e\(\vecs n_2=⟨1,−3,5⟩\):\[\begin{align*} \cos θ &=\dfrac{|\vecs{n}_1⋅\vecs{n}_2|}{‖\vecs{n}_1‖‖\vecs{n}_2‖} \\[4pt] &=\dfrac{|⟨1,1,1⟩⋅⟨1,−3,5⟩|}{\sqrt{1^2+1^2+1^2}\sqrt{1^2+(−3)^2+5^2}} \\[4pt] &=\dfrac{3}{\sqrt{105}} \end{align*}\]
Então\(\theta =\arccos {\frac{3}{\sqrt{105}}} \approx 1.27\) rad.
Assim, o ângulo entre os dois planos é aproximadamente\(1.27\) rad, ou aproximadamente\(73°\).
Encontre a medida do ângulo entre os planos\(x+y−z=3\) e\(3x−y+3z=5.\) dê a resposta em radianos e arredonde para duas casas decimais.
- Dica
-
Use os coeficientes das variáveis em cada equação para encontrar um vetor normal para cada plano.
- Responda
-
\( 1.44\, \text{rad} \)
Quando descobrimos que dois planos são paralelos, talvez precisemos encontrar a distância entre eles. Para encontrar essa distância, simplesmente selecionamos um ponto em um dos planos. A distância desse ponto até o outro plano é a distância entre os planos.
Anteriormente, introduzimos a fórmula para calcular essa distância na Equação\ ref {distanceplanepoint}:
\[d=\dfrac{\vecd{QP}⋅\vecs{n}}{‖\vecs{n}‖}, \nonumber \]
onde\(Q\) é um ponto no plano,\(P\) é um ponto que não está no plano e\(\vec{n}\) é o vetor normal que passa pelo ponto\(Q\). Considere a distância do ponto\((x_0,y_0,z_0)\) ao plano\(ax+by+cz+k=0.\)\((x_1,y_1,z_1)\) Seja qualquer ponto do plano. Substituir na fórmula produz
\[\begin{align*}d =\dfrac{|a(x_0−x_1)+b(y_0−y_1)+c(z_0−z_1)|}{\sqrt{a^2+b^2+c^2}} \\[4pt] =\dfrac{|ax_0+by_0+cz_0+k|}{\sqrt{a^2+b^2+c^2}}.\end{align*}\]
Declaramos esse resultado formalmente no seguinte teorema.
\(P(x_0,y_0,z_0)\)Sejamos um ponto. A distância\(P\) até o plano\(ax+by+cz+k=0\) é dada por
\[d=\dfrac{|ax_0+by_0+cz_0+k|}{\sqrt{a^2+b^2+c^2}}. \nonumber \]
Encontre a distância entre os dois planos paralelos dados por\(2x+y−z=2\) e\(2x+y−z=8.\)
Solução
O ponto\((1,0,0)\) está no primeiro plano. A distância desejada, então, é
\[\begin{align*} d &=\dfrac{|ax_0+by_0+cz_0+k|}{\sqrt{a^2+b^2+c^2}} \\[4pt] &= \dfrac{|2(1)+1(0)+(−1)(0)+(−8)|}{\sqrt{2^2+1^2+(−1)^2}} \\[4pt] &= \dfrac{6}{\sqrt{6}}=\sqrt{6} \,\text{units} \end{align*}\]
Encontre a distância entre planos paralelos\(5x−2y+z=6\)\(5x−2y+z=−3\) e.
- Dica
-
\(x=y=0\)Defina para encontrar um ponto no primeiro plano.
- Responda
-
\(\dfrac{9}{\sqrt{30}} = \dfrac{3\sqrt{30}}{10}\,\text{units} \)
Encontrar a distância de um ponto a uma linha ou de uma linha a um plano parece um procedimento bastante abstrato. Mas, se as linhas representam tubos em uma fábrica de produtos químicos ou tubos em uma refinaria de petróleo ou estradas em um cruzamento de rodovias, confirmar que a distância entre elas atende às especificações pode ser importante e difícil de medir. Uma maneira é modelar os dois tubos como linhas, usando as técnicas deste capítulo, e depois calcular a distância entre eles. O cálculo envolve a formação de vetores ao longo das direções das linhas e o uso do produto cruzado e do produto escalar.
As formas simétricas de duas linhas\(L_1\) e\(L_2\), são
\[L_1:\dfrac{x−x_1}{a_1}=\dfrac{y−y_1}{b_1}=\dfrac{z−z_1}{c_1} \nonumber \]
\[L_2:\dfrac{x−x_2}{a_2}=\dfrac{y−y_2}{b_2}=\dfrac{z−z_2}{c_2}. \nonumber \]
Você deve desenvolver uma fórmula para a distância\(d\) entre essas duas linhas, em termos dos valores\(a_1,b_1,c_1;a_2,b_2,c_2;x_1,y_1,z_1;\) e\(x_2,y_2,z_2.\) A distância entre duas linhas geralmente significa a distância mínima, então esse é o comprimento de um segmento de linha ou o comprimento de um vetor que é perpendicular a ambas as linhas. e cruza as duas linhas.
1. Primeiro, anote dois vetores,\(\vecs{v}_1\) e\(\vecs{v}_2\), que estão ao longo de\(L_1\) e\(L_2\), respectivamente.
2. Encontre o produto cruzado desses dois vetores e chame-o\(\vecs{N}\). Esse vetor é perpendicular a\(\vecs{v}_1\) e\(\vecs{v}_2\), portanto, é perpendicular às duas linhas.
3. A partir do vetor\(\vecs{N}\), forme um vetor unitário\(\vecs{n}\) na mesma direção.
4. Use equações simétricas para encontrar um vetor conveniente\(\vecs{v}_{12}\) que esteja entre quaisquer dois pontos, um em cada linha. Novamente, isso pode ser feito diretamente das equações simétricas.
5. O produto escalar de dois vetores é a magnitude da projeção de um vetor no outro, ou seja,\(\vecs A⋅\vecs B=‖\vecs{A}‖‖\vecs{B}‖\cos θ,\) onde\(θ\) está o ângulo entre os vetores. Usando o produto escalar, encontre a projeção do vetor\(\vecs{v}_{12}\) encontrado na etapa\(4\) sobre o vetor unitário\(\vecs{n}\) encontrado na etapa\(3\). Essa projeção é perpendicular às duas linhas e, portanto, seu comprimento deve ser a distância perpendicular d entre elas. Observe que o valor de\(d\) pode ser negativo, dependendo da escolha do vetor\(\vecs{v}_{12}\) ou da ordem do produto cruzado, portanto, use sinais de valor absoluto ao redor do numerador.
6. Verifique se sua fórmula fornece a distância correta\(|−25|/\sqrt{198}≈1.78\) entre as duas linhas a seguir:
\[L_1:\dfrac{x−5}{2}=\dfrac{y−3}{4}=\dfrac{z−1}{3} \nonumber \]
\[L_2:\dfrac{x−6}{3}=\dfrac{y−1}{5}=\dfrac{z}{7}. \nonumber \]
7. Sua expressão geral é válida quando as linhas são paralelas? Se não, por que não? (Dica: O que você sabe sobre o valor do produto cruzado de dois vetores paralelos? Para onde esse resultado apareceria em sua expressão\(d\)?)
8. Demonstre que sua expressão para a distância é zero quando as linhas se cruzam. Lembre-se de que duas linhas se cruzam se não estiverem paralelas e estiverem no mesmo plano. Portanto, considere a direção de\(\vecs{n}\)\(\vecs{v}_{12}\) e. Qual é o resultado de seu produto escalar?
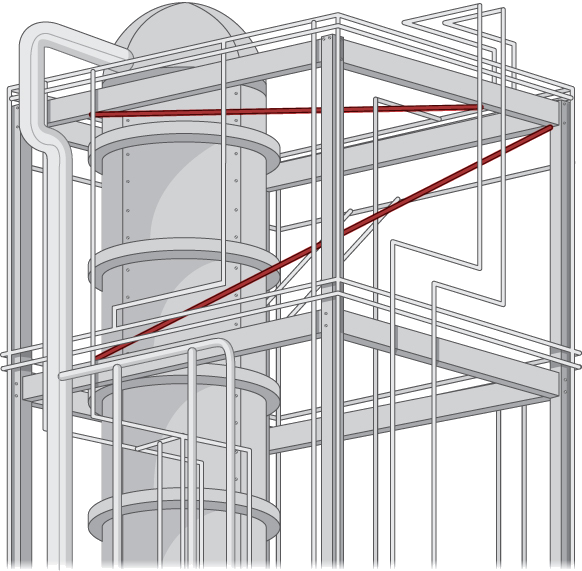
9. Considere a seguinte aplicação. Os engenheiros de uma refinaria determinaram que precisam instalar amortecedores de suporte entre muitos dos tubos de gás para reduzir as vibrações prejudiciais. Para minimizar o custo, eles planejam instalar esses suportes nos pontos mais próximos entre os tubos inclinados adjacentes. Como eles têm esquemas detalhados da estrutura, eles são capazes de determinar os comprimentos corretos dos suportes necessários e, portanto, fabricá-los e distribuí-los para as equipes de instalação sem gastar tempo valioso fazendo medições.
A estrutura da moldura retangular tem as dimensões\(4.0×15.0×10.0\,\text{m}\) (altura, largura e profundidade). Um setor tem um tubo entrando no canto inferior da unidade de estrutura padrão e saindo no canto diametralmente oposto (o mais distante na parte superior); chame assim\(L_1\). Um segundo tubo entra e sai nos dois cantos inferiores opostos diferentes; chame isso\(L_2\) (Figura\(\PageIndex{12}\)).
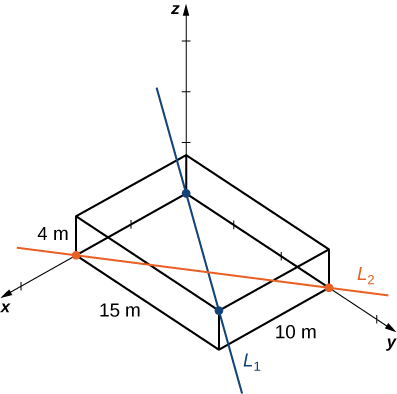
Anote os vetores ao longo das linhas que representam esses tubos, encontre o produto cruzado entre eles a partir do qual criar o vetor unitário\(\vecs n\), defina um vetor que abranja dois pontos em cada linha e, finalmente, determine a distância mínima entre as linhas. (Considere que a origem está no canto inferior do primeiro tubo.) Da mesma forma, você também pode desenvolver as equações simétricas para cada linha e substituí-las diretamente em sua fórmula.
Conceitos-chave
- Em três dimensões, a direção de uma linha é descrita por um vetor de direção. A equação vetorial de uma linha com o vetor de direção\(\vecs v=⟨a,b,c⟩\) passando pelo ponto\(P=(x_0,y_0,z_0)\) é\(\vecs r=\vecs r_0+t\vecs v\), onde\(\vecs r_0=⟨x_0,y_0,z_0⟩\) é o vetor de posição do ponto\(P\). Essa equação pode ser reescrita para formar as equações paramétricas da linha:\(x=x_0+ta,y=y_0+tb\),\(z=z_0+tc\) e. A linha também pode ser descrita com as equações simétricas\(\dfrac{x−x_0}{a}=\dfrac{y−y_0}{b}=\dfrac{z−z_0}{c}\).
- \(L\)Seja uma linha no espaço passando pelo ponto\(P\) com vetor de direção\(\vecs v\). Se\(Q\) for algum ponto que não esteja ligado\(L\), então a distância de\(Q\) para\(L\) é\(d=\dfrac{‖\vecd{PQ}×\vecs v‖}{‖\vecs v‖}.\)
- Em três dimensões, duas linhas podem ser paralelas, mas não iguais, iguais, cruzadas ou inclinadas.
- Dado um ponto\(P\) e um vetor\(\vecs n\), o conjunto de todos os pontos que\(Q\) satisfazem a equação\(\vecs n⋅\vecd{PQ}=0\) forma um plano. A equação\(\vecs n⋅\vecd{PQ}=0\) é conhecida como equação vetorial de um plano.
- A equação escalar de um plano contendo ponto\(P=(x_0,y_0,z_0)\) com vetor normal\(\vecs n=⟨a,b,c⟩\) é\(a(x−x_0)+b(y−y_0)+c(z−z_0)=0\). Essa equação pode ser expressa como\(ax+by+cz+d=0,\) onde\(d=−ax_0−by_0−cz_0.\) Essa forma da equação às vezes é chamada de forma geral da equação de um plano.
- Suponha que um plano com vetor normal\(n\) passe pelo ponto\(Q\). A distância\(D\) do plano até o ponto que\(P\) não está no plano é dada por
\[D=‖\text{proj}_\vecs{n}\vecd{QP}‖=∣\text{comp}_\vecs{n}\vec{QP}∣=\dfrac{∣\vec{QP}⋅\vecs n∣}{‖\vecs n‖.} \nonumber \]
- Os vetores normais dos planos paralelos são paralelos. Quando dois planos se cruzam, eles formam uma linha.
- A medida do ângulo\(θ\) entre dois planos que se cruzam pode ser encontrada usando a equação:\(\cos θ=\dfrac{|\vecs{n}_1⋅\vecs n_2|}{‖\vecs n_1‖‖\vecs n_2‖}\), onde\(\vecs n_1\) e\(\vecs n_2\) são vetores normais dos planos.
- A distância\(D\) do ponto\((x_0,y_0,z_0)\) ao plano\(ax+by+cz+d=0\) é dada por
\[D=\dfrac{|a(x_0−x_1)+b(y_0−y_1)+c(z_0−z_1)|} {\sqrt{a^2+b^2+c^2}}=\dfrac{|ax_0+by_0+cz_0+d|}{\sqrt{a^2+b^2+c^2}} \nonumber \].
Equações-chave
- Equação vetorial de uma linha
\(\vecs r=\vecs r_0+t\vecs v\)
- Equações paramétricas de uma reta
\(x=x_0+ta,\; y=y_0+tb,\)e\(z=z_0+tc\)
- Equações simétricas de uma reta
\(\dfrac{x−x_0}{a}=\dfrac{y−y_0}{b}=\dfrac{z−z_0}{c}\)
- Equação vetorial de um plano
\(\vecs n⋅\vecd{PQ}=0\)
- Equação escalar de um plano
\(a(x−x_0)+b(y−y_0)+c(z−z_0)=0\)
- Distância entre um plano e um ponto
\(d=‖\text{proj}_\vecs{n}\vecd{QP}‖=∣\text{comp}_\vecs{n}\vecd{QP}∣=\dfrac{∣\vecd{QP}⋅\vecs n∣}{‖\vecs n‖}\)
Glossário
- vetor de direção
- um vetor paralelo a uma linha que é usado para descrever a direção, ou orientação, da linha no espaço
- forma geral da equação de um plano
- uma equação na forma em\(ax+by+cz+d=0,\) que\(\vecs n=⟨a,b,c⟩\) é um vetor normal do plano,\(P=(x_0,y_0,z_0)\) é um ponto no plano, e\(d=−ax_0−by_0−cz_0\)
- vetor normal
- um vetor perpendicular a um plano
- equações paramétricas de uma linha
- o conjunto de equações\(x=x_0+ta, y=y_0+tb,\) e a\(z=z_0+tc\) descrição da linha com o vetor de direção\(v=⟨a,b,c⟩\) passando pelo ponto\((x_0,y_0,z_0)\)
- equação escalar de um plano
- a equação\(a(x−x_0)+b(y−y_0)+c(z−z_0)=0\) usada para descrever um plano contendo ponto\(P=(x_0,y_0,z_0)\) com vetor normal\(n=⟨a,b,c⟩\) ou sua forma alternativa\(ax+by+cz+d=0\), onde\(d=−ax_0−by_0−cz_0\)
- linhas de inclinação
- duas linhas que não são paralelas, mas não se cruzam
- equações simétricas de uma linha
- as equações\(\dfrac{x−x_0}{a}=\dfrac{y−y_0}{b}=\dfrac{z−z_0}{c}\) que descrevem a linha com o vetor de direção\(v=⟨a,b,c⟩\) passando pelo ponto\((x_0,y_0,z_0)\)
- equação vetorial de uma linha
- a equação\(\vecs r=\vecs r_0+t\vecs v\) usada para descrever uma linha com vetor de direção\(\vecs v=⟨a,b,c⟩\) passando pelo ponto\(P=(x_0,y_0,z_0)\), onde\(\vecs r_0=⟨x_0,y_0,z_0⟩\), é o vetor de posição do ponto\(P\)
- equação vetorial de um plano
- a equação\(\vecs n⋅\vecd{PQ}=0,\) onde\(P\) é um determinado ponto no plano,\(Q\) é qualquer ponto no plano e\(\vecs n\) é um vetor normal do plano


