11.5: Seções cônicas
- Page ID
- 187885
- Identifique a equação de uma parábola na forma padrão com determinado foco e diretriz.
- Identifique a equação de uma elipse na forma padrão com determinados focos.
- Identifique a equação de uma hipérbole na forma padrão com determinados focos.
- Reconheça uma parábola, elipse ou hipérbole a partir de seu valor de excentricidade.
- Escreva a equação polar de uma seção cônica com excentricidade\(e\).
- Identifique quando uma equação geral de grau dois é uma parábola, elipse ou hipérbole.
As seções cônicas foram estudadas desde a época dos antigos gregos e foram consideradas um importante conceito matemático. Já em 320 a.C., matemáticos gregos como Menaechmus, Appolônio e Arquimedes ficaram fascinados com essas curvas. Appolônio escreveu um tratado inteiro de oito volumes sobre seções cônicas no qual ele foi, por exemplo, capaz de derivar um método específico para identificar uma seção cônica por meio do uso da geometria. Desde então, surgiram importantes aplicações de seções cônicas (por exemplo, em astronomia) e as propriedades das seções cônicas são usadas em radiotelescópios, receptores de antenas parabólicas e até mesmo arquitetura. Nesta seção, discutimos as três seções cônicas básicas, algumas de suas propriedades e suas equações.
As seções cônicas recebem esse nome porque podem ser geradas pela interseção de um plano com um cone. Um cone tem duas partes de formato idêntico chamadas nappes. Uma nuca é o que a maioria das pessoas entende por “cone”, tendo a forma de um chapéu de festa. Um cone circular reto pode ser gerado girando uma linha que passa pela origem ao redor do eixo y, conforme mostrado na Figura\(\PageIndex{1}\).
As seções cônicas são geradas pela interseção de um plano com um cone (Figura\(\PageIndex{2}\)). Se o plano for paralelo ao eixo de revolução (o eixo y), a seção cônica é uma hipérbole. Se o plano for paralelo à linha geradora, a seção cônica é uma parábola. Se o plano for perpendicular ao eixo de revolução, a seção cônica é um círculo. Se o plano cruzar uma nuca em um ângulo com o eixo (diferente de
Parábolas
Uma parábola é gerada quando um plano cruza um cone paralelo à linha geradora. Nesse caso, o avião cruza apenas uma das nappes. Uma parábola também pode ser definida em termos de distâncias.
Uma parábola é o conjunto de todos os pontos cuja distância de um ponto fixo, chamado foco, é igual à distância de uma linha fixa, chamada diretriz. O ponto a meio caminho entre o foco e a diretriz é chamado de vértice da parábola.
Um gráfico de uma parábola típica aparece na Figura\(\PageIndex{3}\). Usando esse diagrama em conjunto com a fórmula da distância, podemos derivar uma equação para uma parábola. Lembre-se da fórmula da distância: Dado o ponto P com coordenadas\((x_1,y_1)\) e o ponto Q com coordenadas,\((x_2,y_2),\) a distância entre eles é dada pela fórmula
\[d(P,Q)=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2}. \nonumber \]
Então, a partir da definição de uma parábola e figura\(\PageIndex{3}\), obtemos
\[d(F,P)=d(P,Q) \nonumber \]
\[\sqrt{(0−x)^2+(p−y)^2}=\sqrt{(x−x)^2+(−p−y)^2}. \nonumber \]
Quadrando os dois lados e simplificando os rendimentos
\[ \begin{align} x^2+(p−y)^2 = 0^2+(−p−y)^2 \\ x^2+p^2−2py+y^2 = p^2+2py+y^2 \\ x^2−2py =2py \\ x^2 =4py. \end{align} \nonumber \]
Agora, suponha que desejemos realocar o vértice. Usamos as variáveis\((h,k)\) para indicar as coordenadas do vértice. Então, se o foco estiver diretamente acima do vértice, ele tem coordenadas\((h,k+p)\) e a diretriz tem a equação\(y=k−p\). Passar pela mesma derivação produz a fórmula\((x−h)^2=4p(y−k)\). Resolver essa equação\(y\) leva ao seguinte teorema.
Dada uma parábola se abrindo para cima com vértice localizado em\((h,k)\) e foco localizado em\((h,k+p)\), onde\(p\) está uma constante, a equação para a parábola é dada por
\[y=\dfrac{1}{4p}(x−h)^2+k. \nonumber \]
Essa é a forma padrão de uma parábola.
Também podemos estudar os casos em que a parábola se abre para baixo, para a esquerda ou para a direita. A equação para cada um desses casos também pode ser escrita na forma padrão, conforme mostrado nos gráficos a seguir.
Além disso, a equação de uma parábola pode ser escrita na forma geral, embora nesta forma os valores de\(h\)\(k\), e não\(p\) sejam imediatamente reconhecíveis. A forma geral de uma parábola é escrita como
\[ax^2+bx+cy+d=0 \label{para1} \]
ou
\[ay^2+bx+cy+d=0.\label{para2} \]
A equação\ ref {para1} representa uma parábola que se abre para cima ou para baixo. A equação\ ref {para2} representa uma parábola que se abre para a esquerda ou para a direita. Para colocar a equação na forma padrão, use o método de completar o quadrado.
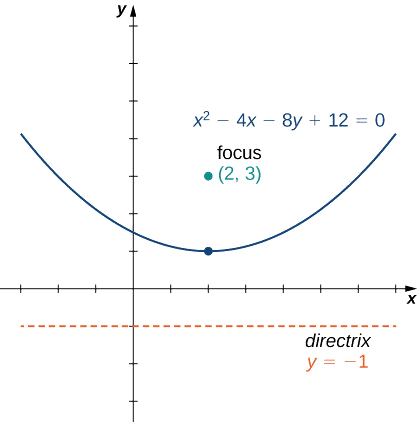
Coloque a equação
\[x^2−4x−8y+12=0 \nonumber \]
na forma padrão e represente graficamente a parábola resultante.
Solução
Como y não está quadrado nessa equação, sabemos que a parábola se abre para cima ou para baixo. Portanto, precisamos resolver essa equação para y, o que colocará a equação na forma padrão. Para fazer isso, primeiro adicione\(8y\) aos dois lados da equação:
\[8y=x^2−4x+12. \nonumber \]
O próximo passo é completar o quadrado no lado direito. Comece agrupando os dois primeiros termos no lado direito usando parênteses:
\[8y=(x^2−4x)+12. \nonumber \]
Em seguida, determine a constante que, quando adicionada entre parênteses, torna a quantidade dentro dos parênteses um trinômio quadrado perfeito. Para fazer isso, pegue metade do coeficiente de x e aumente o quadrado. Isso dá\((\dfrac{−4}{2})^2=4.\) Adicione 4 dentro dos parênteses e subtraia 4 fora dos parênteses, para que o valor da equação não seja alterado:
\[8y=(x^2−4x+4)+12−4. \nonumber \]
Agora combine termos semelhantes e fatore a quantidade dentro dos parênteses:
\[8y=(x−2)^2+8. \nonumber \]
Finalmente, divida por 8:
\[y=\dfrac{1}{8}(x−2)^2+1. \nonumber \]
Essa equação agora está na forma padrão. Comparando isso com a Equação dá\(h=2, k=1\),\(p=2\) e. A parábola se abre, com vértice em\((2,1)\), foco em\((2,3)\) e diretriz\(y=−1\). O gráfico dessa parábola aparece da seguinte forma.
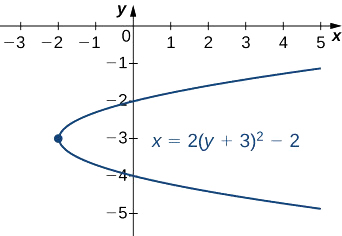
Coloque a equação\(2y^2−x+12y+16=0\) na forma padrão e represente graficamente a parábola resultante.
- Dica
-
Resolver para\(x\). Verifique em qual direção a parábola se abre.
- Responda
-
\[x=2(y+3)^2−2 \nonumber \]
O eixo de simetria de uma parábola vertical (abertura para cima ou para baixo) é uma linha vertical que passa pelo vértice. A parábola tem uma propriedade reflexiva interessante. Suponha que tenhamos uma antena parabólica com uma seção transversal parabólica. Se um feixe de ondas eletromagnéticas, como ondas de luz ou rádio, entrar na antena em uma linha reta de um satélite (paralelo ao eixo de simetria), as ondas refletirão na antena e se acumularão no foco da parábola, conforme mostrado.
Considere uma antena parabólica projetada para coletar sinais de um satélite no espaço. A antena é direcionada diretamente para o satélite e um receptor está localizado no foco da parábola. As ondas de rádio vindas do satélite são refletidas da superfície da parábola para o receptor, que coleta e decodifica os sinais digitais. Isso permite que um pequeno receptor colete sinais de um grande ângulo do céu. As lanternas e os faróis de um carro funcionam segundo o mesmo princípio, mas ao contrário: a fonte da luz (ou seja, a lâmpada) está localizada no foco e a superfície refletora no espelho parabólico focaliza o feixe diretamente à frente. Isso permite que uma pequena lâmpada ilumine um amplo ângulo de espaço na frente da lanterna ou do carro.
Elipses
Uma elipse também pode ser definida em termos de distâncias. No caso de uma elipse, há dois focos (plural de foco) e duas diretrices (plural de diretriz). Examinaremos os diretórios com mais detalhes posteriormente nesta seção.
Uma elipse é o conjunto de todos os pontos para os quais a soma de suas distâncias de dois pontos fixos (os focos) é constante.
Um gráfico de uma elipse típica é mostrado na Figura\(\PageIndex{6}\). Nesta figura, os focos são rotulados como\(F\)\(F′\) e. Ambos têm a mesma distância fixa da origem, e essa distância é representada pela variável\(c\). Portanto, as coordenadas de\(F\) são\((c,0)\) e as coordenadas de\(F′\)\(P′\) são\((−c,0).\) Os pontos\(P\) e estão localizadas nas extremidades do eixo maior da elipse e têm coordenadas\((a,0)\) e\((−a,0)\), respectivamente. O eixo maior é sempre a maior distância da elipse e pode ser horizontal ou vertical. Assim, o comprimento do eixo principal nesta elipse é\(2a\). Além disso,\(P\) e\(P′\) são chamados de vértices da elipse. Os pontos\(Q\)\(Q′\) estão localizados nas extremidades do eixo menor da elipse e têm coordenadas\((0,b)\) e\((0,−b),\) respectivamente. O eixo menor é a menor distância na elipse. O eixo menor é perpendicular ao eixo maior.
De acordo com a definição da elipse, podemos escolher qualquer ponto da elipse e a soma das distâncias desse ponto aos dois focos é constante. Suponha que escolhamos o ponto\(P\). Como as coordenadas do ponto\(P\) são,\((a,0),\) a soma das distâncias é
\[d(P,F)+d(P,F′)=(a−c)+(a+c)=2a. \nonumber \]
Portanto, a soma das distâncias de um ponto arbitrário A com coordenadas também\((x,y)\) é igual\(2a\) a. Usando a fórmula da distância, obtemos
\[d(A,F)+d(A,F′)=2a. \nonumber \]
\[\sqrt{(x−c)^2+y^2}+\sqrt{(x+c)^2+y^2}=2a \nonumber \]
Subtraia o segundo radical de ambos os lados e coloque o quadrado em ambos os lados:
\[\sqrt{(x−c)^2+y^2}=2a−\sqrt{(x+c)^2+y^2} \nonumber \]
\[(x−c)^2+y^2=4a^2−4a\sqrt{(x+c)^2+y^2}+(x+c)^2+y^2 \nonumber \]
\[x^2−2cx+c^2+y^2=4a^2−4a\sqrt{(x+c)^2+y^2}+x^2+2cx+c^2+y^2 \nonumber \]
\[−2cx=4a^2−4a\sqrt{(x+c)^2+y^2}+2cx. \nonumber \]
Agora isole o radical no lado direito e faça o quadrado novamente:
\[−2cx=4a^2−4a\sqrt{(x+c)^2+y^2}+2cx \nonumber \]
\[4a\sqrt{(x+c)^2+y^2}=4a^2+4cx \nonumber \]
\[\sqrt{(x+c)^2+y^2}=a+\dfrac{cx}{a} \nonumber \]
\[(x+c)^2+y^2=a^2+2cx+\dfrac{c^2x^2}{a^2} \nonumber \]
\[x^2+2cx+c^2+y^2=a^2+2cx+\dfrac{c^2x^2}{a^2} \nonumber \]
\[x^2+c^2+y^2=a^2+\dfrac{c^2x^2}{a^2}. \nonumber \]
Isole as variáveis no lado esquerdo da equação e as constantes no lado direito:
\[x^2−\dfrac{c^2x^2}{a^2}+y^2=a^2−c^2 \nonumber \]
\[\dfrac{(a^2−c^2)x^2}{a^2}+y^2=a^2−c^2. \nonumber \]
Divida os dois lados por\(a^2−c^2\). Isso dá a equação
\[\dfrac{x^2}{a^2}+\dfrac{y^2}{a^2−c^2}=1. \nonumber \]
Se nos referirmos à Figura\(\PageIndex{6}\), o comprimento de cada um dos dois segmentos da linha verde é igual\(a\) a. Isso é verdade porque a soma das distâncias do ponto\(Q\) até os focos\(F\)\(F′\) é igual a\(2a\), e os comprimentos desses dois segmentos de linha são iguais. Este segmento de linha forma um triângulo reto com comprimento de hipotenusa\(a\) e comprimento de perna\(c\) e.\(b\) Do teorema de Pitágoras,\(b^2+c^2=a^2\)\(b^2=a^2−c^2\) e. Portanto, a equação da elipse se torna
\[\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1. \nonumber \]
Finalmente, se o centro da elipse for movido da origem para um ponto\((h,k)\), temos a seguinte forma padrão de elipse.
Considere a elipse com centro\((h,k)\), um eixo maior horizontal com comprimento\(2a\) e um eixo menor vertical com comprimento\(2b\). Então, a equação dessa elipse na forma padrão é
\[\dfrac{(x−h)^2}{a^2}+\dfrac{(y−k)^2}{b^2}=1 \label{HorEllipse} \]
e os focos estão localizados em\((h±c,k)\), onde\(c^2=a^2−b^2\). As equações das diretrices são\(x=h±\dfrac{a^2}{c}\).
Se o eixo principal for vertical, a equação da elipse se torna
\[\dfrac{(x−h)^2}{b^2}+\dfrac{(y−k)^2}{a^2}=1 \label{VertEllipse} \]
e os focos estão localizados em\((h,k±c)\), onde\(c^2=a^2−b^2\). As equações das diretrices neste caso são\(y=k±\dfrac{a^2}{c}\).
Se o eixo maior for horizontal, a elipse será chamada horizontal, e se o eixo maior for vertical, a elipse será chamada vertical. A equação de uma elipse está na forma geral se estiver na forma
\[Ax^2+By^2+Cx+Dy+E=0, \nonumber \]
onde A e B são ambos positivos ou negativos. Para converter a equação da forma geral para a forma padrão, use o método de completar o quadrado.
Coloque a equação
\[9x^2+4y^2−36x+24y+36=0 \nonumber \]
na forma padrão e represente graficamente a elipse resultante.
Solução
Primeiro subtraia 36 dos dois lados da equação:
\[9x^2+4y^2−36x+24y=−36. \nonumber \]
Em seguida, agrupe os\(x\)\(y\) termos e os termos juntos e considere o fator comum:
\[(9x^2−36x)+(4y^2+24y)=−36 \nonumber \]
\[9(x^2−4x)+4(y^2+6y)=−36. \nonumber \]
Precisamos determinar a constante que, quando adicionada dentro de cada conjunto de parênteses, resulta em um quadrado perfeito. No primeiro conjunto de parênteses, pegue metade do coeficiente de x e eleve-o ao quadrado. Isso dá\((\dfrac{−4}{2})^2=4.\) No segundo conjunto de parênteses, pegue a metade do coeficiente de y e eleve-o ao quadrado. Isso dá\((\dfrac{6}{2})^2=9.\) Adicione estes dentro de cada par de parênteses. Como o primeiro conjunto de parênteses tem um 9 na frente, na verdade estamos adicionando 36 no lado esquerdo. Da mesma forma, também estamos adicionando 36 ao segundo conjunto. Portanto, a equação se torna
\[9(x^2−4x+4)+4(y^2+6y+9)=−36+36+36 \nonumber \]
\[9(x^2−4x+4)+4(y^2+6y+9)=36. \nonumber \]
Agora, fatore os dois conjuntos de parênteses e divida por 36:
\[9(x−2)^2+4(y+3)^2=36 \nonumber \]
\[\dfrac{9(x−2)^2}{36}+\dfrac{4(y+3)^2}{36}=1 \nonumber \]
\[\dfrac{(x−2)^2}{4}+\dfrac{(y+3)^2}{9}=1. \nonumber \]
A equação agora está na forma padrão. Comparando isso com a Equação\ ref {verteLlipse} fornece\(h=2, k=−3, a=3,\)\(b=2\) e. Esta é uma elipse vertical com centro em\((2,−3)\), eixo maior 6 e eixo menor 4. O gráfico dessa elipse aparece da seguinte forma.

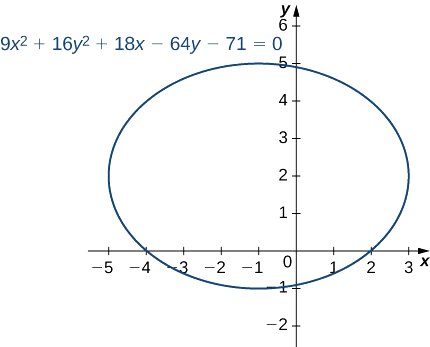
Coloque a equação
\[9x^2+16y^2+18x−64y−71=0 \nonumber \]
na forma padrão e represente graficamente a elipse resultante.
- Dica
-
Mova a constante e complete o quadrado.
- Responda
-
\[\dfrac{(x+1)^2}{16}+\dfrac{(y−2)^2}{9}=1 \nonumber \]
De acordo com a primeira lei do movimento planetário de Kepler, a órbita de um planeta ao redor do Sol é uma elipse com o Sol em um dos focos, conforme mostrado na Figura\(\PageIndex{8A}\). Como a órbita da Terra é uma elipse, a distância do Sol varia ao longo do ano. Um equívoco comum é que a Terra está mais próxima do Sol no verão. Na verdade, no verão, no hemisfério norte, a Terra está mais distante do Sol do que no inverno. A diferença de estação é causada pela inclinação do eixo da Terra no plano orbital. Cometas que orbitam o Sol, como o Cometa Halley, também têm órbitas elípticas, assim como as luas que orbitam os planetas e os satélites que orbitam a Terra.
As elipses também têm propriedades refletivas interessantes: um raio de luz que emana de um foco passa pelo outro foco após a reflexão do espelho na elipse. O mesmo acontece com uma onda sonora. O National Statuary Hall no Capitólio dos EUA em Washington, DC, é uma sala famosa em formato elíptico, conforme mostrado na Figura\(\PageIndex{8B}\). Este salão serviu como ponto de encontro para a Câmara dos Deputados dos EUA por quase cinquenta anos. A localização dos dois focos dessa sala semi-elíptica é claramente identificada por marcas no chão e, mesmo que a sala esteja cheia de visitantes, quando duas pessoas ficam nesses locais e falam uma com a outra, elas podem se ouvir com muito mais clareza do que ouvem alguém por perto. Diz a lenda que John Quincy Adams tinha sua mesa localizada em um dos focos e foi capaz de escutar todos os outros na casa sem precisar ficar de pé. Embora isso seja uma boa história, é improvável que seja verdade, porque o teto original produzia tantos ecos que toda a sala teve que ser pendurada com tapetes para diminuir o ruído. O teto foi reconstruído em 1902 e só então surgiu o agora famoso efeito de sussurro. Outra famosa galeria de sussurros - o local de muitas propostas de casamento - fica na Grand Central Station, na cidade de Nova York.
Hipérbolas
Uma hipérbole também pode ser definida em termos de distâncias. No caso de uma hipérbole, existem dois focos e duas diretrices. As hipérboles também têm duas assíntotas.
Uma hipérbole é o conjunto de todos os pontos em que a diferença entre suas distâncias de dois pontos fixos (os focos) é constante.
Um gráfico de uma hipérbole típica aparece da seguinte forma.
A derivação da equação de uma hipérbole na forma padrão é virtualmente idêntica à de uma elipse. Um pequeno obstáculo está na definição: A diferença entre dois números é sempre positiva. \(P\)Seja um ponto na hipérbole com coordenadas\((x,y)\). Então, a definição da hipérbole dá\(|d(P,F_1)−d(P,F_2)|=constant\). Para simplificar a derivação, suponha que\(P\) esteja no ramo direito da hipérbole, então as barras de valor absoluto caiam. Se estiver no ramo esquerdo, a subtração será revertida. O vértice do ramo direito tem coordenadas\((a,0),\), então
\[d(P,F_1)−d(P,F_2)=(c+a)−(c−a)=2a. \nonumber \]
Portanto, essa equação é verdadeira para qualquer ponto da hipérbole. Retornando às coordenadas\((x,y)\) de\(P\):
\[d(P,F_1)−d(P,F_2)=2a \nonumber \]
\[\sqrt{(x+c)^2+y^2}−\sqrt{(x−c)^2+y^2}=2a. \nonumber \]
Isole o segundo radical e coloque o quadrado em ambos os lados:
\[\sqrt{(x−c)^2+y^2}=-2a+\sqrt{(x+c)^2+y^2} \nonumber \]
\[(x−c)^2+y^2=4a^2-4a\sqrt{(x+c)^2+y^2}+(x+c)^2+y^2 \nonumber \]
\[x^2−2cx+c^2+y^2=4a^2-4a\sqrt{(x+c)^2+y^2}+x^2+2cx+c^2+y^2 \nonumber \]
\[−2cx=4a^2-4a\sqrt{(x+c)^2+y^2}+2cx. \nonumber \]
Agora isole o radical no lado direito e faça o quadrado novamente:
\(−2cx=4a^2-4a\sqrt{(x+c)^2+y^2}+2cx\)
\(-4a\sqrt{(x+c)^2+y^2}=−4a^2−4cx\)
\(-\sqrt{(x+c)^2+y^2}=−a−\dfrac{cx}{a}\)
\((x+c)^2+y^2=a^2+2cx+\dfrac{c^2x^2}{a^2}\)
\(x^2+2cx+c^2+y^2=a^2+2cx+\dfrac{c^2x^2}{a^2}\)
\(x^2+c^2+y^2=a^2+\dfrac{c^2x^2}{a^2}\).
Isole as variáveis no lado esquerdo da equação e as constantes no lado direito:
\[x^2−\dfrac{c^2x^2}{a^2}+y^2=a^2−c^2 \nonumber \]
\[\dfrac{(a^2−c^2)x^2}{a^2}+y^2=a^2−c^2. \nonumber \]
Finalmente, divida os dois lados por\(a^2−c^2\). Isso dá a equação
\[\dfrac{x^2}{a^2}+\dfrac{y^2}{a^2−c^2}=1. \nonumber \]
Agora definimos b para que\(b^2=c^2−a^2\). Isso é possível porque\(c>a\). Portanto, a equação da hipérbole se torna
\[\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1. \nonumber \]
Finalmente, se o centro da hipérbole for movido da origem para o ponto,\((h,k),\) temos a seguinte forma padrão de hipérbole.
Considere a hipérbole com centro\((h,k)\), um eixo maior horizontal e um eixo menor vertical. Então, a equação dessa hipérbole é
\[\dfrac{(x−h)^2}{a^2}−\dfrac{(y−k)^2}{b^2}=1 \label{HorHyperbola} \]
e os focos estão localizados\((h±c,k),\) onde\(c^2=a^2+b^2\). As equações das assíntotas são dadas por\(y=k±\dfrac{b}{a}(x−h).\) As equações das diretrices são
\[x=h±\dfrac{a^2}{\sqrt{a^2+b^2}}=h±\dfrac{a^2}{c} \nonumber \]
Se o eixo principal for vertical, a equação da hipérbole se torna
\[\dfrac{(y−k)^2}{a^2}−\dfrac{(x−h)^2}{b^2}=1 \nonumber \]
e os focos estão localizados\((h,k±c),\) onde\(c^2=a^2+b^2\). As equações das assíntotas são dadas por\(y=k±\dfrac{a}{b}(x−h)\). As equações das diretrices são
\[y=k±\dfrac{a^2}{\sqrt{a^2+b^2}}=k±\dfrac{a^2}{c}. \nonumber \]
Se o eixo maior (eixo transversal) for horizontal, a hipérbole é chamada horizontal, e se o eixo maior for vertical, a hipérbole é chamada vertical. A equação de uma hipérbole está na forma geral se estiver na forma
\[Ax^2+By^2+Cx+Dy+E=0, \nonumber \]
onde A e B têm sinais opostos. Para converter a equação da forma geral para a forma padrão, use o método de completar o quadrado.
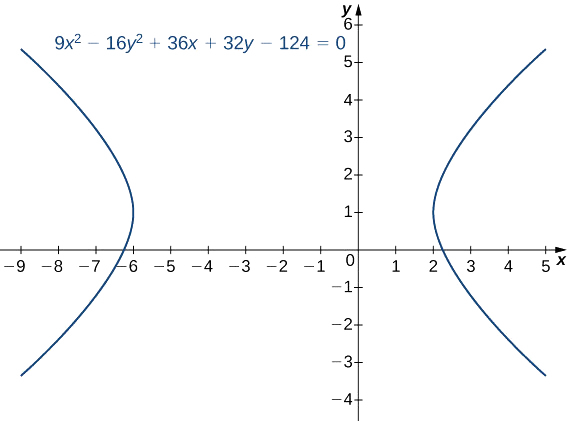
Coloque a equação\(9x^2−16y^2+36x+32y−124=0\) na forma padrão e represente graficamente a hipérbole resultante. Quais são as equações das assíntotas?
Solução
Primeiro, adicione 124 aos dois lados da equação:
\(9x^2−16y^2+36x+32y=124.\)
Em seguida, agrupe os termos x juntos e os termos y juntos e, em seguida, considere os fatores comuns:
\((9x^2+36x)−(16y^2−32y)=124\)
\(9(x^2+4x)−16(y^2−2y)=124\).
Precisamos determinar a constante que, quando adicionada dentro de cada conjunto de parênteses, resulta em um quadrado perfeito. No primeiro conjunto de parênteses, pegue metade do coeficiente de x e eleve-o ao quadrado. Isso dá\((\dfrac{4}{2})^2=4\). No segundo conjunto de parênteses, pegue metade do coeficiente y e aumente o quadrado. Isso dá\((\dfrac{−2}{2})^2=1.\) Adicione estes dentro de cada par de parênteses. Como o primeiro conjunto de parênteses tem um 9 na frente, na verdade estamos adicionando 36 no lado esquerdo. Da mesma forma, estamos subtraindo 16 do segundo conjunto de parênteses. Portanto, a equação se torna
\(9(x^2+4x+4)−16(y^2−2y+1)=124+36−16\)
\(9(x^2+4x+4)−16(y^2−2y+1)=144.\)
Em seguida, fatore os dois conjuntos de parênteses e divida por 144:
\(9(x+2)^2−16(y−1)^2=144\)
\(\dfrac{9(x+2)^2}{144}−\dfrac{16(y−1)^2}{144}=1\)
\(\dfrac{(x+2)^2}{16}−\dfrac{(y−1)^2}{9}=1.\)
A equação agora está na forma padrão. Comparando isso com a Equação\ ref {horHyperbola} dá\(h=−2, k=1, a=4,\)\(b=3\) e. Esta é uma hipérbole horizontal com centro em\((−2,1)\) e assíntotas dadas pelas equações\(y=1±\dfrac{3}{4}(x+2)\). O gráfico dessa hipérbole aparece na Figura\(\PageIndex{10}\).
Coloque a equação\(4y^2−9x^2+16y+18x−29=0\) na forma padrão e represente graficamente a hipérbole resultante. Quais são as equações das assíntotas?
- Dica
-
Mova a constante e complete o quadrado. Verifique em qual direção a hipérbole se abre
- Responda
-
\(\dfrac{(y+2)^2}{9}−\dfrac{(x−1)^2}{4}=1.\)Isso é uma hipérbole vertical. Assíntotas\(y=−2±\dfrac{3}{2}(x−1).\)

As hipérboles também têm propriedades refletivas interessantes. Um raio direcionado para um foco de uma hipérbole é refletido por um espelho hiperbólico em direção ao outro foco. Esse conceito é ilustrado na Figura\(\PageIndex{11}\).
Essa propriedade da hipérbole tem aplicações importantes. É usado na busca da direção do rádio (já que a diferença nos sinais de duas torres é constante ao longo das hipérboles) e na construção de espelhos dentro de telescópios (para refletir a luz vinda do espelho parabólico para a ocular). Outro fato interessante sobre as hipérboles é que, para um cometa entrar no sistema solar, se a velocidade for grande o suficiente para escapar da atração gravitacional do Sol, o caminho que o cometa percorre ao passar pelo sistema solar é hiperbólico.
Excentricidade e diretriz
Uma forma alternativa de descrever uma seção cônica envolve as diretrices, os focos e uma nova propriedade chamada excentricidade. Veremos que o valor da excentricidade de uma seção cônica pode definir com exclusividade essa cônica.
A excentricidade \(e\)de uma seção cônica é definida como a distância de qualquer ponto na seção cônica até seu foco, dividida pela distância perpendicular desse ponto até a diretriz mais próxima. Esse valor é constante para qualquer seção cônica e também pode definir a seção cônica:
- Se\(e=1\), a cônica é uma parábola.
- Se\(e<1\), é uma elipse.
- Se\(e>1,\) for uma hipérbole.
A excentricidade de um círculo é zero. A diretriz de uma seção cônica é a linha que, junto com o ponto conhecido como foco, serve para definir uma seção cônica. Hipérboles e elipses não circulares têm dois focos e duas diretrices associadas. As parábolas têm um foco e uma diretriz.
As três seções cônicas com suas diretrices aparecem na Figura\(\PageIndex{12}\).
Lembre-se da definição de uma parábola que a distância de qualquer ponto da parábola até o foco é igual à distância desse mesmo ponto até a diretriz. Portanto, por definição, a excentricidade de uma parábola deve ser 1. As equações das diretrices de uma elipse horizontal são\(x=±\dfrac{a^2}{c}\). O vértice direito da elipse está localizado em\((a,0)\) e o foco direito está\((c,0)\). Portanto, a distância do vértice ao foco é\(a−c\) e a distância do vértice à diretriz direita é\(\dfrac{a^2}{c}−c.\) Isso dá a excentricidade como
\[e=\dfrac{a−c}{\dfrac{a^2}{c}−a}=\dfrac{c(a−c)}{a^2−ac}=\dfrac{c(a−c)}{a(a−c)}=\dfrac{c}{a}. \nonumber \]
Pois\(c<a\), essa etapa prova que a excentricidade de uma elipse é menor que 1. As diretrices de uma hipérbole horizontal também estão localizadas em\(x=±\dfrac{a^2}{c}\), e um cálculo semelhante mostra que a excentricidade de uma hipérbole também está\(e=\dfrac{c}{a}\). No entanto, neste caso\(c>a\), temos, então a excentricidade de uma hipérbole é maior que 1.
Determine a excentricidade da elipse descrita pela equação
\(\dfrac{(x−3)^2}{16}+\dfrac{(y+2)^2}{25}=1.\)
Solução
A partir da equação, vemos isso\(a=5\)\(b=4\) e. O valor de c pode ser calculado usando a equação\(a^2=b^2+c^2\) de uma elipse. Substituindo os valores de a e b e resolvendo por c, obtém-se\(c=3\). Portanto, a excentricidade da elipse é\(e=\dfrac{c}{a}=\dfrac{3}{5}=0.6.\)
Determine a excentricidade da hipérbole descrita pela equação
\(\dfrac{(y−3)^2}{49}−\dfrac{(x+2)^2}{25}=1.\)
- Dica
-
Primeiro, encontre os valores de a e b e, em seguida, determine c usando a equação\(c^2=a^2+b^2\).
- Responda
-
\(e=\dfrac{c}{a}=\dfrac{\sqrt{74}}{7}≈1.229\)
Equações polares de seções cônicas
Às vezes, é útil escrever ou identificar a equação de uma seção cônica na forma polar. Para fazer isso, precisamos do conceito do parâmetro focal. O parâmetro focal de uma seção cônica p é definido como a distância de um foco até a diretriz mais próxima. A tabela a seguir fornece os parâmetros focais para os diferentes tipos de cônicas, onde a é o comprimento do semi-eixo maior (ou seja, metade do comprimento do eixo principal), c é a distância da origem ao foco e e é a excentricidade. No caso de uma parábola, a representa a distância do vértice até o foco.
| Cônico | \(e\) | \(p\) |
|---|---|---|
| Elipse | \ (e\)” style="alinhamento vertical: meio; ">\(0<e<1\) | \ (p\)” style="alinhamento vertical: médio; ">\(\dfrac{a^2−c^2}{c}=\dfrac{a(1−e^2)}{c}\) |
| Parábola | \ (e\)” style="alinhamento vertical: meio; ">\(e=1\) | \ (p\)” style="alinhamento vertical: médio; ">\(2a\) |
| Hyperbole | \ (e\)” style="alinhamento vertical: meio; ">\(e>1\) | \ (p\)” style="alinhamento vertical: médio; ">\(\dfrac{c^2−a^2}{c}=\dfrac{a(e^2−1)}{c}\) |
Usando as definições do parâmetro focal e da excentricidade da seção cônica, podemos derivar uma equação para qualquer seção cônica em coordenadas polares. Em particular, assumimos que um dos focos de uma determinada seção cônica está no polo. Então, usando a definição das várias seções cônicas em termos de distâncias, é possível provar o seguinte teorema.
A equação polar de uma seção cônica com o parâmetro focal p é dada por
\(r=\dfrac{ep}{1±e\cos θ}\)ou\(r=\dfrac{ep}{1±e\sin θ}.\)
Na equação à esquerda, o eixo principal da seção cônica é horizontal, e na equação à direita, o eixo principal é vertical. Para trabalhar com uma seção cônica escrita na forma polar, primeiro faça com que o termo constante no denominador seja igual a 1. Isso pode ser feito dividindo o numerador e o denominador da fração pela constante que aparece na frente do mais ou menos no denominador. Então, o coeficiente do seno ou cosseno no denominador é a excentricidade. Esse valor identifica a cônica. Se o cosseno aparecer no denominador, a cônica será horizontal. Se o seno aparecer, a cônica será vertical. Se ambos aparecerem, os eixos serão girados. O centro da cônica não está necessariamente na origem. O centro está na origem somente se a cônica for um círculo (ou seja,\(e=0\)).
Identifique e crie um gráfico da seção cônica descrita pela equação
\(r=\dfrac{3}{1+2\cos θ}\).
Solução
O termo constante no denominador é 1, então a excentricidade da cônica é 2. Isso é uma hipérbole. O parâmetro focal p pode ser calculado usando a equação\(ep=3.\) Since\(e=2\), isso fornece\(p=\dfrac{3}{2}\). A função cosseno aparece no denominador, então a hipérbole é horizontal. Escolha alguns valores\(θ\) e crie uma tabela de valores. Em seguida, podemos representar graficamente a hipérbole (Figura\(\PageIndex{13}\)).
| \(θ\) | \(r\) | \(θ\) | \(r\) |
|---|---|---|---|
| \ (θ\)” style="alinhamento vertical: médio; ">0 | \ (r\)” style="alinhamento vertical: médio; ">1 | \ (θ\)” style="alinhamento vertical: meio; ">\(π\) | \ (r\)” style="alinhamento vertical: médio; ">−3 |
| \ (θ\)” style="alinhamento vertical: meio; ">\(\dfrac{π}{4}\) | \ (r\)” style="alinhamento vertical: médio; ">\(\dfrac{3}{1+\sqrt{2}}≈1.2426\) | \ (θ\)” style="alinhamento vertical: meio; ">\(\dfrac{5π}{4}\) | \ (r\)” style="alinhamento vertical: médio; ">\(\dfrac{3}{1−\sqrt{2}}≈−7.2426\) |
| \ (θ\)” style="alinhamento vertical: meio; ">\(\dfrac{π}{2}\) | \ (r\)” style="alinhamento vertical: médio; ">3 | \ (θ\)” style="alinhamento vertical: meio; ">\(\dfrac{3π}{2}\) | \ (r\)” style="alinhamento vertical: médio; ">3 |
| \ (θ\)” style="alinhamento vertical: meio; ">\(\dfrac{3π}{4}\) | \ (r\)” style="alinhamento vertical: médio; ">\(\dfrac{3}{1−\sqrt{2}}≈−7.2426\) | \ (θ\)” style="alinhamento vertical: meio; ">\(\dfrac{7π}{4}\) | \ (r\)” style="alinhamento vertical: médio; ">\(\dfrac{3}{1+\sqrt{2}}≈1.2426\) |
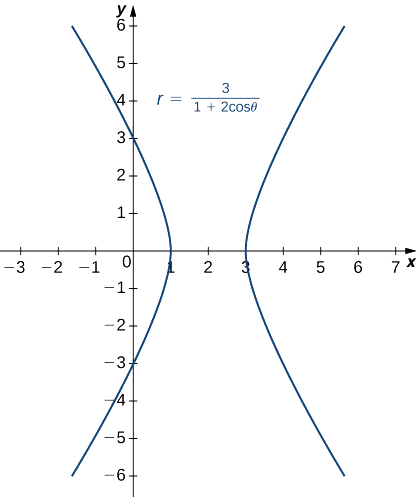
Identifique e crie um gráfico da seção cônica descrita pela equação
\(r=\dfrac{4}{1−0.8 \sin θ}\).
- Dica
-
Primeiro, encontre os valores de e e p e, em seguida, crie uma tabela de valores.
- Responda
-
Aqui\(e=0.8\)\(p=5\) e. Essa seção cônica é uma elipse.
Equações gerais de grau dois
Uma equação geral de grau dois pode ser escrita na forma
\[ Ax^2+Bxy+Cy^2+Dx+Ey+F=0. \nonumber \]
O gráfico de uma equação dessa forma é uma seção cônica. \(B≠0\)Em caso afirmativo, os eixos coordenados são rotacionados. Para identificar a seção cônica, usamos o discriminante da seção cônica\(4AC−B^2.\)
Um dos seguintes casos deve ser verdadeiro:
- \(4AC−B^2>0\). Se sim, o gráfico é uma elipse.
- \(4AC−B^2=0\). Se sim, o gráfico é uma parábola.
- \(4AC−B^2<0\). Se sim, o gráfico é uma hipérbole.
O exemplo mais simples de uma equação de segundo grau envolvendo um termo cruzado é\(xy=1\). Essa equação pode ser resolvida\(y\) para obter\(y=\dfrac{1}{x}\). O gráfico dessa função é chamado de hipérbole retangular, conforme mostrado.
As assíntotas dessa hipérbole são\(x\) os eixos\(y\) coordenados e. Para determinar o ângulo θ de rotação da seção cônica, usamos a fórmula\(\cot 2θ=\frac{A−C}{B}\). Neste caso\(B=1\),\(A=C=0\)\(\cot 2θ=(0−0)/1=0\) e assim por diante\(θ=45°\). O método para representar graficamente uma seção cônica com eixos girados envolve a determinação dos coeficientes da cônica no sistema de coordenadas rotacionadas. Os novos coeficientes são rotulados\(A′,B′,C′,D′,E′,\)\(F′,\) e fornecidos pelas fórmulas
\[ \begin{align} A′ =A\cos^ 2θ+B\cos θ\sin θ+C\sin^2 θ \\ B′ =0 \\ C′ =A\sin^2 θ−B\sin θ\cos θ+C\cos^2θ \\ D′ =D\cos θ+E\sin θ \\ E′ =−D\sin θ+E\cosθ \\ F′ =F. \end{align} \nonumber \]
O procedimento para representar graficamente uma cônica girada é o seguinte:
- Identifique a seção cônica usando o discriminante\(4AC−B^2\).
- Determine\(θ\) usando a fórmula\[\cot2θ=\dfrac{A−C}{B} \label{rot}. \]
- Calcule\(A′,B′,C′,D′,E′\),\(F′\) e.
- Reescreva a equação original usando\(A′,B′,C′,D′,E′\),\(F′\) e.
- Desenhe um gráfico usando a equação rotacionada.
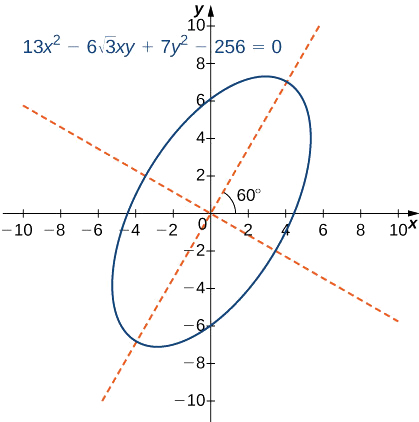
Identifique a cônica e calcule o ângulo de rotação dos eixos para a curva descrita pela equação
\[13x^2−6\sqrt{3}xy+7y^2−256=0. \nonumber \]
Solução
Nesta equação,\(A=13,B=−6\sqrt{3},C=7,D=0,E=0,\)\(F=−256\) e. O discriminante dessa equação é
\[4AC−B^2=4(13)(7)−(−6\sqrt{3})^2=364−108=256. \nonumber \]
Portanto, essa cônica é uma elipse.
Para calcular o ângulo de rotação dos eixos, use Equation\ ref {rot}
\[\cot 2θ=\dfrac{A−C}{B}. \nonumber \]
Isso dá
\(\cot 2θ=\dfrac{A−C}{B}=\dfrac{13−7}{−6\sqrt{3}}=−\dfrac{\sqrt{3}}{3}\).
Portanto\(θ=60^o\),\(2θ=120^o\) e, que é o ângulo de rotação dos eixos.
Para determinar os coeficientes rotacionados, use as fórmulas dadas acima:
\(A′=A\cos^2θ+B\cos θ\sinθ+C\sin^2θ\)
\(=13\cos^260+(−6\sqrt{3})\cos 60 \sin 60+7\sin^260\)
\(=13(\dfrac{1}{2})^2−6\sqrt{3}(\dfrac{1}{2})(\dfrac{\sqrt{3}}{2})+7(\dfrac{\sqrt{3}}{2})^2\)
\(=4,\)
\(B′=0\)
\(C′=A\sin^2θ−B\sin θ\cos θ+C\cos^2θ\)
\(=13\sin^260+(6\sqrt{3})\sin 60 \cos 60+7\cos^260\)
\(=13(\dfrac{\sqrt{3}}{2})^2+6\sqrt{3}(\dfrac{\sqrt{3}}{2})(\dfrac{1}{2})+7(\dfrac{1}{2})^2\)
\(=16,\)
\(D′=D\cos θ+E\sin θ\)
\(=(0)\cos 60+(0)\sin 60\)
\(=0,\)
\(E′=−D\sin θ+E\cos θ\)
\(=−(0)\sin 60+(0)\cos 60\)
\(=0\)
\(F′= F\)
\(=−256.\)
A equação da cônica no sistema de coordenadas rotacionadas se torna
\(4(x′)^2+16(y′)^2=256\)
\(\dfrac{(x′)^2}{64}+\dfrac{(y′)^2}{16}=1\).
Um gráfico dessa seção cônica aparece da seguinte forma.
Identifique a cônica e calcule o ângulo de rotação dos eixos para a curva descrita pela equação
\[3x^2+5xy−2y^2−125=0. \nonumber \]
- Dica
-
Siga as etapas 1 e 2 do método de cinco etapas descrito acima
- Responda
-
A cônica é uma hipérbole e o ângulo de rotação dos eixos é\(θ=22.5°.\)
Conceitos chave
- A equação de uma parábola vertical na forma padrão com determinado foco e diretriz\(p\) é\(y=\dfrac{1}{4p}(x−h)^2+k\) onde está a distância do vértice ao foco e\((h,k)\) são as coordenadas do vértice.
- A equação de uma elipse horizontal na forma padrão é\(\dfrac{(x−h)^2}{a^2}+\dfrac{(y−k)^2}{b^2}=1\) onde o centro tem coordenadas\((h,k)\), o eixo maior tem comprimento 2a, o eixo menor tem comprimento 2b e as coordenadas dos focos são\((h±c,k)\), onde\(c^2=a^2−b^2\).
- A equação de uma hipérbole horizontal na forma padrão é\(\dfrac{(x−h)^2}{a^2}−\dfrac{(y−k)^2}{b^2}=1\) onde o centro tem coordenadas\((h,k)\), os vértices estão localizados e as coordenadas dos focos estão\((h±c,k),\) onde\(c^2=a^2+b^2\).\((h±a,k)\)
- A excentricidade de uma elipse é menor que 1, a excentricidade de uma parábola é igual a 1 e a excentricidade de uma hipérbole é maior que 1. A excentricidade de um círculo é 0.
- A equação polar de uma seção cônica com excentricidade e é\(r=\dfrac{ep}{1±ecosθ}\) ou\(r=\dfrac{ep}{1±esinθ}\), onde p representa o parâmetro focal.
- Para identificar uma cônica gerada pela equação\(Ax^2+Bxy+Cy^2+Dx+Ey+F=0\), primeiro calcule o discriminante\(D=4AC−B^2\). Se\(D>0\) então a cônica é uma elipse, se\(D=0\) então a cônica é uma parábola, e se\(D<0\) então a cônica é uma hipérbole.
Glossário
- seção cônica
- uma seção cônica é qualquer curva formada pela interseção de um plano com um cone de duas nappes
- diretriz
- uma diretriz (plural: diretrices) é uma linha usada para construir e definir uma seção cônica; uma parábola tem uma diretriz; elipses e hipérboles têm duas
- discriminante
- o valor\(4AC−B^2\), que é usado para identificar uma cônica quando a equação contém um termo envolvendo\(xy\), é chamado de discriminante
- foco
- um foco (plural: focos) é um ponto usado para construir e definir uma seção cônica; uma parábola tem um foco; uma elipse e uma hipérbole têm dois
- excentricidade
- a excentricidade é definida como a distância de qualquer ponto da seção cônica até seu foco dividida pela distância perpendicular desse ponto até a diretriz mais próxima
- parâmetro focal
- o parâmetro focal é a distância de um foco de uma seção cônica até a diretriz mais próxima
- forma geral
- uma equação de uma seção cônica escrita como uma equação geral de segundo grau
- eixo principal
- o eixo maior de uma seção cônica passa pelo vértice no caso de uma parábola ou pelos dois vértices no caso de uma elipse ou hipérbole; também é um eixo de simetria da cônica; também chamado de eixo transversal
- eixo menor
- o eixo menor é perpendicular ao eixo maior e cruza o eixo maior no centro da cônica, ou no vértice no caso da parábola; também chamado de eixo conjugado
- nuca
- uma nuca é metade de um cone duplo
- formulário padrão
- uma equação de uma seção cônica mostrando suas propriedades, como localização do vértice ou comprimentos dos eixos maiores e menores
- vértice
- um vértice é um ponto extremo em uma seção cônica; uma parábola tem um vértice em seu ponto de virada. Uma elipse tem dois vértices, um em cada extremidade do eixo maior; uma hipérbole tem dois vértices, um no ponto de virada de cada ramo


