10.3E: Exercícios para a Seção 10.3

Polinômios de Taylor

Nos exercícios 1 a 8, encontre os polinômios de Taylor de grau dois que se aproximam da função dada centrada em um determinado ponto.

1)\( f(x)=1+x+x^2\) em\( a=1\)

2)\( f(x)=1+x+x^2\) em\( a=−1\)

Resposta

\( f(−1)=1;\;f′(−1)=−1;\;f''(−1)=2;\quad p_2(x)=1−(x+1)+(x+1)^2\)

3)\( f(x)=\cos(2x)\) em\( a=π\)

4)\( f(x)=\sin(2x)\) em\( a=\frac{π}{2}\)

Resposta

\( f′(x)=2\cos(2x);\;f''(x)=−4\sin(2x);\quad p_2(x)=−2(x−\frac{π}{2})\)

5)\( f(x)=\sqrt{x}\) em\( a=4\)

6)\( f(x)=\ln x\) em\( a=1\)

Resposta

\( f′(x)=\dfrac{1}{x};\; f''(x)=−\dfrac{1}{x^2};\quad p_2(x)=0+(x−1)−\frac{1}{2}(x−1)^2\)

7)\( f(x)=\dfrac{1}{x}\) em\( a=1\)

8)\( f(x)=e^x\) em\( a=1\)

Resposta

\( p_2(x)=e+e(x−1)+\dfrac{e}{2}(x−1)^2\)

Teorema de Taylor Remainder

Nos exercícios 9 a 14, verifique se a escolha dada\(n\) na estimativa restante\( |R_n|≤\dfrac{M}{(n+1)!}(x−a)^{n+1}\), onde\(M\) é o valor máximo de\( ∣f^{(n+1)}(z)∣\) no intervalo entre\(a\) e o ponto indicado, produz\( |R_n|≤\frac{1}{1000}\). Encontre o valor do polinômio\( p_n\) de Taylor de\( f\) no ponto indicado.

9) [T]\( \sqrt{10};\; a=9,\; n=3\)

10) [T]\( (28)^{1/3};\; a=27,\; n=1\)

Resposta

\( \dfrac{d^2}{dx^2}x^{1/3}=−\dfrac{2}{9x^{5/3}}≥−0.00092…\)quando\( x≥28\) assim for, a estimativa do restante se aplica à aproximação linear\( x^{1/3}≈p_1(27)=3+\dfrac{x−27}{27}\), que dá\( (28)^{1/3}≈3+\frac{1}{27}=3.\bar{037}\), enquanto\( (28)^{1/3}≈3.03658.\)

11) [T]\( \sin(6);\; a=2π,\; n=5\)

12) [T]\( e^2; \; a=0,\; n=9\)

Resposta

Usando a estimativa,\( \dfrac{2^{10}}{10!}<0.000283\) podemos usar a expansão de Taylor de ordem 9 para estimar\( e^x\)\( x=2\) em. como\( e^2≈p_9(2)=1+2+\frac{2^2}{2}+\frac{2^3}{6}+⋯+\frac{2^9}{9!}=7.3887\)... enquanto\( e^2≈7.3891.\)

13) [T]\( \cos(\frac{π}{5});\; a=0,\; n=4\)

14) [T]\( \ln(2);\; a=1,\; n=1000\)

Resposta

Desde\( \dfrac{d^n}{dx^n}(\ln x)=(−1)^{n−1}\dfrac{(n−1)!}{x^n},R_{1000}≈\frac{1}{1001}\). Um tem\(\displaystyle p_{1000}(1)=\sum_{n=1}^{1000}\dfrac{(−1)^{n−1}}{n}≈0.6936\) enquanto\( \ln(2)≈0.6931⋯.\)

Aproximando integrais definidos usando a série Taylor

15) Integre a aproximação\(\sin t≈t−\dfrac{t^3}{6}+\dfrac{t^5}{120}−\dfrac{t^7}{5040}\) avaliada em\( π\) t para aproximar\(\displaystyle ∫^1_0\frac{\sin πt}{πt}\,dt\).

16) Integre a aproximação\( e^x≈1+x+\dfrac{x^2}{2}+⋯+\dfrac{x^6}{720}\) avaliada em\( −x^2\) para aproximar\(\displaystyle ∫^1_0e^{−x^2}\,dx.\)

Resposta

\(\displaystyle ∫^1_0\left(1−x^2+\frac{x^4}{2}−\frac{x^6}{6}+\frac{x^8}{24}−\frac{x^{10}}{120}+\frac{x^{12}}{720}\right)\,dx =1−\frac{1^3}{3}+\frac{1^5}{10}−\frac{1^7}{42}+\frac{1^9}{9⋅24}−\frac{1^{11}}{120⋅11}+\frac{1^{13}}{720⋅13}≈0.74683\)Considerando que\(\displaystyle ∫^1_0e^{−x^2}dx≈0.74682.\)

Mais problemas do teorema de Taylor Remainder

Nos exercícios 17 a 20, determine o menor valor de\(n\) tal forma que a estimativa restante\( |R_n|≤\dfrac{M}{(n+1)!}(x−a)^{n+1}\), onde\(M\) é o valor máximo de\( ∣f^{(n+1)}(z)∣\) no intervalo entre\(a\) e o ponto indicado, produza\( |R_n|≤\frac{1}{1000}\) no intervalo indicado.

17)\( f(x)=\sin x\) em\( [−π,π],\; a=0\)

18)\( f(x)=\cos x\) em\( [−\frac{π}{2},\frac{π}{2}],\; a=0\)

Resposta

Uma vez que\( f^{(n+1)}(z)\) é\(\sin z\) ou\(\cos z\), nós temos\( M=1\). Desde então\( |x−0|≤\frac{π}{2}\), buscamos o menor\(n\) desses\( \dfrac{π^{n+1}}{2^{n+1}(n+1)!}≤0.001\). O menor valor desse tipo é\( n=7\). A estimativa restante é\( R_7≤0.00092.\)

19)\( f(x)=e^{−2x}\) em\( [−1,1],a=0\)

20)\( f(x)=e^{−x}\) em\( [−3,3],a=0\)

Responda

Já que\( f^{(n+1)}(z)=±e^{−z}\) um tem\( M=e^3\). Desde então\( |x−0|≤3\), buscamos o menor\(n\), de tal forma que\( \dfrac{3^{n+1}e^3}{(n+1)!}≤0.001\). O menor valor desse tipo é\( n=14\). A estimativa restante é\( R_{14}≤0.000220.\)

Nos exercícios 21 a 24, o máximo do lado direito da estimativa restante\( |R_1|≤\dfrac{max|f''(z)|}{2}R^2\) em\( [a−R,a+R]\) ocorre em\(a\) ou\( a±R\). Estime o valor máximo de\(R\) tal\( \dfrac{max|f''(z)|}{2}R^2≤0.1\) valor ativado traçando esse máximo em função de\(R\).\( [a−R,a+R]\)

21) [T]\( e^x\) aproximado por\( 1+x,\; a=0\)

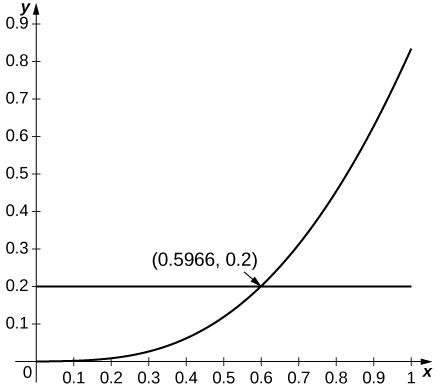
22) [T]\( \sin x\) aproximado por\( x,\; a=0\)

Responda

Como\( \sin x\) está aumentando para pequenos\( x\) e desde então\( \frac{d^2}{dx^2}\left(\sin x\right)=−\sin x\), a estimativa se aplica sempre\( R^2\sin(R)≤0.2\), o que se aplica até\( R=0.596.\)

23) [T]\( \ln x\) aproximado por\( x−1,\; a=1\)

24) [T]\( \cos x\) aproximado por\( 1,\; a=0\)

Responda

Como a segunda derivada de\( \cos x\) é\( −\cos x\) e desde\( \cos x\) está diminuindo\( x=0\), a estimativa se aplica quando\( R^2\cos R≤0.2\) ou\( R≤0.447\).

Série Taylor

Nos exercícios 25 a 35, encontre a série de Taylor da função dada centrada no ponto indicado.

25)\(f(x) = x^4\) em\( a=−1\)

26)\(f(x) = 1+x+x^2+x^3\) em\( a=−1\)

Responda

\( (x+1)^3−2(x+1)^2+2(x+1)\)

27)\(f(x) = \sin x\) em\( a=π\)

28)\(f(x) = \cos x\) em\( a=2π\)

Responda

Os valores das derivadas são os mesmos de\( x=0\)\(\displaystyle \cos x=\sum_{n=0}^∞(−1)^n\frac{(x−2π)^{2n}}{(2n)!}\)

29)\(f(x) = \sin x\) em\( x=\frac{π}{2}\)

30)\(f(x) = \cos x\) em\( x=\frac{π}{2}\)

Responda

\( \cos(\frac{π}{2})=0,\;−\sin(\frac{π}{2})=−1\)então\(\displaystyle \cos x=\sum_{n=0}^∞(−1)^{n+1}\frac{(x−\frac{π}{2})^{2n+1}}{(2n+1)!}\), o que também é\( −\cos(x−\frac{π}{2})\).

31)\(f(x) = e^x\) em\( a=−1\)

32)\(f(x) = e^x\) em\( a=1\)

Responda

Os derivados são\( f^{(n)}(1)=e,\) assim\(\displaystyle e^x=e\sum_{n=0}^∞\frac{(x−1)^n}{n!}.\)

33)\(f(x) = \dfrac{1}{(x−1)^2}\) em\( a=0\) (Dica: diferencie a série Taylor para\( \dfrac{1}{1−x}\).)

34)\(f(x) = \dfrac{1}{(x−1)^3}\) em\( a=0\)

Responda

\(\displaystyle \frac{1}{(x−1)^3}=−\frac{1}{2}\frac{d^2}{dx^2}\left(\frac{1}{1−x}\right)=−\sum_{n=0}^∞\left(\frac{(n+2)(n+1)x^n}{2}\right)\)

35)\(\displaystyle F(x)=∫^x_0\cos(\sqrt{t})\,dt;\quad \text{where}\; f(t)=\sum_{n=0}^∞(−1)^n\frac{t^n}{(2n)!}\) em a=0 (Nota:\( f\) é a série Taylor de\(\cos(\sqrt{t}).)\)

Nos exercícios 36 a 44, calcule a série de Taylor de cada função ao redor\( x=1\).

36)\( f(x)=2−x\)

Responda

\( 2−x=1−(x−1)\)

37)\( f(x)=x^3\)

38)\( f(x)=(x−2)^2\)

Responda

\( ((x−1)−1)^2=(x−1)^2−2(x−1)+1\)

39)\( f(x)=\ln x\)

40)\( f(x)=\dfrac{1}{x}\)

Responda

\(\displaystyle \frac{1}{1−(1−x)}=\sum_{n=0}^∞(−1)^n(x−1)^n\)

41)\( f(x)=\dfrac{1}{2x−x^2}\)

(42)\( f(x)=\dfrac{x}{4x−2x^2−1}\)

Responda

\(\displaystyle x\sum_{n=0}^∞2^n(1−x)^{2n}=\sum_{n=0}^∞2^n(x−1)^{2n+1}+\sum_{n=0}^∞2^n(x−1)^{2n}\)

43)\( f(x)=e^{−x}\)

44)\( f(x)=e^{2x}\)

Responda

\(\displaystyle e^{2x}=e^{2(x−1)+2}=e^2\sum_{n=0}^∞\frac{2^n(x−1)^n}{n!}\)

Série Maclaurin

[T] Nos exercícios 45 - 48, identifique o valor de\(x\) tal que a série dada\(\displaystyle \sum_{n=0}^∞a_n\) seja o valor da série Maclaurin de\( f(x)\) at\( x\). Aproxime o valor do\( f(x)\) uso\(\displaystyle S_{10}=\sum_{n=0}^{10}a_n\).

45)\(\displaystyle \sum_{n=0}^∞\frac{1}{n!}\)

(46)\(\displaystyle \sum_{n=0}^∞\frac{2^n}{n!}\)

Responda

\( x=e^2;\quad S_{10}=\dfrac{34,913}{4725}≈7.3889947\)

47)\(\displaystyle \sum_{n=0}^∞\frac{(−1)^n(2π)^{2n}}{(2n)!}\)

48)\(\displaystyle \sum_{n=0}^∞\frac{(−1)^n(2π)^{2n+1}}{(2n+1)!}\)

Responda

\(\sin(2π)=0;\quad S_{10}=8.27×10^{−5}\)

Nos exercícios 49 a 52, use as funções\( S_5(x)=x−\dfrac{x^3}{6}+\dfrac{x^5}{120}\) e assim\( C_4(x)=1−\dfrac{x^2}{2}+\dfrac{x^4}{24}\) por diante\( [−π,π]\).

49) [T] Trama\(\sin^2x−(S_5(x))^2\) em\( [−π,π]\). Compare a diferença máxima com o quadrado da estimativa do restante de Taylor para\( \sin x.\)

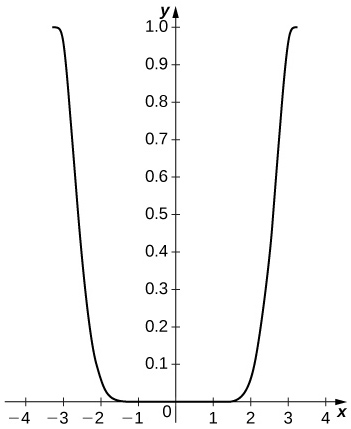
50) [T] Traço\(\cos^2x−(C_4(x))^2\) em\( [−π,π]\). Compare a diferença máxima com o quadrado da estimativa do restante de Taylor para\( \cos x\).

Responda

A diferença é pequena no interior do intervalo, mas se\( 1\) aproxima dos pontos finais. A estimativa restante é\( |R_4|=\frac{π^5}{120}≈2.552.\)

51) [T] Traço\( |2S_5(x)C_4(x)−\sin(2x)|\) em\( [−π,π]\).

52) [T] Compare\( \dfrac{S_5(x)}{C_4(x)}\)\( [−1,1]\) com\( \tan x\). Compare isso com a estimativa do restante de Taylor para a aproximação de\( \tan x\) por\( x+\dfrac{x^3}{3}+\dfrac{2x^5}{15}\).

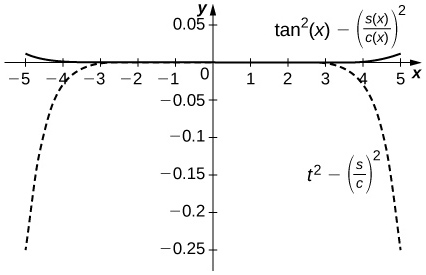
Responda

A diferença está na ordem de\( 10^{−4}\) on,\( [−1,1]\) enquanto o erro de aproximação de Taylor está\( 0.1\) próximo\( ±1\). A curva superior é um gráfico de\(\tan^2x−\left(\dfrac{S_5(x)}{C_4(x)}\right)^2\) e o gráfico tracejado inferior mostra\( t^2−\left(\dfrac{S_5}{C_4}\right)^2\).

53) [T] Lote\( e_4(x)=1+x+\dfrac{x^2}{2}+\dfrac{x^3}{6}+\dfrac{x^4}{24}\) em\( e^x−e_4(x)\) que lugar\( [0,2]\). Compare o erro máximo com a estimativa do restante de Taylor.

54) (Aproximações de Taylor e descoberta de raízes.) Lembre-se de que o método de Newton\( x_{n+1}=x_n−\dfrac{f(x_n)}{f'(x_n)}\) se aproxima de soluções\( f(x)=0\) próximas à entrada\( x_0\).

a. Se\( f\) e\( g\) forem funções inversas, explique por que uma solução de\( g(x)=a\) é o valor\( f(a)\) de\( f\).

b.\( p_N(x)\) Seja o\( N^{\text{th}}\) grau de polinômio Maclaurin de\( e^x\). Use o método de Newton para aproximar soluções\( p_N(x)−2=0\) de\( N=4,5,6.\)

c. Explique por que as raízes aproximadas de\( p_N(x)−2=0\) são valores aproximados de\(\ln(2).\)

Responda

a. As respostas podem variar.
b. A seguir estão os\( x_n\) valores após\( 10\) as iterações do método de Newton para aproximar uma raiz de\( p_N(x)−2=0\): for\( N=4,x=0.6939...;\) for\( N=5,x=0.6932...;\) for\( N=6,x=0.69315...;.\) (Nota:\( \ln(2)=0.69314...\))
c. As respostas podem variar.

Avaliando limites usando a série Taylor

Nos exercícios 55 a 58, use o fato de que se\(\displaystyle q(x)=\sum_{n=1}^∞a_n(x−c)^n\) converge em um intervalo contendo\( c\), então avalie cada limite usando\(\displaystyle \lim_{x→c}q(x)=a_0\) a série de Taylor.

55)\(\displaystyle \lim_{x→0}\frac{\cos x−1}{x^2}\)

56)\(\displaystyle \lim_{x→0}\frac{\ln(1−x^2)}{x^2}\)

Responda

\( \dfrac{\ln(1−x^2)}{x^2}→−1\)

57)\(\displaystyle \lim_{x→0}\frac{e^{x^2}−x^2−1}{x^4}\)

(58)\(\displaystyle \lim_{x→0^+}\frac{\cos(\sqrt{x})−1}{2x}\)

Responda

\(\displaystyle \frac{\cos(\sqrt{x})−1}{2x}≈\frac{(1−\frac{x}{2}+\frac{x^2}{4!}−⋯)−1}{2x}→−\frac{1}{4}\)