10.4: Trabalhando com a série Taylor
- Page ID
- 187791
- Escreva os termos da série binomial.
- Reconheça as expansões de funções comuns da série Taylor.
- Reconheça e aplique técnicas para encontrar a série Taylor para uma função.
- Use a série Taylor para resolver equações diferenciais.
- Use a série Taylor para avaliar integrais não elementares.
Na seção anterior, definimos a série de Taylor e mostramos como encontrar a série de Taylor para várias funções comuns calculando explicitamente os coeficientes dos polinômios de Taylor. Nesta seção, mostramos como usar essas séries de Taylor para derivar séries de Taylor para outras funções. Em seguida, apresentamos duas aplicações comuns de séries de potência. Primeiro, mostramos como as séries de potências podem ser usadas para resolver equações diferenciais. Em segundo lugar, mostramos como as séries de potências podem ser usadas para avaliar integrais quando a antiderivada do integrando não pode ser expressa em termos de funções elementares. Em um exemplo, consideramos\(\displaystyle \int e^{−x^2}dx,\) uma integral que surge com frequência na teoria da probabilidade.
A série binomial
Nosso primeiro objetivo nesta seção é determinar a série de Maclaurin para a função\( f(x)=(1+x)^r\) de todos os números reais\( r\). A série Maclaurin para essa função é conhecida como série binomial. Começamos considerando o caso mais simples:\( r\) é um número inteiro não negativo. Lembramos que, por\( r=0,\,1,\,2,\,3,\,4,\;f(x)=(1+x)^r\) pode ser escrito como
\[\begin{align*} f(x) &=(1+x)^0=1, \\[4pt] f(x) &=(1+x)^1=1+x, \\[4pt] f(x) &=(1+x)^2=1+2x+x^2, \\[4pt] f(x) &=(1+x)^3=1+3x+3x^2+x^3 \\[4pt] f(x) &=(1+x)^4=1+4x+6x^2+4x^3+x^4. \end{align*}\]
As expressões no lado direito são conhecidas como expansões binomiais e os coeficientes são conhecidos como coeficientes binomiais. De forma mais geral, para qualquer número inteiro não negativo\( r\), o coeficiente binomial de\( x^n\) na expansão binomial de\( (1+x)^r\) é dado por
\[\binom{r}{n}=\dfrac{r!}{n!(r−n)!}\label{eq6.6} \]
e
\ [\ begin {align} f (x) &= (1+x) ^r\ nonumber\\ [5pt]
&=\ binom {r} {0} +\ binom {r} {1} x+\ binom {r} {2} x^2+\ binom {r} {3} x^3++\ binom {r} {r-1} x^ {r−1} +\ binom {r} {r} x^r\ nonumber\\ [5pt]
&=\ sum_ {n=0} ^r\ binom {r} {n} x^n.\ label {eq6.7}\ end {align}\]
Por exemplo, usando essa fórmula para\( r=5\), vemos que
\[ \begin{align*} f(x) &=(1+x)^5 \\[4pt] &=\binom{5}{0}1+\binom{5}{1}x+\binom{5}{2}x^2+\binom{5}{3}x^3+\binom{5}{4}x^4+\binom{5}{5}x^5 \\[4pt] &=\dfrac{5!}{0!5!}1+\dfrac{5!}{1!4!}x+\dfrac{5!}{2!3!}x^2+\dfrac{5!}{3!2!}x^3+\dfrac{5!}{4!1!}x^4+\dfrac{5!}{5!0!}x^5 \\[4pt] &=1+5x+10x^2+10x^3+5x^4+x^5. \end{align*}\]
Agora consideramos o caso em que o expoente\(r.\)
é qualquer número real, não necessariamente um número inteiro não negativo. Se não\(r\) for um inteiro não negativo, então\(f(x)=(1+x)^r\) não pode ser escrito como um polinômio finito. No entanto, podemos encontrar uma série de potências para\(f\). Especificamente, procuramos a série Maclaurin para\(f\). Para fazer isso, encontramos as derivadas de\(f\) e as avaliamos em\(x=0\).
\[ \begin{align*} f(x) &=(1+x)^r & f(0) &=1 \\[4pt] f′(x) &=r(1+x)^{r−1} & f'(0) &=r \\[4pt] f''(x) &=r(r−1)(1+x)^{r−2} & f''(0) &=r(r−1) \\[4pt] f'''(x) &=r(r−1)(r−2)(1+x)^{r−3} & f'''(0) &=r(r−1)(r−2) \\[4pt] f^{(n)}(x) &=r(r−1)(r−2)⋯(r−n+1)(1+x)^{r−n} & f^{(n)}(0) &=r(r−1)(r−2)⋯(r−n+1) \end{align*}\]
Concluímos que os coeficientes na série binomial são dados por
\[\dfrac{f^{(n)}(0)}{n!}=\dfrac{r(r−1)(r−2)⋯(r−n+1)}{n!}.\label{eq6.8} \]
Observamos que se\(r\) for um número inteiro não negativo, a\((r+1)^{\text{st}}\) derivada\( f^{(r+1)}\) é a função zero e a série termina. Além disso, se\( r\) for um inteiro não negativo, a Equação\ ref {eq6.8} para os coeficientes concorda com a Equação\ ref {eq6.6} para os coeficientes, e a fórmula para a série binomial concorda com a Equação\ ref {eq6.7} para a expansão binomial finita. De forma mais geral, para denotar os coeficientes binomiais para qualquer número real\( r\), definimos
\[\binom{r}{n}=\dfrac{(r−1)(r−2)⋯(r−n+1)}{n!}. \nonumber \]
Com essa notação, podemos escrever a série binomial para\( (1+x)^r\) como
\[\sum_{n=0}^∞\binom{r}{n}x^n=1+rx+\dfrac{r(r−1)}{2!}x^2+⋯+\dfrac{r(r−1)⋯(r−n+1)}{n!}x^n+⋯. \label{bin1} \]
Agora precisamos determinar o intervalo de convergência para a série binomial Equation\ ref {bin1}. Nós aplicamos o teste de proporção. Consequentemente, consideramos
\[\begin{align*} \dfrac{|a_{n+1}|}{|a_n|} &=\dfrac{|r(r−1)(r−2)⋯(r−n)|x||^{n+1}}{(n+1)!}⋅\dfrac{n}{|r(r−1)(r−2)⋯(r−n+1)||x|^n} \\[4pt] &=\dfrac{|r−n||x|}{|n+1|} \end{align*}\].
Desde
\[\lim_{n→∞}\dfrac{|a_{n+1}|}{|a_n|}=|x|<1 \nonumber \]
se e somente se\( |x|<1\), concluímos que o intervalo de convergência para a série binomial é\( (−1,1)\). O comportamento nos endpoints depende de\( r\). Pode-se mostrar que para\( r≥0\) a série converge em ambos os pontos finais; para\( −1<r<0\), a série converge em\( x=1\) e diverge em\( x=−1\); e para\( r<−1\), para, a série diverge em ambos os pontos finais. A série binomial converge para\( (1+x)^r\) in\( (−1,1)\) para todos os números reais\( r\), mas provar esse fato mostrando que o restante\( R_n(x)→0\) é difícil.
Para qualquer número real\( r\), a série Maclaurin para\( f(x)=(1+x)^r\) é a série binomial. Ele converge para\( f\) para\( |x|<1\), e nós escrevemos
\[(1+x)^r=\sum_{n=0}^∞\binom{r}{n}x^n=1+rx+\dfrac{r(r−1)}{2!}x^2+⋯+r\dfrac{(r−1)⋯(r−n+1)}{n!}x^n+⋯ \nonumber \]
para\( |x|<1\).
Podemos usar essa definição para encontrar a série binomial\( f(x)=\sqrt{1+x}\) e usar a série para aproximar\( \sqrt{1.5}\).
- Encontre a série binomial para\( f(x)=\sqrt{1+x}\).
- Use o polinômio Maclaurin de terceira ordem\( p_3(x)\) para estimar\( \sqrt{1.5}\). Use o teorema de Taylor para limitar o erro. Use um utilitário gráfico para comparar os gráficos de\( f\)\( p_3\) e.
Solução
a. Aqui\( r=\dfrac{1}{2}\). Usando a definição para a série binomial, obtemos
\ (\ displaystyle\ qquad\ begin {align*}\ sqrt {1+x} &=1+\ dfrac {1} {2} x+\ dfrac {(1/2) (−1/2)} {2!} x^2+\ dfrac {(1/2) (−1/2) (−3/2)} {3!} x^3+\\ [5pt]
&=1+\ dfrac {1} {2} x−\ dfrac {1} {2!} \ dfrac {1} {2^2} x^2+\ dfrac {1} {3!} \ dfrac {1⋅3} {2^3} x^3−+\ dfrac {(−1) ^ {n+1}} {n!} \ dfrac {1⋅3⋅5( 2n−3)} {2^n} x^n+\\ [5pt]
&=1+\ sum_ {n=1} ^∞\ dfrac {(−1) ^ {n+1}} {n!} \ dfrac {1⋅3⋅5( 2n−3)} {2^n} x^n.\ end {align*}\)
b. A partir do resultado na parte a., o polinômio Maclaurin de terceira ordem é
\( p_3(x)=1+\dfrac{1}{2}x−\dfrac{1}{8}x^2+\dfrac{1}{16}x^3\).
Portanto,
\( \sqrt{1.5}=\sqrt{1+0.5}≈1+\dfrac{1}{2}(0.5)−\dfrac{1}{8}(0.5)^2+\dfrac{1}{16}(0.5)^3≈1.2266.\)
Do teorema de Taylor, o erro satisfaz
\( R_3(0.5)=\dfrac{f^{(4)}(c)}{4!}(0.5)^4\)
para alguns\( c\) entre\( 0\)\( 0.5\) e. Como\( f^{(4)}(x)=−\dfrac{15}{2^4(1+x)^{7/2}}\), e o valor máximo de\( ∣f^{(4)}(x)∣\) no intervalo\( (0,0.5)\) ocorre em\( x=0\), temos
\( |R_3(0.5)|≤\dfrac{15}{4!2^4}(0.5)^4≈0.00244.\)
A função e o polinômio de Maclaurin\( p_3\) estão representados graficamente na Figura\(\PageIndex{1}\).
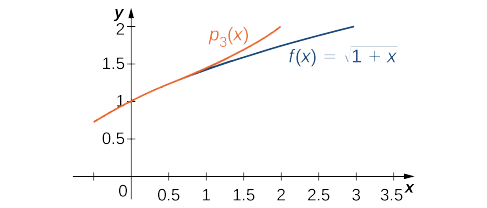
Encontre a série binomial para\( f(x)=\dfrac{1}{(1+x)^2}\).
- Dica
-
Use a definição de série binomial para\( r=−2\).
- Responda
-
\(\displaystyle \sum_{n=0}^∞(−1)^n(n+1)x^n\)
Funções comuns expressas como série Taylor
Neste ponto, derivamos a série de Maclaurin para funções exponenciais, trigonométricas e logarítmicas, bem como funções da forma\( f(x)=(1+x)^r\). Na Tabela\(\PageIndex{1}\), resumimos os resultados dessas séries. Observamos que a convergência da série Maclaurin para\( f(x)=\ln(1+x)\) no ponto final\( x=1\) e a série Maclaurin para\( f(x)=\tan^{−1}x\) nos pontos finais\( x=1\) e se\( x=−1\) baseia em um teorema mais avançado do que apresentamos aqui. (Consulte o teorema de Abel para uma discussão sobre esse ponto mais técnico.)
| Função | Série Maclaurin | Intervalo de convergência |
|---|---|---|
| \( f(x)=\dfrac{1}{1−x}\) | \(\displaystyle \sum_{n=0}^∞x^n\) | \( −1<x<1\) |
| \( f(x)=e^x\) | \(\displaystyle \sum_{n=0}^∞\dfrac{x^n}{n!}\) | \( −∞<x<∞\) |
| \( f(x)=\sin x\) | \(\displaystyle \sum_{n=0}^∞(−1)^n\dfrac{x^{2n+1}}{(2n+1)!}\) | \( −∞<x<∞\) |
| \( f(x)=\cos x\) | \(\displaystyle \sum_{n=0}^∞(−1)^n\dfrac{x^{2n}}{(2n)!}\) | \( −∞<x<∞\) |
| \( f(x)=\ln(1+x)\) | \(\displaystyle \sum_{n=0}^∞(−1)^{n+1}\dfrac{x^n}{n}\) | \( −1<x<1\) |
| \( f(x)=\tan^{−1}x\) | \(\displaystyle \sum_{n=0}^∞(−1)^n\dfrac{x^{2n+1}}{2n+1}\) | \( −1<x<1\) |
| \( f(x)=(1+x)^r\) | \(\displaystyle \sum_{n=0}^∞\binom{r}{n}x^n\) | \( −1<x<1\) |
No início do capítulo, mostramos como você pode combinar séries de potência para criar novas séries de potência. Aqui usamos essas propriedades, combinadas com a série Maclaurin na Tabela\(\PageIndex{1}\), para criar a série Maclaurin para outras funções.
Encontre a série Maclaurin de cada uma das seguintes funções usando uma das séries listadas na Tabela\(\PageIndex{1}\).
- \( f(x)=\cos\sqrt{x}\)
- \( f(x)=\sinh x\)
Solução
a. Usando a série Maclaurin para,\( \cos x\) descobrimos que a série Maclaurin para\( \cos\sqrt{x}\) é dada por
\(\displaystyle \sum_{n=0}^∞\dfrac{(−1)^n(\sqrt{x})^{2n}}{(2n)!}=\sum_{n=0}^∞\dfrac{(−1)^nx^n}{(2n)!}=1−\dfrac{x}{2!}+\dfrac{x^2}{4!}−\dfrac{x^3}{6!}+\dfrac{x^4}{8!}−⋯.\)
Esta série converge\( \cos\sqrt{x}\) para todos\( x\) no domínio de\( \cos\sqrt{x}\); isto é, para todos\( x≥0\).
b. Para encontrar a série Maclaurin para,\( \sinh x,\) usamos o fato de que
\( \sinh x=\dfrac{e^x−e^{−x}}{2}.\)
Usando a série Maclaurin para\( e^x\), vemos que o\(n^{\text{th}}\) termo na série Maclaurin para\(\sinh x\) é dado por
\( \dfrac{x^n}{n!}−\dfrac{(−x)^n}{n!}.\)
\( n\)Mesmo assim, esse termo é zero. Por\( n\) estranho, esse termo é\( \dfrac{2x^n}{n!}\). Portanto, a série Maclaurin para\(\sinh x\) tem apenas termos de ordem ímpar e é dada por
\(\displaystyle \sum_{n=0}^∞\dfrac{x^{2n+1}}{(2n+1)!}=x+\dfrac{x^3}{3!}+\dfrac{x^5}{5!}+⋯.\)
Encontre a série Maclaurin para\( \sin(x^2).\)
- Dica
-
Use a série Maclaurin para\( \sin x.\)
- Responda
-
\(\displaystyle \sum_{n=0}^∞\dfrac{(−1)^nx^{4n+2}}{(2n+1)!}\)
Também mostramos anteriormente neste capítulo como as séries de potência podem ser diferenciadas termo a termo para criar uma nova série de potências. No exemplo\(\PageIndex{3}\), diferenciamos a série binomial de\( \sqrt{1+x}\) termo a termo para encontrar a série binomial para\( \dfrac{1}{\sqrt{1+x}}\). Observe que poderíamos construir a série binomial\( \dfrac{1}{\sqrt{1+x}}\) diretamente da definição, mas diferenciar a série binomial para\( \sqrt{1+x}\) é um cálculo mais fácil.
Use a série binomial\( \sqrt{1+x}\) para encontrar a série binomial para\( \dfrac{1}{\sqrt{1+x}}\).
Solução
As duas funções estão relacionadas por
\( \dfrac{d}{dx}\sqrt{1+x}=\dfrac{1}{2\sqrt{1+x}}\),
então a série binomial para\( \dfrac{1}{\sqrt{1+x}}\) é dada por
\(\displaystyle \dfrac{1}{\sqrt{1+x}}=2\dfrac{d}{dx}\sqrt{1+x}=1+\sum_{n=1}^∞\dfrac{(−1)^n}{n!}\dfrac{1⋅3⋅5⋯(2n−1)}{2^n}x^n.\)
Encontre a série binomial para\( f(x)=\dfrac{1}{(1+x)^{3/2}}\)
- Dica
-
Diferencie a série para\( \dfrac{1}{\sqrt{1+x}}\)
- Responda
-
\(\displaystyle \sum_{n=1}^∞\dfrac{(−1)^n}{n!}\dfrac{1⋅3⋅5⋯(2n−1)}{2^n}x^n\)
Neste exemplo, diferenciamos uma série conhecida de Taylor para construir uma série de Taylor para outra função. A capacidade de diferenciar séries de potências termo a termo as torna uma ferramenta poderosa para resolver equações diferenciais. Agora mostramos como isso é feito.
Resolvendo equações diferenciais com séries de potências
Considere a equação diferencial
\[y′(x)=y.\nonumber \]
Lembre-se de que esta é uma equação separável de primeira ordem e sua solução é\(y=Ce^x\). Essa equação é facilmente resolvida usando técnicas discutidas anteriormente no texto. Para a maioria das equações diferenciais, no entanto, ainda não temos ferramentas analíticas para resolvê-las. As séries de potências são uma ferramenta extremamente útil para resolver muitos tipos de equações diferenciais. Nessa técnica, procuramos uma solução da forma\(\displaystyle y=\sum_{n=0}^∞c_nx^n\) e determinamos quais seriam os coeficientes. No próximo exemplo, consideramos um problema de valor inicial que envolve ilustrar\(y′=y\) a técnica.
Use a série de potências para resolver o problema do valor inicial\(y′=y,\quad y(0)=3.\)
Solução
Suponha que exista uma solução de série de potência
\(\displaystyle y(x)=\sum_{n=0}^∞c_nx^n=c_0+c_1x+c_2x^2+c_3x^3+c_4x^4+⋯.\)
Diferenciando esta série termo a termo, obtemos
\( y′=c_1+2c_2x+3c_3x^2+4c_4x^3+⋯.\)
Se\(y\) satisfaz a equação diferencial, então
\( c_0+c_1x+c_2x^2+c_3x^3+⋯=c_1+2c_2x+3c_3x^2+4c_3x^3+⋯.\)
Usando a singularidade das representações de séries de potência, sabemos que essas séries só podem ser iguais se seus coeficientes forem iguais. Portanto,
\( c_0=c_1,\)
\( c_1=2c_2,\)
\( c_2=3c_3,\)
\( c_3=4c_4,\)
÷
Usando a condição inicial\( y(0)=3\) combinada com a representação da série de potência
\( y(x)=c_0+c_1x+c_2x^2+c_3x^3+⋯\),
nós descobrimos isso\( c_0=3\). Agora estamos prontos para resolver o resto dos coeficientes. Usando o fato de que\( c_0=3\), temos
\ [\ begin {align*} c_1&=c_0=3=\ dfrac {3} {1!} ,\\ [5pt]
c_2&=\ dfrac {c_1} {2} =\ dfrac {3} {2} =\ dfrac {3} {2!} ,\\ [5pt]
c_3&=\ dfrac {c_2} {3} =\ dfrac {3} {3⋅2} =\ dfrac {3} {3!} ,\\ [5pt]
c_4&=\ dfrac {c_3} {4} =\ dfrac {3} {4⋅3⋅2} =\ dfrac {3} {4!}. \ end {align*}\]
Portanto,
\[y=3\left[1+\dfrac{1}{1!}x+\dfrac{1}{2!}x^2+\dfrac{1}{3!}x^3\dfrac{1}{4!}x^4+⋯\right]=3\sum_{n=0}^∞\dfrac{x^n}{n!}.\nonumber \]
Você pode reconhecer
\[\sum_{n=0}^∞\dfrac{x^n}{n!}\nonumber \]
como a série Taylor para\( e^x\). Portanto, a solução é\( y=3e^x\).
Use séries de potência para resolver\( y′=2y,\quad y(0)=5.\)
- Dica
-
As equações para os primeiros coeficientes\( c_n\) satisfarão\( c_0=2c_1,\,c_1=2⋅2c_2,\,c_2=2⋅3c_3,\,….\) Em geral, para todos\( n≥0,\;c_n=2(n+1)C_{n+1}\).
- Responda
-
\( y=5e^{2x}\)
Agora, consideramos um exemplo envolvendo uma equação diferencial que não podemos resolver usando métodos discutidos anteriormente. Esta equação diferencial
\[y′−xy=0\nonumber \]
é conhecida como equação de Airy. Ele tem muitas aplicações em física matemática, como modelar a difração da luz. Aqui, mostramos como resolvê-lo usando séries de potência.
Use séries de potência para resolver\(y''−xy=0\) com as condições iniciais\( y(0)=a\) e\( y'(0)=b.\)
Solução
Procuramos uma solução do formulário
\[y=\sum_{n=0}^∞c_nx^n=c_0+c_1x+c_2x^2+c_3x^3+c_4x^4+⋯\nonumber \]
Diferenciando essa função termo por termo, obtemos
\ [\ begin {align*} y′&=c_1+2c_2x+3c_3x^2+4c_4x^3+,\\ [4pt]
y"&=2⋅1c_2+3⋅2c_3x+4⋅3c_4x^2+. \ end {align*}\]
Se\(y\) satisfizer a equação\( y''=xy\), então
\( 2⋅1c_2+3⋅2c_3x+4⋅3c_4x^2+⋯=x(c_0+c_1x+c_2x^2+c_3x^3+⋯).\)
Usando [link] sobre a exclusividade das representações de séries de potência, sabemos que coeficientes do mesmo grau devem ser iguais. Portanto,
\( 2⋅1c_2=0,\)
\( 3⋅2c_3=c_0,\)
\( 4⋅3c_4=c_1,\)
\( 5⋅4c_5=c_2,\)
÷
De forma mais geral\( n≥3\), pois temos\( n⋅(n−1)c_n=c_{n−3}\). Na verdade, todos os coeficientes podem ser escritos em termos de\( c_0\)\( c_1\) e. Para ver isso, primeiro observe isso\( c_2=0\). Então
\( c_3=\dfrac{c_0}{3⋅2}\),
\( c_4=\dfrac{c_1}{4⋅3}\).
\( c_5,\,c_6,\,c_7\)Pois, vemos que
\ [\ begin {align*} c_5&=\ dfrac {c_2} {5⋅4} =0,\\ [5pt]
c_6&=\ dfrac {c_3} {6⋅5} =\ dfrac {c_0} {6⋅5⋅3⋅2},\\ [5pt]
c_7&=\ dfrac {c_4} {7⋅6} =\ dfrac {c_1} {7⋅6⋅4⋅3}. \ end {align*}\]
Portanto, a solução em série da equação diferencial é dada por
\( y=c_0+c_1x+0⋅x^2+\dfrac{c_0}{3⋅2}x^3+\dfrac{c_1}{4⋅3}x^4+0⋅x^5+\dfrac{c_0}{6⋅5⋅3⋅2}x^6+\dfrac{c_1}{7⋅6⋅4⋅3}x^7+⋯.\)
A condição inicial\( y(0)=a\) implica\( c_0=a\). Diferenciando esta série termo por termo e usando o fato de que\( y′(0)=b\), concluímos isso\( c_1=b\).
Portanto, a solução desse problema de valor inicial é
\( y=a\left(1+\dfrac{x^3}{3⋅2}+\dfrac{x}{6⋅5⋅3⋅2}+⋯\right)+b\left(x+\dfrac{x^4}{4⋅3}+\dfrac{x^7}{7⋅6⋅4⋅3}+⋯\right).\)
Use a série de potência para resolver\( y''+x^2y=0\) com a condição inicial\( y(0)=a\)\( y′(0)=b\) e.
- Dica
-
Os coeficientes satisfazem\( c_0=a,\,c_1=b,\,c_2=0,\,c_3=0,\) e para\( n≥4,\; n(n−1)c_n=−c_{n−4}\).
- Responda
-
\(y=a\left(1−\dfrac{x^4}{3⋅4}+\dfrac{x^8}{3⋅4⋅7⋅8}−⋯\right)+b\left(x−\dfrac{x^5}{4⋅5}+\dfrac{x^9}{4⋅5⋅8⋅9}−⋯\right)\)
Avaliando integrais não elementares
Resolver equações diferenciais é uma aplicação comum de séries de potências. Agora, passamos para uma segunda aplicação. Mostramos como as séries de potências podem ser usadas para avaliar integrais envolvendo funções cujas antiderivadas não podem ser expressas usando funções elementares.
Uma integral que surge frequentemente em aplicações na teoria da probabilidade é\(\displaystyle \int e^{−x^2}\,dx.\) Infelizmente, a antiderivada do integrando não\( e^{−x^2}\) é uma função elementar. Por função elementar, queremos dizer uma função que pode ser escrita usando um número finito de combinações algébricas ou composições de funções exponenciais, logarítmicas, trigonométricas ou de potência. Observamos que o termo “função elementar” não é sinônimo de função não complicada. Por exemplo, a função\( f(x)=\sqrt{x^2−3x}+e^{x^3}−\sin(5x+4)\) é uma função elementar, embora não seja uma função de aparência particularmente simples. Qualquer integral da forma em\(\displaystyle \int f(x)\,dx\) que a antiderivada de\( f\) não possa ser escrita como uma função elementar é considerada uma integral não elementar.
integrais não elementares não podem ser avaliadas usando as técnicas básicas de integração discutidas anteriormente. Uma forma de avaliar essas integrais é expressando o integrando como uma série de potências e integrando termo por termo. Demonstramos essa técnica considerando\(\displaystyle \int e^{−x^2}\,dx.\)
- Express\(\displaystyle \int e^{−x^2}dx\) como uma série infinita.
- Avalie\(\displaystyle \int ^1_0e^{−x^2}dx\) dentro de um erro de\( 0.01\).
Solução
a. A série Maclaurin para\( e^{−x^2}\) é dada por
\ [\ begin {align*} e^ {−x^2} &=\ sum_ {n=0} ^∞\ dfrac {(−x^2) ^n} {n!} \\ [5pt]
&=1−x^2+\ dfrac {x^4} {2!} −\ dfrac {x^6} {3!} ++ (−1) ^n\ dfrac {x^ {2n}} {n!} +\\ [5pt]
&=\ sum_ {n=0} ^∞ (−1) ^n\ dfrac {x^ {2n}} {n!}. \ end {align*}\]
Portanto,
\ [\ begin {align*}\ int e^ {−x^2}\, dx&=\ int\ left (1−x^2+\ dfrac {x^4} {2!} −\ dfrac {x^6} {3!} ++ (−1) ^n\ dfrac {x^ {2n}} {n!} +\ right)\, dx\\ [5pt]
&=C+x−\ dfrac {x^3} {3} +\ dfrac {x^5} {5.2!} −\ dfrac {x^7} {7,3!} ++ (−1) ^n\ dfrac {x^ {2n+1}} {(2n+1) n!} +. \ end {align*}\]
b. Usando o resultado da parte a. temos
\[ \int ^1_0e^{−x^2}\,dx=1−\dfrac{1}{3}+\dfrac{1}{10}−\dfrac{1}{42}+\dfrac{1}{216}−⋯.\nonumber \]
A soma dos primeiros quatro termos é de aproximadamente\( 0.74\). Pelo teste de série alternada, essa estimativa é precisa dentro de um erro menor que\( \dfrac{1}{216}≈0.0046296<0.01.\)
Express\(\displaystyle \int \cos\sqrt{x}\,dx\) como uma série infinita. Avalie\(\displaystyle \int ^1_0\cos\sqrt{x}\,dx\) dentro de um erro de\( 0.01\).
- Dica
-
Use a série encontrada em Example\(\PageIndex{6}\).
- Responda
-
\(\displaystyle C+\sum_{n=1}^∞(−1)^{n+1}\dfrac{x^n}{n(2n−2)!}\)A integral definida está aproximadamente dentro\( 0.514\) de um erro de\( 0.01\).
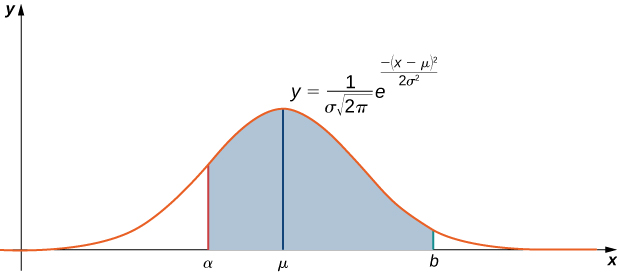
Como mencionado acima, a integral\(\displaystyle \int e^{−x^2}\,dx\) surge frequentemente na teoria da probabilidade. Especificamente, ele é usado ao estudar conjuntos de dados que são normalmente distribuídos, o que significa que os valores dos dados estão sob uma curva em forma de sino. Por exemplo, se um conjunto de valores de dados é normalmente distribuído com média\( μ\) e desvio padrão\( σ\), a probabilidade de que um valor escolhido aleatoriamente esteja entre\( x=a\) e\( x=b\) é dada por
\[\dfrac{1}{σ\sqrt{2π}}\int ^b_ae^{−(x−μ)^2/(2σ^2)}\,dx.\label{probeq} \]
(Veja a Figura\(\PageIndex{2}\).)
Para simplificar essa integral, normalmente deixamos\( z=\dfrac{x−μ}{σ}\). Essa quantidade\(z\) é conhecida como a\(z\) pontuação de um valor de dados. Com essa simplificação, a equação integral\ ref {probeq} se torna
\[\dfrac{1}{\sqrt{2π}}\int ^{(b−μ)/σ}_{(a−μ)/σ}e^{−z^2/2}\,dz. \nonumber \]
No exemplo\(\PageIndex{7}\), mostramos como podemos usar essa integral no cálculo de probabilidades.
Suponha que um conjunto de pontuações de testes padronizados seja normalmente distribuído com média\( μ=100\) e desvio padrão\( σ=50\). Use a Equação\ ref {probeq} e os primeiros seis termos da série Maclaurin para para\( e^{−x^2/2}\) aproximar a probabilidade de que uma pontuação de teste selecionada aleatoriamente esteja entre\( x=100\)\( x=200\) e. Use o teste de séries alternadas para determinar a precisão de sua aproximação.
Solução
Como\( μ=100,σ=50,\) e estamos tentando determinar a área sob a curva de\( a=100\) até\( b=200\), a equação integral\ ref {probeq} se torna
\[ \dfrac{1}{\sqrt{2π}}\int ^2_0e^{−z^2/2}\,dz.\nonumber \]
A série Maclaurin para\( e^{−x^2/2}\) é fornecida por
\ [\ begin {align*} e^ {−x^2/2} &=\ sum_ {n=0} ^∞\ dfrac {\ left (−\ dfrac {x^2} {2}\ direita) ^n} {n!} \\ [5pt]
&=1−\ dfrac {x^2} {2^1⋅1!} +\ dfrac {x^4} {2^2⋅2!} −\ dfrac {x^6} {2^3⋅3!} ++ (−1) ^n\ dfrac {x^ {2n}} {2^n⋅n}! +\\ [5pt]
&=\ sum_ {n=0} ^∞ (−1) ^n\ dfrac {x^ {2n}} {2^n⋅n!}. \ end {align*}\]
Portanto,
\ [\ begin {align*}\ dfrac {1} {\ sqrt {2π}}\ int e^ {−z^2/2}\, dz&=\ dfrac {1} {\ sqrt {2π}}\ int\ left (1−\ dfrac {z^2} {2^1⋅1!} +\ dfrac {z^4} {2^2⋅2!} −\ dfrac {z^6} {2^3⋅3!} ++ (−1) ^n\ dfrac {z^ {2n}} {2^n⋅n!} +\ direita) dz\\ [5pt]
&=\ dfrac {1} {\ sqrt {2π}}\ left (C+z−\ dfrac {z^3} {3⋅2^1⋅1!} +\ dfrac {z^5} {5⋅2^2⋅2!} −\ dfrac {z^7} {7⋅2^3⋅3!} ++ (−1) ^n\ dfrac {z^ {2n+1}} {(2n+1) 2^n⋅n!} +\ right)\ end {align*}\]
\[\dfrac{1}{\sqrt{2π}}\int ^2_0e^{−z^2/2}\,dz=\dfrac{1}{\sqrt{2π}}\left(2−\dfrac{8}{6}+\dfrac{32}{40}−\dfrac{128}{336}+\dfrac{512}{3456}−\dfrac{2^{11}}{11⋅2^5⋅5!}+⋯\right)\nonumber \]
Usando os primeiros cinco termos, estimamos que a probabilidade é de aproximadamente 0,4922. Pelo teste de série alternada, vemos que essa estimativa é precisa de
\[ \dfrac{1}{\sqrt{2π}}\dfrac{2^{13}}{13⋅2^6⋅6!}≈0.00546.\nonumber \]
Análise
Se você estiver familiarizado com a teoria da probabilidade, você pode saber que a probabilidade de um valor de dados estar dentro de dois desvios padrão da média é de aproximadamente\( 95\%.\) Aqui calculamos a probabilidade de que um valor de dados esteja entre a média e dois desvios padrão acima da média, então a estimativa deve ser por aí\( 47.5\%\). A estimativa, combinada com o limite de precisão, está dentro desse intervalo.
Use os primeiros cinco termos da série Maclaurin para\( e^{−x^2/2}\) estimar a probabilidade de que uma pontuação de teste selecionada aleatoriamente esteja entre\( 100\)\( 150\) e. Use o teste de série alternada para determinar a precisão dessa estimativa.
- Dica
-
Avalie\(\displaystyle \int ^1_0e^{−z^2/2}\,dz\) usando os primeiros cinco termos da série Maclaurin para\( e^{−z^2/2}\).
- Responda
-
A estimativa é de aproximadamente\( 0.3414.\) Esta estimativa é precisa\( 0.0000094.\)
Outra aplicação na qual surge uma integral não elementar envolve o período de um pêndulo. O integral é
\[\int ^{π/2}_0\dfrac{dθ}{\sqrt{1−k^2\sin^2θ}}\nonumber \].
Uma integral dessa forma é conhecida como integral elíptica do primeiro tipo. Integrais elípticas surgiram originalmente ao tentar calcular o comprimento do arco de uma elipse. Agora, mostramos como usar séries de potência para aproximar essa integral.
O período de um pêndulo é o tempo necessário para que um pêndulo faça um giro completo para frente e para trás. Para um pêndulo com comprimento\( L\) que faz um ângulo máximo\( θ_{max}\) com a vertical, seu período\( T\) é dado por
\[ T=4\sqrt{\dfrac{L}{g}}\int ^{π/2}_0\dfrac{dθ}{\sqrt{1−k^2\sin^2θ}}\nonumber \]
onde\( g\) está a aceleração devida à gravidade e\( k=\sin\left(\dfrac{θ_{max}}{2}\right)\) (veja a Figura\(\PageIndex{3}\)). (Observamos que essa fórmula para o período surge de um modelo não linearizado de um pêndulo. Em alguns casos, para simplificação, um modelo linearizado é usado e\(\sin θ\) é aproximado por\( θ\).)
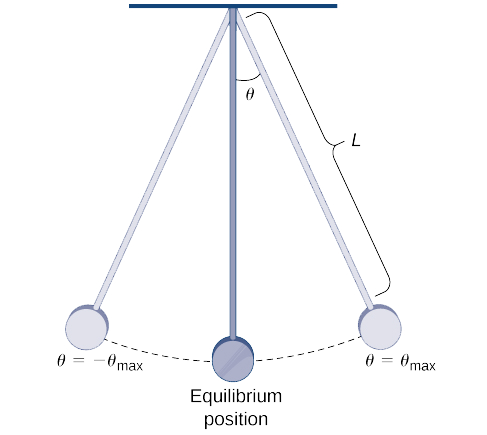
Use a série binomial
\[ \dfrac{1}{\sqrt{1+x}}=1+\sum_{n=1}^∞\dfrac{(−1)^n}{n!}\dfrac{1⋅3⋅5⋯(2n−1)}{2^n}x^n\nonumber \]
para estimar o período desse pêndulo. Especificamente, aproxime o período do pêndulo se
- você usa somente o primeiro termo na série binomial, e
- você usa os dois primeiros termos na série binomial.
Solução
Usamos a série binomial, substituindo x por\( −k^2\sin^2θ.\) Então, podemos escrever o período como
\[ T=4\sqrt{\dfrac{L}{g}}\int ^{π/2}_0\left(1+\dfrac{1}{2}k^2\sin^2θ+\dfrac{1⋅3}{2!2^2}k^4\sin^4θ+⋯\right)\,dθ.\nonumber \]
a. Usando apenas o primeiro termo no integrando, a estimativa de primeira ordem é
\[ T≈4\sqrt{\dfrac{L}{g}}\int ^{π/2}_0\,dθ=2π\sqrt{\dfrac{L}{g}}.\nonumber \]
Se\( θ_{max}\) é pequeno, então\( k=\sin\left(\dfrac{θ_{max}}{2}\right)\) é pequeno. Afirmamos que quando\( k\) é pequeno, essa é uma boa estimativa. Para justificar essa alegação, considere
\[ \int ^{π/2}_0\left(1+\frac{1}{2}k^2\sin^2θ+\dfrac{1⋅3}{2!2^2}k^4\sin^4θ+⋯\right)\,dθ.\nonumber \]
Uma vez que\( |\sin x|≤1\), essa integral é limitada por
\[ \int ^{π/2}_0\left(\dfrac{1}{2}k^2+\dfrac{1.3}{2!2^2}k^4+⋯\right)\,dθ\;<\;\dfrac{π}{2}\left(\dfrac{1}{2}k^2+\dfrac{1⋅3}{2!2^2}k^4+⋯\right).\nonumber \]
Além disso, pode-se mostrar que cada coeficiente do lado direito é menor que\( 1\) e, portanto, que essa expressão é limitada por
\( \dfrac{πk^2}{2}(1+k^2+k^4+⋯)=\dfrac{πk^2}{2}⋅\dfrac{1}{1−k^2}\),
que é pequeno para\( k\) pequeno.
b. Para valores maiores de\( θ_{max}\), podemos aproximar\( T\) usando mais termos no integrando. Usando os dois primeiros termos na integral, chegamos à estimativa
\[ T≈4\sqrt{\frac{L}{g}}\int ^{π/2}_0\left(1+\dfrac{1}{2}k^2\sin^2θ\right)\,dθ=2π\sqrt{\dfrac{L}{g}}\left(1+\dfrac{k^2}{4}\right).\nonumber \]
As aplicações da série Taylor nesta seção têm como objetivo destacar sua importância. Em geral, as séries de Taylor são úteis porque nos permitem representar funções conhecidas usando polinômios, fornecendo assim uma ferramenta para aproximar valores de funções e estimar integrais complicadas. Além disso, eles nos permitem definir novas funções como séries de potências, fornecendo assim uma ferramenta poderosa para resolver equações diferenciais.
Conceitos-chave
- A série binomial é a série Maclaurin para\( f(x)=(1+x)^r\). Ele converge para\( |x|<1\).
- A série Taylor para funções geralmente pode ser derivada por operações algébricas com uma série Taylor conhecida ou pela diferenciação ou integração de uma série Taylor conhecida.
- As séries de potência podem ser usadas para resolver equações diferenciais.
- A série Taylor pode ser usada para ajudar a aproximar integrais que não podem ser avaliadas por outros meios.
Glossário
- série binomial
- a série Maclaurin para\( f(x)=(1+x)^r\); é dada por\(\displaystyle (1+x)^r=\sum_{n=0}^∞\binom{r}{n}x^n=1+rx+\dfrac{r(r−1)}{2!}x^2+⋯+\dfrac{r(r−1)⋯(r−n+1)}{n!}x^n+⋯\) para\( |x|<1\)
- integral não elementar
- uma integral para a qual a antiderivada do integrando não pode ser expressa como uma função elementar


