10.4E: Exercícios para a Seção 10.4

Last updated
Save as PDF

Page ID: 187797

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Nos exercícios 1 a 4, use as substituições apropriadas para anotar a série de Maclaurin para o binômio dado.

1)$(1−x)^{1/3}$

2)$(1+x^2)^{−1/3}$

Responda: $\displaystyle (1+x^2)^{−1/3}=\sum_{n=0}^∞\left(n^{−\frac{1}{3}}\right)x^{2n}$

3)$(1−x)^{1.01}$

4)$(1−2x)^{2/3}$

Responda: $\displaystyle (1−2x)^{2/3}=\sum_{n=0}^∞(−1)^n2^n\left(n^{\frac{2}{3}}\right)x^n$

Nos exercícios 5 a 12, use a substituição$(b+x)^r=(b+a)^r\left(1+\dfrac{x−a}{b+a}\right)^r$ na expansão binomial para encontrar a série de Taylor de cada função com o centro dado.

5)$\sqrt{x+2}$ em$a=0$

6)$\sqrt{x^2+2}$ em$a=0$

Responda: $\displaystyle \sqrt{2+x^2}=\sum_{n=0}^∞2^{(1/2)−n}\left(n^{\frac{1}{2}}\right)x^{2n};(|x^2|<2)$

7)$\sqrt{x+2}$ em$a=1$

8)$\sqrt{2x−x^2}$ em$a=1$ (Dica:$2x−x^2=1−(x−1)^2$)

Responda: $\sqrt{2x−x^2}=\sqrt{1−(x−1)^2}$então$\displaystyle \sqrt{2x−x^2}=\sum_{n=0}^∞(−1)^n\left(n^{\frac{1}{2}}\right)(x−1)^{2n}$

9)$(x−8)^{1/3}$ em$a=9$

10)$\sqrt{x}$ em$a=4$

Responda: $\sqrt{x}=2\sqrt{1+\frac{x−4}{4}}$então$\displaystyle \sqrt{x}=\sum_{n=0}^∞2^{1−2n}\left(n^{\frac{1}{2}}\right)(x−4)^n$

11)$x^{1/3}$ em$a=27$

12)$\sqrt{x}$ em$x=9$

Responda: $\displaystyle \sqrt{x}=\sum_{n=0}^∞3^{1−3n}\left(n^{\frac{1}{2}}\right)(x−9)^n$

Nos exercícios 13 a 14, use o teorema binomial para estimar cada número, computando termos suficientes para obter uma estimativa precisa de um erro de no máximo$1/1000.$

13) [T]$(15)^{1/4}$ usando$(16−x)^{1/4}$

14) [T]$(1001)^{1/3}$ usando$(1000+x)^{1/3}$

Responda: $\displaystyle 10(1+\frac{x}{1000})^{1/3}=\sum_{n=0}^∞10^{1−3n}(^{\frac{1}{3}}_n)x^n$. Usando, por exemplo, uma estimativa de quarto grau em$x=1$ fornece,$(1001)^{1/3}≈10\left(1+\left(1^{\frac{1}{3}}\right)10^{−3}+\left(2^{\frac{1}{3}}\right)10^{−6}+\left(3^{\frac{1}{3}}\right)10^{−9}+\left(3^{\frac{1}{3}}\right)10^{−12}\right)=10\left(1+\frac{1}{3.10^3}−\frac{1}{9.10^6}+\frac{5}{81.10^9}−\frac{10}{243.10^{12}}\right)=10.00333222...$ enquanto$(1001)^{1/3}=10.00332222839093....$ dois termos seriam suficientes para uma precisão de três dígitos.

Nos exercícios 15 a 18, use a aproximação binomial$\sqrt{1−x}≈1−\frac{x}{2}−\frac{x^2}{8}−\frac{x^3}{16}−\frac{5x^4}{128}−\frac{7x^5}{256}$ para$|x|<1$ para aproximar cada número. Compare esse valor com o valor dado por uma calculadora científica.

15) [T]$\frac{1}{\sqrt{2}}$ usando$x=\frac{1}{2}$ em$(1−x)^{1/2}$

16) [T]$\sqrt{5}=5×\frac{1}{\sqrt{5}}$ usando$x=\frac{4}{5}$ em$(1−x)^{1/2}$

Responda: A aproximação é$2.3152$; o valor CAS é$2.23….$

17) [T]$\sqrt{3}=\frac{3}{\sqrt{3}}$ usando$x=\frac{2}{3}$ em$(1−x)^{1/2}$

18) [T]$\sqrt{6}$ usando$x=\frac{5}{6}$ em$(1−x)^{1/2}$

Responda: A aproximação é$2.583…$; o valor CAS é$2.449….$

19) Integre a aproximação binomial de$\sqrt{1−x}$ para encontrar uma aproximação de$\displaystyle ∫^x_0\sqrt{1−t}\,dt$.

20) [T] Lembre-se de que o gráfico de$\sqrt{1−x^2}$ é um semicírculo superior de raio$1$. Integre a aproximação binomial de$\sqrt{1−x^2}$ até ordenar$8$ de até$x=−1$$x=1$ até estimar$\frac{π}{2}$.

Responda: $\sqrt{1−x^2}=1−\frac{x^2}{2}−\frac{x^4}{8}−\frac{x^6}{16}−\frac{5x^8}{128}+⋯.$Assim,$\displaystyle ∫^1_{−1}\sqrt{1−x^2}\,dx=\left[x−\frac{x^3}{6}−\frac{x^5}{40}−\frac{x^7}{7⋅16}−\frac{5x^9}{9⋅128}+⋯\right]\Big|^1_{−1}≈2−\frac{1}{3}−\frac{1}{20}−\frac{1}{56}−\frac{10}{9⋅128}+error=1.590...$ considerando que$\frac{π}{2}=1.570...$

Nos exercícios 21 a 24, use a expansão$(1+x)^{1/3}=1+\frac{1}{3}x−\frac{1}{9}x^2+\frac{5}{81}x^3−\frac{10}{243}x^4+⋯$ para escrever os primeiros cinco termos (não necessariamente um polinômio quártico) de cada expressão.

21)$(1+4x)^{1/3};\;a=0$

22)$(1+4x)^{4/3};\;a=0$

Responda: $(1+x)^{4/3}=(1+x)(1+\frac{1}{3}x−\frac{1}{9}x^2+\frac{5}{81}x^3−\frac{10}{243}x^4+⋯)=1+\frac{4x}{3}+\frac{2x^2}{9}−\frac{4x^3}{81}+\frac{5x^4}{243}+⋯$

23)$(3+2x)^{1/3};\;a=−1$

24)$(x^2+6x+10)^{1/3};\;a=−3$

Responda: $(1+(x+3)^2)^{1/3}=1+\frac{1}{3}(x+3)^2−\frac{1}{9}(x+3)^4+\frac{5}{81}(x+3)^6−\frac{10}{243}(x+3)^8+⋯$

25) Use$(1+x)^{1/3}=1+\frac{1}{3}x−\frac{1}{9}x^2+\frac{5}{81}x^3−\frac{10}{243}x^4+⋯$ com$x=1$ para aproximar$2^{1/3}$.

26) Use a aproximação de$(1−x)^{2/3}=1−\frac{2x}{3}−\frac{x^2}{9}−\frac{4x^3}{81}−\frac{7x^4}{243}−\frac{14x^5}{729}+⋯$$|x|<1$ para aproximar$2^{1/3}=2.2^{−2/3}$.

Responda: Duas vezes a aproximação é$1.260…$ enquanto$2^{1/3}=1.2599....$

27) Encontre a$25^{\text{th}}$ derivada de$f(x)=(1+x^2)^{13}$ at$x=0$.

28) Encontre a$99^{\text{th}}$ derivada de$f(x)=(1+x^4)^{25}$.

Responda: $f^{(99)}(0)=0$

Nos exercícios 29 a 36, encontre a série Maclaurin de cada função.

29)$f(x)=xe^{2x}$

30)$f(x)=2^x$

Responda: $\displaystyle \sum_{n=0}^∞\frac{(\ln(2)x)^n}{n!}$

31)$f(x)=\dfrac{\sin x}{x}$

32)$f(x)=\dfrac{\sin(\sqrt{x})}{\sqrt{x}},(x>0),$

Responda: Para$\displaystyle x>0,\, \sin(\sqrt{x})=\sum_{n=0}^∞(−1)^n\frac{x^{(2n+1)/2}}{\sqrt{x}(2n+1)!}=\sum_{n=0}^∞(−1)^n\frac{x^n}{(2n+1)!}$.

33)$f(x)=\sin(x^2)$

34)$f(x)=e^{x^3}$

Responda: $\displaystyle e^{x^3}=\sum_{n=0}^∞\frac{x^{3n}}{n!}$

35)$f(x)=\cos^2x$ usando a identidade$\cos^2x=\frac{1}{2}+\frac{1}{2}\cos(2x)$

36)$f(x)=\sin^2x$ usando a identidade$\sin^2x=\frac{1}{2}−\frac{1}{2}\cos(2x)$

Responda: $\displaystyle \sin^2x=−\sum_{k=1}^∞\frac{(−1)^k2^{2k−1}x^{2k}}{(2k)!}$

Nos exercícios 37 a 44, encontre a série Maclaurin de$\displaystyle F(x)=∫^x_0f(t)\,dt$ integrando a série Maclaurin$f$ termo a termo. Se não$f$ estiver estritamente definido em zero, você pode substituir o valor da série Maclaurin em zero.

37)$\displaystyle F(x)=∫^x_0e^{−t^2}\,dt;\; f(t)=e^{−t^2}=\sum_{n=0}^∞(−1)^n\frac{t^{2n}}{n!}$

38)$\displaystyle F(x)=\tan^{−1}x;\; f(t)=\frac{1}{1+t^2}=\sum_{n=0}^∞(−1)^nt^{2n}$

Responda: $\displaystyle \tan^{−1}x=\sum_{k=0}^∞\frac{(−1)^kx^{2k+1}}{2k+1}$

39)$\displaystyle F(x)=\tanh^{−1}x; \; f(t)=\frac{1}{1−t^2}=\sum_{n=0}^∞t^{2n}$

40)$\displaystyle F(x)=\sin^{−1}x; \; f(t)=\frac{1}{\sqrt{1−t^2}}=\sum_{k=0}^∞\left(k^{\frac{1}{2}}\right)\frac{t^{2k}}{k!}$

Responda: $\displaystyle \sin^{−1}x=\sum_{n=0}^∞\left(n^{\frac{1}{2}}\right)\frac{x^{2n+1}}{(2n+1)n!}$

41)$\displaystyle F(x)=∫^x_0\frac{\sin t}{t}\,dt; \; f(t)=\frac{\sin t}{t}=\sum_{n=0}^∞(−1)^n\frac{t^{2n}}{(2n+1)!}$

(42)$\displaystyle F(x)=∫^x_0\cos\left(\sqrt{t}\right)\,dt; \; f(t)=\sum_{n=0}^∞(−1)^n\frac{x^n}{(2n)!}$

Responda: $\displaystyle F(x)=\sum_{n=0}^∞(−1)^n\frac{x^{n+1}}{(n+1)(2n)!}$

43)$\displaystyle F(x)=∫^x_0\frac{1−\cos t}{t^2}\,dt; \; f(t)=\frac{1−\cos t}{t^2}=\sum_{n=0}^∞(−1)^n\frac{t^{2n}}{(2n+2)!}$

44)$\displaystyle F(x)=∫^x_0\frac{\ln(1+t)}{t}\,dt; \; f(t)=\sum_{n=0}^∞(−1)^n\frac{t^n}{n+1}$

Responda: $\displaystyle F(x)=\sum_{n=1}^∞(−1)^{n+1}\frac{x^n}{n^2}$

Nos exercícios 45 - 52, calcule pelo menos os primeiros três termos diferentes de zero (não necessariamente um polinômio quadrático) da série Maclaurin de$f$.

45)$f(x)=\sin\left(x+\frac{π}{4}\right)=\sin x\cos\left(\frac{π}{4}\right)+\cos x\sin\left(\frac{π}{4}\right)$

(46)$f(x)=\tan x$

Responda: $x+\dfrac{x^3}{3}+\dfrac{2x^5}{15}+⋯$

47)$f(x)=\ln(\cos x)$

48)$f(x)=e^x\cos x$

Responda: $1+x−\dfrac{x^3}{3}−\dfrac{x^4}{6}+⋯$

49)$f(x)=e^{\sin x}$

50)$f(x)=\sec^2x$

Responda: $1+x^2+\dfrac{2x^4}{3}+\dfrac{17x^6}{45}+⋯$

51)$f(x)=\tanh x$

52)$f(x)=\dfrac{\tan\sqrt{x}}{\sqrt{x}}$ (veja expansão para$\tan x$)

Responda: Usando a expansão para$\tan x$ doações$1+\dfrac{x}{3}+\dfrac{2x^2}{15}$.

Nos exercícios 53 a 56, determine o raio de convergência da série Maclaurin de cada função.

53)$\ln(1+x)$

54)$\dfrac{1}{1+x^2}$

Responda: $\displaystyle \frac{1}{1+x^2}=\sum_{n=0}^∞(−1)^nx^{2n}$então,$R=1$ pelo teste de proporção.

55)$\tan^{−1}x$

(56)$\ln(1+x^2)$

Responda: $\displaystyle \ln(1+x^2)=\sum_{n=1}^∞\frac{(−1)^{n−1}}{n}x^{2n}$então,$R=1$ pelo teste de proporção.

57) Encontre a série Maclaurin de$\sinh x=\dfrac{e^x−e^{−x}}{2}$.

58) Encontre a série Maclaurin de$\cosh x=\dfrac{e^x+e^{−x}}{2}$.

Responda: Adicione série$e^x$ e$e^{−x}$ termo por termo. Termos ímpares cancelam$\displaystyle \cosh x=\sum_{n=0}^∞\frac{x^{2n}}{(2n)!}$ e.

59) Diferencie termo a termo a série Maclaurin de$\sinh x$ e compare o resultado com a série Maclaurin de$\cosh x$.

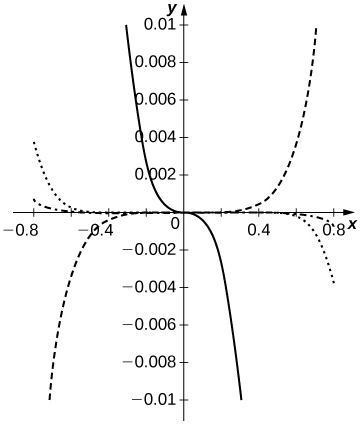
60) [T] Seja$\displaystyle S_n(x)=\sum_{k=0}^n(−1)^k\frac{x^{2k+1}}{(2k+1)!}$ e$\displaystyle C_n(x)=\sum_{n=0}^n(−1)^k\frac{x^{2k}}{(2k)!}$ denote os respectivos polinômios de Maclaurin de grau$2n+1$ de$\sin x$ e grau$2n$ de$\cos x$. Faça um gráfico dos erros$\dfrac{S_n(x)}{C_n(x)}−\tan x$$n=1,..,5$ e compare-os com os$x+\dfrac{x^3}{3}+\dfrac{2x^5}{15}+\dfrac{17x^7}{315}−\tan x$ de$\left(−\frac{π}{4},\frac{π}{4}\right)$.

Responda

A proporção$\dfrac{S_n(x)}{C_n(x)}$ se aproxima$\tan x$ melhor do que$p_7(x)=x+\dfrac{x^3}{3}+\dfrac{2x^5}{15}+\dfrac{17x^7}{315}$ para$N≥3$. As curvas tracejadas são$\dfrac{S_n}{C_n}−\tan x$ para$n=1,\, 2$. A curva pontilhada corresponde a$n=3$, e a curva tracejada corresponde$n=4$ a. A curva sólida é$p_7−\tan x$.

$Esse gráfico tem duas curvas. A primeira é uma função decrescente que passa pela origem. A segunda é uma linha quebrada, que é uma função crescente que passa pela origem. As duas curvas estão muito próximas da origem.$

61) Use a identidade$2\sin x\cos x=\sin(2x)$ para encontrar a expansão da série de potência de$\sin^2x$ at$x=0$. (Dica: integre a série Maclaurin de$\sin(2x)$ termo a termo.)

62) Se$\displaystyle y=\sum_{n=0}^∞a_nx^n$, encontre as expansões da série de potência de$xy′$$x^2y''$ e.

Responda: Pelo teorema da diferenciação termo a termo,$\displaystyle y′=\sum_{n=1}^∞na_nx^{n−1}$ então$\displaystyle y′=\sum_{n=1}^∞na_nx^{n−1}xy′=\sum_{n=1}^∞na_nx^n$, considerando que$\displaystyle y′=\sum_{n=2}^∞n(n−1)a_nx^{n−2}$ sim$\displaystyle xy''=\sum_{n=2}^∞n(n−1)a_nx^n$.

63) [T] Suponha que$\displaystyle y=\sum_{k=0}^∞a^kx^k$ satisfaça$y′=−2xy$$y(0)=0$ e. Mostre isso$a_{2k+1}=0$ para todos$k$ e para isso$a_{2k+2}=\dfrac{−a_{2k}}{k+1}$. Faça um gráfico da soma parcial$S_{20}$ de$y$ no intervalo$[−4,4]$.

64) [T] Suponha que um conjunto de pontuações de testes padronizados seja normalmente distribuído com média$μ=100$ e desvio padrão$σ=10$. Configure uma integral que represente a probabilidade de que a pontuação do teste esteja entre$90$$110$ e e use a integral do polinômio de grau$10$ Maclaurin de$\frac{1}{\sqrt{2π}}e^{−x^2/2}$ para estimar essa probabilidade.

Responda: A probabilidade é$\displaystyle p=\frac{1}{\sqrt{2π}}∫^{(b−μ)/σ}_{(a−μ)/σ}e^{−x^2/2}\,dx$ onde$a=90$ e$b=100$, ou seja,$\displaystyle p=\frac{1}{\sqrt{2π}}∫^1_{−1}e^{−x^2/2}\,dx=\frac{1}{\sqrt{2π}}∫^1_{−1}\sum_{n=0}^5(−1)^n\frac{x^{2n}}{2^nn!}\,dx=\frac{2}{\sqrt{2π}}\sum_{n=0}^5(−1)^n\frac{1}{(2n+1)2^nn!}≈0.6827.$

65) [T] Suponha que um conjunto de pontuações de testes padronizados seja normalmente distribuído com média$μ=100$ e desvio padrão$σ=10$. Configure uma integral que represente a probabilidade de que a pontuação do teste esteja entre$70$$130$ e e use a integral do polinômio de grau$50$ Maclaurin de$\frac{1}{\sqrt{2π}}e^{−x^2/2}$ para estimar essa probabilidade.

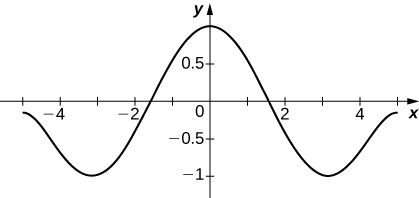
66) [T] Suponha que$\displaystyle \sum_{n=0}^∞a_nx^n$ converja para uma função$f(x)$ tal que$f(0)=1,\, f′(0)=0$,$f''(x)=−f(x)$ e. Encontre uma fórmula para$a_n$ e plote a soma parcial$S_N$ de$N=20$ em$[−5,5].$

Responda

Como no problema anterior, obtém-se$a_n=0$ se$n$ é ímpar e$a_n=−(n+2)(n+1)a_{n+2}$ se$n$ é par, então$a_0=1$ leva$a_{2n}=\dfrac{(−1)^n}{(2n)!}$ a.

$Este gráfico é uma curva de onda simétrica em relação à origem. Tem um pico em y = 1 acima da origem. Tem pontos mais baixos em -3 e 3.$

67) [T] Suponha que$\displaystyle \sum_{n=0}^∞a_nx^n$ converja para uma função$f(x)$ tal que$f(0)=0,\; f′(0)=1$,$f''(x)=−f(x)$ e. Encontre uma fórmula para um e plote a soma parcial$S_N$ de$N=10$ on$[−5,5]$.

68) Suponha que$\displaystyle \sum_{n=0}^∞a_nx^n$ converja para uma função$y$ tal que$y''−y′+y=0$ onde$y(0)=1$ e$y'(0)=0.$ encontre uma fórmula que se relacione$a_{n+2},\;a_{n+1},$ e calcule e$a_0,...,a_5$.

Responda: $\displaystyle y''=\sum_{n=0}^∞(n+2)(n+1)a_{n+2}x^n$e$\displaystyle y′=\sum_{n=0}^∞(n+1)a_{n+1}x^n$ assim$y''−y′+y=0$ implica isso$(n+2)(n+1)a_{n+2}−(n+1)a_{n+1}+a_n=0$ ou$a_n=\dfrac{a_{n−1}}{n}−\dfrac{a_{n−2}}{n(n−1)}$ para todos$n⋅y(0)=a_0=1$ e$y′(0)=a_1=0,$ assim por diante$a_2=\frac{1}{2},\;a_3=\frac{1}{6}\;,a_4=0$,$a_5=−\frac{1}{120}$ e.

69) Suponha que$\displaystyle \sum_{n=0}^∞a_nx^n$ converja para uma função$y$ tal que$y''−y′+y=0$ onde$y(0)=0$$y′(0)=1$ e. Encontre uma fórmula que se relacione$a_{n+2},\;a_{n+1}$ e calcule e$a_1,...,a_5$.

O erro ao aproximar a integral$\displaystyle ∫^b_af(t)\, dt$ pelo de uma aproximação de Taylor$\displaystyle ∫^b_aPn(t) \,dt$ é no máximo$\displaystyle ∫^b_aR_n(t) \,dt$. Nos exercícios 70 a 71, a estimativa do restante de Taylor$R_n≤\frac{M}{(n+1)!}|x−a|^{n+1}$ garante que a integral do polinômio de Taylor da ordem dada se aproxime da integral de$f$ com um erro menor que$\frac{1}{10}$.

a. Avalie a integral do polinômio de Taylor apropriado e verifique se ele se aproxima do valor de CAS com um erro menor que$\frac{1}{100}$.

b. Compare a precisão da estimativa integral do polinômio com a estimativa do restante.

70) [T]$\displaystyle ∫^π_0\frac{\sin t}{t}\, dt;\quad P_s=1−\frac{x^2}{3!}+\frac{x^4}{5!}−\frac{x^6}{7!}+\frac{x^8}{9!}$ (Você pode supor que o valor absoluto da nona derivada de$\frac{\sin t}{t}$ é limitado por$0.1$.)

Responda: a. (Prova)
b. Temos$R_s≤\frac{0.1}{(9)!}π^9≈0.0082<0.01.$ Temos$\displaystyle ∫^π_0\frac{\sin t}{t}\,dt=1.85194...$,$\displaystyle ∫^π_0\left(1−\frac{x^2}{3!}+\frac{x^4}{5!}−\frac{x^6}{7!}+\frac{x^8}{9!}\right)\,dx=π−\frac{π^3}{3⋅3!}+\frac{π^5}{5⋅5!}−\frac{π^7}{7⋅7!}+\frac{π^9}{9⋅9!}=1.852...,$ enquanto que, portanto, o erro real é de aproximadamente$0.00006.$

71) [T]$\displaystyle ∫^2_0e^{−x^2}\,dx;\; p_{11}=1−x^2+\frac{x^4}{2}−\frac{x^6}{3!}+⋯−\frac{x^{22}}{11!}$ (Você pode assumir que o valor absoluto da$23^{\text{rd}}$ derivada de$e^{−x^2}$ é menor que$2×10^{14}$.)

Os exercícios a seguir (72-73) tratam das integrais de Fresnel.

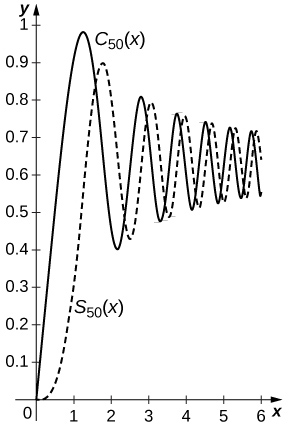
72) As integrais de Fresnel são definidas por$\displaystyle C(x)=∫^x_0\cos(t^2)\,dt$$\displaystyle S(x)=∫^x_0\sin(t^2)\,dt$ e. Calcule a série de potências de$C(x)$$S(x)$ e e e plote as somas$C_N(x)$ e$S_N(x)$ dos primeiros termos$N=50$ diferentes de zero em$[0,2π]$.

Responda

Desde$\displaystyle \cos(t^2)=\sum_{n=0}^∞(−1)^n\frac{t^{4n}}{(2n)!}$ e$\displaystyle \sin(t^2)=\sum_{n=0}^∞(−1)^n\frac{t^{4n+2}}{(2n+1)!}$, um tem$\displaystyle S(x)=\sum_{n=0}^∞(−1)^n\frac{x^{4n+3}}{(4n+3)(2n+1)!}$$\displaystyle C(x)=\sum_{n=0}^∞(−1)^n\frac{x^{4n+1}}{(4n+1)(2n)!}$ e. As somas dos primeiros termos$50$ diferentes de zero são plotadas abaixo com$C_{50}(x)$ a curva sólida e$S_{50}(x)$ a curva tracejada.

$Esse gráfico tem duas curvas. A primeira é uma curva sólida chamada Csub50 (x). Começa na origem e é uma onda que diminui gradualmente em amplitude. O mais alto que ele atinge é y = 1. A segunda curva é chamada de Ssub50 (x). É uma onda que diminui gradualmente em amplitude. O mais alto que atinge é 0,9. Está muito próximo do padrão da primeira curva, com uma ligeira mudança para a direita.$

73) [T] As integrais de Fresnel são usadas em aplicações de projeto para estradas e ferrovias e outras aplicações devido às propriedades de curvatura da curva com coordenadas$(C(t),S(t))$. Faça um gráfico da curva$(C_{50},S_{50})$ para$0≤t≤2π$, cujas coordenadas foram calculadas no exercício anterior.

74) Faça uma estimativa$\displaystyle ∫^{1/4}_0\sqrt{x−x^2}\,dx$ aproximando$\sqrt{1−x}$ usando a aproximação binomial$\displaystyle 1−\frac{x}{2}−\frac{x^2}{8}−\frac{x^3}{16}−\frac{5x^4}{2128}−\frac{7x^5}{256}$.

Responda: $\displaystyle ∫^{1/4}_0\sqrt{x}\left(1−\frac{x}{2}−\frac{x^2}{8}−\frac{x^3}{16}−\frac{5x^4}{128}−\frac{7x^5}{256}\right)\,dx =\frac{2}{3}2^{−3}−\frac{1}{2}\frac{2}{5}2^{−5}−\frac{1}{8}\frac{2}{7}2^{−7}−\frac{1}{16}\frac{2}{9}2^{−9}−\frac{5}{128}\frac{2}{11}2^{−11}−\frac{7}{256}\frac{2}{13}2^{−13}=0.0767732...$Considerando que$\displaystyle ∫^{1/4}_0\sqrt{x−x^2}\, dx=0.076773.$

75) [T] Use a aproximação de Newton do binômio$\sqrt{1−x^2}$ para aproximar da$π$ seguinte forma. O círculo$(\frac{1}{2},0)$ centrado no raio$\frac{1}{2}$ tem semicírculo superior$y=\sqrt{x}\sqrt{1−x}$. O setor desse círculo delimitado pelo$x$ eixo -entre$x=0$ e$x=\frac{1}{2}$ e pela união da linha$(\frac{1}{4},\frac{\sqrt{3}}{4})$ corresponde ao$\frac{1}{6}$ do círculo e tem área$\frac{π}{24}$. Este setor é a união de um triângulo reto com altura$\frac{\sqrt{3}}{4}$ e base$\frac{1}{4}$ e a região abaixo do gráfico entre$x=0$$x=\frac{1}{4}$ e. Para encontrar a área desta região, você pode escrever$y=\sqrt{x}\sqrt{1−x}=\sqrt{x}×(\text{binomial expansion of} \sqrt{1−x})$ e integrar termo a termo. Use essa abordagem com a aproximação binomial do exercício anterior para estimar$π$.

76) Use a aproximação$T≈2π\sqrt{\frac{L}{g}}(1+\frac{k^2}{4})$ para aproximar o período de um pêndulo com comprimento em$10$ metros e ângulo máximo$θ_{max}=\frac{π}{6}$ onde$k=\sin\left(\frac{θ_{max}}{2}\right)$. Compare isso com a estimativa de ângulo pequeno$T≈2π\sqrt{\frac{L}{g}}$.

Responda: $T≈2π\sqrt{\frac{10}{9.8}}\left(1+\frac{\sin^2(θ/12)}{4}\right)≈6.453$segundos. A estimativa do pequeno ângulo é$T≈2π\sqrt{\frac{10}{9.8}≈6.347}$. O erro relativo é de cerca de uma$2$ porcentagem.

77) Suponha que um pêndulo tenha um período de$2$ segundos e um ângulo máximo de$θ_{max}=\frac{π}{6}$. Use$T≈2π\sqrt{\dfrac{L}{g}}\left(1+\dfrac{k^2}{4}\right)$ para aproximar o comprimento desejado do pêndulo. Qual comprimento é previsto pela estimativa de ângulo pequeno$T≈2π\sqrt{\frac{L}{g}}$?

78) Avalie$\displaystyle ∫^{π/2}_0\sin^4θ\,dθ$ na aproximação$\displaystyle T=4\sqrt{\frac{L}{g}}∫^{π/2}_0\left(1+\frac{1}{2}k^2\sin^2θ+\frac{3}{8}k^4\sin^4θ+⋯\right)\,dθ$ para obter uma estimativa aprimorada para$T$.

Responda: $\displaystyle ∫^{π/2}_0\sin^4θ\, dθ=\frac{3π}{16}.$Conseqüentemente$T≈2π\sqrt{\frac{L}{g}}\left(1+\frac{k^2}{4}+\frac{9}{256}k^4\right).$

79) [T] Uma fórmula equivalente para o período de um pêndulo com amplitude$\displaystyle θ_{max}$ é$T(θ_{max})=2\sqrt{2}\sqrt{\frac{L}{g}}∫^{θ_{max}}_0\frac{dθ}{\sqrt{\cos θ}−\cos(θ_{max})}$ onde$L$ está o comprimento do pêndulo e$g$ é a constante de aceleração gravitacional. Quando$θ_{max}=\frac{π}{3}$ chegarmos$\dfrac{1}{\sqrt{\cos t−1/2}}≈\sqrt{2}\left(1+\frac{t^2}{2}+\frac{t^4}{3}+\frac{181t^6}{720}\right)$. Integre essa aproximação para estimar$T(\frac{π}{3})$ em termos de$L$$g$ e. Supondo$g=9.806$ metros por segundo ao quadrado, encontre um comprimento$L$ aproximado em$T(\frac{π}{3})=2$ segundos.

Colaboradores

Template:ContribOpenStaxCalc