10.3: Série Taylor e Maclaurin

Objetivos de

• Descreva o procedimento para encontrar um polinômio de Taylor de uma determinada ordem para uma função.
• Explique o significado e a importância do teorema de Taylor com o restante.
• Estime o restante de uma aproximação da série Taylor de uma determinada função.

Nas duas seções anteriores, discutimos como encontrar representações de séries de potência para certos tipos de funções — especificamente, funções relacionadas a séries geométricas. Aqui, discutimos representações de séries de potência para outros tipos de funções. Em particular, abordamos as seguintes questões: Quais funções podem ser representadas por séries de potências e como encontramos essas representações? Se pudermos encontrar uma representação de série de potência para uma função específica\(f\) e a série convergir em algum intervalo, como podemos provar que a série realmente converge para\(f\)?

Visão geral da série Taylor/Maclaurin

Considere uma função\(f\) que tenha uma representação de série de potências em\(x=a\). Então a série tem a forma

\[\sum_{n=0}^∞c_n(x−a)^n=c_0+c_1(x−a)+c_2(x−a)^2+ \dots. \label{eq1} \]

Quais devem ser os coeficientes? Por enquanto, ignoramos questões de convergência, mas nos concentramos no que a série deveria ser, se houver. Voltaremos para discutir a convergência mais adiante nesta seção. Se a série Equation\ ref {eq1} for uma representação para\(f\) at\(x=a\), certamente queremos que a série seja igual\(f(a)\) a\(x=a\) a. Avaliando a série em\(x=a\), vemos que

\[\sum_{n=0}^∞c_n(x−a)^n=c_0+c_1(a−a)+c_2(a−a)^2+\dots=c_0.\label{eq2} \]

Assim, a série é igual\(f(a)\) ao coeficiente\(c_0=f(a)\). Além disso, gostaríamos que a primeira derivada da série de potências fosse igual\(f′(a)\) a\(x=a\). Equação de diferenciação\ ref {eq2} termo a termo, vemos que

\[\dfrac{d}{dx}\left( \sum_{n=0}^∞c_n(x−a)^n \right)=c_1+2c_2(x−a)+3c_3(x−a)^2+\dots.\label{eq3} \]

Portanto,\(x=a,\) na derivada é

\[\dfrac{d}{dx}\left( \sum_{n=0}^∞c_n(x−a)^n \right)=c_1+2c_2(a−a)+3c_3(a−a)^2+\dots=c_1.\label{eq4} \]

Portanto, a derivada da série é igual\(f′(a)\) se o coeficiente\(c_1=f′(a).\) Continuando dessa maneira, procuramos coeficientes\(c_n\) de forma que todas as derivadas da série de potências Equation\ ref {eq4} concordem com todas as derivadas correspondentes de\(f\) at\(x=a\). As segunda e terceira derivadas da Equação\ ref {eq3} são dadas por

\[\dfrac{d^2}{dx^2} \left(\sum_{n=0}^∞c_n(x−a)^n \right)=2c_2+3⋅2c_3(x−a)+4⋅3c_4(x−a)^2+\dots\label{eq5} \]

e

\[\dfrac{d^3}{dx^3} \left( \sum_{n=0}^∞c_n(x−a)^n \right)=3⋅2c_3+4⋅3⋅2c_4(x−a)+5⋅4⋅3c_5(x−a)^2+⋯.\label{eq6} \]

Portanto, at\(x=a\), a segunda e a terceira derivadas

\[\dfrac{d^2}{dx^2} \left(\sum_{n=0}^∞c_n(x−a)^n\right)=2c_2+3⋅2c_3(a−a)+4⋅3c_4(a−a)^2+\dots=2c_2\label{eq7} \]

e

\[\dfrac{d^3}{dx^3} \left(\sum_{n=0}^∞c_n(x−a)^n\right)=3⋅2c_3+4⋅3⋅2c_4(a−a)+5⋅4⋅3c_5(a−a)^2+\dots =3⋅2c_3\label{eq8} \]

igual\(f''(a)\) e\(f'''(a)\), respectivamente, se\(c_2=\dfrac{f''(a)}{2}\)\(c_3=\dfrac{f'''(a)}{3⋅2}\) e. De forma mais geral, vemos que se\(f\) tem uma representação de série de potência em\(x=a\), então os coeficientes devem ser dados por\(c_n=\dfrac{f^{(n)}(a)}{n!}\). Ou seja, a série deve ser

\[\sum_{n=0}^∞\dfrac{f^{(n)}(a)}{n!}(x−a)^n=f(a)+f′(a)(x−a)+\dfrac{f''(a)}{2!}(x−a)^2+\dfrac{f'''(a)}{3!}(x−a)^3+⋯ \nonumber \]

Esta série de potência\(f\) é conhecida como série Taylor para\(f\) at\(a.\) If\(x=0\), então esta série é conhecida como a série Maclaurin para\(f\).

Definição\(\PageIndex{1}\): Maclaurin and Taylor series

Se\(f\) tem derivadas de todas as ordens em\(x=a\), então a série de Taylor para a função\(f\) at\(a\) é

\[\sum_{n=0}^∞\dfrac{f^{(n)}(a)}{n!}(x−a)^n=f(a)+f′(a)(x−a)+\dfrac{f''(a)}{2!}(x−a)^2+⋯+\dfrac{f^{(n)}(a)}{n!}(x−a)^n+⋯ \nonumber \]

A série Taylor para\(f\) em 0 é conhecida como a série Maclaurin para\(f\).

Mais adiante nesta seção, mostraremos exemplos de como encontrar séries de Taylor e discutiremos as condições sob as quais a série de Taylor para uma função convergirá para essa função. Aqui, declaramos um resultado importante. Lembre-se de que as representações da série Power são únicas. Portanto, se uma função\(f\) tem uma série de potência em\(a\), então ela deve ser a série Taylor para\(f\) at\(a\).

Exclusividade da série Taylor

Se uma função\(f\) tem uma série de potências em a que converge para\(f\) algum intervalo aberto contendo\(a\), então essa série de potência é a série Taylor para\(f\) at\(a\).

A prova segue diretamente daquela discutida anteriormente.

Para determinar se uma série de Taylor converge, precisamos examinar sua sequência de somas parciais. Essas somas parciais são polinômios finitos, conhecidos como polinômios de Taylor.

Polinômios de Taylor

A soma\(n^{\text{th}}\) parcial da série de Taylor para uma função\(f\) at\(a\) é conhecida como polinômio de Taylor de\(n^{\text{th}}\) grau. ^{Por exemplo, as somas parciais 0, 1, 2 e 3 ª da série Taylor são dadas por}

\[\begin{align*} p_0(x) &=f(a) \\[4pt] p_1(x) &=f(a)+f′(a)(x−a) \\[4pt]p_2(x) &=f(a)+f′(a)(x−a)+\dfrac{f''(a)}{2!}(x−a)^2\ \\[4pt]p_3(x) &=f(a)+f′(a)(x−a)+\dfrac{f''(a)}{2!}(x−a)^2+\dfrac{f'''(a)}{3!}(x−a)^3 \end{align*}\]

respectivamente. ^{Essas somas parciais são conhecidas como polinômios Taylor de 0, 1º, 2º e 3º graus de Taylor de\(f\) at\(a\), respectivamente.} Se\(x=a\), então esses polinômios são conhecidos como polinômios de Maclaurin para\(f\). Agora fornecemos uma definição formal dos polinômios de Taylor e Maclaurin para uma função\(f\).

Definição\(\PageIndex{2}\): Maclaurin polynomial

Se\(f\) tem\(n\) derivadas em\(x=a\), então o polinômio de Taylor de\(n^{\text{th}}\) -grau de\(f\) at\(a\) é

\[p_n(x)=f(a)+f′(a)(x−a)+\dfrac{f''(a)}{2!}(x−a)^2+\dfrac{f'''(a)}{3!}(x−a)^3+⋯+\dfrac{f^{(n)}(a)}{n!}(x−a)^n. \nonumber \]

O polinômio de Taylor em\(n^{\text{th}}\) -grau para\(f\) at\(0\) é conhecido como polinômio Maclaurin de\(n^{\text{th}}\) grau -para\(f\).

Agora, mostramos como usar essa definição para encontrar vários polinômios de Taylor para\(f(x)=\ln x\) at\(x=1\).

Exemplo\(\PageIndex{1}\): Finding Taylor Polynomials

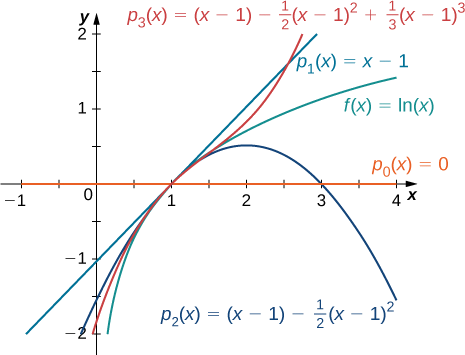
Encontre os polinômios de Taylor\(p_0,p_1,p_2\) e\(p_3\) para\(f(x)=\ln x\) em\(x=1\). Use um utilitário gráfico para comparar o gráfico de\(f\) com os gráficos de\(p_0,p_1,p_2\)\(p_3\) e.

Solução

Para encontrar esses polinômios de Taylor, precisamos avaliar\(f\) suas três primeiras derivadas em\(x=1\).

\ [\ begin {align*} f (x) &=\ ln x & f (1) &=0\\ [5pt]
f′( x) &=\ dfrac {1} {x} e f′( 1) &=1\\ [5pt]
f “(x) &=−\ dfrac {1} {x^2} & f “(1) &=−1\ [5pt]
f"' (x) &=\ dfrac {2} {x^3} & f"' (1) &=2\ end {align*}\]

Portanto,

\[\begin{align*} p_0(x) &= f(1)=0,\\[4pt]p_1(x) &=f(1)+f′(1)(x−1) =x−1,\\[4pt]p_2(x) &=f(1)+f′(1)(x−1)+\dfrac{f''(1)}{2}(x−1)^2 = (x−1)−\dfrac{1}{2}(x−1)^2 \\[4pt]p_3(x) &=f(1)+f′(1)(x−1)+\dfrac{f''(1)}{2}(x−1)^2+\dfrac{f'''(1)}{3!}(x−1)^3=(x−1)−\dfrac{1}{2}(x−1)^2+\dfrac{1}{3}(x−1)^3 \end{align*}\]

Os gráficos\(y=f(x)\) e os três primeiros polinômios de Taylor são mostrados na Figura\(\PageIndex{1}\).

Figura\(\PageIndex{1}\): A função\(y=\ln x\) e os polinômios de Taylor\(p_0,p_1,p_2\) e\(p_3\) at\(x=1\) estão plotados neste gráfico.

Exercício\(\PageIndex{1}\)

Encontre os polinômios de Taylor\(p_0,p_1,p_2\) e\(p_3\) para\(f(x)=\dfrac{1}{x^2}\) em\(x=1\).

Dica

Encontre as três primeiras derivadas de\(f\) e avalie-as em\(x=1.\)

Responda

\ [\ begin {align*} p_0 (x) &=1\\ [5pt]
p_1 (x) &=1−2 (x−1)\ [5pt] p_2 (x) &=1−2 (x−1) +3 (x−1)
^2\\ [5pt] p_3 (x) &=1−2 (x−1) +3 (x−1) ^2\\ [5pt]
p_3 (x) &=1−2 (x−1) +3 (x−1) ^2\\ [5pt] p_3 (x) &=1−x−1) ^2−4 (x−1) ^3\ end {align*}\]

Agora mostramos como encontrar polinômios de Maclaurin para\(e^x, \sin x,\)\(\cos x\) e. Conforme mencionado acima, os polinômios de Maclaurin são polinômios de Taylor centrados em zero.

Exemplo\(\PageIndex{2}\): Finding Maclaurin Polynomials

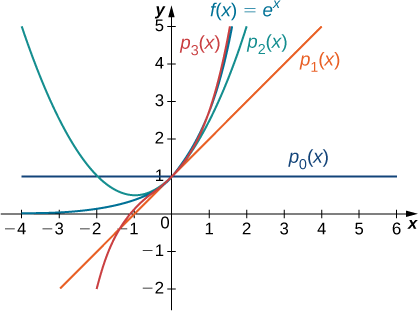
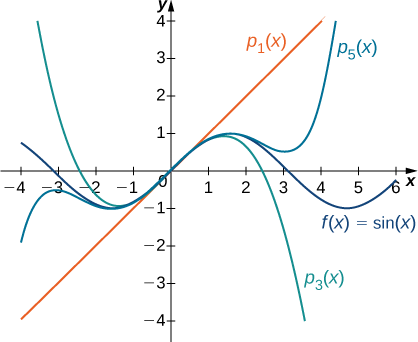
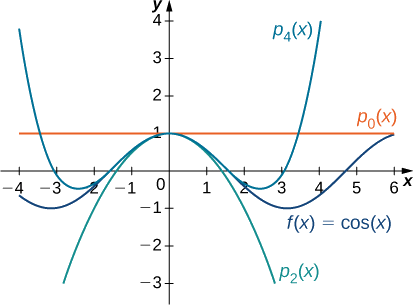
Para cada uma das seguintes funções, encontre fórmulas para os polinômios de Maclaurin\(p_0,p_1,p_2\)\(p_3\) e. Encontre uma fórmula para o polinômio de Maclaurin em\(n^{\text{th}}\) -grau e escreva-a usando a notação sigma. Use um utilitário gráfico para comparar os gráficos de\(p_0,p_1,p_2\) e\(p_3\) com\(f\).

1. \(f(x)=e^x\)
2. \(f(x)=\sin x\)
3. \(f(x)=\cos x\)

Solução

Desde então\(f(x)=e^x\), sabemos disso\(f(x)=f′(x)=f''(x)=⋯=f^{(n)}(x)=e^x\) para todos os números inteiros positivos\(n\). Portanto,

\[f(0)=f′(0)=f''(0)=⋯=f^{(n)}(0)=1 \nonumber \]

para todos os números inteiros positivos\(n\). Portanto, temos

\ (\ begin {align*} p_0 (x) &=f (0) =1,\\ [5pt]
p_1 (x) &=f (0) +f′( 0) x=1+x,\\ [5pt]
p_2 (x) &=f (0) +f′( 0) x+\ dfrac {f "(0)} {2!} x^2=1+x+\ dfrac {1} {2} x^2,\\ [5pt]
p_3 (x) &=f (0) +f′( 0) x+\ dfrac {f "(0)} {2} x^2+\ dfrac {f"' (0)} {3!} x^3=1+x+\ dfrac {1} {2} x^2+\ dfrac {1} {3!} x^3,\ end {align*}\)

\ (\ displaystyle\ begin {align*} p_n (x) &=f (0) +f′( 0) x+\ dfrac {f "(0)} {2} x^2+\ dfrac {f"' (0)} {3!} x^3++\ dfrac {f^ {(n)} (0)} {n!} x^n\\ [5 pontos]
&=1+x+\ dfrac {x^2} {2!} +\ dfrac {x^3} {3!} ++\ dfrac {x^n} {n!} \\ [5pt]
&=\ sum_ {k=0} ^n\ dfrac {x^k} {k!} \ end {align*}\).

A função e os três primeiros polinômios de Maclaurin são mostrados na Figura\(\PageIndex{2}\).

Figura\(\PageIndex{2}\): O gráfico mostra a função\(y=e^x\) e os polinômios de Maclaurin\(p_0,\,p_1,\,p_2\)\(p_3\) e.

b. Para\(f(x)=\sin x\), os valores da função e suas primeiras quatro derivadas em\(x=0\) são dados da seguinte forma:

\ [\ begin {align*} f (x) &=\ sin x & f (0) &=0\\ [5pt]
f′( x) &=\ cos x & f′( 0) &=1\\ [5pt]
f "(x) &=−\ sin x & f “(0) &=0\\ [5pt]
f"' (x) &=−\ cos x & f"' (0) &=−1\\ [5pt]
f^ {(4)} (x) &=\ sin x & f^ {(4)} (0) &=0. \ end {align*}\]

Como a quarta derivada é\(\sin x,\) o padrão se repete. Ou seja,\(f^{(2m)}(0)=0\) e\(f^{(2m+1)}(0)=(−1)^m\) para\(m≥0.\) Assim, temos

\ (\ begin {align*} p_0 (x) &=0,\\ [5pt]
p_1 (x) &=0+x=x,\\ [5pt]
p_2 (x) &=0+x+0=x,\\ [5pt]
p_3 (x) &=0+x+0−\ dfrac {1} {3!} x^3=x−\ dfrac {x^3} {3!} ,\\ [5pt]
p_4 (x) &=0+x+0−\ dfrac {1} {3!} x^3+0=x−\ dfrac {x^3} {3!} ,\\ [5pt]
p_5 (x) &=0+x+0−\ dfrac {1} {3!} x^3+0+\ dfrac {1} {5!} x^5=x−\ dfrac {x^3} {3!} +\ dfrac {x^5} {5!} ,\ end {align*}\)

e para\(m≥0\),

\ [\ begin {align*} p_ {2m+1} (x) =p_ {2m+2} (x) &=x−\ dfrac {x^3} {3!} +\ dfrac {x^5} {5!} −+ (−1) ^m\ dfrac {x^ {2m+1}} {(2m+1)!} \\ [5pt]
&=\ sum_ {k=0} ^m (−1) ^k\ dfrac {x^ {2k+1}} {(2k+1)!}. \ end {align*}\]

Os gráficos da função e seus polinômios de Maclaurin são mostrados na Figura\(\PageIndex{3}\).

Figura\(\PageIndex{3}\): O gráfico mostra a função\(y=\sin x\) e os polinômios de Maclaurin\(p_1,\, p_3\)\(p_5\) e.

c. Para\(f(x)=\cos x\), os valores da função e suas primeiras quatro derivadas em\(x=0\) são dados da seguinte forma:

\ [\ begin {align*} f (x) &=\ cos x & f (0) &=1\\ [5pt]
f′( x) &=−\ sin x & f′( 0) &=0\\ [5pt]
f "(x) &=−\ cos x & f “(0) &=−1\\ [5pt]
f"' (x) &=\ sin x & f"' (0) &=0\\ [5pt]
f^ {(4)} (x) &=\ cos x e f^ {(4)} (0) &=1. \ end {align*}\]

Como a quarta derivada é\(\sin x\), o padrão se repete. Em outras palavras,\(f^{(2m)}(0)=(−1)^m\) e\(f^{(2m+1)}=0\) para\(m≥0\). Portanto,

\ (\ begin {align*} p_0 (x) &=1,\\ [5pt]
p_1 (x) &=1+0=1,\\ [5pt]
p_2 (x) &=1+0−\ dfrac {1} {2!} x^2=1−\ dfrac {x^2} {2!} ,\\ [5pt]
p_3 (x) &=1+0−\ dfrac {1} {2!} x^2+0=1−\ dfrac {x^2} {2!} ,\\ [5pt]
p_4 (x) &=1+0−\ dfrac {1} {2!} x^2+0+\ dfrac {1} {4!} x^4=1−\ dfrac {x^2} {2!} +\ dfrac {x^4} {4!} ,\\ [5pt]
p_5 (x) &=1+0−\ dfrac {1} {2!} x^2+0+\ dfrac {1} {4!} x^4+0=1−\ dfrac {x^2} {2!} +\ dfrac {x^4} {4!} ,\ end {align*}\)

e para\(n≥0\),

\ [\ begin {align*} p_ {2m} (x) &=p_ {2m+1} (x)\\ [5pt]
&=1−\ dfrac {x^2} {2!} +\ dfrac {x^4} {4!} −+ (−1) ^m\ dfrac {x^ {2m}} {(2m)!} \\ [5pt]
&=\ sum_ {k=0} ^m (−1) ^k\ dfrac {x^ {2k}} {(2k)!}. \ end {align*}\]

Gráficos da função e dos polinômios de Maclaurin aparecem na Figura\(\PageIndex{4}\).

Figura\(\PageIndex{4}\): A função\(y=\cos x\) e os polinômios\(p_0,p_2\) de Maclaurin\(p_4\) estão plotados neste gráfico.

Exercício\(\PageIndex{2}\)

Encontre fórmulas para os polinômios de Maclaurin\(p_0,\,p_1,\,p_2\) e\(p_3\) para\(f(x)=\dfrac{1}{1+x}\).

Encontre uma fórmula para o polinômio Maclaurin de\(n^{\text{th}}\) grau. Escreva sua resposta usando a notação sigma.

Dica

Avalie as quatro primeiras derivadas de\(f\) e procure um padrão.

Responda

\(\displaystyle p_0(x)=1;\;p_1(x)=1−x;\;p_2(x)=1−x+x^2;\;p_3(x)=1−x+x^2−x^3;\;p_n(x)=1−x+x^2−x^3+⋯+(−1)^nx^n=\sum_{k=0}^n(−1)^kx^k\)

Teorema de Taylor com resto

Lembre-se de que o polinômio de Taylor em\(n^{\text{th}}\) -grau para uma função\(f\) at\(a\) é a soma\(n^{\text{th}}\) parcial da série Taylor para\(f\) at\(a\). Portanto, para determinar se a série de Taylor converge, precisamos determinar se a sequência dos polinômios de Taylor\({p_n}\) converge. No entanto, não queremos apenas saber se a sequência de polinômios de Taylor converge, queremos saber se ela converge para\(f\). Para responder a essa pergunta, definimos o restante\(R_n(x)\) como

\[R_n(x)=f(x)−p_n(x). \nonumber \]

Para que a sequência de polinômios de Taylor converja\(f\), precisamos que o restante\(R_n\) converja para zero. Para determinar se\(R_n\) converge para zero, introduzimos o teorema de Taylor com o restante. Esse teorema não é apenas útil para provar que uma série de Taylor converge para sua função relacionada, mas também nos permitirá quantificar o quão bem o polinômio de Taylor em\(n^{\text{th}}\) -grau se aproxima da função.

Aqui procuramos um limite em\(|R_n|.\) Considere o caso mais simples:\(n=0\). \(p_0\)Seja o ^10º polinômio de Taylor em\(a\) para uma função\(f\). O restante\(R_0\) satisfaz

\(R_0(x)=f(x)−p_0(x)=f(x)−f(a).\)

Se\(f\) é diferenciável em um intervalo\(I\) contendo\(a\) e\(x\), então, pelo Teorema do Valor Médio, existe um número real\(c\) entre\(a\) e\(x\) tal que\(f(x)−f(a)=f′(c)(x−a)\). Portanto,

\[R_0(x)=f′(c)(x−a). \nonumber \]

Usando o Teorema do Valor Médio em um argumento similar, podemos mostrar que se\(f\) é\(n\) vezes diferenciável em um intervalo\(I\) contendo\(a\) e\(x\), então o\(n^{\text{th}}\) restante\(R_n\) satisfaz

\[R_n(x)=\dfrac{f^{(n+1)}(c)}{(n+1)!}(x−a)^{n+1} \nonumber \]

para algum número real\(c\) entre\(a\)\(x\) e. É importante observar que o valor\(c\) no numerador acima não é o centro\(a\), mas sim um valor desconhecido\(c\) entre\(a\)\(x\) e. Essa fórmula nos permite obter um limite para o restante\(R_n\). Se por acaso soubermos que\(∣f^{(n+1)}(x)∣\) é limitado por algum número real\(M\) nesse intervalo\(I\), então

\[|R_n(x)|≤\dfrac{M}{(n+1)!}|x−a|^{n+1} \nonumber \]

para todos\(x\) no intervalo\(I\).

Agora declaramos o teorema de Taylor, que fornece a relação formal entre uma função\(f\) e seu polinômio de Taylor de\(n^{\text{th}}\) grau\(p_n(x)\). Esse teorema nos permite limitar o erro ao usar um polinômio de Taylor para aproximar o valor de uma função e será importante para provar que uma série de Taylor para\(f\) converge para\(f\).

Teorema de Taylor com resto

\(f\)Seja uma função que pode ser diferenciada\(n+1\) vezes em um intervalo\(I\) contendo o número real\(a\). \(p_n\)Seja o polinômio de Taylor em\(n^{\text{th}}\) -grau de\(f\) at\(a\) e let

\[R_n(x)=f(x)−p_n(x) \nonumber \]

seja o\(n^{\text{th}}\) restante. Então, para cada um\(x\) no intervalo\(I\), existe um número real\(c\) entre\(a\) e\(x\) tal que

\[R_n(x)=\dfrac{f^{(n+1)}(c)}{(n+1)!}(x−a)^{n+1} \nonumber \].

Se existe um número real\(M\) tal que\(∣f^{(n+1)}(x)∣≤M\) para todos\(x∈I\), então

\[|R_n(x)|≤\dfrac{M}{(n+1)!}|x−a|^{n+1} \nonumber \]

para todos\(x\) em\(I\).

Prova

Fixe um ponto\(x∈I\) e introduza a função de\(g\) forma que

\[g(t)=f(x)−f(t)−f′(t)(x−t)−\dfrac{f''(t)}{2!}(x−t)^2−⋯−\dfrac{f^{(n)}(t)}{n!}(x−t)^n−R_n(x)\dfrac{(x−t)^{n+1}}{(x−a)^{n+1}}. \nonumber \]

Afirmamos que\(g\) satisfaz os critérios do teorema de Rolle. Como\(g\) é uma função polinomial (in\(t\)), é uma função diferenciável. Além disso,\(g\) é zero em\(t=a\) e\(t=x\) porque

\[ \begin{align*} g(a) &=f(x)−f(a)−f′(a)(x−a)−\dfrac{f''(a)}{2!}(x−a)^2+⋯+\dfrac{f^{(n)}(a)}{n!}(x−a)^n−R_n(x) \\[4pt] &=f(x)−p_n(x)−R_n(x) \\[4pt] &=0, \\[4pt] g(x) &=f(x)−f(x)−0−⋯−0 \\[4pt] &=0. \end{align*}\]

Portanto,\(g\) satisfaz o teorema de Rolle e, consequentemente, existe\(c\) entre\(a\) e\(x\) tal que agora\(g′(c)=0.\) calculamos\(g′\). Usando a regra do produto, notamos que

\[\dfrac{d}{dt}\left[\dfrac{f^{(n)}(t)}{n!}(x−t)^n\right]=−\dfrac{f^{(n)}(t)}{(n−1)!}(x−t)^{n−1}+\dfrac{f^{(n+1)}(t)}{n!}(x−t)^n. \nonumber \]

Consequentemente,

\ [\ begin {align} g′( t) &=−f′( t) + [f′( t) −f "(t) (x−t)] +\ left [f" (t) (x−t) −\ dfrac {f"' (t)} {2!} (x−t) ^2\ direita] +\ nonumber\\
&\ quad+\ left [\ dfrac {f^ {(n)} (t)} {(n−1)!} (x−t) ^ {n−1} −\ dfrac {f^ {(n+1)} (t)} {n!} (x−t) ^n\ right] + (n+1) R_n (x)\ dfrac {(x−t) ^n} {(x−a) ^ {n+1}}\ end {align}\ nonumber\].

Observe que há um efeito telescópico. Portanto,

\[g'(t)=−\dfrac{f^{(n+1)}(t)}{n!}(x−t)^n+(n+1)R_n(x)\dfrac{(x−t)^n}{(x−a)^{n+1}} \nonumber \].

Pelo teorema de Rolle, concluímos que existe um número\(c\) entre\(a\) e\(x\) tal que\(g′(c)=0.\) Desde

\[g′(c)=−\dfrac{f^{(n+1})(c)}{n!}(x−c)^n+(n+1)R_n(x)\dfrac{(x−c)^n}{(x−a)^{n+1}} \nonumber \]

concluímos que

\[−\dfrac{f^{(n+1)}(c)}{n!}(x−c)^n+(n+1)R_n(x)\dfrac{(x−c)^n}{(x−a)^{n+1}}=0. \nonumber \]

Adicionando o primeiro termo do lado esquerdo aos dois lados da equação e dividindo os dois lados da equação por,\(n+1,\) concluímos que

\[R_n(x)=\dfrac{f^{(n+1)}(c)}{(n+1)!}(x−a)^{n+1} \nonumber \]

conforme desejado. Deste fato, conclui-se que, se existe\(M\) tal coisa que,\(∣f^{(n+1)}(x)∣≤M\) para todos\(x\)\(I\), então

\[|R_n(x)|≤\dfrac{M}{(n+1)!}|x−a|^{n+1} \nonumber \].

□

O teorema de Taylor não apenas nos permite provar que uma série de Taylor converge para uma função, mas também nos permite estimar a precisão dos polinômios de Taylor na aproximação dos valores da função. Começamos examinando as aproximações lineares e quadráticas de\(f(x)=\sqrt[3]{x}\) at\(x=8\) e determinamos a precisão dessas aproximações na estimativa\(\sqrt[3]{11}\).

Exemplo\(\PageIndex{3}\): Using Linear and Quadratic Approximations to Estimate Function Values

Considere a função\(f(x)=\sqrt[3]{x}\).

1. Encontre o primeiro e o segundo polinômios de Taylor para\(f\) at\(x=8\). Use um utilitário gráfico para comparar esses polinômios com\(f\) near\(x=8.\)
2. Use esses dois polinômios para estimar\(\sqrt[3]{11}\).
3. Use o teorema de Taylor para limitar o erro.

Solução:

a. Para\(f(x)=\sqrt[3]{x}\), os valores da função e suas duas primeiras derivadas em\(x=8\) são os seguintes:

\ [\ begin {align*} f (x) &=\ sqrt [3] {x}, & f (8) &=2\\ [5pt]
f′( x) &=\ dfrac {1} {3x^ {2/3}}, & f′( 8) &=\ dfrac {1} {12}\\ [5pt] f “(x) &=\ dfrac {1} {12}\\ [5pt]
f “(x) &=\ dfrac {1} {12}\\ [5pt] f “(x) &=\ dfrac {1}\ frac {−2} {9x^ {5/3}}, & f “(8) &=−\ dfrac {1} {144.} \ end {align*}\]

Assim, o primeiro e o segundo polinômios de Taylor em\(x=8\) são dados por

\ (\ begin {align*} p_1 (x) &=f (8) +f′( 8) (x−8)\\ [5pt]
&=2+\ dfrac {1} {12} (x−8)\ end {align*}\)

\ (\ begin {align*} p_2 (x) &=f (8) +f′( 8) (x−8) +\ dfrac {f "(8)} {2!} (x−8) ^2\\ [5pt]
&=2+\ dfrac {1} {12} (x−8) −\ dfrac {1} {288} (x−8) ^2. \ end {align*}\)

A função e os polinômios de Taylor são mostrados na Figura\(\PageIndex{5}\).

Figura\(\PageIndex{5}\): Os gráficos\(f(x)=\sqrt[3]{x}\) e as aproximações lineares e quadráticas\(p_1(x)\) e\(p_2(x)\)

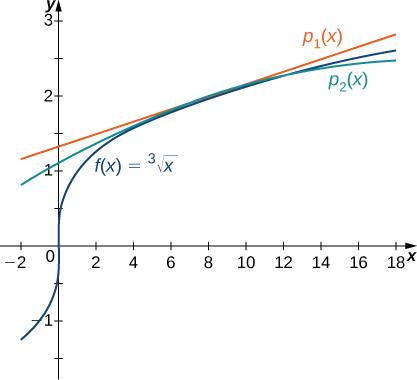
b. Usando o primeiro polinômio de Taylor em\(x=8\), podemos estimar

\[\sqrt[3]{11}≈p_1(11)=2+\dfrac{1}{12}(11−8)=2.25. \nonumber \]

Usando o segundo polinômio de Taylor em\(x=8\), obtemos

\[\sqrt[3]{11}≈p_2(11)=2+\dfrac{1}{12}(11−8)−\dfrac{1}{288}(11−8)^2=2.21875. \nonumber \]

c. Por nota, existe um c no intervalo de\((8,11)\) tal forma que o restante ao se aproximar\(\sqrt[3]{11}\) pelo primeiro polinômio de Taylor satisfaz

\[R_1(11)=\dfrac{f''(c)}{2!}(11−8)^2. \nonumber \]

Não sabemos o valor exato de\(c,\), então encontramos um limite superior\(R_1(11)\) determinando o valor máximo de\(f''\) no intervalo\((8,11)\). Desde então\(f''(x)=−\dfrac{2}{9x^{5/3}}\), o maior valor para\(|f''(x)|\) nesse intervalo ocorre em\(x=8\). Usando o fato de que\(f''(8)=−\dfrac{1}{144}\), obtemos

\(|R_1(11)|≤\dfrac{1}{144⋅2!}(11−8)^2=0.03125.\)

Da mesma forma, para estimar\(R_2(11)\), usamos o fato de que

\(R_2(11)=\dfrac{f'''(c)}{3!}(11−8)^3\).

Desde então\(f'''(x)=\dfrac{10}{27x^{8/3}}\), o valor máximo de\(f'''\) no intervalo\((8,11)\) é\(f'''(8)≈0.0014468\). Portanto, temos

\(|R_2(11)|≤\dfrac{0.0011468}{3!}(11−8)^3≈0.0065104.\)

Exercício\(\PageIndex{3}\):

Encontre o primeiro e o segundo polinômios de Taylor para\(f(x)=\sqrt{x}\) at\(x=4\). Use esses polinômios para estimar\(\sqrt{6}\). Use o teorema de Taylor para limitar o erro.

Dica

Avalie\(f(4),f′(4),\) e\(f''(4).\)

Responda

\(p_1(x)=2+\dfrac{1}{4}(x−4);p_2(x)=2+\dfrac{1}{4}(x−4)−\dfrac{1}{64}(x−4)^2;p_1(6)=2.5;p_2(6)=2.4375;\)

\(|R_1(6)|≤0.0625;|R_2(6)|≤0.015625\)

Exemplo\(\PageIndex{4}\): Approximating \(\sin x\) Using Maclaurin Polynomials

Do exemplo\(\PageIndex{2b}\), os polinômios de Maclaurin para\(\sin x\) são dados por

\[p_{2m+1}(x)=p_{2m+2}(x)=x−\dfrac{x^3}{3!}+\dfrac{x^5}{5!}−\dfrac{x^7}{7!}+⋯+(−1)^m\dfrac{x^{2m+1}}{(2m+1)!} \nonumber \]

para\(m=0,1,2,….\)

1. Use o quinto polinômio de Maclaurin para\(\sin x\) para aproximar\(\sin\left(\dfrac{π}{18}\right)\) e limitar o erro.
2. Para quais valores do\(x\) quinto polinômio de Maclaurin\(\sin x\) se aproxima de dentro\(0.0001\)?

Solução

uma.

O quinto polinômio de Maclaurin é

\[p_5(x)=x−\dfrac{x^3}{3!}+\dfrac{x^5}{5!} \nonumber \].

Usando esse polinômio, podemos estimar da seguinte forma:

\[\sin\left(\dfrac{π}{18}\right)≈p_5\left(\dfrac{π}{18}\right)=\dfrac{π}{18}−\dfrac{1}{3!}\left(\dfrac{π}{18}\right)^3+\dfrac{1}{5!}\left(\dfrac{π}{18}\right)^5≈0.173648. \nonumber \]

Para estimar o erro, use o fato de que o sexto polinômio de Maclaurin é\(p_6(x)=p_5(x)\) e calcule um limite em\(R_6(\dfrac{π}{18})\). Por nota, o restante é

\[R_6\left(\dfrac{π}{18}\right)=\dfrac{f^{(7)}(c)}{7!}\left(\dfrac{π}{18}\right)^7 \nonumber \]

para alguns\(c\) entre 0\(\dfrac{π}{18}\) e. Usando o fato de que\(x\),\(∣f^{(7)}(x)∣≤1\) para todos, descobrimos que a magnitude do erro é no máximo

\[\dfrac{1}{7!}⋅\left(\dfrac{π}{18}\right)^7≤9.8×10^{−10}. \nonumber \]

b.

Precisamos encontrar os valores de\(x\) tal forma que

\[\dfrac{1}{7!}|x|^7≤0.0001. \nonumber \]

Resolvendo essa desigualdade para\(x\), temos que o quinto polinômio de Maclaurin fornece uma estimativa de dentro de\(0.0001\) tão longo quanto\(|x|<0.907.\)

Exercício\(\PageIndex{4}\)

Use o quarto polinômio de Maclaurin para\(\cos x\) para aproximar\(\cos\left(\dfrac{π}{12}\right).\)

Dica

O quarto polinômio de Maclaurin é\(p_4(x)=1−\dfrac{x^2}{2!}+\dfrac{x^4}{4!}\).

Responda

0,96593

Agora que podemos limitar o restante\(R_n(x)\), podemos usar esse limite para provar que uma série de Taylor para\(f\) a converge para\(f\).

Representando funções com as séries Taylor e Maclaurin

Agora discutimos questões de convergência para a série Taylor. Começamos mostrando como encontrar uma série de Taylor para uma função e como encontrar seu intervalo de convergência.

Exemplo\(\PageIndex{5}\): Finding a Taylor Series

Encontre a série Taylor\(f(x)=\dfrac{1}{x}\) em\(x=1\). Determine o intervalo de convergência.

Solução

\(f(x)=\dfrac{1}{x},\)Pois os valores da função e suas primeiras quatro derivadas em\(x=1\) são

\ [\ begin {align*} f (x) &=\ dfrac {1} {x} & f (1) &=1\\ [5pt]
f′( x) &=−\ dfrac {1} {x^2} e f′( 1) &=−1\\ [5pt]
f "(x) &=\ dfrac {2} {x^3} e f “(1) &=2! \\ [5pt]
f"' (x) &=−\ dfrac {3⋅2} {x^4} & f"' (1) &=−3! \\ [5pt]
f^ {(4)} (x) &=\ dfrac {4⋅3⋅2} {x^5} e f^ {(4)} (1) &=4!. \ end {align*}\]

Ou seja, temos\(f^{(n)}(1)=(−1)^nn!\) para todos\(n≥0\). Portanto, a série Taylor para\(f\) at\(x=1\) é dada por

\(\displaystyle \sum_{n=0}^∞\dfrac{f^{(n)}(1)}{n!}(x−1)^n=\sum_{n=0}^∞(−1)^n(x−1)^n\).

Para encontrar o intervalo de convergência, usamos o teste de proporção. Nós descobrimos que

\(\dfrac{|a_{n+1}|}{|a_n|}=\dfrac{∣(−1)^{n+1}(x−1)n^{+1}∣}{|(−1)^n(x−1)^n|}=|x−1|\).

Assim, a série converge, se\(|x−1|<1.\) isso é, a série converge para\(0<x<2\). Em seguida, precisamos verificar os endpoints. Em\(x=2\), vemos que

\(\displaystyle \sum_{n=0}^∞(−1)^n(2−1)^n=\sum_{n=0}^∞(−1)^n\)

diverge pelo teste de divergência. Da mesma forma, em\(x=0,\)

\(\displaystyle \sum_{n=0}^∞(−1)^n(0−1)^n=\sum_{n=0}^∞(−1)^{2n}=\sum_{n=0}^∞1\)

diverge. Portanto, o intervalo de convergência é\((0,2)\).

Exercício\(\PageIndex{5}\)

Encontre a série Taylor para\(f(x)=\dfrac{1}{2}\) at\(x=2\) e determine seu intervalo de convergência.

Dica

\(f^{(n)}(2)=\dfrac{(−1)^nn!}{2^{n+1}}\)

Responda

\(\dfrac{1}{2}\displaystyle \sum_{n=0}^∞\left(\dfrac{2−x}{2}\right)^n\). O intervalo de convergência é\((0,4)\).

Sabemos que a série Taylor encontrada neste exemplo converge no intervalo\((0,2)\), mas como sabemos se ela realmente converge para\(f\)? Consideramos essa questão de forma mais geral em um momento, mas neste exemplo, podemos responder a essa pergunta escrevendo

\[ f(x)=\dfrac{1}{x}=\dfrac{1}{1−(1−x)}. \nonumber \]

Ou seja,\(f\) pode ser representado pela série geométrica\(\displaystyle \sum_{n=0}^∞(1−x)^n\). Como esta é uma série geométrica, ela converge\(\dfrac{1}{x}\) desde que\(|1−x|<1.\) Portanto, a série Taylor encontrada em Example converge para\(f(x)=\dfrac{1}{x}\)\((0,2).\)

Agora, consideramos a questão mais geral: se uma série de Taylor para uma função\(f\) converge em algum intervalo, como podemos determinar se ela realmente converge para\(f\)? Para responder a essa pergunta, lembre-se de que uma série converge para um valor específico se e somente se sua sequência de somas parciais convergir para esse valor. Dada uma série de Taylor para\(f\) at\(a\), a soma\(n^{\text{th}}\) parcial é dada pelo polinômio de Taylor de\(n^{\text{th}}\) -grau\(p_n\). Portanto, para determinar se a série Taylor converge para\(f\), precisamos determinar se

\(\displaystyle \lim_{n→∞}p_n(x)=f(x)\).

Desde o restante\(R_n(x)=f(x)−p_n(x)\), a série Taylor converge para\(f\) se e somente se

\(\displaystyle \lim_{n→∞}R_n(x)=0.\)

Agora, declaramos esse teorema formalmente.

Convergência da série Taylor

Suponha que\(f\) tenha derivadas de todos os pedidos em um intervalo\(I\) contendo\(a\). Em seguida, a série Taylor

\[\sum_{n=0}^∞\dfrac{f^{(n)}(a)}{n!}(x−a)^n \nonumber \]

converge\(f(x)\) para todos\(x\) em\(I\) se e somente se

\[\lim_{n→∞}R_n(x)=0 \nonumber \]

para todos\(x\) em\(I\).

Com esse teorema, podemos provar que uma série de Taylor para\(f\) at a converge para\(f\) se pudermos provar que o restante\(R_n(x)→0\). Para provar isso\(R_n(x)→0\), normalmente usamos o limite

\[|R_n(x)|≤\dfrac{M}{(n+1)!}|x−a|^{n+1} \nonumber \]

do teorema de Taylor com o restante.

No próximo exemplo, encontramos a série Maclaurin para\(e^x\) e\(\sin x\) e mostramos que essas séries convergem para as funções correspondentes de todos os números reais, provando que os restos são\(R_n(x)→0\) para todos os números reais\(x\).

Exemplo\(\PageIndex{6}\): Finding Maclaurin Series

Para cada uma das funções a seguir, encontre a série Maclaurin e seu intervalo de convergência. Use o Note para provar que a série Maclaurin para\(f\) converge para\(f\) esse intervalo.

1. \(e^x\)
2. \(\sin x\)

Solução

a. Usando o polinômio de Maclaurin de\(n^{\text{th}}\) grau para\(e^x\) encontrado no Exemplo a., descobrimos que a série Maclaurin para\(e^x\) é dada por

\(\displaystyle \sum_{n=0}^∞\dfrac{x^n}{n!}\).

Para determinar o intervalo de convergência, usamos o teste de proporção. Desde

\(\dfrac{|a_{n+1}|}{|a_n|}=\dfrac{|x|^{n+1}}{(n+1)!}⋅\dfrac{n!}{|x|^n}=\dfrac{|x|}{n+1}\),

nós temos

\(\displaystyle \lim_{n→∞}\dfrac{|a_{n+1}|}{|a_n|}=\lim_{n→∞}\dfrac{|x|}{n+1}=0\)

para todos\(x\). Portanto, a série converge absolutamente para todos e\(x\), portanto, o intervalo de convergência é\((−∞,∞)\). Para mostrar que a série converge\(e^x\) para todos\(x\), usamos o fato de que\(f^{(n)}(x)=e^x\) para todos\(n≥0\) e\(e^x\) é uma função crescente ativada\((−∞,∞)\). Portanto, para qualquer número real\(b\), o valor máximo de\(e^x\) para todos\(|x|≤b\) é\(e^b\). Assim,

\(|R_n(x)|≤\dfrac{e^b}{(n+1)!}|x|^{n+1}\).

Já que acabamos de mostrar isso

\(\displaystyle \sum_{n=0}^∞\dfrac{|x|^n}{n!}\)

converge para todos\(x\), pelo teste de divergência, sabemos que

\(\displaystyle \lim_{n→∞}\dfrac{|x|^{n+1}}{(n+1)!}=0\)

para qualquer número real\(x\). Ao combinar esse fato com o teorema da compressão, o resultado é\(\displaystyle \lim_{n→∞}R_n(x)=0.\)

b. Usando o polinômio de Maclaurin de\(n^{\text{th}}\) grau para\(\sin x\) encontrado no Exemplo b., descobrimos que a série Maclaurin para\(\sin x\) é dada por

\(\displaystyle \sum_{n=0}^∞(−1)^n\dfrac{x^{2n+1}}{(2n+1)!}\).

Para aplicar o teste de proporção, considere

\ [\ begin {align*}\ dfrac {|a_ {n+1} |} {|a_n|} &=\ dfrac {|x|^ {2n+3}} {(2n+3)!} ==\ dfrac {(2n+1)!} {|x|^ {2n+1}}\\ [5pt]
&=\ dfrac {|x|^2} {(2n+3) (2n+2)}\ end {align*}. \ nonumber\]

Desde

\(\displaystyle \lim_{n→∞}\dfrac{|x|^2}{(2n+3)(2n+2)}=0\)

para todos\(x\), obtemos o intervalo de convergência como\((−∞,∞).\) Para mostrar que a série Maclaurin converge para\(\sin x\), veja\(R_n(x)\). Para cada um\(x\) existe um número real\(c\) entre\(0\) e\(x\) tal que

\(R_n(x)=\dfrac{f^{(n+1)}(c)}{(n+1)!}x^{n+1}\).

Já que\(∣f^{(n+1)}(c)∣≤1\) para todos os números inteiros\(n\) e todos os números reais \(c\), temos

\(|R_n(x)|≤\dfrac{|x|^{n+1}}{(n+1)!}\)

para todos os números reais\(x\). Usando a mesma ideia da parte a., o resultado é\(\displaystyle \lim_{n→∞}R_n(x)=0\) para todos e\(x\), portanto, a série Maclaurin para\(\sin x\) converge\(\sin x\) para todos os reais\(x\).

Exercício\(\PageIndex{6}\)

Encontre a série Maclaurin para\(f(x)=\cos x\). Use o teste de proporção para mostrar que o intervalo de convergência é\((−∞,∞)\). Mostre que a série Maclaurin converge\(\cos x\) para todos os números reais\(x\).

Dica

Use os polinômios de Maclaurin para\(\cos x.\)

Responda

\(\displaystyle \sum_{n=0}^∞\dfrac{(−1)^nx^{2n}}{(2n)!}\)

Pelo teste de razão, o intervalo de convergência é\((−∞,∞).\) Desde\(|R_n(x)|≤\dfrac{|x|^{n+1}}{(n+1)!}\), a série converge\(\cos x\) para todos os reais\(x\).

Provando isso\(e\) is Irrational

Neste projeto, usamos os polinômios de Maclaurin\(e^x\) para provar que isso\(e\) é irracional. A prova se baseia em supor que isso\(e\) seja racional e chegue a uma contradição. Portanto, nas etapas a seguir, supomos que\(e=r/s\) para alguns números inteiros\(r\) e\(s\) onde\(s≠0.\)

1. Escreva os polinômios de Maclaurin\(p_0(x),p_1(x),p_2(x),p_3(x),p_4(x)\) para\(e^x\). Avalie\(p_0(1),p_1(1),p_2(1),p_3(1),p_4(1)\) para estimar\(e\).
2. Vamos\(R_n(x)\) indicar o restante ao usar\(p_n(x)\) para estimar\(e^x\). Portanto\(R_n(x)=e^x−p_n(x)\),,\(R_n(1)=e−p_n(1)\) e. Supondo que\(e=\dfrac{r}{s}\) para números inteiros\(r\) e\(s\), avalie\(R_0(1),R_1(1),R_2(1),R_3(1),R_4(1).\)
3. Usando os resultados da parte 2, mostre que para cada restante\(R_0(1),R_1(1),R_2(1),R_3(1),R_4(1),\) podemos encontrar um número inteiro\(k\) tal que\(kR_n(1)\) seja um inteiro para\(n=0,1,2,3,4.\)
4. Anote a fórmula para o polinômio Maclaurin de\(n^{\text{th}}\) -grau\(p_n(x)\) para\(e^x\) e o restante correspondente\(R_n(x).\) Mostre que\(sn!R_n(1)\) é um número inteiro.
5. Use o teorema de Taylor para escrever uma fórmula explícita para\(R_n(1)\). Conclua isso e\(R_n(1)≠0\), portanto,\(sn!R_n(1)≠0\).
6. Use o teorema de Taylor para encontrar uma estimativa de\(R_n(1)\). Use essa estimativa combinada com o resultado da parte 5 para mostrar isso\(|sn!R_n(1)|<\dfrac{se}{n+1}\). Conclua que se\(n\) for grande o suficiente, então\(|sn!R_n(1)|<1\). Portanto,\(sn!R_n(1)\) é um número inteiro com magnitude menor que 1. Assim,\(sn!R_n(1)=0\). Mas da parte 5, nós sabemos disso\(sn!R_n(1)≠0\). Chegamos a uma contradição e, consequentemente, a suposição original de que e é racional deve ser falsa.

Conceitos-chave

• Os polinômios de Taylor são usados para aproximar funções próximas a um valor\(x=a\). Os polinômios de Maclaurin são polinômios de Taylor em\(x=0\).
• Os polinômios de Taylor em\(n^{\text{th}}\) -graus para uma função\(f\) são as somas parciais da série Taylor para\(f\).
• Se uma função\(f\) tem uma representação de série de potência em\(x=a\), então ela é dada por sua série de Taylor em\(x=a\).
• Uma série de Taylor para\(f\) converge para\(f\) se e somente se\(\displaystyle \lim_{n→∞}R_n(x)=0\) onde\(R_n(x)=f(x)−p_n(x)\).
• A série Taylor para\(e^x, \sin x\) e\(\cos x\) converge para as respectivas funções para todos os x reais.

Equações-chave

• Série Taylor para a função\(f\) no ponto\(x=a\)

\(\displaystyle \sum_{n=0}^∞\dfrac{f^{(n)}(a)}{n!}(x−a)^n=f(a)+f′(a)(x−a)+\dfrac{f''(a)}{2!}(x−a)^2+⋯+\dfrac{f^{(n)}(a)}{n!}(x−a)^n+⋯\)

Glossário

Polinômio de Maclaurin

um polinômio de Taylor centrado em\(0\); o polinômio de Taylor de\(n^{\text{th}}\) -grau para\(f\) at\(0\) é o polinômio de Maclaurin de\(n^{\text{th}}\) -grau para\(f\)

Série Maclaurin

uma série Taylor para uma função\(f\) em\(x=0\) é conhecida como série Maclaurin para\(f\)

Polinômios de Taylor

o polinômio de Taylor em\(n^{\text{th}}\) -grau para\(f\) at\(x=a\) é\(p_n(x)=f(a)+f′(a)(x−a)+\dfrac{f''(a)}{2!}(x−a)^2+⋯+\dfrac{f^{(n)}(a)}{n!}(x−a)^n\)

Série Taylor

uma série de potências em\(a\) que converge para uma função\(f\) em algum intervalo aberto contendo\(a\).

Teorema de Taylor com o restante

para uma função\(f\) e o polinômio de Taylor em\(n^{\text{th}}\) -grau para\(f\) at\(x=a\), o restante\(R_n(x)=f(x)−p_n(x)\) satisfaz\(R_n(x)=\dfrac{f^{(n+1)}(c)}{(n+1)!}(x−a)^{n+1}\)

para alguns\(c\) entre\(x\) e\(a\); se existe um intervalo\(I\) contendo\(a\) e um número real\(M\) tal que\(∣f^{(n+1)}(x)∣≤M\) para todos\(x\) em\(I\), então\(|R_n(x)|≤\dfrac{M}{(n+1)!}|x−a|^{n+1}\)