10.2E: Exercícios para a Seção 10.2

1) Se\(\displaystyle f(x)=\sum_{n=0}^∞\frac{x^n}{n!}\) e\(\displaystyle g(x)=\sum_{n=0}^∞(−1)^n\frac{x^n}{n!}\), encontre a série de potência de\(\frac{1}{2}\big(f(x)+g(x)\big)\) e de\(\frac{1}{2}\big(f(x)−g(x)\big)\).

Responda

\(\displaystyle \frac{1}{2}\big(f(x)+g(x)\big)=\sum_{n=0}^∞\frac{x^{2n}}{(2n)!}\)\(\displaystyle \frac{1}{2}\big(f(x)−g(x)\big)=\sum_{n=0}^∞\frac{x^{2n+1}}{(2n+1)!}\)e.

2) Se\(\displaystyle C(x)=\sum_{n=0}^∞\frac{x^{2n}}{(2n)!}\) e\(\displaystyle S(x)=\sum_{n=0}^∞\frac{x^{2n+1}}{(2n+1)!}\), encontre a série de potência de\(C(x)+S(x)\) e de\(C(x)−S(x)\).

Nos exercícios 3 a 6, use frações parciais para encontrar a série de potência de cada função.

3)\(\dfrac{4}{(x−3)(x+1)}\)

Responda

\(\displaystyle \frac{4}{(x−3)(x+1)}=\frac{1}{x−3}−\frac{1}{x+1}=−\frac{1}{3(1−\frac{x}{3})}−\frac{1}{1−(−x)}=−\frac{1}{3}\sum_{n=0}^∞\left(\frac{x}{3}\right)^n−\sum_{n=0}^∞(−1)^nx^n=\sum_{n=0}^∞\left((−1)^{n+1}−\frac{1}{3n+1}\right)x^n\)

4)\(\dfrac{3}{(x+2)(x−1)}\)

5)\(\dfrac{5}{(x^2+4)(x^2−1)}\)

Responda

\(\displaystyle \frac{5}{(x^2+4)(x^2−1)}=\frac{1}{x^2−1}−\frac{1}{4}\frac{1}{1+\left(\frac{x}{2}\right)^2}=−\sum_{n=0}^∞x^{2n}−\frac{1}{4}\sum_{n=0}^∞(−1)^n\left(\frac{x}{2}\right)^n=\sum_{n=0}^∞\left((−1)+(−1)^{n+1}\frac{1}{2^{n+2}}\right)x^{2n}\)

6)\(\dfrac{30}{(x^2+1)(x^2−9)}\)

Nos exercícios 7 a 10, expresse cada série como uma função racional.

7)\(\displaystyle \sum_{n=1}^∞\frac{1}{x^n}\)

Responda

\(\displaystyle \frac{1}{x}\sum_{n=0}^∞\frac{1}{x^n}=\frac{1}{x}\cdot \frac{1}{1−\frac{1}{x}}=\frac{1}{x−1}\)

8)\(\displaystyle \sum_{n=1}^∞\frac{1}{x^{2n}}\)

9)\(\displaystyle \sum_{n=1}^∞\frac{1}{(x−3)^{2n−1}}\)

Responda

\(\displaystyle \frac{1}{x−3}\cdot \frac{1}{1−\frac{1}{(x−3)^2}}=\frac{x−3}{(x−3)^2−1}\)

10)\(\displaystyle \sum_{n=1}^∞\left(\frac{1}{(x−3)^{2n−1}}−\frac{1}{(x−2)^{2n−1}}\right)\)

Os exercícios 11 a 16 exploram as aplicações de anuidades.

11) Calcule os valores atuais\(P\) de uma anuidade na qual $10.000 devem ser pagos anualmente por um período de 20 anos, assumindo taxas de juros de\(r=0.03,\, r=0.05\),\(r=0.07\) e.

Responda

\(P=P_1+⋯+P_{20}\)onde\(P_k=10,000\dfrac{1}{(1+r)^k}\). Então\(\displaystyle P=10,000\sum_{k=1}^{20}\frac{1}{(1+r)^k}=10,000\frac{1−(1+r)^{−20}}{r}\). Quando,\(r=0.03, \,P≈10,000×14.8775=148,775.\) quando,\(r=0.05, \,P≈10,000×12.4622=124,622.\) quando\(r=0.07, \, P≈105,940\).

12) Calcule os valores atuais\(P\) das anuidades nas quais $9.000 devem ser pagos anualmente perpetuamente, assumindo taxas de juros de\(r=0.03,\, r=0.05\)\(r=0.07\) e.

13) Calcule os pagamentos anuais\(C\) a serem dados por 20 anos em anuidades com valor atual de $100.000, assumindo as respectivas taxas de juros de\(r=0.03,\, r=0.05,\) e\(r=0.07.\)

Responda

Em geral,\(P=\dfrac{C(1−(1+r)^{−N})}{r}\) por\(N\) anos de pagamentos, ou\(C=\dfrac{Pr}{1−(1+r)^{−N}}\). \(N=20\)Pois e\(P=100,000\), temos\(C=6721.57\)\(r=0.03; \, C=8024.26\) quando\(r=0.05\), quando e\(C≈9439.29\) quando\(r=0.07\).

14) Calcule os pagamentos anuais\(C\) a serem dados perpetuamente em anuidades com valor presente de $100.000, assumindo as respectivas taxas de juros de\(r=0.03, \,r=0.05,\)\(r=0.07\) e.

15) Suponha que uma anuidade tenha um valor atual\(P=1\) de milhões de dólares. Qual taxa de juros\(r\) permitiria pagamentos anuais perpétuos de $50.000?

Responda

Em geral,\(P=\dfrac{C}{r}.\) portanto,\(r=\dfrac{C}{P}=5×\frac{10^4}{10^6}=0.05.\)

16) Suponha que uma anuidade tenha um valor atual\(P=10\) de milhões de dólares. Qual taxa de juros\(r\) permitiria pagamentos anuais perpétuos de $100.000?

Nos exercícios 17 a 20, expresse a soma de cada série de potências em termos de séries geométricas e, em seguida, expresse a soma como uma função racional.

17)\(x+x^2−x^3+x^4+x^5−x^6+⋯\) (Dica: poderes do grupo\(x^{3k}, \, x^{3k−1},\)\(x^{3k−2}\) e.)

Responda

\((x+x^2−x^3)(1+x^3+x^6+⋯)=\dfrac{x+x^2−x^3}{1−x^3}\)

18)\(x+x^2−x^3−x^4+x^5+x^6−x^7−x^8+⋯\) (Dica: poderes de grupo\(x^{4k}, \, x^{4k−1},\), etc.)

19)\(x−x^2−x^3+x^4−x^5−x^6+x^7−⋯\) (Dica: poderes do grupo\(x^{3k}, \, x^{3k−1}\),\(x^{3k−2}\) e.)

Responda

\((x−x^2−x^3)(1+x^3+x^6+⋯)=\dfrac{x−x^2−x^3}{1−x^3}\)

20)\(\displaystyle \frac{x}{2}+\frac{x^2}{4}−\frac{x^3}{8}+\frac{x^4}{16}+\frac{x^5}{32}−\frac{x^6}{64}+⋯\) (Dica: poderes do grupo\(\left(\dfrac{x}{2}\right)^{3k}, \, \left(\dfrac{x}{2}\right)^{3k−1},\)\(\left(\dfrac{x}{2}\right)^{3k−2}\) e.)

Nos exercícios 21 a 24, determine a série de potências\(f(x)g(x)\) dada\(f\) e\(g\) conforme definida.

21)\(\displaystyle f(x)=2\sum_{n=0}^∞x^n,g(x)=\sum_{n=0}^∞nx^n\)

Responda

\(a_n=2, \, b_n=n\)então\(\displaystyle c_n=\sum_{k=0}^nb_ka_{n−k}=2\sum_{k=0}^nk=(n)(n+1)\) e\(\displaystyle f(x)g(x)=\sum_{n=1}^∞n(n+1)x^n\)

22)\(\displaystyle f(x)=\sum_{n=1}^∞x^n,\; g(x)=\sum_{n=1}^∞\frac{1}{n}x^n\). Expresse os coeficientes de\(f(x)g(x)\) em termos de\(\displaystyle H_n=\sum_{k=1}^n\frac{1}{k}\).

23)\(\displaystyle f(x)=g(x)=\sum_{n=1}^∞\left(\frac{x}{2}\right)^n\)

Responda

\(a_n=b_n=2^{−n}\)então\(\displaystyle c_n=\sum_{k=1}^nb_ka_{n−k}=2^{−n}\sum_{k=1}^n1=\frac{n}{2^n}\) e\(\displaystyle f(x)g(x)=\sum_{n=1}^∞n\left(\frac{x}{2}\right)^n\)

24)\(\displaystyle f(x)=g(x)=\sum_{n=1}^∞nx^n\)

Nos exercícios 25 a 26, diferencie a expansão da série dada de\(f\) termo a termo para obter a expansão da série correspondente para a derivada de\(f.\)

25)\(\displaystyle f(x)=\frac{1}{1+x}=\sum_{n=0}^∞(−1)^nx^n\)

Responda

A derivada de\(f\) é\(\displaystyle −\frac{1}{(1+x)^2}=−\sum_{n=0}^∞(−1)^n(n+1)x^n\).

26)\(\displaystyle f(x)=\frac{1}{1−x^2}=\sum_{n=0}^∞x^{2n}\)

Nos exercícios 27 - 28, integre a expansão da série dada de\(f\) zero a termo\(x\) para obter a expansão da série correspondente para a integral indefinida de\(f\).

27)\(\displaystyle f(x)=\frac{2x}{(1+x^2)^2}=\sum_{n=1}^∞(−1)^n(2n)x^{2n−1}\)

Responda

A integral indefinida de\(f\) é\(\displaystyle \frac{1}{1+x^2}=\sum_{n=0}^∞(−1)^nx^{2n}\).

28)\(\displaystyle f(x)=\frac{2x}{1+x^2}=2\sum_{n=0}^∞(−1)^nx^{2n+1}\)

Nos exercícios 29 a 32, avalie cada série infinita identificando-a como o valor de uma derivada ou integral de uma série geométrica.

29) Avalie\(\displaystyle \sum_{n=1}^∞\frac{n}{2^n}\) como\(f′\left(\frac{1}{2}\right)\) onde\(\displaystyle f(x)=\sum_{n=0}^∞x^n\).

Responda

\(\displaystyle f(x)=\sum_{n=0}^∞x^n=\frac{1}{1−x}; \; f′(\frac{1}{2})=\sum_{n=1}^∞\frac{n}{2^{n−1}}=\frac{d}{dx}(1−x)^{−1}\Big|_{x=1/2}=\frac{1}{(1−x)^2}\Big|_{x=1/2}=4\)então\(\displaystyle \sum_{n=1}^∞\frac{n}{2^n}=2.\)

30) Avalie\(\displaystyle \sum_{n=1}^∞\frac{n}{3^n}\) como\(f′\left(\frac{1}{3}\right)\) onde\(\displaystyle f(x)=\sum_{n=0}^∞x^{6n}\).

31) Avalie\(\displaystyle \sum_{n=2}^∞\frac{n(n−1)}{2^n}\) como\(f''\left(\frac{1}{2}\right)\) onde\(\displaystyle f(x)=\sum_{n=0}^∞x^n\).

Responda

\(\displaystyle f(x)=\sum_{n=0}^∞x^n=\frac{1}{1−x}; \; f''\left(\frac{1}{2}\right)=\sum_{n=2}^∞\frac{n(n−1)}{2^{n−2}}=\frac{d^2}{dx^2}(1−x)^{−1}\Big|_{x=1/2}=\frac{2}{(1−x)^3}\Big|_{x=1/2}=16\)então\(\displaystyle \sum_{n=2}^∞n\frac{(n−1)}{2^n}=4.\)

32) Avalie\(\displaystyle \sum_{n=0}^∞\frac{(−1)^n}{n+1}\) como\(\displaystyle ∫^1_0f(t) \, dt\) onde\(\displaystyle f(x)=\sum_{n=0}^∞(−1)^nx^{2n}=\frac{1}{1+x^2}\).

Nos exercícios 33 a 39, dado que\(\displaystyle \frac{1}{1−x}=\sum_{n=0}^∞x^n\), use a diferenciação ou integração termo a termo para encontrar séries de potências para cada função centrada em um determinado ponto.

33)\(f(x)=\ln x\) centrado em\(x=1\) (Dica:\(x=1−(1−x)\))

Responda

\(\displaystyle ∫\sum(1−x)^n\,dx=∫\sum(−1)^n(x−1)^n\,dx=\sum \frac{(−1)^n(x−1)^{n+1}}{n+1}\)

34)\(\ln(1−x)\) em\(x=0\)

35)\(\ln(1−x^2)\) em\(x=0\)

Responda

\(\displaystyle −∫^{x^2}_{t=0}\frac{1}{1−t}dt=−\sum_{n=0}^∞∫^{x^2}_0t^ndx−\sum_{n=0}^∞\frac{x^{2(n+1)}}{n+1}=−\sum_{n=1}^∞\frac{x^{2n}}{n}\)

36)\(f(x)=\dfrac{2x}{(1−x^2)^2}\) em\(x=0\)

37)\(f(x)=\tan^{−1}(x^2)\) em\(x=0\)

Responda

\(\displaystyle ∫^{x^2}_0\frac{dt}{1+t^2}=\sum_{n=0}^∞(−1)^n∫^{x^2}_0t^{2n}dt=\sum_{n=0}^∞(−1)^n\frac{t^{2n+1}}{2n+1}∣^{x^2}_{t=0}=\sum_{n=0}^∞(−1)^n\frac{x^{4n+2}}{2n+1}\)

38)\(f(x)=\ln(1+x^2)\) em\(x=0\)

39)\(\displaystyle f(x)=∫^x_0\ln t\,dt\) onde\(\displaystyle \ln(x)=\sum_{n=1}^∞(−1)^{n−1}\frac{(x−1)^n}{n}\)

Responda

A integração termo a prazo oferece\(\displaystyle ∫^x_0\ln t\,dt=\sum_{n=1}^∞(−1)^{n−1}\frac{(x−1)^{n+1}}{n(n+1)}=\sum_{n=1}^∞(−1)^{n−1}\left(\frac{1}{n}−\frac{1}{n+1}\right)(x−1)^{n+1}=(x−1)\ln x+\sum_{n=2}^∞(−1)^n\frac{(x−1)^n}{n}=x\ln x−x.\)

40) [T] Avalie a expansão da série de potência\(\displaystyle \ln(1+x)=\sum_{n=1}^∞(−1)^{n−1}\frac{x^n}{n}\) em\(x=1\) para mostrar que\(\ln(2)\) é a soma da série harmônica alternada. Use o teste de séries alternadas para determinar quantos termos da soma são necessários para estimar com\(\ln(2)\) precisão de dentro\(0.001,\) e encontrar essa aproximação.

41) [T] Subtraia a série infinita de\(\ln(1−x)\) de\(\ln(1+x)\) para obter uma série de potência para\(\ln\left(\dfrac{1+x}{1−x}\right)\). Avalie em\(x=\frac{1}{3}\). Qual é o menor\(N\) para que a soma\(N^{\text{th}}\) parcial dessa série se aproxime\(\ln(2)\) com um erro menor que\(0.001\)?

Responda

Nós temos\(\displaystyle \ln(1−x)=−\sum_{n=1}^∞\frac{x^n}{n}\) isso\(\displaystyle \ln(1+x)=\sum_{n=1}^∞(−1)^{n−1}\frac{x^n}{n}\). Assim,\(\displaystyle \ln\left(\frac{1+x}{1−x}\right)=\sum_{n=1}^∞\big(1+(−1)^{n−1}\big)\frac{x^n}{n}=2\sum_{n=1}^∞\frac{x^{2n−1}}{2n−1}\). Quando\(x=\frac{1}{3}\) obtemos\(\displaystyle \ln(2)=2\sum_{n=1}^∞\frac{1}{3^{2n−1}(2n−1)}\). Nós temos\(\displaystyle 2\sum_{n=1}^3\frac{1}{3^{2n−1}(2n−1)}=0.69300…\), enquanto\(\displaystyle 2\sum_{n=1}^4\frac{1}{3^{2n−1}(2n−1)}=0.69313…\) e\(\ln(2)=0.69314…;\) portanto,\(N=4\).

Nos exercícios 42 a 45, usando uma substituição, se indicada, expresse cada série em termos de funções elementares e encontre o raio de convergência da soma.

(42)\(\displaystyle \sum_{k=0}^∞(x^k−x^{2k+1})\)

43)\(\displaystyle \sum_{k=1}^∞\frac{x^{3k}}{6k}\)

Responda

\(\displaystyle \sum_{k=1}^∞\frac{x^k}{k}=−\ln(1−x)\)então\(\displaystyle \sum_{k=1}^∞\frac{x^{3k}}{6k}=−\frac{1}{6}\ln(1−x^3)\). O raio de convergência é igual\(1\) ao do teste de razão.

44)\(\displaystyle \sum_{k=1}^∞(1+x^2)^{−k}\) usando\(y=\dfrac{1}{1+x^2}\)

45)\(\displaystyle \sum_{k=1}^∞2^{−kx}\) usando\(y=2^{−x}\)

Responda

Se\(y=2^{−x}\), então\(\displaystyle \sum_{k=1}^∞y^k=\frac{y}{1−y}=\frac{2^{−x}}{1−2^{−x}}=\frac{1}{2^x−1}\). Se\(a_k=2^{−kx}\), então\(\dfrac{a_{k+1}}{a_k}=2^{−x}<1\) quando\(x>0\). Então, a série converge para todos\(x>0\).

46)\(x^3\) Mostre que, até os poderes\(y^3\),\(\displaystyle E(x)=\sum_{n=0}^∞\frac{x^n}{n!}\) satisfaz\(E(x+y)=E(x)E(y)\).

47) Diferencie a série\(\displaystyle E(x)=\sum_{n=0}^∞\frac{x^n}{n!}\) termo a termo para mostrar que\(E(x)\) é igual à sua derivada.

Responda

As respostas podem variar.

48) Mostre que se\(\displaystyle f(x)=\sum_{n=0}^∞a_nx^n\) é uma soma de poderes pares, ou seja,\(a_n=0\) se\(n\) for ímpar, então\(\displaystyle F=∫^x_0f(t)\, dt\) é uma soma de potências ímpares, enquanto se\(I\) é uma soma de potências ímpares, então\(F\) é uma soma de poderes pares.

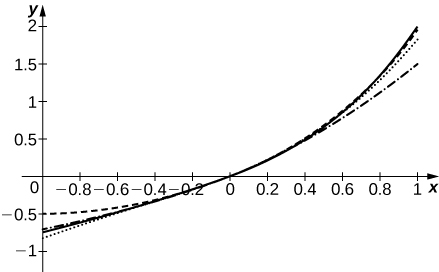
49) [T] Suponha que os coeficientes an da série\(\displaystyle \sum_{n=0}^∞a_nx^n\) sejam definidos pela relação de recorrência\(a_n=\dfrac{a_{n−1}}{n}+\dfrac{a_{n−2}}{n(n−1)}\). Para\(a_0=0\) e\(a_1=1\), calcule e plote as somas\(\displaystyle S_N=\sum_{n=0}^Na_nx^n\) de\(N=2,3,4,5\) em\([−1,1].\)

Responda

A curva sólida é\(S_5\). A curva tracejada é\(S_2\), pontilhada é\(S_3\) e tracejada é\(S_4\)

50) [T] Suponha que os coeficientes an da série\(\displaystyle \sum_{n=0}^∞a_nx^n\) sejam definidos pela relação de recorrência\(a_n=\dfrac{a_{n−1}}{\sqrt{n}}−\dfrac{a_{n−2}}{\sqrt{n(n−1)}}\). Para\(a_0=1\) e\(a_1=0\), calcule e plote as somas\(\displaystyle S_N=\sum_{n=0}^Na_nx^n\) de\(N=2,3,4,5\) on\([−1,1]\).

51) [T] Dada a expansão da série de potências\(\displaystyle \ln(1+x)=\sum_{n=1}^∞(−1)^{n−1}\frac{x^n}{n}\), determine quantos termos\(N\) da soma avaliada em\(x=−1/2\) são necessários para aproximar a\(\ln(2)\) precisão de\(1/1000.\) Avalie a soma parcial correspondente\(\displaystyle \sum_{n=1}^N(−1)^{n−1}\frac{x^n}{n}\).

Responda

Quando\(\displaystyle x=−\frac{1}{2}, \;−\ln(2)=\ln\left(\frac{1}{2}\right)=−\sum_{n=1}^∞\frac{1}{n2^n}\). \(\displaystyle \sum^∞_{n=11}\frac{1}{n2^n}<\sum_{n=11}^∞\frac{1}{2^n}=\frac{1}{2^{10}},\)Uma vez\(\displaystyle \sum_{n=1}^{10}\frac{1}{n2^n}=0.69306…\) que se tem\(\ln(2)=0.69314…;\), portanto,\(N=10.\)

52) [T] Dada a expansão da série de potência\(\displaystyle \tan^{−1}(x)=\sum_{k=0}^∞(−1)^k\frac{x^{2k+1}}{2k+1}\), use o teste de série alternada para determinar quantos termos\(N\) da soma avaliada em\(x=1\) são necessários para aproximar a\(\tan^{−1}(1)=\frac{π}{4}\) precisão de\(1/1000.\) Avalie a soma parcial correspondente\(\displaystyle \sum_{k=0}^N(−1)^k\frac{x^{2k+1}}{2k+1}\).

53) [T] Lembre-se de que,\(\tan^{−1}\left(\frac{1}{\sqrt{3}}\right)=\frac{π}{6}.\) assumindo um valor exato de\(\frac{1}{\sqrt{3}})\), estime\(\frac{π}{6}\) avaliando somas parciais\(S_N\left(\frac{1}{\sqrt{3}}\right)\) da expansão da série de potência\(\displaystyle \tan^{−1}(x)=\sum_{k=0}^∞(−1)^k\frac{x^{2k+1}}{2k+1}\) em\(x=\frac{1}{\sqrt{3}}\). Qual é o menor número\(N\) desse tipo que\(6S_N\left(\frac{1}{\sqrt{3}}\right)\) se aproxima\(π\) com precisão de dentro\(0.001\)? Quantos termos são necessários para que a precisão seja interna\(0.00001\)?

Responda

\(\displaystyle 6S_N\left(\frac{1}{\sqrt{3}}\right)=2\sqrt{3}\sum_{n=0}^N(−1)^n\frac{1}{3^n(2n+1).}\)Um tem\(π−6S_4\left(\frac{1}{\sqrt{3}}\right)=0.00101…\) e\(π−6S_5\left(\frac{1}{\sqrt{3}}\right)=0.00028…\), portanto,\(N=5\) é a menor soma parcial com precisão dentro de\(0.001.\) Além disso,\(π−6S_7\left(\frac{1}{\sqrt{3}}\right)=0.00002…\) enquanto\(π−6S_8\left(\frac{1}{\sqrt{3}}\right)=−0.000007…\) assim\(N=8\) é a menor\(N\) para dar precisão a dentro\(0.00001.\)

Colaboradores

Template:ContribOpenStaxCalc