9.5: Séries alternadas
- Page ID
- 188350
- Use o teste de série alternada para testar a convergência de uma série alternada.
- Estime a soma de uma série alternada.
- Explique o significado da convergência absoluta e da convergência condicional.
Até agora, neste capítulo, discutimos principalmente séries com termos positivos. Nesta seção, apresentamos séries alternadas — aquelas séries cujos termos se alternam em signo. Mostraremos em um capítulo posterior que essas séries geralmente surgem quando se estuda séries de potência. Depois de definir séries alternadas, introduzimos o teste de séries alternadas para determinar se essa série converge.
O teste de série alternada
Uma série cujos termos alternam entre valores positivos e negativos é uma série alternada. Por exemplo, a série
\[\sum_{n=1}^∞ \left(−\dfrac{1}{2} \right)^n=−\dfrac{1}{2}+\dfrac{1}{4}−\dfrac{1}{8}+\dfrac{1}{16}− \ldots \label{eq1} \]
e
\[\sum_{n=1}^∞\dfrac{(−1)^{n+1}}{n}=1−\dfrac{1}{2}+\dfrac{1}{3}−\dfrac{1}{4}+\ldots \label{eq2} \]
são ambas séries alternadas.
Qualquer série cujos termos alternam entre valores positivos e negativos é chamada de série alternada. Uma série alternada pode ser escrita no formulário
\[\sum_{n=1}^∞(−1)^{n+1}b_n=b_1−b_2+b_3−b_4+ \ldots \label{eq3} \]
ou
\[\sum_{n−1}^∞(−1)^nb_n=−b_1+b_2−b_3+b_4−\ldots \label{eq4} \]
Onde\( b_n≥0\) para todos os números inteiros positivos\(n\).
A série (1), mostrada na Equação\ ref {eq1}, é uma série geométrica. Já que\( |r|=|−1/2|<1,\) a série converge. A série (2), mostrada na Equação\ ref {eq2}, é chamada de série harmônica alternada. Mostraremos que, enquanto a série harmônica diverge, a série harmônica alternada converge. Para provar isso, examinamos a sequência de somas parciais\( \{S_k\}\) (Figura 1).
Considere os termos estranhos\( S_{2k+1}\) para\( k≥0\). Desde\( 1/(2k+1)<1/2k,\)
\[S_{2k+1}=S_{2k−1}−\dfrac{1}{2k}+\dfrac{1}{2k+1}<S_{2k−1}. \nonumber \]
Portanto,\( \{S_{2k+1}\}\) é uma sequência decrescente. Além disso,
\[S_{2k+1}=\left(1−\dfrac{1}{2}\right)+\left(\dfrac{1}{3}−\dfrac{1}{4}\right)+ \ldots + \left(\dfrac{1}{2k−1}−\dfrac{1}{2k}\right)+\dfrac{1}{2k+1}>0. \nonumber \]
Portanto,\( \{S_{2k+1}\}\) está limitado abaixo. Uma vez que\( \{S_{2k+1}\}\) é uma sequência decrescente limitada abaixo, pelo Teorema da Convergência Monótona,\( \{S_{2k+1}\}\) converge. Da mesma forma, os termos pares\( \{S_{2k}\}\) formam uma sequência crescente que é limitada acima porque
\[S_{2k}=S_{2k−2}+\dfrac{1}{2k−1}−\dfrac{1}{2k}>S_{2k−2} \nonumber \]
e
\[S_{2k}=1+ \left(−\dfrac{1}{2}+\dfrac{1}{3}\right)+\ldots + \left(−\dfrac{1}{2k−2}+\dfrac{1}{2k−1}\right)−\dfrac{1}{2k}<1. \nonumber \]
Portanto, pelo Teorema da Convergência Monótona, a sequência\( \{S_{2k}\}\) também converge. Desde
\[S_{2k+1}=S_{2k}+\dfrac{1}{2k+1}, \nonumber \]
nós sabemos que
\[\lim_{k→∞}S_{2k+1}=\lim_{k→∞}S_{2k}+\lim_{k→∞}\dfrac{1}{2k+1}. \nonumber \]
Deixando\(\displaystyle S=\lim_{k→∞}S_{2k+1}\) e usando o fato de\( 1/(2k+1)→0,\) concluirmos isso\(\displaystyle \lim_{k→∞}S_{2k}=S\). Como os termos ímpares e os termos pares na sequência de somas parciais convergem para o mesmo limite\( S\), pode-se mostrar que a sequência de somas parciais converge para e\( S\), portanto, a série harmônica alternada converge para\( S\).
Também pode ser mostrado isso\( S=\ln 2,\) e podemos escrever
\[\sum_{n=1}^∞\dfrac{(−1)^{n+1}}{n}=1−\dfrac{1}{2}+\dfrac{1}{3}−\dfrac{1}{4}+a\ldots=\ln (2). \nonumber \]
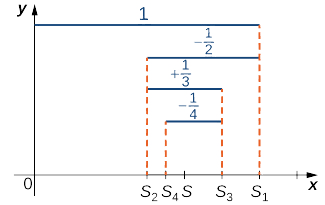
□
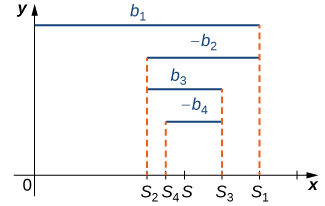
De forma mais geral, qualquer série alternada de forma (3) (Equação\ ref {eq3}) ou (4) (Equação\ ref {eq4}) converge tanto quanto\( b_1≥b_2≥b_3≥⋯\) e\( b_n→0\) (Figura 2). A prova é semelhante à prova da série harmônica alternada.
Uma série alternada do formulário
\[\sum_{n=1}^∞(−1)^{n+1}b_n \nonumber \]ou\[\sum_{n=1}^∞(−1)^nb_n \nonumber \]
converge se
- \( 0≤b_{n+1}≤b_n\)para todos\( n≥1\) e
- \(\displaystyle \lim_{n→∞}b_n=0.\)
Isso é conhecido como teste de série alternada.
Observamos que esse teorema é verdadeiro de forma mais geral, desde que exista algum número inteiro\( N\) tal que\( 0≤b_{n+1}≤b_n\) para todos\( n≥N.\)
Para cada uma das séries alternadas a seguir, determine se a série converge ou diverge.
- \(\displaystyle \sum^∞_{n=1}\frac{(−1)^{n+1}}{n^2}\)
- \(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{n}{n+1}\)
Solução
a. Desde então\( \dfrac{1}{(n+1)^2}<\dfrac{1}{n^2}\) e\( \dfrac{1}{n^2}→0,\) a série convergem.
b. Já que\( n→∞\),\( n/(n+1)↛0\) como, não podemos aplicar o teste de séries alternadas. Em vez disso, usamos o enésimo termo teste para divergência. Já que\(\displaystyle \lim_{n→∞}\dfrac{n}{n+1}=1≠0,\) a série diverge.
Determine se a série\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{n}{2^n}\) converge ou diverge.
- Dica
-
Está\( \left\{\frac{n}{2^n}\right\}\) diminuindo? O que é\(\displaystyle \lim_{n→∞}\frac{n}{2^n}\)?
- Responda
-
A série converge.
Restante de uma série alternada
É difícil calcular explicitamente a soma da maioria das séries alternadas, então normalmente a soma é aproximada usando uma soma parcial. Ao fazer isso, estamos interessados na quantidade de erro em nossa aproximação. Considere uma série alternada
\[\sum_{n=1}^∞(−1)^{n+1}b_n \nonumber \]
satisfazendo as hipóteses do teste de séries alternadas. Vamos\( S\) denotar a soma dessa série e\( {S_k}\) ser a sequência correspondente de somas parciais. Na Figura\( \PageIndex{2}\), vemos que para qualquer número inteiro\( N≥1\), o restante\( R_N\) satisfaz
\[|R_N|=|S−S_N|≤|S_{N+1}−S_N|=b_{n+1}. \nonumber \]
Considere uma série alternada do formulário
\[\sum_{n=1}^∞(−1)^{n+1}b_n \nonumber \]ou\[\sum_{n=1}^∞(−1)^nb_n \nonumber \]
que satisfaz as hipóteses do teste de séries alternadas. Vamos\( S\) denotar a soma da série e\( S_N\) denotar a soma\(N^{\text{th}}\) parcial. Para qualquer número inteiro\( N≥1\), o restante\( R_N=S−S_N\) satisfaz
\[|R_N|≤b_{N+1}. \nonumber \]
Em outras palavras, se as condições do teste de séries alternadas se aplicarem, o erro na aproximação da série infinita pela soma\(N^{\text{th}}\) parcial\( S_N\) é, no máximo, do tamanho do próximo termo\( b_{N+1}\).
Considere a série alternada
\[ \sum_{n=1}^∞\dfrac{(−1)^{n+1}}{n^2}. \nonumber \]
Use a estimativa do restante para determinar um limite no erro\( R_{10}\) se aproximarmos a soma da série pela soma parcial\( S_{10}\).
Solução
Do teorema mencionado acima,\[ |R_{10}|≤b_{11}=\dfrac{1}{11^2}≈0.008265. \nonumber \]
Encontre um limite para\( R_{20}\) ao aproximar\(\displaystyle \sum^∞_{n=1}\frac{(−1)^{n+1}}{n}\) em\( S_{20}\).
- Dica
-
\( |R_{20}|≤b_{21}\)
- Responda
-
\( 0.04762\)
Convergência absoluta e condicional
Considere uma série\(\displaystyle \sum_{n=1}^∞a_n\) e a série relacionada\(\displaystyle \sum_{n=1}^∞|a_n|\). Aqui discutimos as possibilidades da relação entre a convergência dessas duas séries. Por exemplo, considere a série harmônica alternada\(\displaystyle \sum_{n=1}^∞\frac{(−1)^{n+1}}{n}\). A série cujos termos são o valor absoluto desses termos é a série harmônica,\(\displaystyle \sum_{n=1}^∞\left|\frac{(−1)^{n+1}}{n}\right|=\sum_{n=1}^∞\frac{1}{n}.\) pois como a série harmônica alternada converge, mas a série harmônica diverge, dizemos que a série harmônica alternada exibe convergência condicional.
Em comparação, considere a série\(\displaystyle \sum_{n=1}^∞\frac{(−1)^{n+1}}{n^2}.\) A série cujos termos são os valores absolutos dos termos desta série é a série.\(\displaystyle \sum_{n=1}^∞\frac{1}{n^2}.\) Uma vez que ambas as séries convergem, dizemos que a série\(\displaystyle \sum_{n=1}^∞\frac{(−1)^{n+1}}{n^2}\) apresenta convergência absoluta.
Uma série\(\displaystyle \sum^∞_{n=1}a_n\) exibe convergência absoluta se\(\displaystyle \sum^∞_{n=1}|a_n|\) convergir. Uma série\(\displaystyle \sum^∞_{n=1}a_n\) exibe convergência condicional se\(\displaystyle \sum^∞_{n=1}a_n\) converge, mas\(\displaystyle \sum^∞_{n=1}|a_n|\) diverge.
Conforme mostrado pela série harmônica alternada, uma série\(\displaystyle \sum^∞_{n=1}a_n\) pode convergir, mas\(\displaystyle \sum^∞_{n=1}|a_n|\) pode divergir. No teorema a seguir, no entanto, mostramos que se\(\displaystyle \sum^∞_{n=1}|a_n|\) converge, então\(\displaystyle \sum^∞_{n=1}a_n\) converge.
Se\(\displaystyle \sum^∞_{n=1}|a_n|\) converge, então\(\displaystyle \sum^∞_{n=1}a_n\) converge.
Suponha que isso\(\displaystyle \sum_{n=1}^∞|a_n|\) converja. Mostramos isso usando o fato de que\( a_n=|a_n\) ou\( a_n=−|a_n|\) e, portanto,\( |a_n|+a_n=2|a_n|\) ou\( |a_n|+a_n=0\). Portanto,\( 0≤|a_n|+a_n≤2|a_n|\). Consequentemente, pelo teste de comparação, uma vez que\( 2\sum^∞_{n=1}|a_n|\) converge, a série
\[\sum_{n=1}^∞(|a_n|+a_n) \nonumber \]
converge. Usando as propriedades algébricas para séries convergentes, concluímos que
\[\sum_{n=1}^∞a_n=\sum_{n=1}^∞(|a_n|+a_n)−\sum_{n=1}^∞|a_n| \nonumber \]
converge.
□
Para cada uma das séries a seguir, determine se a série converge absolutamente, converge condicionalmente ou diverge.
- \(\displaystyle \sum^∞_{n=1}\frac{(−1)^{n+1}}{3n+1}\)
- \(\displaystyle \sum^∞_{n=1}\frac{\cos(n)}{n^2}\)
Solução
a. Podemos ver que
\(\displaystyle \sum_{n=1}^∞\left|\dfrac{(−1)^{n+1}}{3n+1}\right|=\sum_{n=1}^∞\dfrac{1}{3n+1}\)
diverge usando o teste de comparação de limites com a série harmônica. Na verdade,
\(\displaystyle \lim_{n→∞}\dfrac{1/(3n+1)}{1/n}=\dfrac{1}{3}\).
Portanto, a série não converge absolutamente. No entanto, uma vez que
\( \dfrac{1}{3(n+1)+1}<\dfrac{1}{3n+1}\)e\( \dfrac{1}{3n+1}→0\),
a série converge. Podemos concluir que\(\displaystyle \sum^∞_{n=1}\frac{(−1)^{n+1}}{3n+1}\) converge condicionalmente.
b. Observando que,\( |\cos n|≤1,\) para determinar se a série converge absolutamente, compare
\(\displaystyle \sum_{n=1}^∞\left|\dfrac{\cos n}{n^2}\right|\)
com a série\(\displaystyle \sum^∞_{n=1}\frac{1}{n^2}\). Uma vez que\(\displaystyle \sum^∞_{n=1}\frac{1}{n^2}\) converge, pelo teste de comparação,\(\displaystyle \sum^∞_{n=1}\left|\frac{\cos n}{n^2}\right|\) converge e, portanto,\(\displaystyle \sum^∞_{n=1}\frac{\cos n}{n^2}\) converge absolutamente.
Determine se a série\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{n}{2n^3+1}\) converge absolutamente, converge condicionalmente ou diverge.
- Dica
-
Verifique primeiro a convergência absoluta.
- Resposta
-
A série converge absolutamente.
Para ver a diferença entre convergência absoluta e condicional, veja o que acontece quando reorganizamos os termos da série harmônica alternada\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{1}{n}\). Mostramos que podemos reorganizar os termos para que a nova série diverja. Certamente, se reorganizarmos os termos de uma soma finita, a soma não muda. No entanto, quando trabalhamos com uma soma infinita, coisas interessantes podem acontecer.
Comece adicionando o suficiente dos termos positivos para produzir uma soma maior do que algum número real.\( M=10\) Por exemplo, deixe\( M=10,\) e encontre um número inteiro\( k\) tal que
\[1+\dfrac{1}{3}+\dfrac{1}{5}+⋯+\dfrac{1}{2k−1}>10 \nonumber \]
(Podemos fazer isso porque a série\(\displaystyle \sum^∞_{n=1}\frac{1}{2n−1}\) diverge até o infinito.) Em seguida, subtraia\( 1/2\). Em seguida, adicione mais termos positivos até que a soma chegue a 100. Ou seja, encontre outro número inteiro\( j>k\) tal que
\[(1+\dfrac{1}{3}+⋯+\dfrac{1}{2k−1}−\dfrac{1}{2}+\dfrac{1}{2k+1}+ \ldots +\dfrac{1}{2j+1}>100. \nonumber \]
Em seguida, subtraia\( 1/4.\) Continuando dessa maneira, encontramos uma maneira de reorganizar os termos na série harmônica alternada para que a sequência de somas parciais da série reorganizada seja ilimitada e, portanto, diverja.
Os termos da série harmônica alternada também podem ser reorganizados para que a nova série converja para um valor diferente. Em Exemplo, mostramos como reorganizar os termos para criar uma nova série para a qual converja\( 3\ln(2)/2\). Ressaltamos que a série harmônica alternada pode ser rearranjada para criar uma série que converge para qualquer número real\( r\); no entanto, a prova desse fato está além do escopo deste texto.
Em geral, qualquer série\(\displaystyle \sum^∞_{n=1}a_n\) que converja condicionalmente pode ser reorganizada para que a nova série diverja ou converja para um número real diferente. Uma série que converge absolutamente não tem essa propriedade. Para qualquer série\(\displaystyle \sum^∞_{n=1}a_n\) que converja absolutamente, o valor de\(\displaystyle \sum^∞_{n=1}a_n\) é o mesmo para qualquer reorganização dos termos. Esse resultado é conhecido como Teorema do Rearranjo de Riemann, que está além do escopo deste livro.
Use o fato de que
\[ 1−\dfrac{1}{2}+\dfrac{1}{3}−\dfrac{1}{4}+\dfrac{1}{5}−⋯=\ln 2 \nonumber \]
para reorganizar os termos na série harmônica alternada para que a soma da série rearranjada seja\( 3\ln (2)/2.\)
Solução
Deixe
\[ \sum_{n=1}^∞a_n=1−\dfrac{1}{2}+\dfrac{1}{3}−\dfrac{1}{4}+\dfrac{1}{5}−\dfrac{1}{6}+\dfrac{1}{7}−\dfrac{1}{8}+⋯. \nonumber \]
Uma vez que\(\displaystyle \sum_{n=1}^∞a_n=\ln (2)\), pelas propriedades algébricas das séries convergentes,
\[ \sum_{n=1}^∞\dfrac{1}{2}a_n=\dfrac{1}{2}−\dfrac{1}{4}+\dfrac{1}{6}−\dfrac{1}{8}+⋯=\dfrac{1}{2}\sum_{n=1}^∞a_n=\dfrac{\ln 2}{2}. \nonumber \]
Agora, apresente a série de\(\displaystyle \sum_{n=1}^∞b_n\) forma que, para todos\( b_{2n}=a_n/2.\),\( n≥1, b_{2n−1}=0\) e então
\[ \sum_{n=1}^∞b_n=0+\dfrac{1}{2}+0−\dfrac{1}{4}+0+\dfrac{1}{6}+0−\dfrac{1}{8}+⋯=\dfrac{\ln 2}{2}. \nonumber \]
Em seguida, usando as propriedades de limite algébrico de séries convergentes, uma vez que\(\displaystyle \sum_{n=1}^∞a_n\) e\(\displaystyle \sum_{n=1}^∞b_n\) convergem, a série\(\displaystyle \sum_{n=1}^∞(a_n+b_n)\) converge e
\[ \sum_{n=1}^∞(a_n+b_n)=\sum_{n=1}^∞a_n+\sum_{n=1}^∞b_n=\ln 2+\dfrac{\ln 2}{2}=\dfrac{3\ln 2}{2}. \nonumber \]
Agora, adicionando os termos correspondentes\( b_n\),\( a_n\) e vemos que
\[ \sum_{n=1}^∞(a_n+b_n)=(1+0)+\left(−\dfrac{1}{2}+\dfrac{1}{2}\right)+\left(\dfrac{1}{3}+0\right)+\left(−\dfrac{1}{4}−14\right)+\left(\dfrac{1}{5}+0\right)+\left(−\dfrac{1}{6}+\dfrac{1}{6}\right)+\left(\dfrac{1}{7}+0\right)+\left(\dfrac{1}{8}−\dfrac{1}{8}\right)+⋯=1+\dfrac{1}{3}−\dfrac{1}{2}+\dfrac{1}{5}+\dfrac{1}{7}−\dfrac{1}{4}+⋯. \nonumber \]
Percebemos que a série no lado direito do sinal de igual é um rearranjo da série harmônica alternada. Uma vez\(\displaystyle \sum_{n=1}^∞(a_n+b_n)=3\ln (2)/2,\) que concluímos que
\[ 1+\dfrac{1}{3}−\dfrac{1}{2}+\dfrac{1}{5}+\dfrac{1}{7}−\dfrac{1}{4}+⋯=\dfrac{3\ln (2)}{2}. \nonumber \]
Portanto, encontramos um rearranjo da série harmônica alternada com a propriedade desejada.
Conceitos-chave
- Para uma série alternada,\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}b_n,\) se for\( b_{k+1}≤b_k\) para todos\( k\) e\( b_k→0\) à medida\( k→∞,\) que a série alternada converge.
- Se\(\displaystyle \sum^∞_{n=1}|a_n|\) converge, então\(\displaystyle \sum^∞_{n=1}a_n\) converge.
Equações-chave
- Séries alternadas
\(\displaystyle \sum_{n=1}^∞(−1)^{n+1}b_n=b_1−b_2+b_3−b_4+⋯\)ou
\(\displaystyle \sum_{n=1}^∞(−1)^nb_n=−b_1+b_2−b_3+b_4−⋯\)
Glossário
- convergência absoluta
- se a série\(\displaystyle \sum^∞_{n=1}|a_n|\) convergir,\(\displaystyle \sum^∞_{n=1}a_n\) diz-se que a série converge absolutamente
- séries alternadas
- uma série da forma\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}b_n\) ou\(\displaystyle \sum^∞_{n=1}(−1)^nb_n\), onde\( b_n≥0\), é chamada de série alternada
- teste de série alternada
- para uma série alternada de qualquer forma, se\( b_{n+1}≤b_n\) para todos os inteiros\( n≥1\) e\( b_n→0\), então uma série alternada converge
- convergência condicional
- se a série\(\displaystyle \sum^∞_{n=1}a_n\) converge, mas a série\(\displaystyle \sum^∞_{n=1}|a_n|\) diverge,\(\displaystyle \sum^∞_{n=1}a_n\) diz-se que a série converge condicionalmente


