9.5E: Exercícios para a Seção 9.5

Nos exercícios 1 a 30, indique se cada uma das séries a seguir converge de forma absoluta, condicional ou não.

1)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{n}{n+3}\)

2)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{\sqrt{n}+1}{\sqrt{n}+3}\)

Responda

Esta série diverge pelo teste de divergência. Os termos não tendem a zero.

3)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{1}{\sqrt{n+3}}\)

4)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{\sqrt{n+3}}{n}\)

Responda

Converge condicionalmente pelo teste de série alternada, pois\(\sqrt{n+3}/n\) está diminuindo e seu limite é 0. Não converge absolutamente em comparação com a\(p\) série -,\(p=1/2\).

5)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{1}{n!}\)

6)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{3^n}{n!}\)

Responda

Converge absolutamente por limite, em comparação com,\(3^n/4^n,\) por exemplo.

7)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\left(\frac{n−1}{n}\right)^n\)

8)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\left(\frac{n+1}{n}\right)^n\)

Responda

Diverge por teste de divergência desde então\(\displaystyle \lim_{n→∞}|a_n|=e\) e não\(0\).

9)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\sin^2n\)

10)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\cos^2n\)

Responda

Diverge pelo teste de divergência, pois seus termos não tendem a zero. O limite da sequência de seus termos não existe.

11)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\sin^2(1/n)\)

12)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\cos^2(1/n)\)

Responda

\(\displaystyle \lim_{n→∞}\cos^2(1/n)=1.\)Diverge por teste de divergência.

13)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\ln(1/n)\)

14)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\ln(1+\frac{1}{n})\)

Responda

Converge por teste de série alternada.

15)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{n^2}{1+n^4}\)

16)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{n^e}{1+n^π}\)

Responda

Converge condicionalmente por meio de teste de série alternada. Não converge absolutamente por limite em comparação com a\(p\) série -,\(p=π−e\)

Solução:

17)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}2^{1/n}\)

18)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}n^{1/n}\)

Responda

Diverge; os termos não tendem a zero.

19)\(\displaystyle \sum^∞_{n=1}(−1)^n(1−n^{1/n})\) (Dica:\(n^{1/n}≈1+\ln(n)/n\) para grandes\(n\).)

20)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}n\left(1−\cos\left(\frac{1}{n}\right)\right)\) (Dica:\(\cos(1/n)≈1−1/n^2\) para grandes\(n\).)

Responda

Converge por teste de série alternada. Não converge absolutamente por limite em comparação com séries harmônicas.

21)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}(\sqrt{n+1}−\sqrt{n})\) (Dica: racionalize o numerador.)

22)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\left(\frac{1}{\sqrt{n}}−\frac{1}{\sqrt{n+1}}\right)\) (Dica: multiplique e depois racionalize o numerador.)

Responda

Converge absolutamente por comparação de limites com\(p\) -series,\(p=3/2\), depois de aplicar a dica.

23)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}(\ln(n+1)−\ln n)\)

24)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}n(\tan^{−1}(n+1)−\tan^{−1}n)\) (Dica: use o teorema do valor médio.)

Responda

Converge por teste de série alternada, pois\( n(\tan^{−1}(n+1)−\tan^{−1}n)\) está diminuindo para zero para grandes\(n\). Não converge absolutamente por comparação de limites com séries harmônicas após a aplicação da dica.

25)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}((n+1)^2−n^2)\)

26)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\left(\frac{1}{n}−\frac{1}{n+1}\right)\)

Responda

Converge absolutamente, pois\( a_n=\dfrac{1}{n}−\dfrac{1}{n+1}\) são termos de uma série telescópica.

27)\(\displaystyle \sum^∞_{n=1}\frac{\cos(nπ)}{n}\)

28)\(\displaystyle \sum^∞_{n=1}\frac{\cos(nπ)}{n^{1/n}}\)

Responda

Os termos não tendem a zero. A série diverge por teste de divergência.

29)\(\displaystyle \sum^∞_{n=1}\frac{1}{n}\sin(\frac{nπ}{2})\)

30)\(\displaystyle \sum^∞_{n=1}\sin(nπ/2)\sin(1/n)\)

Responda

Converge por teste de série alternada. Não converge absolutamente por limite em comparação com séries harmônicas.

Nos exercícios 31 a 36, use a estimativa\(|R_N|≤b_{N+1}\) para encontrar um valor\(N\) que garanta que a soma dos primeiros\(N\) termos da série alternada seja\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}b_n\) diferente da soma infinita no máximo pelo erro dado. Calcule a soma parcial\(S_N\) para isso\(N\).

31)\(b_n=1/n,\) erro [T]\( <10^{−5}\)

32)\(b_n=1/\ln(n), n≥2,\) erro [T]\(<10^{−1}\)

Responda

\( \ln(N+1)>10, N+1>e^{10}, N≥22026; S_{22026}=0.0257…\)

33)\(b_n=1/\sqrt{n},\) erro [T]\(<10^{−3}\)

34) [T]\(b_n=1/2^n\), erro\(<10^{−6}\)

Responda

\(2^{N+1}>10^6\)ou\(N+1>6\ln(10)/\ln(2)=19.93.\) ou\(N≥19; S_{19}=0.333333969…\)

35)\(b_n=ln(1+\dfrac{1}{n}),\) erro [T]\( <10^{−3}\)

36)\(b_n=1/n^2,\) Erro [T]\(<10^{−6}\)

Responda

\((N+1)^2>10^6\)ou\(N>999; S_{1000}≈0.822466.\)

Para os exercícios 37 a 45, indique se cada uma das afirmações a seguir é verdadeira ou falsa. Se a afirmação for falsa, forneça um exemplo em que ela seja falsa.

37)\( b_n≥0\) Está diminuindo e\(\displaystyle \lim_{n→∞}b_n=0\), em seguida,\(\displaystyle \sum_{n=1}^∞(b_{2n−1}−b_{2n})\) converge absolutamente.

38) Se\( b_n≥0\) está diminuindo, então\(\displaystyle \sum_{n=1}^∞(b_{2n−1}−b_{2n})\) converge absolutamente.

Responda

Verdadeiro \(b_n\)não precisa tender a zero, pois se\(\displaystyle c_n=b_n−\lim b_n\), então\(c_{2n−1}−c_{2n}=b_{2n−1}−b_{2n}.\)

39) Se\( b_n≥0\) e\(\displaystyle \lim_{n→∞}b_n=0\) depois\(\displaystyle \sum_{n=1}^∞(\frac{1}{2}(b_{3n−2}+b_{3n−1})−b_{3n})\) convergir.

40) Se\(b_n≥0\) está diminuindo e\(\displaystyle \sum_{n=1}^∞(b_{3n−2}+b_{3n−1}−b_{3n})\) converge, então\(\displaystyle \sum_{n=1}^∞b_{3n−2}\) converge.

Responda

Verdadeiro \(b_{3n−1}−b_{3n}≥0,\)portanto, a convergência de\(\displaystyle \sum b_{3n−2}\) segue do teste de comparação.

41) Se\(b_n≥0\) está diminuindo e\(\displaystyle \sum_{n=1}^∞(−1)^{n−1}b_n\) converge condicionalmente, mas não absolutamente, então\(b_n\) não tende a zero.

42) Deixe\(a^+_n=a_n\) se\(a_n≥0\) e\( a^−_n=−a_n\) se\(a_n<0\). (Além disso,\( a^+_n=0\) se\(a_n<0\) e\(a^−_n=0\) se\(a_n≥0\).) Se\(\displaystyle \sum_{n=1}^∞a_n\) converge condicionalmente, mas não absolutamente, então\(\displaystyle \sum_{n=1}^∞a^+_n\) nem\(\displaystyle \sum_{n=1}^∞a^−_n\) converge.

Responda

Verdadeiro Se um converge, o mesmo acontece com o outro, o que implica convergência absoluta.

43) Suponha que\(a_n\) seja uma sequência de números reais positivos e que\(\displaystyle \sum_{n=1}^∞a_n\) converja.

44) Suponha que\(b_n\) seja uma sequência arbitrária de uns e menos uns. \(\displaystyle \sum_{n=1}^∞a_nb_n\)Necessariamente converge?

45) Suponha que\(a_n\) seja uma sequência que\(\displaystyle \sum_{n=1}^∞a_nb_n\) converja para cada sequência possível\(b_n\) de zeros e uns. \(\displaystyle \sum_{n=1}^∞a_n\)Converge absolutamente?

Responda

Sim. Pegue\(b_n=1\) se\(a_n≥0\) e\( b_n=0\) se\(a_n<0\). Em seguida,\(\displaystyle \sum_{n=1}^∞a_nb_n=\sum_{n:a_n≥0}a_n\) converge. Da mesma forma, pode-se mostrar\(\displaystyle \sum_{n:a_n<0}a_n\) convergências. Como as duas séries convergem, a série deve convergir absolutamente.

Nos exercícios 46 a 49, as séries não satisfazem as hipóteses do teste de séries alternadas, conforme declarado. Em cada caso, indique qual hipótese não foi satisfeita. Indique se a série converge absolutamente.

(46)\(\displaystyle \sum_{n=1}^∞(−1)^{n+1}\frac{\sin^2n}{n}\)

47)\(\displaystyle \sum_{n=1}^∞(−1)^{n+1}\frac{\cos^2n}{n}\)

Responda

Não está diminuindo. Não converge absolutamente.

48)\(\displaystyle 1+\frac{1}{2}−\frac{1}{3}−\frac{1}{4}+\frac{1}{5}+\frac{1}{6}−\frac{1}{7}−\frac{1}{8}+⋯\)

49)\(\displaystyle 1+\frac{1}{2}−\frac{1}{3}+\frac{1}{4}+\frac{1}{5}−\frac{1}{6}+\frac{1}{7}+\frac{1}{8}−\frac{1}{9}+⋯\)

Responda

Não alternando. Pode ser expresso como\(\displaystyle \sum_{n=1}^∞\left(\frac{1}{3n−2}+\frac{1}{3n−1}−\frac{1}{3n}\right),\) o que diverge em comparação com\(\displaystyle \sum_{n=1}^∞\frac{1}{3n−2}.\)

50) Mostre que a série alternada\(\displaystyle 1−\frac{1}{2}+\frac{1}{2}−\frac{1}{4}+\frac{1}{3}−\frac{1}{6}+\frac{1}{4}−\frac{1}{8}+⋯\) não converge. Qual hipótese do teste de séries alternadas não foi atendida?

51) Suponha que isso\(\displaystyle \sum a_n\) converja absolutamente. Mostre que a série que consiste em termos positivos\(a_n\) também converge.

Responda

Deixe\(a^+_n=a_n\) se\(a_n≥0\) e\(a^+_n=0\) se\( a_n<0\). Então,\(a^+_n≤|a_n|\) para todos\(n\), a sequência de somas parciais de\( a^+_n\) está aumentando e limitada acima pela sequência de somas parciais de\( |a_n|\), que converge; portanto,\(\displaystyle \sum_{n=1}^∞a^+_n\) converge.

52) Mostre que a série alternada\(\displaystyle \frac{2}{3}−\frac{3}{5}+\frac{4}{7}−\frac{5}{9}+⋯\) não converge. Qual hipótese do teste de séries alternadas não foi atendida?

53) A fórmula\(\displaystyle \cos θ=1−\frac{θ^2}{2!}+\frac{θ^4}{4!}−\frac{θ^6}{6!}+⋯\) será derivada no próximo capítulo. Use o restante\(|R_N|≤b_{N+1}\) para encontrar um limite para o erro na estimativa\(\cos θ\) pela quinta soma parcial\(1−θ^2/2!+θ^4/4!−θ^6/6!+θ^8/8!\) para\(θ=1, θ=π/6,\) e\(θ=π.\)

Responda

\(N=5\)Pois um tem\(∣R_N∣b_6=θ^{10}/10!\). Quando\(θ=1, R_5≤1/10!≈2.75×10^{−7}\). Quando\(θ=π/6,\)\(R_5≤(π/6)^{10}/10!≈4.26×10^{−10}\). Quando\(θ=π, R_5≤π^{10}/10!=0.0258.\)

54) A fórmula\(\sin θ=θ−\dfrac{θ^3}{3!}+\dfrac{θ^5}{5!}−\dfrac{θ^7}{7!}+⋯\) será derivada no próximo capítulo. Use o restante\(|R_N|≤b_{N+1}\) para encontrar um limite para o erro na estimativa\(\sin θ\) pela quinta soma parcial\(θ−θ^3/3!+θ^5/5!−θ^7/7!+θ^9/9!\) para\(θ=1, θ=π/6,\) e\(θ=π.\)

55) Quantos termos em\(\cos θ=1−\dfrac{θ^2}{2!}+\dfrac{θ^4}{4!}−\dfrac{θ^6}{6!}+⋯\) são necessários para aproximar a\(\cos 1\) precisão de um erro de no máximo\( 0.00001\)?

Responda

Deixe\( b_n=1/(2n−2)!.\) então\(R_N≤1/(2N)!<0.00001\) quando\((2N)!>10^5\) ou\(N=5\) e\(\displaystyle 1−\frac{1}{2!}+\frac{1}{4!}−\frac{1}{6!}+\frac{1}{8!}=0.540325…\), enquanto\(\cos 1=0.5403023…\)

56) Quantos termos em\(\sin θ=θ−\dfrac{θ^3}{3!}+\dfrac{θ^5}{5!}−\dfrac{θ^7}{7!}+⋯\) são necessários para aproximar a\(\sin 1\) precisão de um erro de no máximo\(0.00001?\)

57) Às vezes, a série alternada\(\displaystyle \sum_{n=1}^∞(−1)^{n−1}b_n\) converge para uma certa fração de uma série absolutamente convergente\(\displaystyle \sum_{n=1}^∞b_n\) em uma taxa mais rápida. Diante disso\(\displaystyle \sum_{n=1}^∞\frac{1}{n^2}=\frac{π^2}{6}\), encontre\(\displaystyle S=1−\frac{1}{2^2}+\frac{1}{3^2}−\frac{1}{4^2}+⋯\). Qual das séries\(\displaystyle 6\sum_{n=1}^∞\frac{1}{n^2}\) e\(\displaystyle S\sum_{n=1}^∞\frac{(−1)^{n−1}}{n^2}\) fornece uma melhor estimativa do\(π^2\) uso de\(1000\) termos?

Responda

Deixe\(\displaystyle T=\sum\frac{1}{n^2}.\) então\(T−S=\dfrac{1}{2}T\), então\(S=T/2\). \(\displaystyle \sqrt{6×\sum_{n=1}^{1000}1/n^2}=3.140638…; \sqrt{\frac{1}{2}×\sum_{n=1}^{1000}(−1)^{n−1}/n^2}=3.141591…; π=3.141592….\)A série alternada é mais precisa para\(1000\) os termos.

As séries alternadas nos exercícios 58 e 59 convergem para determinados múltiplos de\(π\). Encontre o valor\(N\) previsto pela estimativa restante, de forma que a soma\(N^{\text{th}}\) parcial da série se aproxime com precisão do lado esquerdo de dentro do erro dado. Encontre o mínimo\(N\) para o qual o limite de erro é válido e forneça o valor aproximado desejado em cada caso. Até\(15\) casas decimais,\( π=3.141592653589793….\)

58)\(\displaystyle \frac{π}{4}=\sum_{n=0}^∞\frac{(−1)^n}{2n+1},\) erro [T]\(<0.0001\)

59)\(\displaystyle \frac{π}{\sqrt{12}}=\sum_{k=0}^∞\frac{(−3)^{−k}}{2k+1},\) Erro [T]\(<0.0001\)

Responda

\(N=6, S_N=0.9068\)

60) [T] A série\(\displaystyle \sum_{n=0}^∞\frac{\sin(x+πn)}{x+πn}\) desempenha um papel importante no processamento do sinal. Mostre que\(\displaystyle \sum_{n=0}^∞\frac{\sin(x+πn)}{x+πn}\) converge sempre\(0<x<π\). (Dica: use a fórmula para o seno de uma soma de ângulos.)

61) [T] Se\(\displaystyle \sum_{n=1}^N(−1)^{n−1}\frac{1}{n}→ln2,\) o que é\(\displaystyle 1+\frac{1}{3}+\frac{1}{5}−\frac{1}{2}−\frac{1}{4}−\frac{1}{6}+\frac{1}{7}+\frac{1}{9}+\frac{1}{11}−\frac{1}{8}−\frac{1}{10}−\frac{1}{12}+⋯?\)

Responda

\(\ln(2).\)A soma\(n^{\text{th}}\) parcial é a mesma da série harmônica alternada.

62) [T] Faça um gráfico da série\(\displaystyle \sum_{n=1}^{100}\frac{\cos(2πnx)}{n}\) para\(0≤x<1\). Explique por que\(\displaystyle \sum_{n=1}^{100}\frac{\cos(2πnx)}{n}\) diverge quando\(x=0,1\). Como a série se comporta para os outros\(x\)?

63) [T] Faça um gráfico da série\(\displaystyle \sum_{n=1}^{100}\frac{\sin(2πnx)}{n}\)\(0≤x<1\) e comente sobre seu comportamento

Responda

A série salta rapidamente perto dos pontos finais. Pois,\(x\) longe dos pontos finais, o gráfico tem a aparência de\( π(1/2−x)\).

64) [T] Faça um gráfico da série\(\displaystyle \sum_{n=1}^{100}\frac{\cos(2πnx)}{n^2}\)\( 0≤x<1\) e descreva seu gráfico.

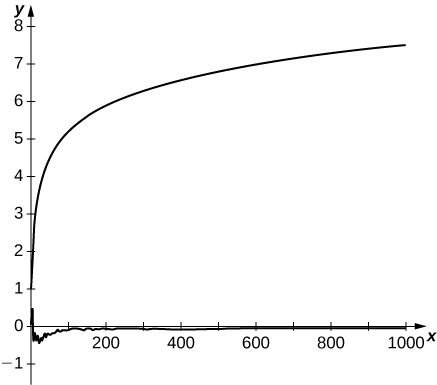
65) [T] A série harmônica alternada converge devido ao cancelamento entre seus termos. Sua soma é conhecida porque o cancelamento pode ser descrito explicitamente. Uma série harmônica aleatória é uma das formas\(\displaystyle \sum_{n=1}^∞\frac{S_n}{n}\), onde\(s_n\) é uma sequência gerada aleatoriamente\(±1's\) na qual os valores\(±1\) têm a mesma probabilidade de ocorrer. Use um gerador de números aleatórios para produzir\(1000\) aleatoriamente\(±1's\) e traçar as somas parciais\(\displaystyle S_N=\sum_{n=1}^N\frac{s_n}{n}\) de sua sequência harmônica aleatória\(N=1\) para\(1000\). Compare com um gráfico das primeiras somas\(1000\) parciais da série harmônica.

Responda

Aqui está um resultado típico. A curva superior consiste em somas parciais da série harmônica. A curva inferior traça somas parciais de uma série harmônica aleatória.

66) [T] As estimativas de\(\displaystyle \sum_{n=1}^∞\frac{1}{n^2}\) podem ser aceleradas escrevendo suas somas parciais como\(\displaystyle \sum_{n=1}^N\frac{1}{n^2}=\sum_{n=1}^N\frac{1}{n(n+1)}+\sum_{n=1}^N\frac{1}{n^2(n+1)}\) e lembrando que\(\displaystyle \sum_{n=1}^N\frac{1}{n(n+1)}=1−\frac{1}{N+1}\) converge para uma como\( N→∞.\) Compare a estimativa de\(π^2/6\) usar as somas\(\displaystyle \sum_{n=1}^{1000}\frac{1}{n^2}\) com a estimativa usando\(\displaystyle 1+\sum_{n=1}^{1000}\frac{1}{n^2(n+1)}\).

67) [T] A transformação de Euler reescreve\(\displaystyle S=\sum_{n=0}^∞(−1)^nb_n\) como\(\displaystyle S=\sum_{n=0}^∞(−1)^n2^{−n−1}\sum_{m=0}^n(^n_m)b_{n−m}\). Para a série harmônica alternada, ela assume a forma\(\displaystyle \ln(2)=\sum_{n=1}^∞\frac{(−1)^{n−1}}{n}=\sum_{n=1}^∞\frac{1}{n2^n}\). Calcule somas parciais de\(\displaystyle \sum_{n=1}^∞\frac{1}{n2^n}\) até que tenham\(\ln(2)\) precisão aproximada de dentro\(0.0001\). Quantos termos são necessários? Compare essa resposta com o número de termos da série harmônica alternada que são necessários para estimar\(\ln(2)\).

Responda

Pelo teste de séries alternadas,\(|S_n−S|≤b_{n+1},\) então\(10^4\) são necessários termos da série harmônica alternada para estimar\(\ln(2)\) para dentro\(0.0001\). As primeiras somas\(10\) parciais da série\(\displaystyle \sum_{n=1}^∞\frac{1}{n2^n}\) são (até quatro decimais)\( 0.5000,0.6250,0.6667,0.6823,0.6885,0.6911,0.6923,0.6928,0.6930,0.6931\) e a décima soma parcial está dentro\(0.0001\) de\(\ln(2)=0.6931….\)

68) [T] No texto, foi afirmado que uma série condicionalmente convergente pode ser reorganizada para convergir para qualquer número. Aqui está um fato um pouco mais simples, mas semelhante. Se\(a_n≥0\) é\(a_n→0\) tal que,\(n→∞\) mas\(\displaystyle \sum_{n=1}^∞a_n\) diverge, então, dado qualquer número,\(A\) há uma sequência\(s_n\) de\( ±1's\) tal que\(\displaystyle \sum_{n=1}^∞a_ns_n→A.\) Mostre isso da\(A>0\) seguinte forma.

a. Defina recursivamente\(s_n\) por “\( s_n=1\)se”\(\displaystyle S_{n−1}=\sum_{k=1}^{n−1}a_ks_k<A\) e “de\( s_n=−1\) outra forma”.

b. Explique por que, eventualmente\(S_n≥A,\) e por qualquer coisa\(m\) maior do que isso\(n\),\(A−a_m≤S_m≤A+a_m\).

c. Explique por que isso implica que\( S_n→A\), como\( n→∞.\)